Computers, Materials & Continua DOI:10.32604/cmc.2022.017916
Article

Optical Flow with Learning Feature for Deformable Medical Image Registration

Jinrong Hu1, Lujin Li1, Ying Fu1, Maoyang Zou1, Jiliu Zhou1 and Shanhui Sun2,*

1Department of Computer Science, Chengdu University of Information Technology, Chengdu, 610225, China
2Curacloud Corporation, 999 Third Ave, Suite 700 Seattle, WA, 98104, USA
*Corresponding Author: Shanhui Sun. Email: shanhuis@curacloudcorp.com
Received: 17 February 2021; Accepted: 13 April 2021

Abstract: Deformable medical image registration plays a vital role in medical image applications, such as placing different temporal images at the same time point or different modality images into the same coordinate system. Various strategies have been developed to satisfy the increasing needs of deformable medical image registration. One popular registration method is estimating the displacement field by computing the optical flow between two images. The motion field (flow field) is computed based on either gray-value or handcrafted descriptors such as the scale-invariant feature transform (SIFT). These methods assume that illumination is constant between images. However, medical images may not always satisfy this assumption. In this study, we propose a metric learning-based motion estimation method called Siamese Flow for deformable medical image registration. We train metric learners using a Siamese network, which produces an image patch descriptor that guarantees a smaller feature distance in two similar anatomical structures and a larger feature distance in two dissimilar anatomical structures. In the proposed registration framework, the flow field is computed based on such features and is close to the real deformation field due to the excellent feature representation ability of the Siamese network. Experimental results demonstrate that the proposed method outperforms the Demons, SIFT Flow, Elastix, and VoxelMorph networks regarding registration accuracy and robustness, particularly with large deformations.

Keywords: Deformation registration; feature extraction; optical flow; convolutional neural network

1  Introduction

Medical image registration refers to seeking one or a series of spatial transformations for a medical image (moving image) to achieve spatial and anatomical position correspondence to another fixed image [1–3]. In many clinical applications, medical image registration can provide complementary information for accurate diagnosis and tumor treatment planning. For instance, aligning a map of important anatomical structures to patient images provides useful guidance for preoperative and intraoperative planning in neurosurgery. In addition, image registration technology is used to put studied patient images into a common coordinate system to study anatomical and functional variations in the population. Image registration is also used to compensate for motion, such as breathing and cardiac motions, in dynamic images. In computer-aided diagnosis and radiation therapy, image registration also plays an important role in aligning and tracking tumor growth in longitudinal images.

Deformable image registration is an active field of medical image analysis [4–6], and many studies have investigated this topic [7–9]. The optical flow-based method [10–12] was proposed to estimate object motion in two successive images in [13]. Thirion et al. [14] proposed the Demons image registration algorithm based on the similarity between the deformation field and the optical flow field. The Demons approach solves the image registration problem by considering the optical flow and calculates the optical flow field based on the difference in intensity of pixels between the fixed and moving images. Due to nonuniform illumination and abnormal lesions in medical images, the intensity difference-based optical flow method cannot correctly estimate the deformation field, and it is difficult to achieve accurate registration results.

To overcome this problem, Ce Liu et al. proposed the scale-invariant feature transform (SIFT) Flow algorithm, which computes the optical flow field based on the difference in SIFT features of a pixel between fixed and moving images [15–16]. Although this method can obtain a more accurate deformation field than traditional optical flow methods, such as Demons, it also has limitations: (1) because SIFT features are based on gradient information, the SIFT Flow method mismatches SIFT features and cannot accurately register medical images with weak contrast and complex structures; and (2) because a SIFT feature is a low-level image feature and cannot represent a higher level or abstract image feature [17], the SIFT Flow method cannot robustly estimate the deformation field or effectively register medical images with large deformations.

Recently, in the field of computer vision, machine-learning methods have been used to learn feature descriptions from large datasets. In particular, convolutional neural networks (CNNs) have strong feature representation abilities and exhibit good performance for various computer vision tasks [18–20]. In this study, we propose a deep metric learning feature-based optical flow method (Siamese Flow) for deformable medical image registration. This method is composed of three primary steps: deep metric learning feature extraction, deformation field estimation and warping. Specifically, we obtain image patches that are densely clustered around a given pixel. Then, we extract the deep metric learning feature of the pixel using the Siamese network [21]. Finally, we calculate the optical flow field based on these in-depth learning features and obtain the registered image by warping the moving image using the computed deformation field.

To construct the proposed registration framework, the learned image patch representation using deep contrastive metric learning and the deformation field estimation using such learned representations are developed. The learned image patch representation uses the Siamese network to train the metric learner, which produces an image patch descriptor that guarantees a smaller feature distance in two similar anatomical structures and a larger feature distance in two dissimilar anatomical structures. Unlike the SIFT feature and general deep learning features, such as those from the Visual Geometry Group (VGG) networks [22], the proposed deep metric learning feature is more discriminative and more stable. The proposed Siamese Flow method can thus solve the optical flow field with regard to the real deformation field. To our knowledge, this is the first study that combines contrastive metric learning into optical flow to solve the problem of deformable medical image registration. Experimental results show that the proposed method outperforms the Demons [14], SIFT Flow [16], Elastix [23], and VoxelMorph [24] networks regarding registration accuracy and robustness, particularly with large deformations.

2  Method

Fig. 1 shows an overview of the proposed Siamese Flow method, which consists of three primary components: Siamese feature extraction, deformation field estimation and warping. Among these components, Siamese feature extraction is the most critical. After obtaining the deformation field, we obtain the registered image by warping the moving image according to the determined deformation field.

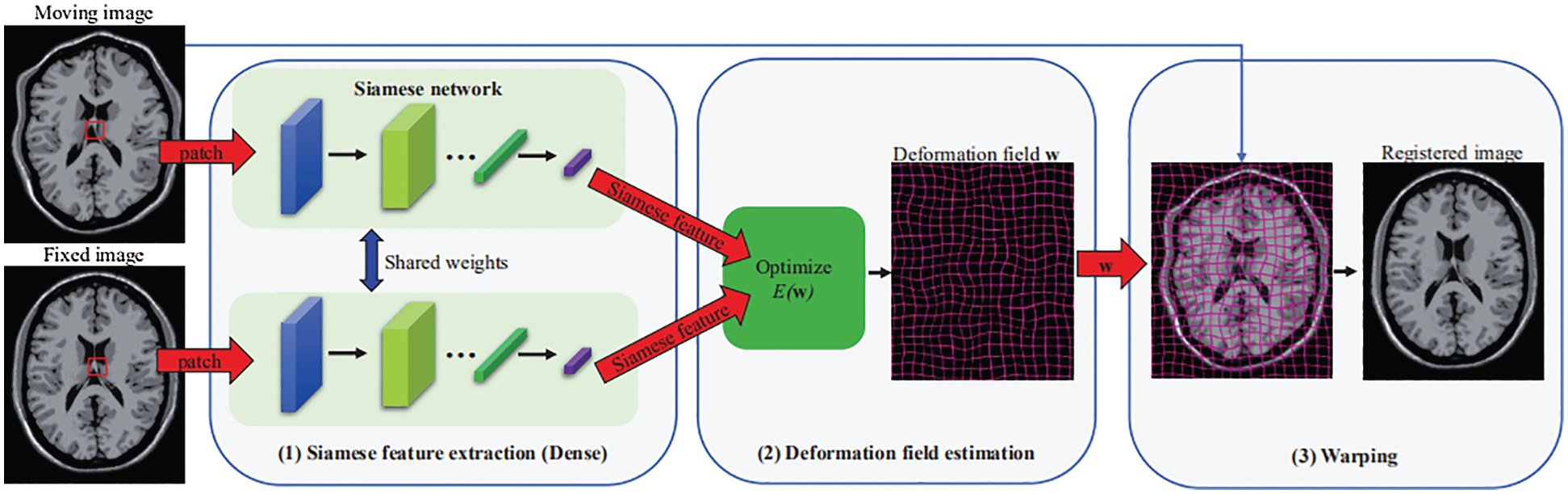
Figure 1: Overview of the proposed image registration framework using the Siamese Flow method

2.1 Siamese Feature Extraction

In the context of image registration, a good local image representation can significantly improve the corresponding point matching performance, leading to an accurate and robust deformation field. To perform this process accurately without using manually designed features, we propose to learn local image representations directly from the data using contrastive metric learning, a Siamese network.

Fig. 2 shows the structure of the proposed Siamese network, which consists of two CNN networks, in which we share computations across two networks. The input of each network is an image patch of size 15 × 15. The output of the network is a 128-dimensional feature representation. The convolution layers of each network use a 3 × 3 convolution kernel with a stride of 1 following a leaky rectified linear unit (LeakyReLU) activation function. In addition, the fully connected layers (Dense 1 and Dense 2) use an ReLU activation function, and we add a dropout layer after the flattened layer to mitigate overfitting. Network parameters are shown in Fig. 2.

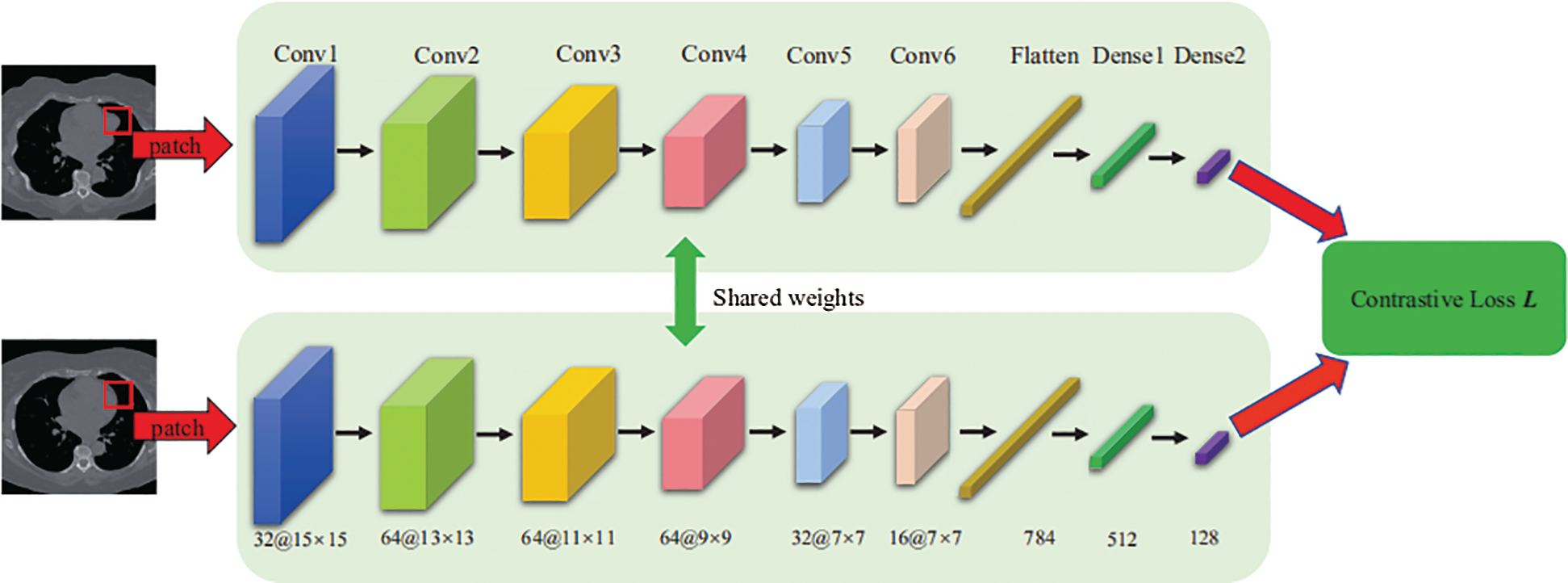
Figure 2: Architecture of the Siamese network

The proposed Siamese network makes a discriminative image feature by minimizing a contrastive loss function, which is shown as follows:

L=12N∑i=1N⁡yidi2+(1−yi)max(margin−di,0)2(1)

where N is the number of input sample pairs; di=||xi1−xi22|| is the Euclidean distance of each pair; margin is a constant value of 1; and yi is the binary label for input pairs, where 1 indicates that it is a positive sample pair without deformation, and 0 indicates that it is a negative sample pair with deformation.

The mapping learned using contrastive metric learning can make the Euclidean distance between the Siamese features small for two patches without deformation and large for two patches with deformation. Therefore, compared with the SIFT feature and general deep learning features, such as the VGG [22], the proposed Siamese feature extracted by the Siamese network is more discriminative in the context of the image registration problem.

2.2 Deformation Field Estimation

Inspired by the SIFT Flow method, we incorporate the learned feature representation into an optical flow-based image registration framework to estimate a dense deformation field. The goal of this method is to match the Siamese features densely in two images and then minimize the energy loss function to obtain the displacement vector for each pixel. We defined the energy loss function as follows:

E(w)=∑p⁡min(||S1(p)−S2(p+w(p))||1,t)(2a)

+∑p⁡η(|u(p)|+|v(p)|)(2b)

+∑p,q∈ε⁡min(α|u(p)−u(q)|,d)+min(α|v(p)−v(q)|,d)(2c)

where S1 and S2 are the Siamese feature vectors of the fixed and moving images; w(p)=(u(p),v(p)) is the flow vector at pixel location p = (x,y); ε contains all the spatial neighborhoods (an eight-neighbor system is used); and η and α are used to maintain the desired balance between the terms. The first term Eq. (2a) accounts for the dissimilarity of the Siamese feature between the fixed and moving images; the second term Eq. (2b) provides a regularization on the first-order magnitude of w; and the third term Eq. (2c) enforces a smooth flow field, which constrains the flow vectors of adjacent pixels to be similar. We use the thresholds t and d to consider matching outliers and flow discontinuities. These thresholds allow large deformations in soft tissues and discontinuous displacements between adjacent tissues. Due to large deformations, such as those caused by cardiac and respiratory motions, the weight of α in Eq. (2c) should be larger than that of η in Eq. (2b).

To optimize the objective function E(w), we use a dual-layer loopy belief propagation (BP-S) [25] method that is similar to that used in SIFT Flow. In addition, we use a coarse-to-fine matching scheme to speed up optimization [26]. Finally, we warp the moving image to obtain the registered result based on the deformation field using cubic spline interpolation [27].

3  Experiment and Results

3.1 Dataset and Ground Truth

We validated the proposed method with the BrainWeb [28–30], EXPIRE10 [31], and ACDC [32] datasets, as well as with our own nasopharyngeal carcinoma (NPC) patient data. BrainWeb is a simulated brain database (SBD) produced by an MRI simulator and contains simulated brain MRI data based on two anatomical models: normal and multiple sclerosis (MS). Full 3-dimensional data volumes were simulated using three sequences (T1-, T2- and PD-weighted) and a variety of slice thicknesses, noise levels, and levels of intensity nonuniformity. This dataset has rich image texture information and good image quality. EMPIRE10 is a lung dataset that contains 30 clinical chest CT scans and their corresponding masks obtained using the lung segmentation method that was proposed by Rikxoorta et al. [33]. ACDC is a multislice cine MRI clinical cardiac dataset that contains 150 patients. Finally, NPC is a 3D CT and MRI clinical nasopharyngeal cancer dataset that includes 100 patients (male/female: 52/48; mean age ± standard deviation: 50.3 ± 11.2 years old; age range: 21–76 years old), who underwent chemoradiotherapy or radiotherapy at West China Hospital.

We randomly selected 45 T1 and T2 images from BrainWeb and 30 MRI lung images from EXPIPE10 to create training and validation datasets. Furthermore, to obtain the corresponding moving images, we deformed those images using the method proposed by Patrice et al. [34] with the deformation level parameter λ from 50 to 200 to control the degree of deformation. Then, we densely extracted image patches with a size of 15 × 15 pixels from the fixed and moving images. We used the patch pairs as the training data and validation data. A patch pair received a positive label if the patches were generated from the same location of the same fixed image; a negative label was applied if the patches were created from the same place of the fixed and moving images. Fig. 3 shows example patches with positive and negative labels. The patches in pairs with positive labels are identical; there is a deformation between the patch pair with a negative label.

Figure 3: Some positive and negative sample pairs for Siamese network training. (a) BrainWeb T1 positive sample pair (b) BrainWeb T2 positive sample pair (c) EXPIPE10 positive sample pairs (d) BrainWeb T1 negative sample pair (e) BrainWeb T2 negative sample pair (f) EXPIPE10 negative sample pair

3.2 Experiment Setup

We compared the proposed Siamese Flow to Demons [14], SIFT Flow [16], the Elastix toolbox [23], and VoxelMorph [24]. The Elastix toolbox consists of a collection of algorithms that are commonly used to solve rigid and nonrigid medical image registration problems. VoxelMorph is a self-supervised end-to-end deep learning-based registration method and is one of the most advanced existing methods.

We generated image patch pairs following Section 3.1 and used 6,000,000 and 1,200,000 patch pairs as training and validation data for the Siamese network, respectively. We implemented the Siamese network using Keras, where the training batch size was 512, the optimizer was RMSprop [35] with momentum, and the initial learning rate was 0.001 with a momentum of 0.9. The training of each epoch took approximately 52 s on an NVIDIA Tesla K40C GPU. We trained the Siamese network with 200 epochs, and it converged before the end of training.

In the experiments, for the Demons parameters, we set the number of histogram levels and iterations to 1024 and 50, respectively. For the SIFT Flow parameters, we set η to 0.005, α to 2, and the number of iterations to 200. For the elasticity parameters, we chose advanced Mattes mutual information as the optimization criterion, adaptive stochastic gradient descent as the optimization routine, and B-splines (BSPLINE) as the transformation model. We used the four image pyramids (resolutions), each with 500 iterations. For VoxelMorph, we used the mean squared error (MSE) as the loss function and implemented EMPIRE10 and BrainWeb as training datasets to train the model using the released code from the authors [36].

3.3 Evaluation Indices

3.3.1 Root Mean Squared Difference (RMSD)

The RMSD measures the difference between the two images and has the following definition:

RMSD=1|ΩI|∑xi∈ΩI⁡(I1(χi)−I2(xi))2(3)

where I1 and I2 are images; I1(p) and I2(p) are the gray values at location p = (x,y); ΩI is the image domain of I1 and I2; and |ΩI| is the number of pixels in I1 or I2. The smaller the RMSD value between the registered and fixed images is, the more accurate the registration result is.

3.3.2 DICE Coefficient

We also compare the corresponding regions of interest (ROIs) of fixed and moving images. The method behind this comparison assumes that the ROI is given in the fixed image and that the corresponding ROI in the moving image is computed by warping the ROI in the fixed image using a computed deformation field. We use the DICE coefficient to determine this comparison evaluation index [37]. The DICE coefficient is defined as follows:

DICE=2|X∩⁡Y||X|+|Y|(4)

where X and Y are the ROIs of the two images, and X∩⁡Y is the overlapping ROI. For images from EMPIRE10, the ROI is the lung segmentation. For images from ACDC, the ROIs are the annotated left ventricular endocardium (LV), right ventricular endocardium (RV) and myocardium (MC). Fig. 4 shows examples of lung and cardiac images and their masks.

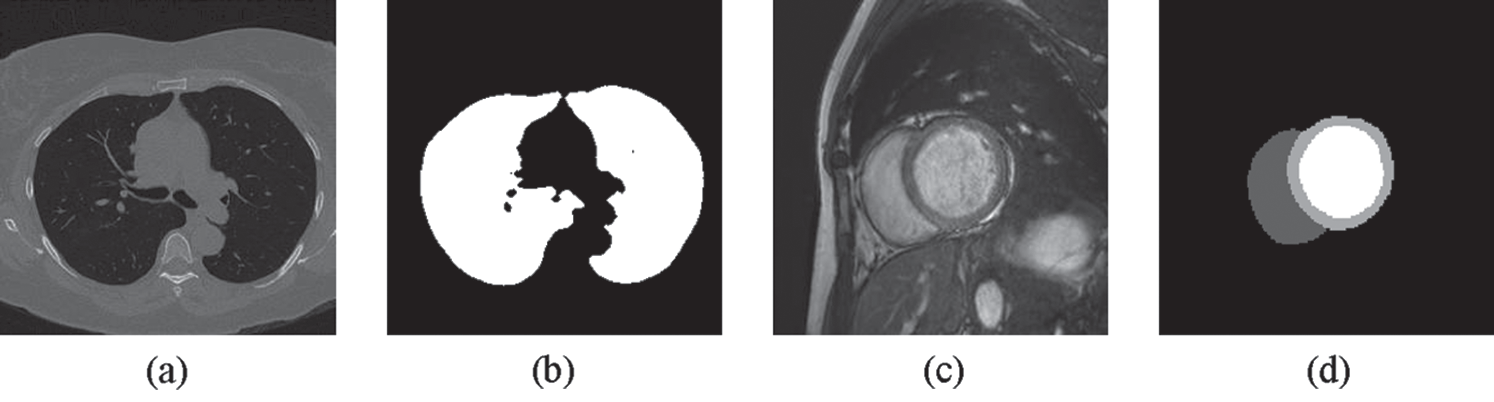
Figure 4: Examples of (a) a lung image (b) its lung mask (c) a cardiac image and (d) its LV, RV and MC masks

3.3.3 Mutual Information (MI)

MI measures the similarity between the two images, and the following is one of the standard mathematical definitions for MI:

MI(I1,I2)=E(I1)+E(I2)−E(I1,I2)(5)

where E(I1) and E(I2) are the individual entropies and E(I1,I2) is the joint entropy. When two similar images are perfectly aligned, the joint entropy E(I1,I2) is minimized, and thus, MI reaches its maximum. Thus, the greater the MI value between the registered and fixed images is, the more accurate the registration result is.

3.4 Registration Accuracy

We randomly chose twenty images from BrainWeb and EMPIRE10 as the fixed images and deformed them with a specific deformation level λ from 50 to 200 with a step of 50 to create the moving images. There are a total of 160 paired fixed and deformable moving images used to validate the registration accuracy of the five methods.

Tab. 1 summarizes the average RMSD indices of the five compared methods with the BrainWeb and EMPIRE10 datasets. Tab. 2 summarizes the average DICE indices of the five methods with the EMPIRE10 dataset. The results shown in Tabs. 1 and 2 demonstrate that the proposed approach outperforms Demons, SIFT Flow, and the most advanced methods (Elastix and VoxelMorph) in all cases in terms of RMSD and DICE.

Figs. 5 and 6 show two examples of registration results with different methods (Demons, SIFT Flow, Elastix, VoxelMorph, and the proposed Siamese Flow) from the test BrainWeb and EMPIRE10 datasets. Fig. 5a is the fixed T1 image; Fig. 5b is the moving T1 image; Fig. 5c is the heatmap between the fixed and moving images; Figs. 5d–5h are the registered images obtained by Demons, SIFT Flow, Elastix, VoxelMorph and Siamese Flow, respectively; and Figs. 5i–5m are the heatmaps between the fixed and registered images. The heatmap shows the absolute difference between the fixed and registered images. Figs. 5 and 6 show that the heatmaps of the five methods are consistent with their RMSD and DICE results, and the proposed Siamese Flow achieves the most accurate registration results.

3.5 Cross-Modality

To demonstrate the cross-modality registration capability of the proposed method, we applied the proposed method to two new tasks (multimodality applications). The first task was to register T1 and T2 images from BrainWeb, and the second task was to register CT and MRI images from NPC. For the two tasks, we trained the Siamese networks on image patch pairs taken from the T1-T2 slices of BrainWeb and the CT-MR slices of NPC. For each task, we used 150,000 and 40,000 patch pairs as training data and validation data, respectively.

We randomly chose fifteen paired T1-T2 and CT-MR images from BrainWeb and NPC separately, took T1 and CT as the fixed images, and deformed the paired T2 and MRI with a specific deformation level λ from 50 to 200 with a step of 50 to create the moving images. There are a total of 120 paired fixed and distorted moving images to validate the proposed method's ability to register the multimodality registration.

Tab. 3 summarizes the average MI of the five compared methods on the BrainWeb and NPC datasets. The results presented in Tab. 3 demonstrate that the proposed approach outperforms VoxelMorph, Demons, SIFT Flow, and the most advanced cross-modality registration method Elastix in all cases.

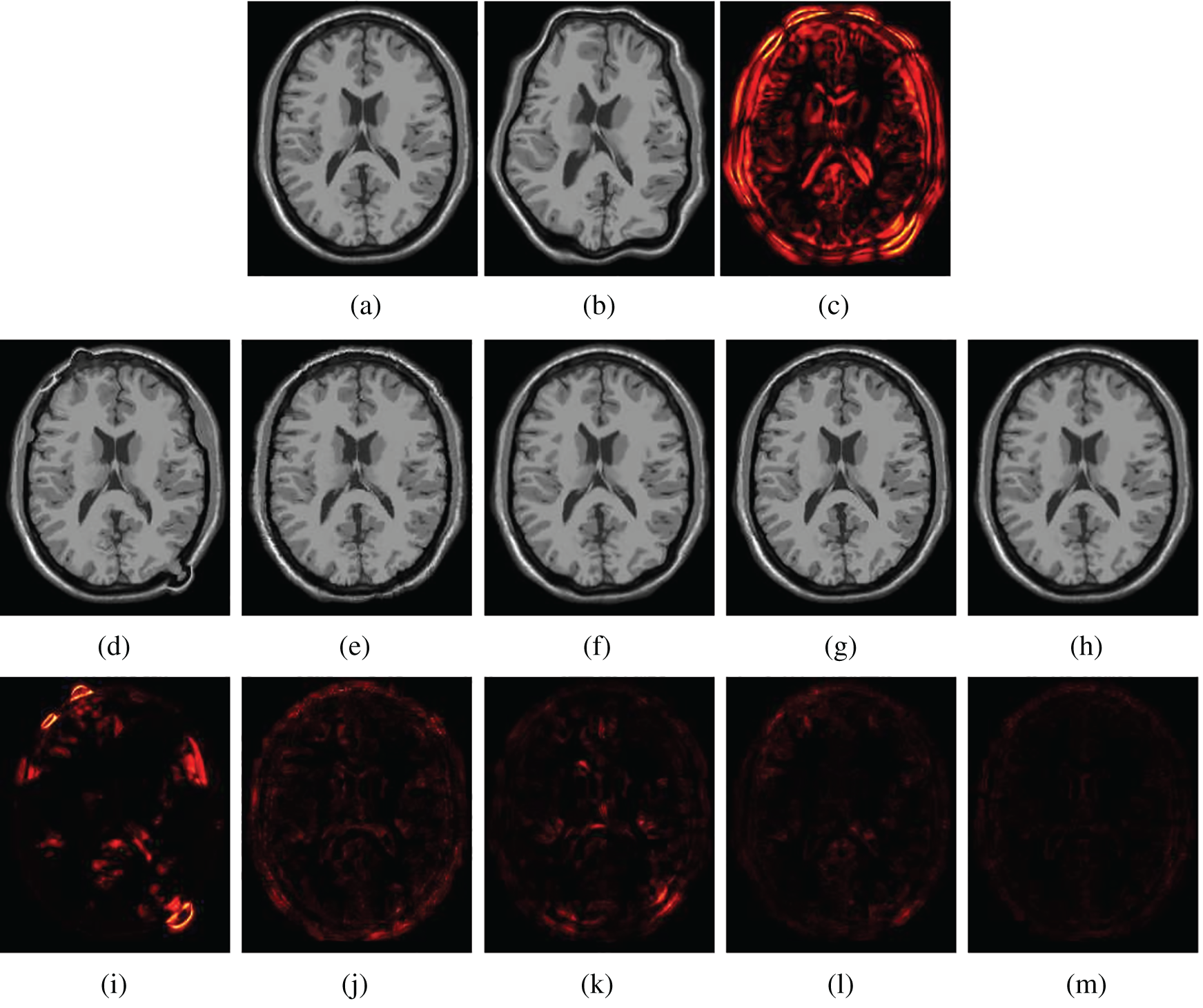
Figure 5: Visualization of registration accuracy results using a heatmap for a randomly selected BrainWeb T1 image and its deformable image (λ = 150). (a) Fixed T1 (b) Moving T1 (c) Heatmap of the fixed and moving T1 (d) Demons (e) SIFT Flow (f) Elastix (g) VoxelMorph (h) Siamese Flow (i) Heatmap of Demons (j) Heatmap of SIFT Flow (k) Heatmap of Elastix (I) Heatmap of VoxelMorph (m) Heatmap of Siamese Flow

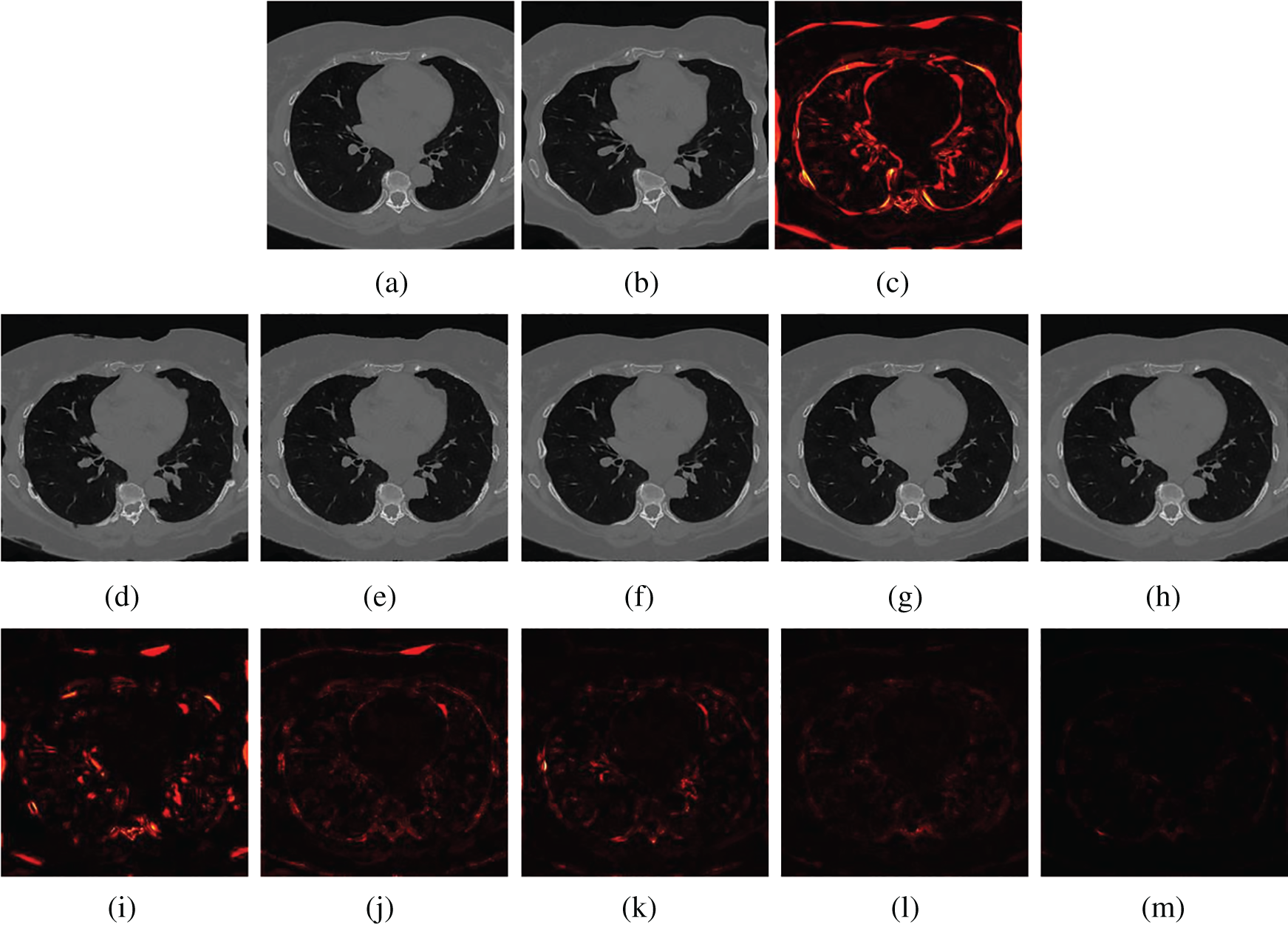
Figure 6: Visualization of registration accuracy results using a heatmap for a randomly selected EMPIRE10 image and its deformable image (λ = 150). (a) Fixed image (b) Moving image (c) Heatmap between the fixed and moving image (d) Demons (e) SIFT Flow (f) Elastix (g) VoxelMorph (h) Siamese Flow (i) Heatmap of Demons (j) Heatmap of SIFT Flow (k) Heatmap of Elastix (I) Heatmap of VoxelMorph (m) Heatmap of Siamese Flow

Figs. 7 and 8 show how well different registration algorithms perform in the application of registering a pair of images from the different image modalities. Fig. 7a is the fixed T1 MR image; Fig. 7b is the corresponding T2 MR slice (ground truth); Fig. 7c is the moving T2 MR image generated by distorting image (b) with λ=150; Fig. 7d is the ground truth T2 MR image overlayed on the fixed T1 image; Fig. 7e is the moving T2 MR image overlayed on the fixed T1 image; and Figs. 7f–7j are the registration results obtained by Demons, SIFT Flow, Elastix, VoxelMorph and Siamese Flow overlayed on the fixed T1 image, respectively. The proposed method is shown to achieve better registration accuracy than Elastix when registering images from cross-modalities.

3.6 Large-Deformation and Unseen Dataset

Large deformations due to heartbeat and respiration effects lead to a challenging deformable image registration task. In this section, we investigated registration performance in the case of the large deformable motion of cardiac tissue from ACDC for the five compared methods. The cardiac cine MRI scans in ACDC consist of short-axis cardiac image slices, each containing 20 time points that encompass the entire cardiac cycle. An expert annotated the LV, the RV and the MC at end diastolic (ED) and end systolic (ES) time points. To facilitate quantitative evaluation, we took the images in the ED and ES phases as fixed and moving images, respectively. We also trained the Siamese network on the image patches taken from the MR slices from BrainWeb and EMPIRE10, and the testing images were randomly selected from ACDC (unseen dataset and body part).

Tab. 4 shows the average DICE of the annotated LV, RV and MC regions that correspond to the registered images obtained by the five methods for ED and ES frames from the ACDC dataset. Tab. 4 shows that the proposed Siamese Flow achieves the highest average DICE.

Fig. 9 shows a comparison among different registration algorithms with large deformations and unseen datasets. Fig. 9a shows one fixed image randomly selected from ACDC; Fig. 9b is the corresponding moving image at the ES time point; and Figs. 9c–9h are superimposed LV, RV and MC regions of the ground truth (red) and the deformed regions of the registered image (green). Specifically, Fig. 9c is the result before registration; and Figs. 9d–9h are the results after registration using Demons, SIFT Flow, Elastix, VoxelMorph and Siamese Flow, respectively. Fig. 9 shows that the deformed region attained by Siamese Flow achieves the closest alignment with the ground truth region.

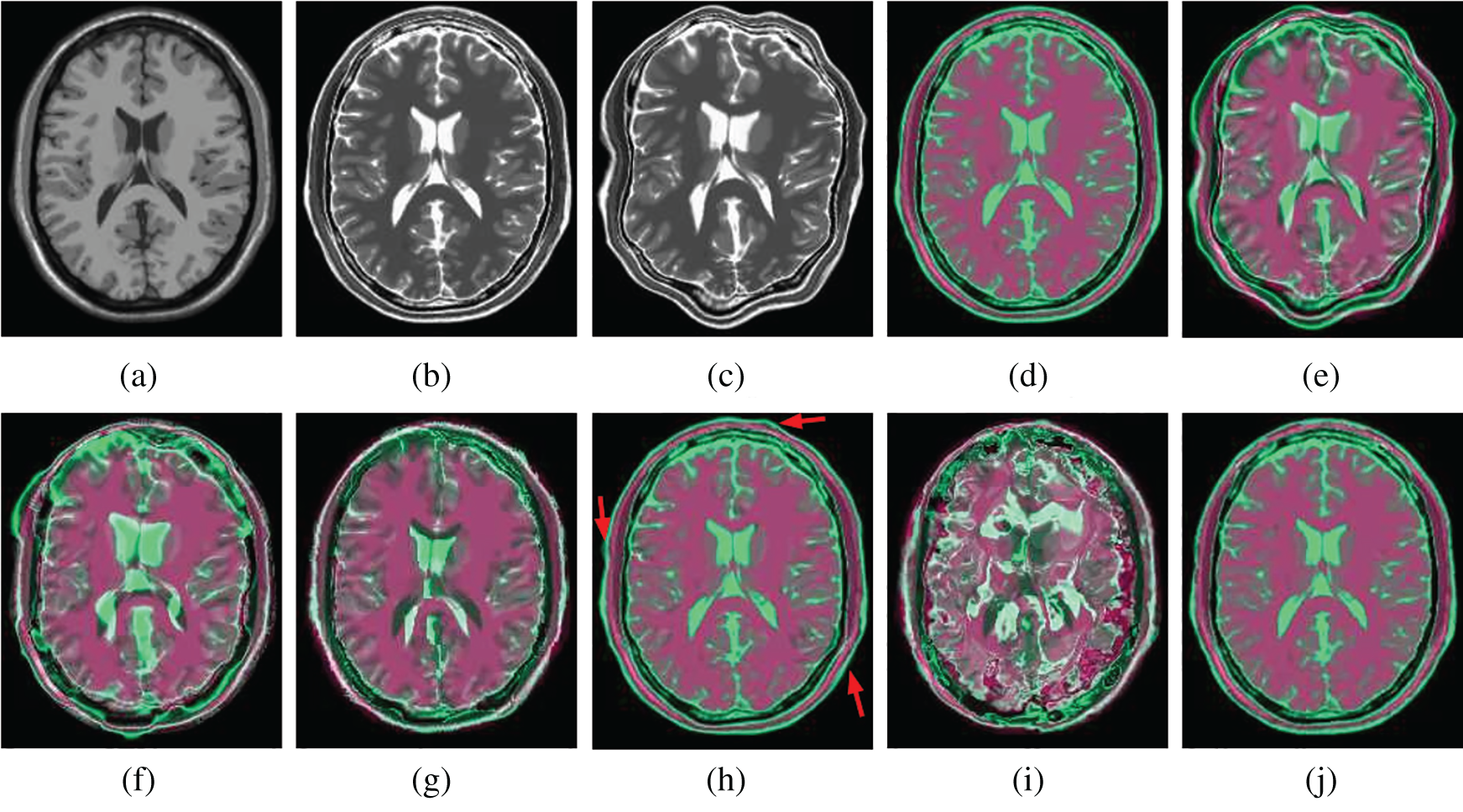
Figure 7: Illustration example of T1-T2 images from BrainWeb with different registration methods. (a) Fixed T1 (b) True T2 (c) Initial moving image (d) Ground truth overlay (e) Unregistered (f) Demons (g) SIFT Flow (h) Elastix (i) VoxelMorph (j) Siamese Flow

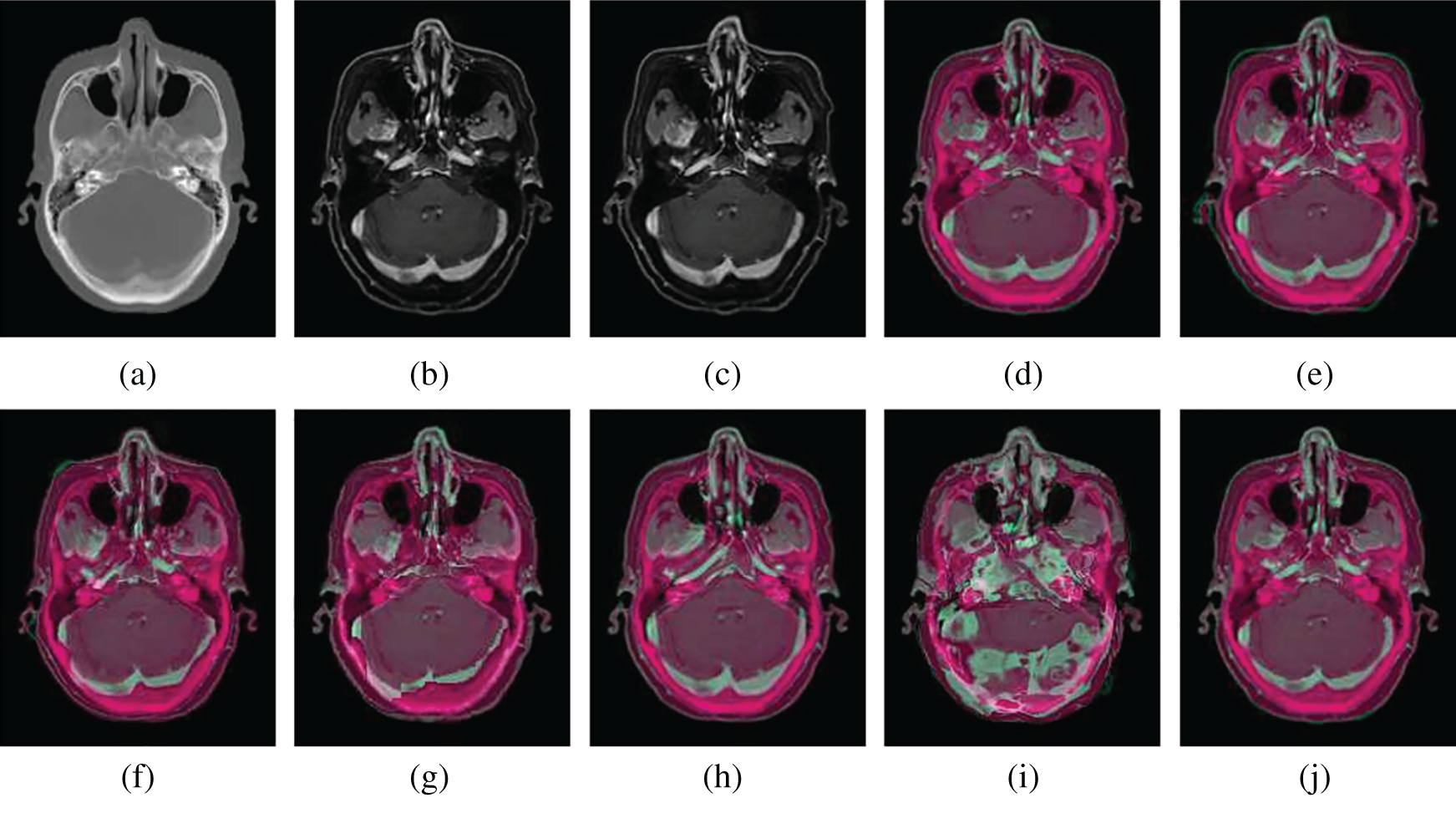
Figure 8: Illustration examples of CT-MR slices from NPCs with different registration methods. (a) Fixed CT (b) True MR (c) Initial moving image (d) Ground truth overlay (e) Unregistered (f) Demons (g) SIFT Flow (h) Elastix (i) VoxelMorph (j) Siamese Flow

4  Discussion

In this study, we proposed a deep learning feature-based optical flow method (Siamese Flow) for deformable medical image registration. Experimental results show that the proposed method outperforms Demons, SIFT Flow, and the most advanced existing methods (Elastix and VoxelMorph) with regard to registration accuracy, robustness, and large deformation.

The registration accuracy results (Tabs. 1 and 2, and Figs. 5 and 6) show that the proposed Siamese Flow method performs better than the comparison methods regarding RMSD, DICE, and heatmap visualization. Demons, SIFT Flow, and Siamese Flow are optical flow-based registration methods that align the fixed and moving images by minimizing image dissimilarities in the context of the optical flow approach. The feature representation derived from the proposed deep learning approach outperforms handcrafted features, such as SIFT Flow and pixel intensity-based approaches. The proposed approach thus produces better registration accuracy than Demons and SIFT Flow-based approaches.

Conversely, Elastix and VoxelMorph perform image registration via an optimizer that maximizes the intensity-based similarity between the overall fixed and moving images. The cost function thus plays an essential role in these methods to achieve an accurate registration result. Using the same cost function, we observed that the RMSD and DICE results in these two algorithms are similar. While it is a challenging task to design an optimal cost function in a specific task, we do not need to use an explicit image registration cost function in the proposed approach because image similarity is learned via metric learning and contrastive samples prepared in the learning stage. From comparative experiments that consider RMSD and DICE indices as well as heatmap visualization on BrainWeb and EMPIRE10, we observed that the proposed approach outperformed these two methods.

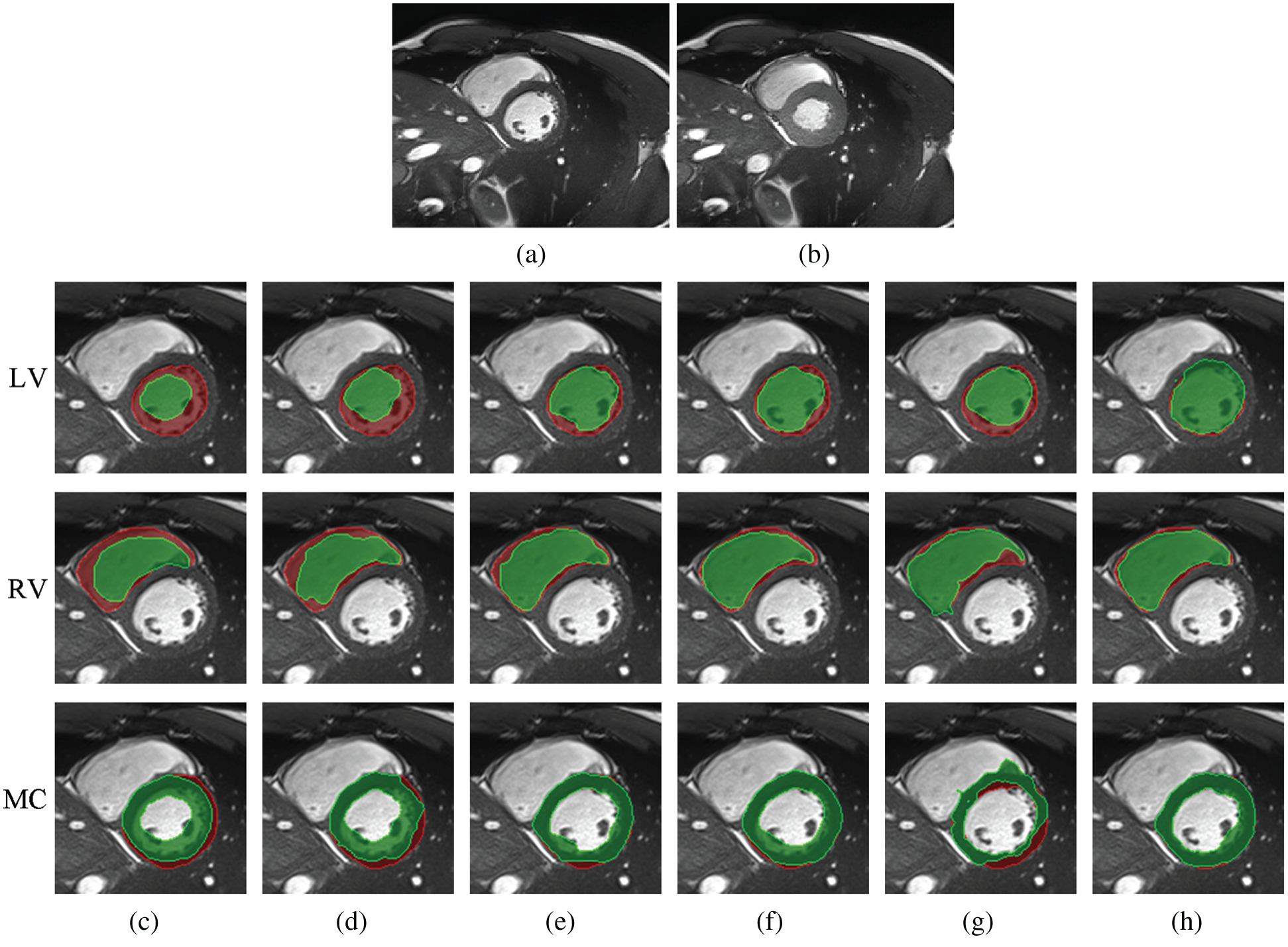
Figure 9: Example results for large-deformation cardiac-motion registration. (a) Fixed image (ED time point) (b) Moving image (ES time point) (c) unregistered (d) Demons (e) SIFT Flow (f) Elastix (g) VoxelMorph (h) Siamese Flow

From the results in Tab. 3, Figs. 7, and 8, the proposed algorithm is shown to be capable of registering multimodal deformable images. Demons and VoxelMorph fail to align two images in the case of appearance variations across different modalities because they assume that illumination is constant between images. SIFT Flow also fails because the SIFT feature is based on the gradient information and does not consider multimodal information. Unlike Demons, SIFT Flow and VoxelMorph, Elastix and Siamese Flow perform well in these cross-modality registration tasks. In addition, from the MI results in Tab. 3 and the color coding results in Figs. 7 and 8, particularly the red arrows pointing in Fig. 7h, Siamese Flow is shown to perform better than Elastix, which uses handcrafted mutual information as a cost function to measure image similarity under a global statistical assumption. However, Siamese Flow calculates image similarity via metric learning image features, making it more suitable for deformable medical image registration and allowing it to produce more accurate results.

Better registration is reflected by closer alignment of the fixed and moving images. Based on the DICE results in Tab. 4 and the superimposed LV, RV and MC regions in Fig. 9, Siamese Flow is shown to be capable of managing large tissue or organ deformations and achieves the best performance among all investigated methods. The Demons approach fails to align two images because the underlying assumptions (constant gray values and constant gradient) are unsatisfactory in optical flow estimation. VoxelMorph fails to attain accurate registered results due to the large unseen deformation level. SIFT Flow obtains alignment results that are comparable to those of Elastix for this large-deformation registration task. Elastix fails to align two images under a certain iteration number (e.g., 500 iterations). SIFT Flow also fails to use the handcrafted SIFT feature. In contrast, Siamese Flow is successful in all of these cases because the learned image patch representation is robust and generalizable, even to large deformations.

Furthermore, Tab. 4 and Fig. 9 show that Siamese Flow can generalize different tasks without retraining the model. The model learns a generic local descriptor that is applicable to other unseen datasets (ACDC) and unseen body parts (cardiac).

5  Conclusion

In this study, we presented a deep metric learning feature-based optical flow method for deformable medical image registration. In this framework, the critical components are the learned image patch representation that uses contrastive loss and the proposed optical flow that uses this learned representation. Experimental results show that the proposed Siamese Flow-based registration method performs better than pixel intensity and SIFT feature-based optical flow methods. Additionally, the proposed method outperforms conventional intensity-based image registration methods, such as Elastix, and end-to-end deep learning-based image registration methods, such as VoxelMorph, with regard to registration accuracy, robustness, and ability to manage large deformations.

In the future, we plan to extend the proposed algorithm as follows. First, we plan to investigate the end-to-end deep learning feature-based optical flow method (Siamese Flow) for deformable image registration to reduce computation time. Second, we plan to investigate the deep learning feature-based optical flow method for multimodality deformable image registration. Last, we plan to use the proposed algorithm to register lungs with large deformations to evaluate regional lung deformation.

Funding Statement: This study was supported in part by the Sichuan Science and Technology Program (2019YFH0085, 2019ZDZX0005, 2019YFG0196) and in part by the Foundation of Chengdu University of Information Technology (No. KYTZ202008).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  F. P. Oliveira and J. M. R. Tavares, “Medical image registration: A review,” Computer Methods in Biomechanics and Biomedical Engineering, vol. 17, no. 2, pp. 73–93, 2014. [Google Scholar]

 2.  M. Y. Zou, J. R. Hu, H. Zhang, X. Wu, J. He et al., “Rigid medical image registration using learning-based interest points and features,” Computers, Materials & Continua, vol. 60, no. 2, pp. 511–525, 2019. [Google Scholar]

 3.  J. Hu, Z. W. Luo, X. Wang, S. H. Sun, Y. B. Yin et al., “End-to-end multimodal image registration via reinforcement learning,” Medical Image Analysis, vol. 68, no. 2021, pp. 101878–101890, 2021. [Google Scholar]

 4.  A. Sotiras, C. Davatzikos and N. Paragios, “Deformable medical image registration: A survey,” IEEE Transactions on Medical Imaging, vol. 32, no. 7, pp. 1153–1190, 2013. [Google Scholar]

 5.  Y. Fu, Y. Lei, T. Wang, W. J. Curran, T. J. Liu et al., “Deep learning in medical image registration: A review,” Physics in Medicine & Biology, vol. 65, no. 20, pp. 20TR01, 2020. [Google Scholar]

 6.  G. Haskins, U. Kruger and P. Yan, “Deep learning in medical image registration: A survey,” Machine Vision and Applications, vol. 31, no. 8, pp. 1–18, 2020. [Google Scholar]

 7.  O. Weistrand and S. Svensson, “The anaconda algorithm for deformable image registration in radiotherapy,” Medical Physics, vol. 42, no. 1, pp. 40–53, 2015. [Google Scholar]

 8.  B. D. D. Vos, F. F. Berendsen, M. A. Viergever, M. Staring and I. Išgum, “End-to-end unsupervised deformable image registration with a convolutional neural network,” In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support Springer, Cham, Switzerland: Springer International Publishing, pp. 204–212, 2017. [Google Scholar]

 9.  G. Balakrishnan, A. Zhao, M. R. Sabuncu, J. Guttag and A. V. Dalca, “An unsupervised learning model for deformable medical image registration,” in Proc. CVPR, Salt Lake City, UT, USA, pp. 9252–9260, 2018. [Google Scholar]

10. T. Vercauteren, X. Pennec, A. Perchant and N. Ayache, “Diffeomorphic demons: Efficient non-parametric image registration,” NeuroImage, vol. 45, no. 1, pp. S61–S72, 2009. [Google Scholar]

11. A. Gooya, G. Biros and C. Davatzikos, “Deformable registration of glioma images using em algorithm and diffusion reaction modeling,” IEEE Transactions on Medical Imaging, vol. 30, no. 2, pp. 375–390, 2010. [Google Scholar]

12. X. Yang, R. Kwitt and M. Niethammer, “Fast predictive image registration,” Deep Learning and Data Labeling for Medical Applications, vol. 10008, pp. 48–57, 2016. [Google Scholar]

13. B. K. Horn and B. G. Schunck, “Determining optical flow,” Artificial Intelligence, vol. 17, no. 1–3, pp. 185–203, 1981. [Google Scholar]

14. J. P. Thirion, “Image matching as a diffusion process: An analogy with Maxwell's demons,” Medical Image Analysis, vol. 2, no. 3, pp. 243–260, 1998. [Google Scholar]

15. C. Liu, J. Yuen, A. Torralba, J. Sivic and W. T. Freeman, “Sift flow: Dense correspondence across different scenes,” in Proc. ECCV, Berlin, Heidelberg, France, pp. 28–42, 2008. [Google Scholar]

16. C. Liu, J. Yuen and A. Torralba, “Sift flow: Dense correspondence across scenes and its applications,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 33, no. 5, pp. 978–994, 2010. [Google Scholar]

17. Y. L. Boureau, F. Bach, Y. LeCun and J. Ponce, “Learning mid-level features for recognition,” in Proc. CVPR, San Francisco, CA, USA, pp. 2559–2566, 2010. [Google Scholar]

18. L. Zheng, Y. Zhao, S. Wang, J. Wang and Q. Tian, “Good practice in cnn feature transfer,” arXiv preprint arXiv:1604.00133, pp. 1–9, 2016. [Online]. Available: https://arxiv.org/pdf/1604.00133.pdf. [Google Scholar]

19. S. Zagoruyko and N. Komodakis, “Learning to compare image patches via convolutional neural networks,” in Proc. CVPR, Boston, MA, USA, pp. 4353–4361, 2015. [Google Scholar]

20. M. Simonovsky, B. Gutiérrez-Becker, D. Mateus, N. Navab and N. Komodakis, “A deep metric for multimodal registration,” in Proc. MICCAI, Athens, ATH, Greece, pp. 10–18, 2016. [Google Scholar]

21. S. Chopra, R. Hadsell and Y. LeCun, “Learning a similarity metric discriminatively, with application to face verification,” in Proc. CVPR, San Diego, CA, USA, pp. 539–546, 2005. [Google Scholar]

22. K. Simonyan and A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” in Proc. ICLR, San Diego, CA, United states, pp. 1–14, 2015. [Google Scholar]

23. S. Klein, M. Staring, K. Murphy, M. A. Viergever and J. P. Pluim, “Elastix: A toolbox for intensity-based medical image registration,” IEEE Transactions on Medical Imaging, vol. 29, no. 1, pp. 196–205, 2009. [Google Scholar]

24. G. Balakrishnan, A. Zhao, M. R. Sabuncu, J. Guttag and A. V. Dalca,“Voxelmorph: A learning framework for deformable medical image registration,” IEEE Transactions on Medical Imaging, vol. 38, no. 8, pp. 1788–1800, 2019. [Google Scholar]

25. A. Shekhovtsov, I. Kovtun and V. Hlaváč, “Efficient mrf deformation model for non-rigid image matching,” Computer Vision and Image Understanding, vol. 112, no. 1, pp. 91–99, 2008. [Google Scholar]

26. Y. Hu, R. Song and Y. Li, “Efficient coarse-to-fine patch match for large displacement optical flow,” in Proc. CVPR, Las Vegas, NV, USA, pp. 5704–5712, 2016. [Google Scholar]

27. H. Hou and H. Andrews, “Cubic splines for image interpolation and digital filtering,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 26, no. 6, pp. 508–517, 1978. [Google Scholar]

28. C. A. Cocosco, V. Kollokian, R. Kwan, G. B. Pike and A. C. Evans, “Brainweb: Online interface to a 3d mri simulated brain database,” NeuroImage, vol. 5, pp. 425, 1997. [Google Scholar]

29. R. Kwan, A. C. Evans and G. B. Pike, “Mri simulation-based evaluation of image-processing and classification methods,” IEEE Transactions on Medical Imaging, vol. 18, no. 11, pp. 1085–1097, 1999. [Google Scholar]

30. R. Kwan, A. C. Evans and G. B. Pike, “An extensible mri simulator for post-processing evaluation,” in Proc. VBC, Berlin, Heidelberg, Germany, pp. 135–140, 1996. [Google Scholar]

31. K. Murphy, B. V. Ginneken, J. M. Reinhardt, S. Kabus and K. Ding, “Evaluation of registration methods on thoracic ct: The empire10 challenge,” IEEE Transactions on Medical Imaging, vol. 30, no. 11, pp. 1901–1920, 2011. [Google Scholar]

32. O. Bernard, A. Lalande, C. Zotti, F. Cervenansky and X. Yang, “Deep learning techniques for automatic mri cardiac multi-structures segmentation and diagnosis: Is the problem solved?,” IEEE Transactions on Medical Imaging, vol. 37, no. 11, pp. 2514–2525, 2018. [Google Scholar]

33. E. M. Rikxoort, B. Hoop, M. A. Viergever, M. Prokop and B. Ginneken, “Automatic lung segmentation from thoracic computed tomography scans using a hybrid approach with error detection,” Medical Physics, vol. 36, no. 7, pp. 2934–2947, 2009. [Google Scholar]

34. P. Y. Simard, D. Steinkraus and J. C. Platt, “Best practices for convolutional neural networks applied to visual document analysis,” in Proc. ICDAR, Edinburgh, Scotland, UK, pp. 958–963, 2003. [Google Scholar]

35. T. Tieleman and G. Hinton, “Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude,” COURSERA: Neural Networks for Machine Learning, vol. 4, no. 2, pp. 26–31, 2012. [Google Scholar]

36. P. Christoffersen and K. Jacobs, “The importance of the loss function in option valuation,” Journal of Financial Economics, vol. 72, no. 2, pp. 291–318, 2004. [Google Scholar]

37. N. Tustison and J. Gee, “Introducing dice, jaccard, and other label overlap measures to itk,” Insight, vol. 2, pp. 1–4, 2009. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.