Computers, Materials & Continua DOI:10.32604/cmc.2022.021577
Article

Chaotic Whale Optimized Fractional Order PID Controller Design for Desalination Process

F. Kavin1,* and R. Senthilkumar2

1Department of Electronics and Instrumentation Engineering, Saveetha Engineering College, Thandalam, Chennai, 602105, India
2Department of Electrical and Electronics Engineering, Saveetha Engineering College, Thandalam, Chennai, 602105, India
*Corresponding Author: F. Kavin. Email: kavinleer@gmail.com
Received: 07 July 2021; Accepted: 19 August 2021

Abstract: The main aim of this work is to design a suitable Fractional Order Proportionl Integral Derivative (FOPID) controller with Chaotic Whale Optimization Algorithm (CWOA) for a RO desalination system. Continuous research on Reverse Osmosis (RO) desalination plants is a promising technique for satisfaction with sustainable and efficient RO plants. This work implements CWOA based FOPID for the simulation of reverse osmosis (RO) desalination process for both servo and regulatory problems. Mathematical modeling is a vital constituent of designing advanced and developed engineering processes, which helps to gain a deep study of processes to predict the performance, more efficiently. Numerous approaches have been employed for mathematical models based on mass and heat transfer and concentration of permeable flow rate. Incorporation of FOPID controllers is broadly used to improve the dynamic response of the system, at the same time, to reduce undershoot or overshoot, steady state error and hence improve the response. The performances of the FOPID controller with optimization is compared in terms of measures such as Integral Time Absolute Error (ITAE) and Integral Square Error (ISE). Simulation results with FOPID on desalination process achieved rise time of 0.0311 s, settling time of 0.0489 s and 0.7358% overshoot, better than the existing techniques available in the literatures.

Keywords: Desalination; FOPID; integral of absolute error; reverse osmosis; water treatment

1  Introduction

Due to the rapid growth in population and higher standards of living, water scarcity is one of the most important issues faced by the people in day-to-day life. Fresh water is used every day for many purposes. Moreover, the mortality rate has been increasing annually, due to the lack of adequate water supply and proper sanitation [1]. Numerous solutions have been proposed to provide sufficient fresh water, which involves desalination. Desalination is the standardized technique to reduce water insufficiency by the way of converting the untiring supply of seawater into freshwater resources, thus can be used in healthcare applications. Nowadays, several desalination plants work based on the semi permeable membrane technique known as reverse osmosis [2]. Among the desalination techniques, RO desalination offers the merits of low-energy consumption [3]. Reverse osmosis is the technique used to purify the water through a semipermeable membrane by separating the salt from it [4]. In natural osmosis, the membrane avoids the amount of salts, and it permits the fresh water to pass through the membrane [5]. Two types of pressure is maintained in this process in which the pressure on the dilute side lowered and the pressure will be raised on the concentration side [6].

In order to identify the best result for this issue, it becomes significantly necessary to implement and establish large volume of desalination plants with accurate operating control strategies [7]. Conventional Proportionl Integral Derivative (PID) is the extreme distinctive controller employed in the process industries in past few years, due to its simplicity, easy design and availability of many tuning methodologies. PID controllers are not enough to provide agreeable performance. FOPID controller is well suitable for control system that consists of five parameters. It is easy to implement with low complexity, as compared to PID. FOPID controller makes the system performance better, as compared to the conventional PID controller, due to the presence of non-integer proportional and integral gain. In RO process instrumentation and control, it becomes mandatory to maintain the desired level and monitor every process such as flow rates and pressure, feed flow and the quality of water generated (pH, conductivity and turbidity), feed pressure controls, and operated level of tanks [8].

Perez et al., (2019) [1] have proposed the design of an Expert Model based Predictive Controller for effective and accurate control of the critical variables of the seawater RO desalination plant. The controller was designed to overcome the problems of PID controller. Batlle et al., (2017) [2] suggested a new technique for the RO desalination plant, which aims to design a suitable controller for the desalination plant system using reverse osmosis technique. Rathore et al., (2019) [3] have presented a whale optimisation algorithm based PID controller for reverse osmosis desalination plant. The permeate flux and conductivity parameters are estimated. Patnana et al., (2018) [4] developed a novel technique for desalination plant, which uses PID controller and salp swarm optimization algorithm. For parameter tuning of PID controller the minimization of integral of square error (ISE) is applied. Noeiaghdam et al., (2021) [5] illustrated a novel approach to implement a novel approach, to determine the suitable idea of the reverse osmosis desalination plant system. Phuc et al., (2017) [6] suggested a robust controller for desalination plant, which aims to overcome the limitation of external disturbances. It is analyzed by using multiple input multiple output systems, presented an optimization framework for the reverse osmosis desalination plant.

Various techniques are proposed by the researchers for desalination plant. Several types of controllers are designed, but they are not efficient and takes much time for computation. Hence, these models cannot be used for satisfactory performance, and it does not provide effective solution for the growing demand of portable water. Hence, the present work deals with the FOPID controller with CWOA optimization that makes system more robust and effective for different applications. The CWOA based FOPID controller is proposed, ITAE and ISE are the time domain measures performance [7–8].

The main contributions of the research include

•   To design efficient fractional order PID controllers, to control a RO seawater desalination plant.

•   Development of mathematical modeling for Reverse Osmosis [9] process

•   The permeate flux and conductivity parameters have been analyzed.

•   Better time domain specification [10] performance is achieved using FOPID control structure for a desalination plant system [11].

The paper is structured as follows. Section 2 explains the process description of the proposed work. Section 3, briefly presents the mathematical modeling of reverse osmosis desalination plant. The simulation results and discussion is developed in Section 4. Section 5 presents the conclusion and future work of the research.

2  Process Description

The desalination system consists of pretreated water tank, membrane assembly which is separated into two sides, one the concentrate side and the other is permeate side. The membrane assembly provides one or more semi permeable membrane to separate the pure water from the concentrated side [12]. Pretreated water is passed to the membrane assembly via a high pressure pump, and a section of concentrated brine discharge that comes out from the reverse osmosis is recycled [13] to water tank.

Figure 1: Block schematic of reverse osmosis process

The high-pressure pump supplies the pressure needed to enable the water to pass through the membrane. Likewise, a small section of permeate side that comes out via membrane assembly get recycled to the equalization tank [14]. Untreated water is pre-treated and stored in a tank. Untreated water is pumped to the membrane assembly with the help of high pressure pump to overcome osmotic pressure [15]. Two sensors namely conductivity sensor σs and flux sensor φs used to measure the output variables is shown in Fig. 1. In this process, the manipulated input variables [16] are measured at the feed side the measured variables are the rejection valve θv and the speed variator Sv. In radial direction [17], the permeate comes out from the reverse osmosis and the axial flow stream enters as rejection (or) brine.

3  Mathematical Modeling

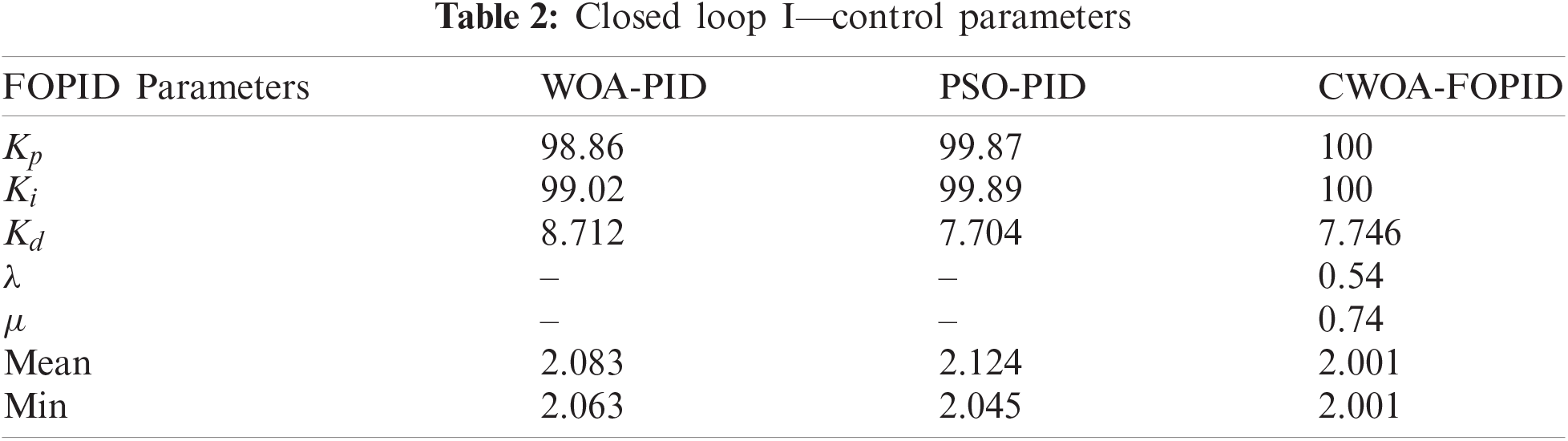
The generalized unit transfer model of RO desalination plant system can be represented as follows and the parameter specification are shown in Tab. 1.

[H(S)]=[H11(S)H12(S)H21(S)H22(S)] (1)

H11(S)=φsSv=g111+d11S (2)

H12(S)=φsθv=−b12S2+a1b1s+b12 (3)

H21(S)=σsSv=−b22S2+a2b2s+b22 (4)

H22(S)=σsφv=g221+d22S (5)

where φs is the flux sensor output, Sv is the input of speed variator, φv is the rejection valve, σs is the conductivity sensor output.

4  Proposed RO Treatment Control Loop Design

Basically, two FOPID controllers applied for the process of reverse osmosis desalination system. The two control loops are separately tuned, hence the two outputs could not be interrelated [18]. The interrelation is cancelled by employing feed-forward compensators. This method is said to be decoupling. In the proposed technique, two compensators are designed as feed forward, hence the two FOPID controllers can tuned without any difficulties [19]. The RO control loop design is shown in Fig. 2.

4.1 Design of Decoupler

Decoupler is needed for the design to cancel the effect of interaction of the system. Fig. 3 illustrates the simplified decoupler along with the plant [20].

The transfer function of decoupler is represented as

CD(S)=[1hd12(S)hd21(S)1] (6)

where,

hd12(S)=−Hp12(S)Hp11(S) (7)

hd21(S)=−Hp21(S)Hp22(S) (8)

By designing, hd12(S) and hd21(S), the two effects can be easily eliminated.

Figure 2: Control loop design for reverse osmosis

Figure 3: Simplified decoupler

4.2 FOPID Controller Design

FOPID Controller is the advanced version of PID controller. FOPID controller improves the system performance more efficiently [21].

The FOPID controller transfer function is given as,

Hc(s)=u(s)e(s)=kp+kIs−λ+kDsμ (9)

where Hc(s) is the transfer function of the controller, e(s) is the error value, and (s) is the resultant output. kp,kI and kD are the gains for proportional, integral, and derivative terms for the FOPID controller [22]. The expression λ is the fractional element of integral parts and μ is the fractional element of derivative parts as clearly shown in Fig. 4.

The FOPID controller function is given as,

u(t)=Kpe(t)+KiD−λe(t)+KdDμe(t) (10)

Figure 4: Block schematic of FOPID controller

The FOPID controller design solving five equations with five unknowns KP, KI, KD, λ, and μ related to the system [23]. By selecting the value μ as 1, the PID controller is improved in the modified form.

The transfer function for the FOPID Controller can be represented by CFOPID(S) and CP(S). The reference input r(s), error input e(s) and actual input y(s) are the three input variables, as shown in Fig. 5.

Figure 5: Structure of FOPID based RO system

The FOPID controller is tuned in an optimal way, which offers optimal performance of FOPID controller, based on fitness function.

4.3 Proposed Chaotic Whale Optimization Algorithm for RO Desalination Plant

Whale optimization algorithm describes the hunting characteristics of humpback for solving optimization issues. The hunting mechanism for observing the foraging character of humpback in whales known as bubble bet method is proposed in [24]. Moreover, the whale makes a bubble surround, while hunting. The WOA algorithm assumes that the best search solution with the increasing number of iterations from start to a maximum number of iterations [25]. To find the best search agent, the remaining search agents update their location towards the best search agent.

The mathematical humpback behavior of whales can be represented as

E→=|D→.Y∗→(t)−Y→(t)| (11)

Y→(t+1)=Y∗→(t)−B→.E→ (12)

where B→ and E→ are the vector coefficients for convergence value,

t is the recent iteration,

Y∗→ is the best result positive vector

Y→ is the positive vector

The formula for B→ and E→ vectors can be represented as,

B→=2a→.r→-r→ (13)

E→=2.r→ (14)

The value of ‘a’ ranges from 0 to 2,

‘r’ is the random vector at the interval [0,1]

Two main approaches for hunting the humpback whales are:

     i)  shrinking encircling mechanism and

    ii)  spiral position update

Shrinking encircling mechanism: some features like shrinking the search environment while moving towards the prey is achieved when the value of a is reduced from 2 to 0 [26].

Spiral update position: The humpback whales moving along a spiral path is mathematically denoted as

Y→(t+1)=E′.→ebk.cos(2πl)+Y→(t) (15)

Y→(t+1)={Y→(t)−B→.E→if  s≤0.5E′.→ebk.cos(2πl)+Y→(t)}if s≥0.5} (16)

where ‘s’ is the random number in interval [0,1]

Chaotic Whale Optimization performs by changing the parameter r in B→ and E→. The parameter ks is the tent chaotic maps for searching best agents. By solving the multi objective problem, chaotic map can improve the performance.

B→=2a→.ks→−a→ (17)

E→=2ks→ (18)

The advanced model is created by replacing the parameter ‘s’ in Eq. (16)

Y→(t+1)={Y→(t)−B→.E→ if ks≤0.5E′.→ebk.cos(2πl)+Y→(t)} if ks≥0.5} (19)

The proposed CWOA flowchart is shown in Fig. 6.

Figure 6: Flowchart for proposed CWOA for RO

4.4 Design Procedure of FOPID Controller Using CWOA

In FOPID controller design, the parameters are optimized with the aid of Chaotic Whale Optimization algorithm as shown in Fig. 7. The error performance namely ISE is considering the fitness function [27]. It is represented as

E(Y)=∫0∞|e(t)|2dt (20)

With respect to the condition 0 < = kp < = 5, 0 < = ki < = 5 and the fitness function can be evaluated as

FTi=1Fi(y) (21)

whereas the search with suitable FTi values can be investigated again [28]

Figure 7: Schematic of FOPID controller using proposed CWOA

5  Simulation Results and Discussion

In this section, the simulations results are presented for FOPID controllers with Chaotic Whale Optimization Algorithm (CWOA) [29] and the performance measures are analyzed. It demonstrates the two output variable to validate the permeate flux and conductivity parameters for reverse osmosis desalination plant model. By analyzing the performance, few of the techniques are compared namely, the PSO optimization using PID controller [30], Whale optimization algorithm using PID controller and the proposed method.

The closed loop performance for the proposed method using fractional order PID controller with Chaotic Whale Optimization algorithm is shown in Fig. 8. It is clearly evident that, the proposed method provides better performance compared to the existing WOA-PID method.

Figure 8: Closed loop performance of reverse osmosis desalination plant

Fig. 9 shows the step response obtained for control loop I, by using the FOPID controller parameters Kp, Ki, Kd, λ and μ. It is analyzed with the help of WOA-PID, PSO-PID and CWOA-FOPID for flux rate, at a constant pressure value of 700 psi is applied. From the results, the proposed method gives better step response. Tab. 2 demonstrates the closed loop I parameters by using WOA-PID, PSO-PID and CWOA-FOPID algorithms. Tab. 3 shows the closed loop I performance parameters such as overshoot, settling time and the rise time of WOA-PID, PSO-PID and CWOA-FOPID algorithms. The performance of Chaotic Whale Optimization Algorithm based FOPID controller provides better results in terms of settling time, rise time and overshoot than WOA-PID and PSO-PID controllers. Hence, it is proved that the proposed CWOA-FOPID controller is very well suitable for the reverse osmosis desalination system.

Figure 9: Step response for control loop I

The step response for control loop II is shown in Fig. 10. The results obtained by using the FOPID controller parameters Kp, Ki, Kd, λ and μ are analyzed. The applied algorithms are WOA-PID, PSO-PID and CWOA-FOPID, in case of conductivity loop. From the results, the proposed CWOA-FOPID method gives better step response than the existing techniques such as WOA-PID and PSO-PID.

Figure 10: Step response for control loop II

5.1 Performance and Evaluations

The closed loop II parameter by using WOA-PID, PSO-PID and CWOA-FOPID algorithms are listed in Tab. 4. The closed loop II time domain specifications such as rise time, settling time and peak overshoot are observed in Tab. 5. The performance of proposed CWOA based FOPID controller provides better ISE performance in terms of rise time, settling time and peak overshoot, compared to the existing WOA-PID and PSO-PID controllers.

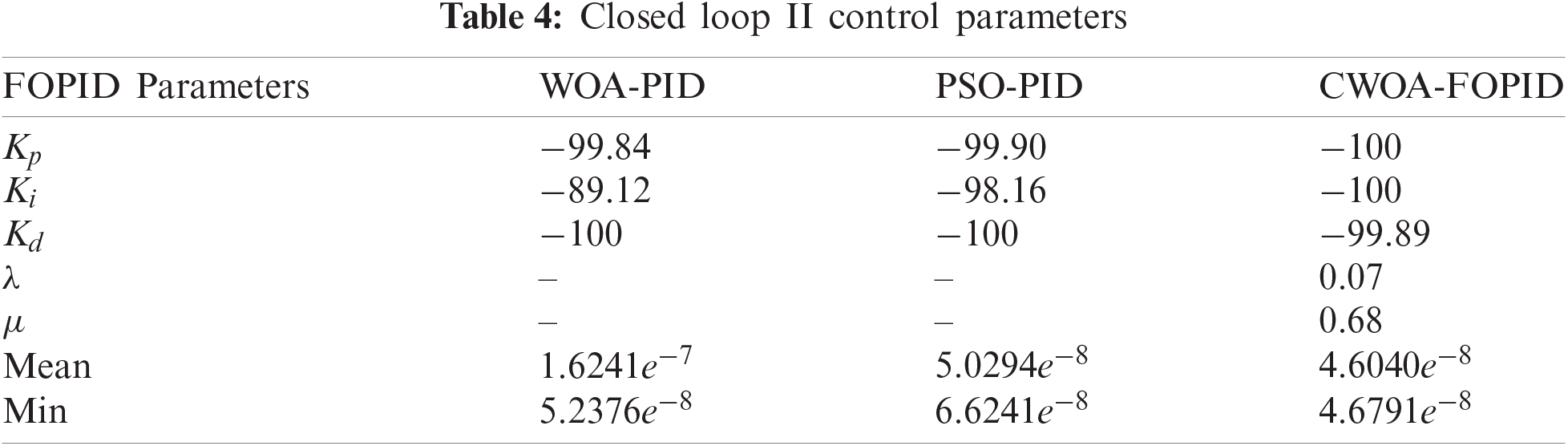
Fig. 11 shows the ITAE performance for reverse osmosis desalination plant model, which clearly gives the error reduction performance. Moreover, it is proved that the error reduction for the proposed system is increased than existing WOA-PID. Fig. 12 illustrates the ISE performance for reverse osmosis desalination plant model, which clearly illustrates the error reduction performance using FOPID controller. The error amplitude of existing WOA-PID system is increased initially, later drastically reduced to zero in 3 seconds. Hence, the error is minimized using the proposed CWOA-FOPID technique. The rise time and settling time are very less by using the proposed technique, as compared to other techniques such as WOA-PID and PSO-PID techniques.

Figure 11: ITAE performance of proposed method

Figure 12: ISE performance of proposed CWOA based FOPID

Fig. 13 shows the step response of the fractional order PID controller with improved performance. Fig. 14 shows the settling time response using FOPID controller with various optimization techniques.

Figure 13: Step response of proposed FOPID controller

In comparison, the proposed system provides better results in terms of settling time, as compared to the existing system such as WOA-PID and PSO-PID.

Tab. 6 shows the performance evaluation of various techniques applied for reverse osmosis desalination plant system. Various techniques such as WOA-PID, Expert-MPC, SSO-PID, TLBO-PID, SOS-PID and the proposed CWOA-FOPID are compared. The time domain specification such as such as rise time, settling time and overshoot are noticed to be better with the proposed technique. Moreover, it is proved that the proposed CWOA–FOPID technique using reverse osmosis process for the desalination plant is suitable for various applications. The proposed CWOA–FOPID has 0.0311 s as rise time, 0.0489 s as settling time and 0.7358% overshoot.

Fig. 15 illustrates the performance comparison of various techniques, applied for reverse osmosis desalination plant system. Various techniques such as WOA-PID, Expert-MPC, SSO-PID, TLBO-PID, SOS-PID and the proposed CWOA-FOPID are applied for the comparison. The time domain specifications such as rise time, settling time and overshoot are given. In addition, it is clearly verified that the proposed CWOA-FOPID technique using reverse osmosis process for the desalination plant is suitable for healthcare applications and provides better rise time, settling time and overshoot. The proposed CWOA-FOPID method gives the result of 0.0311 s as rise time, 0.0489 s as settling time and 0.7358% overshoot, better than the existing techniques such as WOA-PID, Expert MPC, SSO-PID, TLBO-PID, SOS-PID.

Figure 14: Settling time response for proposed CWOA based FOPID

Figure 15: Performance graph for various techniques used for reverse osmosis desalination plant

5.2 Experimental Setup and Discussion

This section discusses the RO system performance with FOPID controller. The reverse osmosis unit was designed and manufactured at California. The desalination unit was fabricated and interlinked with a high pressure solenoid valves which is not manual controlled via a control unit.

The basic components used are as follows: High-Pressure Pump (HPP) is used to manufacture by an optimal flow depends on salinity and volume of the system with speed of 1350 rpm. Low-Pressure Pump (LPP) is applied to guarantee the pressure entering the high-pressure pump, to minimize cavitation at the suction. The Booster Pump (BP) is used to increase the pressure of feed water and to raise the feed water pressure to the HPP working level. Low-pressure switch is employed in the setup, which makes the system turn on and off. The impurity water from sea with total dissolved solids with 48345 ppm is used for this setup. The lower pressure switch categories the entering water into two ways. The low pressure pump is used to allow the water and increases its pressure. One way to allow the high-pressure pump that can increase the seawater pressure to the desired system as shown in Fig. 16. The fraction in the derivative part improves the closed loop performance.

Fig. 17 shows the comparative analysis for experimental and the proposed method. It is proved that the proposed method gives better performance. Figs. 18 and 19 illustrates that the proposed method is suitable for RO plant, as it provides the best performance compared to experimentation.

Figure 16: Photograph for desalination plant system

Figure 17: Comparison of experimental and simulation result

Figure 18: Comparison of experimental and simulation result for permeable flux

Figure 19: Comparison of experimental and simulation result for permeable conductivity vs. system pressure

6  Conclusion

In this paper, FOPID controller with Chaotic Whale Optimization Algorithm (CWOA) is proposed for the reverse osmosis desalination system. A mathematical model of a reverse osmosis desalination plant has been presented. Before designing the FOPID controller, initially decoupling is performed to reject the effect of interaction. The time domain specification such as rise time, settling time and peak overshoot are analyzed. From the simulation results, it is proved that that the proposed technique is able to achieve better ISE and ITAE error performance. The result shows that, the proposed FOPID controller with Chaotic Whale optimization algorithm yields better result in terms of error performance. The study shows that the CWOA based FOPID controllers outperform the existing ones and found to be suitable for various applications. Moreover, the experimental result is compared to the proposed CWOA based FOPID technique and it is proved that the proposed method yields better results in improved time domain specifications.

7  Future Work

The work can be extended by applying other metaheuristic technique and studying the system performance for reverse osmosis desalination plant system.

Acknowledgement: The authors with a deep sense of gratitude would thank the supervisor for his guidance and constant support rendered during this research.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  R. R. Perez, J. S. Moriano, G. P. Zuniga and M. E. S. Angles, “Real-time implementation of an expert model predictive controller in a pilot-scale reverse osmosis plant for brackish and seawater desalination,” Applied Sciences, vol. 9, no. 14, pp. 2932, 2019. [Google Scholar]

 2.  V. F. Batlle, R. R. Perez and A. L. Saez, “Fractional order robust control of a reverse osmosis seawater desalination plant,” IFAC-PapersOnline, vol. 50, no. 1, pp. 14545–14550, 2017. [Google Scholar]

 3.  N. S. Rathore and V. P. Singh, “Whale optimisation algorithm-based controller design for reverse osmosis desalination plants,” International Journal of Intelligent Engineering Informatics, vol. 7, no. 1, pp. 77–88, 2019. [Google Scholar]

 4.  N. Patnana, S. Pattnaik and V. Singh, “Salp swarm optimization based PID controller tuning for doha reverse osmosis desalination plant,” International Journal of Pure and Applied Mathematics, vol. 119, no. 12, pp. 12707–12720, 2018. [Google Scholar]

 5.  S. Noeiaghdam, D. Sidorov, A. Tynda, A. Zamyshlyaeva, A. Dreglea et al., “A valid dynamical control on the reverse osmosis system using the CESTAC method,” Mathematics, vol. 9, no. 1, pp. 48, 2021. [Google Scholar]

 6.  B. D. H. Phuc, S. S. You, H. S. Choi and S. K. Jeong, “Advanced control synthesis for reverse osmosis water desalination processes,” Water Environment Research, vol. 89, no. 11, pp. 1932–1941, 2017. [Google Scholar]

 7.  Z. Hadadian, S. Zahmatkesh, M. Ansari, A. Haghighi, E. Moghimipour et al., “Mathematical and experimental modeling of reverse osmosis (RO) process,” Korean Journal of Chemical Engineering, vol. 38, no. 6, pp. 366–379, 2021. [Google Scholar]

 8.  F. Moazeni and J. Khazaei, “Optimal design and operation of an islanded water-energy network including a combined electro dialysis reverse osmosis desalination unit,” Renewable Energy, vol. 167, no. 9, pp. 395–408, 2021. [Google Scholar]

 9.  C. Liu and L. Song, “Energy analysis and efficiency assessment of reverse osmosis desalination process,” Desalination, vol. 276, no. 1–3, pp. 352–358, 2011. [Google Scholar]

10. R. Dashtpour and S. N. A. Zubaidy, “Energy efficient reverse osmosis desalination process,” International Journal of Environmental Science and Development, vol. 3, no. 4, pp. 339, 2012. [Google Scholar]

11. S. Vrkalovic, E. C. Lunca and L. D. Borlea, “Model-free sliding mode and fuzzy controllers for reverse osmosis desalination plants,” International Journal of Artificial Intelligence, vol. 16, no. 2, pp. 208–222, 2018. [Google Scholar]

12. N. Rathore, S. Natwar and V. P. Singh, “Design of optimal PID controller for the reverse osmosis using teacher-learner-based-optimization,” Membrane Water Treatment, vol. 9, no. 2, pp. 129–136, 2018. [Google Scholar]

13. S. M. Kargar and R. Mehrad, “Robust model predictive control for a small reverse osmosis desalination unit subject to uncertainty and actuator fault,” Water Supply, vol. 20, no. 4, pp. 1229–1240, 2020. [Google Scholar]

14. Z. Mohamed, Y. Messlem, A. Gouichiche and T. Mohamed, “Super-twisting sliding mode control and robust loop shaping design of RO desalination process powered by PV generator,” Desalination, vol. 458, no. 9, pp. 122–135, 2019. [Google Scholar]

15. C. S. Karavas, A. G. Konstantinos and G. Papadakis, “Optimal technical and economic configuration of photovoltaic powered reverse osmosis desalination systems operating in autonomous mode,” Desalination, vol. 466, pp. 97–106, 2019. [Google Scholar]

16. R. Mehrad and S. K. Mohamad, “Integrated model predictive fault-tolerant control, and fault detection based on the parity space approach for a reverse osmosis desalination unit,” Transactions of the Institute of Measurement and Control, vol. 42, no. 10, pp. 1882–1894, 2020. [Google Scholar]

17. C. Yoram, P. D. Christofides, A. Rahardianto, A. R. Bartman, A. Zhu et al., “Apparatus, system and method for integrated filtration and reverse osmosis desalination,” U. S. Patent, vol. 113, p. 790, 2017. [Google Scholar]

18. D. Karimanzira and T. Rauschenbach, “Deep learning based model predictive control for a reverse osmosis desalination plant,” Journal of Applied Mathematics and Physic, vol. 8, no. 12, pp. 2713–2731, 2020. [Google Scholar]

19. P. Kofinas and A. I. Dounis, “Online tuning of a PID controller with a fuzzy reinforcement learning MAS for flow rate control of a desalination unit,” Electronics, vol. 8, no. 2, pp. 231, 2019. [Google Scholar]

20. S. Srivastava, S. V. P. Kumar and S. Sadistap, “Design and development of reverse osmosis (RO) plant status monitoring system for early fault prediction and predictive maintenance,” Applied Water Science, vol. 8, no. 6, pp. 1–10, 2018. [Google Scholar]

21. G. Kyriakarakos, A. I. Dounis, K. G. Arvanitis and G. Papadakis, “Design of a fuzzy cognitive maps variable-load energy management system for autonomous PV-reverse osmosis desalination systems: A simulation survey,” Applied Energy, vol. 187, pp. 575–584, 2017. [Google Scholar]

22. P. Z. Gustavo, R. P. Raul, J. S. Moriano and V. S. Zurita, “Fault detection and isolation system based on structural analysis of an industrial seawater reverse osmosis desalination plant,” Processes, vol. 8, no. 9, pp. 1100, 2020. [Google Scholar]

23. M. A. M. Khan, S. Rehman and F. A. Sulaiman, “A hybrid renewable energy system as a potential energy source for water desalination using reverse osmosis: A review,” Renewable and Sustainable Energy Reviews, vol. 97, pp. 456–477, 2018. [Google Scholar]

24. B. D. Hong, S. S. You, T. W. Lim and H. S. Kim, “Dynamical analysis and control synthesis of RO desalination process against water hammering,” Desalination, vol. 402, no. 1, pp. 133–142, 2017. [Google Scholar]

25. M. Bachar, A. Naddami, A. Fahli and H. Mohamed, “A new mobile and hybrid desalination unit with solar energy and enhanced reverse osmosis,” in Proc. of Renewable and Sustainable Energy Conf. (IRSECRabat, Morocco, pp. 1–5, 2018. [Google Scholar]

26. L. Hongli, L. Song, L. Shao, Z. Tan, X. Chen et al., “Design of LT-MED seawater desalination temperature control system based on dynamic matrix predictive fuzzy PID control algorithm,” in Proc. of IEEE Int. Conf. on Mechatronics and Automation (ICMAChangchun, China, pp. 293–297, 2018. [Google Scholar]

27. N. S. Rathore and V. P. Singh, “Design of optimal PID controller for the reverse osmosis using teacher-learner-based-optimization,” Membrane Water Treatment, vol. 9, no. 2, pp. 129–136, 2018. [Google Scholar]

28. N. S. Rathore, V. P. Singh and B. D. Hong, “A modified controller design based on symbiotic organisms search optimization for desalination system,” Journal of Water Supply: Research and Technology-Aqua, vol. 68, no. 5, pp. 337–345, 2019. [Google Scholar]

29. Y. H. Cai, N. Galili, Y. Gelman, M. Herzberg, J. Gilron, “Evaluating the impact of pretreatment processes on fouling of reverse osmosis membrane by secondary wastewater,” Journal of Membrane Science, vol. 623, pp. 119054, 2021. [Google Scholar]

30. N. Patnana, S. Pattnaik, T. Varshney and V. P. Singh, “Self-learning salp swarm optimization based PID design of doha RO plant,” Algorithms, vol. 13, no. 11, pp. 287, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.