DOI:10.32604/cmc.2022.022063

| Computers, Materials & Continua DOI:10.32604/cmc.2022.022063 |  |
| Article |
Improved DHOA-Fuzzy Based Load Scheduling in IoT Cloud Environment
1Department of Information Science & Engineering, CMR Institute of Technology, Bengaluru, 560037, India
2Department of Computer Application, CMR Institute of Technology, Bangalore, 560037, India
3School of Computing, Woldia Institute of Technology, Woldia University, Ethiopia
4Department of Commerce, School of Commerce, Finance and Accountancy, Christ University, Bangalore, 560029, India
5Department of Computer Science, College of Science & Art at Mahayil, King Khalid University, Saudi Arabia
6Faculty of Computer and IT, Sana'a University, Yemen
7Department of Information Systems, College of Computer and Information Sciences, Princess Nourah Bint Abdulrahman University, Saudi Arabia
8Department of Computer and Self Development, Preparatory Year Deanship, Prince Sattam bin Abdulaziz University, Alkharj, Saudi Arabia
*Corresponding Author: Fahd N. Al-Wesabi. Email: Falwesabi@kku.edu.sa
Received: 26 July 2021; Accepted: 26 August 2021
Abstract: Internet of things (IoT) has been significantly raised owing to the development of broadband access network, machine learning (ML), big data analytics (BDA), cloud computing (CC), and so on. The development of IoT technologies has resulted in a massive quantity of data due to the existence of several people linking through distinct physical components, indicating the status of the CC environment. In the IoT, load scheduling is realistic technique in distinct data center to guarantee the network suitability by falling the computer hardware and software catastrophe and with right utilize of resource. The ideal load balancer improves many factors of Quality of Service (QoS) like resource performance, scalability, response time, error tolerance, and efficiency. The scholar is assumed as load scheduling a vital problem in IoT environment. There are many techniques accessible to load scheduling in IoT environments. With this motivation, this paper presents an improved deer hunting optimization algorithm with Type II fuzzy logic (IDHOA-T2F) model for load scheduling in IoT environment. The goal of the IDHOA-T2F is to diminish the energy utilization of integrated circuit of IoT node and enhance the load scheduling in IoT environments. The IDHOA technique is derived by integrating the concepts of Nelder Mead (NM) with the DHOA. The proposed model also synthesized the T2L based on fuzzy logic (FL) systems to counterbalance the load distribution. The proposed model finds useful to improve the efficiency of IoT system. For validating the enhanced load scheduling performance of the IDHOA-T2F technique, a series of simulations take place to highlight the improved performance. The experimental outcomes demonstrate the capable outcome of the IDHOA-T2F technique over the recent techniques.
Keywords: Load scheduling; internet of things; cloud computing; metaheuristics; fuzzy logic
In recent times, Internet of Things (IoT) was developed as the most important revolution in information and communication technology (ICT) production [1]. By IoT, Internet connections extended over standard smart devices namely smartphone and tablet for different range of devices (machine, vehicle, sensors, and so on.) for accomplishing several distinct applications and services namely health care, medicinal treatment, traffic controller, energy organization, vehicle network, and so on. This generates a massive number of information which require that exists saved, processed, and analyzed for obtaining valuable data for meeting user aim as well as requires [2]. Also, the number and scale of applications and services are improving quickly that needs processing ability which even one of the powerful smart devices could not presently meet. The Cloud environment that is recognized as huge resource center which permits ubiquitous access for sharing as well as providing resources to users flexible with virtualization approach is a potential platform for supporting IoT progresses. Limitations of recent smart devices are minimization by getting time utilization and resource intensive tasks for powerful computing environment namely Cloud computing (CC) but exit the easy task to smart device for handling. But, if relating IoT as well as CC, novel issues appear [3].
An IoT is enormous advantage to their lives, assisting those by relating many sensors and actuators. Besides, relating to many requests to varying devices all simultaneously is a general subject for scholar analyzing the IoT. It could not only interfere with the smooth efficiency of an IoT ecosystems along with lead to load balancing (LB) issues. Researches are thoroughly examined LB in allocated environment and network [4]. The LB is 2 modes: unaware (allocating the request similarly to every server, regardless of its load) and conscious (transmitting the request from worse loaded servers). LB goals at making sure which processor in the model does approximately a similar load of work at all particular times. LB amongst every virtual device is a vital topic in IoT due to many desires and variety of resources. It can be important topic in IoT; it can be helpful if any points are overload, some under-loaded and remainder is idle with no interfering with the effective model [5].
An optimum load balancer improves many factors of Quality of Service (QoS) like resource performance, scalability, response time, error tolerance, and efficiency [6]. It can be need for a non-linear technique for handling this problem as their aim for improving the LB and reducing energy utilization as NPhard problem. An IoT is difficult for wireless gadget/hub interrelating with sending packages for everyone or another gadget/hub, not containing some outline control information for routing. IoT centers are unrestricted amount of schemes and flexibility to different hubs. An important problem in IoT is the secured broadcast from source-destination. At this point, it can be presented LB manner for minimized the energy utilization of combined circuit of IoT node and enhance the LB in IoT platform [7]. Kumar et al. [8] establish a task processing structure which is the decision making ability for selecting the optimum resource at runtime for processing the application (different and difficult nature) at virtual machine (VM) utilizing modified particle swarm optimization (PSO) technique in end-user deadline. The presented technique offers non-dominance group of optimum solutions and enhances different effective parameters (task acceptance ratio, throughput, time, and cost) by sequence of experimentations on distinct synthetic datasets utilizing Cloudsim tool.
This paper presents an improved deer hunting optimization algorithm with Type II fuzzy logic (IDHOA-T2F) model to load scheduling in IoT environments. The goal of the IDHOA-T2F is to diminish the energy utilization of integrated circuit of IoT node and enhance the load scheduling in IoT environments. The IDHOA technique is derived by integrating the concepts of Nelder Mead (NM) with the DHOA. The proposed model also synthesized the T2L based on fuzzy logic (FL) systems to counterbalance the load distribution. The proposed model finds useful to improve the efficiency of IoT systems. For validating the enhanced load scheduling performance of the IDHOA-T2F technique, a series of simulations take place to highlight the improved performance.
The rest of the paper is organized as follows. Section 2 offers the related works, Section 3 provides the proposed model, Section 4 validates the results, and Section 5 concludes the paper.
Ma et al. [9] present the deadline and cost-aware scheduling technique which minimizing the executing cost of progress in deadline constraint from IaaS approach. Assuming the VM efficiency difference and acquisition delay, it can be initial separate tasks as to varying levels based on topological framework so no dependencies exist among tasks at a similar level. In 3 strings are utilized for coding the genes in presented technique for optimum reproduce the heterogeneous and resilient features of cloud environment. Afterward, the heterogeneous earliest finish time (HEFT) was utilized for generating those with minimal completion time as well as cost. Fadlallah et al. [10] planned and validated greedy scheduling and LB techniques for improving the consumption of resources. It can be shown a comparative analysis with longest cloudlet fact processing (LCFP), shortest cloudlet fact processing (SCFP), and Min-Min heuristic techniques. The selection of an individual's 3 techniques was dependent upon the performance and simplicity of its systems, as described in the works, to allocate task to device.
Narman et al. [11] presented dynamic dedicate server scheduling to heterogeneous as well as homogeneous methods for effectively giving wanted service by regarding priorities of requests. Refaat et al. [12] present a novel scheduling approach to control real time and soft service request in Fog methods that are named decentralize load-balance scheduling (DLBS). The projected techniques give decentralization LB control technique. This technique allocates the load depends on kind of service request and load status of all fog nodes. Gawali et al. [13] introduce a heuristic technique which comprises the modified analytic hierarchy process (MAHP), bandwidth aware divisible scheduling (BATS) + BAR optimization, longest expected processing time preemption (LEPT), and divide-and-conquer techniques for performing task scheduling (TS) and resource allocation (RA). During this method, all tasks are managed earlier their actual distribution to cloud resource employing MAHP method. The resource is distributed utilizing the collective BATS + BAR optimization technique that assumes the bandwidth and load of cloud resource as constraint. Wang et al. [14] analyses the feature of IoT request and intend to an enhanced Poisson task method with new approach for predicting the arrivals of IoT requests. It can be present an adaptive energy performance method for adjusting the priority of an optimized objective. Lastly, an energy-efficient VM scheduling technique was presented for maximizing the energy performance of data center.
In Maamari et al. [15], a dynamic adaptive PSO (DAPSO) algorithm was executed for improving the efficiency of basic PSO technique for optimizing the task runtime by minimized the makespan of specific task set, and at once, maximized resource consumption. Therefore, a TS technique is presented for scheduling the independence task on CC. The presented technique was assumed an amalgamation of DAPSO technique and the Cuckoo search (CS) technique is named MDAPSO. Ni et al. [16] presented a 3-layer scheduling method dependent on whale-Gaussian cloud. In the second layer of approach, the whale optimization approach dependent upon Gaussian cloud technique (GCWOAS2) was utilized to multi-objective TS in CC that is for minimizing the completion time of task through efficiently employing the VM resource and for keeping the LB of all VM, decreasing the effective cost of model. In the GCWOAS2 approach, opposition-based learning (OBL) method was initially utilized for initializing the scheduling approach for generating the optimum scheduling method. Though several load scheduling methods are available in the literature, there is still need to explore and improve the scheduling performance on the IoT and cloud environment.
In this study, a new IDHOA-T2F technique has been presented for load scheduling in IoT cloud environment. The IDHOA-T2F technique involves a T2F system with distinct input variables for scheduling load in the IoT cloud environment. Besides, the IDHOA technique is applied to appropriately select the membership functions (MFs) of the T2F system. The IDHOA-T2F technique has established a multi-objective fitness function (FF) dependent upon load balancing (LB) and energy utilization and implemented.
where
The detailed working of these processes is given in the succeeding sections.
Type-2 fuzzy set (T2F) has considered as fuzzy membership operation; i.e., the value of membership (membership degree) of all elements of set is fuzzy set in 0 and 1. The structure of T2F model is shown in Fig. 1. The sets are utilized in conditions where it can be uncertainty on the values of similar membership. Uncertainty is the procedure of either the membership function (MF) or most of their parameter [17]. Assume that transition from normal to fuzzy sets. Therefore, perfectly it can be required for utilizing fuzzy sets type-
In the mathematical way, a T2FS is referred as
where
where
Type-2 MFs: Type-2 fuzzy logic (T2FL) methods were considered as the procedure of its MFs. In 2 varying MFs: (a) a classic type-l MF and (b) a blurred type- 1 MF which signifies the type-2 MF.

Figure 1: Structure of T2F model
The uncertainty in first membership of T2FS
The upper as well as lower MFs, denoted by
Fuzzifier: The MF type-2 offers many degrees of membership to all inputs. So, the uncertainty is further signified. This illustration permits us to taken to account that is unnoticed by type-l. The fuzzifier map the input vector
Rules: The common procedure of
where
Inference Engine: In fuzzy model interval type-2 utilizing the minimal or product
where
Type Reducer: Afterward the rule is fired and inference is applied, the attained T2F system resultant in type-1 fuzzy (T1F) system was calculated. During this part, the accessible techniques for computing the centroid of T2F system utilizing the extension lead rule are discussed. The centroid of T1F system A is provided as:
where n indicates the amount of discretized domains of
Defuzzifier: For getting a crisp output from T1FL system, the type-reduced set is defuzzified. One of the general techniques for finding the centroid of type-reduced set. When the type_reduced set Y implies discretized to n point, at that time the subsequent written offers the centroid of type_reduced set as:
It is calculated the output utilizing the iterative Karnik Mendel Algorithms. So, the defuzzified output of
With
3.2 Design of IDHOA Technique for MF Selection
In order to choose the optimal MFs of the T2FS approach, the IDHOA is derived. A new meta-heuristic DHO technique was presented [18] that is simulated as hunting of deer by a set of hunters. For hunting the deer, the hunter surrounds it and travels near dependent upon any approaches. The approaches contain the concern of different parameters as wind angle, deer place, etc. Co-operation amongst the hunter is another essential condition which creates the hunting effectual. Eventually, it can influence the target dependent upon place of leader and successor. An objective functions of this presented technique is provided in Eq. (16).
The steps for weight optimized utilizing DHO technique are discussed under Because of the different capabilities of deer, it simply escapes from hunting by predators. The technique begins with vector of arbitrary population is named hunters. This procedure is defined as:
where m represents the amount of hunters population (weight) and the entire amount of weight implemented to optimized are signified as X. It can be determined in Eq. (18) [18],
where, the arbitrary number containing range 0 and 1 has signified as a, and the current iteration is signified as J. At this point, θ refers the wind angle. After, the place propagation with successor place
After initializing the optimum place, all weights in population effort to influence which optimum place [19]. Then, the place upgradation model starts by modelling the surrounding performance that is determined in Eq. (19),
where,
where the maximal iteration is signified as
The position angle upgradation has been regarded for increasing the search space. For making the hunting model effectual, it can be important for determining the position angle of hunter. According to position angle, the place upgrade was carried out utilizing in Eq. (22),
where the optimum place has signified as
The separate place was established very opposite to position angle so the prey doesn't take some awareness of hunter.
In the exploration, K vector has been established within the surrounding performance. Primarily, the arbitrary search model was performed regarding the value of K lesser to 1. Eventually, the place upgrade model occurs on the basis of successor position instead of assuming the optimum place. Afterward, the global search is carried out utilizing the Eq. (23),
The place upgraded model was performed for identifying the optimum place (for instance, end condition). The flowchart of the DHOA technique is depicted in Fig. 2.

Figure 2: Flowchart of the DHOA technique
The IDHOA technique is derived by integrating the concepts of Nelder Mead (NM) with the DHOA. In NM simplex search is part of common class of direct search techniques. It can be most famous technique to resolve unconstrained non-linear optimized issues without utilizing derivatives [20–22]. In general, it can be utilized for local optimization. The NM technique tend for minimizing a non-linear scalar function of n variables by utilizing only the estimation of objective functions. Primarily, the NM technique carries out their initial simplex,
This section investigates the performance of the proposed IDHOA-T2F technique under different aspects. A brief total energy consumption analysis of the IDHOA-T2F technique takes place in Tab. 1 and Fig. 3. From the outcomes, it can be demonstrated that the IDHOA-T2F approach has accomplished least TEC over the other techniques. For instance, with 100 resources, the IDHOA-T2F technique has offered a lower TEC of 26J whereas the ACO-PSO, GA, and social spider optimization algorithm (SSOA) techniques have provided a maximum TEC of 76J, 58J, and 34J respectively. In addition, with 150 resources, the IDHOA-T2F approach has existed a minimal TEC of 53J whereas the ACO-PSO, GA, and SSOA methods have given a superior TEC of 65J, 74J, and 63J correspondingly. Likewise, with 250 resources, the IDHOA-T2F technique has accessible a lower TEC of 80J whereas the ACO-PSO, GA, and SSOA methodologies have provided a higher TEC of 203J, 143J, and 96J correspondingly.
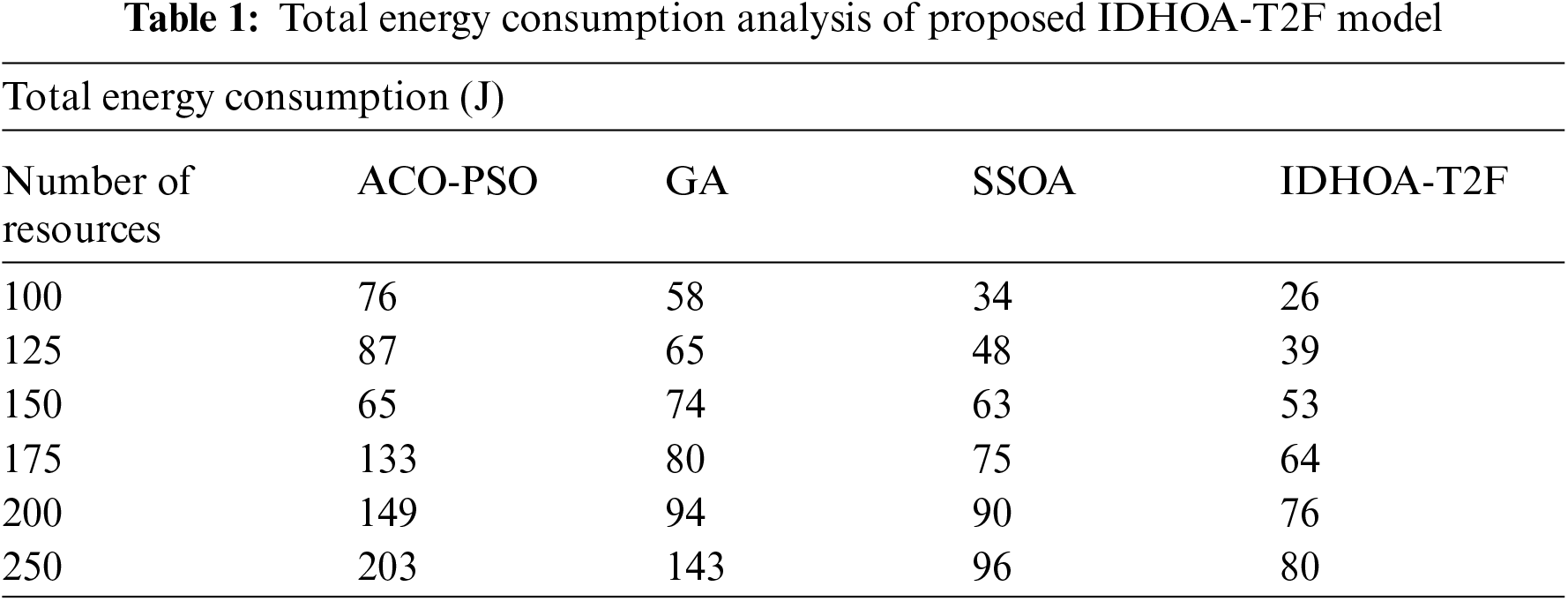

Figure 3: Total energy consumption analysis of IDHOA-T2F model
Tab. 2 and Fig. 4 offer the load balance degree analysis of the IDHOA-T2F technique under varying data sizes. From the obtained values, it is ensured that the IDHOA-T2F technique has resulted in a higher load balance degree compared to other techniques. For instance, with the data size of 100, the IDHOA-T2F technique has resulted in an increased load balance degree with 0.59 whereas the TEENA, MOFA, and SSOA techniques have accomplished a reduced load balance degree of 0.19, 0.42, and 0.52 respectively. In line with, the data size of 300, the IDHOA-T2F approach has resulted in an improved load balance degree of 0.8 whereas the TEENA, MOFA, and SSOA manners have accomplished a minimal load balance degree of 0.45, 0.59, and 0.75 correspondingly. At the same time, with the data size of 500, the IDHOA-T2F method has resulted in a maximum load balance degree of 0.92 whereas the TEENA, MOFA, and SSOA manners have accomplished a lesser load balance degree of 0.65, 0.79, and 0.87 correspondingly.
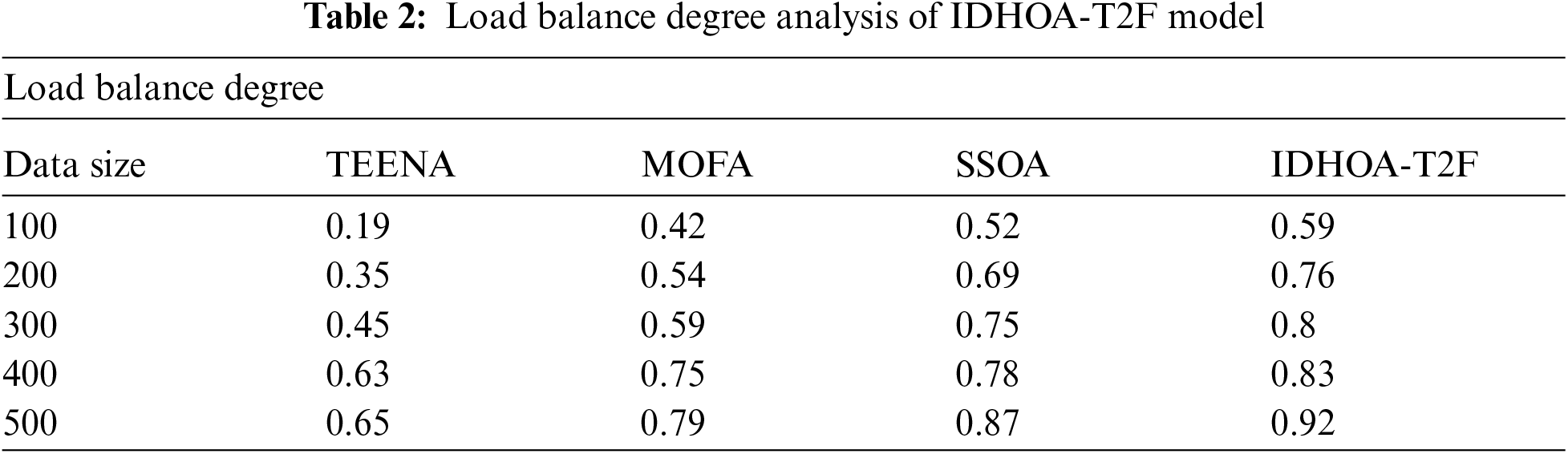

Figure 4: Load balance degree analysis of IDHOA-T2F model
Brief fitness analysis of the IDHOA-T2F technique takes place under different iterations and runs in Tab. 3 and Fig. 5. The IDHOA-T2F technique has resulted in a better fitness value under all iterations. For instance, with iteration 10, the IDHOA-T2F technique has obtained a fitness value of 0.40, 0.38, and 0.37 under three distinct runs 1–3 respectively. Moreover, with iteration 50, the IDHOA-T2F method has reached a fitness value of 0.22, 0.21, and 0.14 under 3 different runs 1–3 correspondingly. Furthermore, with iteration 150, the IDHOA-T2F algorithm has gained a fitness value of 0.17, 0.16, and 0.11 under three varying runs 1–3 respectively. Additionally, with iteration 350, the IDHOA-T2F method has obtained a fitness value of 0.15, 0.13, and 0.10 under three various runs 1–3 correspondingly. In the same way, with iteration 550, the IDHOA-T2F methodology has attained a fitness value of 0.14, 0.12, and 0.10 under 3 distinct runs 1–3 respectively. At last, with iteration 850, the IDHOA-T2F approach has achieved a fitness value of 0.13, 0.12, and 0.10 under three distinct runs 1–3 correspondingly.
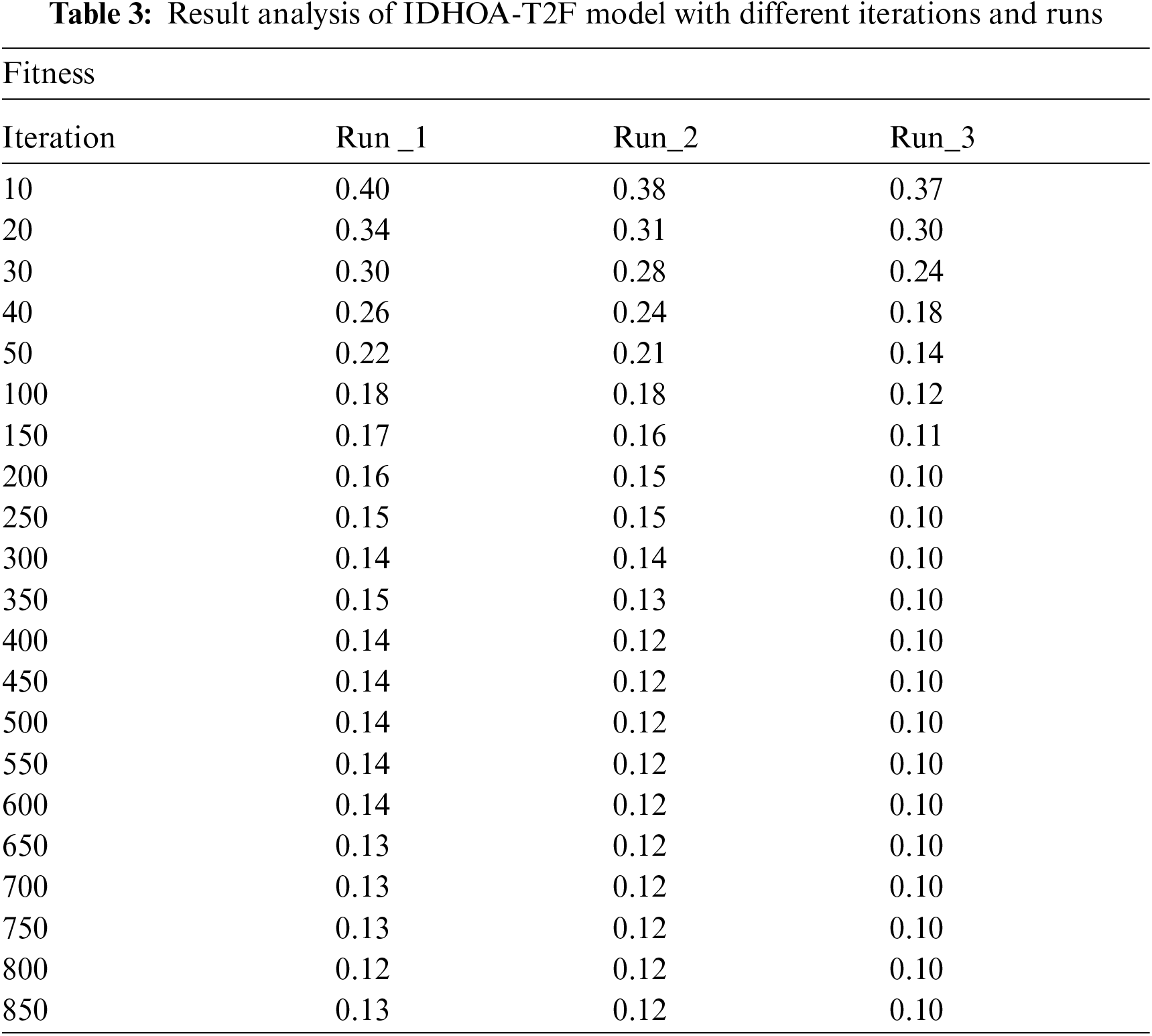

Figure 5: Result analysis of IDHOA-T2F model with different runs
For ensuring the improved performance of IDHOA-T2F technique, a comparison study is made in Tab. 4 and Fig. 6. The experimental outcomes stated that the IDHOA-T2F approach has accomplished superior performance over the SSOA technique. For instance, with 10 iterations, the IDHOA-T2F technique has attained a lower fitness function of 0.37 whereas the SSOA has obtained an increased fitness value of 0.40. In addition, with 100 iterations, the IDHOA-T2F method has reached a lesser fitness function of 0.12 whereas the SSOA has attained a maximum fitness value of 0.23. Similarly, with 350 iterations, the IDHOA-T2F algorithm has gained a lesser fitness function of 0.10 whereas the SSOA has obtained an improved fitness value of 0.19. Moreover, with 500 iterations, the IDHOA-T2F methodology has attained a minimal fitness function of 0.10 whereas the SSOA has obtained an enhanced fitness value of 0.19. Furthermore, with 700 iterations, the IDHOA-T2F technique has obtained a lower fitness function of 0.10 whereas the SSOA has reached a superior fitness value of 0.19. At last, with 850 iterations, the IDHOA-T2F technique has obtained the least fitness function of 0.10 whereas the SSOA has gained an improved fitness value of 0.19. The experimental outcomes demonstrate the promising outcome of IDHOA-T2F technique over the recent techniques due to the inclusion of T2F and IDHOA.


Figure 6: Comparative analysis of IDHOA-T2F model with distinct iterations
In this study, a new IDHOA-T2F technique has been presented for load scheduling in IoT cloud environment. The IDHOA-T2F technique involves a T2F system with distinct input variables for scheduling load in the IoT cloud environment. Besides, the IDHOA technique is applied to appropriately select the MFs of the T2F system. The proposed model finds useful to improve the efficiency of IoT models. For validating the enhanced load scheduling efficiency of the IDHOA-T2F technique, a series of simulations take place to highlight the improved performance. The experimental outcomes demonstrate the promising outcome of IDHOA-T2F technique over the recent techniques. In future, the outcome of the IDHOA-T2F technique is extended to the design of context aware route planning in the IoT cloud platform.
Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work under grant number (RGP 2/209/42). This research was funded by the Deanship of Scientific Research at Princess Nourah bint Abdulrahman University through the Fast-Track Path of Research Funding Program.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. X. Rui, J. Wu, J. Zhao and M. S. Khamesinia, “Load balancing in the internet of things using fuzzy logic and shark smell optimization algorithm,” Circuit World, vol. 47, pp. 335–344, 2020. [Google Scholar]
2. K. Shankar, E. Perumal, M. Elhoseny and P. Thanh Nguyen, “An iot-cloud based intelligent computer-aided diagnosis of diabetic retinopathy stage classification using deep learning approach,” Computers, Materials & Continua, vol. 66, no. 2, pp. 1665–1680, 2021. [Google Scholar]
3. V. Porkodi, A. R. Singh, A. R. W. Sait, K. Shankar, E. Yang et al., “Resource provisioning for cyber–physical–social system in cloud-fog-edge computing using optimal flower pollination algorithm,” IEEE Access, vol. 8, pp. 105311–105319, 2020. [Google Scholar]
4. Z. Ghanbari, N. J. Navimipour, M. Hosseinzadeh and A. Darwesh, “Resource allocation mechanisms and approaches on the internet of things,” Cluster Computing, vol. 22, no. 4, pp. 1253–1282, 2019. [Google Scholar]
5. N. Krishnaraj, M. Elhoseny, E. L. Lydia, K. Shankar and O. ALDabbas, “An efficient RADIX TRIE -based semantic visual indexing model for large-scale image retrieval in cloud environment,” Software: Practice and Experience, vol. 51, no. 3, pp. 489–502, 2021. [Google Scholar]
6. A. F. S. Devaraj, M. Elhoseny, S. Dhanasekaran, E. L. Lydia and K. Shankar, “Hybridization of firefly and improved multi-objective particle swarm optimization algorithm for energy efficient load balancing in cloud computing environments,” Journal of Parallel and Distributed Computing, vol. 142, pp. 36–45, 2020. [Google Scholar]
7. M. Hnatiuc, O. Geman, A. G. Avram, D. Gupta and K. Shankar, “Human signature identification using iot technology and gait recognition,” Electronics, vol. 10, no. 7, pp. 852, 2021. [Google Scholar]
8. M. Kumar and S. C. Sharma, “PSO-Based novel resource scheduling technique to improve QoS parameters in cloud computing,” Neural Computing and Applications, vol. 32, no. 16, pp. 12103–12126, 2020. [Google Scholar]
9. X. Ma, H. Gao, H. Xu and M. Bian, “An iot-based task scheduling optimization scheme considering the deadline and cost-aware scientific workflow for cloud computing,” EURASIP Journal on Wireless Communications and Networking, vol. 2019, no. 1, pp. 249, 2019. [Google Scholar]
10. G. Fadlallah, D. Rebaine and H. Mcheick, “A greedy scheduling approach for peripheral mobile intelligent systems,” IoT, vol. 2, no. 2, pp. 249–274, 2021. [Google Scholar]
11. H. S. Narman, M. S. Hossain, M. Atiquzzaman and H. Shen, “Scheduling internet of things applications in cloud computing,” Annals of Telecommunication, vol. 72, no. 1–2, pp. 79–93, 2017. [Google Scholar]
12. H. E. Refaat and M. A. Mead, “DLBS: Decentralize load-balance scheduling algorithm for real-time iot services in mist computing,” International Journal of Advanced Computer Science and Applications, vol. 10, no. 9, pp. 92–100, 2019. [Google Scholar]
13. M. B. Gawali and S. K. Shinde, “Task scheduling and resource allocation in cloud computing using a heuristic approach,” Journal of Cloud Computing, vol. 7, no. 1, pp. 4, 2018. [Google Scholar]
14. B. Wang and F. Liu, “Task arrival based energy efficient optimization in smart-IoT data center,” Mathematical Biosciences and Engineering, vol. 18, no. 3, pp. 2713–2732, 2021. [Google Scholar]
15. A. A. Maamari and F. A. Omara, “Task scheduling using pso algorithm in cloud computing environments,” International Journal of Grid Distribution Computing, vol. 8, no. 5, pp. 245–256, 2015. [Google Scholar]
16. L. Ni, X. Sun, X. Li and J. Zhang, “GCWOAS2: Multiobjective task scheduling strategy based on Gaussian cloud-whale optimization in cloud computing,” Computational Intelligence and Neuroscience, vol. 2021, pp. 1–17, 2021. [Google Scholar]
17. H. A. Hagras, “A hierarchical type-2 fuzzy logic control architecture for autonomous mobile robots,” IEEE Transactions on Fuzzy Systems, vol. 12, no. 4, pp. 524–539, 2004. [Google Scholar]
18. G. Brammya, S. Praveena, N. N. Preetha, R. Ramya, B. Rajakumar et al., “Deer hunting optimization algorithm: A new nature-inspired meta-heuristic paradigm,” The Computer Journal, vol. bxy133, pp. 1–20, 2019. https://doi.org/10.1093/comjnl/bxy133. [Google Scholar]
19. G. Agarwal and H. Om, “Performance of deer hunting optimization based deep learning algorithm for speech emotion recognition,” Multimedia Tools and Applications, vol. 80, no. 7, pp. 9961–9992, 2021. [Google Scholar]
20. M. J. Blondin, J. Sanchis, P. Sicard and J. M. Herrero, “New optimal controller tuning method for an avr system using a simplified ant colony optimization with a new constrained nelder–mead algorithm,” Applied Soft Computing, vol. 62, pp. 216–229, 2018. [Google Scholar]
21. A. Baby and J. S. Raj, “An efficient load balancing using Bee foraging technique with random stealing,” IOSR Journal of Computer Engineering (IOSR-JCE), vol. 17, no. 2, pp. 97–104, 2015. [Google Scholar]
22. J. S. Raj, K. S. Hridya and V. Vasudevan, “Augmenting hierarchical load balancing with intelligence in grid environment,” International Journal of Grid and Distributed Computing, vol. 5, no. 2, pp. 9–18, 2012. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |