Computers, Materials & Continua DOI:10.32604/cmc.2022.022291
Article

A Zero-Watermark Scheme Based on Quaternion Generalized Fourier Descriptor for Multiple Images

Baowei Wang1,2,3,*, Weishen Wang1, Peng Zhao1 and Naixue Xiong4

1School of Computer Science, Nanjing University of Information Science and Technology, Nanjing, 210044, China
2Jiangsu Collaborative Innovation Center of Atmospheric Environment and Equipment Technology (CICAEET), Nanjing, 210044, China
3Engineering Research Center of Digital Forensics, Ministry of Education, Nanjing, 210044, China
4Department of Mathematics and Computer Science, Northeastern State University, Tahlequah, OK, 74464, USA
*Corresponding Author: Baowei Wang. Email: wang@nuist.edu.cn
Received: 03 August 2021; Accepted: 16 September 2021

Abstract: Most of the existing zero-watermark schemes for medical images are only appropriate for a single grayscale image. When they protect a large number of medical images, repeating operations will cause a significant amount of time and storage costs. Hence, this paper proposes an efficient zero-watermark scheme for multiple color medical images based on quaternion generalized Fourier descriptor (QGFD). Firstly, QGFD is utilized to compute the feature invariants of each color image, then the representative features of each image are selected, stacked, and reshaped to generate a feature matrix, which is then binarized to get a binary feature image. Copyright information can be converted into the copyright image by using QR code technology, which contains more information. Finally, the zero-watermark image is constructed by executing the XOR operation on the copyright image and the feature image scrambled by the Cat map. In the experiment, different parameters are selected to determine the maximum number of images that the proposed scheme can protect simultaneously while achieving good robustness. The experimental results demonstrate that the proposed scheme can effectively resist common attacks, geometric attacks and joint attacks, and effectively improve the operation efficiency of the algorithm, thus effectively decreasing the time and storage cost of copyright protection for lots of medical images.

Keywords: Copyright protection; color medical image; zero-watermark; QGFD

1  Introduction

With the development of multimedia technology and information processing technology, digitization has become an important means of information sharing and transmission, and it is widely used in many fields. In recent years, the rapid application of digitization in the medical field has benefited from the development of medical imaging technology and equipment, as well as the urgent need for hospital information construction. The medical images obtained by medical imaging equipment, such as CT images, ultrasound images, X-ray images, and fundus color images, can provide an important reference basis for clinical diagnosis and scientific research, and promote the convenience and development of remote consultation and remote cooperation. However, the content of medical images contains the patient's personal and medical information. Once these images are intercepted and stolen during the process of shared transmission and local storage, this will lead to information security issues such as infringement of patient privacy and leakage of medical data. Therefore, how to effectively avoid these security problems has become an urgent need. In recent years, mature digital watermark technology [1–8] that integrates knowledge from multiple parties has been widely used in fields such as copyright certification protection and digital content forensics. It modifies the image data to embed watermark information that is invisible to the naked eye, and realize the ownership protection and traceability of the image. However, medical images are an important basis for the diagnosis of patients, and no modification is allowed on them, so as not to affect the quality and integrity of the images. Therefore, how to protect medical images non-destructively has become the key to research.

In 2001, Wen et al. [9] put forward the concept of zero-watermark for the first time, which effectively avoids the problem that image quality is affected by the traditional method of modifying image data. As a lossless watermark technology, zero-watermark is more suitable for the protection of medical images and can effectively guarantee the integrity and quality of the images. Since the introduction of zero-watermark, many scholars have devoted themselves to the research of zero-watermark technology, and have achieved many excellent scientific research results. However, most zero-watermark algorithms [10–15] are only applicable to a single image. As the number of images that need to be protected increases, the repetitive operation of these algorithms will bring higher time and storage costs. In recent years, the emergence of zero-watermark algorithms [16–18] for multiple images can protect two or three or more images simultaneously, but these algorithms essentially group grayscale images for protection. When the number of images that need to be protected increases sharply, like the zero-watermark algorithm for a single image, these algorithms will also cause higher time and storage costs, and reduce the efficiency of the algorithm.

To the above problems, this paper proposes an efficient zero-watermark scheme for multiple color medical images. Firstly, QGFD is used to calculate the feature invariants of each image. Because the invariants obtained by QGFD have better stability, the algorithm has strong robustness. Then, the main representative features of each image are selected, stacked, reshaped, and formed into a feature matrix, and then the binary feature image can be obtained by binarization according to the mean of the elements of the feature matrix. Integrating the features of multiple images into a matrix effectively improves the efficiency of the algorithm and saves the cost of storage space during copyright protection. The QR code technology is introduced to convert copyright information into copyright images so that it contains more copyright information. Finally, Cat map is used to scramble the copyright image and the feature image, and the XOR operation is performed on the scrambled two images to get the zero-watermark image. The use of Cat map enhances the security of the proposed scheme. The experimental results show that the proposed scheme using QGFD has strong robustness in dealing with various attacks, and can effectively reduce the time and storage cost of a large number of medical image protection, and improve the execution efficiency of the algorithm.

The rest of the paper is organized as follows: Section 2 summarizes the main related work of zero-watermark; Section 3 introduces related background knowledge principles; Section 4 presents the proposed zero-watermark scheme; Section 5 demonstrates and analyzes the performance of the proposed scheme; Section 6 summarizes the work of the paper.

2  Related Work

In 2001, Wen et al. [9] proposed the concept of zero-watermark. Each image has feature information that is different from other images, which can be used to construct a zero-watermark without modifying the data. They apply the discrete cosine transform (DCT) to the image to obtain the robust features of the image and build the zero-watermark image based on them. Their method overcomes the problem that the traditional watermark algorithm is difficult to resist the statistical attack and verifies the feasibility of the proposed zero-watermark algorithm. Subsequently, Wen et al. [19] proposed a zero-watermark method based on high-order cumulants, which has achieved good performance in dealing with noise attacks and small-angle rotation attacks. Chen et al. [20] proposed an image copyright protection scheme based on the wavelet domain. It uses the low-frequency component of the image obtained by the wavelet transform to construct the feature matrix and carries out the digital signature according to the security parameters. Finally, it is saved to the third-party certification body and adds the time stamp according to the date and time. This scheme can effectively resist common image processing attacks and geometric attacks, and has strong robustness. Chang et al. [21] innovatively paid attention to the edge features of the image and used Sobel technology to extract features. This is a relatively novel method, and the robustness of the method can be enhanced by adjusting the strength of the watermark. Tsai et al. [22] proposed a lossless image watermark scheme based on α-trimmed mean algorithm and support vector machine (SVM). The scheme trains SVM to record the relationship between image feature information and watermark, and uses the trained SVM to recover the watermark to confirm the ownership of copyright. The α-trimmed mean algorithm can effectively reduce the influence of noise and improve the robustness of the algorithm. Subsequently, Tsai et al. [23] obtained image feature invariants based on discrete Fourier transform (DFT) and SVM, and the optimal parameters were determined by particle swarm optimization (PSO) algorithm, thus to some extent making up for the shortcomings of some algorithms in dealing with geometric attacks.

Shao et al. [16] proposed a watermark algorithm based on orthogonal Fourier-Mellin moments (OFMM) and chaotic mapping, which mapped two images into the real and imaginary parts of the complex number respectively to obtain a whole structure and then calculated the invariants of the OFMM. Experimental results show that the proposed algorithm has good robustness and can reduce the storage space. Subsequently, Shao et al. [24] applied quaternion moment to the image watermark algorithm. The quaternion can make full use of the color information of the image to construct the watermark by its excellent characteristics. They also demonstrated the robustness and feasibility of quaternion moments such as quaternion Fourier-Melin moments (QFMMs) and quaternion Zernike moments (QZMs) through experiments. Aiming at the problem that existing algorithms only target grayscale images and are difficult to effectively resist geometric attacks, Wang et al. [25] proposed a zero-watermark algorithm based on quaternion exponential moments. This algorithm calculates the quaternion exponential moments of color images and constructs the feature image based on it. Finally, the XOR operation is performed on the feature image and the logo image to get the zero-watermark image. Experiments show that the proposed algorithm has certain robustness in resisting geometric attacks. Wang et al. [14] adopted the polar complex exponential transform (PCET) to compute the coefficients of the image, combined with logical mapping to randomly select the coefficients used to construct the features, and created the feature image based on these coefficients. Like most methods, they also utilize the XOR operation to combine the logo image and the feature image to get a zero-watermark. The attacks test demonstrates that it has a certain degree of robustness and ensures the security of the algorithm. Xia et al. [12] used the quaternion polar harmonic transformation (QPHT) to calculate the image coefficients, and selected more accurate coefficients according to certain rules and constructed a zero-watermark based on these robust coefficients. They describe how the accuracy coefficients are selected, and the presented experimental results also show that the proposed scheme is robust against some attacks. Jiang et al. [26] proposed a color image zero-watermark algorithm based on tensor mode expansion. The algorithm divides an image into four images of R, G, B component and grayscale, and then combines them into two three-dimensional tensors, and then performs tensor mode expansion on the combined tensor, and finally uses singular value decomposition and DCT processes the expanded data to obtain the feature image of the color image. Aiming at the inaccuracy and inefficiency of the existing calculation methods based on moments, Yang et al. [27] creatively combined the fast quaternion generic polar complex exponential transformation (FQGPCET) to obtain the image moments. The image moments calculated by this transformation have good stability and distinguishability. The experimental results also show that the moments obtained by the proposed method have certain robustness and have good time complexity. Wang et al. [28] extended the generalized orthogonal Fourier-Mellin moments (GOFMMs) suitable for grayscale images to the field of color image processing, namely quaternion GOFMMs. They use the polar coordinate pixel stitching method to calculate the GOFMMs, and use all the four-dimensional features of the accurate quaternion GOFMMs of the color image to construct feature information, thereby generating a zero-watermark image. Wang et al. [18] used PCET to calculate the amplitude of each image, and compared the amplitude of the same position of each image to construct all features, thereby eliminating the correlation between different images and improving the discrimination. The experimental results show that this method achieves certain robustness and makes the constructed zero-watermark have a certain degree of discrimination.

3  Relevant Knowledge

3.1 Quaternion Description of Color Images

The knowledge of quaternion theory was first proposed by Hamilton [29] in 1843, but it was not applied to specific scenarios. Sangwine [30] took the lead in applying it to color images and proved the feasibility of quaternion theory in 1996. Similar to a complex number having one real part and one imaginary part, a quaternion contains one real part and three imaginary parts, as shown in Eq. (1).

q=a+bi+cj+dk#(1)

where, q represents a quaternion, a,b,c,d represent real numbers, i,j,k are imaginary units. Similar to the complex number, the conjugate and magnitude of the quaternion q are q¯=a−bi−cj−dk and |q|=a2+b2+c2+d2 respectively. If a=0, q is a pure quaternion, and if |q|=1, q is a unit pure quaternion. The relationship between the quaternion imaginary units is similar to the relationship between the complex imaginary units, as shown in Eq. (2).

{i2=j2=k2=ijk=−1ij=−ji=k,jk=−kj=i,ki=−ik=j#(2)

According to the relationship between imaginary units shown in Eq. (2), it can be known that q1⋅q2≠q2⋅q1, that is, the multiplication of quaternion does not follow the commutative law. However, this does not affect the overall description of a color image f(x,y) by a pure quaternion, as shown in Eq. (3).

f(x,y)=fR(x,y)i+fG(x,y)j+fB(x,y)k#(3)

where, fR(x,y),fG(x,y), and fB(x,y) are respectively the three-color components of the color image: Red, Green, and Blue. Obviously, the color image processing based on quaternion can reflect the integrity of the color image, and can keep the color information of the color image well, and can really treat the color image as a vector whole.

3.2 Quaternion Generic Fourier Descriptor

Let f(r,θ) be an RGB color image in polar coordinates. Since the quaternion multiplication does not satisfy the commutative law, then the quaternion polar Fourier transform (QPFT) of f(r,θ) has two forms, that is, the left QPFT and the right QPFT [31], as show in Eqs. (4) and (5).

QFR,TL(ρ,ϕ)=∑r⁡∑n⁡exp[μ2π((r/R)ρ+(2πn/T)ϕ)]f(r,θn)#(4)

QFR,TR(ρ,ϕ)=∑r⁡∑n⁡f(r,θn)exp⁡[μ2π((r/R)ρ+(2πn/T)ϕ)]#(5)

where, R represents the radial frequency and T represents angular frequency. 0≤r<R, 0≤n<T, 0≤ρ<R,0≤ϕ<T, θn=n×(2π/T). Unit pure quaternion μ=(i+j+k)/3. The QPFT mentioned in this paper refers to the left form.

Since the conjugate of two quaternions q1 and q2 satisfies q1⋅q2¯=q2¯⋅q1¯, the left and right QPFT of the same color image can be derived from each other, as shown in Eq. (6).

QFR,TL(ρ,ϕ)=∑r⁡∑n⁡exp[μ2π((r/R)ρ+(2πn/T)ϕ)]f(r,θn)=∑r⁡∑n⁡f(r,θn)¯exp[−μ2π((r/R)ρ+(2πn/T)ϕ)]¯=−∑r⁡∑n⁡f(r,θn)exp[−μ2π((r/R)ρ+(2πn/T)ϕ)]¯=−QFR,TR(−ρ,−ϕ)¯ #(6)

Similar to the idea of general Fourier transform [32], the steps of QPFT are as follows: Firstly, the image in polar space is transformed into a two-dimensional rectangular image in Cartesian space, then the two-dimensional quaternion discrete Fourier transform is applied to it, finally the coefficients of the quaternion polar Fourier transform can be achieved. Quaternion generalized polar Fourier descriptor, as shown in Eq. (7).

QD={∥QF(0,0)∥,∥QF(0,1)∥,…,∥QF(0,T)∥,…,∥QF(R,0)∥,…,∥QF(R,T)∥} #(7)

The coefficient matrix obtained after QGFD has a certain law, that is, coefficients with high energy values are mainly distributed in the upper left corner of the coefficient matrix. It has a strong energy gathering effect and is particularly suitable for constructing robust features, as shown in Fig. 1. The invariance of the QGFD has been expounded and proved in the paper [31]. The rotation attack on the original image will transform into the translation of the polar coordinate image, and the periodicity shows that QGFD is invariant to rotation. The translation is invariable by moving the origin of coordinates to the centroid, and the zero-order geometric moment is normalized to obtain the scaling invariance of the image by adjusting the size of the image.

Figure 1: Spectral distribution diagram with zero frequency component shifted to the center: (a) Flat view, (b) Three-dimensional view

4  Proposed Scheme

The proposed scheme aims to protect as many images as possible simultaneously while being efficient and cost-saving. Therefore, assuming that the fixed size of the feature matrix is N×N, select the first f feature of each image as the representation vector, and the maximum number of images that can be protected simultaneously can be obtained as Q=(N×N)/f. The proposed scheme consists of a zero-watermark generation part and a verification part. In the zero-watermark generation part, the invariant feature matrix of each color image is firstly calculated by using QGFD, and then the first f features are selected as the representations of each image. Then, the representations of each image are connected end to end to form the principal eigenvector, which is reconstructed into the feature matrix. Then the binary feature image can be obtained by binarization of the feature matrix. Finally, the scrambled QR code image and scrambled feature image are performed XOR operation to generate a zero-watermark image. The zero-watermark verification part is similar to the generation part in feature extraction, but the main difference is that the copyright image (QR code) is obtained by XOR operation between scrambled feature image and zero-watermark image.

4.1 Zero-Watermark Generation

The key to the process of zero-watermark generation is to make full use of the feature information of the image to construct a robust feature matrix, to obtain the zero-watermark image, and save it in the Intellectual Property Protection (IPR) agency. The generation process of zero-watermark is shown in Fig. 2. Detailed steps are described as follows:

Step 1: Set the radial frequency R=m and angular frequency T=n, calculate the invariant features of each image (Oi,i=1,2,…,Q) by using QGFD, then the description matrix of each image with the size of m×n can be obtained, and the first f features are selected as the characterization vector V={vi∣i=1,2,…,f} of each image;

Step 2: The features of these images are stacked as the main feature vector P={Vi∣i=1,2,…,Q}, which is remodeled into a feature matrix B of size N×N. If it is insufficient, zero is filled to fill the matrix.

Step 3: The mean ave of the elements in the feature matrix B is calculated, and the feature matrix is binarized according to the mean by Eq. (8). If the value of the elements in the matrix is greater than or equal to the mean ave, take 1; otherwise, take 0, then the binary feature image F can be obtained.

Fij={1, Bij≥ave0, Bij<ave,i,j=1,2,…,N.#(8)

Step 4: The copyright information provided by the copyright owner is converted into the copyright image C by using QR code technology. The feature image F and the copyright image C are scrambled by Cat map, and the scrambling parameter is used as the Key for copyright verification, which is saved by the copyright owner.

Step 5: A zero-watermark image W is able to be acquired by performing the XOR manipulation on the scrambled feature image F′ and the copyright image C′ by Eq. (9), which is saved to the trusted third party IPR agency as the basis for copyright verification.

Fij′⊕Cij′=Wij,i,j=1,2,…,N.#(9)

4.2 Zero-Watermark Verification

The key to the zero-watermark verification process is to recover the copyrighted image according to the key provided by the copyright owner, to determine the ownership of multiple images to be verified. The verification process of zero-watermark is shown in Fig. 3. Detailed steps are described as follows:

Step 1: The values of R and T set in the generation stage are used as the basis to calculate the invariant features of each image (O^i,i=1,2,…,Q) to be verified by using QGFD. Then the description matrix of each image to be verified with the size of m×n can be obtained, and the first f features are selected as the characterization vector V^={v^i∣i=1,2,…,f} of each image;

Step 2: The features of these images are stacked as the principal eigenvector P^={V^i∣i=1,2,…,Q}, which is remodeled into a feature matrix B^ of size N×N. If it is insufficient, zero is filled to fill the matrix.

Step 3: The mean ave^ of the elements in the feature matrix B^ is calculated, and the feature matrix is binarized according to the mean by Eq. (10). If the value of the elements in the matrix is greater than or equal to the mean ave^, take 1; otherwise, take 0, then the binary feature image F^ can be obtained.

F^ij={1, B^ij≥ave^0, B^ij<ave^,i,j=1,2,…,N.#(10)

Step 4: According to the Key provided by the copyright owner, the feature image F^ obtained is scrambled by Cat map, and the XOR operation is performed on the zero-watermark image W saved by IPR and the scrambled feature image F^′, then the disordered image C^′ can be obtained by Eq. (11).

Wij⊕F^ij′=C^ij′, i,j=1,2,…,N.#(11)

Step 5: Then Cat map is used to reverse scramble the disordered image C^′, and the meaningful copyright image C^ can be recovered. Then compare the similarity between the recovered copyright image C^ and the copyright image C saved by the copyright owner. If the ratio is greater than or equal to the set threshold, the copyright verification is successful; otherwise, it fails.

Figure 2: Schematic diagram of the multiple color medical images zero-watermark generation

Figure 3: Schematic diagram of the multiple color medical images zero-watermark verification

5  Experiments and Results

In this section, we conduct an attack test on the proposed scheme, and demonstrate the robustness of the scheme, and analyze the experimental results. We also determine the optimal parameters, and compare our scheme with other excellent schemes, and finally analyze the security proposed scheme. The color fundus images in the ODIR-5K data set [33] are chosen as the experimental images, and six of the images in the data set are shown in Fig. 4. In the experiment, we set the fixed size of the feature matrix to 64×64, and take different values for the number of features f, the radial frequency R, and the angular frequency T. Under the premise of ensuring good robustness, the proposed scheme is sought to protect the maximum number of images simultaneously, thereby reducing the time and storage costs, and improving the efficiency of copyright protection.

5.1 Robust Performance Against Various Attacks

In this paper, we use the normalized correlation (NC) [34] value to evaluate the robustness of the proposed scheme, and the calculation formula is shown in Eq. (12).

NC(W,W^)=∑i⁡∑j⁡W(i,j)W^(i,j)∑i⁡∑j⁡W(i,j)2∑i⁡∑j⁡W^(i,j)2#(12)

where W and W^ represent the original copyright image and the recovered copyright image respectively. To find the optimal parameters, we set invariants and variations, and assign different values to f, R, and T. To test and demonstrate the robustness of the proposed scheme against various attacks, we select attacks such as noise, JPEG compression, and mosaic as common attacks. The parameter of Gaussian noise is the mean, and the variance is set to the default value of 0.01 in the experiment. Geometric attacks include such as rotation, scaling, translation, and mirroring. Several attacks from common attacks and geometric attacks are randomly selected to form a joint attack.

Figure 4: Six color fundus images in the ODIR-5K dataset

(1)   Set f = 8, that is, the value of f remains unchanged, adjust the values of R and T, and test the robustness of the algorithm.

The experimental results show that the proposed algorithm can deal with most of the attacks in common, geometric, and joint attacks, and has good robustness, as shown in Tabs. 1 and 2. When dealing with image compression attacks and joint attacks (bold content), the algorithm's robustness against these two attacks also increases as the values of R and T increase. When (R,T)=(87,97), the robustness of the algorithm has achieved good results, as shown in Fig. 5. As the cropping ratio increases, the robustness of the proposed algorithm shows a downward trend, but it still maintains good robustness, as shown in Tab. 2.

(2)   Set R = 50 and T = 60, adjust the value of f and test the robustness of the algorithm.

Experimental results show that the algorithm can still resist most attacks by giving different values of f, as shown in Tabs. 3 and 4. However, when dealing with image compression, mosaic and joint attack (bold content) attacks, the robustness of the algorithm is not ideal. Especially when f is less than 13, the algorithm performance is average. However, as the value of f increases, the ability of the algorithm to deal with the above attacks is also enhanced, as shown in Fig. 6.

(3)   Set f, R, and T all increase simultaneously to test the robustness of the algorithm.

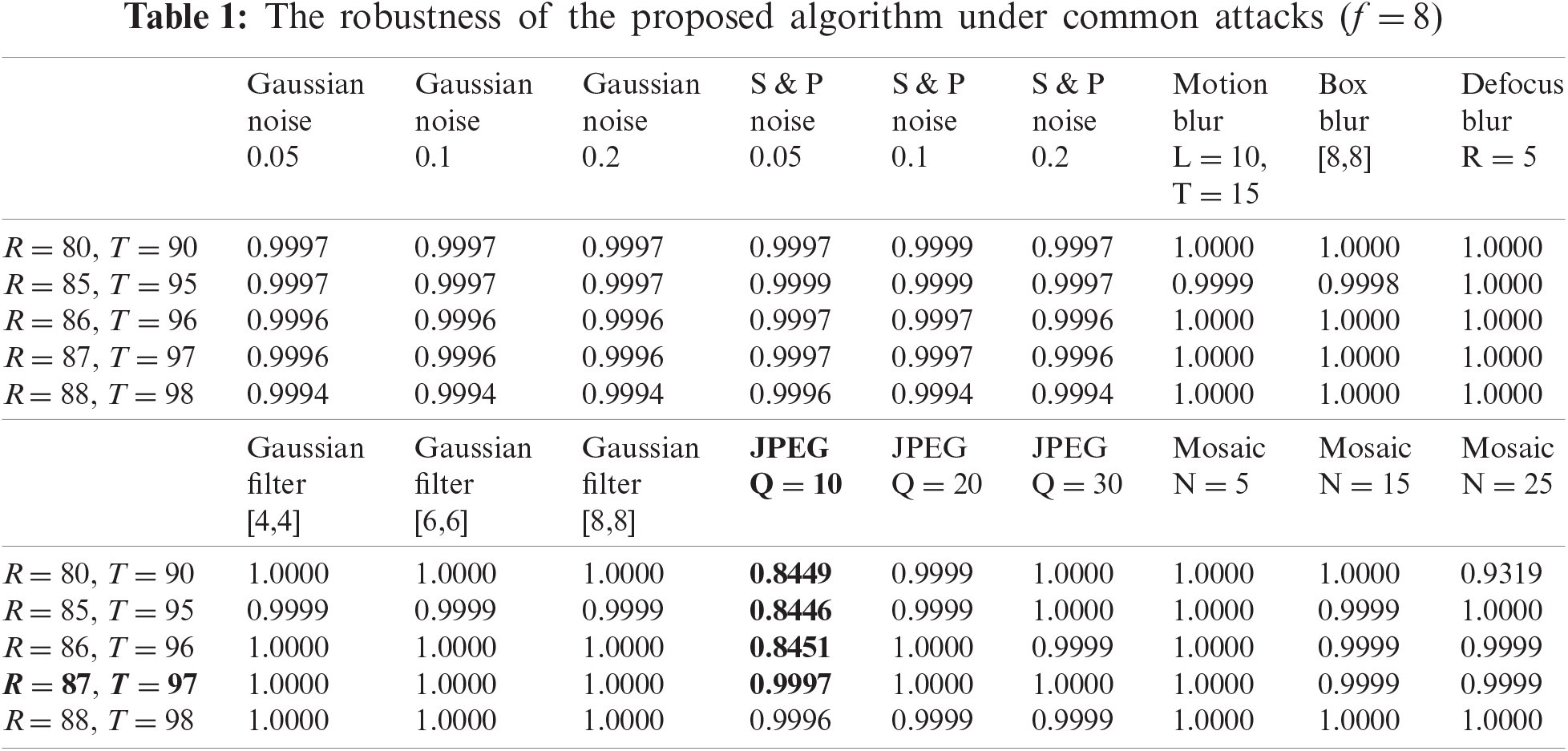
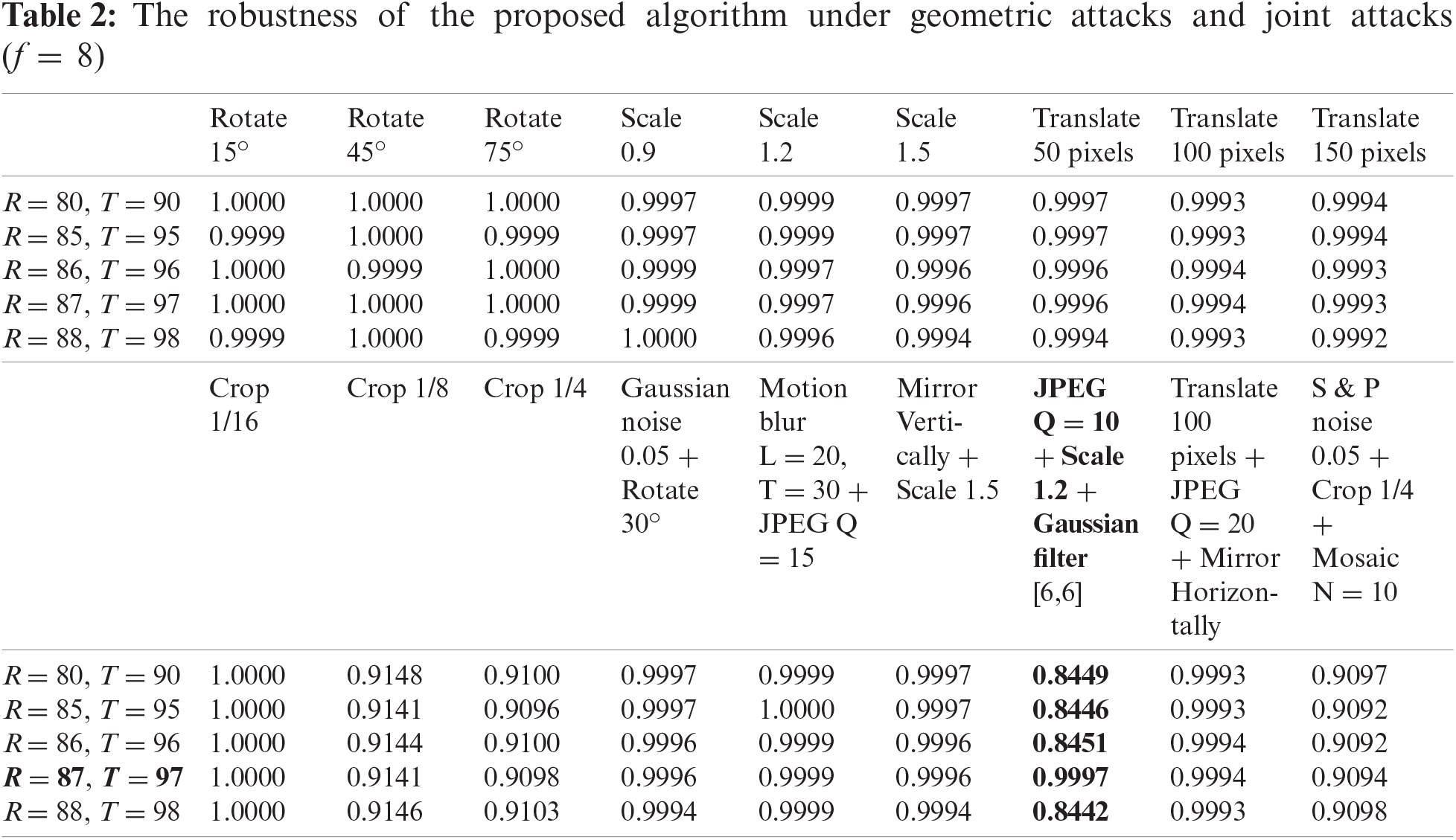
Figure 5: The robustness to JPEG attack and joint attack varies with parameters

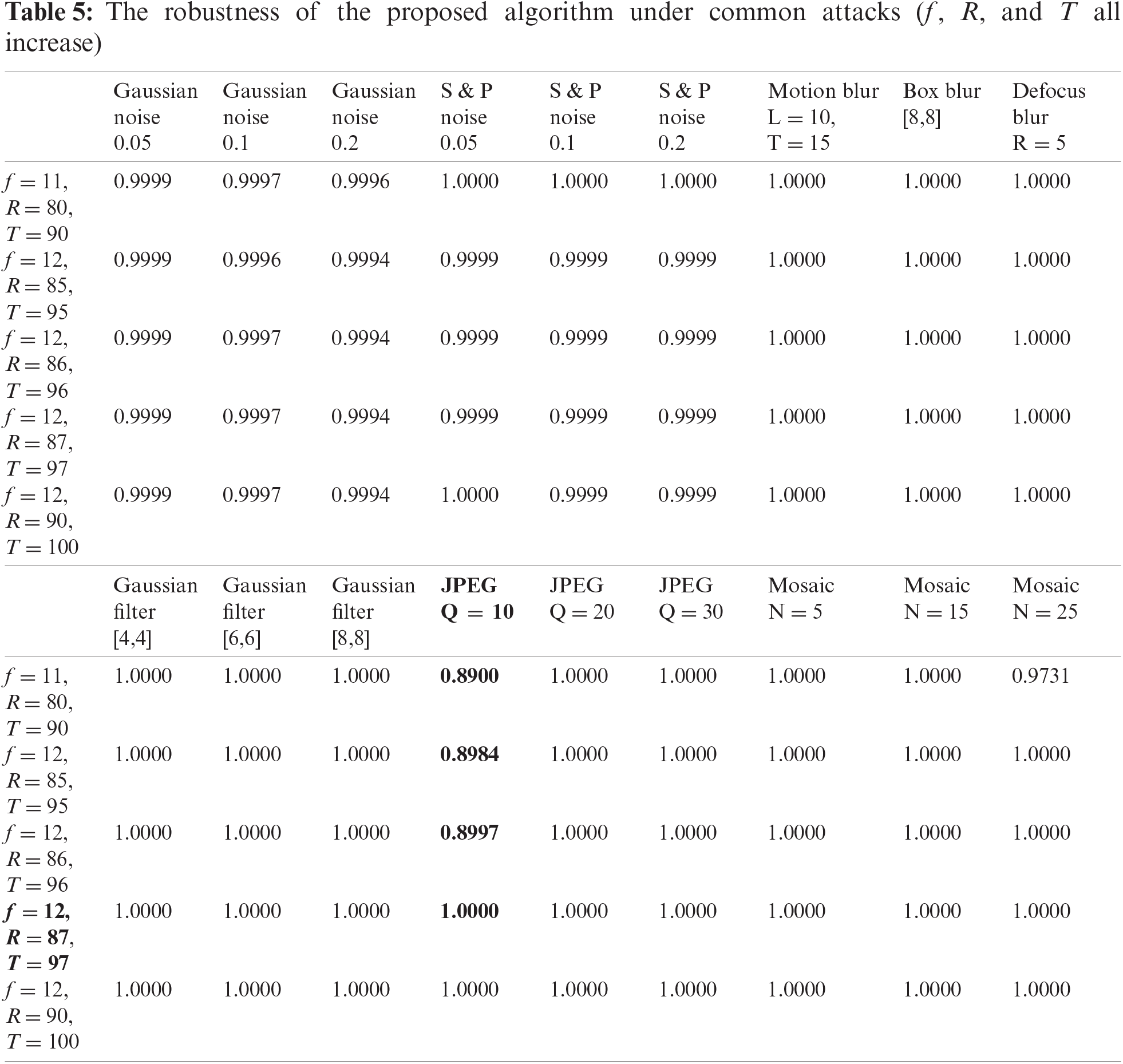
From the experimental results in Tabs. 5 and 6, it can be clearly seen that the proposed algorithm can resist most attacks and has good robustness. We also find that when the values of f, R, and T are small, the robustness of the algorithm against JPEG attacks and joint attacks (bold content) is not ideal. However, as the values increase, the robustness also improves, and the best results are achieved when f = 12, R = 87, and T = 97, as shown in Fig. 7.

In summary, when f=8,R=87,T=97, the proposed algorithm can simultaneously protect 512 images; when f=13,R=50,T=60, the proposed algorithm can simultaneously protect 315 images; when f=12,R=87,T=97, the proposed algorithm can simultaneously protect 341 images. Although the algorithm using the first group of parameters can simultaneously protect more images, the zero-watermark algorithm pays more attention to robustness, and the algorithm using the third group of parameters is more robust than the first group. Therefore, the optimal parameter of the proposed algorithm should be the third group. According to the results of the attack test, we set 0.9 as the threshold for the copyright verification of the color fundus image.

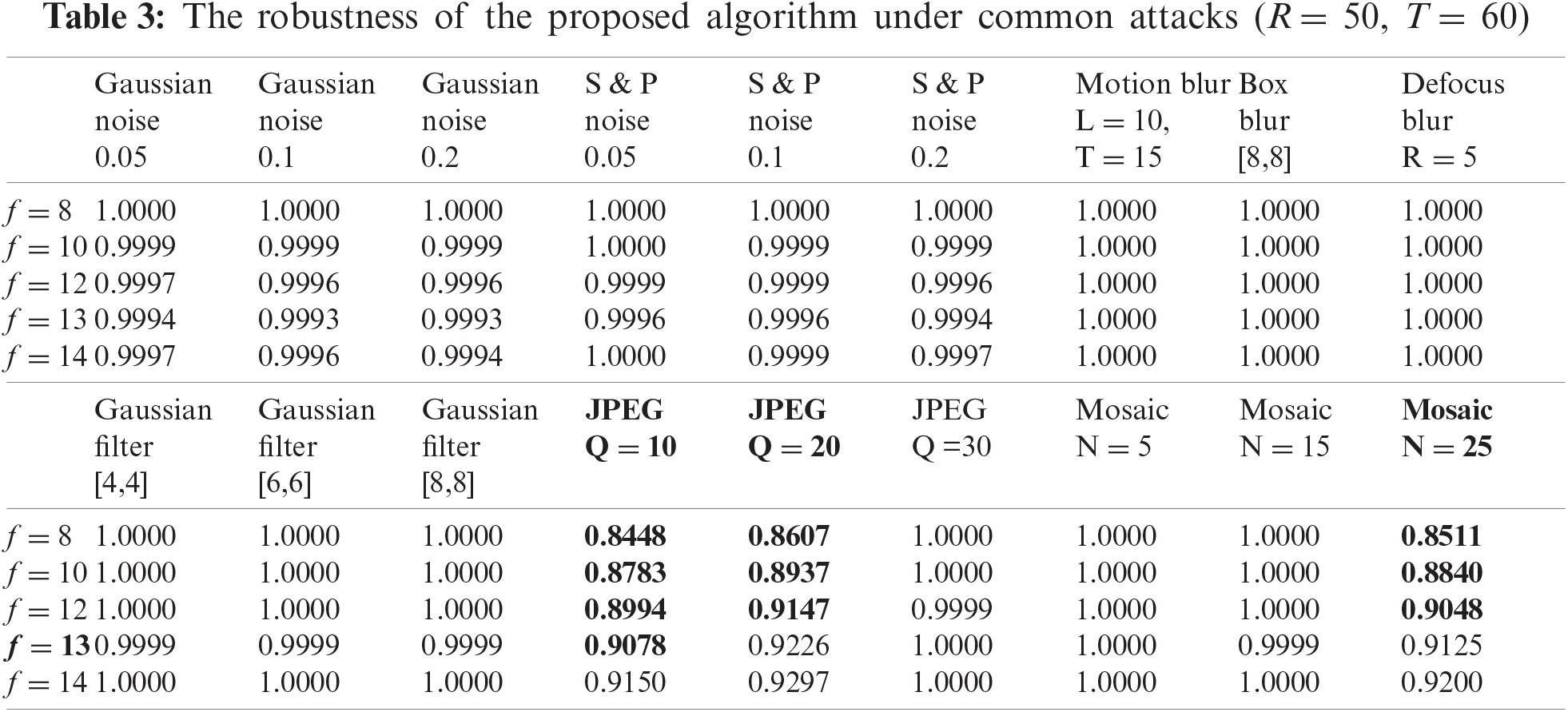
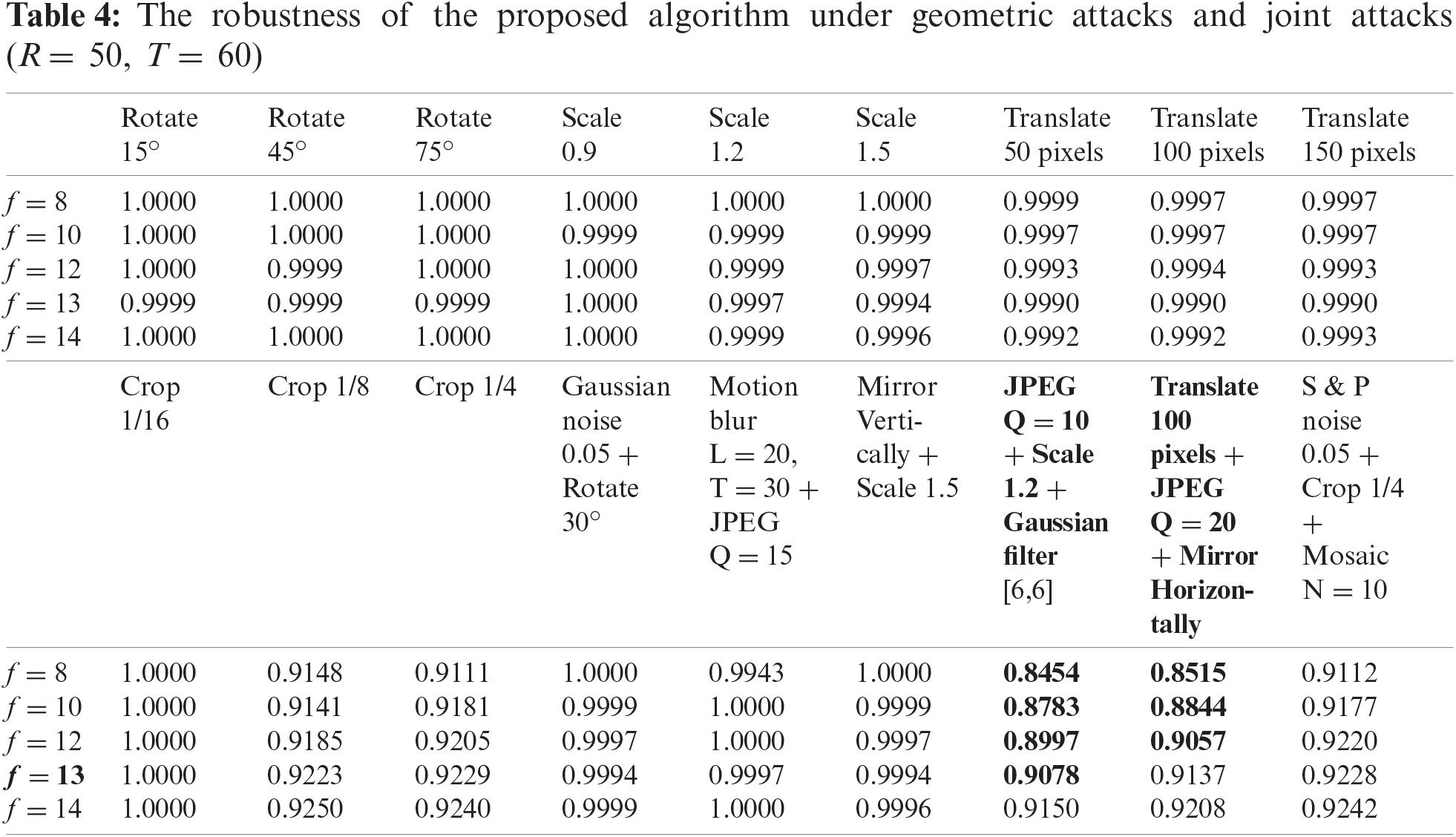
Figure 6: The change of robustness as the value of f increases

5.2 Comparison of Robustness and Running Time

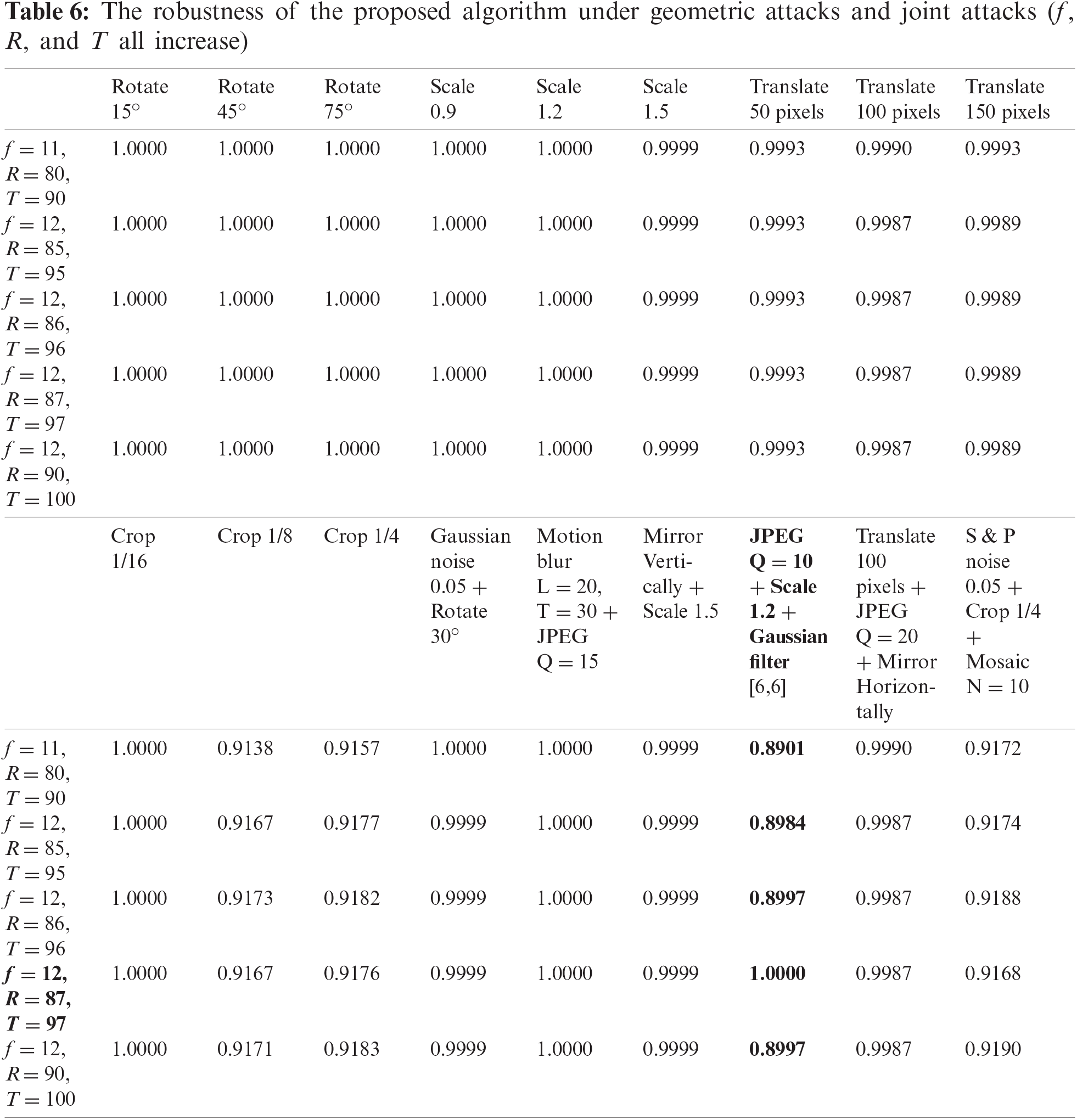
Based on the optimal parameters obtained from the analysis of experimental results in Section 5.1, we compare the robustness and running time with three excellent zero-watermark schemes: Scheme I ([18]), Scheme II ([24]), and Scheme III ([27]). The NC values and running time of the three schemes are obtained by averaging 341 images, the comparison results are shown in Tab. 7 and Fig. 8. It can be seen from the comparison results that the proposed scheme has stronger robustness in dealing with most attacks, especially in dealing with attacks such as image compression, rotation, and joint attacks. However, the robustness of the proposed scheme is weak when resisting a large-scale cropping attack, but it still has a good effect. It can be seen from Tab. 7 that compared with the three schemes, the execution time of the proposed scheme for each image is shorter. The main reason for the longer execution time of the other three schemes is that the computational amount will increase sharply when copyright protection is performed on larger-size images. In summary, compared with the other three excellent zero-watermark schemes, the proposed scheme has better robustness in dealing with various attacks and has higher operating efficiency in large-size image processing.

5.3 Algorithm Security Analysis

The security of the zero-watermark algorithm is as important as its robustness. If there is no scrambling encryption for the copyright or feature images, malicious attackers will likely reproduce a similar algorithm to generate specific feature images. The copyright image is obtained by performing the XOR operation on the generated feature image and the stolen zero-watermark image, thereby destroying the fairness of copyright verification and causing losses to the true copyright owner. Therefore, Cat map is used to scramble and reverse scramble the feature image and the copyright image, and the scrambling parameter is used as the key to be saved by the copyright owner. Even if the malicious attackers use the similar zero-watermark algorithm, the copyright image obtained is still a scrambled image, so it is impossible to pass the NC value verification. Only when the key is used for anti-scrambling can the copyright owner of the image be confirmed. Therefore, the security of the zero-watermark algorithm can be enhanced to some extent by using the Cat map.

Figure 7: The effect of robustness as values are increased

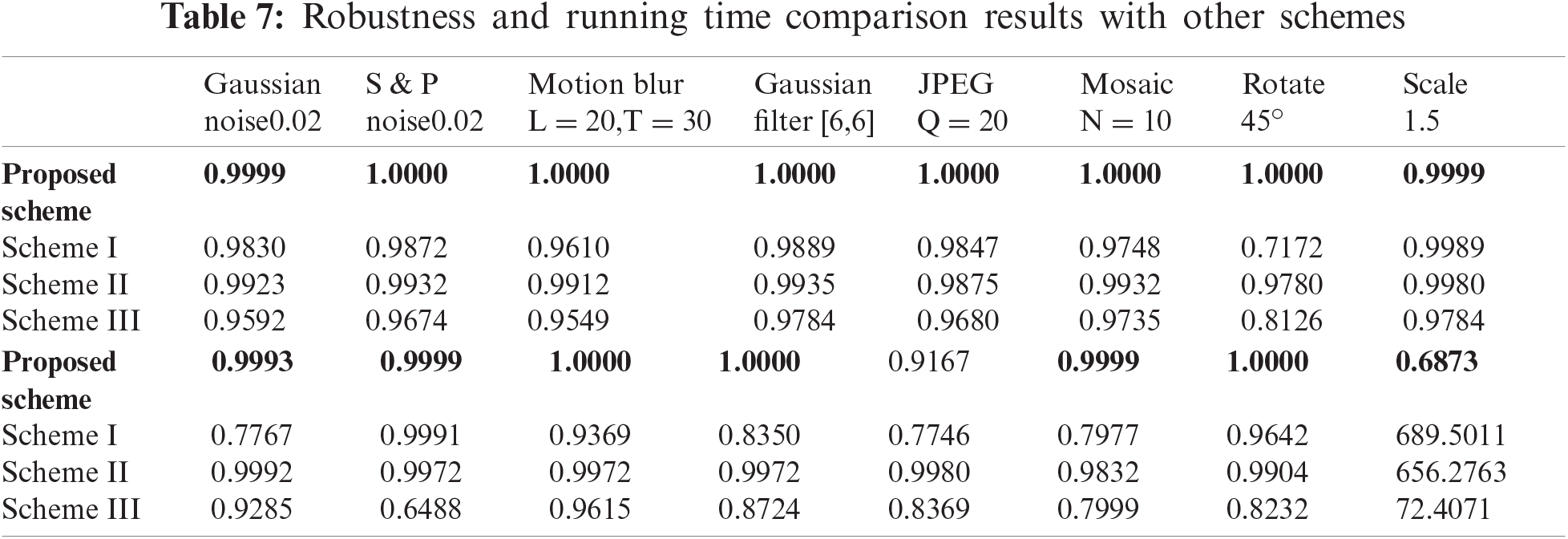
Figure 8: The robustness comparison of different schemes

6  Conclusion

Although existing zero-watermark algorithms can protect a single grayscale medical image, most algorithms will bring high time and storage costs when protecting a large number of images due to repetitive operation. Therefore, this paper proposes an efficient zero-watermark scheme for multiple color medical images based on QGFD and QR code. This method firstly uses QGFD to calculate the robust features of each image, and then select the representative features of each image from these robust features to form a feature matrix, and then binarize the feature matrix to obtain the feature image. Finally, the XOR operation combines the encrypted copyright image with the encrypted feature image to get a zero-watermark image. In the experiment, we divided the experiment into three aspects, namely, f is unchanged, R and T are assigned different values; R and T are unchanged, f is assigned different values; f, R, and T are all assigned different values. The optimal parameters are sought to make the algorithm have better robustness and can protect more images. The experimental results show that the proposed scheme has achieved good robustness in dealing with various attacks, and the optimal parameters have been determined according to the results. Comparative experiments show that the proposed scheme not only has stronger robustness and higher execution efficiency but also can greatly and effectively reduce the time and storage cost of medical image copyright protection. The future work is to improve the execution efficiency of the algorithm further and improve the algorithm's robustness against large-scale cropping attacks.

Funding Statement: This work is supported by the National Natural Science Foundation of China [Grant Numbers 61972207, U1836208, U1836110, 61672290]; the Major Program of the National Social Science Fund of China [Grant Number 17ZDA092], by the National Key R&D Program of China [Grant Number 2018YFB1003205]; by the Collaborative Innovation Center of Atmospheric Environment and Equipment Technology (CICAEET) fund, China; by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD) fund.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  R. Thanki, S. Borra, V. Dwivedi and K. Borisagar, “An efficient medical image watermarking scheme based on FDCuT–DCT,” Engineering Science and Technology, An International Journal, vol. 20, no. 4, pp. 1366–1379, 2017. [Google Scholar]

 2.  N. R. Zhou, A. W. Luo and W. P. Zou, “Secure and robust watermark scheme based on multiple transforms and particle swarm optimization algorithm,” Multimedia Tools and Applications, vol. 78, no. 2, pp. 2507–2523, 2019. [Google Scholar]

 3.  S. M. Mousavi, A. Naghsh, A. A. Manaf and S. Abu-Bakar, “A robust medical image watermarking against salt and pepper noise for brain MRI images,” Multimedia Tools and Applications, vol. 76, no. 7, pp. 10313–10342, 2017. [Google Scholar]

 4.  Z. T. Li, J. X. Xie, G. M. Zhu, X. Peng, Y. R. Xie et al., “Block-based projection matrix design for compressed sensing,” Chinese Journal of Electronics, vol. 25, no. 3, pp. 551–555, 2016. [Google Scholar]

 5.  J. Liu, J. Li, J. Cheng, J. Ma, N. Sadiq et al., “A novel robust watermarking algorithm for encrypted medical image based on dtcwt-dct and chaotic map,” Computers, Materials & Continua, vol. 61, no. 2, pp. 889–910, 2019. [Google Scholar]

 6.  N. Jayashree and R. S. Bhuvaneswaran, “A robust image watermarking scheme using z-transform, discrete wavelet transform and bidiagonal singular value decomposition,” Computers, Materials & Continua, vol. 58, no. 1, pp. 263–285, 2019. [Google Scholar]

 7.  Z. T. Li, J. W. Kang, R. Yu, D. D. Ye, Q. Y. Deng et al., “Consortium blockchain for secure energy trading in industrial internet of things,” IEEE Transactions on Industrial Informatics, vol. 8, no. 14, pp. 3690–3700, 2018. [Google Scholar]

 8.  B. Wang and P. Zhao, “An adaptive image watermarking method combining SVD and wang-landau sampling in DWT domain,” Mathematics, vol. 8, pp. 691, 2020. [Google Scholar]

 9.  Q. Wen, T. F. Sun and S. X. Wang, “Based zero-watermark digital watermarking technology,” in Proc. 3rd China Inf. Hiding Multimedia Secur. Workshop (CIHWXian, China, pp. 102–109, 2001. [Google Scholar]

10. H. H. Tsai, Y. S. Lai and S. C. Lo, “A zero-watermark scheme with geometrical invariants using SVM and PSO against geometrical attacks for image protection,” Journal of Systems and Software, vol. 86, no. 2, pp. 335–348, 2013. [Google Scholar]

11. X. Q. Wu, J. B. Li, U. A. Bhatti and Y. W. Chen, “Logistic map and contourlet-based robust zero watermark for medical images,” in Innovation in Medicine and Healthcare Systems, and Multimedia, Singapore: Springer, pp. 115–123, 2019. [Google Scholar]

12. Z. Q. Xia, X. Y. Wang, W. J. Zhou, R. Li, C. P. Wang et al., “Color medical image lossless watermarking using chaotic system and accurate quaternion polar harmonic transforms,” Signal Processing, vol. 157, pp. 108–118, 2019. [Google Scholar]

13. C. P. Wang, X. Y. Wang, Z. Q. Xia, C. Zhang and X. J. Chen, “Geometrically resilient color image zero-watermarking algorithm based on quaternion exponent moments,” Journal of Visual Communication and Image Representation, vol. 41, pp. 247–259, 2016. [Google Scholar]

14. C. P. Wang, X. Y. Wang, X. J. Chen and C. Zhang, “Robust zero-watermarking algorithm based on polar complex exponential transform and logistic mapping,” Multimedia Tools and Applications, vol. 76, no. 24, pp. 26355–26376, 2017. [Google Scholar]

15. J. Liu, J. Li, Y. Chen, X. Zou, J. Cheng et al., “A robust zero-watermarking based on sift-dct for medical images in the encrypted domain,” Computers, Materials & Continua, vol. 61, no. 1, pp. 363–378, 2019. [Google Scholar]

16. Z. H. Shao, Y. Y. Shang, Y. Zhang, X. L. Liu and G. D. Guo, “Robust watermarking using orthogonal Fourier–Mellin moments and chaotic map for double images,” Signal Processing, vol. 20, pp. 522–531, 2016. [Google Scholar]

17. Z. Q. Xia, X. Y. Wang, X. X. Li, C. P. Wang, S. Unar et al., “Efficient copyright protection for three CT images based on quaternion polar harmonic Fourier moments,” Signal Processing, vol. 164, pp. 368–379, 2019. [Google Scholar]

18. W. B. Wang, Y. Li and S. L. Liu, “A polar complex exponential transform-based zero-watermarking for multiple medical images with high discrimination,” Security and Communication Networks, vol. 2021, no. 2, pp. 1–13, 2021. [Google Scholar]

19. Q. Wen, T. F. Sun and S. X. Wang, “Concept and application of zero-watermark,” Chinese Journal of Electronics, vol. 31, no. 2, pp. 214–216, 2003. [Google Scholar]

20. T. H. Chen, G. Horng and W. B. Lee, “A publicly verifiable copyright-proving scheme resistant to malicious attacks,” IEEE Transactions on Industrial Electronics, vol. 52, no. 1, pp. 327–334, 2005. [Google Scholar]

21. C. C. Chang and P. Y. Lin, “Adaptive watermark mechanism for rightful ownership protection,” Journal of Systems and Software, vol. 81, no. 7, pp. 1118–1129, 2008. [Google Scholar]

22. H. H. Tsai, H. C. Tseng and Y. S. Lai, “Robust lossless image watermarking based on α-trimmed mean algorithm and support vector machine,” Journal of Systems and Software, vol. 83, no. 6, pp. 1015–1028, 2010. [Google Scholar]

23. H. H. Tsai, Y. S. Lai and S. C. Lo, “A zero-watermark scheme with geometrical invariants using SVM and PSO against geometrical attacks for image protection,” Journal of Systems and Software, vol. 86, no. 2, pp. 335–348, 2013. [Google Scholar]

24. Z. H. Shao, Y. Y. Shang, R. Zeng, H. Z. Shu, G. Coatrieux et al., “Robust watermarking scheme for color image based on quaternion-type moment invariants and visual cryptography,” Signal Processing: Image Communication, vol. 48, pp. 12–21, 2016. [Google Scholar]

25. C. P. Wang, X. Y. Wang, Z. Q. Xia, C. Zhang and X. J. Chen, “Geometrically resilient color image zero-watermarking algorithm based on quaternion exponent moments,” Journal of Visual Communication and Image Representation, vol. 41, pp. 247–259, 2016. [Google Scholar]

26. F. F. Jiang, T. G. Gao and D. Li, “A robust zero-watermarking algorithm for color image based on tensor mode expansion,” Multimedia Tools and Applications, vol. 79, no. 11, pp. 7599–7614, 2020. [Google Scholar]

27. H. Y. Yang, S. R. Qi, P. P. Niu and X. Y. Wang, “Color image zero-watermarking based on fast quaternion generic polar complex exponential transform,” Signal Processing: Image Communication, vol. 82, no. 115747, 2020. [Google Scholar]

28. X. Y. Wang, L. Wang, J. L. Tian, P. P. Niu and H. Y. Yang, “Color image zero-watermarking using accurate quaternion generalized orthogonal Fourier–Mellin moment,” Journal of Mathematical Imaging and Vision, vol. 63, no. 6, pp. 708–734, 2021. [Google Scholar]

29. W. R. Hamilton, Elements of Quaternions. London: Longmans, Green, & Company, 1866. [Google Scholar]

30. S. J. Sangwine, “Fourier transforms of colour images using quaternion or hypercomplex, numbers,” Electronics Letters, vol. 32, no. 21, pp. 1979–1980, 1996. [Google Scholar]

31. H. Li, Z. W. Liu, Y. L. Huang and Y. G. Shi, “Quaternion generic Fourier descriptor for color object recognition,” Pattern Recognition, vol. 48, no. 12, pp. 3895–3903, 2015. [Google Scholar]

32. D. S. Zhang and G. J. Lu, “Shape-based image retrieval using generic Fourier descriptor,” Signal Processing: Image Communication, vol. 17, no. 10, pp. 825–848, 2020. [Google Scholar]

33. Shanggong Medical Technology Co. Ltd. (SGOcular Disease Intelligent Recognition ODIR-5K, 2019. [Online]. Available: https://odir2019.grand-challenge.org. [Google Scholar]

34. S. H. Wang and Y. P. Lin, “Wavelet tree quantization for copyright protection watermarking,” IEEE Transactions on Image Processing, vol. 13, no. 2, pp. 154–165, 2004. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.