Computers, Materials & Continua DOI:10.32604/cmc.2022.022524
Article

Diabetic Retinopathy Detection Using Classical-Quantum Transfer Learning Approach and Probability Model

Amna Mir1, Umer Yasin1, Salman Naeem Khan1, Atifa Athar3,*, Riffat Jabeen2 and Sehrish Aslam1

1Department of Physics, Comsats University Islamabad, Lahore Campus, Lahore, 54000, Pakistan
2Department of Statistics, Comsats University Islamabad, Lahore Campus, Lahore, 54000, Pakistan
3Department of Computer Science, Comsats University Islamabad, Lahore Campus, Lahore, 54000, Pakistan
*Corresponding Author: Atifa Athar. Email: atifaathar@cuilahore.edu.pk
Received: 10 August 2021; Accepted: 19 October 2021

Abstract: Diabetic Retinopathy (DR) is a common complication of diabetes mellitus that causes lesions on the retina that affect vision. Late detection of DR can lead to irreversible blindness. The manual diagnosis process of DR retina fundus images by ophthalmologists is time consuming and costly. While, Classical Transfer learning models are extensively used for computer aided detection of DR; however, their maintenance costs limits detection performance rate. Therefore, Quantum Transfer learning is a better option to address this problem in an optimized manner. The significance of Hybrid quantum transfer learning approach includes that it performs heuristically. Thus, our proposed methodology aims to detect DR using a hybrid quantum transfer learning approach. To build our model we extract the APTOS 2019 Blindness Detection dataset from Kaggle and used inception-V3 pre-trained classical neural network for feature extraction and Variational Quantum classifier for stratification and trained our model on Penny Lane default device, IBM Qiskit BasicAer device and Google Cirq Simulator device. Both models are built based on PyTorch machine learning library. We bring about a contrast performance rate between classical and quantum models. Our proposed model achieves an accuracy of 93%–96% on the quantum hybrid model and 85% accuracy rate on the classical model. So, quantum computing can harness quantum machine learning to do work with power and efficiency that is not possible for classical computers.

Keywords: Diabetic Retinopathy (DR); quantum transfer learning; inception-V3; variational quantum circuit; image classification

1  Introduction

Diabetic retinopathy (DR) is the most common form of diabetic eye disease [1]. Diabetic retinopathy usually only affects people who have chronic diabetes (diagnosed or undiagnosed). Diabetic retinopathy causes an array of long-term systemic complications that have considerable impact on the patients as the disease typically affect individuals in their most reproductive years. The World Health Organization has declared that, in 2030 diabetes will be the most serious and 7th highest death causing disease across world. DR occurs due to the damage of tiny blood vessels in the retina due to chronic diabetics. This may cause hemorrhages, exudates and even swelling of the retina can cause blind spots blurry vision. Diabetic Retinopathy is a major cause of vision loss and blindness affecting millions of people across the globe. If DR is diagnosed early, it can be managed using available treatments. Regular eye fundus examination is necessary because DR do not present any symptoms at early stages. The retinal abnormalities in DR also include Hemorrhages (HM), “Cotton wool” spots, Microaneurysm (MA), Retinal neovascularization, hard exudates, which are clearly presented in Fig. 1.

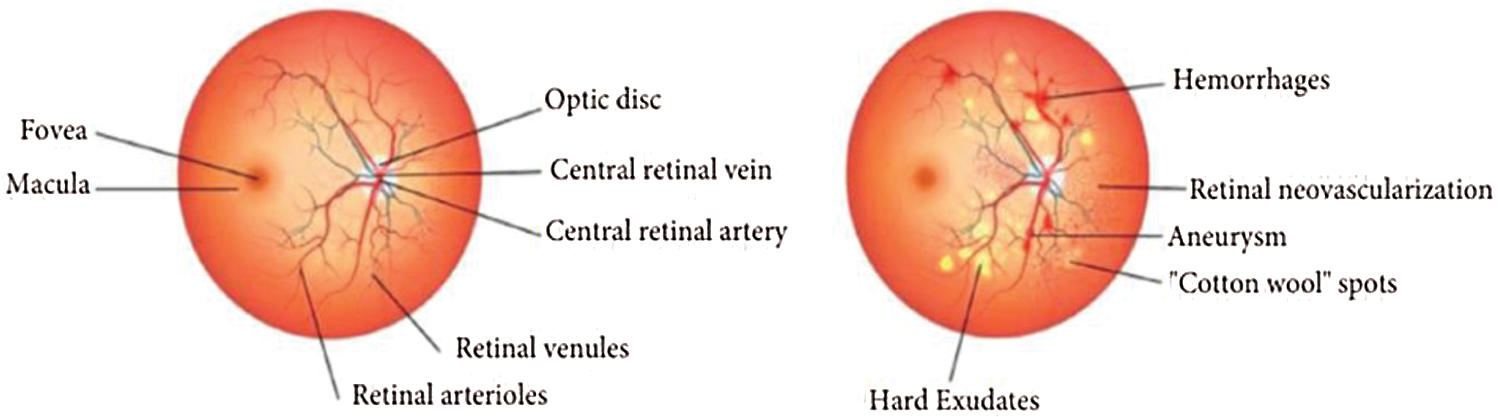
Figure 1: Normal eye and Infected eye [2]

In recent years, classical transfer learning approaches are used in the field of image classification, segmentation, and screening for DR. However, limited detection performance rates are hinderance to computer aided diagnostic. A breakthrough in the field of quantum computing can help in giving the ophthalmologist a second opinion to solve this problem by using hybrid quantum transfer learning approach. This quantum approach can result into more efficient detection of DR in patients as compared to the classical transfer learning [3,4]. Quantum transfer learning and Principal Component Analysis (PCA) is currently used in various medical diagnostics [2]. Zhang [5] used pathological images for Non-Hodgkin Lymphoma analysis. Similarly, classification of Arabic sign language is done using same hybrid approach [6]. Therefore, this work presents a hybrid approach of quantum learning model for DR detection.

This paper presents a hybrid approach for early detection of DR. We have compared the results of our three hybrid Quantum Transfer Learning models with one classical Transfer Learning model. We have labeled our data set into two categories i.e., no DR or DR. To build Quantum Transfer learning model, we have used inception-V3 [7] pre trained neural network for feature extraction and used quantum variational circuit for classification. Further our model is trained on penny lane default device, IBM Qiskit BasicAer device and Google Cirq Simulator device. We have built Classical transfer model on the same parameters and learning rates as defined in Quantum transfer learning model. Moreover, both models are based on pytorch machine learning Library. Our proposed model achieves an accuracy of 93%–96% on hybrid models and 85% accuracy rate on classical model. Quantum transfer learning approach has many advantages over conventional diagnostic techniques. This approach has less probability of human error and it is found to be more efficient and rapid way of finding the lesions in retina. Quantum computing approaches are great for solving optimization problems as compared to classical computing approaches.

2  Literature Review

Transfer learning refers to a technique for predictive modeling on a different but somehow similar problem that can be used partially or entirely to accelerate the training and improve the performance of a model. It can train deep neural network with comparatively small size of data. If a previously trained artificial neural network is successful in solving a particular problem, it can be reused with some additional training to solve a problem. Let’s consider a pre-trained deep neural network with the data set used for the solution of a problem. Transfer learning can be used to accelerates the training of neural networks as either a weight initialization scheme or feature extraction method that is retrained to solve a different or similar problem with a new dataset.

Quantum machine learning extends the concept of transfer learning, widely applied in modern machine learning algorithms, to the emerging context of hybrid neural networks composed of classical and quantum elements. In Quantum transfer learning we focus mainly on the paradigm in which a pre-trained classical network is modified and augmented by a final quantum layer. We can use any pre trained classical neural network according to our problem for feature extraction. To classify these features with the help of “dressed quantum circuit” we need to reduce output-dimensional feature vector to final dimensions with linear transformation [8]. We commonly use variational quantum classifier to classify output features from built-in neural network and variational quantum classifier used in this regard as presented in Fig. 2.

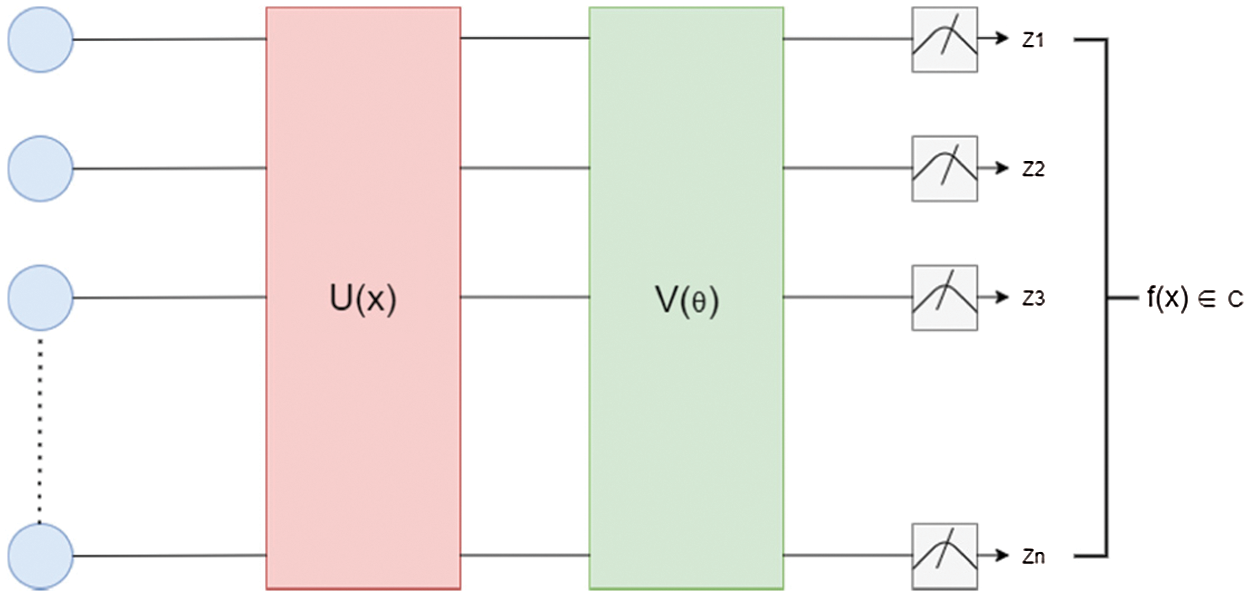
Figure 2: Variational Quantum Classifier with embedding layers U(x) and variational circuit V(θ) and final measurements in classical output f(x)εc

In Fig. 2 we have presented three basic components (embedding layers U(x), variational circuit V(θ) and final measurements) on which Variational Quantum Classifier (VQC) is built [9]. We have adopted a different method to get data into quantum computers and we have used four major data encoding techniques like: Basis Encoding, Amplitude Encoding, Angle Encoding and Higher order embedding.

One of the most important components in VQC is variational circuit. Fig. 3 presents variational circuit for one qubit operation.

Figure 3: Simple case of one Qubit

In past, many works have been reported to solve DR problem by using classical machine learning approaches using different datasets. Mansour [10] used a deep convolution neural network using transfer learning for feature extraction when building a computer aided diagnosis for DR.

To avoid the time and resource consumption, Mohammadian [11] fine-tuned the Inception-V3 and Xception pre-trained models to classify the DR dataset into two classes. After using data augmentation to balance the dataset, an accuracy score of 87.12% on the Inception-V3, and 74.49% on the Xception model is reported. Wan et al. [12] implemented transfer learning and hyper parameter tuning on the pre-trained models AlexNet, VggNet-s, VggNet-16, VggNet-19, GoogleNet and RestNet using the Kaggle dataset and compared their performances. The highest accuracy score was that of VggNet-s model, which reached 95.68% when training with hyper-parameter tuning. Transfer learning was used to work around the problem of insufficient training dataset in for retinal vessel segmentation. Dutta et al. [13] used 2000 fundus images to train a shallow feed forward neural network, deep neural network and VggNet-16 model. On a test dataset of 300 images, the shallow neural network scored an accuracy of 42%, and the deep neural network scored 86.3% while the VggNet-16 scored 78.3% accuracy.

It is quite evident from the majority of the work in diabetic retinopathy detection revolves around the use of various transfer learning models and performance comparison of these models. It is also observed that less emphasis has been given on improvement of quality of the diabetic retinopathy dataset which could lead to more accurate results. It is important to highlight the fact that the reliability of results generated from the transfer learning model depends on the features of the dataset. Google’s recent achievement of quantum supremacy marked the first glimpse of this promised power. This is reminiscent of how machine learning evolved towards deep learning with the advent of new computational capabilities. These new algorithms use parameterized quantum transformations called parameterized quantum circuits (PQCs), Quantum Neural Networks (QNNs), Variational quantum circuits and Dressed quantum circuits. In analogy with classical transfer learning, the parameters of a variational quantum circuits are then optimized with respect to a cost function via either black-box optimization heuristics or gradient-based methods.

3  Limitations of Existing Works and Contributions

A tabular comparison has been outlined to discuss the limitations and contributions of the existing works.

4  Material and Method

4.1 Dataset

The dataset we used in our study is a publicly available retinal fundus images database from Kaggle (APTOS 2019 Blindness Detection) [14] consisting of 3662 images. This database is formed by technicians as they traveled in rural areas to take images for ophthalmologist’s review regarding diagnosis. This process is time and resource consuming. Therefore, in current study this dataset is used to get computer aided ability to screen images without the help of ophthalmologists for timely detection of disease. The obtained dataset was weed up and a clean dataset was created. The resulting dataset is labeled into two categories. In order to train our model, we have used 789 non-DR and 738 DR images. Validation of our model is carried out by using 384 images from which 198 non-DR and 186 DR images of patients. We test out model on 1738 different and random images to evaluate performance of both types of models i.e., Classical transfer learning-based model and Quantum transfer learning based model. Distribution of training data with labels of Non-DR and DR is presented in Fig. 4.

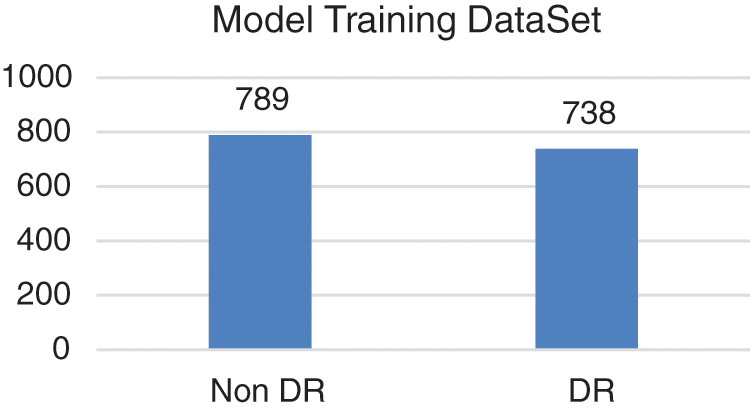
Figure 4: Distribution of training data with labels of Non-DR and DR

4.2 Quantum Devices

The Quantum Computing device used in our study is Penny-lane default device, IBM QiskitBasicaer and Google Cirq Simulator device. These simulators are noiseless to avoid any error.

4.3 Image Pre-Processing

In current work, APTOS 2019 Blindness Detection dataset is taken from Kaggle and labelled into two categories with the help of provided file in Kaggle documentation. Furthermore, resizing of imbalance images is done to 350 by 350. These images are further processed to remove extra black pixel part to covert image as input in our inception V3 pre-trained neural network. After this we have converted our images into tensor vector because machine learning model always input data in the form of vectors. We have done some normalization of parameters like ( [0.485,0.456,0.406]) to remove any misbalancing during resizing of images [15,16].

5  Proposed Hybrid Quantum Transfer Learning Model

We have proposed hybrid Quantum transfer learning model, in which we have used inception-v3 pre trained neural network for feature extraction. Inception-v3 is a pre-trained convolutional neural network model that is 48 layers deep that is used to reduce images to 2048-dimensional feature vector [1].

To classify these features with the help of 4-qubit “dressed quantum circuit” we have reduced 2048-dimensional feature vector to 4 dimensions with linear transformation [8]. Variational quantum classifier, built for our problem is presented in Fig. 5.

Figure 5: Variational quantum classifier of (four qubits)

Following steps are performed to build quantum classifier

1. Firstly, we have initialized 4 qubits in |0) state and then apply Hadamard (H) gate on these 4 qubits to make them in superposition state of zero and one [1].

2. Then we have applied, additional transformation to encode our classical data with unitary circuit. To perform this operation, we encoded our 4-dimensional feature vector as a parameters or weights into our circuit consisting of Ry(fi) gates and U (α, β, θ, γ) circuit.

3. We have a sequence of trainable variational layers having an entanglement layer and a data encoding circuit. We have 3 CNOT gates in the entanglement layer which makes all qubits, entangled

4. In the end we have done measurements on each 4-qubits to get the expected value along the z-operator.

Fig. 6, clearly presents the complete flow of our proposed model from first block A (inception V3) to its final measurement block (between Non-DR or DR (0,1)).

Figure 6: Flowchart of the proposed Quantum Transfer learning model

6  Experimental Evaluation

We have trained two models, first is classical model using classical transfer learning and second is quantum model using quantum transfer learning with the same training data set and parameters. We have setup learning rate 0.0004 which is same for both models and used Adam optimization algorithm and Cross Entropy function as activation function. Online google Colab notebook is being used to run our model.

We have evaluated our model with five basic standards: Accuracy, Precision, Recall, f1-score and specificity with the following formulas.

Accurcay=Tp+TNTp+TN+Fp+FN(1)

Precision=TpTp+Fp(2)

Recall=TpTp+FN(3)

Specificity=TNTN+FN(4)

F1=2×Recall×PrecisionRecall×Precision(5)

Where