DOI:10.32604/cmc.2022.022673

| Computers, Materials & Continua DOI:10.32604/cmc.2022.022673 |  |
| Article |
An Improved DeepNN with Feature Ranking for Covid-19 Detection
1Faculty of Computers and Artificial Intelligence, Benha University, Benha, 13518, Egypt
2University of Jeddah, College of Computer Science and Engineering, Jeddah, 21493, Kingdom of Saudi Arabia
3Faculty of Computers and Information, Damietta University, Damietta, 34711, Egypt
*Corresponding Author: Noha E. El-Attar. Email: noha.ezzat@fci.bu.edu.eg
Received: 15 August 2021; Accepted: 15 September 2021
Abstract: The outbreak of Covid-19 has taken the lives of many patients so far. The symptoms of COVID-19 include muscle pains, loss of taste and smell, coughs, fever, and sore throat, which can lead to severe cases of breathing difficulties, organ failure, and death. Thus, the early detection of the virus is very crucial. COVID-19 can be detected using clinical tests, making us need to know the most important symptoms/features that can enhance the decision process. In this work, we propose a modified multilayer perceptron (MLP) with feature selection (MLPFS) to predict the positive COVID-19 cases based on symptoms and features from patients’ electronic medical records (EMR). MLPFS model includes a layer that identifies the most informative symptoms to minimize the number of symptoms base on their relative importance. Training the model with only the highest informative symptoms can fasten the learning process and increase accuracy. Experiments were conducted using three different COVID-19 datasets and eight different models, including the proposed MLPFS. Results show that MLPFS achieves the best feature reduction across all datasets compared to all other experimented models. Additionally, it outperforms the other models in classification results as well as time.
Keywords: Covid-19; feature selection; deep learning
The COVID-19 virus is still spreading rapidly. Although some vaccines have been developed to provide acquired immunity against Covid19, no vaccine exists to completely prevent coronavirus infection in humans. Therefore, early diagnosis of (COVID-19) patients is crucial for disease diagnosis and control. As a result, it is essential to classify and analyze COVID-19 data, particularly in epidemic areas, to save medical experts’ time and effort. Data mining is considered an effective technique for detecting and predicting several medical issues due to its ability to find and extract meaningful information and patterns from medical datasets. There are several types of data mining-based classification algorithms. To name a few, artificial neural networks (ANN), support vector machines (SVM), K-nearest neighbors (KNN), and random forest (RF) [1]. Even though classification models are primarily reliant on extracting features that characterize data instances, these extracted features may contain lots of unnecessary or redundant features. From this standpoint, selecting the most important and relevant features, especially for high-dimensional data, enhances the classification model accuracy and minimizes the time cost.
In general, the traditional feature selection approaches are classified into three types; filter approach, wrapper approach, and embedded approach, as shown in Fig. 1 [2]. Filter methods are classifier-independent, where they select the features’ subsets based on specific given criteria [3]. Correlation-based feature selection, fast correlated-based filter, and Relief are examples of filter methods [4]. The main drawback of this methodology is that it ignores feature dependencies and relationships between classifiers, resulting in a misclassified model [5]. On the other hand, wrapper and embedded techniques are classifier-dependent. Their methods take into consideration feature interaction, resulting in increased algorithm classification accuracy. Wrapper approaches, such as forward selection and backward elimination, assess a potential subset based on the accuracy rate of a given classifier.
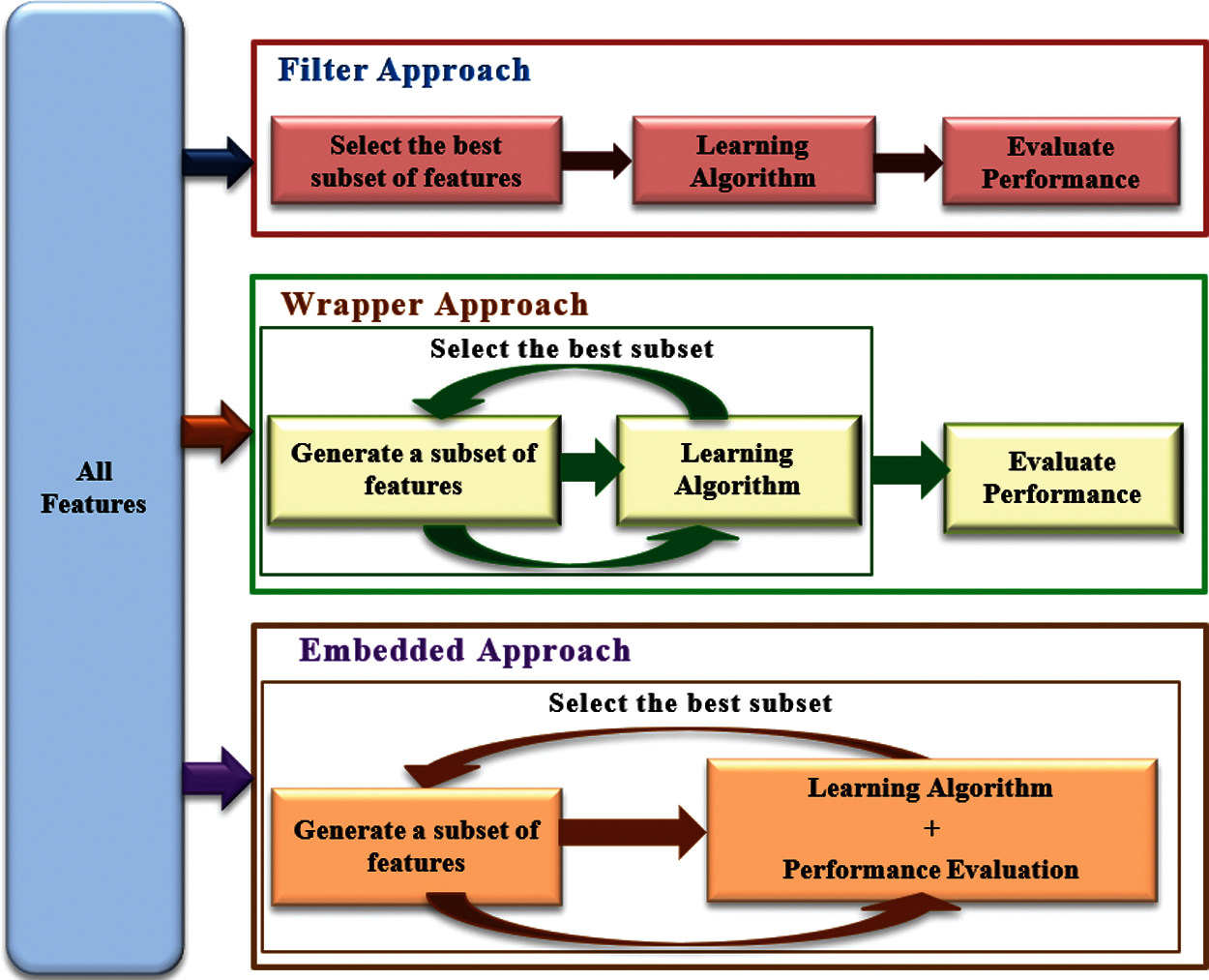
Figure 1: Feature selection approaches
In contrast, embedded methods (e.g., LASSO and RIDGE regression) incorporate feature selection inside the classification process. Although wrapper and embedded methods usually gain a high level of classification accuracy, they take a longer time to execute than filter approaches [3]. Therefore, many researchers have developed hybrid approaches to select the most critical features [5].
Machine learning models have been widely leveraged in big data to establish efficient predictive models. However, a critical issue with ML techniques is the high dimension of the dataset. For instance, sometimes, the feature subset size is much larger than the pattern size, which may decrease the classifier's performance. Therefore, determining the feature importance for high-dimensional variables and data has gotten attention in recent years to improve the accuracy of classification models [6].
One of the recent trends to enhance classification accuracy is using deep learning networks by creating more profound and more sophisticated networks such as convolutional neural networks, recurrent neural networks, radial basis function neural networks, and multilayer perceptrons [7]. Deep neural networks (DNN) have generally been viewed as black-box techniques due to their complicated construction. Despite their high predictive power in many learning problems (e.g., system identification, text classification, pattern recognition, and medical diagnosis), they don't reveal which features significantly impact prediction accuracy. In addition, the trainable parameters needed by these networks in both the training and testing stages have become increasingly complicated, necessitating a large amount of memory and processing resources [7]. Feature selection could be adopted and integrated during the learning process to eliminate non-significant features based on a particular fitness function value of a predefined threshold and help identify the inputs that control the outcome [8,9]. In common, feature selection (FS) algorithms are used as preprocessors before learning to detect the most relevant features and neglect the non-significant ones. After that, the machine learning algorithm gives the same importance level to all extracted features and applies the induction algorithm [10]. This technique may reduce classification performance because less relevant characteristics may play a significant role in the learning problem. As a result, a ranking based on the importance of the features of the learning problems may be more valuable [11].
In recent years, different strategies have been presented to perform the feature importance ranking (FIR) process for DNNs, such as regularization, greedy search, and averaged input gradient [11]. Regularization strategies are based on detracting the first hidden layer's weights, which helps reduce the number of parameters in a DNN and finding heuristic approaches for feature selection. Lasso and random forest are examples of regularization strategies [8]. The Greedy search strategy effectively optimizes problems to find the optimal global solution at an acceptable response time. However, this strategy ordinarily causes high computational costs and may produce solutions far from the optimal ones. Averaged input gradient is an approach to population-wise FIR methods, which uses the average of all prominence maps derived from individual instances and the global population [11].
The contribution of this paper is to modify the classification model to learn faster according to the weight of features’ importance. Rather than dealing with all features identically, the model will handle the features according to their importance and utilize this importance’ knowledge in the learning process, leading to better classification accuracy. This study proposes a modified MLP network by adding a new hidden layer that plays the feature selection process role. The proposed FS layer depends on ranking the features’ importance according to their weights based on a threshold produced by a nonlinear function. The more important the features, the more discriminative power they have. The rest of the paper is organized as follows; Section 2 displays the literature review on feature selection and feature importance and their effectiveness on classification models. Section 3 represents the materials and methodologies as preliminaries to the proposed algorithm. The proposed algorithm is discussed in Section 4, followed by the experiment details and the final results in Section 5. Finally, the conclusion is reviewed in Section 6.
As neural networks have been widely used in classification problems, many researchers have tended to enhance their capabilities in learning and classification by modifying their structure or applying feature selection techniques. For instance, in Wang et al. [12], have combined a bottom-up feature extraction and a top-down cognitive bias into one cohesive structure to produce a new attentional neural network structure. As the authors mentioned, this framework could efficiently handle noisy and complicated segmentation problems with a high level of accuracy. Another study used neural networks in feature selection presented by Bugata et al. [9]. In this study, the authors developed neural networks to find the significant input variables and produce a supervised feature selection method called sparse neural network layer with normalizing constraints. Also, Mocanu et al. [13] have replaced the traditional ANN's fully connected layer with sparse layers to enhance the classification accuracy. Ho et al. [8] have developed a theoretical criterion for using the adaptive group lasso to obtain significant features of NNs. Akintola et al. [14] have scrutinized the influence of filter-based classification techniques on predicting software defects. They have evaluated the FilterSubsetEval, CFS, and PCA algorithms on available datasets from the metric data program software repository and NASA. They have used Naïve Bayes and KNN, J48 Decision Tree, and MLP as classifiers. Another novel approach to constrained feature selection has been proposed by Rostami et al. [15]. The presented approach is a pairwise constraints-based method for feature selection and dimensionality reduction.
Increasing the data dimension encouraged researchers to adopt different types of DNN due to their robust capabilities in classification and prediction. Therefore, several works of literature have developed feature selection and feature ranking techniques to improve the classification performance of the DNNs. In Liu et al. [16], have proposed an improved feature derivation and selection method for a hybrid deep learning approach. They have used the deep neural network (DNN) and multilayer bi-directional long short-term memory (BiLSTM) with the attention mechanism to forecast overdue repayment behavior. Jiang et al. [17] have proposed an improved feature selection approach by integrating the CNN with the Relief algorithm. Also, Kaddar et al. in [7] have used the ANOVA technique to find the non-redundant representation in CNN by obtaining the feature maps with various neuron responses. In the same context, Nasir et al. [18] have proposed a deep convolutional neural network (DCNN) for real-time document classification based on the Pearson correlation coefficient to select the optimal feature subset. Another study using correlation coefficient and the automatic modulation classification (AMC) scheme has been presented by Lee et al. [19]. In [5], a feature selection framework based on recurrent neural networks (RNN) has been proposed. This research presented different feature selection approaches based on the RNN architecture: long short-term memory (LSTM), bidirectional LSTM, and gated recurrent unit (GRU). Also, a deep neural network-based feature selection (NeuralFS) was presented in [20]. Another supervised feature selection approach based on developing the first layer in DNN has been presented in [21] and [6].
As we mentioned before, FIR is another direction to enhance classification performance, as presented by Iqbal [11]. The authors of this study introduced a Correlation Assisted Neural Network (CANN) that calculates the feature importance weight based on the correlation coefficient between the class label and the features. Furthermore, M. Wojtas and K. Chen have handled the population-wise feature importance ranking by presenting an innovative dual-network architecture to obtain an optimal feature subset and rank the importance of the selected features [22].
Several studies have been interested in increasing the classification performance of clinical diagnosis systems by selecting the essential features. For instance, Bron et al. [23] have introduced feature selection based on SVM weights to enhance the computer-aided diagnosis system for dementia. Also, in Christo et al. [24], have proposed a correlation-based ensemble feature selector for clinical diagnosis. They have adapted three types of evolutionary algorithms (i.e., the lion optimization algorithm, the glowworm swarm optimization algorithm, and differential evolution) for feature selection. Then, they applied AdaBoostSVM as a classifier in a gradient descendant backpropagation neural network. In recent years, neural networks have been widely combined and integrated with several FS methods to enhance classification performance, such as combining NN with a feature selection method to analyze the specificity of HIV-1 protease [25]. Likewise, integrating NN and 10-fold cross-validations to diagnose liver cancer [26]. Combining the paired-input nonlinear knockoff filter with the MLP in [27]. Random forest in [28], Naive Bayes, and SVM classifiers [29] are other algorithms used in recent studies of FS problems.
Regarding COVID-19, which is still the focus of the world's attention, several works of literature have tried to handle different aspects of this disease. To name a few, analyzing its viral infections, classifying its textual clinical reports, and detecting the significant features for predicting its patients. For instance, Khanday et al. [30] have proposed a learning model to detect COVID-19 from textual clinical reports based on classical and ensemble machine learning algorithms. They used term frequency/inverse document frequency, report length, a bag of words as feature engineering techniques, and logistic regression (LR) with multinomial Naïve Bayes as a classifier. Likewise, Avila et al. [31] have introduced a Naïve-Bayes machine learning model to predict qRT-PCR test results, considered one of the most widely used clinical exams for COVID-19. Another machine learning algorithm based on feature importance has been presented in by Mondal et al. [32] to diagnose COVID-19. In this study, the authors applied MLP, XGBoost, and LR to classify COVID-19 patients based on a clinical dataset from Brazil. In, one more COVID-19 diagnosis strategy has been proposed by Shaban et al. [1]. This strategy is based on a novel hybrid feature selection method that consists of two stages to select the essential features: a fast selection stage as a filter selection method and an accurate selection stage based on a genetic algorithm as a wrapper selection method. As another use for machine learning, Mollalo et al. [33] have used MLP and LR to forecast the cumulative COVID-19 incidence rates across the United States. Finally, Tab. 1 summarizes some of the recent studies that address the FS importance.

Clinical reports and laboratory analysis are two of the most popular tools for diagnosing Covid-19 cases. Three types of datasets in the form of clinical reports have been used in this study. The first dataset is available at1. This dataset was collected from the SARS-CoV-2 RT-PCR and other laboratory tests performed on nearly 6000 Covid-19 cases during their visits to the emergency room. It includes 109 features and one class label. The second covid-19 dataset includes clinical features for symptomatic and asymptomatic patients (e.g., comorbidities, vitals, epidemiologic factors, clinician-assessed symptoms, and patient-reported symptoms). This dataset consists of 34475 records with 41 features and one class label and can be found at2. The third dataset focuses on predicting intensive care unit (ICU) admission for positive COVID-19 cases based on clinical data. It comprises 1926 cases with 228 features and one class label, and it is available at3.
Recently, constructing learning networks deeper and more complicated has emerged to improve the performance of learning and classification processes. Consequently, the trainable parameters required by these deep networks in the learning process (i.e., training and testing phases) have become increasingly complicated, which necessitates using a massive amount of power and memory resources. A multilayer neural network such as the multilayer perceptron (MLP) model is an example of these types of deep networks. MLP is a feedforward neural network containing hidden layers between its input and output layers, as depicted in Fig. 2. It is classified as a supervised learning algorithm used for classification and regression [34].
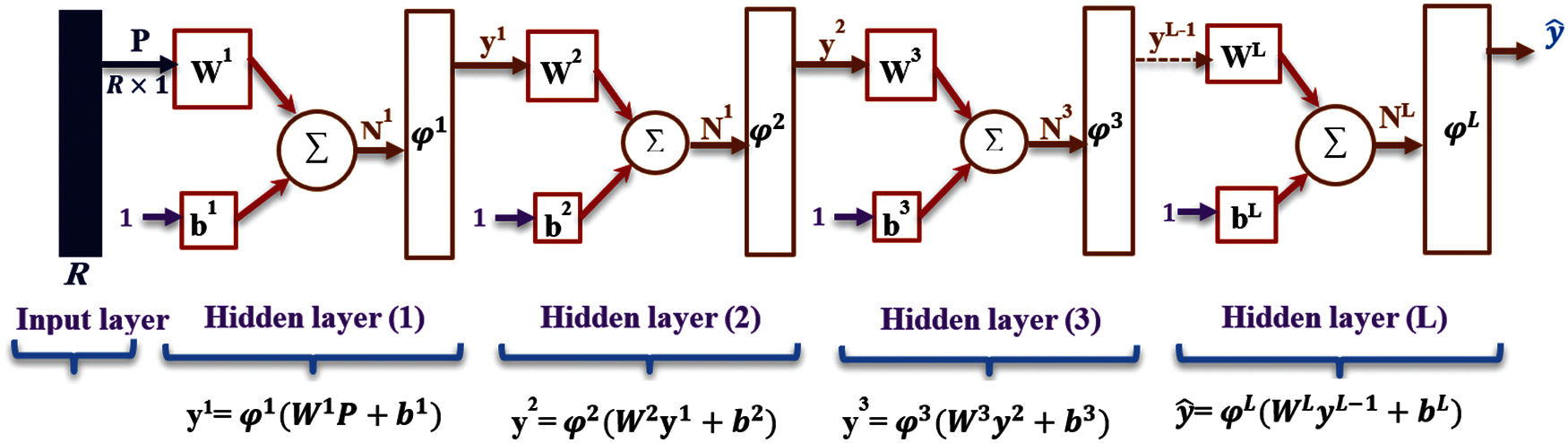
Figure 2: The architecture of multilayer perceptron network
In more detail, each layer in MLP is made up of nodes and contains its weight matrix, W, and bias b. Each node in the fully connected network has a connection with every node in the following layers. The input layer distributes the inputs to the subsequent layers based on a linear activation function without a threshold by equation. After that, the hidden layers process the input values based on one or more nonlinear activation functions to feed the output layer. Finally, the output layer used a linear activation function to produce the outcome
Some additional notations are used to distinguish between the variables of the hidden layers as follows: superscripts to define the number of the layer, and subscripts to define the number of the neurons in the current layer (e.g.,

4 The Proposed Multilayer Perceptron Network-Based Feature Selection (MLPFS)
In this study, a modified MLP with an additional FS layer has been proposed to improve the accuracy of Covid 19 detection. As depicted in Fig. 3, the proposed MLPFS architecture is constructed from three bunches. The initial bunch consists of the input and feature selection layers, which are connected in a one-to-one manner. Every input node in the input layer only connects with its corresponding node in the FS layer. The second bunch contains the hidden layers in which nodes are fully connected and pass forward. Finally, the third bunch is the output layer that uses a nonlinear activation function to produce a binary output form. The pseudo-code of the proposed MLPFS algorithm is shown in Algorithm 2.
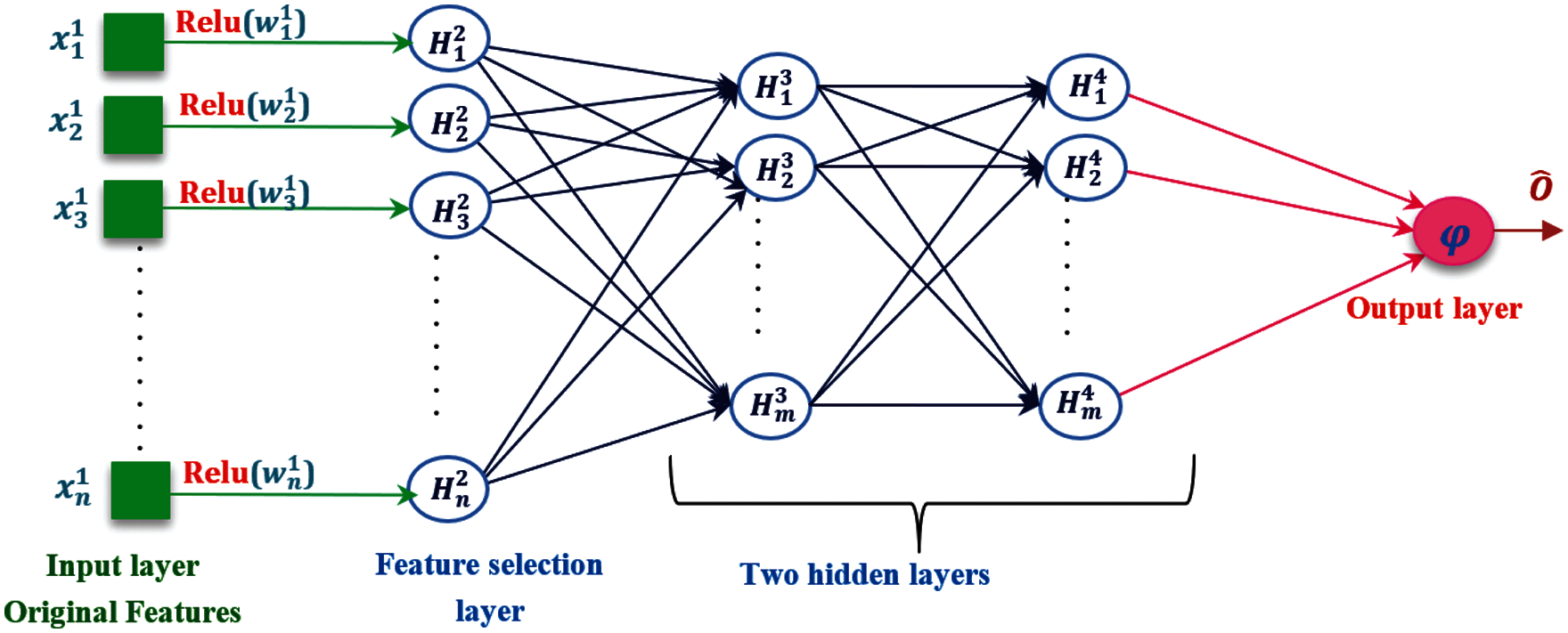
Figure 3: The architecture of the proposed MLPFS network

1-Input and Feature Selection Bunch
This bunch is considered the adaptive phase in the proposed MLPFS network, where it contains the FS layer that modifies its node weights based on the importance of the original features during the training phase to keep only the features that surpass the Rectified Linear Unit (ReLU) activation function [37]. Initially, the number of neurons in the input layer is always equal to the number of the original features of the utilized dataset, and every input neuron connects with only one neuron in the FS layer. The initial weights of these connections are justified based on a modified version of the Gaussian distribution in Eq. (3) [38].
where, n is the number of input features, and
where m is the number of the significant features.
By completing this bunch, the learning rates of the connections between the output of the FS layer (i.e., new values of input features) and the first hidden layer nodes will be adjusted by the new feature importance values. In more detail, based on the Relu threshold, all produced negative weights will be converted to zero and omitted. Then the heuristic process begins by ranking the importance of the features with positive weights (i.e., more essential features have higher overall connection weights, while redundant and irrelevant features have a lower overall connection weight). Finally, the outcome of this bunch will feed the rest of the network to achieve the learning process based on the chosen classifier.
2-Hidden Layers and Output Bunches
The input of this bunch is the selected features
Tab. 2 displays the parameters for the proposed MLPFS according to the utilized dataset. The utilized activation functions in the hidden layers and the output layer are Relu and sigmoid, respectively. Eqs. (7) and (8) calculate the outcome of the output layer.

5 Experiment Results and Discussion
The proposed MLP based FS (MLPFS) algorithm results are shown here. The effectiveness of these proposed enhancements is highlighted, demonstrating the MLPFS algorithm's performance in feature selection and classification processes. As indicated in Tabs. 4–6, we compared the proposed algorithm to other existing techniques to have a consistent comparison. The proposed MLPFS algorithm is compared to some filter-based feature selection algorithms with different classifiers such as Pearson correlation with neural network [41], chi-square with neural network [42], Chi-square with support vector machine [43], chi-square with boosted decision tree [44], and chi-square and logistic regression [45]. Also, the proposed MLPFS is compared to wrapper-based feature selection algorithms such as deep SVM [46] and cancelOut deep neural networks [6]. The utilized algorithms were tested on the three covid-19 data sets and evaluated based on their predictive accuracy and processing time. The parameters used in all of the algorithms are shown in Tab. 3. Python was used to implement this experiment using the Keras 0.2.0 library, integrated into the TensorFlow open-source library [47]. The implementation has been run on an Intel(R) Core i7 2.81 GHz CPU with 8 GB RAM and the Windows 10 operating system.

5.1 Performance Evaluation Measures
To evaluate the performance of the proposed MLPFS algorithm, the statistical results for all algorithms used in the comparison are calculated, including the number of selected features (SF), AUC, and processing time. In addition, confusion matrix values (i.e., TP, TN, FP, and FN) are used to find the classifier's performance in terms of accuracy, precision, sensitivity, and F score [48].
• Accuracy: The accuracy metric (
• Precision: it presents the ratio of true positives to all the predicted positive patterns. It is calculated by Eq. (10):
• Sensitivity or Recall: it presents the ratio of true positives to all the positives patterns in the dataset. It is calculated by Eq. (11):
• F1 score: it measures the accuracy of the model on the dataset. It can be calculated by Eq. (12):
5.2 Statistical Results Analysis
The performance of the proposed MLPFS algorithm for feature selection and classification is investigated in terms of feature size, accuracy, and processing time. The final result of feature size in the three utilized datasets is displayed in Tabs. 4–6. As shown, the proposed MLPFS model achieved a higher reduction in features compared to the other experimented models. It achieved almost 33% feature reduction for the first dataset, 34% reduction for the second dataset, and 35% reduction for the third dataset. The scored feature reduction is higher than the other models by at least 7% for the first dataset, 8% for the second dataset, and around 13% for the third dataset. MLPFS succeeded in identifying the most common COVID-19 symptoms amongst the most informative features concerning the features’ importance. For instance, applying MLPFS on the second Covid-19 data set gives the highest weight to smell loss, respiratory rate, and cough severity. On the other hand, these same symptoms came with less weights in the cancelout DNN algorithm [6].



Moreover, MLPFS has recorded an accuracy rate of 91.4%, 98.4%, and 88.4% for the SARS-CoV-2 RT-PCR, second Covid-19, and ICU datasets, respectively. Cancelout DNN achieved the second higher accuracy with 90.9%, 97.4%, and 84.5% for the three datasets. The Chi & LR achieved the third-highest accuracies with 90.6%, 97.4%, and 80.5% for the three datasets. Despite achieving the same accuracy for dataset1, Chi-square & NN achieved higher accuracy by around 1% than Pearson & NN for both dataset2 and dataset3. Chi & SVM and Chi & boosted DT achieved almost the same accuracies for all the datasets. Deep SVM achieved the lowest accuracy of 66.7% for the first dataset, with a high deviation from an average of around 0.2.
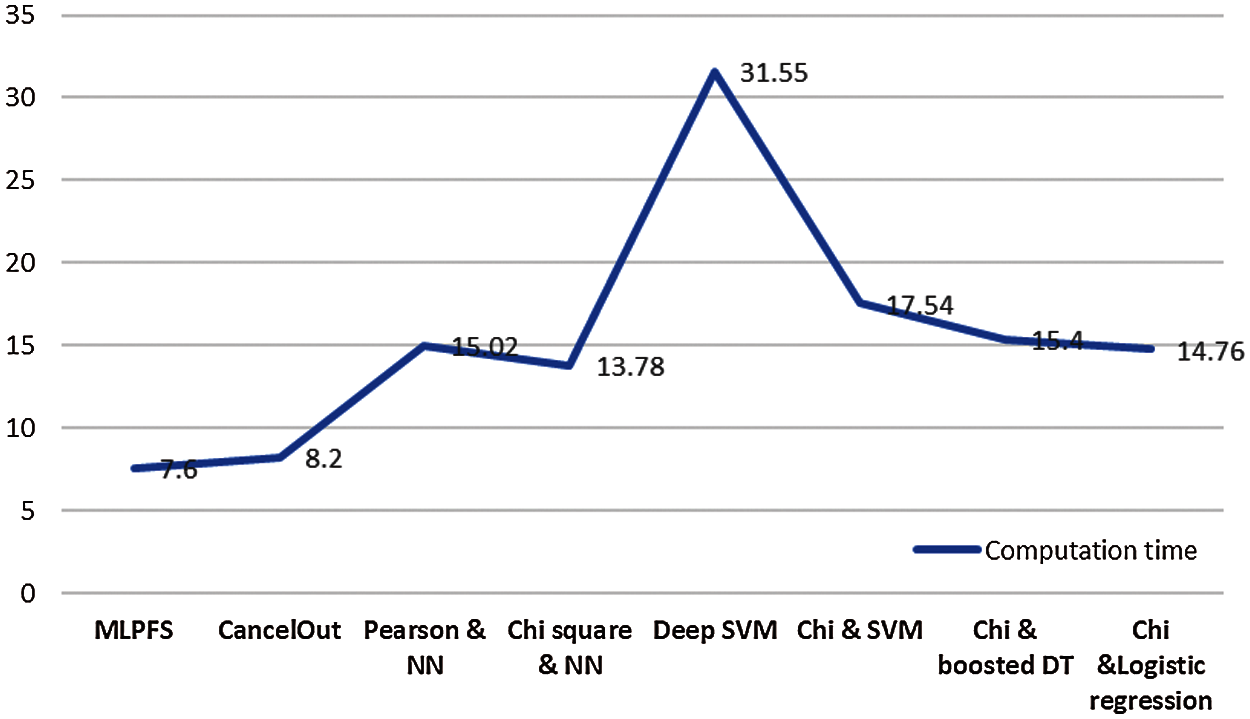
Figure 4: Computation time for the tested algorithms on SARS-CoV-2 RT-PCR data set
Additionally, results indicate that MLPFS achieved at least 8% and 2% higher precision for the first and third datasets. Also, it achieved nearly 2%, 1% higher recall and 26%, 9% higher f1 score for the second and third datasets. Regarding the processing time, as depicted in Figs. 4–6, the MLPFS has been recorded as the minimum processing time compared to the other experimented models where it finished the complete process in 7.6, 28.7, and 5.01 s for the three used datasets respectively. The Cancelout DNN is next in speed with 8.2, 29.5, and 5.2 s. Finally, validation accuracy per epoch for the eight algorithms on the three utilized datasets is displayed in Figs. 7–9.
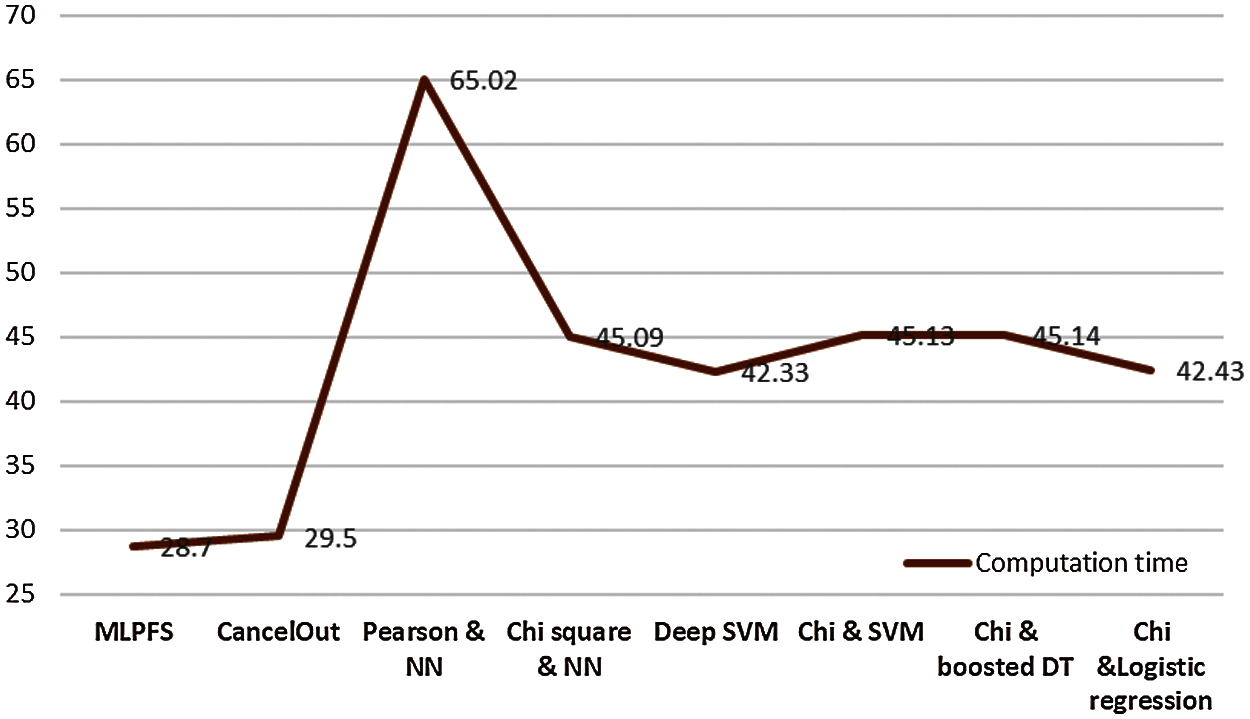
Figure 5: Computation time for the tested algorithms on second Covid-19 data set
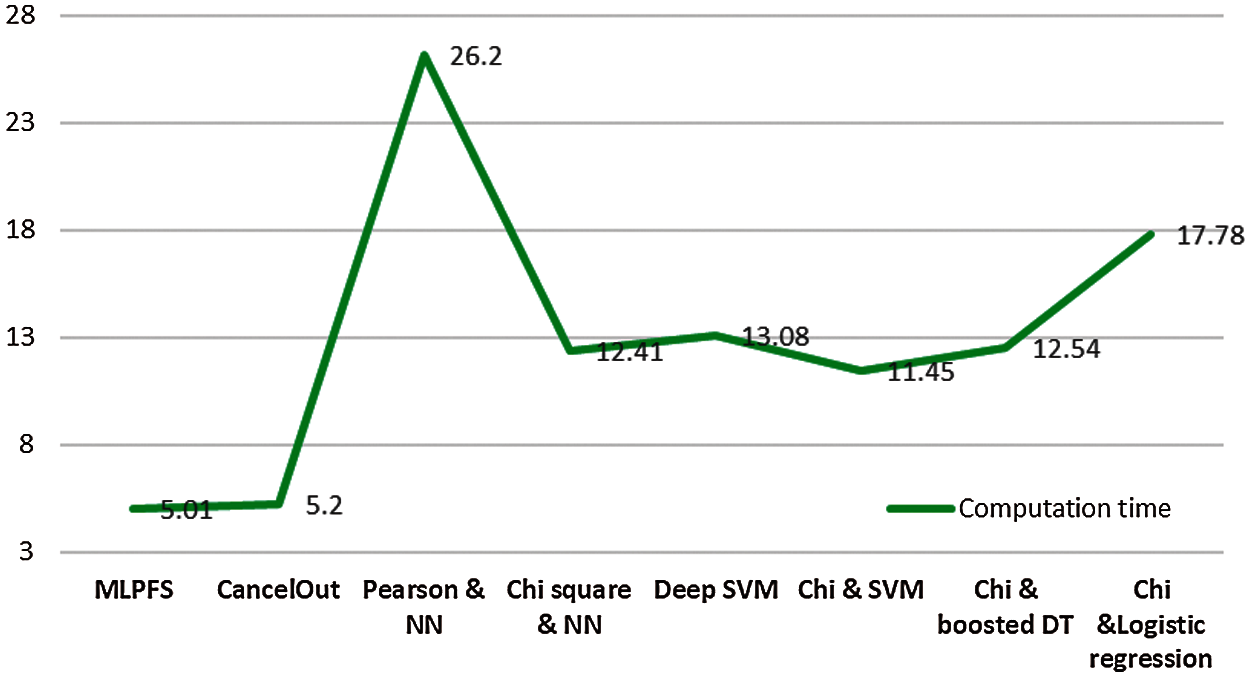
Figure 6: Computation time for the tested algorithms on ICU data set
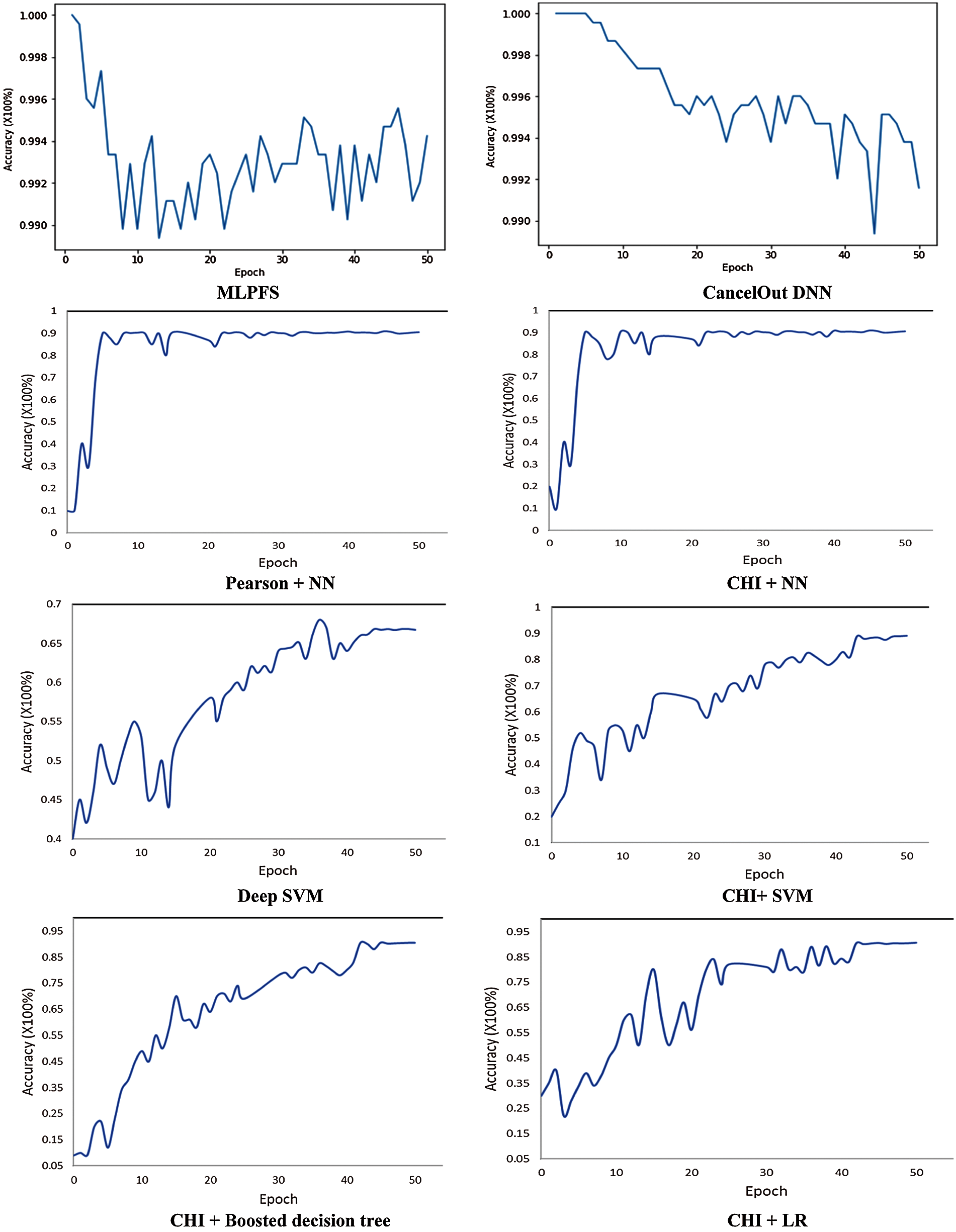
Figure 7: Validation accuracy per epoch for SARS-CoV-2 RT-PCR
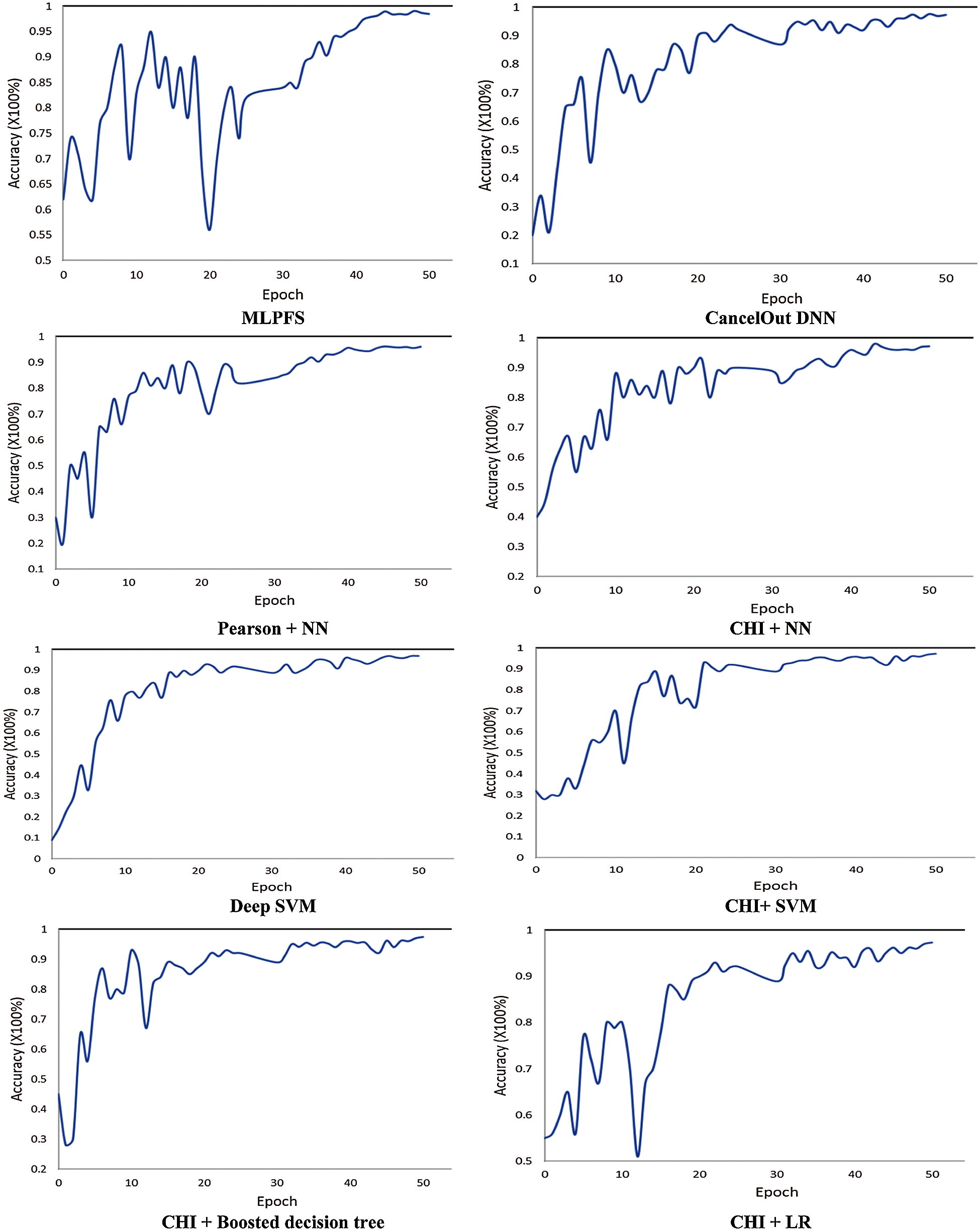
Figure 8: Validation accuracy per epoch for second Covid-19 dataset
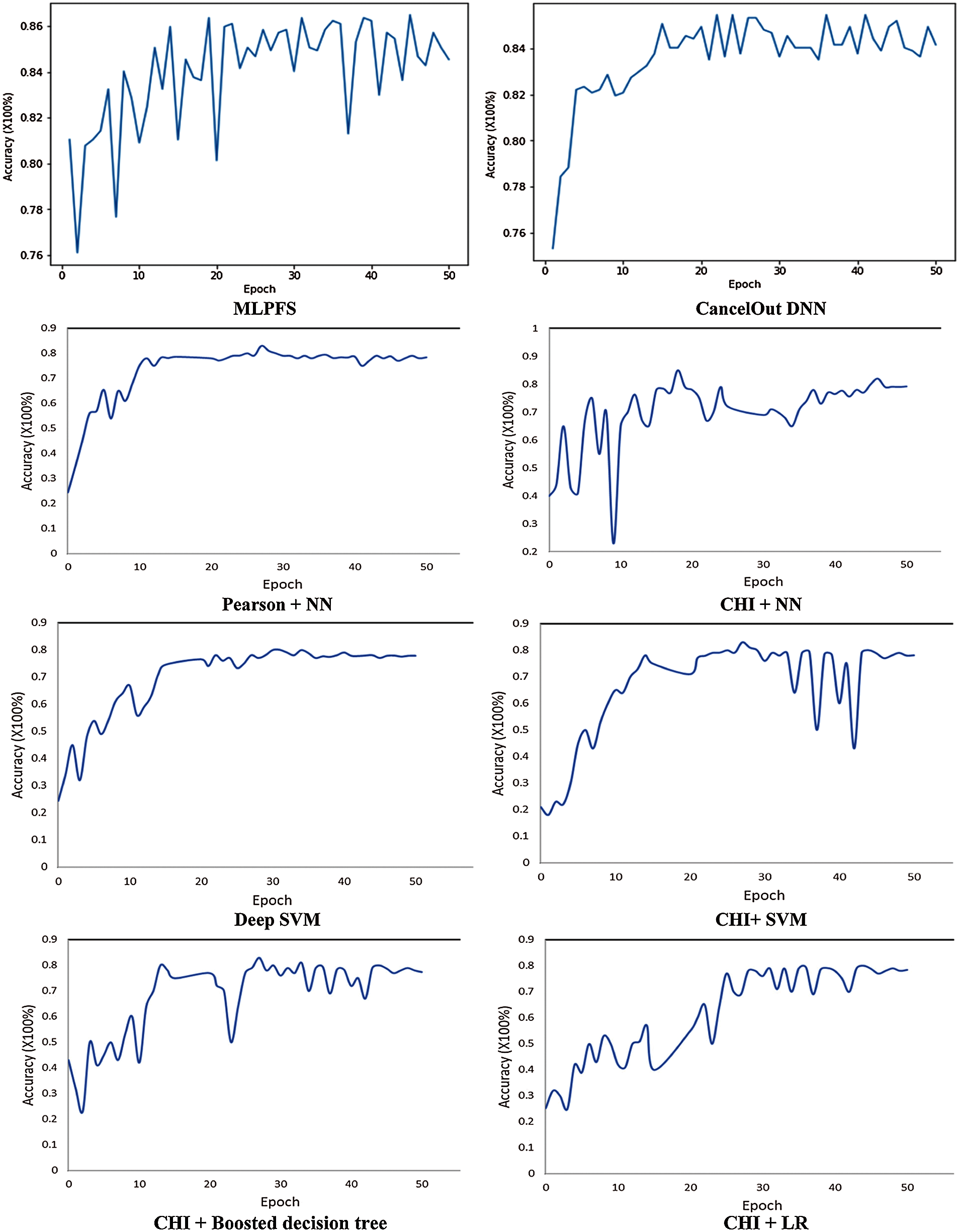
Figure 9: Validation accuracy per epoch for ICU dataset
Up to now, COVID-19 is still a pandemic and threatens the lives of many people. Data mining techniques play an essential role in diagnosing and treating COVID-19. This work presents MLPFS, an MLP-based classification model for COVID-19 prediction with a feature selection and weighting layer. Three Clinical COVID-19 datasets were used for our experiment. MLPFS's performance was evaluated against seven different classification models. The evaluation results showed that MLPFS outperformed all the other tested in terms of accuracy indicators, number of extracted features, and processing time.
1https://www.kaggle.com/einsteindata4u/covid19
2https://github.com/mdcollab/covidclinicaldata
3https://www.kaggle.com/S%C3%ADrio-Libanes/covid19
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors have declared that there is no conflict of interest. And there are non-financial competing interests.
1. W. M. Shaban, A. H. Rabie, A. I. Saleh and M. A. Abo-elsoud, “A new COVID-19 patients detection strategy (CPDS) based on hybrid feature selection and enhanced KNN classifier,” Knowledge-Based Syststems, vol. 205, pp. 1–18, 2020. [Google Scholar]
2. M. Babiker, E. Karaarslan and Y. Hoşcan, “A hybrid feature-selection approach for finding the digital evidence of web application attacks,” Turkish Journal of Electrical Engineering & Computer Sciecne, vol. 27, no. 6, pp. 4102–4117, 2019. [Google Scholar]
3. J. Zhang, X. Hu, P. Li, W. He, Y. Zhang et al., “A hybrid feature selection approach by correlation-based filters and SVM-RFE,” in Proc. Int. Conf. of Pattern Recognition, Stockholm, Sweden, pp. 3684–3689, 2014. [Google Scholar]
4. N. S. Marono, A. A. Betanzos and M. T. Sanroman, “Filter methods for feature selection–A comparative study,” In Intelligent Data Engineering and Automated Learning, vol. 4881, UK, Springer-Verlag, Berlin Heidelberg, pp. 178–187, 2014. [Google Scholar]
5. S. Chowdhury, X. Dong and X. Li, “Recurrent neural network based feature selection for high dimensional and low sample size micro-array data,” in Proc. Int. Conf. on Big Data, Big Data, CA, USA, pp. 4823–4828, 2019. [Google Scholar]
6. V. Borisov, J. Haug and G. Kasneci, “Cancelout: A layer for feature selection in deep neural networks,” in Proc. Int. Conf. on Artificial Neural Networks, Munich, Germany, pp. 72–83, 2019. [Google Scholar]
7. B. Kaddar, H. Fizazi and D. E. Mansouri, “Convolutional neural network features selection based on analysis of variance,” in Proc. Int. Conf. on Theoretical and Applicative Aspects of Computer Science, Skikda, Algeria, 2019. [Google Scholar]
8. L. S. Ho and V. Dinh, “Consistent feature selection for neural networks via adaptive group lasso,” in Proc. NeurIPS, Vancouver, Canada, pp. 1–31, 2020. [Google Scholar]
9. P. Bugata and P. Drotar, “Feature selection based on a sparse neural-network layer with normalizing constraints,” IEEE Transactions on Cybernetics, vol. 14, no. 8, pp. 1–12, 2021. [Google Scholar]
10. M. R. Hossain, A. M. Than Oo and A. B. Shawkat Ali, “The combined effect of applying feature selection and parameter optimization on machine learning techniques for solar power prediction,” American Journal of Energy Research, vol. 1, no. 1, pp. 7–16, 2013. [Google Scholar]
11. R. A. Iqbal, “Correlation aided neural networks: a correlation based approach of using feature importance to improve performance,” in Proc. Int. Conf. on Informatics, Electronics & Vision, Dhaka, Bangladesh, pp. 70–75, 2012. [Google Scholar]
12. Q. Wang, J. Zhang, S. Song and Z. Zhang, “Attentional neural network: Feature selection using cognitive feedback,” in Proc. Int. Conf. on Neural Information Processing Systems, USA, pp. 2033–2041, 2014. [Google Scholar]
13. D. C. Mocanu, E. Mocanu, P. Stone, P. H. Nguyen, M. Gibescu et al., “Scalable training of artificial neural networks with adaptive sparse connectivity inspired by network science,” Nature Communication, vol. 9, no. 1, pp. 1–12, 2018. [Google Scholar]
14. A. G. Akintola, A. Balogun, F. B. Lafenwa-Balogun and H. A. Mojeed, “Comparative analysis of selected heterogeneous classifiers for software defects prediction using filter-based feature selection methods,” FUOYE Journal of Engineering and Technology, vol. 3, no. 1, pp. 1–6, 2018. [Google Scholar]
15. M. Rostami, K. Berahmand and S. Forouzandeh, “A novel method of constrained feature selection by the measurement of pairwise constraints uncertainty,” Journal of Big Data, vol. 7, no. 1, pp. 1–21, 2020. [Google Scholar]
16. B. Liu, Z. Zhang, J. Yan, N. Zhang, H. Zha et al., “A deep learning approach with feature derivation and selection for overdue repayment forecasting,” Applied Science, vol. 10, no. 23, pp. 1–18, 2020. [Google Scholar]
17. H. Jiang, Q. Hu, Z. Zhi, J. Gao, Z. Gao et al., “Convolution neural network model with improved pooling strategy and feature selection for weld defect recognition,” Welding in the World, vol. 65, no. 4, pp. 731–744, 2021. [Google Scholar]
18. I. M. Nasir, M. A. Khan, M. Yasmin, J. H. Shah, M. Gabryel et al., “Pearson correlation-based feature selection for document classification using balanced training Inzamam,” Sensors, vol. 20, pp. 1–18, 2020. [Google Scholar]
19. S. H. Lee, K. Y. Kim and Y. Shin, “Effective feature selection method for deep learning-based automatic modulation classification scheme using higher-order statistics,” Applied Sciences, vol. 10, no. 2, pp. 1–14, 2020. [Google Scholar]
20. Y. Huang, W. Jin, Z. Yu and B. Li, “Supervised feature selection through deep neural networks with pairwise connected structure,” Knowledge-Based Systems, vol. 204, pp. 106–202, 2020. [Google Scholar]
21. D. Roy, K. S. Murty and C. K. Mohan, “Feature selection using deep neural networks,” in Proc. Int. Joint Conf. on Neural Networks, Killarney, Ireland, 2015. [Google Scholar]
22. M. A. Wojtas and K. Chen, “Feature importance ranking for deep learning,” in Proc. NeurIPS, Vancouver, Canada, pp. 1–10, 2020. [Google Scholar]
23. E. E. Bron, M. Smits, W. J. Niessen and S. Klein, “Feature selection based on the SVM weight vector for classification of dementia,” IEEE Journal of Biomedical Health and Informatics, vol. 19, no. 5, pp. 1617–1626, 2015. [Google Scholar]
24. V. R. Christo, H. Nehemiah, B. Minu and A. Kannan, “Correlation-based ensemble feature selection using bioinspired algorithms and classification using backpropagation neural network,” Computational and Mathematical Methods in Medecin, vol. 2019, pp. 1–17, 2019. [Google Scholar]
25. H. Liu, X. Shi, D. Guo, Z. Zhao and Yimin, “Feature selection combined with neural network structure optimization for HIV-1 protease cleavage site prediction,” Biomed Research International, vol. 2015, pp. 1–11, 2015. [Google Scholar]
26. S. Kim and J. Park, “Hybrid feature selection method based on neural networks and cross-validation for liver cancer with microarray,” IEEE Access, vol. 6, pp. 78214–78224, 2018. [Google Scholar]
27. Y. Y. Lu, Y. Fan, J. Lv and W. S. Noble, “Deeppink: Reproducible feature selection in deep neural networks,” in Proc. NeurIPS, Montréal, Canada, pp. 1–11, 2018. [Google Scholar]
28. R. C. Chen, C. Dewi, S. W. Huang and R. E. Caraka, “Selecting critical features for data classification based on machine learning methods,” Journal of Big Data, vol. 7, no. 1, pp. 1–26, 2020. [Google Scholar]
29. K. Thirumoorthy and K. Muneeswaran, “Feature selection for text classification using machine learning approaches,” National Academy Science Letter, pp. 1–6, 2021. https://doi.org/10.1007/s40009-021-01043-0. [Google Scholar]
30. A. M. Khanday, S. T. Rabani, Q. R. Khan, N. Rouf and M. Mohi Ud Din, “Machine learning based approaches for detecting COVID-19 using clinical text data,” International Journal of Information Technology, vol. 12, no. 3, pp. 731–739, 2020. [Google Scholar]
31. E. Avila, A. Kahmann, C. Alho and M. Dorn, “Hemogram data as a tool for decision-making in COVID-19 management: Applications to resource scarcity scenarios,” PeerJ, vol. 2020, no. 6, pp. 1–14, 2020. [Google Scholar]
32. M. R. Mondal, S. Bharati, P. Podder and P. Podder, “Data analytics for novel coronavirus disease,” Informatics in Medicine Unlocked, vol. 20, pp. 2–13, 2020. [Google Scholar]
33. A. Mollalo, K. M. Rivera and B. Vahedi, “Artificial neural network modeling of novel coronavirus (COVID19) incidence rates across the continental United States,” International Journal of Environmental Research and Public Health, vol. 17, no. 12, pp. 1–13, 2020. [Google Scholar]
34. B. Keshtegar, S. Heddam and H. Hosseinabadi, “The employment of polynomial chaos expansion approach for modeling dissolved oxygen concentration in river,” Environmental Earth Science, vol. 78, no. 1, pp. 1–18, 2019. [Google Scholar]
35. J. M. Nazzal, I. M. El-Emary, S. A. Najim and A. Ahliyya, “Multilayer perceptron neural network (MLPs) for analyzing the properties of Jordan oil shale,” World Applied Sciences Journal, vol. 5, no. 5, pp. 546–552, 2008. [Google Scholar]
36. A. Salem, A. Sharieh, A. Sleit and R. Jabri, “Enhanced authentication system performance based on keystroke dynamics using classification algorithms,” KSII Transaction on Internet and Information Systems, vol. 13, no. 8, pp. 4076–4092, 2019. [Google Scholar]
37. Y. Wang, Y. Li, Y. Song and X. Rong, “The influence of the activation function in a convolution neural network model of facial expression recognition,” Applied Science, vol. 10, no. 5, pp. 1–20, 2020. [Google Scholar]
38. K. He, X. Zhang, S. Ren and J. Sun, “Delving deep into rectifiers: Surpassing human-level performance on imagenet classification,” in Proc. IEEE Int. Conf. of Computer Vision, Santiago, Chile, pp. 1026–1034, 2015. [Google Scholar]
39. M. Hosseinzadeh, O. H. Ahmed, M. Y. Ghafour, F. Safara, H. Karaman et al., “A multiple multilayer perceptron neural network with an adaptive learning algorithm for thyroid disease diagnosis in the internet of medical things,” Journal of Supercomputing, vol. 77, no. 4, pp. 3616–3637, 2021. [Google Scholar]
40. H. P. N. Nagarajan, H. Mokhtarian, H. Jafarian, S. Dimassi, S. Baskrani-Balani et al., “Knowledge-based design of artificial neural network topology for additive manufacturing process modeling: A new approach and case study for fused deposition modeling,” Journal of Mechanical Desgin, vol. 141, no. 2, pp. 1–12, 2019. [Google Scholar]
41. A. F. Daru, M. B. Hanif and E. Widodo, “Improving neural network performance with feature selection using Pearson correlation method for diabetes disease detection,” JUITA Journal Informatica, vol. 9, no. 1, pp. 123, 2021. [Google Scholar]
42. O. S. Bachri, Kusnadi, M. Hatta and O. D. Nurhayati, “Feature selection based on CHI square in artificial neural network to predict the accuracy of student study period,” International Journal of Civil Engeering Technology, vol. 8, no. 8, pp. 731–739, 2017. [Google Scholar]
43. O. Al-Harbi, “A comparative study of feature selection methods for dialectal arabic sentiment classification using support vector machine,” Information Retrieval Technology, vol. 19, no. 1, pp. 167–176, 2019. [Google Scholar]
44. Y. Coadou, “Boosted decision trees and applications,” EPJ Web of Conferences, vol. 55, pp. 1–25, 2013. [Google Scholar]
45. B. Umaña-Hermosilla, H. de la Fuente-Mella, C. Elórtegui-Gómez and M. Fonseca-Fuentes, “Multinomial logistic regression to estimate and predict the perceptions of individuals and companies in the face of the covid-19 pandemic in the Ñuble region, Chile,” Sustainability, vol. 12, no. 22, pp. 1–20, 2020. [Google Scholar]
46. Z. Qi, B. Wang, Y. Tian and P. Zhang, “When ensemble learning meets deep learning: A new deep support vector machine for classification,” Knowledge-Based Systems, vol. 107, pp. 54–60, 2016. [Google Scholar]
47. M. Abadi, P. Barham, J. Chen, Z. Chen, A. Davis et al., “Tensorflow: A system for large-scale machine learning,” in Proc. 12th USENIX Symposium on Operating Systems Design and Implementation, Savannah, GA, USA, pp. 265–283, 2016. [Google Scholar]
48. M. Sokolova, N. Japkowicz and S. Szpakowicz, “Beyond accuracy, F-score and ROC: A family of discriminant measures for performance evaluation,” in Proc. Australasian Joint Conf. on Artificial Intelligence, Hobart, Australia, pp. 1015–1021, 2006. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |