Computers, Materials & Continua DOI:10.32604/cmc.2022.023657
Article

Design of QoS Aware Routing Protocol for IoT Assisted Clustered WSN

Ashit Kumar Dutta1, S. Srinivasan2, Bobbili Prasada Rao3, B. Hemalatha4, Irina V. Pustokhina5, Denis A. Pustokhin6 and Gyanendra Prasad Joshi7,*

1Department of Computer Science and Information Systems, College of Applied Sciences, Almaarefa University, Riyadh, 13713, Kingdom of Saudi Arabia
2Saveetha School of Engineering, Saveetha Institute of Medical and Technical Sciences, Saveetha Nagar, Thandalam, Chennai, 602105, India
3Department of Electrical and Electronics Engineering, Vignan's Institute of Information Technology, Visakhapatnam, 530049, India
4Department of Electronics and Communication Engineering, Thirumalai Engineering College, Kancheepuram, 631551, India
5Department of Entrepreneurship and Logistics, Plekhanov Russian University of Economics, 117997, Moscow, Russia
6Department of Logistics, State University of Management, 109542, Moscow, Russia
7Department of Computer Science and Engineering, Sejong University, Seoul, 05006, Korea
*Corresponding Author: Gyanendra Prasad Joshi. Email: joshi@sejong.ac.kr
Received: 15 September 2021; Accepted: 20 October 2021

Abstract: In current days, the domain of Internet of Things (IoT) and Wireless Sensor Networks (WSN) are combined for enhancing the sensor related data transmission in the forthcoming networking applications. Clustering and routing techniques are treated as the effective methods highly used to attain reduced energy consumption and lengthen the lifetime of the WSN assisted IoT networks. In this view, this paper presents an Ensemble of Metaheuristic Optimization based QoS aware Clustering with Multihop Routing (EMO-QoSCMR) Protocol for IoT assisted WSN. The proposed EMO-QoSCMR protocol aims to achieve QoS parameters such as energy, throughput, delay, and lifetime. The proposed model involves two stage processes namely clustering and routing. Firstly, the EMO-QoSCMR protocol involves cross-entropy rain optimization algorithm based clustering (CEROAC) technique to select an optimal set of cluster heads (CHs) and construct clusters. Besides, oppositional chaos game optimization based routing (OCGOR) technique is employed for the optimal set of routes in the IoT assisted WSN. The proposed model derives a fitness function based on the parameters involved in the IoT nodes such as residual energy, distance to sink node, etc. The proposed EMO-QoSCMR technique has resulted to an enhanced NAN of 64 nodes whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS methods have resulted in a lesser NAN of 2, 10, 42, and 51 rounds. The performance of the presented protocol has been evaluated interms of energy efficiency and network lifetime.

Keywords: Internet of things; wireless sensor networks; clustering; routing; metaheuristics; cluster head selection; QoS parameters

1  Introduction

Internet of Things (IoT) is globally suggested to use in various applications for interlinking various networks. In recent days IoTs are used in various heterogeneous networks such as medical networks, vehicular networks, mobile networks as well as sensor networks [1]. In particular, the sensor network or WSN can improve the distributed intelligence and communication protocols for smart devices and various other equipment, which is combined to form a novel futuristic internet solution in IoT. The WSNs are emerging as an advanced platform that is useful in lots of applications like healthcare, environmental monitoring, intelligence surveillance, smart cities, military, etc. In these applications, small sensors act as nodes to collect and transmit the information to a base station or sink node [2]. An individual sensor node is a self-operating device which is connected wirelessly and is spatially distributed. So every individual node can simultaneously sense, process, and interact with one another. The price of IoT systems has decreased dramatically, opening up a number of possibilities to boost potential innovation and deployments [3]. Researchers have been exploring the Wireless Sensor Networks technology (WSNs) for over a decade and, along with numerous routing methods, different techniques have been proposed by the researchers with regard to reducing the packet and frame size of medium access control (MAC) and physical layers. Various other unsophisticated processes, energy combination with applied fusion techniques, time, placement, and safety mechanisms have been made aware of. They enrich fundamental infrastructures, high-level abstractions that are assisted by operating system designs, and large-scale management systems to handle data generated in an appropriate way [4]. The energy control of the IoT networks is now becoming self-sufficient. Fig. 1 illustrates the overview of WSN.

Figure 1: Overview of WSN

WSN provides extremely flexible control and monitoring at an efficient cost since they are infrastructure-less and autonomous [5]. The costs of a single node are efficient as the node in WSN are constrained based on the memory, processing, energy, as well as transmission resource. Since energy is one of the key problems, where IoT serves as a compromising region which links billions of WSNs. In MANET the networks node are free to transfer everywhere in the network. The importance and functioning of the present system in industry are occasionally converted to the consistent solution render with IoT. Although IoT assures opportunity to establish the reliable system, energy utilization seem to be a key constraint in IoT network.

In general, the dynamic nature of the WSN environments is because of the absence/presence of the hurdle, exhaustion of sensor battery, mobility of the sensor, sink nodes, and unstable weather situations between the nodes in the network. Because of the fact, that there is a continuous variation in the routes among the nodes, that require reacting and tracing via efficient routing protocols [6]. Thus, carrying out the network routings is one of the key challenges due to the nonstatic node that arbitrarily moves in the predefined searching area. Secure node multi-casting routing approach improves the security by electing the route according to the less amount of communications as well generate a bandwidth minimum multi-cast trees. This would resist each threat involving wormhole attacks. For IoT applications, the message is distributed to some nodes via multi-cast transmission. The multi-cast routing protocols establish multicast routes to send data packets among source and destination. For example, applications in IoT with multi-cast transmissions update the price in a market on electronic shelf labels. Literature divides the routing protocol into geographic and non-geographic based protocols. In the event of nongeographic-based solution, the requested packet is flooded from the multi-cast source to each destination node, while, in geographic based multi-cast routing, the node knows the position by a GPS device [7]. Multi-channel routing reduces the congestion and interference to improve the data rate and reduce the energy utilization which ensures multiple QoS limitations. Alternatively, the network topology from adoptive to dynamic assists better efficiency in multi-media communications of IoT. It is necessary to effective multi-cast routing protocol for addressing the need for multi-media communication in a high dynamic IoT environment.

Shende et al. [8] proposes an energy aware multipath routing protocol depending on the optimization, CrowWhale-ETR, i.e., the incorporation of WOA & CSA depending on the objective function developed by the trust factor and energy of the node. At first, the energy and trust of the node are calculated to establish the route i.e., optimally selected by a CWOA approach. These optimally selected paths are utilized to transmit the information, where the trust and energy of a single node are upgraded after the single communication, thus the secured node could be elected, and that enhances the secured transmission in the network. Tandon et al. [9] propose a Bio-inspired cross-layer routing (BiHCLR) protocol to achieve effectively and energy preserving routing in WSN assisted IoT. Initially, the deployed sensor nodes are arranged in the form of a grid as per the grid-based routing strategy. Then to enable energy preservation in BiHCLR, the fuzzy logic approach is executed to select the Cluster Head (CH) for every cell of the grid. Then a hybrid bio-inspired algorithm is used to select the routing path. The hybrid algorithm combines moth search and Salp Swarm optimization techniques.

Chouhan et al. [10] present the multipath routing protocol with the presented optimization algorithm, called TSGWO method in the IoT enabled WSN system. With the multipath routing protocol, the multi-path is developed using multi-path source nodes to many destinations. The multi-path source node packet is forward to multiple destinations at the same time. Initially, the node in IoT enabled WSN system is inspired together and perform the CH election with FGSA approach, and later the multi-path routing method is made based on the presented TSGWO algorithm where the routing paths are elected by taking into account the fitness variables such as trust factors and QoS parameters.

In Sunitha et al. [11], very much efficient and robust Evolutionary computing enabled WSN routing protocols are improved to energy efficacy and QoS. This presented method encompasses 2 major features NCAMND mines/exploits the network parameters or dynamic node for identifying malicious node, and EC-DDFP models learn through network or node connectivity and accessibility data to attain a dual disjoint path without shared component for ensuring energy effective routing and QoS centric. Jazebi et al. [12] proposed a routing system for IoT with SFLA method. RISA employs SFLA for finding content based paths among the source node and destination node. RISA could decrease power utilization as well as enhance the lifetime of network with a suitable data aggregation system.

Jaiswal et al. [13] propose a GWO based CH election method for WSN consider different aspects such as node degree, energy levels of the node, intracluster distance, priority factor, and sink distance. Also, this study addresses the routing via QoS aware relay nodes election for a reliable and effective intercluster routing from CH to BS. In Hajiee et al. [14], an ETOR approach is presented based on a new hybrid FF. The method has 2 major phases: one is for selecting a secured node according to the tolerance constant and another is for selecting an opportunistic node from the secured node to implement routing. ETOR employs the multipath route techniques using an intracluster and intercluster multihop transmission method. Furthermore, the secure and optimal routes are elected according to a new hybrid FF.

Shafiq et al. [15] introduce the RCBRP algorithm for identifying the routing path where lesser energy is expended for enhancing the lifetime of the network. The system is proposed in 6 phases for exploring transmission. Also, proposed the 2 approaches: i) routing and energy effective clustering approach and ii) power utilization and distance measurement approach. The system consumes lesser energy and balances the load by clustering the smart device. Ruan et al. [16] proposed a PUDCRP approach. In the PUDCRP algorithm, the distribution of the cluster would alter vigorously while few nodes get fail. The PSO algorithms are employed for determining the areas where the candidate CH node is placed. The adoptive clustering approach depending on node distribution makes the cluster distribution highly reasonable that balances the power utilization of the system efficiently. Though several clustering and routing techniques are available in the literature, only few works have focused on QoS aware clustering and routing process. Therefore, it is needed to design effective QoS aware clustering with routing techniques for IoT assisted WSN.

This paper presents an Ensemble of Metaheuristic Optimization based QoS aware Clustering with Multihop Routing (EMO-QoSCMR) Protocol for IoT assisted WSN. The proposed EMO-QoSCMR protocol aims to achieve QoS parameters such as energy, throughput, delay, and lifetime. The proposed model involves two stage processes namely clustering and routing. Firstly, the EMO-QoSCMR protocol involves cross-entropy rain optimization algorithm based clustering (CEROAC) technique to select an optimal set of cluster heads (CHs) and construct clusters. Besides, oppositional chaos game optimization based routing (OCGOR) technique is employed for the optimal set of routes in the IoT assisted WSN. The proposed model derives a fitness function based on the parameters involved in the IoT nodes. The performance of the presented protocol has been evaluated interms of energy efficiency and network lifetime.

2  The Proposed EMO-QoSCMR Technique

In this study, the EMO-QoSCMR protocol is designed to accomplish QoS in WSN by accomplishing energy efficiency and maximizing network lifetime. The EMO-QoSCMR protocol involves a two stage process namely CEROAC based clustering and OCGOR based routing. The detailed operations of these modules are given in the following.

2.1 Process Involved in CEROAC Based Clustering

At this stage, the CEROAC technique is derived to select the CHs and organize clusters. In ROA, the rain behaviours are inspired as it is determined in the traditional subsection. All the solutions to a problem can be referred to as raindrops. Based on this issue, few points in the answer space is determined in an arbitrary manner as raindrop falls on the ground. The main feature of a drop of rain is the radius. The radius of all the raindrops might be constrained as time passes and it is improved as raindrops are connected to alternative drops. Once the primary answer population is made, the radius of all droplets is assigned in a random fashion to a constraint range. In addition, every droplet validates the neighbourhood according to the size. Individual droplet which isn't yet connected just verify the end limits of the position that has covered. To solve the issue in dimension space, all the droplets are composed of n variables. Therefore, in the first phase, the minimum and maximum limits of the parameter are validated as the limit is calculated by the radius of the droplets [17]. Followed by, two endpoints of the parameter are tested and it is continued until attaining the last parameter. Next, the cost of initial droplets is updated by shifting in a downward direction. It is implemented for all the droplets, as well as the cost, and place of all the droplets would be allocated. The radius of droplets would be altered in two manners:

Once 2 droplets using radius r1 & r2, they are closer to one another with the general field and they connect to develop large droplets of radius R:

R=(r1n+r2n)1/n(1)

Let n be the amount of parameters for each droplet. Once a droplet using radius r1 isn't moved, according to the soil features, which is shown as α, water is observed with the soil.

R=(αr1n)1/n(2)

Apparently, αdemonstrates the amount of droplets which was absorbed in each iteration from zero to hundred percent. Moreover, it determines the minimum value for the droplet radius rmin, whereas droplets with the least radius of that rmin will be reduced.

As abovementioned, the population values can be decreased afterward few iterations, and maximal droplet is placed with a large area of analysis. By improving the analyses method, the local possible search of drop is proportionally maximized to the diameter of droplet. Hence, by increasing the amount of rounds, weak droplets get vanished or are linked to strong drops using the maximal area of analysis, and the primary population will be intensively decreased and discover the accurate answer (s). It is supposed that there are some variants between the recently proposed optimization method in ROA and the newly presented search models placed RFA approach, i.e., given below:

•   In ROA, the early population numbers are adapted afterward each iteration due to the link of neighbouring drop. It leads to enhance the search ability of a method and considerably reduce the optimization cost.

•   When the size of droplets is altered, the connecting of adjacent droplet or adsorption with the soils are carried out. Such performances modify the possible search of all the droplets and classify the droplet.

•   In RFA, and alternative searching methods, each population is made up of neighbour points and the droplets are improved one-step in an arbitrary manner. Likewise, all the populations identify the optimum path to the least points. When the path is established, it is moved in downwards iteratively using step, and the cost function is decreased in an individual iteration.

Based on the idealization and approximation of the models, the rain methods are described. In depth, tuning parameters of these methods such as basic raindrops radius, initial raindrops amount (population amount), etc. Followed by, the values are assigned to each droplet based on the cost function. Next, all the droplets are shifted in downwards direction. Therefore, nearer droplet is integrated with each other, that results in enhanced result. When droplets are ended at the lowest points, the radius begins to reduce gradually caused the precision of the answer to be improved. Subsequently, it is relevant for identifying an extremal point of the objective function.

In order to improve the performance of the ROA, CEROAC technique is derived by the inclusion of the CE concept. The CE approach for optimization could be determined in the following equation.

S(x∗)=maxx∈X⁡S(x),(3)

Whereas γ∗ represent the maximal on the provided set X, the x∗ denotes the maximum x.S indicates the efficiency metric. While evaluating sample X iteratively, a set of indicators function I{S(X)≥γ} are determine. I{S(X)≥γ} represent the S(x) as above in the level γ for sample x. For a vector u, m of likelihood density function parameter, the optimization problems could be converted to estimate the likelihood Pu(S(X)≥γ). Integrating with indicator function, the likelihood could be evaluated as follows:

l(γ)=Pu(S(X)≥γ)=∑x⁡I{S(X)≥γ}f(x,u)=EuI{S(X)≥γ},(4)

Whereas P denotes the likelihood related to the likelihood density function (., u), and Eu represents the probability function. If γ=γ∗,l(γ) could be evaluated by:

argmax1N∑i=1N⁡I{S(X)≥γ}lnf(Xi,v).(5)

Xi is generated with the help of f(.,v). It is noteworthy that the CE approach find the improved sampling density f(.,v∗) thus the optimum solutions could be sampled [18].

The process of CE could be summarised into 3 major stages:

1.    Produce an arbitrary instance from Gaussian distribution using mean mu and standard deviation s.

2.    Choose a certain amount of optimal samples from the entire sample.

3.    Upgrade mu & s according to the optimal samples using best fitness.

To increase the network lifespan of a clustered based WSN, the CEROAC technique is derived to choose an optimal set of best positions CH. To satisfy this aim, a multiobjective FF is created that has 4 variables like degree of node, residual node energy, coverage ratio, and intracluster distance. The derivation and definition of this parameter can be expressed in the following:

Node Energy (Nodeenergy): The presented clustering protocol utilizes maximal energy node as an optimal candidate for the election of CH. As a CH endure further responsibilities like data aggregation and cluster management when compared to CM, it must have improved energy budget for facilitating balanced power utilization in the network. It is determined as the residual energy of the sensors.

MinimizeNodeenergy=∑i=1m⁡1ECHi(6)

Now ECHi denotes residual energy of ith CH and m represent amount of CHs.

(b)   Degree of node (Nodedegree): It is determined as an amount of sensors accessible from a CH. It is employed for balancing the load at CH [19].

MinimizeNodedegree=∑i=1m⁡|CMi|(7)

Here, |CMi| is the number of cluster members of the ith CH.

(c)   Intracluster distance (Dintro−cluster): It is determined as the normal intracluster distance of CH from its CM. This variable ensures the quality of cluster and increases the connection quality among CH and CMs.

MinimizeDintra−cluster=∑j=1m⁡[∑i=1|CMj|⁡d(CHj,CMi)|CMj|](8)

Now, d(CHj, CMi) is the Euclidean distance among jth CH & ith CM.

(d)   Coverage of CH (CCH): The major goal of this variable is to remove the unclustered sensors and to guarantee participation of the few left-out sensors in the clustering. This variable reduces the amount of left-out nodes which cannot be a portion of the cluster. Therefore, enhance the coverage of the elected CH. The parameter could be calculated in the following equation:

MinimizeCHcoverage=(N−m)−∑j=1m⁡|CMj|∑j=1m⁡|CMj|(9)

where N indicates an overall amount of sensors, m denotes amount of CHs and |CMj| represent quantity of cluster members in the jth cluster.

The last multi-objective FF (F) could be equated as weighted amount of the aforementioned 4 variables which are given in the following equation:

F=w1×Nodeenergy+w2×Nodedegree+w3×Dintro−cluster+w4×CHcoveroge(10)

Linear programming equations for an optimum location CH election problems are given below:

subject to

Nodeenergy>Eth(11)

Nodedegree≤NDth(12)

Dinfro−cluster<Tmax(13)

w1+w2+w3+w4=1,w1,w2,w3,andw4∈(0,1)(14)

Here, Eth is threshold node energy, NDth denotes the threshold value of node amount value is initiated by N/m.Tmax represents the maximal broadcast range of a sensor.

2.2 Process Involved in OCGOR Based Routing

At this stage, the OCGOR based routing technique is designed to elect an optimal set of routes to sink nodes. The CGO technique has been presented dependent upon the projected rules of chaos theory. The fundamental models of fractals and chaos games were employed for formulating a mathematical method to the CGO technique. Due to the fact that several natural evolution techniques continue a population of solutions that are progressed with arbitrary alteration as well as selection. The CGO technique assumes the amount of solution candidates (S) during this determination that signifies few suitable seeds inside a Sierpinski triangle. The Sierpinski triangle has been assumed as search space to solution candidates from the optimized technique. The mathematical model of these features is as follows:

S=S1:Sn=[S11S21Si1Sn1S12S22⋮Si2Sn2S1jS2jSijSnj⋯⋱⋯S1d⋮Snd](15)

i=1,2…n.J=1,2….d. Where n implies the amount of eligible seeds (solution candidate) inside the Sierpinski triangle (search space), and d represents the dimensional of these seeds. The first places of these eligible seeds were defined arbitrarily in the search space as:

S1j(0)=S1,minj+R(S1,minj−S1,maxj)(16)

where R represents the arbitrary number from the interval of 0 and 1. The procedure to the initial seed has been demonstrated under:

Seedi1=Si+xi∗(yi∗Globalbest−zi∗MeanValue)(17)

where xi,yi,zi signifies the arbitrary integer of 0 or 1 for demonstrating the possibilities of rolling a dice. Afterward, the schematic presentation of explained procedure to the second seed has been formalized as under [20]:

Seedi2=Globalbest+xi∗(yi∗Si−zi∗MeanValue)(18)

A schematic demonstration of seeds 3rd and 4th has been explained as under:

Seedi3=MeanValue+xi∗(yi∗Si−zi∗Globalbest)(19)

Seedi4=Si(Sik=Sik+Rand)(20)

where k implies the arbitrary integer from the interval of 0 and 1. The CGO technique, distinct formulations were projected to xi that manages the movement restricts of seeds.

xi={2∗rand(Ψ∗rand)+1(Ω∗rand)+∼Ω(21)

where Rand represents the uniformly distributed arbitrary number from the interval of 0 and 1. But Ψ and Ω are arbitrary integers from the interval of 0 and 1.

To boost the convergence rate of the CGO algorithm, OBL concept is employed. OBL concepts are utilized for enhancing the quality of initial population solutions with the divergence of the solution. The OBL scheme searches in each direction in the search space, namely opposite and original solution directions. At last, the OBL concepts consider the appropriate solution from every solution.

The opposite amount x could be defined as a real value over the interval x∈[lb,ub]. The opposite amount of x could be represented as x~ and employed for computing the value:

x~=lb+ub−x(22)

The aforementioned formula could be normalized to apply in a search space with multiple dimensions. So, for normalization, each search agent and the corresponding opposite positions can be defined using Eqs. (23)–(24):

x=[x1,x2,x3,…xD](23)

x~=[x~1,x~2,x~3,…,x~D](24)

The value of each individual component in x~ could be calculated as Eq. (25):

x~j=lbj+ubj−xjwherej=1,2,3,…,D(25)

Now, the fitness function is f(.). Once the fitness value f(x~) of the opposite solutions exceed f(x) of the actual solutions x, then x=x~; otherwise x=x.

The process included in the CGO algorithm is listed as follows.

Population initiation X as xi where (i=1,2,…, n) .

Compute the opposite position of individuals OX as x~i where (i=1,2,…, n).

Elect the n fittest individuals from {X∪⁡OX} and denote the novel primary population of CGO algorithm.

In routing, the FF of the OCGOR technique implies the data forwarding route in CH to sink node. The importance of FF is related to CH being reachable from the network, and further locations are added in the sink. The superiority of FF is interrelated to m+1, where m represents the number of CH included in the system. Now, Fi=(Fi,1(t), Fi,2(t)…Fi,m+1(t)) be ith FF, and the location Fi,d,∀i1≤ i≤m+1,∀d1≤ d≤m+1, determine next hop send the data to BS. It is highly focused on determining optimum route from CH to sink. It can be achieved with the help of FF in various sub objectives such as node degree, intervehicle distance, and energy. For delivering data, successive hop achieves the data and transferring to BS. Therefore, maximum RE of next hop is prominently prioritized. Moreover, key sub objective using energy f1 is enhanced by:

f1=∑i=1m⁡ECHi(26)

Distance is represented as distance between CH to next hop & sink. While the distance is minimum afterward the energy utilization rate is also diminished. The next objectives to minimize the distance amongst CHs to sink is estimated by:

f2=1∑i=1m⁡dis(CHi,NH)+dis(NH,BS)(27)

Node degree represents the number of vehicles in next hop. When the next hop is comprised of limited CH members, then it employs minimum energy in attained data in neighbouring members and remains active for a long period. Later, the next hop using limited node degree is prominently selected. Lastly, node degree is determined based on node degree of f3 as follows:

f3=1Σi=1mIi(28)

Afterward, the weighted sum model is executed for each sub objective and transformed as single objective as shown in Eq. (29). Now α1,α2 & α3 represents the weight assigned to all the sub objectives, and αiε(0,1) and α1+α2+α3=1.

Fitness=α1(f1)+α2(f2)+α3(f3)(29)

3  Performance Validation

This section investigates the performance analysis of the EMO-QoSCMR with existing techniques under different dimensions. The proposed model is simulated using MATLAB. Tab. 1 shows the result analysis of EMO-QoSCMR model under count of rounds interms of TEC.

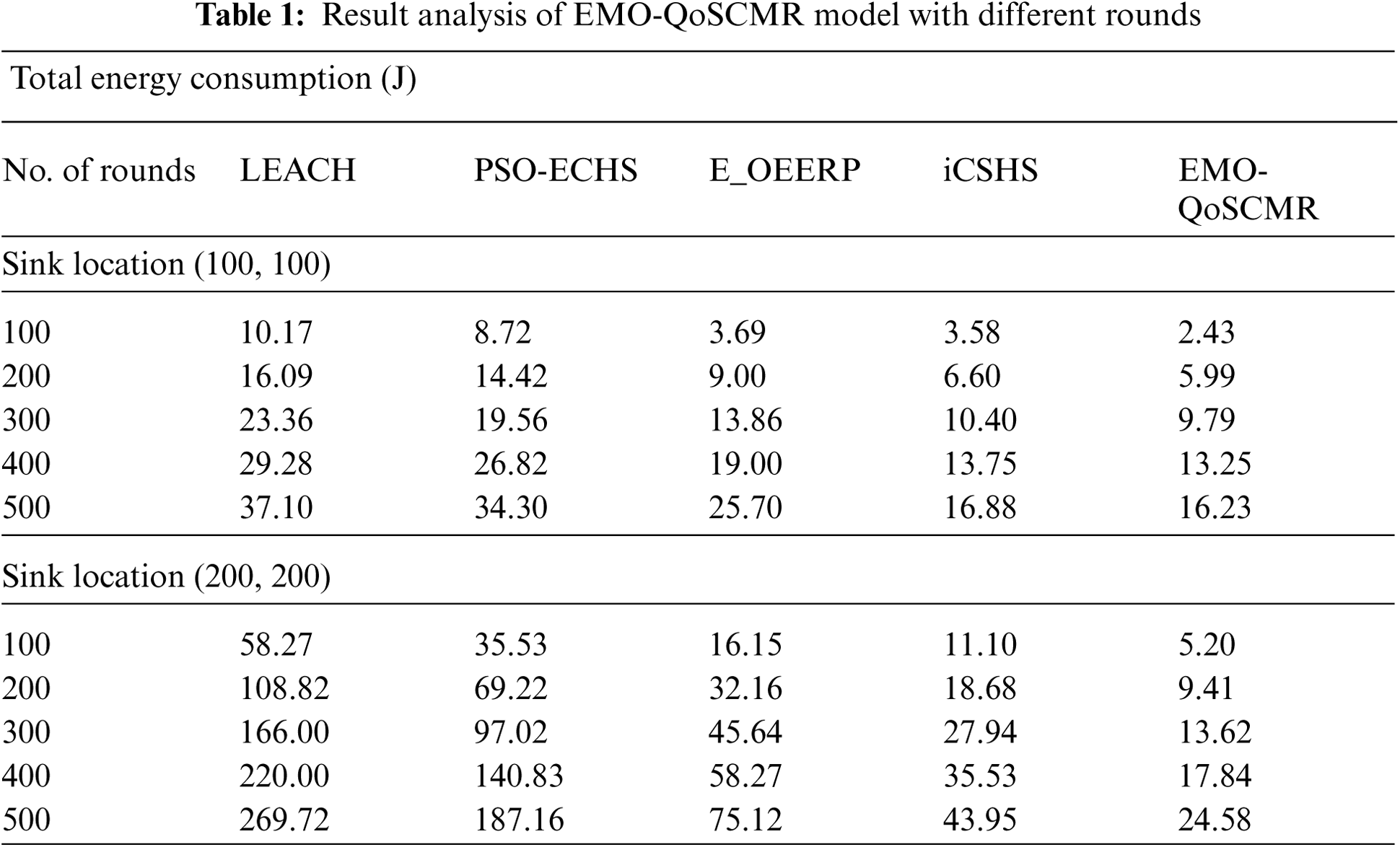
Fig. 2 investigates the TEC analysis of the EMO-QoSCMR technique with other techniques under different rounds and sink locations of (100, 100). The figure showcased that the EMO-QoSCMR technique has resulted in the least TEC. For instance, with 100 rounds, the EMO-QoSCMR technique has accomplished a minimal TEC of 2.43J whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS techniques have obtained a maximum TEC of 10.17J, 8.72J, 3.69J, and 3.58J respectively. In addition, with 300 rounds, the EMO-QoSCMR technique has accomplished a lesser TEC of 9.79J whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS methods have gained a maximal TEC of 23.36J, 19.56J, 13.86J, and 10.40J correspondingly. Moreover, with 500 rounds, the EMO-QoSCMR technique has accomplished a lower TEC of 16.23J whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS approaches have gained a higher TEC of 37.10J, 34.30J, 25.70J, and 16.88J correspondingly.

Fig. 3 examines the TEC analysis of the EMO-QoSCMR technique with other techniques under varying rounds and sink locations of (200, 200). The figure outperformed that the EMO-QoSCMR approach has resulted in a lower TEC. For instance, with 100 rounds, the EMO-QoSCMR manner has accomplished a minimal TEC of 5.20J whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS techniques have obtained a maximum TEC of 58.27J, 35.53J, 16.15J, and 11.10J correspondingly. Likewise, with 300 rounds, the EMO-QoSCMR algorithm has accomplished a reduced TEC of 13.62J whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS techniques have obtained a maximal TEC of 166J, 97.02J, 45.64J, and 27.94J respectively. Besides, with 500 rounds, the EMO-QoSCMR manner has accomplished a lower TEC of 24.58J whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS methods have gained an increased TEC of 269.72J, 187.16J, 75.12J, and 43.95J correspondingly.

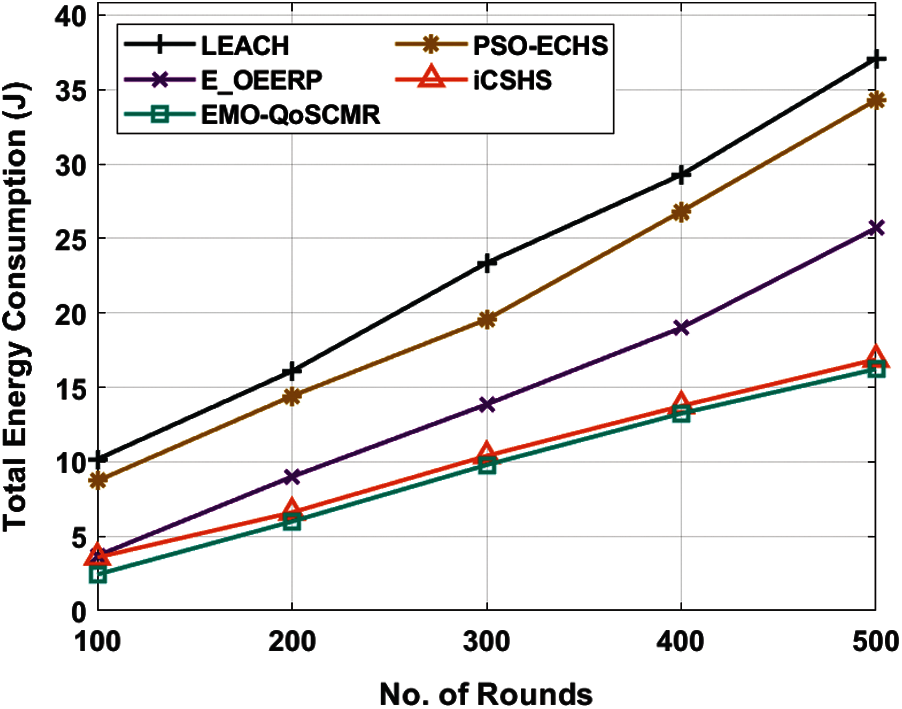
Figure 2: TEC analysis of EMO-QoSCMR model under sink location (100, 100)

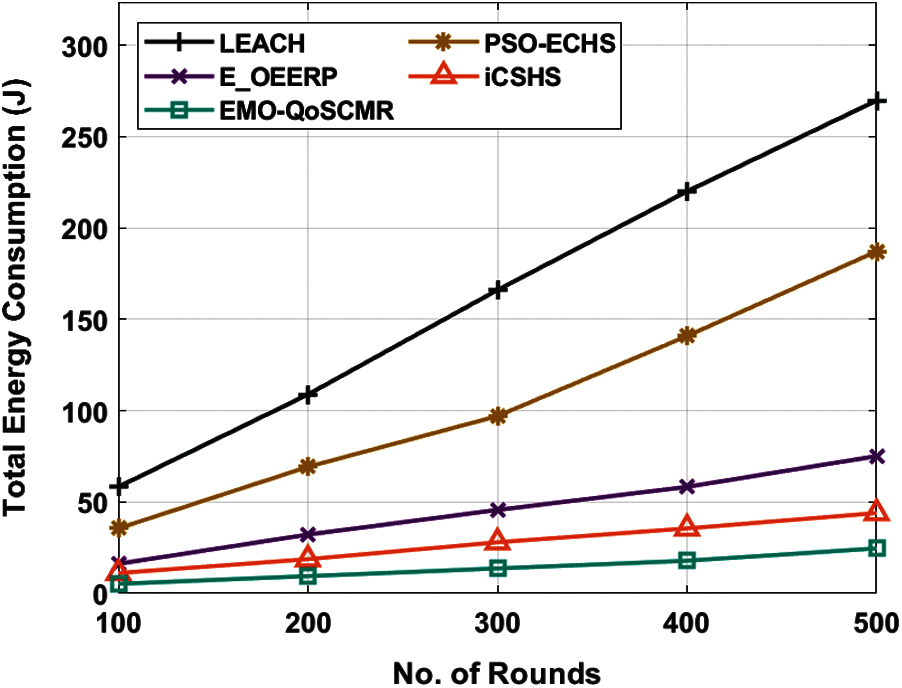
Figure 3: TEC analysis of EMO-QoSCMR model under sink location (200, 200)

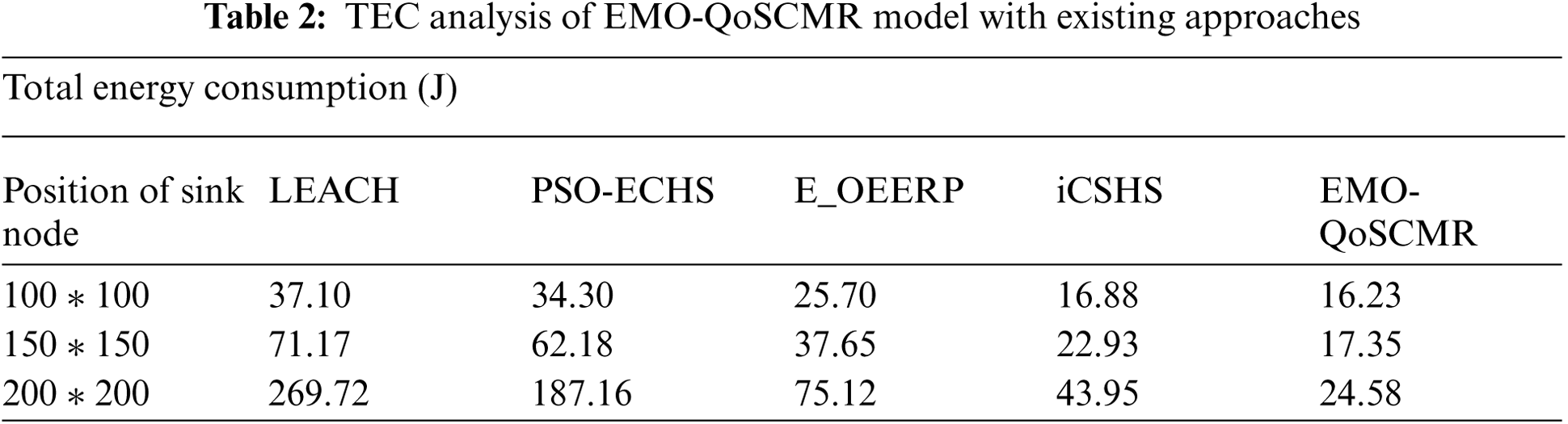
An overall TEC analysis of the EMO-QoSCMR technique with existing techniques takes place in Tab. 2 and Fig. 4 under varying positions of sink node. The figure demonstrated that the EMO-QoSCMR technique has offered the least TEC over the other existing techniques. For instance, with 100 * 100 position of sink node, the EMO-QoSCMR technique has obtained a lower TEC of 16.23J whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS techniques have attained a higher TEC of 37.10J, 34.30J, 25.70J, and 16.88J respectively. Also, with 150 * 150 position of sink node, the EMO-QoSCMR method has achieved a lesser TEC of 17.35J whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS techniques have attained a higher TEC of 71.17J, 187.16J, 75.12J, and 43.95J correspondingly. Besides, with 200 * 200 position of sink node, the EMO-QoSCMR technique has obtained a reduced TEC of 24.58J whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS methodologies have gained a maximal TEC of 269.72J, 187.16J, 75.12J, and 43.95J correspondingly.

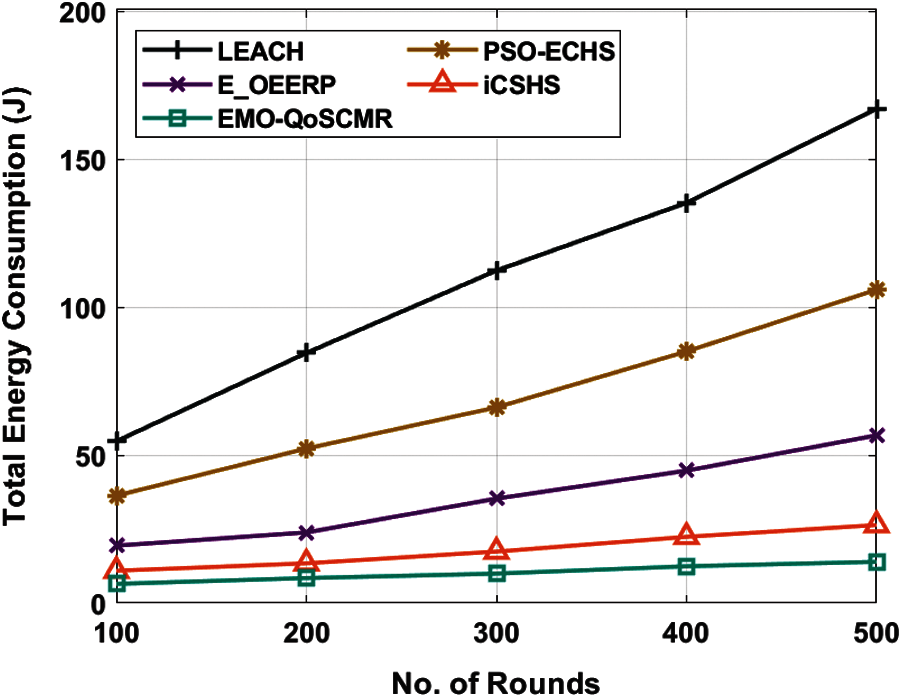
Figure 4: Result analysis of EMO-QoSCMR model interms of TEC

Tab. 3 offers the network lifetime analysis of the EMO-QoSCMR technique over the other techniques under diverse sink locations.

Fig. 5 investigates the results analysis of the EMO-QoSCMR technique interms of Number of Alive Nodes (NAN) with the sink location of 100, 100. The figure depicted that the EMO-QoSCMR technique has gained an increased NAN over the other techniques. For instance, with 200 rounds, the EMO-QoSCMR technique has offered an improved NAN of 197 nodes whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS techniques have resulted in a reduced NAN of 139, 160, 188, and 196 rounds. Meanwhile, with 800 rounds, the EMO-QoSCMR approach has existed a higher NAN of 145 nodes whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS methods have resulted in a lesser NAN of 61, 79, 132, and 141 rounds. Eventually, with 1200 rounds, the EMO-QoSCMR manner has offered a superior NAN of 116 nodes whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS techniques have resulted in a reduced NAN of 31, 41, 99, and 111 rounds. Likewise, with 1600 rounds, the EMO-QoSCMR technique has offered an improved NAN of 94 nodes whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS manners have resulted in a minimum NAN of 12, 23, 79, and 85 rounds. Similarly, with 2000 rounds, the EMO-QoSCMR technique has offered an improved NAN of 79 nodes whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS approaches have resulted in a minimum NAN of 6, 16, 54, and 65 rounds.

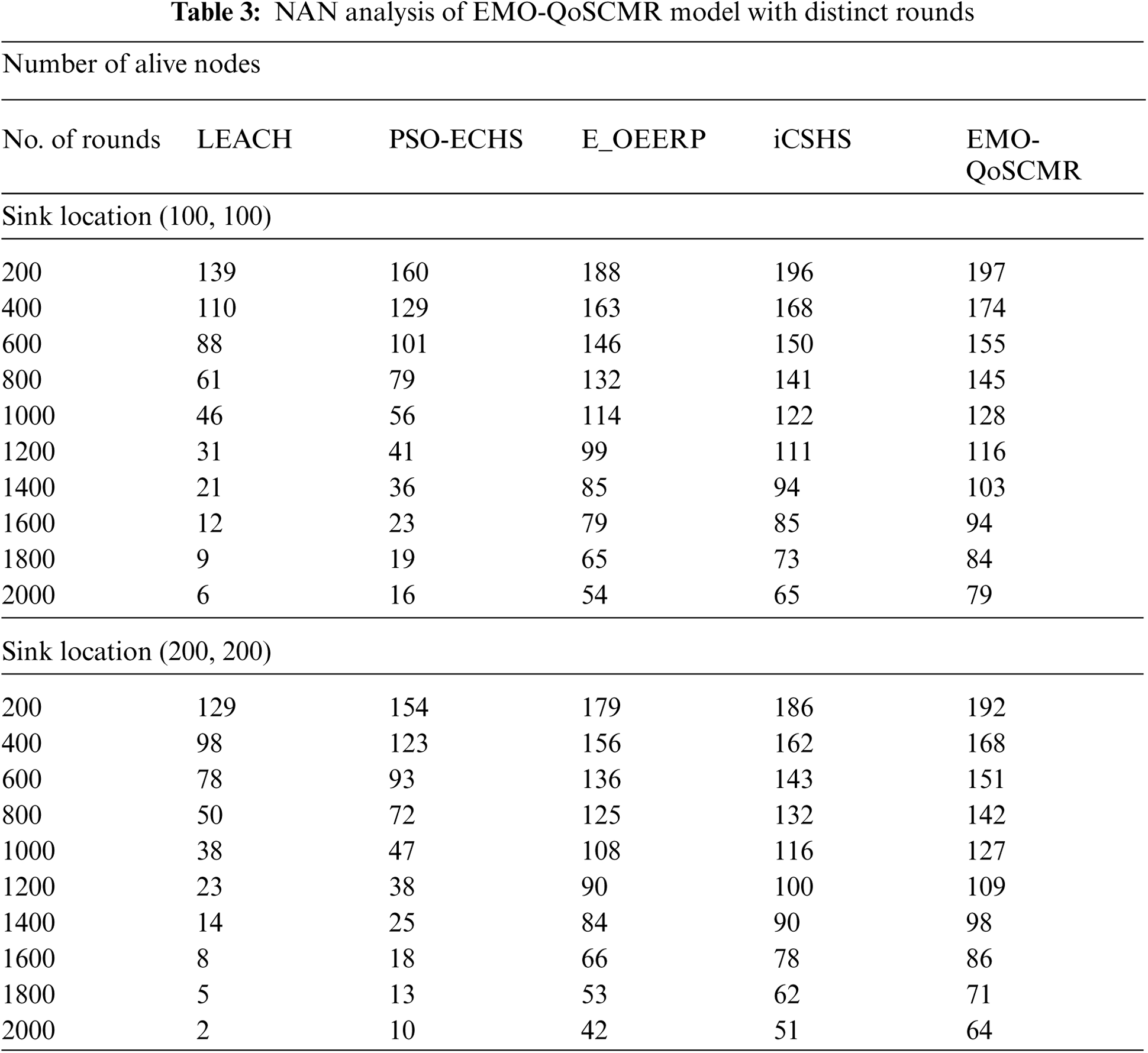
Fig. 6 inspects the outcomes analysis of the EMO-QoSCMR approach with respect to NAN with the sink location of 200, 200. The figure depicted that the EMO-QoSCMR technique has gained an increased NAN over the other algorithms. For instance, with 200 rounds, the EMO-QoSCMR technique has offered a maximal NAN of 192 nodes whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS techniques have resulted in a reduced NAN of 129, 154, 179, and 186 rounds. Meanwhile, with 800 rounds, the EMO-QoSCMR manner has presented a higher NAN of 142 nodes whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS techniques have resulted in a reduced NAN of 50, 72, 125, and 132 rounds. Followed by, with 1200 rounds, the EMO-QoSCMR system has offered an enhanced NAN of 109 nodes whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS manners have resulted in a reduced NAN of 23, 38, 90, and 100 rounds. Similarly, with 1600 rounds, the EMO-QoSCMR technique has offered a maximum NAN of 86 nodes whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS techniques have resulted in a minimum NAN of 8, 18, 66, and 78 rounds. Also, with 2000 rounds, the EMO-QoSCMR technique has accessible an enhanced NAN of 64 nodes whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS methods have resulted in a lesser NAN of 2, 10, 42, and 51 rounds.

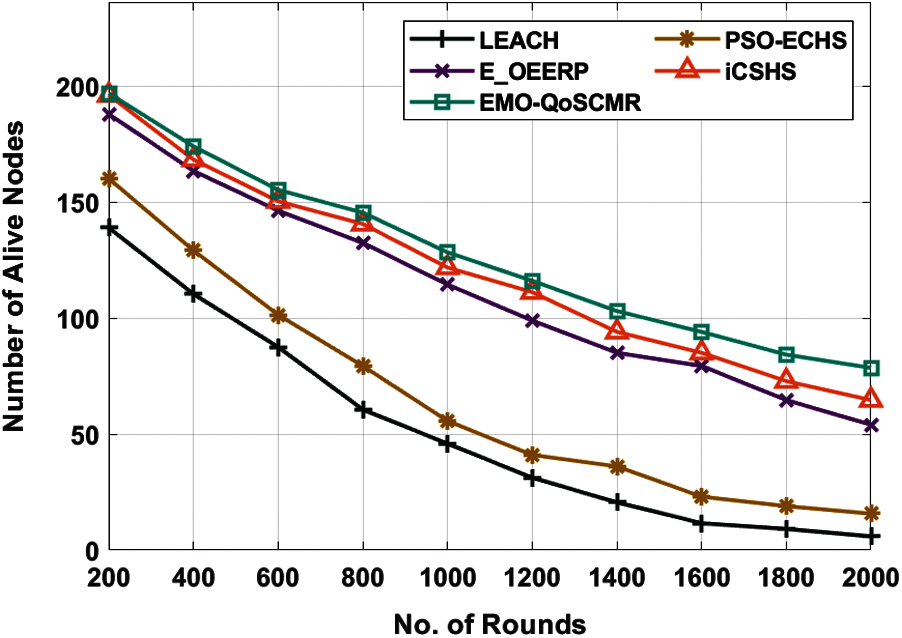
Figure 5: NAN analysis of EMO-QoSCMR model under sink location (100, 100)

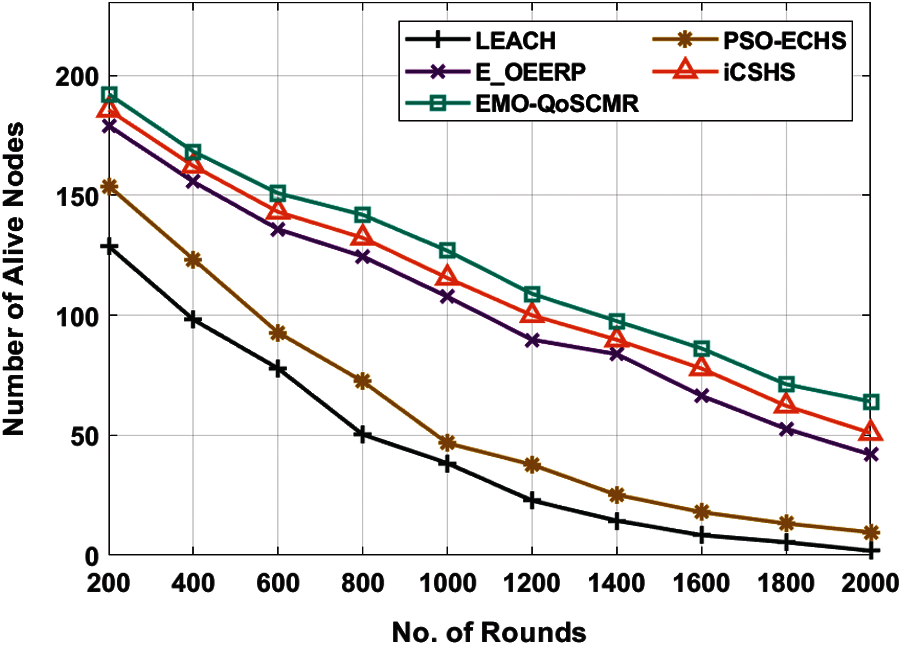
Figure 6: NAN analysis of EMO-QoSCMR model under sink location (200, 200)

4  Conclusion

In this study, the EMO-QoSCMR protocol is designed to accomplish QoS in WSN by accomplishing energy efficiency and maximizing network lifetime. The EMO-QoSCMR protocol involves a two stage process namely CEROAC based clustering and OCGOR based routing. The proposed EMO-QoSCMR protocol aims to achieve QoS parameters such as energy, throughput, delay, and lifetime. In addition, the EMO-QoSCMR protocol involves OCGOR for the optimal set of routes in the IoT assisted WSN. The proposed model derives a fitness function based on the parameters involved in the IoT nodes. The proposed EMO-QoSCMR technique has resulted to an enhanced NAN of 64 nodes whereas the LEACH, PSO-ECHS, E-OEERP, and iCSHS methods have resulted in a lesser NAN of 2, 10, 42, and 51 rounds. The performance of the presented protocol has been evaluated interms of energy efficiency and network lifetime. As a part of future scope, the data aggregation and MAC scheduling techniques can be designed to improve the overall performance of the WSN.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  X. M. Huang, R. Yu, J. W. Kang, Z. Q. Xia and Y. Zhang, “Software defined networking for energy harvesting internet of things,” IEEE Internet of Things Journal, vol. 5, no. 3, pp. 1389–1399, 2018. [Google Scholar]

 2.  J. Wang, X. Gu, W. Liu, A. K. Sangaiah, and H. -J. Kim, “An empower hamilton loop based data collection algorithm with mobile agent for WSNs,” Human-Centric Computing and Information Sciences, vol. 9, no. 1, pp. 18, 2019. [Google Scholar]

 3.  J. Uthayakumar, M. Elhoseny and K. Shankar, “Highly reliable and low-complexity image compression scheme using neighborhood correlation sequence algorithm in wsn,” IEEE Transactions on Reliability, vol. 69, no. 4, pp. 1398–1423, 2020. [Google Scholar]

 4.  B. Yin and X. T. Wei, “Communication-efficient data aggregation tree construction for complex queries in IoT applications,” IEEE Internet of Things Journal, vol. 6, no. 2, pp. 3352–3363, 2018. [Google Scholar]

 5.  S. Arjunan and P. Sujatha, “Lifetime maximization of wireless sensor network using fuzzy based unequal clustering and ACO based routing hybrid protocol,” Applied Intelligence, vol. 48, no. 8, pp. 2229–2246, 2018. [Google Scholar]

 6.  X. Yin, K. Q. Zhang, B. Li, A. K. Sangaiah, J. Wang, “A task allocation strategy for complex applications in heterogeneous cluster-based wireless sensor networks,” International Journal of Distributed Sensor Networks, vol. 14, no. 8, pp. 1–15, 2018. [Google Scholar]

 7.  T. Vaiyapuri, V. S. Parvathy, V. Manikandan, N. Krishnaraj, D. Gupta et al., “A novel hybrid optimization for cluster-based routing protocol in information-centric wireless sensor networks for iot based mobile edge computing,” Wireless Personal Communications, 2021. https://doi.org/10.1007/s11277-021-08088-w. [Google Scholar]

 8.  D. K. Shende and S. S. Sonavane, “CrowWhale-ETR: CrowWhale optimization algorithm for energy and trust aware multicast routing in WSN for IoT applications,” Wireless Networks, vol. 26, no. 6, pp. 4011–4029, 2020. [Google Scholar]

 9.  A. Tandon, P. Kumar, V. Rishiwal, M. Yadav and P. Yadav, “A bio-inspired hybrid cross-layer routing protocol for energy preservation in wsn-assisted iot,” KSII Transactions on Internet and Information Systems, vol. 15, no. 4, pp. 1317–1341, 2021. [Google Scholar]

10. N. Chouhan and S. C. Jain, “Tunicate swarm grey wolf optimization for multi-path routing protocol in iot assisted wsn networks,” Journal of Ambient Intelligence and Humanized Computing, 2020. https://doi.org/10.1007/s12652-020-02657-w. [Google Scholar]

11. R. Sunitha and J. Chandrikab, “Evolutionary computing assisted wireless sensor network mining for qos-centric and energy-efficient routing protocol,” International Journal of Engineering, vol. 33, no. 5, pp. 791–797, 2020. [Google Scholar]

12. S. J. Jazebi and A. Ghaffari, “RISA: Routing scheme for internet of things using shuffled frog leaping optimization algorithm,” Journal of Ambient Intelligence and Humanized Computing, vol. 11, no. 10, pp. 4273–4283, 2020. [Google Scholar]

13. K. Jaiswal and V. Anand, “A grey-wolf based optimized clustering approach to improve qos in wireless sensor networks for iot applications,” Peer-to-Peer Networking and Applications, vol. 14, no. 4, pp. 1943–1962, 2021. [Google Scholar]

14. M. Hajiee, M. Fartash and N. O. Eraghi, “An energy-aware trust and opportunity based routing algorithm in wireless sensor networks using multipath routes technique,” Neural Processing Letters, vol. 53, no. 4, pp. 2829–2852, 2021. [Google Scholar]

15. M. Shafiq, H. Ashraf, A. Ullah, M. Masud, M. Azeem et al., “Robust cluster-based routing protocol for iot-assisted smart devices in wsn,” Computers, Materials & Continua, vol. 67, no. 3, pp. 3505–3521, 2021. [Google Scholar]

16. D. Ruan and J. Huang, “A PSO-based uneven dynamic clustering multi-hop routing protocol for wireless sensor networks,” Sensors, vol. 19, no. 8, pp. 1835, 2019. [Google Scholar]

17. I. V. Pustokhina, D. A. Pustokhin, P. T. Nguyen, M. Elhoseny and K. Shankar, “Multi-objective rain optimization algorithm with WELM model for customer churn prediction in telecommunication sector,” Complex & Intelligent Systems, 2021. https://doi.org/10.1007/s40747-021-00353-6. [Google Scholar]

18. R. Tang, S. Fong, N. Dey, R. Wong and S. Mohammed, “Cross entropy method based hybridization of dynamic group optimization algorithm,” Entropy, vol. 19, no. 10, pp. 533, 2017. [Google Scholar]

19. G. P. Gupta and S. Jha, “Integrated clustering and routing protocol for wireless sensor networks using cuckoo and harmony search based metaheuristic techniques,” Engineering Applications of Artificial Intelligence, vol. 68, pp. 101–109, 2018. [Google Scholar]

20. S. Talatahari and M. Azizi, “Chaos game optimization: A novel metaheuristic algorithm,” Artificial Intelligence Review, vol. 54, no. 2, pp. 917–1004, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.