Computers, Materials & Continua DOI:10.32604/cmc.2022.020472
Article

E-mail Spam Classification Using Grasshopper Optimization Algorithm and Neural Networks

Sanaa A. A. Ghaleb1,3,4, Mumtazimah Mohamad1, Syed Abdullah Fadzli1 and Waheed A.H.M. Ghanem2,3,4,*

1Faculty of Informatics and Computing, Universiti Sultan Zainal Abidin, Kuala Terengganu, 22200, Malaysia
2Faculty of Ocean Engineering Technology and Informatics, Universiti Malaysia Terengganu, Kuala Terengganu, 21030, Malaysia
3Faculty of Engineering, University of Aden, Aden, Yemen
4Faculty of Education (Aden-Saber), University of Aden, Aden, Yemen
*Corresponding Author: Waheed A. H. M. Ghanem. Email: Waheedghanem@umt.edu.my
Received: 25 May 2021; Accepted: 30 August 2021

Abstract: Spam has turned into a big predicament these days, due to the increase in the number of spam emails, as the recipient regularly receives piles of emails. Not only is spam wasting users’ time and bandwidth. In addition, it limits the storage space of the email box as well as the disk space. Thus, spam detection is a challenge for individuals and organizations alike. To advance spam email detection, this work proposes a new spam detection approach, using the grasshopper optimization algorithm (GOA) in training a multilayer perceptron (MLP) classifier for categorizing emails as ham and spam. Hence, MLP and GOA produce an artificial neural network (ANN) model, referred to (GOAMLP). Two corpora are applied Spam Base and UK-2011 Web spam for this approach. Finally, the finding represents evidence that the proposed spam detection approach has achieved a better level in spam detection than the status of the art.

Keywords: Grasshopper optimization algorithm; multilayer perceptron; artificial neural network; spam detection approach

1  Introduction

Despite the popularity of social networking services to spread messages over the Internet, email remains at the forefront of social, academic, and business communications [1]. E-mail is a major means of disseminating information around the world at no cost via smartphones and computers, which have made e-mail messages more and more popular [2]. It is a quick means of communication for companies, government departments, and universities as well, and are used to save documents and facilitate their circulation among employees, to facilitate communication, conduct, and complete work. Notwithstanding the substantial benefits of utilizing email, the communication technology is followed by a huge number of non-requested emails and infrequently deceptive emails, represented as spam email (SE). SE is the most irritating phenomenon on the Internet that challenges individuals and global firms like Yahoo, Google, and Microsoft [3]. Two basic methods can be used for spam detection: Machine learning (ML) and knowledge filtering (KF) [4]. In a KF method, a view to create patterns and populate the detection database, different elements of the messages are analyzed using guideline filtering. When a pattern matches one of the detection policies, the message is labelled as spam. In comparison, an ML is more effective than a KF and does not require rules [5]. In order to know the classification rules in email messages, specific algorithms are used. Due to the efficacy of the ML methods, many algorithms have been used to detect spam [6].

Systematic review literature showed that the ML method in purifying mail achieves effective categorization. They include ANNs [7], Support vector machines (SVM) [8], and Naive bayes (NB) [9]. Some researchers have provided combined ML algorithms or hybridized algorithms to achieve an accurate, detection and pattern recognition method [10]. However, the use of traditional training methods depend on the gradient algorithm, has drawbacks as compared to swarm intelligence that can be applied to ANNs specifically [11–13] Gradient descent is a local search algorithm that the existing solution to generate a new solution; nevertheless, it lacks good exploration and tends to be trapped in the local minima of the search space [14–16]. In contrast, metaheuristics algorithms are an optimal solution because they have a balance between intensification and diversification and can address simultaneous adaptation in ANNs components. One of these techniques that are becoming popular in Neural networks (NN) training is the nature inspired metaheuristic algorithms (NIMAs). This is a very popular algorithm in this category; these include Genetic algorithm (GA) [17], Grasshopper optimization algorithm (GOA) [18], Ant colony optimization (ACO) [19], Particle swarm optimization (PSO) [20], and BAT algorithm [21]. This research introduces a modified ML technique of the MLP referred to as a GOA. The major benefits of this GOA are a few controlling parameters, adaptive intensification and diversification search patterns, and a gradient-free mechanism. Our approach is represented as GOAMLP, where GOA is adopted for MLPs training. The application of these algorithms in NN training for spam classification is extensively evaluated, and their performances are compared with current and traditional metaheuristic algorithms.

Several stochastic global optimization (SGO) approaches demonstrate higher accuracy and computational efficiency compared to trajectory driven approaches like Backpropagation (BP). When applying SGO techniques for trained NNs, problems related to BP are resolved [22]. SGO methods are normally inspired by physical and biological instances like PSO, ACO, or GA, etc. For example, some studies utilized the PSO for explaining the structure of the MLP model for addressing real world challenges [23]. The authors applied GA to modify the variables of an ANNs [24].

Some studies utilized several techniques concurrently. For example, research by [25] uses GA to adjust the weights of the studies model, which in turn improves the model's performance. However, the authors used a special dataset to evaluate the model. Reference [26] designed a detecting model by training BPNN via GA, where it optimizes weights of the BPNN, enhances accuracy. However, GA cannot guarantee an optimal solution. Additionally, Reference [27] introduced the negative selection algorithm (NSA) to develop variables of BPNN. The algorithm of the email is classified as self and non-self. The dataset that was used in this work is Spam Base using MLP and SVM classifiers. However, this model does not offer better performance. Reference [28] introduced the memetic algorithm (MA) which is a furtherance of convectional GA, which was applied in optimizing the relationship between weights in NN for SD. The dataset that was used in this was work Spam Base using Feedforward neural network (FFNN) classifier. However, MA lacks local optimal. Reference [29] presented Krill herd algorithm (KH), to classify ham and spam. The result demonstrates more accuracy and speedy convergence than the convectional BP paradigm. The dataset that was used in this work is SpamAssassin using FFNN classifiers. However, this model does not perform better. Reference [30] proposed spam detection model, by Biogeography-based optimization (BBO) algorithm based trained on ANN. The datasets that were used in this work are the Spam Base dataset and SpamAssassin using ANN classifiers. However, BBO lack exploiting the solutions. Reference [31] use of GA in a modification to standard ANNs and an artificial immune system for spam detection and SpamAssassin corpus was utilized for simulations. Lastly, Reference [32] proposed a new SD approach by ANNs to EBAT algorithm. The dataset that was used in this work is Spam Base and UK-2011 Web spam. This research introduces a new spam detection approach created by the most promising GOA in training MLP to address challenges faced by traditional MLP training algorithms. Two corpora are applied Spam Base and UK-2011 Web spam for this approach with better performance.

2  Methodology

The implementation of the SD approach regarding ANNs trained through GOA, as presented in Fig. 1. The aim of the new GOAMLP model was to achieve a promising score in terms of detection accuracy, global convergence, law false positive prediction, and in identifying SE with the help of the new metaheuristic algorithm called GOA algorithm for training the ANNs.

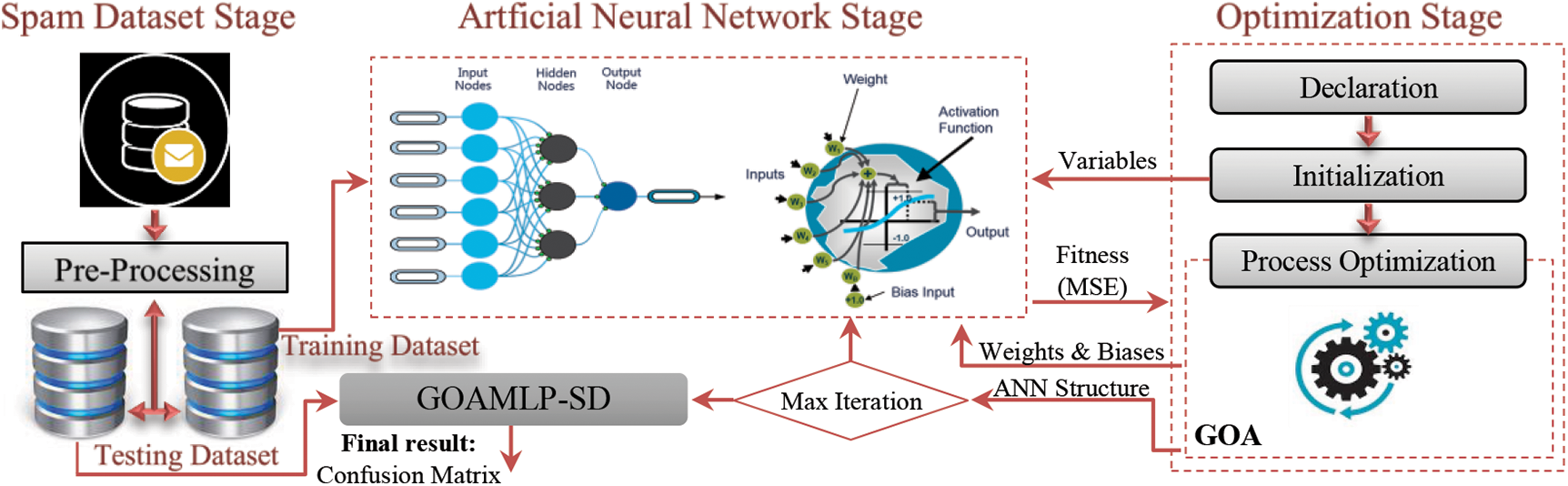
Figure 1: The GOAMLP-SD approach

MLPs were prevalent in the spam detection approach due to their efficiency in classifying mail as wanted or spam. This sort of tool considers the system's common components, the environment of electronic mailing, and statistically significant departures from expected user nature. These tools have open and extendable architectures that aid in the creation of intelligent character models in the environment. The protocol composes determining structure and variables of ANNs to learn the relationship between the incoming patterns and the target output through training. The training comprises? the protocol specifying the structure and variables of ANNs to learn the relationship between incoming patterns and target outputs. By decreasing the value of the MSE, the ANN structure and weights (w) & biases (B) of the ANNs were obtained. Then, the knowledge base (structure and w and B) is updated. The maximum number of iterations parameter (given in Fig. 1) determines when the training process should end. The final stage is carried out after obtaining the most suitable model in terms of the best ANNs structure and w and B, which were built by using the training dataset.

2.1 Grasshopper Optimization Algorithm (GOA)

The GOA is a lately proposed swarm-primarily based totally meta-heuristic [33]. As these algorithms are viewed alone in nature, they establish a big swarm of all insects. These insects construct swarm pests that negatively affect farmers and agriculture. The grasshopper's life cycle includes two stages. The nymph moves slowly a small distance, while the adult age jumps high and travels a great distance; form their movement corresponds to exploration and exploitation. A version that shows the swarming conduct of the grasshopper becomes provided in [34] and is repetitive here:

Xi=Si+Gi+Ai(1)

Xi indicates location ith grasshopper, Si shows the social interaction (SI) presented in Eq. (2), Gi indicates the gravitational force on ith grasshopper, and Ai indicates wind advection:

Si=∑810j=1j≠iN⁡s(dij)dij^(2)

N indicates the number of grasshoppers, dij indicates the length within ith and jthgrasshoppers, parameter s indicates the social forces assessed by the following Eq. (3), and dij=|xi−xj|/dij represents the unit vector from ith to ithgrasshopper.

s(r)=fer/l−e−r(3)

f and l are the attraction intensity and attraction length scale, correspondingly. In this algorithm, the SI is divided into three regions: stable, attraction, and repulsion. The “s” function gives values close to 0 with distances greater than 10 returns. If the distance between the locusts is greater, the function “s” cannot follow as strong forces. This problem can be resolved by the Gi component using the following Eq. (4):

Gi=−ge^g(4)

where g indicates gravitational variable, and e^g indicates unity vector toward the centre of earth. The wind advection Ai in Eq. (1) is computed by the following Eq. (5).

Ai=uew^(5)

u indicates continuous flow and ew^ is unity vector in wind direction. thus, their motion is closely related to the wind direction. Next plugging the values of S, G, and A in Eq. (1), the last Eq. becomes:

Xi=∑j=1,j≠iN⁡s(|xj−xi|)xj−xidij−ge^g+uew^(6)

Eq. (6) is not able to be used at once to resolve optimization problems, because the grasshoppers fast attain the comfort 0, and the swarm gadget does now no longer converge to a goal location by Saremi et al.. An enhanced version of this Eq. (7) is given as:

Xid=c(∑j=1,j≠iN⁡cubd−lbd2s(|xjd−xid|xj−xidij))+Td^(7)

where ubdandlbd are indicating the lower and upper bounds in Dth dimension, respectively. Td^ indicates the best solution found so far in the Dth dimension space, and argument c indicates the decreasing coefficient to detract from the stable, attraction, and repulsion areas. The argument c mitigates the stable area directly to count iterations and is given as:

c=cmax−Itercmax−cminitermax(8)

The parameter c1 is like the inertial w in PSO. Decrease the locust's movement in an optimal solution. Coefficient c balances the intensification and diversification. of the whole swarm by the optimal solution. The parameter c2 is used to reduce the repulsion, comfort, and attraction zones among grasshoppers. In addition, component [cubd−lbd2] linearly creases the way for grasshoppers to intensify and diversify.

The second part s(|xj−xi|) reveals a grasshopper could be repelled by searching or employing. Parameter cmax indicates the least value, cmin indicates most value, Iter is new iteration, and itermax reveals the most iterations. The GOA pseudo-code is displayed in Algorithm 1. How GOA does, at this point it is worth pointing out to initialize all the parameters such as the maximum No. of iterations, c1 & c2, and no. of populations. For each grasshopper xd, GOA starts with generating a random set xid and calculating the fitness function (FF) and the best grasshopper Td then is chosen with the best FF. After selecting the grasshopper from the previous step, three steps are performed through: 1) Normalizing the lengths amongst grasshoppers in Xid to [1,4]; 2). Modifying current grasshopper xi ∈ Xid by utilizing Eq. (7); 3) Adjusting the boundaries for the new grasshopper in the population. Finally, until the end criterion is reached, grasshopper position updates are made periodically. The grasshopper's position and the best target's fitness are returned as the best estimate for the global optimal.

2.2 The GOA Adaptation Process

The meta-heuristic algorithms have already shown great potential in solving the problem of classification or prediction of ANNs by tuning the w and B of the NN. In these approaches, the process of training involves using appropriate ANNs architecture, w and B representation, termination condition(s), and FF. Through these four aspects are adapted in GOA to suit its functions as a training method for ANNs, to provide the required needs through the ANN training process, therefore the training method using the approach algorithm in this work named as GOAMLP. The grasshopper algorithm's capacity to work with NNs has already been tested and compared to other algorithms, with encouraging results [35], our new approach is motivated by recent developments in the field. There are three basic techniques of using the meta-heuristic algorithm to train NNs. In the first stage, the algorithms are used to fixed right ANNs architecture for NNs during the learning process. Modifying the architecture could involve changing the relationship among the neurons, hidden layers, and hidden neurons. In the second stage, the algorithms are used to locate w and B that enable a minimal MSE that denotes the cost function of the NNs. The training algorithm finds appropriate values for all relation w and B to reduce the general error of the ANNs.

In the final stage, the algorithms is applied to modify the variables of the gradient descent learning algorithms. In our Reference [36] used the method which is discovering maximum w and B throughout the training. Nevertheless, this research utilizes the GOA was proposed lately, to find the optimal ANNs. GOA is shown in Algorithm 2. At the beginning of Algorithm 2, all the variables of the GOA and the NNs model are provoke, namely, cmax, cmin, itermax, then the lower and upper bounds; then a set of solutions is created unselective. The GOA has different parameters, like solution vector size (SVS), that denote the no. of success in the SV. Solution in SV is xi (i = 1, 2 …, D) is a D-dimensional vector, the dimension of solutions is described by Eq. (9). That is, D is decision variables. The ranges are given by XL and XU vectors are indicating lower and upper bounds, with uniform distance of the SV. The SV is a vector of the best SV obtained. Eq. (9) represent unit vector of SVS × D. The SV dimension is set prior to address the algorithm. Each SV is also related to a quality value regarding objective function (f(x)). Algorithm 2 illustrates that GOAMLP is same as other algorithms, that start by initializing solution memory vector denoting MLP w. Calculates the initial fitness value for every grasshopper (solution) in line 3. The MSE for individual grasshopper (solution) in the whole SV is verified and MSE of global minimum derivation in lines 4–9. In line 10, is calculated the GOA parameter Td^ and loops given to maximum iteration in line 11. Then parameterc of the GOA is updated.

SV=[x11x12⋯x1Dx21x22⋯x2Dx31x32⋯x3D⋯⋯⋱⋯xSV1xSV2⋯xSVD][f(x1)f(x2)f(x3)⋮f(xSV)](9)

Lines 13 to 19 comprise providing a little change to the GOA operator in early testing of the probability parameter P and choosing one of two alternative approaches to balance the application of the GOA operator to either the ANNs structure or its w and B.

The possibility to know the answer a parent is proportional to the amount by that its fitness is a smaller amount than other of the opposite solution's fitness. The GOA optimization process is used with a 50% probability in the ANN structure, and there is a 50% that applies the optimization process to w and B during the current iteration. If the GOA optimization is to be applied to the parental structure, the w and B neurons will be randomly attached or eliminated to fit the ANNs architecture of the solution. The no. of neurons in w and B of the SV is computed using Eqs. (11)–(13). This technology provides the GOAMLP to obtain an expanded quality of solutions with optimized ANNs structures of w and B. An efficient FF that considers both the no. of w and B connections and the error to be minimized helps the algorithm improve the FF using a small-scale model. Finding new solutions by updating GOA. If the no. of iterations exceeds the maximum no. of generations, the iterations will be stopped. Moreover, this process requires to review the active w and B connections to find the architecture of ANNs. Responsibility for selecting the ANN architecture rests with the GOA when obtaining a solution. The GOAMLP pseudocode is introduced in Algorithm 2. The solutions in the sample have two components, the first component encodes the ANNs architecture. When the result of applying random operator, P decides that the structure of the MLP is modified by another location of the grasshopper, SS determined as a binary pattern [0, 1] denoting the grasshopper's location in binary vector using a sigmoid function as presented in Eq. (10).

f(x)=1/1+e−x(10)

Eq. (10) is used on output of Eq. (9) during the process of GOA to the architecture of ANNs. When the result of the Eq. (10) is less than a specific number in the range 0, 1 thereafter the result from Eq. (10) is set to 0, on the other hand, this result is modified to one. Secondly part, locates that the w and B in ANNs model are modified. Motion of every grasshopper within ss direction is between [−1, 1]. The first population architecture solution is indiscriminately given, and the length of w and B is determined to match every structure. Finally, the w and B values are randomly generated. The MSE for a grasshopper (solution) in all SV is verified and the MSE of global minima in lines 20–25. In line 26, the GOA parameter, namely, Td^ is updated. Line 27 saves the best solution with minimum MSE. The iter parameter is increased by 1 in line 28. Lastly, the good solution to the minimum MSE is recognized in line 30.

2.2.1 Solution Representation of ANN Structure by Using GOAMLP

The biases associated to every neuron are in hidden and output layers. The GOAMLP solution is represented by two one-dimensional vectors: 1) ANNs structure SV indicates the amount of inputs, the amount of hidden layers and amount of neurons at every hidden layer in ANNs. 2) w and B SV indicates trained MLP. Each of those SV has an extraordinary representation. The value in the structure SV includes 0 or 1, whilst each value in the w and B SV have a real number between [−1, +1]. The dimension of the w and B SV is equal to w for each layer of the MLP model, in addition to no. of B in each layer. This length is computed in the use of Eq. (11). As such the total w and B depend on nodes and hidden layers, as shown in Eqs. (12) and (13).

DistanceofwandBvector=w+B(11)

w=(I×N)+((N×N)×(H−1))+(N×O)(12)

B=H×N+O(13)

w denotes weights, B equals biases, I stand for nodes in the input layer, N means No. of nodes in every hidden layer, H denote hidden layers, and O means No of nodes in the output layer. With regard to identifying hidden nodes in MLP, some protocols suggested in the existing state-of-arts and no understanding amongst investigators on the most beneficial rule of application.

2.2.2 Fitness Function(FF)

This FF that can be utilized to assess the quality of the solutions to minimize the values obtained. In essence, this training method is similar to the previous studies [37,38]. Supposing input nodes number is N, H denote hidden nodes, and O denote output nodes, then the output ith hidden node is computed as:

1/(1+exp(−(∑i=1N⁡Wij.Xi−Bj))),j=1,2,…,H(14)

Sj= ∑i=1N⁡wij.Xi−Bj, wij is the associated weight from ith node in input layer to the jth node in the hidden layer, βj is the bias of jth hidden node, and Xi is ith input. Then final output is stated as:

Ok=∑i=1N⁡Wkj.f(Sj)−Bk,k=1,2,…,O,(15)

wkj is associated weight for the jth hidden node to the kth output node and βk is the bias (threshold) of the kth output node. Lastly, the learning error E (FF) is:

Ek=∑i=1O⁡(Oik−dik)2(16)

MSE=∑k=1q⁡Ekq(17)

where q are No. of trained, dik is expected output of ith input unit if the kth sample trained is utilizes, and Oik is real output of ithinput unit if the kth trained sample applied. Hence, the FF of ith sample trained is stated as:

Fitness(xi)=MSE(xi)(18)

3  Validation of the Proposed

In this section the experiments for compared models were performed with a laptop configuration Core i5, 8 GB RAM, 2.4 GHz CPU, and MATLAB R2014a. The GOAMLP classifier is evaluated using the two data sets. The first dataset is Spam Base and consists of 4601 instances with 57 features. It consists of 1813 spam and 2788 legitimate emails. The dataset was obtained from the UCI [39]. The second dataset is UK-2011 Web spam which consists of 3766 instances with eleven features. It consists of 1998 spam and 1768 legitimate emails. The features described as follows [40].

3.1 Parameters and Algorithms

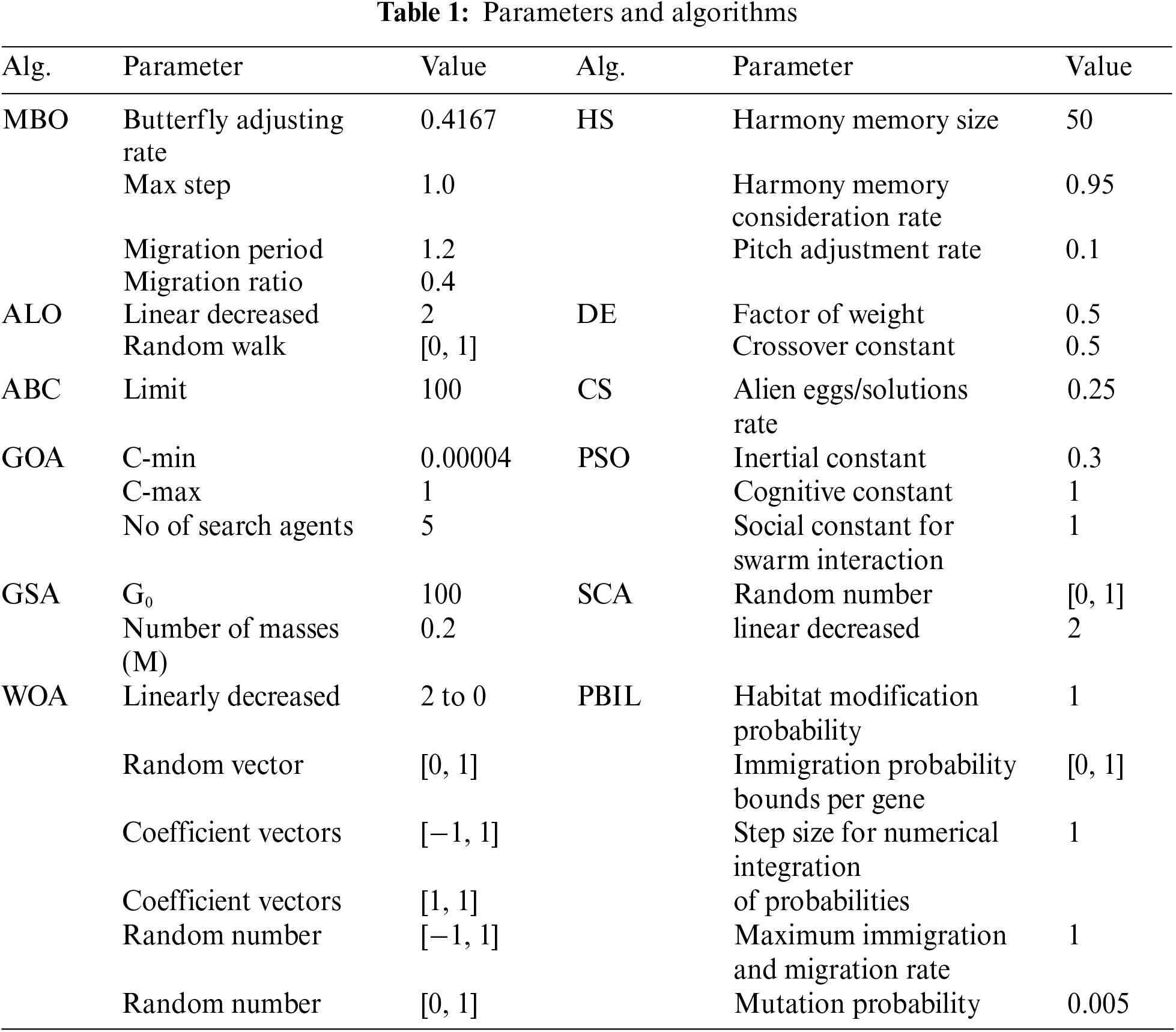
Different algorithms have been studied that analyse the reliability of the new model. All control variables of algorithms were set to the same values, SV solution, and dimensionality of SD that denotes features of the dataset. Shown in Tab. 1 the parameters of the models utilized in the performance analysis.

3.2 Criteria for Performance Evaluation for GOAMLP

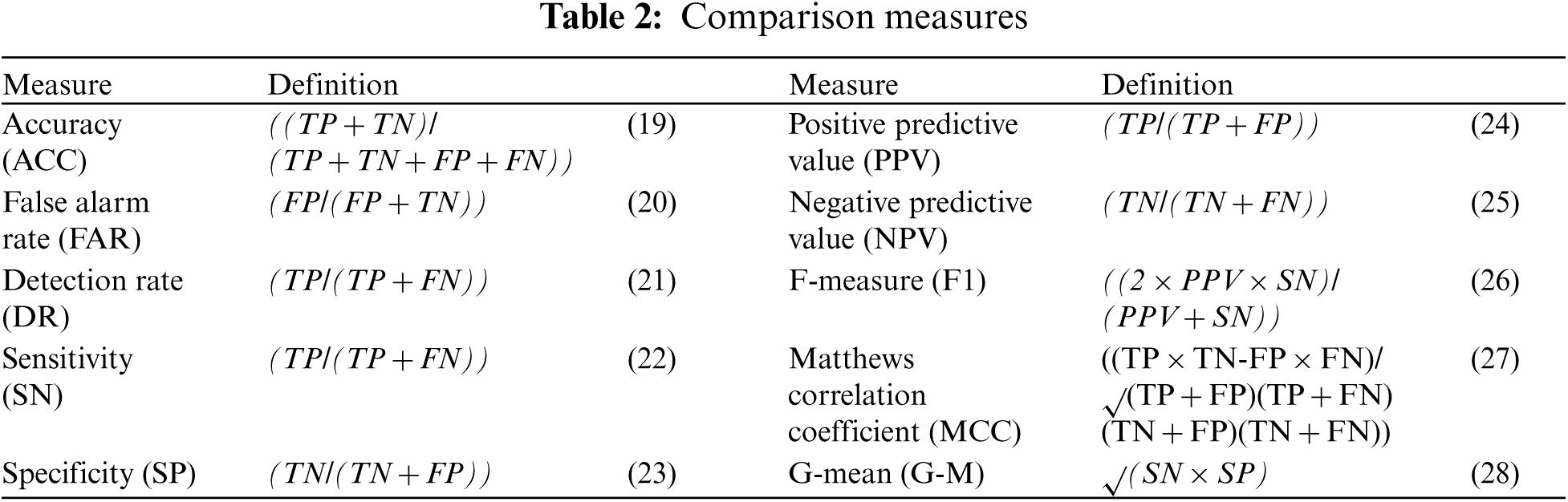
The proposed model compared ten basic measurements popularly applied in evaluating performance of the GOAMLP SD approach. The confusion matrix consists of four values include false negative (FN), true positive (TP), true negative (TN), and false positive (FP) rates. Tab. 2 displayed the performance metrics.

4  Results and Discussion

As mentioned, this study uses two standard datasets to measure performance on data in different domains. Therefore, as is obligatory to normalize values of features to allow effective application to MLPs training, the minimum to maximum normalization technique was applied. The results from datasets are described as follows:

4.1 Scenario 1 the Spam Base Dataset

The results of GOAMLP SD approach and related models are computed using the Eqs. (19)–(28) in Tab. 2. The last three columns of the range ACC (R-ACC), range DR (R-DR), and range FAR (R-FAR). Tab. 3 summarize the results of GOAMLP spam detection approach. In term of accuracy, we find that the GOAMLP algorithm is the most accurate while the ALOMLP and the CSMLP give us closely the same lower percentage.

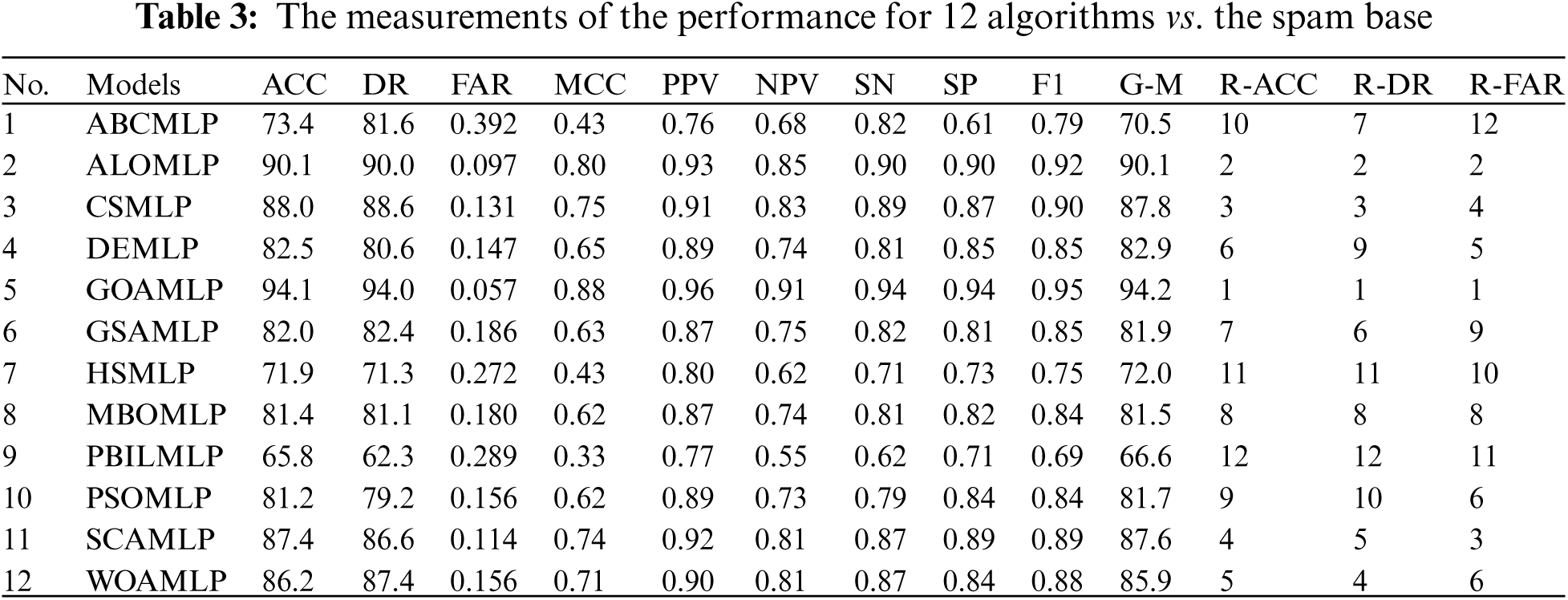
Results recorded by the ALOMLP algorithm were roughly similar to GOAMLP with an ACC of 90.1%, DR of 90.0%, and FAR of 0.097; the CSMLP algorithm was rated third with regard to ACC and DR and rated 4th with regard to FAR of 88.0%, 88.6%, and 0.131, respectively. The SCAMLP was rated third with regard to FAR of 0.114 but rated fourth with regard to the ACC of 87.4%. The WOAMLP was rated 5th with regard to ACC, rated 4th with regard to DR, and rated sixth with regard to FAR of 86.2%, 87.4%, and 0.156, respectively. On another hand, the PBILMLP algorithm has an inferior.

Fig. 2 demonstrates the results of GOAMLP and other MLP algorithms when applied to this dataset, in terms of both the convergence speed of the MSE with the ultimate algorithm result. Investigating the convergence curves, we observe that GOAMLP significantly outperforms the other algorithms in terms of the convergence speed, which shows the goodness of fit the suggested algorithm trained. Fig. 3 highlights the confusion matrix (CM) for the new model together with some algorithms. Due to the limited space, but their randomly selected 2 out of 12 algorithms to prove GOAMLP's performance against algorithms.

Figure 2: The measurements of the performance for 12 algorithms vs. the spam base dataset

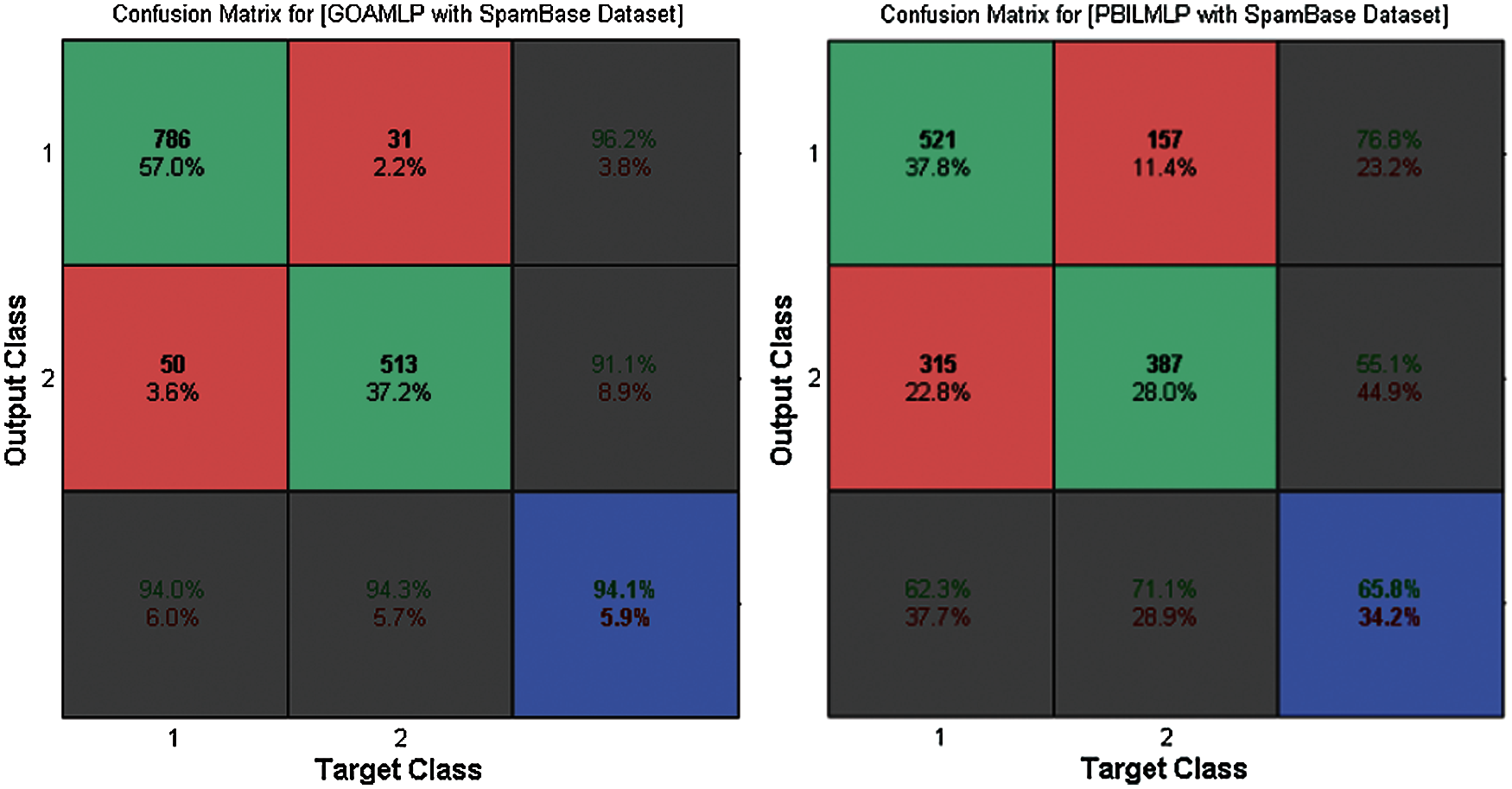
Figure 3: The confusion matrix for GOAMLP and PBILMLP vs. spam base dataset

4.2 Scenario 2 the UK-2011 Web Spam Dataset

Tab. 4, Figs. 4 and 5 summarize the results of GOAMLP SD approach. The GOAMLP SD approach achieved high ranking in 92.7%, 93.4%, and 0.078, correspondingly. Our proposed SD approach is followed by the following models: WOAMLP is rated second with regard to ACC at a rate of 91.6%, second with regard to DR at a rate of 93.0%, and third respecting FAR at a rate of 0.097; the MBOMLP algorithm is rated third with regard to ACC at a rate of 88.9%, 6th regarding DR at a rate of 86.4%, and second with regard to FAR at a rate of 0.088; and ALOMLP model is rated fourth regarding ACC at a rate of 87.5%, third regarding DR at a rate of 89.2%, and seventh concerning FAR at a rate of 0.140.

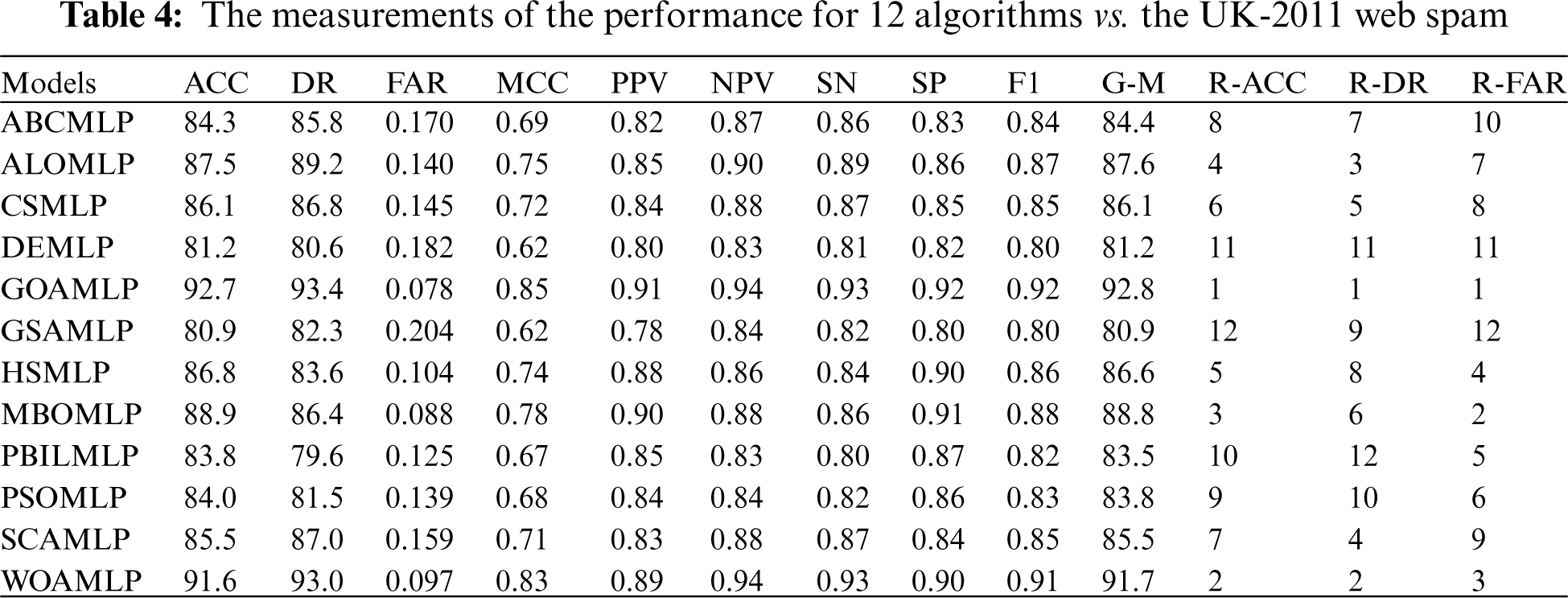
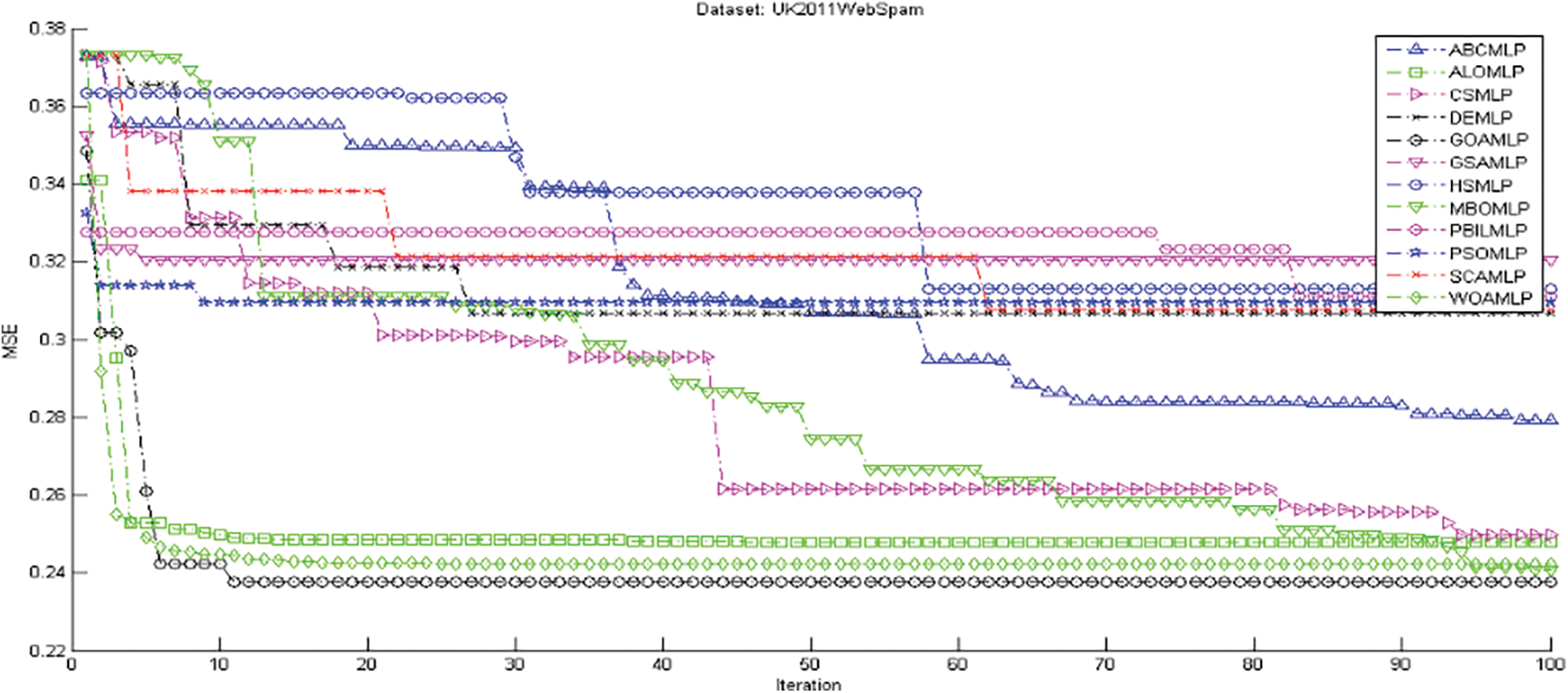
Figure 4: The measurements of the performance for 12 algorithms vs. the UK-2011Web spam dataset

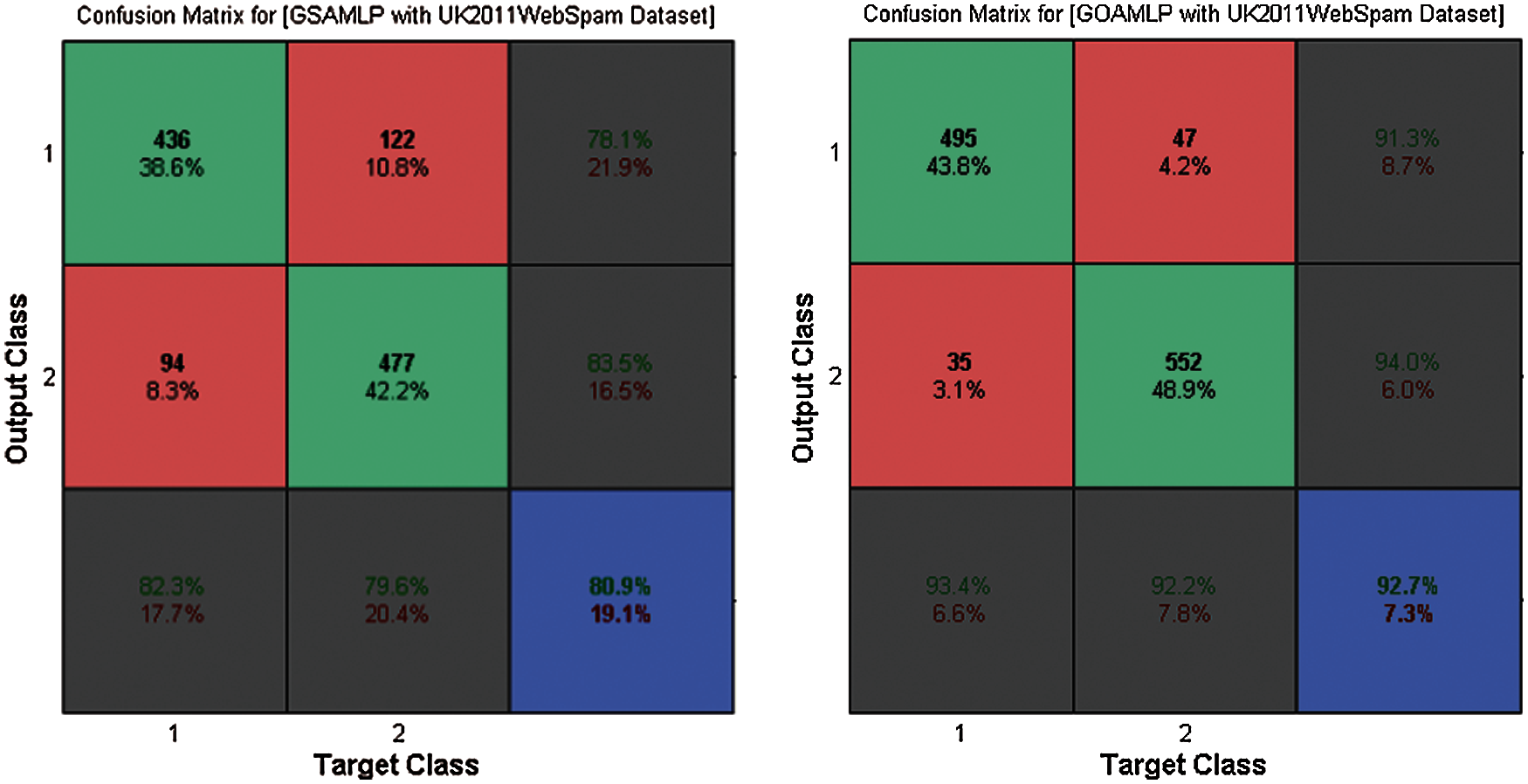
Figure 5: The confusion matrix for GOAMLP and GSAMLP vs. UK-2011Web spam dataset

In the area of speed of convergence, Fig. 4 demonstrates GOAMLP SD approach achieved faster convergence rate. Fig. 5 shows that the GOAMLP SD approach generally performed better with ACC, DR, and FAR.

4.3 Scenario 3 Performance Comparison of Proposed Approaches and Other Methods

Tab. 5 illustrated the comparisons of results of the proposed models with some methods of SD.

4.4 Statistical T-Test

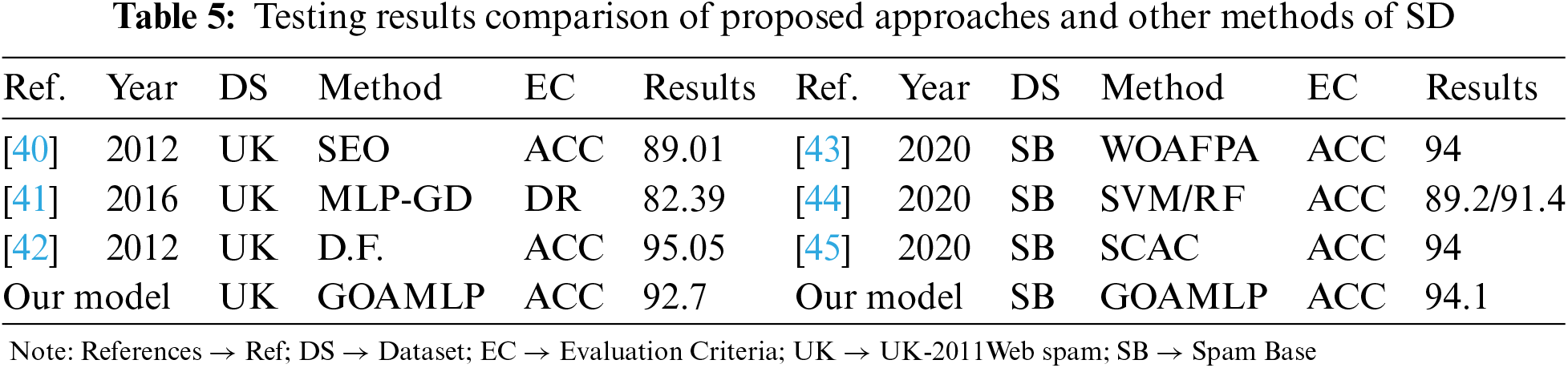
The difference between the models was tested for statistical significance using a t-test. The analysis shown in Tab. 6 shows a high correlation between the mean of the GOAMLP model at 0.05 alpha levels compared with the other models. The null hypothesis (H0) is the negation of any relationship between model 1 (M1) and model 2 (M2); M1 indicates as GOAMLP in all the tests. The statistical importance level was set at 0.05, that is, the alternative hypothesis will be considered when the p-value is less than 0.05 at the 95% confidence level. Meanwhile, Tab. 6 shows p-values by paired t-tests among GOAMLP and other models, as well as the analysis of ACC, DR, and FAR. In Tab. 6, all the p-values of < 0.05 reveal that the hypothesis of GOAMLP superiority can be accepted, as the GOAMLP model achieved significantly better results than other models in all of the cases except for the test between ALOMLP and GOAMLP with Spam Base dataset.

5  Conclusion

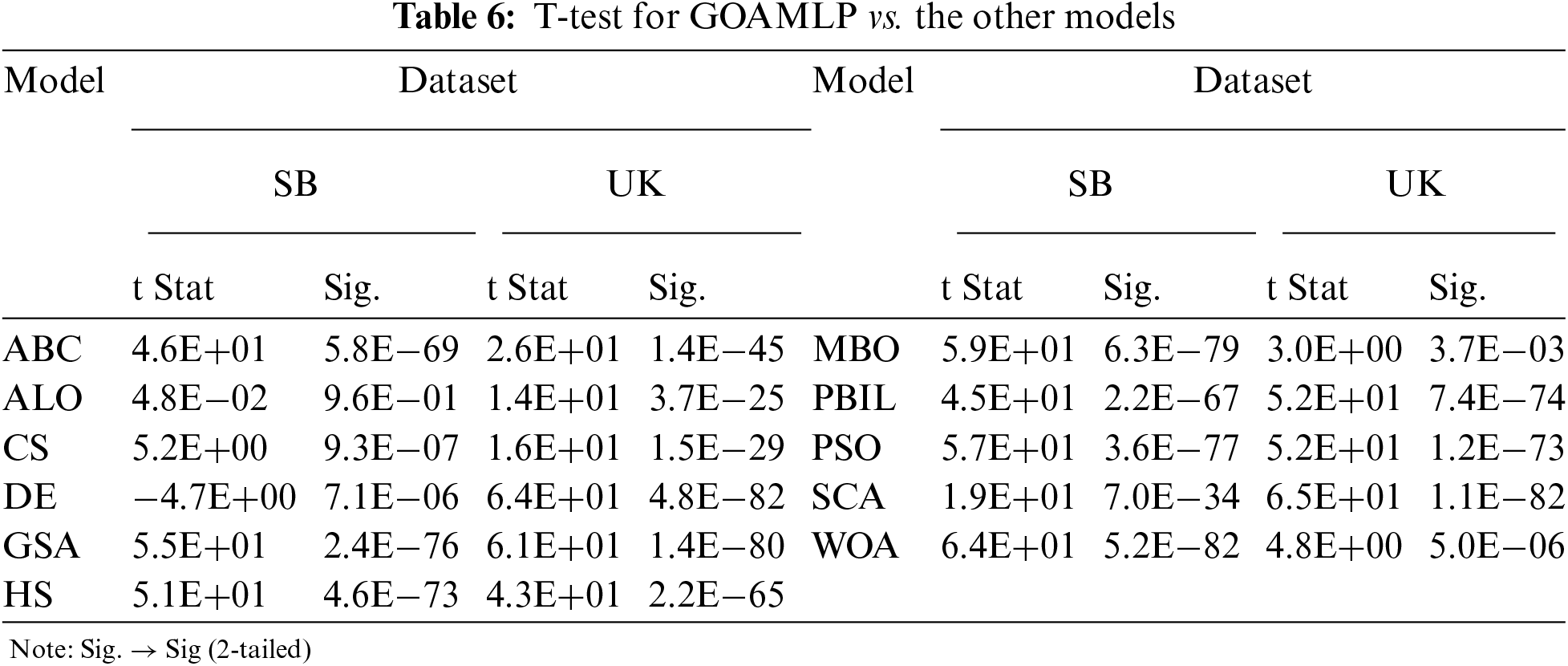
This work introduced a novel approach for SD, namely, the GOAMLP. The focus was on the applicability of the GOA to train MLP. The performance of the proposed GOAMLP compared to the most recent SD. The work utilized 12 algorithms to train the MLP. The GOAMLP was trained against the benchmark datasets of Spam Base, and UK-2011Web spam and had classification accuracies of 94.1%, and 92.7%, detecting rates of 94.0%, and 93.4%, respectively; and finally, false alarm rates of 0.057, and 0.078. These results are higher than the result from other models that were tested using the same datasets. The outcomes display the adequacy of the proposed approach for spam detectors. All approaches were measured with regard to features of SD datasets.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Shuaib, S. M. Abdulhamid, O. S. Adebayo, O. Osho, I. Idris et al., “Whale optimization algorithm-based email spam feature selection method using rotation forest algorithm for classification,” SN Applied Sciences, vol. 1, no. 5, pp. 390, 2019. [Google Scholar]

 2.  E. G. Dada, J. S. Bassi, H. Chiroma, S. M. Adetunmbid, A. O. Abdulhami et al., “Machine learning for email spam filtering: Review, approaches and open research problems,” Heliyon, vol. 5, no. 6, pp. e01802, 2019. [Google Scholar]

 3.  A. Arram, H. Mousa and A. Zainal, “Spam detection using hybrid artificial neural network and genetic algorithm,” in IEEE Int. Conf. on Intellient Systems Design and Applications, Salangor, Malaysia, pp. 336–340, 2013. [Google Scholar]

 4.  S. Jan, I. Maqsood, A. Ahmed, Z. Wadud and I. Ahmad, “Investigating the use of email application in illiterate and semiilliterate population,” Computers, Materials & Continua, Singapore Malaysia, vol. 62, no. 3, pp. 1473–1486, 2020. [Google Scholar]

 5.  S. A. A. Ghaleb, M. Mohamad, E. F. H. S. Abdullah and W. A. H. M. Ghanem, “Spam classification based on supervised learning using grasshopper optimization algorithm and artificial neural network,” in Int. Conf. on Advances in Cyber Security Springer, Singapore Malaysia, pp. 420–434, 2020. [Google Scholar]

 6.  S. A. A. Ghaleb, M. Mohamad, E. F. H. S. Abdullah and W. A. H. M. Ghanem, “An integrated model to email spam classification using an enhanced grasshopper optimization algorithm to train a multilayer perceptron neural network,” in Int. Conf. on Advances in Cyber Security Springer, Singapore Malaysia, pp. 402–419, 2020. [Google Scholar]

 7.  O. I. Abiodun, A. Jantan, A. E. Omolara, K. V. Dada, N. A. Mohamed et al., “State-of-the-art in artificial neural network applications: A survey,” Heliyon, vol. 4, no. 11, pp. e00938, 2018. [Google Scholar]

 8.  S. O. Olatunji, “Improved email spam detection model based on support vector machines,” Neural Computing and Applications, vol. 31, no. 3, pp. 691–699, 2019. [Google Scholar]

 9.  D. D. Arifin, Shaufiah and M. A. Bijaksana, “Enhancing spam detection on mobile phone short message service (SMS) performance using FP-growth and naive Bayes classifier,” in Indonesia IEEE Asia Pacific Conference onWireless and Mobile (APWiMob), pp. 80–84, 2016. [Google Scholar]

10. O. I. Abiodun, A. Jantan, A. E. Omolara, K. V. Dada, A. M. Umar et al., “Comprehensive review of artificial neural network applications to pattern recognition,” IEEE Access, vol. 7, pp. 158820–158846, 2019. [Google Scholar]

11. S. Amjad and F. S. Gharehchopogh, “A novel hybrid approach for email spam detection based on scatter search algorithm and K-nearest neighbors,” Journal of Advances in Computer Engineering and Technology, vol. 5, no. 3, pp. 169–178, 2019. [Google Scholar]

12. T. A. Xia, “Constant time complexity spam detection algorithm for boosting throughput on rule-based filtering systems,” IEEE Access, vol. 8, pp. 82653–82661, 2020. [Google Scholar]

13. S. Hakak, M. Alazab, S. Khan, T. R. Gadekallu, P. K. R. Maddikunta et al., “An ensemble machine learning approach through effective feature extraction to classify fake news,” Future Generation Computer Systems, vol. 117, pp. 47–58, 2021. [Google Scholar]

14. S. Mirjalili, “How effective is the grey wolf optimizer in training multi-layer perceptrons,” Applied Intelligence, vol. 43, no. 1, pp. 150–161, 2015. [Google Scholar]

15. W. A. H. M. Ghanem and A. Jantan, “A cognitively inspired hybridization of artificial bee colony and dragonfly algorithms for training multi-layer perceptrons,” Cognitive Computation, vol. 10, no. 6, pp. 1096–1134, 2018. [Google Scholar]

16. W. A. H. M. Ghanem and A. Jantan, “A training a neural network for cyberattack classification applications using hybridization of an artificial bee colony and monarch butterfly optimization,” Neural Processing Letters, vol. 51, no. 1, pp. 905–946, 2020. [Google Scholar]

17. A. Arram, H. Mousa and A. Zainal, “Spam detection using hybrid artificial neural network and genetic algorithm,” in IEEE Int. Conf. on Intellient Systems Design and Applications, Singapore Malaysia, pp. 336–340, 2013. [Google Scholar]

18. S. Z. Mirjalili, S. Mirjalili, S. Saremi, H. Faris and I. Aljarah, “Grasshopper optimization algorithm for multi-objective optimization problems,” Applied Intelligence, vol. 48, no. 4, pp. 805–820, 2018. [Google Scholar]

19. E. S. M. El-Alfy, “Discovering classification rules for email spam filtering with an ant colony optimization algorithm,” in IEEE Congress on Evolutionary Computation, pp. 1778–1783, 2009. [Google Scholar]

20. I. Idris, A. Selamat, N. T. Nguyen, S. Omatu, O. Krejcar et al., “A combined negative selection algorithm particle swarm optimization for an email spam detection system,” Engineering Applications of Artificial Intelligence, vol. 39, pp. 33–44, 2015. [Google Scholar]

21. R. R. Rajalaxmi and A. Ramesh, “Binary bat approach for effective spam classification in online social networks,” Australian Journal of Basic and Applied Sciences, vol. 8, no, 18, pp. 383–388, 2014. [Google Scholar]

22. V. K. Ojha, A. Abraham and V. Snášel, “Metaheuristic design of feedforward neural networks: A review of two decades of research,” Engineering Applications of Artificial Intelligence, vol. 60, pp. 97–116, 2017. [Google Scholar]

23. J. Yu, L. Xi and S. Wang, “An improved particle swarm optimization for evolving feedforward artificial neural networks,” Neural Processing Letters, vol. 26, no. 3, pp. 217–231, 2007. [Google Scholar]

24. F. H. F. Leung, H. K. Lam, S. H. Ling, and P. K. S. Tam, “Tuning of the structure and parameters of neural network using an improved genetic algorithm,” Proc. 27th Annu, in IEEE Industrial Electronics Society, vol. 14, pp. 25–30, 2001. [Google Scholar]

25. S. Mizuta, T. Sato, D. Lao, M. Ikeda and T. Shimizu, “Structure design of neural networks using genetic algorithms,” Complex Systems, vol. 13, no. 2, pp. 161–176, 2001. [Google Scholar]

26. K. Manjusha and R. Kumar, “Spam mail classification using combined approach of Bayesian and neural network,” in IEEE Int. Conf. on Computational Intelligence and Communication Networks, pp. 145–149, 2010. [Google Scholar]

27. I. Idris, “E-mail spam classification with artificial neural network and negative selection algorithm,” International Journal of Computer Science & Communication Networks, vol. 1, no. 3, pp. 227–231, 2011. [Google Scholar]

28. S. Singh, A. Chand and S. P. Lal, “Improving spam detection using neural networks trained by memetic algorithm,” in IEEE Int. Conf. on Computational Intelligence, Modelling and Simulation, Seoul, Korea (Southpp. 55–60, 2013. [Google Scholar]

29. H. Faris, I. Aljarah and J. Alqatawna, “Optimizing feedforward neural networks using krill herd algorithm for e-mail spam detection,” in IEEE Amman, Jordan Conf. on Applied Electrical Engineering and ComputingTechnologies (AEECT), pp. 1–5, 2015. [Google Scholar]

30. A. Rodan, H. Faris and J. Alqatawna, “Optimizing feedforward neural networks using biogeography-based optimization for e-mail spam identification,” International Journal of Communications, Network and System Sciences, vol. 9, no. 1, pp. 19, 2016. [Google Scholar]

31. G. K. Tak and S. Tapaswi, “Query based approach towards spam attacks using artificial neural network,” International Journal of Artificial Intelligence & Applications, vol. 1, no. 4, pp. 82–99, 2010. [Google Scholar]

32. A. Jantan, W. A. H. M. Ghanem and S. A. A. Ghaleb, “Using modified bat algorithm to train neural networks for spam detection,” Journal of Theoretical & Applied Information Technology, vol. 95, no. 24, pp. 6788–6799, 2017. [Google Scholar]

33. S. Saremi, S. Mirjalili and A. Lewis, “Grasshopper optimisation algorithm: Theory and application,” Advances in Engineering Software, vol. 105, pp. 30–47, 2017. [Google Scholar]

34. S. A. A. Ghaleb, M. Mohamad, E. F. H. S. Abdullah and W. A. H. M. Ghanem, “Integrating mutation operator into grasshopper optimization algorithm for global optimization,” Soft Computing, pp. 1–44, 2021. https://doi.org/10.1007/s00500-021-05752-y. [Google Scholar]

35. A. A. Heidari, H. Faris, I. Aljarah and S. Mirjalili, “An efficient hybrid multilayer perceptron neural network with grasshopper optimization,” Soft Computing, vol. 23, no. 17, pp. 7941–7958, 2019. [Google Scholar]

36. W. A. H. M. Ghanem and A. Jantan, “A new approach for intrusion detection system based on training multilayer perceptron by using enhanced bat algorithm,” Neural Computing and Applications, vol. 4, no. 107, pp. 1–34, 2020. [Google Scholar]

37. W. A. H. M. Ghanem, A. Jantan, S. A. A. Ghaleb and A. B. Nasser, “An efficient intrusion detection model based on hybridization of artificial bee colony and dragonfly algorithms for training multilayer perceptrons,” IEEE Access, vol. 8, pp. 130452–130475, 2020. [Google Scholar]

38. W. A. H. M. Ghanem, Y. A. B. El-Ebiary, M. Abdulnab, M. Tubishat, N. A. Alduais et al., “Metaheuristic based IDS using multi-objective wrapper feature selection and neural network classification,” in Int. Conf. on Advances in Cyber Security, Springer, pp. 384–401, 2020. [Google Scholar]

39. M. Hopkins, E. Reeber, G. Forman and J. Suermondt, “Spambase dataset. Hewlett-Packard labs,” [Online]. Available: https://archive.ics.uci.edu/ml/datasets/SpamBase, 1999. [Google Scholar]

40. H. A. Wahsheh, M. N. Al-Kabi and I. M. Alsmadi, “A link and content hybrid approach for arabic web spam detection,” International Journal of Intelligent Systems and Applications, vol. 5, no. 1, pp. 30–43, 2012. [Google Scholar]

41. M. Alsaleh and A. Alarifi, “Analysis of web spam for non-English content: Toward more effective language-based classifiers,” Plos One, vol. 11, no. 11, pp. 1–25, 2016. [Google Scholar]

42. A. Alarifi and M. Alsaleh, “Web spam: A study of the page language effect on the spam detection features,” Int. Conf. on Machine Learning and Applications ICMLA, vol. 2, pp. 216–221, 2012. [Google Scholar]

43. H. Mohmmadzadeh and F. S. Gharehchopogh, “A novel hybrid whale optimization algorithm with flower pollination algorithm for feature selection: Case study email spam detection,” Preprints, pp. 1–28, 2020. [Google Scholar]

44. O. E. Taylor and P. S. Ezekiel, “A model to detect spam email using support vector classifier and random forest classifier,” International Journal of Computer Science and Mathematical Theory, vol. 6, no. 1, pp. 1–11, 2020. [Google Scholar]

45. R. M. A. Mohammad, “An improved multi-class classification algorithm based on association classification approach and its application to spam emails,” International Journal of Computer Science IAENG, vol. 47, no. 2, pp. 187–198, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.