Computers, Materials & Continua DOI:10.32604/cmc.2022.023068
Article

Binary Fruit Fly Swarm Algorithms for the Set Covering Problem

Broderick Crawford1,*, Ricardo Soto1, Hanns de la Fuente Mella1, Claudio Elortegui1, Wenceslao Palma1, Claudio Torres-Rojas1, Claudia Vasconcellos-Gaete2, Marcelo Becerra1, Javier Peña1 and Sanjay Misra3

1Pontificia Universidad Católica de Valparaíso, Valparaíso, 2362807, Chile
2LERIA, Université d'Angers, Angers, 49000, France
3Department of Computer Science and Communication, Ostfold University College, Halden, Norway
*Corresponding Author: Broderick Crawford. Email: broderick.crawford@pucv.cl
Received: 27 August 2021; Accepted: 21 October 2021

Abstract: Currently, the industry is experiencing an exponential increase in dealing with binary-based combinatorial problems. In this sense, metaheuristics have been a common trend in the field in order to design approaches to solve them successfully. Thus, a well-known strategy consists in the use of algorithms based on discrete swarms transformed to perform in binary environments. Following the No Free Lunch theorem, we are interested in testing the performance of the Fruit Fly Algorithm, this is a bio-inspired metaheuristic for deducing global optimization in continuous spaces, based on the foraging behavior of the fruit fly, which usually has much better sensory perception of smell and vision than any other species. On the other hand, the Set Coverage Problem is a well-known NP-hard problem with many practical applications, including production line balancing, utility installation, and crew scheduling in railroad and mass transit companies. In this paper, we propose different binarization methods for the Fruit Fly Algorithm, using S-shaped and V-shaped transfer functions and various discretization methods to make the algorithm work in a binary search space. We are motivated with this approach, because in this way we can deliver to future researchers interested in this area, a way to be able to work with continuous metaheuristics in binary domains. This new approach was tested on benchmark instances of the Set Coverage Problem and the computational results show that the proposed algorithm is robust enough to produce good results with low computational cost.

Keywords: Set covering problem; fruit fly swarm algorithm; metaheuristics; binarization methods; combinatorial optimization problem

1  Introduction

The Set Covering Problem (SCP) is a well-known NP-hard class covering problem, which consists of finding a subset of columns in a zero-one matrix such that it covers all rows of the matrix at minimum cost. It has important practical applications, such as: localization of emergency services [1], scheduling of crews in mass transit companies [2], routing of vehicles [3], reconstruction of sibling relationships [4].

Considering the complex nature of SCP, the huge size of the real data sets and the variety of methods designed to approach similar problems, SCP has been solved by exact methods, metaheuristics and other techniques, such as hyperheuristics [5] or with Machine Learning techniques [6–8]. Solving by exact methods is mainly based on Branch-and-Bound, Branch-and-Cut and Lagrangean heuristics [9].

Resolution by metaheuristics includes Genetic Algorithms [10], Tabu Search [11], Ant Colony Optimization [12], Artificial Bee Colonies [13], Firefly Algorithms [14], Cat Swarm Optimization [15], Cuckoo Search [16], Teaching-learning Based Optimization [17] and Shuffled Frog Jumping Algorithm [18], Binary Black Hole Algorithms [19]. Previous work [20] propose the use of binarization techniques in order to improve the solutions of combinatorial problems like the SCP, but they lack explanation on how the binarization affects the metaheuristics, also the previous work don't propose a pre-processing phase to reduce the computational cost of the instances of the SCP.

In this paper, we present a new approach to solving the SCP based on Wen Tsao-Pan's Fruit Fly Swarm Algorithm (FFSA) [21]. This metaheuristic is based on the foraging behavior of fruit flies, which use the senses of smell and vision to find their food; in terms of the algorithm, these senses are represented by a combination of local (smell) and global (vision) searches to improve the quality of solutions. Since FFSA was developed for continuous spaces and SCP is a binary problem, our work contributes to propose several binarization methods for a continuous algorithm in order to promote a better distribution between exploration/exploitation. In order to achieve this balance, we present eight different transfer functions and five discretization methods, generating a total of 39 variations to the original BFFSA. The results of this work suggests that BFFSA (the binary version of FFSA) is a robust algorithm, capable to produce good results at a low computational cost.

This article is organized as follows: A brief description of the Set Coverage Problem in Section 2, the presentation of Pan's Fruit Fly Algorithm in Section 3, an adaptation of Pan's metaheuristic to work in a binary search space in Section 4. Our proposal with the description of the functions and methods used to allow the algorithm to run in discrete spaces in Section 5. Finally, we present our results, conclusions, and possible future lines of research in Sections 6 and 7.

2  Set Covering Problem

The SCP is a classical covering problem and is defined as a binary matrix A where ai,j∈{0,1} is the value of each cell in the matrix and i,j are the size of m-rows and n-columns, respectively:

(a11a12⋯a1na21a22⋯a2n⋮⋯⋯⋮am1am2⋯amn)(1)

Defining the column j satisfies a row i if aij is equal to 1 and this will be the contrary case if this is 0. In addition, it has an associated cost c∈C, where C={c1,c2,…,cn} together with i∈{1,2,…,m} and j∈{1,2,…,n} are the sets of rows and columns, respectively. The problem results in the following objective: to minimize the cost of the subset S⊆J, with the constraint that all rows i∈I are covered by at least one column j∈J. It is taken into consideration that when the column j is in the subset of solution S, this is equal to 1 and 0 otherwise. The SCP can be defined as the following:

MinimizeZ=∑j=1n⁡cjxj(2)

Subject to Eqs. (3) and (4):

∑j=1n⁡ai,jxj≥1∀i∈I(3)

xj∈{0,1}∀j∈J(4)

One of the many practical applications of this problem is the location of fire stations. Lets consider a city divided in a finite number of areas which need to locate and build fire stations. Each one of these areas need to be covered by at least one station, but a single fire station can only bring coverage to its own area and the adjacent ones; also, the problem requires that the number of stations to build needs to be the minimum.

Intentionally, we have selected an instance of SCP with m=11 and n=11 to represent it graphically in Fig. 1 and by Eqs. (5)–(16). When a SCP formulation has a constant cost (a value of 1 in this case), we will refer to it as an Unicost SCP instance.

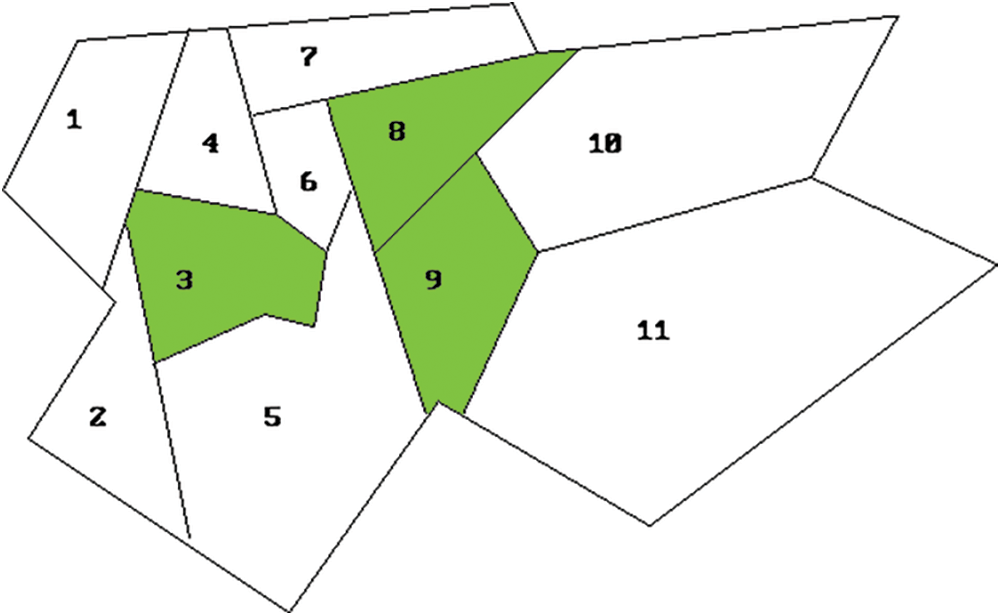
Figure 1: Solution to the practical example of SCP

MinimizeZ=∑j=111⁡cjxj(5)

Subject to:

AREA1=x1+x2+x3+x4≥1(6)

AREA2=x1+x2+x3+x5≥1(7)

AREA3=x1+x2+x3+x4+x5+x6≥1(8)

AREA4=x1+x3+x4+x6+x7≥1(9)

AREA5=x2+x3+x5+x6+x8+x9≥1(10)

AREA6=x3+x4+x5+x6+x7+x8≥1(11)

AREA7=x4+x6+x7+x8≥1(12)

AREA8=x5+x6+x7+x8+x9+x10≥1(13)

AREA9=x5+x8+x9+x10+x11≥1(14)

AREA10=x8+x9+x10+x11≥1(15)

AREA11=x9+x10+x11≥1(16)

As the SCP is a NP-hard class problem, one of the many difficulties that benchmarks arise is their size and the computational time associated. To solve this, many authors propose to do a pre-processing of the problem before apply any exact method or metaheuristic in order to obtain instances that are equivalent to original but smaller in terms of rows and columns. In the next section, we describe the methods used in this research.

2.1 Pre-Processing

To accelerate the problem solving, we introduce a preprocessing phase before run the metaheuristic to reduce the size of instances and improve the performance of the algorithm. In this article, we use two methods that have proven to be more effective: Column Domination [22] and Column Inclusion [23].

Column Domination: It consists into deleting the redundant columns without affecting the final solution. In other words, if the rows belonging to the column j can be covered by another column with a cost lower than cj, then the column j is dominated and it can be removed. This method is detailed in the Algorithm 1.

Column Inclusion: If a row is covered by only one column after the above domination, that column must be included in the optimal solution, and there is no need to evaluate its feasibility.

3  Fruit Fly Swarm Algorithm

The FFSA is a bio-inspired metaheuristic [21] based on the foraging behavior of fruit flies or vinegar flies for finding food, considering that their smell (osphresis) and vision senses are much better than in any other specie. The foraging behavior processes consider smell the food source, fly to it and then visualize the same food source to determine a better direction.

In Fig. 2, there is a graphical representation of these foraging search processes. Consider S1, S2 and S3 as fruit flies from our population. During the smell-based search, the flies will randomly move across the search space, so their new positions will be (X1,Y1), (X2,Y2) and (X3,Y3) respectively; then, in the next phase, flies will be evaluated in their smell concentration (fitness function) to determine which one is the best in the group; for our example, we are using the reciprocal of distance to the origin (1/Disti) as fitness function. Finally, and knowing which one is the best fruit fly, the population will move into its direction to get closer to the food source.

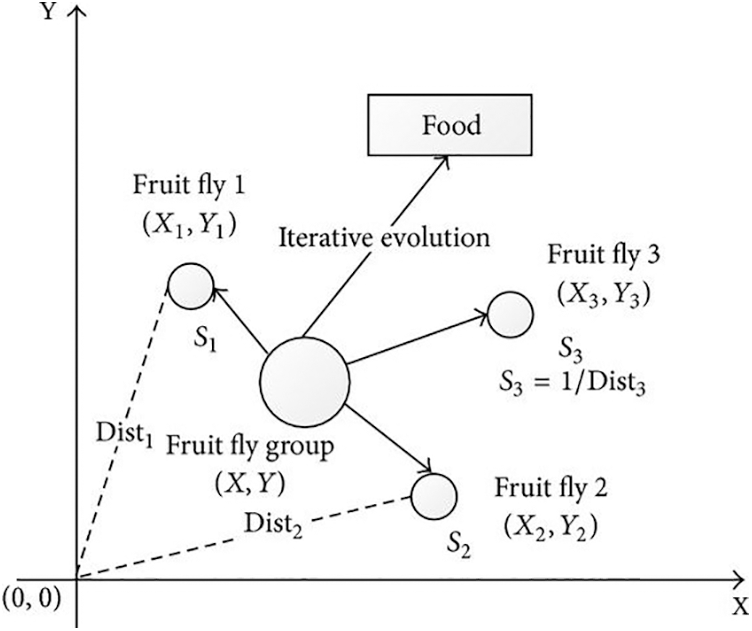
Figure 2: Food searching of a group of fruit flies

The traditional FFSA consists of 4 phases. These are: initialization, smell-based search, population evaluation, and vision-based search. In the initialization phase, parameters are set and the fruit flies (solutions) are created randomly with a very sensitive osphresis and vision organs. During the smell-based search phase, flies use their senses to feel all kinds of smells in the air and fly towards the corresponding locations. Then, the flies are evaluated to find the best concentration of smell. When they are near to food, in the vision-based search phase, they fly toward the food source using their vision organ. The pseudocode of these phases is detailed in Algorithm 2.

The FFSA has been successfully used to solve continuous problems such as: the financial distress [21], web auction logistics service [24], power load forecasting [25], design of key control characteristics for automobile parts [26] and distribution of pollution particles [27].

4  Binary-Fruit Fly Swarm Algorithm

In contrast with traditional FFSA, the BFFSA [28] uses a discrete binary string (Fig. 3) to represent a solution and a probability vector to generates the population (Fig. 4); then, the value of each bit of the fruit flies goes from zero to one (and vice versa) to exploit the neighborhood in the smell-based search process and perform a global vision-based search to improve the exploration ability. This new algorithm, detailed later in pseudocode (Algorithm 3), preserves the four phases but adds three search methods: Smell-based, Local-Vision-based and Global-Vision-based. Also, these methods will add new parameters to perform searches; all of them are detailed in Tab. 1.

Figure 3: Representation of a fruit fly (solution) in BFFSA

Figure 4: Representation of the probability vector in BFFSA

This article proposes and evaluates new instances for BFFSA, created from the combination of the original binary algorithm, eight transfer functions and two discrete methods, in order to improve solutions.

4.1 Initialization

In the BFFSA, each fruit fly is a solution represented by a n-bit binary vector, where n is the number of columns in the instance to solve. Thus, in a fruit fly Fi, the value Fd represents the dth binary decision bit, d∈[1,n]. All fruit flies are generated by an n-dimensional probability vector p(t), where t represents generation (or iteration) with t∈[1,gen]. Then, the p(t)d is the probability in the dth dimension of the fruit fly Fi to be 1 during generation t. The pseudocode for this phase is detailed in Algorithm 4.

To generate a uniformly distributed population in the search space, the probability vector must be p(0)=[0.5,0.5,…,0.5], so all columns have fifty percent probability of being selected. In the next generation, a new population with N fruit flies will be generated using this probability vector.

4.2 Smell-Based Search

In this phase, we create S neighbors randomly around each fruit fly Fi using the smell-based search. Each one of these neighbors are generated using the following method: first, we select randomly L-bits, and then we flip these L columns values to the opposite binary value. For example, if we have a 9-bit fruit fly and L=3, the smell-based search may produce a neighbor like the one represented in Fig. 5.

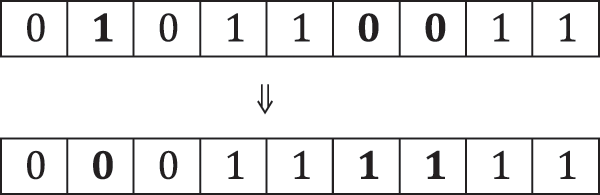
Figure 5: Creation of a neighbor during smell-based search

At this point, a population with (N⋅S)− fruit flies is evaluated using the objective function. In case to get unfeasible solutions, we apply a repair operator. This additional phase will be explained later (SubSection 4.5).

4.3 Local-Vision-Based Search

Once all solutions in the neighborhood are feasible, the fruit flies are evaluated with the vision sense (the objective function) to find the best local neighbor and fly towards it. If a better neighbor is found, then the whole neighborhood will fly towards it and this recently discovered “local best” fruit fly will replace the previous solution; otherwise, solution will remain the same.

4.4 Global-Vision-Based Search

This search works on the exploration ability (Eqs. (17) and (18)), considering that previous phases are more focused into the exploitation ability. To update the next fruit flies generation, this phase updates the probability vector with the differential information between the best fruit fly Fbest and two random fruit flies (F1 and F2) to set a coefficient for the vision sensitivity b to enhance the exploration.

Δd(t+1)=Fbestd+0.5(F1d−F2d)(17)

pd(t+1)=1(1+e−b(Δd(t+1)−0.5)(18)

As we can see in the Eq. (17), the algorithm have a high probability of exploration in the first steps of the search, because the two random fruit flies tend to be far away one of the other, but always with the guide of the best fruit fly Fbest. Once the flies are stuck on close positions, they tend to perform more exploitation with the smell-based search and the local-vision-based search.

4.5 Repair Operator

A common issue with metaheuristics is the generation of unfeasible solutions during an iteration. For the SCP, this means that some individuals will not cover all rows and a subset of constraints may be violated. To solve this issue, the algorithm implements a repair operator to make all individuals feasible and eliminate redundancy. The method described in [29] calculates a ratio between the cost of an uncovered column (cj) and the number of uncovered rows covered by that column; once all rows are covered and the solution is feasible, the operator includes an optimization step to eliminate any redundant column (Algorithm 5).

5  Proposed Binarization Methods for the BFFSA

In this article, we propose to modify the original BFFSA with a two-step binarization technique (Fig. 6), which will transform the solution from R to an “InterSpace” (in Z) and then to the binary space. Following a procedure similar to the one proposed in [30,31], we will replace the equation for global searching (Eq. (18)) with one of the eight transfer functions (Eqs. (19)–(26)) showed in the Tab. 2. Specifically, our idea is to replace the calculation for the differential information b(Δid−0.5), with one of these eight transfer functions in order to define the probability to move an element of the solution from 1 to 0 (or vice versa), forcing the fruit flies to be in the interval [0, 1]. With this change, we force to have a controlled balance between exploration and exploitation in all the search steps of the algorithm. Thus, we promote the search of new areas meanwhile we search better solution in known promising areas.

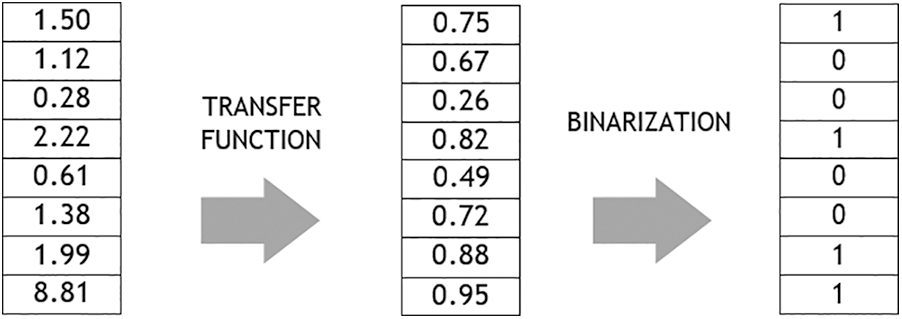
Figure 6: Classic binarization scheme

It is important to note that of the S-shaped (left-hand in Fig. 7) and V-shaped (right-hand in Fig. 7) functions presented here, the original BFFSA uses the transfer function PS2 with a standard discretization method. In this paper, we test a universe of 40 different instances of the algorithm, where 39 of the 40 are new variations realized by our research.

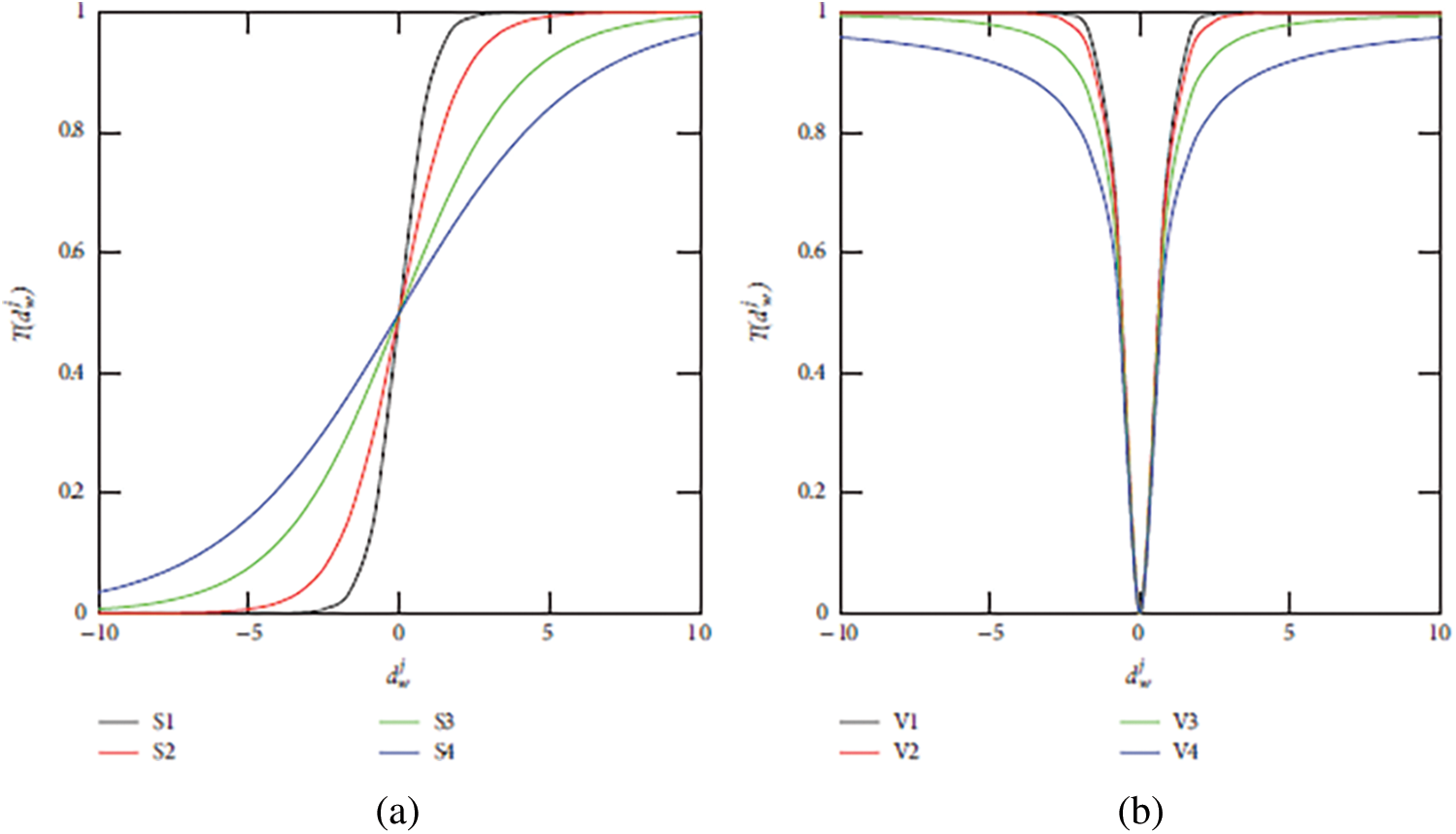
Figure 7: (a) S and (b) V transfer functions

After updating the probability vector with one of these S-shaped or V-shaped transfer functions, an element of a fruit fly will be updated using one of the following discretization methods: Standard, Complement, Static Probability, Elitist and Elitist Roulette, detailed in Tab. 3 with the Eqs. (27)–(31), respectively. In all of them, Fd represents the dth position of the fruit fly Fi, Fbest is the best fruit fly in the current generation and α is the static probability.

6  Experiment Results

The modified BFFSA with the transfer functions proposed has been implemented in Java in a Common KVM processor of 2.66 GHz with 4 GB RAM computer, running Microsoft Windows 7. The parameter tuning for the algorithm is detailed in Tab. 4.

All the datasets tested are from Beasley's OR Library 3. In total, we solved 65 data files; instances 4, 5, 6 are from [36], instances A, B, C, D are from [22] and instances NRE, NRF, NRG, NRH are the unknown-solution problem set from [37]. Details of datasets are described in Tab. 5.

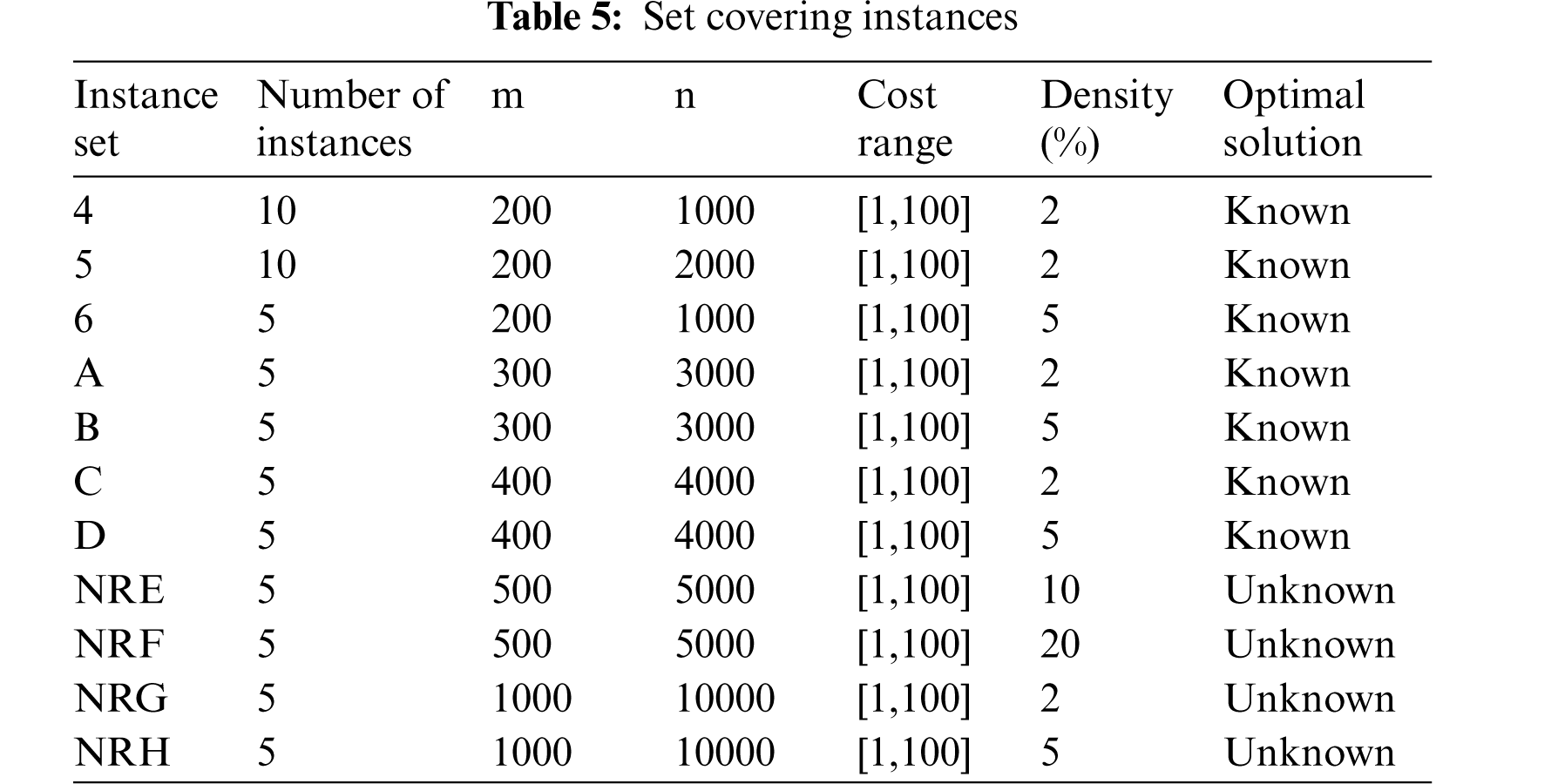
For each instance, we report the average values obtained after run 30 times each algorithm.

6.1 Comparison of Proposed BFFSA with Other Metaheuristics

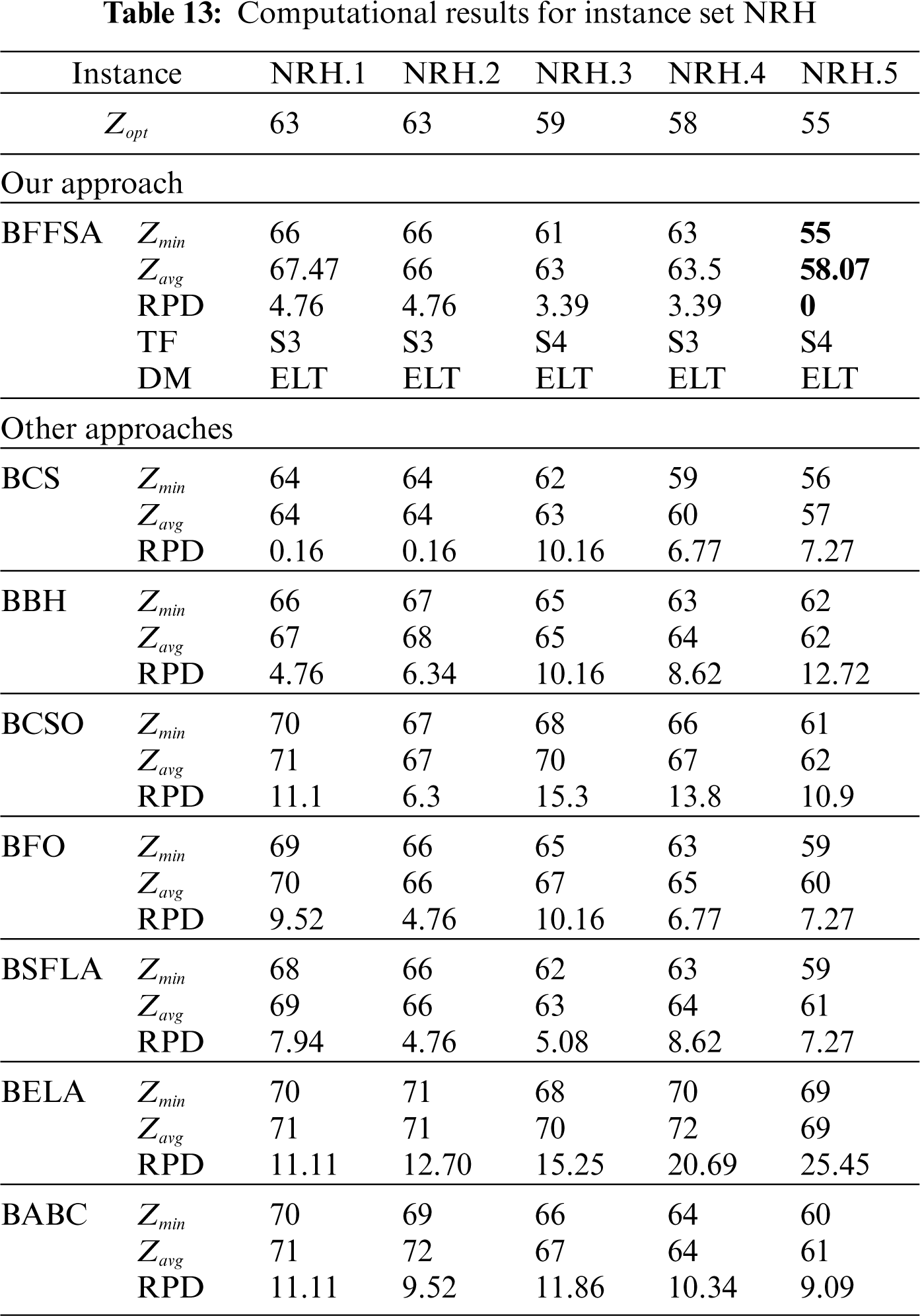
The Tabs. 6–13 show the detailed results obtained by different instances of our modified BFFSA. In all of them, the results are presented along with the transfer function (TF) and discretization method (DM) used in each case, and compared with other metaheuristics in terms of minimum and maximum number of optimal founded (ZMIN, ZMAX) and the relative percentage deviation (RPD), which represents the deviation of the objective value Z (fitness) from ZOPT (Eq. (32)).

RPD=100(ZMIN−ZOPT)ZOPT(32)

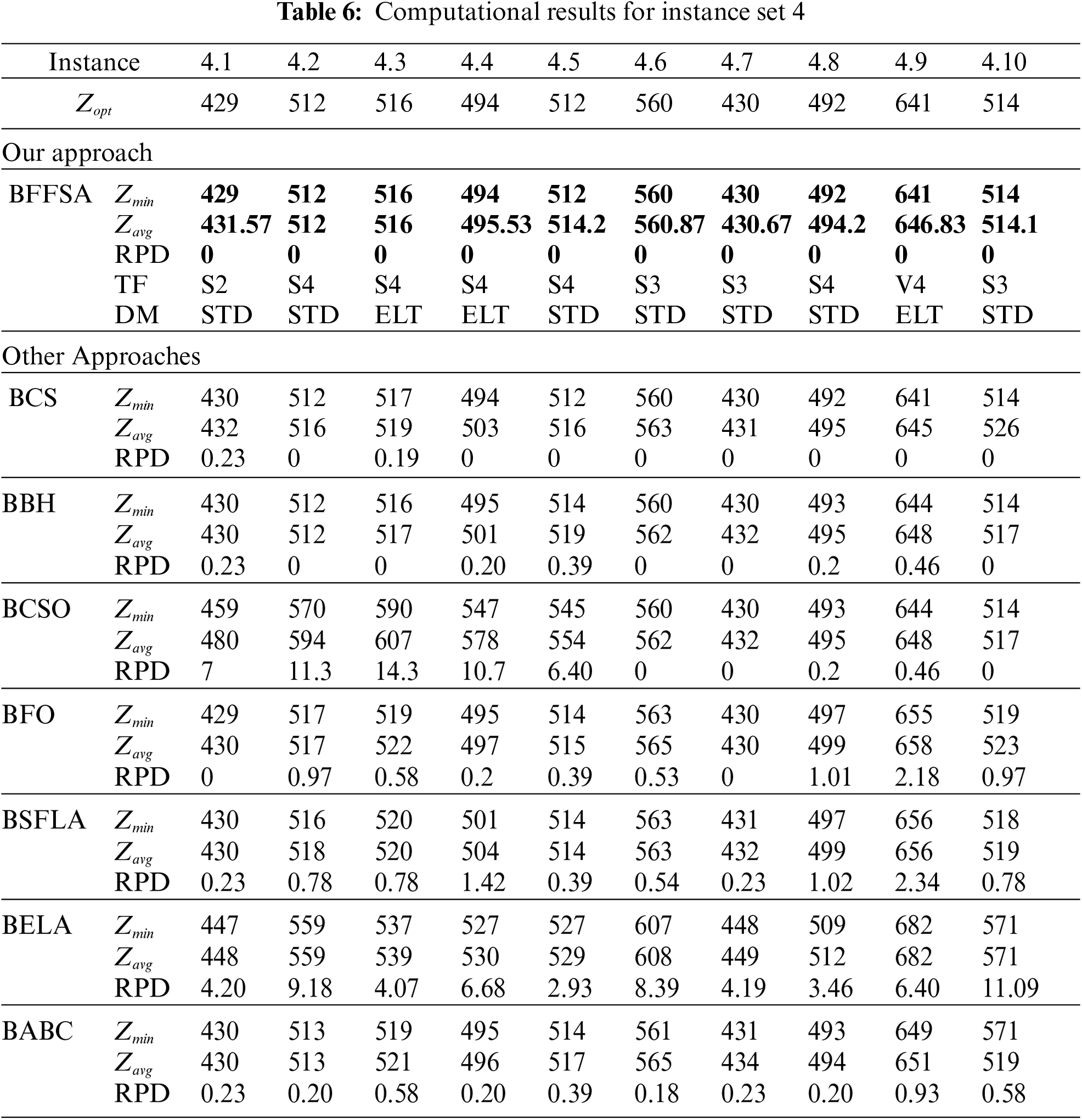
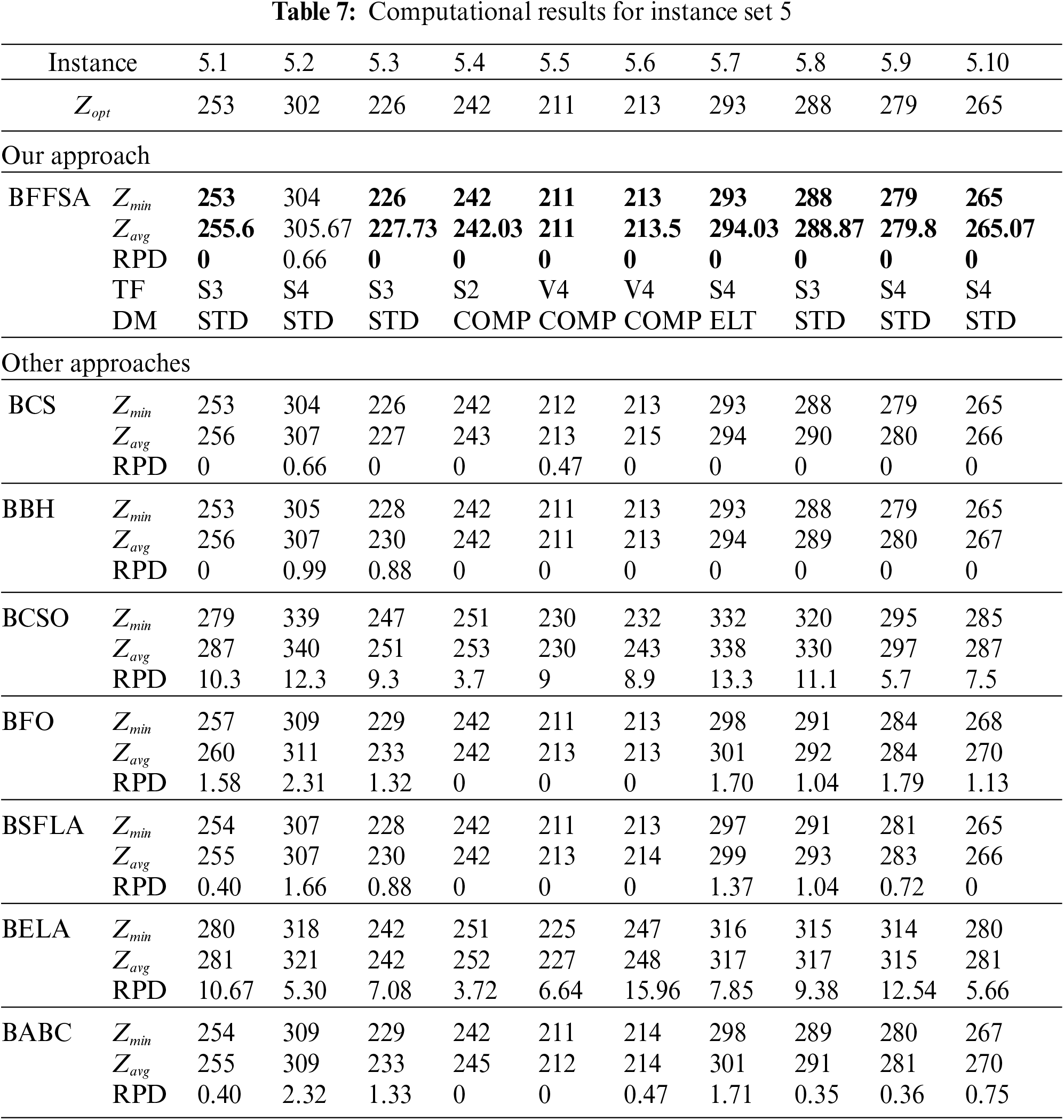
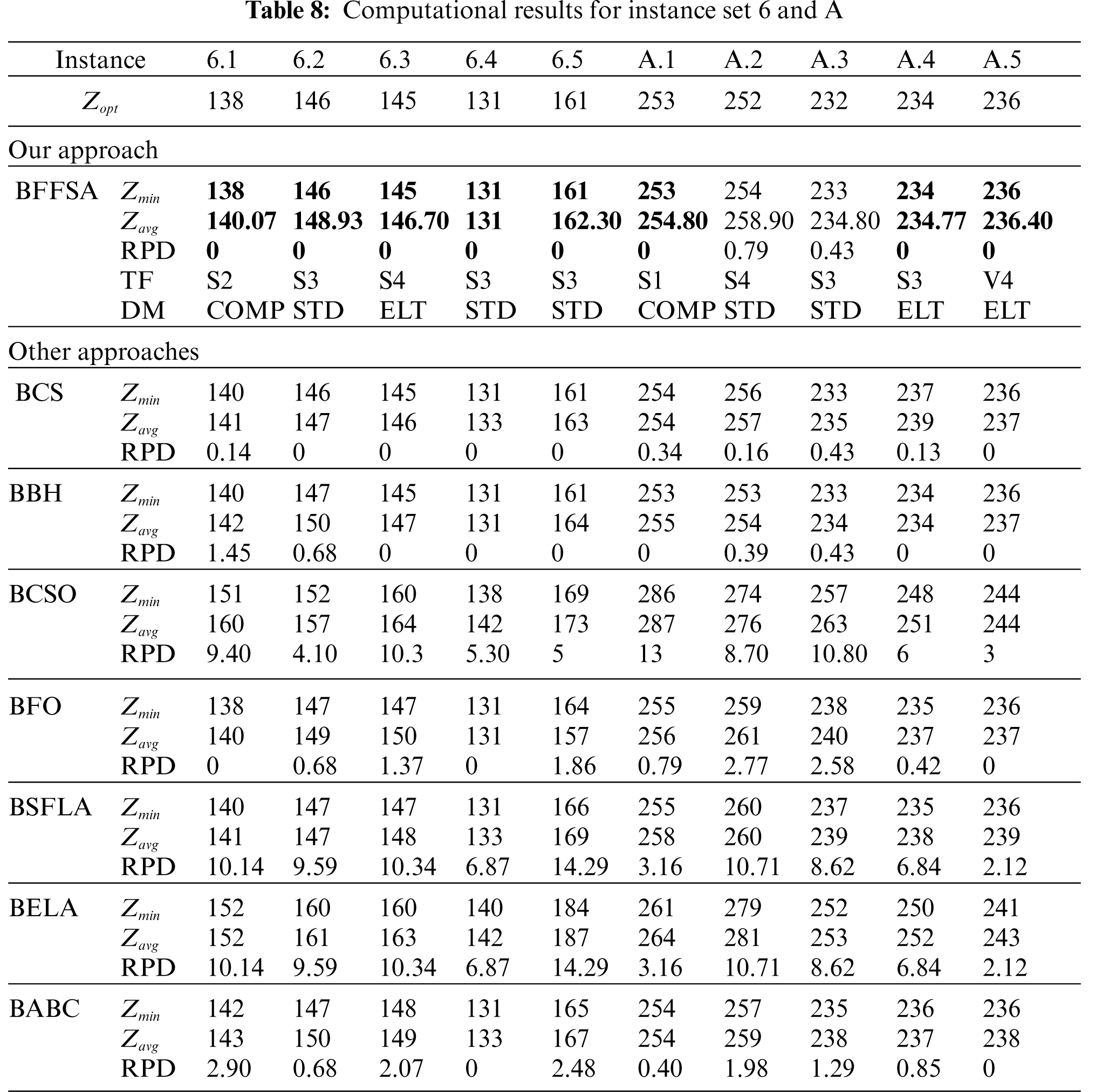
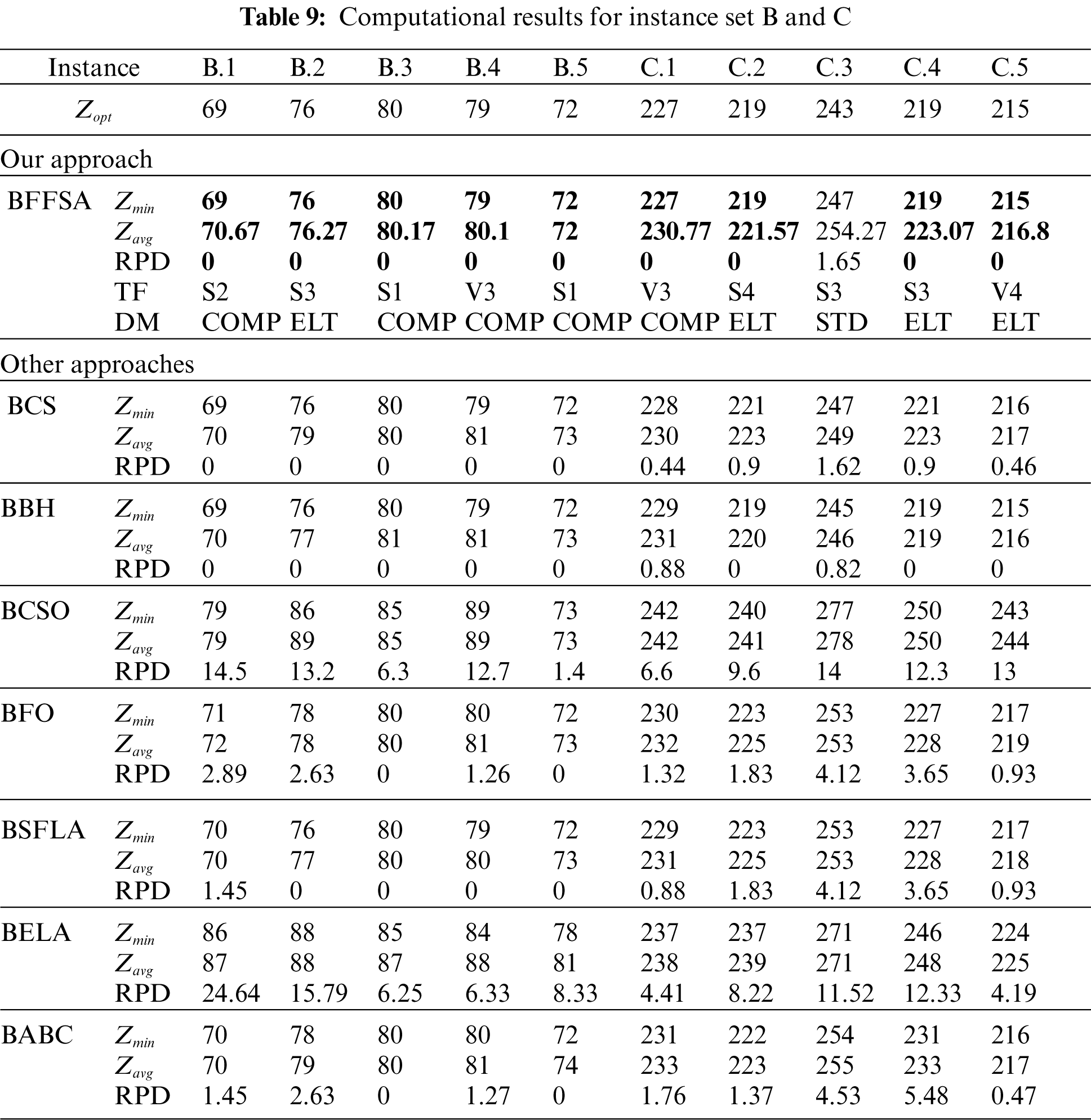
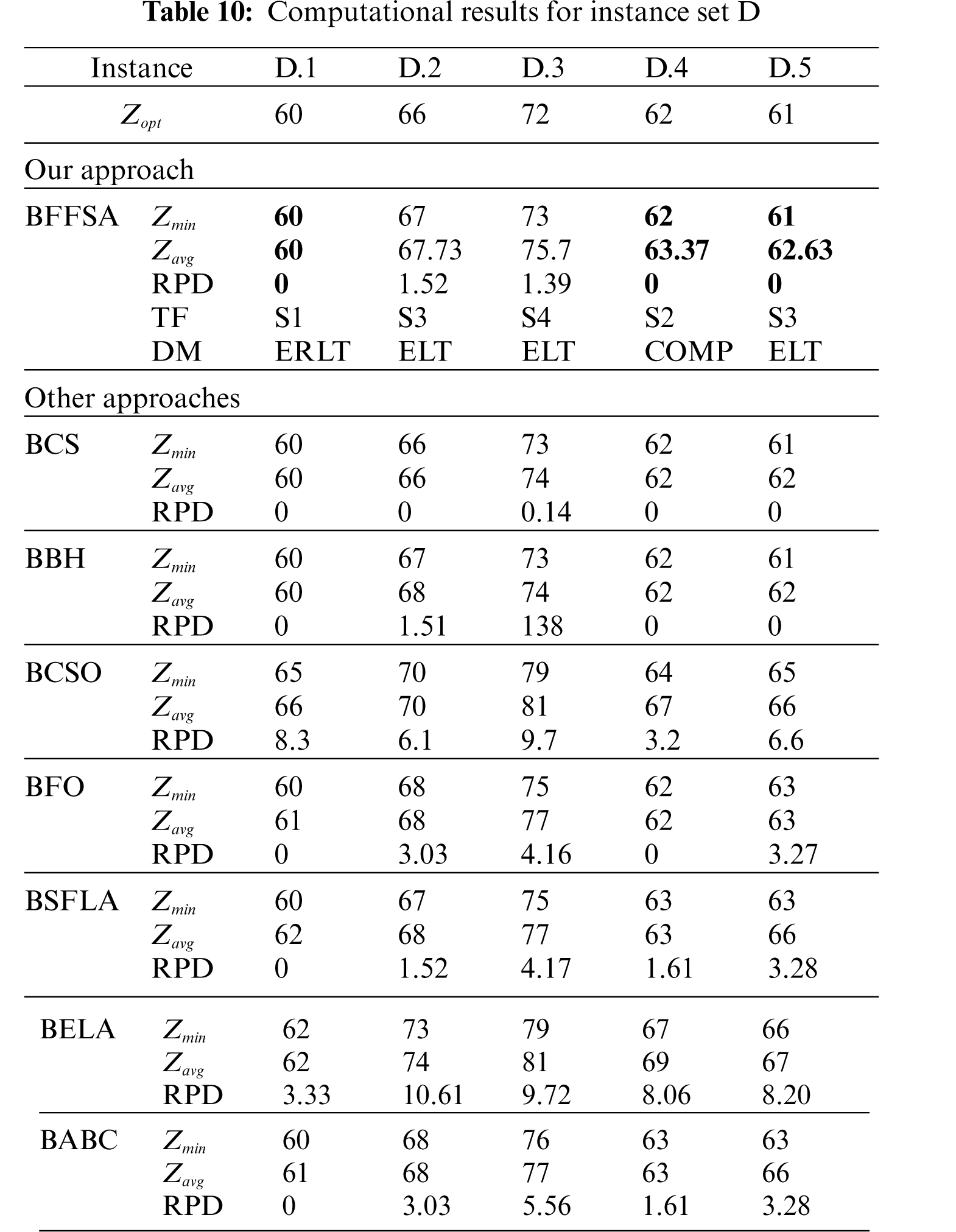
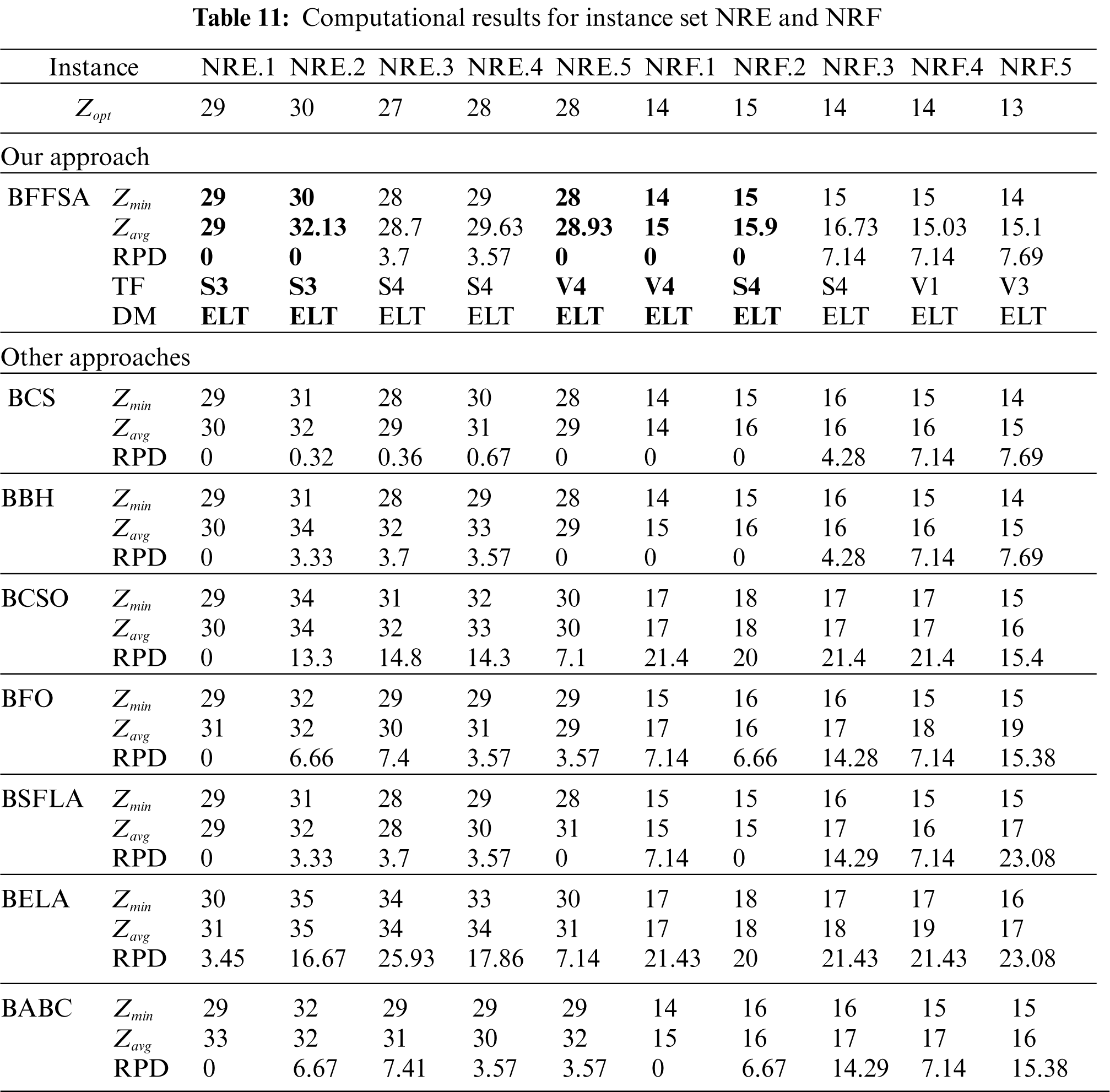
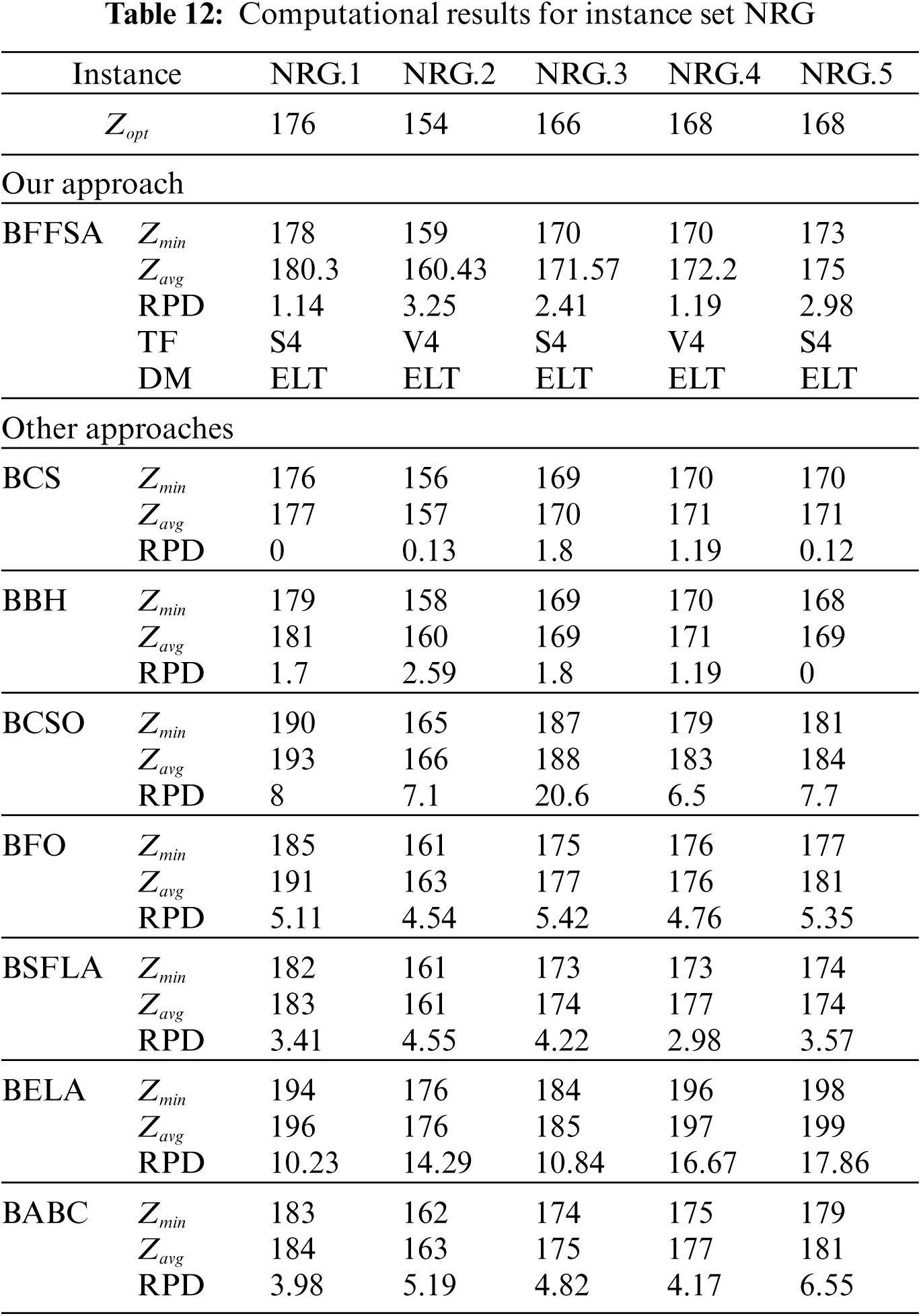
For comparison purposes, we consider the values reported in [16] for Binary Cuckoo Search (BCS) and Binary Black Hole (BBH); also, we have taken results for Binary Cat Swarm Optimization (BCSO) [15], Binary Firefly Optimization (BFO) [13], Binary Shuffled Frog Leap Algorithm (BSFLA) [18], Binary Electromagnetism-like Algorithm (BELA) [38] and Binary Artificial Bee Colony (BABC) [39].

Tab. 6 presents the results obtained from instance set 4. in this case our algorithm was better to all others in comparison, as it reached optimal values in all instances; BCSO, BSFLA, BELA and BABC are unable to achieve optimal values and BFO reached only two. The closest methods in comparison were BCS with eight optimal and BBH with five.

Tab. 7 describes the results from instance set 5. Once again, our algorithm got the best results along with BCS and BBH. Algorithms BCSO and BELA are unable to solve optimally any instance, BABC found only two optimal values, BFO reached three and BSFLA got four.

Tab. 8 illustrates the results from instance sets 6 and A. Our algorithm performed well, reaching eight optimal values (the whole set 6 and 3 from set A). BBH was slightly better than BCS this time, BCSO and BELA are unable to optimally solve any instance, BABC is capable to find only two optimal values (one in each set), BFO reached three and BSFLA got four.

Tab. 9 shows the results from instance set B and C. In case of set B, our algorithm had a very good performance, reaching all the optimal values, just like BCS and BBH. For instance set C, situation is similar, as BFFSA reached four out of five optimal values, outperforming all other methods.

Tab. 10 shows the results from instance set D. Here, the BFFSA and BBH (3 optimal values each one) could not reach results of BCS. However, we can still say this is an acceptable result, considering that all other approaches got less than 30% of optimal values.

For the NRE and NRF sets described in Tab. 11, only two RPD = 0 per set are reached by the BFFSA algorithm. Other approaches fail in general to find optimum values as the instance set becomes harder. Only BCS and BBH are closer to our results. BSFLA and BABC achieve one optimum for the instances belonging to set NRF, while BBH and BCS reach three.

Finally, for the hardest instance sets NRG and NRH (see Tabs. 12 and 13), we observe that the RPD obtained by the proposed BBFOA is good enough to compete with the approaches like BCS and BBH, as in the three cases, they could only reached one optimal value.

7  Conclusion

This article proposes several variations to BFFSA (39 to be precise), created by adding to the original BFFSA different transfer functions and discrete methods in order to improve the solutions obtained. All of these BBFOA-variations were tested into 65 SCP instances and the values reported correspond to the algorithm with the best performance. From our results, we conclude that variations presented are robust enough to compete with other algorithms as we were able to find many optimal solutions with a little parameter tuning.

We observed that best combinations of transfer functions and discretization methods depend on the instance size. For small instances (4, 5, 6, A, B, C, D) best results were achieved with transfer functions pS3 and pS4 plus the Standard discretization, whereas for huge instances (NRE, NRF, NRG, NRH) the best combinations are the same transfer functions pS3 and pS4, but with the Elitist method. A point to remark is that the use of the Elitist discretization is not exclusive for this algorithm and problem; other articles like [40] report good results with it.

In the future, we are interested in the hybridization of BFFSA with other meta-heuristics or apply an hyper-heuristics version. In the short term, we expect to test our algorithms on other SCP libraries, such like the Unicost (available at OR-Library website) or Italian railways [41] benchmarks. Due to the good results and the simplicity of this algorithm, it could be used to solve other combinatorial problems.

Acknowledgement: Marcelo Becerra-Rozas and Javier Peña are supported by Grant DI Interdisciplinary Undergraduate Research/VRIEA/PUCV/039.421/2021.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  D. Šarac, M. Kopić, K. Mostarac, M. Kujačić and B. Jovanović, “Application of set covering location problem for organizing the public postal network,” PROMET-Traffic&Transportation, vol. 28, pp. 403–413, 2016. [Google Scholar]

 2.  M. Mesquita and A. Paias, “Set partitioning/covering-based approaches for the integrated vehicle and crew scheduling problem,” Computers & Operations Research, vol. 35, pp. 1562–1575, 2008. [Google Scholar]

 3.  V. Cacchiani, V. C. Hemmelmayr and F. Tricoire, “A set-covering based heuristic algorithm for the periodic vehicle routing problem,” Discrete Applied Mathematics, vol. 163, pp. 53–64, 2014. [Google Scholar]

 4.  W. A. Chaovalitwongse, T. Y. Berger-Wolf, B. Dasgupta and M. V. Ashley, “Set covering approach for reconstruction of sibling relationships,” Optimisation Methods and Software, vol. 22, pp. 11–24, 2007. [Google Scholar]

 5.  D. Tapia, B. Crawford, R. Soto, F. Cisternas-Caneo, J. Lemus-Romani et al., “A Q-learning hyperheuristic binarization framework to balance exploration and exploitation,” in Applied Informatics: Third International Conference, ICAI 2020, Ota, Nigeria, 2020. [Google Scholar]

 6.  B. Crawford, R. Soto, J. Lemus-Romani, M. Becerra-Rozas, J. M. Lanza-Gutiérrez et al., “Q-Learnheuristics: Towards data-driven balanced metaheuristics,” Mathematics, vol. 9, pp. 1–26, 2021. [Google Scholar]

 7.  R. Soto, G. Astorga, J. Lemus-Romani, S. Misra, M. Castillo et al., “Balancing exploration-exploitation in the set covering problem resolution with a self-adaptive intelligent water drops algorithm,” Advances in Science, Technology and Engineering Systems, vol. 6, pp. 134–145, 2021. [Google Scholar]

 8.  D. Tapia, B. Crawford, R. Soto, W. Palma, J. Lemus-Romani et al., “Embedding Q-learning in the selection of metaheuristic operators: The enhanced binary grey wolf optimizer case,” in de 2021 IEEE Int. Conf. on Automation/XXIV Congress of the Chilean Association of Automatic Control (ICA-ACCA), Santiago, Chile, 2021. [Google Scholar]

 9.  A. Caprara, P. Toth and M. Fischetti, “Algorithms for the set covering problem,” Annals of Operations Research, vol. 98, pp. 353–371, 2000. [Google Scholar]

10. R. -L. Wang and K. Okazaki, “An improved genetic algorithm with conditional genetic operators and its application to set-covering problem,” Soft Computing, vol. 11, pp. 687–694, 2007. [Google Scholar]

11. M. Caserta, “Tabu search-based metaheuristic algorithm for large-scale set covering problems,” in Metaheuristics, Springer, Boston, MA: Springer, pp. 43–63, 2007. [Google Scholar]

12. Z. -G. Ren, Z. -R. Feng, L. -J. Ke and Z. -J. Zhang, “New ideas for applying ant colony optimization to the set covering problem,” Computers & Industrial Engineering, vol. 58, pp. 774–784, 2010. [Google Scholar]

13. B. Crawford, R. Soto, R. Cuesta and F. Paredes, “Application of the artificial bee colony algorithm for solving the set covering problem,” The Scientific World Journal, vol. 2014, pp. 1–8, 2014. [Google Scholar]

14. B. Crawford, R. Soto, M. O. Suárez, F. Paredes and F. Johnson, “Binary firefly algorithm for the set covering problem,” in de 2014 9th Iberian Conf. on Information Systems and Technologies (CISTI), Barcelona, Spain, pp.65–73, 2014. [Google Scholar]

15. B. Crawford, R. Soto, N. Berrı́os, F. Johnson and F. Paredes, “Binary cat swarm optimization for the set covering problem,” in de 2015 10th Iberian Conf. on Information Systems and Technologies (CISTI), Águeda, Aveiro, Portugal, 2015. [Google Scholar]

16. R. Soto, B. Crawford, R. Olivares, J. Barraza, I. Figueroa et al., “Solving the non-unicost set covering problem by using cuckoo search and black hole optimization,” Natural Computing, vol. 16, pp. 213–229, 2017. [Google Scholar]

17. B. Crawford, R. Soto, F. Aballay, S. Misra, F. Johnson et al., “A teaching-learning-based optimization algorithm for solving set covering problems,” in de Int. Conf. on Computational Science and its Applications, Banff, Alberta, Canada, 2015. [Google Scholar]

18. B. Crawford, R. Soto, C. Peña, W. Palma, F. Johnson et al., “Solving the set covering problem with a shuffled frog leaping algorithm,” in de Asian Conf. on Intelligent Information and Database Systems, Bali, Indonesia, 2015. [Google Scholar]

19. J. Garcı́a, B. Crawford, R. Soto and P. Garcı́a, “A multi dynamic binary black hole algorithm applied to set covering problem,” in de nt. Conf. on Harmony Search Algorithm, Bilbao, Spain, 2017. [Google Scholar]

20. B. Crawford, R. Soto, C. Torres-Rojas, C. Peña, M. Riquelme-Leiva et al., “A binary fruit fly optimization algorithm to solve the set covering problem.” in Int. Conf. on Computational Science and its Applications, Springer, Cham, 2015. [Google Scholar]

21. W. -T. Pan, “A new fruit fly optimization algorithm: Taking the financial distress model as an example,” Knowledge-Based Systems, vol. 26, pp. 69–74, 2012. [Google Scholar]

22. J. E. Beasley, “An algorithm for set covering problem,” European Journal of Operational Research, vol. 31, pp. 85–93, 1987. [Google Scholar]

23. M. L. Fisher and P. Kedia, “Optimal solution of set covering/partitioning problems using dual heuristics,” Management Science, vol. 36, pp. 674–688, 1990. [Google Scholar]

24. S. -M. Lin, “Analysis of service satisfaction in web auction logistics service using a combination of fruit fly optimization algorithm and general regression neural network,” Neural Computing and Applications, vol. 22, pp. 783–791, 2013. [Google Scholar]

25. H. -Z. Li, S. Guo, C. -J. Li and J. -Q. Sun, “A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm,” Knowledge-Based Systems, vol. 37, pp. 378–387, 2013. [Google Scholar]

26. Y. Xing, “Design and optimization of key control characteristics based on improved fruit fly optimization algorithm,” Kybernetes, vol. 42, no. 3, pp. 466–481, 2013. [Google Scholar]

27. Z. He, H. Qi, Y. Yao and L. Ruan, “Inverse estimation of the particle size distribution using the fruit fly optimization algorithm,” Applied Thermal Engineering, vol. 88, pp. 306–314, 2015. [Google Scholar]

28. L. Wang, X. -L. Zheng and S. -Y. Wang, “A novel binary fruit fly optimization algorithm for solving the multidimensional knapsack problem,” Knowledge-Based Systems, vol. 48, pp. 17–23, 2013. [Google Scholar]

29. J. E. Beasley and P. C. Chu, “A genetic algorithm for the set covering problem,” European Journal of Operational Research, vol. 94, pp. 392–404, 1996. [Google Scholar]

30. J. M. Lanza-Gutierrez, B. Crawford, R. Soto, N. Berrios, J. A. Gomez-Pulido et al., “Analyzing the effects of binarization techniques when solving the set covering problem through swarm optimization,” Expert Systems with Applications, vol. 70, pp. 67–82, 2017. [Google Scholar]

31. B. Crawford, R. Soto, G. Astorga, J. Garcı́a, C. Castro et al., “Putting continuous metaheuristics to work in binary search spaces,” Complexity, vol. 2017, pp. 1–19, 2017. [Google Scholar]

32. M. Olivares-Suarez, W. Palma, F. Paredes, E. Olguín and E. Norero, “A binary coded firefly algorithm that solves the set covering problem,” Science and Technology, vol. 17, pp. 252–264, 2014. [Google Scholar]

33. S. Mirjalili and A. Lewis, “S-shaped versus V-shaped transfer functions for binary particle swarm optimization,” Swarm and Evolutionary Computation, vol. 9, pp. 1–14, 2013. [Google Scholar]

34. Z. W. Geem, J. H. Kim and G. V. Loganathan, “A new heuristic optimization algorithm: Harmony search,” Simulation, vol. 76, pp. 60–68, 2001. [Google Scholar]

35. N. Rajalakshmi, D. P. Subramanian and K. Thamizhavel, “Performance enhancement of radial distributed system with distributed generators by reconfiguration using binary firefly algorithm,” Journal of the Institution of Engineers (IndiaSeries B, vol. 96, pp. 91–99, 2015. [Google Scholar]

36. E. Balas and A. Ho, “Set covering algorithms using cutting planes, heuristics, and subgradient optimization: A computational study,” in de Combinatorial Optimization, Berlin, Heidelberg: Springer, pp. 37–60, 1980. [Google Scholar]

37. J. E. Beasley, “A lagrangian heuristic for set-covering problems,” Naval Research Logistics (NRL), vol. 37, pp. 151–164, 1990. [Google Scholar]

38. R. Soto, B. Crawford, A. Munoz, F. Johnson and F. Paredes, “Pre-processing, repairing and transfer functions can help binary electromagnetism-like algorithms,” in de Artificial Tntelligence Perspectives and Applications, Switzerland, Cham: Springer, pp. 89–97, 2015. [Google Scholar]

39. R. Cuesta, B. Crawford, R. Soto and F. Paredes, “An artificial bee colony algorithm for the set covering problem,” in de Modern Trends and Techniques in Computer Science, Switzerland, Cham: Springer, pp. 53–63, 2014. [Google Scholar]

40. N. Ghorbani, E. Babaei and F. Sadikoglu, “Bema: Binary exchange market algorithm,” Procedia Computer Science, vol. 120, pp. 656–663, 2017. [Google Scholar]

41. S. Ceria, P. Nobili and A. Sassano, “A Lagrangian-based heuristic for large-scale set covering problems,” Mathematical Programming, vol. 81, pp. 215–228, 1998. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.