Computers, Materials & Continua DOI:10.32604/cmc.2022.023697
Article

Robust Authentication and Session Key Agreement Protocol for Satellite Communications

Somayeh Soltani1, Seyed Amin Hosseini Seno1, Juli Rejito2 and Rahmat Budiarto3,*

1Department of Computer Engineering, Ferdowsi University of Mashhad, Mashhad, 9177948974, Iran
2Faculty of Mathematics and Science, Universitas Padjadjaran, Jatinangor, 45363, Indonesia
3Faculty of Computer Science, Universitas Mercu Buana, Jakarta, 11650, Indonesia
*Corresponding Author: Rahmat Budiarto. Email: rahmat.budiarto@mercubuana.ac.id
Received: 17 September 2021; Accepted: 08 December 2021

Abstract: Satellite networks are recognized as the most essential communication infrastructures in the world today, which complement land networks and provide valuable services for their users. Extensive coverage and service stability of these networks have increased their popularity. Since eavesdropping and active intrusion in satellite communications are much easier than in terrestrial networks, securing satellite communications is vital. So far, several protocols have been proposed for authentication and key exchange of satellite communications, but none of them fully meet the security requirements. In this paper, we examine one of these protocols and identify its security vulnerabilities. Moreover, we propose a robust and secure authentication and session key agreement protocol using the elliptic curve cryptography (ECC). We show that the proposed protocol meets common security requirements and is resistant to known security attacks. Moreover, we prove that the proposed scheme satisfies the security features using the Automated Validation of Internet Security Protocols and Applications (AVISPA) formal verification tool and On-the fly Model-Checker (OFMC) and ATtack SEarcher (ATSE) model checkers. We have also proved the security of the session key exchange of our protocol using the Real or Random (RoR) model. Finally, the comparison of our scheme with similar methods shows its superiority.

Keywords: Satellite communications; authentication; session key agreement; secure communication; security protocols; formal verification

1  Introduction

Nowadays, mobile satellite networks are used to provide advanced personal communication services. These services complement terrestrial networks, providing benefits such as global coverage and increasing mobility and reliability for users. Satellite communications are valuable in an emergency and when other networks are unable to operate. Users can use satellite phones anytime and anywhere, including seas, islands, and high mountains, where land-based networks cannot provide services [1–3]. Furthermore, multicast applications delivery such as multimedia content distribution is perfectly performed by satellite systems [4,5].

While there are many different types of satellites, Low-Earth-Orbit (LEO) satellites are used more in mobile communications. These satellites are at shorter distances from Earth, so they have higher signal strength and lower latency [6,7]. However, unlike the Geosynchronous-Equatorial-Orbit (GEO) satellite, which alone covers the entire surface of the earth, several LEO satellites are required for this purpose [8].

The LEO satellite is a land-based satellite located less than 2000 km above the earth, which enables communication between mobile devices and the network control center through gateways [8,9]. Fig. 1 illustrates a general overview of satellite communications. The four basic components of these communications are mobile users, the network control center (NCC), LEOs, and gateways. Mobile users need to register with NCC to use the services. Gateways communicate between LEOs and the NCC.

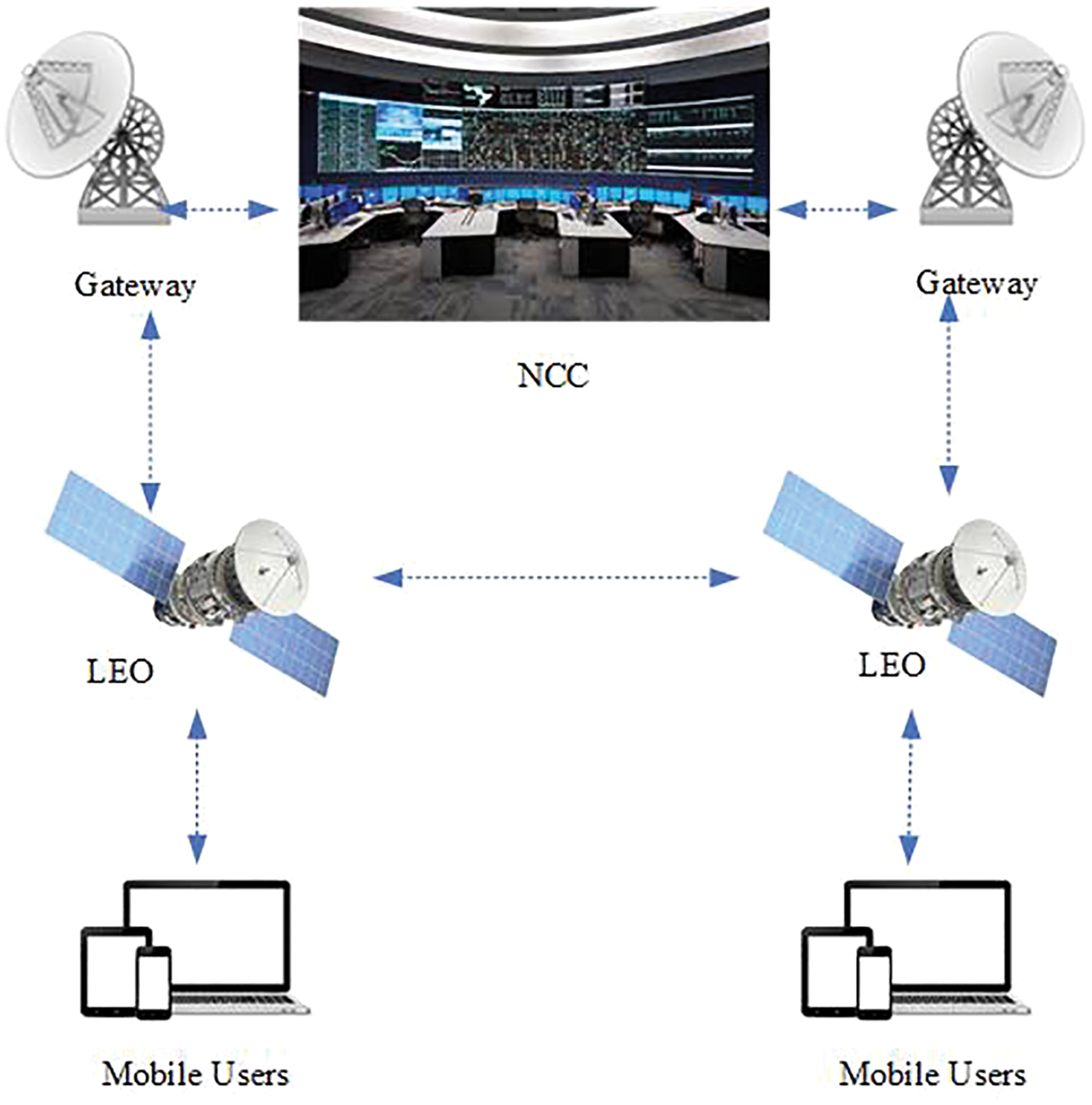
Figure 1: An overview of satellite communications

Because satellite communications are more susceptible to security attacks due to their broadcast nature, these communications need to be secure. Therefore, a session key is required for each communication session to encrypt the messages. There is also a need for strong authentication of both parties.

In recent years, various protocols for securing satellite communications have been proposed, most of which have security flaws. In particular, some authentication and key management protocols have provided ECC-based solutions leveraging the elliptic curve discrete logarithm problem (ECDLP) [10–14]. In this paper, we examine Qi et al.'s work [12] and show its security vulnerabilities. We propose a secure and robust protocol for key exchange in satellite communications, which is resistant to known security attacks and satisfies the security requirements. Further, a thorough analysis of the proposed protocol shows that it performs better in terms of security than other ECC-based protocols.

The contributions of this paper are as follows:

•   Analysis of key exchange protocol introduced by Qi et al. [12] and security vulnerabilities are revealed.

•   A secure ECC-based authentication and key exchange protocol that resists common attacks and meets common security requirements.

•   A thorough security analysis of the proposed protocol and its resistance to various types of attacks.

•   Formal security verification of the proposed protocol on AVISPA tool, considering different model checking techniques that the proposed protocol meets different security requirements.

•   The proof of security of the proposed key exchange protocol using the RoR model.

The rest of the paper is structured as follows: In Section 2, some essential related works are discussed. Section 3 provides background information on elliptic curve cryptography and the threat models. Section 4 describes Qi et al.'s protocol [12] and analyzes its security. Section 5 describes the proposed authentication and key exchange protocol for satellite communications. The security analysis of the proposed method is described in Section 6. In Section 7, the proposed protocol is compared with other similar protocols in terms of time complexity, communication cost, and security features. Finally, Section 8 is devoted to the conclusion.

2  Related Works

To provide satellite communications over unsecured networks, Cruickshank [15] developed the first satellite communication protocol in 1996. Since then, many protocols were introduced to secure satellite communications, and later on, other researchers take turns finding out weaknesses and flaws in those protocols and propose improved protocols.

Chen et al. [16] proposed an authentication mechanism for mobile satellite communication systems. Later on, Lasc et al. [17] showed that Chen et al.'s protocol was not resistant to the Denial of Service (DoS) attack and then suggested an improvement. Next, Chang et al. [18] revealed that Lasc et al.'s protocol was susceptible to impersonation attack through a stolen smart card. Then they proposed an authentication protocol for satellite communications. The newly proposed protocol was claimed to be resistant to all kinds of attacks. However, Zhang et al. [19] showed that the protocol proposed by Chang et al. was not resistant against the DoS attack and the impersonation attack.

Lee et al. [20] introduced an authentication and key exchange protocol for mobile satellite communications systems and claimed that it is resistant to all kinds of attacks. Later, Zhang et al. [21] revealed that Lee et al.'s protocol was not resistant against replay attacks, DoS attacks, and attacks from a stolen smart card. Then they developed a new protocol for satellite communication authentication. In 2018, Qi et al. [10] stated that Zhang et al.’ protocol was insecure against the stolen-verifier attack and DoS attack. Then they proposed an ECC-based protocol for satellite communication authentication. In 2019, Ostad-sharif et al. [11] showed that Qi and Chen's protocol could not meet the security requirements of perfect forward secrecy and did not resist the ephemeral secret leakage attack.

Liu et al. [22] proposed a Lightweight protocol for satellite communications authentication. Later on, Qi et al. [12] showed that the protocol proposed by Liu et al. does not meet the perfect forward security requirement. Then they introduced an authentication protocol based on ECC. In this paper, we prove that the protocol of Qi et al. is not resistant to Known-session-specific temporary information attacks and insider attacks.

Altaf et al. [14] proposed an authentication and key agreement scheme which is based on the (ECDLP problem. Then, Chen and Chen [13] proved that Altaf et al.'s protocol does not provide perfect forward secrecy. Moreover, we found that their scheme is vulnerable to DoS attack. The attacker can resend the request message to the NCC many times and force it to do the time-expensive point multiplication operation many times and thus overwhelms the NCC. Furthermore, Hosseini-Seno et al. [23] have proposed an authentication and key management protocol to provide patient privacy in Tele-medical information system. The proposed protocol cautiously considers all aspects of security requirements including the perfect forward secrecy.

3  Preliminaries

3.1 Elliptic Curve Cryptography (ECC)

ECC uses the elliptic curve y2=x3+ax+b over the finite field Fp, where p is a prime number with typically 256-bit (or more) length. All operations in the filed Fp are in the modular form. Therefore, the ECC is defined as (1):

Ep(a,b):y2=x3+ax+b(modp)∪⁡{O}(1)

where a,b∈Fp, 4a3+27b2modp≠0, and O is the point at infinity.

The ECC Ep(a,b) is an Abelian group with addition as the group operation. Therefore, the addition of every two points on the curve leads to a new point on the curve. We can simulate scalar multiplication using the addition operation. The multiplication of scalar k in point R is k.

R=R+⋯+R⏟ktimes

The building block for elliptic curve cryptography is the elliptic curve discrete logarithm problem: Given two points R and S over Ep(a,b), find k such that S=k.R. If the parameters of the elliptic curve are properly chosen, the ECDLP is believed to be infeasible with current technology [24].

To select a suitable elliptic curve, in addition to determining the values of a, b, and p, we should also define the generator G. In some elliptic curves, all points on the curve (n) can be generated with a single G. In this case, the curve has only one subgroup (h=1). Sometimes, the curve has several subgroups (h>1), and it is necessary to find a separate generator for each one. In the proposed method, we use ECCs with h=1, such as secp192r1 [25]. Therefore, the ECC parameters in the proposed method are shown with a five-tuple ⟨a,b,p,n,G⟩.

3.2 Threat Models

The most popular threat model is the Dolev-Yao model [26], which is an abstract model of agents’ capabilities. The Dolev-Yao model strips away the extraneous details of communications and shows a simple view of exchanged messages. The Dolev-Yao model presents term of algebra and models the protocol messages as terms. It presents some term derivation rules which define how agents can build new terms from the old ones.

Suppose Ag, K, and N represent the set of agents, keys, and nonces, respectively. We define the set of basic terms as B=Ag∪⁡N∪⁡K. We denote the public key and private key of the agent A∈Ag using pk(A) and sk(A), respectively. Moreover, for A,B∈Ag we use k(A,B) to denote the shared symmetric key between them. The inverse of each k∈K is defined in (2)--(4).

inv(pk(A))=sk(A)(2)

inv(sk(A))=pk(A)(3)

inv(k(A,B))=k(A,B)(4)

The term syntax in Dolev-Yao model is defined in (5).

t::=t0|pair(t0,t1)|hash(t)|symE(t,k)|pubE(t,k),(5)

where t0,t1∈B and k∈K.

The intruder in the Dolev-Yao model is one of the agents and has access to the hash function, public keys of all agents, his private key, and his shared key with other entities. Moreover, the intruder has full control over all communication messages between agents. He can eavesdrop, intercept, or replay the messages [27]. However, in examining the strength of security protocols, a stricter threat model such as the Canetti–Krawczyk (CK) [28] model is usually used. The attacker in the CK model not only has complete control over communications but also has the ability to obtain secret data in the system's memories. Therefore, the adversary may access private keys of parties or session-specific temporary keys. We consider the CK treat model in the analysis of our protocol.

4  Review and Analysis of Qi et al. Protocol

This section analyzes the protocol introdued by Qi et al. [12]. The protocol consists of four phases, namely, 1) initialization, 2) user registration, 3) login and authentication with key agreement, and 4) password update. In the registration phase, each user firstly selects his ID and password (IDi,pwi), and sends them to the NCC with IDi,mpi=H(IDi||pwi) via a secure channel [12].

When the message is received, the NCC checks that the selected IDi does not belong to a duplicate user. It then performs the operations in the registration phase and finally delivers the smart card to the user. During the login and authentication phase, the user enters his smart card into the card reader and then inputs the user and password (IDi,pwi). If it is determined that the smart card belongs to the person, the user and the NCC agree on a shared key of (SKi=αβ.G) by transmitting messages to each other. So, from now on, the user and the NCC can communicate using the shared key.

We demonstrate that the protocol proposed by Qi et al. is vulnerable against attacks, as follows.

Known Session-Specific Temporary Information Attack

If the random parameters generated in a protocol are captured by the attacker, the session key should not be revealed. However, in the Qi et al.'s protocol, the session key SKi=αβ.G is generally made up of random numbers α and β and a base point, which is considered general. So, by revealing random numbers, the attacker gains the key to the session.

Insider Attack

It is assumed that the internal attacker (here NCC) tries to obtain the password of each user. Since the user sends the mpi′=H(IDi||pwi) and IDi to the NCC, and the password is usually short, the internal attacker on the NCC side can guess the password using the hash table.

5  The Proposed Protocol

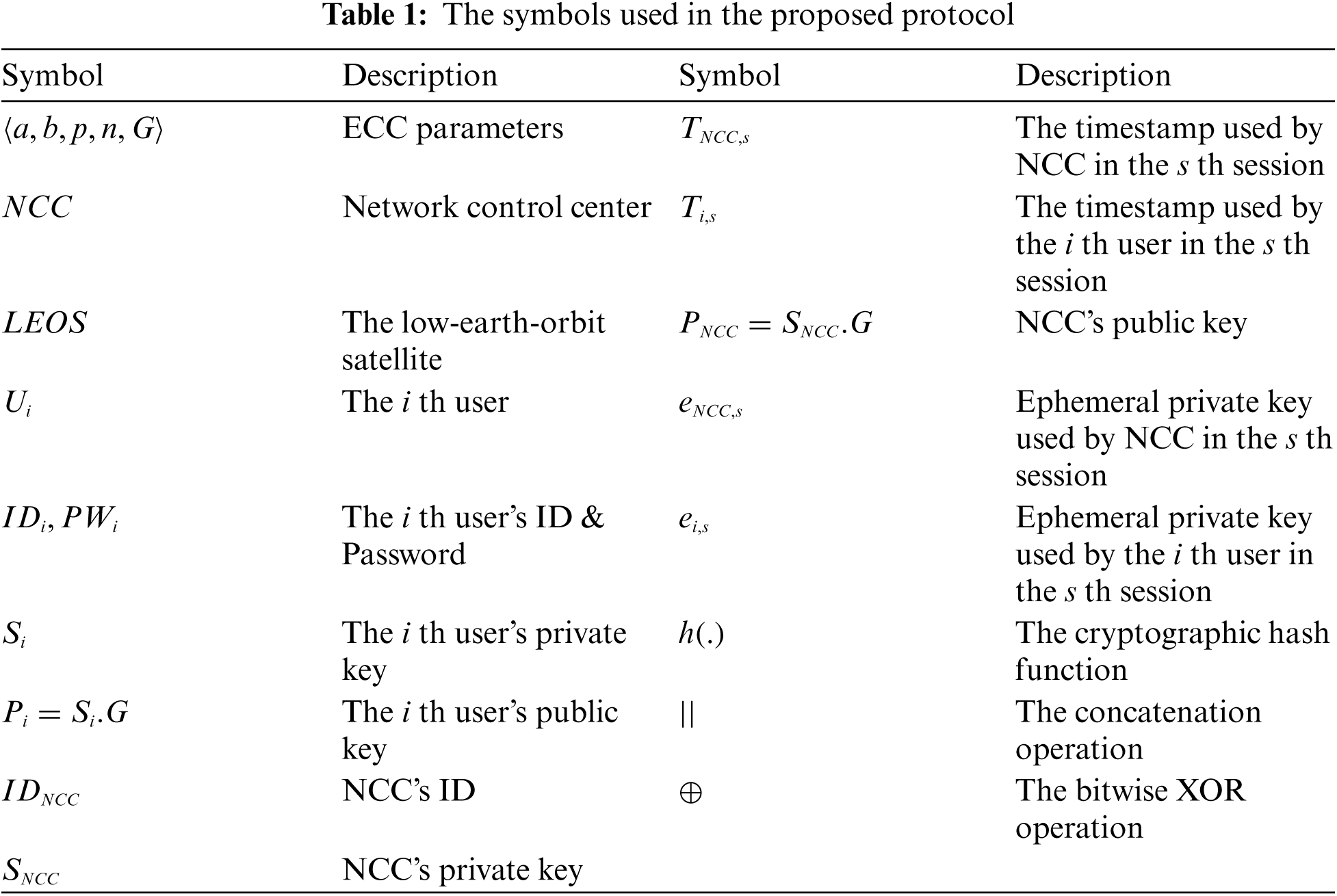
The proposed protocol uses elliptic curve encryption and consists of initialization, registration, and authentication and key agreement steps. Tab. 1 shows the symbols used in the proposed protocol.

5.1 Initialization Phase

In this phase, the NCC sets some parameters to be used in authentication and key management. As explained in the previous section, to use the ECC cryptosystem, the NCC needs to set the five-tuple ⟨a,b,p,n,G⟩. Besides, the NCC chooses a random number SNCC∈Fp and computes its related public key PNCC=SNCC.G. Moreover, the NCC needs to choose the hash function h(.).

5.2 Registration Phase

To use the NCC services, the user needs to register first. The steps of user registration are depicted in Fig. 2 and are as follows:

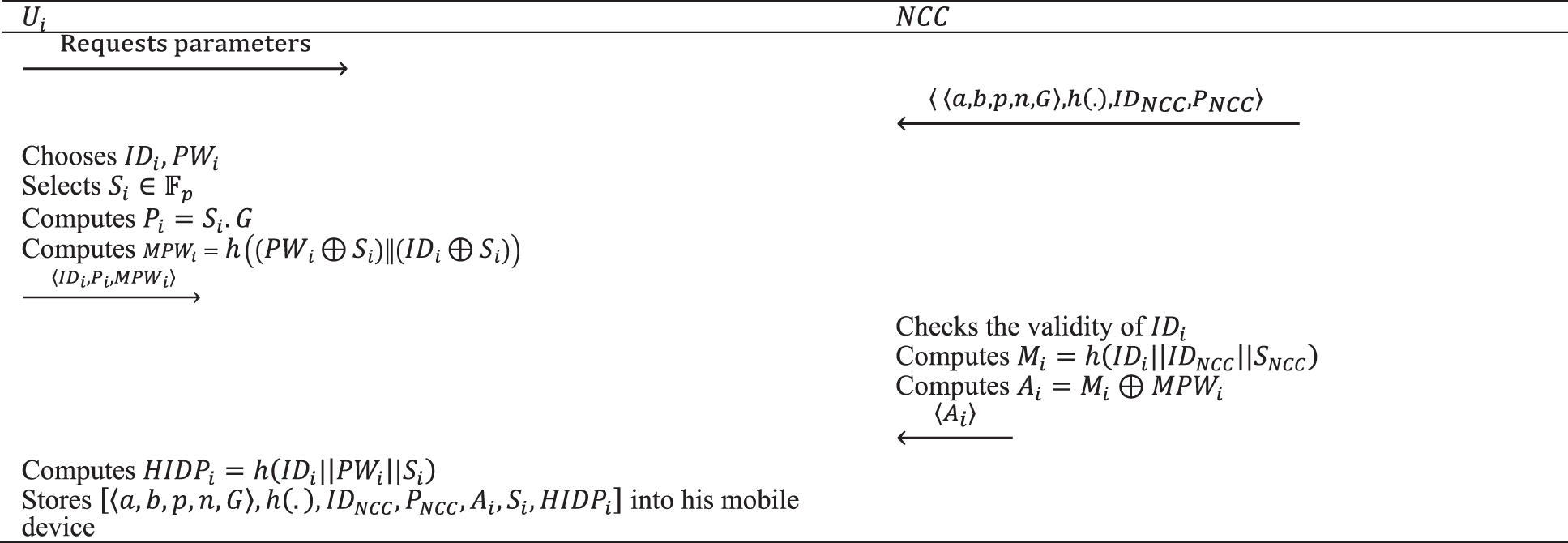
Figure 2: The registration phase of the proposed protocol

Step 1. The user Ui first asks the NCC via a secure channel to send him the initialized parameters, ⟨⟨a,b,p,n,G,h(.),IDNCC,PNCC⟩.

Step 2. After receiving the necessary parameters, the user chooses an ID and password. He also selects a random number Si∈Fp as the private key and calculates his public key Pi=Si.G. The user then calculates his masked password to hide his password from the NCC. The masked password is defined in (6).

MPWi=h((PWi⊕Si)||(IDi⊕Si))(6)

Finally, he sends the triple ⟨IDi,Pi,MPWi⟩ through the secure channel to the NCC.

Step 3. Upon receiving ⟨IDi,Pi,MPWi⟩, the NCC checks the validity of IDi. If the ID is legitimate, the NCC computes Mi, which is a combination of the user's identity, the NCC's identity, and the NCC's private key as defined in (7).

Mi=h(IDi||IDNCC||SNCC)(7)

Then, the NCC performs the XOR operation on Mi and MPWi to calculate Ai as defined in (8).

Ai=Mi⊕MPWi(8)

Finally, the NCC sends ⟨Ai⟩ to Ui via the secure channel.

Step 4. The user calculates the hash of his identity, his password, and his private key as defined in (9).

HIDPi=h(IDi||PWi||Si)(9)

Finally, he stores [⟨a,b,p,n,G⟩,h(.),IDNCC,PNCC,Ai,Si,HIDPi] in his mobile device.

5.3 Authentication and Key Agreement Phase

Upon completion of the registration, the user and the NCC start a two-way authentication and key exchange process to communicate with each other via an insecure channel. A complete description of this phase is given in Fig. 3 and is described in the following steps:

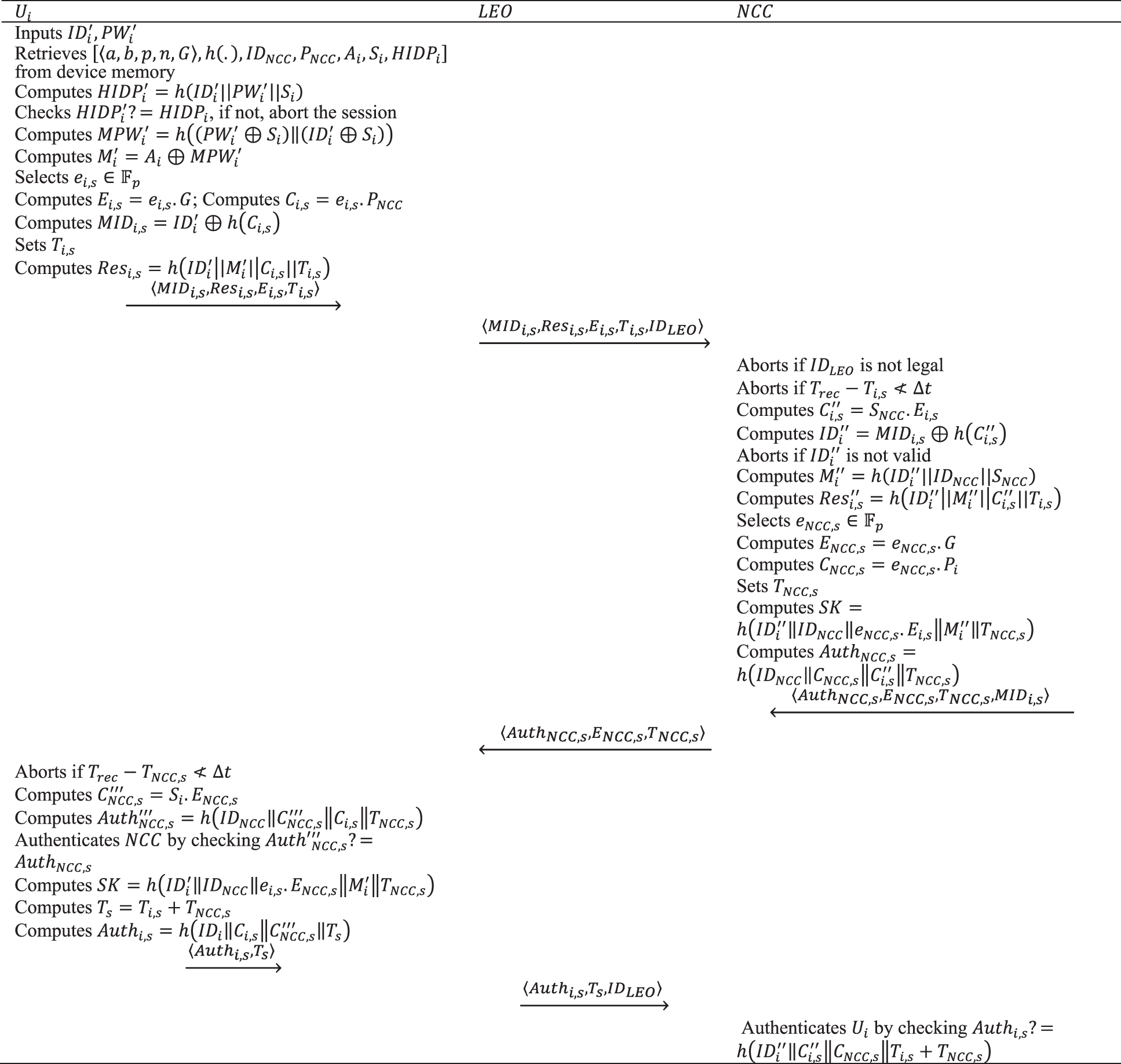
Figure 3: The authentication and key agreement phase of the proposed protocol

Step 1. The user enters his identity and password (IDi′,PWi′). Here, the ID and password are shown using the prime symbol to indicate that these values are re-entered in this step and may differ from the ID and password values in the previous phase. Then [⟨a,b,p,n,G⟩,h(.),IDNCC,PNCC,Ai,Si,HIDPi] is extracted from the mobile device memory. After that, HIDPi′ is calculated and checked to see if this value is the same as HIDPi in the device memory (10).

HIDPi′=h(IDi′||PWi′||Si)(10)

MPWi′=h((PWi′⊕Si)∥(IDi′⊕Si))(11)

Mi′=Ai⊕MPWi′(12)

Ci,s=ei,s.PNCC(13)

Then the mobile device calculates the masked identity of the user for this session as defined in (14).

MIDi,s=IDi′⊕h(Ci,s)(14)

The mobile device then sets the timestamp Ti,s and calculates Resi,s as defined in (15).

Resi,s=h(IDi′||Mi′||Ci,s||Ti,s)(15)

Finally, the mobile device sends the four-tuple ⟨MIDi,s,Resi,s,Ei,s,Ti,s⟩ to the LEO. Upon receiving the four-tuple, the LEO adds its own identity IDLEO to it and forwards the five-tuple ⟨MIDi,s,Resi,s,Ei,s,Ti,s,IDLEO⟩ to the NCC.

Step 2. Upon receiving the message ⟨MIDi,s,Resi,s,Ei,s,Ti,s,IDLEO⟩, the NCC checks the validity of the LEO. Then it verifies the freshness of the message by checking that the difference between receiving time (Trec) and the timestamp Ti,s is less than Δt. Afterward, it calculates Ci,s′′ as defined in (16).

Ci,s′′=SNCC.Ei,s(16)

Moreover, the NCC computes IDi′′ as defined in (18), and it aborts the session if it is not valid.

IDi′′=MIDi,s⊕h(Ci,s′′)(17)

Note that here we use the double prime symbol to indicate that the variables are calculated in a new step of the protocol.

Then the NCC calculates Mi′′ and Resi,s′′ as defined in (18) and (19).

Mi′′=h(IDi′′||IDNCC||SNCC)(18)

Resi,s′′=h(IDi′′||Mi′′||Ci,s′′||Ti,s)(19)

Then the NCC selects the ephemeral private key of the session, eNCC,s∈Fp, and computes the ephemeral public key, ENCC,s=eNCC,s.G. Moreover, the NCC calculates another secret, CNCC,s, as defined in (20).

CNCC,s=eNCC,s.Pi(20)

The NCC then sets the timestamp TNCC,s and calculates the session key, SK, and the verifier, AuthNCC,s, as defined in (21) and (22).

SK=h(IDi′′∥IDNCC∥eNCC,s.Ei,s∥Mi′′∥TNCC,s)(21)

AuthNCC,s=h(IDNCC∥CNCC,s∥Ci,s′′∥TNCC,s)(22)

Finally, the NCC sends the four-tuple ⟨AuthNCC,s,ENCC,s,TNCC,s,MIDi,s⟩ to the LEO, and the LEO forwards the triple ⟨AuthNCC,s,ENCC,s,TNCC,s⟩ to the mobile device.

Step 3. The mobile device verifies the freshness of the received message by checking Trec−TNCC,s≮Δt, and it ends the session if the message is not fresh. It then calculates CNCC,s′′′ and AuthNCC,s′′′ as defined in (23) and (24).

CNCC,s′′′=Si.ENCC,s(23)

AuthNCC,s′′′=h(IDNCC∥CNCC,s′′′∥Ci,s∥TNCC,s)(24)

Then, the mobile device checks whether AuthNCC,s′′′ is equal to AuthNCC,s. If it is true, it calculates the shared session key as defined in (25).

SK=h(IDi′∥IDNCC∥ei,s.ENCC,s∥Mi′∥TNCC,s)(25)

Next, the mobile device computes Ts=Ti,s+TNCC,s and creates Authi,s as defined in (26).

Authi,s=h(IDi∥Ci,s∥CNCC,s′′′∥Ts)(26)

Finally, it sends ⟨Authi,s,Ts⟩ to the LEO, and the LEO forwards ⟨Authi,s,Ts,IDLEO⟩ to the NCC.

Step 4. The NCC authenticates the user by checking whether the received Authi,s is equal to h(IDi′′∥Ci,s′′∥CNCC,s∥Ti,s+TNCC,s).

6  Security Analysis of the Proposed Protocol

In this section, we describe the security features, the robustness against several security attacks of the proposed protocol, and formally verify the correctness of the proposed protocol in terms of satisfying security features using AVISPA.

6.1 Security Features

6.1.1 Mutual Authentication

Key agreement protocols require the parties to authenticate each other. In our proposed method, the user selects the ephemeral private key ei,s and generates the ephemeral public key Ei,s and the secret key Ci,s. To request services, the user sends Ei,s and some other messages to the NCC and keeps Ci,s hidden. Except for the user, the only entity that can reproduce Ci,s is NCC. The NCC reproduces the Ci,s using Ei,s and incorporates it into its authentication message (AuthNCC,s). On the other hand, the NCC selects the ephemeral private key eNCC,s, from which it generates the ephemeral public key ENCC,s and the secret key CNCC,s. The NCC sends the ENCC,s to the user and holds the secret key CNCC,s. Except for NCC, the only entity that can reproduce CNCC,s is the user. The user can regenerate CNCC,s and AuthNCC,s. If the reconstructed AuthNCC,s is equal to the sent AuthNCC,s, NCC will be authenticated to the user. The user then inserts CNCC,s in his authentication message (Authi,s) and sends it to the NCC. If Authi,s is equal to h(IDi∥Ci,s∥CNCC,s), the user is authenticated for NCC.

6.1.2 Session Key Security

The session key generated in the proposed method is shared between the user and the NCC, and no other entity can access the session key. The session key on the server-side is calculated with SK=h(IDi′′∥IDNCC∥eNCC,s.Ei,s∥Mi′′∥TNCC,s)=h(IDi′′∥IDNCC∥eNCC,s.Ei,s∥h(IDi′′||IDNCC||SNCC)∥TNCC,s), which requires knowing the ephemeral private key eNCC,s and the private key SNCC. The session key on the user side is calculated with SK=h(IDi′∥IDNCC∥ei,s.ENCC,s∥Mi′∥TNCC,s)=h(IDi′∥IDNCC∥ei,s.ENCC,s∥Ai⊕h(PWi′⊕Si)∥TNCC,s) and requires knowledge of the ephemeral private key ei,s, the private key Si, the password PWi, and Ai.

6.1.3 Perfect Forward Secrecy

The perfect forward secrecy guarantees the security of the session key, even though the long-term secret keys of parties are compromised. The proposed method preserves this feature because the session key is built using both long-term private keys and temporary secret keys. Even if the adversary A gets access to Si and SNCC, he cannot guess the session key.

6.1.4 User Anonymity

The proposed method does not send the user identity in plain text over insecure channels, but the masked user identity, MIDi,s=IDi′⊕h(Ci,s), is sent. Only the NCC can calculate Ci,s using SNCC and know the user ID. Therefore, user anonymity is preserved against other entities.

6.2 Security Attacks

6.2.1 Replay Attack

Our proposed method is resistant against the replay attack because, in addition to sending the timestamp Ti,s explicitly, we also embed it in the Resi,s message. So, if the adversary A updates the timestamp Ti,s to Tnewi,s and resends the message ⟨MIDi,s,Resi,s,Ei,s,Tnewi,s⟩, the NCC detects the attack by checking Resi,s. Also, if the attacker repeats the message ⟨AuthNCC,s,ENCC,s,TnewNCC,s⟩ by changing the timestamp TNCC,s, the user will notice the attack by checking AuthNCC,s.

6.2.2 Man-in-the-Middle Attack

If the adversary A interrupts the communication between the valid user Ui and the NCC, he should be able to send legitimate message ⟨MIDi,s,Resi,s,Ei,s,Ti,s⟩ to the NCC. However, to build a valid Resi,s, the adversary has to know the password and the private key of Ui.

6.2.3 Insider Attack

The user does not send the password to NCC in the registration phase explicitly but sends it in hidden form, MPWi=h((PWi⊕Si)∥(IDi⊕Si)). Since the NCC does not know the user's private key Si, it cannot guess the user's password.

6.2.4 Impersonation Attack

If the adversary A wants to impersonate the user, he must be able to forget the request message ⟨MIDi,s,Resi,s,Ei,s,Ti,s⟩. Assuming that the adversary is one of the users, he can generate a random number ei,s and the secret key Ci,s and create MIDi,s by accessing the user ID. He can also generate Ei,s and Ti,s, but he cannot generate RESi,s without Mi, and knowing Mi relies on knowing Ai and the user password PWi or knowing the NCC's private key, SNCC.

6.2.5 Known-Session-Specific Temporary Information Attack

If the attacker accesses the temporary session parameters in any way, he should not be able to access the session key. Since the session key, SK=h(IDi′′∥IDNCC∥eNCC,s.Ei,s∥Mi′′∥TNCC,s), in our scheme is composed of both temporary and long-term parameters, it is resistant to this attack.

6.2.6 Smart Card Loss Attack

If the user's mobile device (or smart card) is stolen, the adversary A should not be able to impersonate the user. Our proposed method is resistant to this attack because even if the adversary access smart card information [⟨a,b,p,n,G⟩,h(.),IDNCC,PNCC,Ai,Si,HIDPi], he cannot impersonate the user without the correct ID and password.

6.2.7 Stolen Verifier Attack

In our proposed method, NCC does not store any information about users other than their ID. Therefore, if the adversary accesses the NCC database, it will not receive any additional information.

6.2.8 DoS Attack

Denial of Service attacks can be done on satellite communications entities, including the users and the NCC. By persuading the NCC to perform a large number of heavy-weight point multiplication operations on the elliptic curve, the attacker causes the NCC to crash and makes it impossible to provide services to authorized users. Our proposed protocol is resistant to this attack because if one of the users wants to carry out this attack against the NCC, he himself will suffer the same heavy-weight operations. Also, due to the resistance of the proposed method to replay attacks, the adversary is not able to resend the request message to the NCC. For the same reason, it is not possible to perform this attack on system users.

6.3 Formal Security Analysis with AVISPA

AVISPA is a role-based language that provides a formal language for specifying protocols and security properties and uses several back-ends to analyze them [29,30]. Each participant in the protocol is represented by a role, which communicates with other roles by channels. The HLPSL specification is translated to an intermediate format, which is then analyzed by some back-ends. The four back-ends used by AVISPA include Tree Automata-based Protocol Analyzer (TA4SP), OFMC [31], Constraint Logic-based Attack Searcher (CL-ATSE) [32], and satisfiability-based Model-Checker (SATMC) [33].

We have implemented our protocol in the HLPSL language. We have defined a role for the user, role_Ui, and a role for the NCC, role_NCC. We have also defined a session role that specifies a session of the protocol. In addition, we have considered an environment role and defined three sessions in it. The first session is between the user and the NCC. In the second session, the intruder impersonates the user, and in the third session, the intruder impersonates the NCC. In addition, we have defined the intruder's knowledge and the security goals.

The goal of secrecy_of sec_1 examines the confidentiality of ei,s for the user. If the goal is satisfied by the protocol, the secrecy of ei,s is guaranteed. Similarly, the goal of secrecy_of sec_2 checks the confidentiality of eNCC,s for the NCC. Moreover, the goal of secrecy_of sec_3 examines that the SK is confidential between the user and the NCC, and the attacker cannot access it. Besides, the goals authentication_on auth_1 and authentication_on auth_2 examine the mutual authentication of the user and the NCC. The goal predicates request(Ui, NCC, auth_1, Eis) in role_Ui and witness(NCC, Ui, auth_1, Eis’) in role_NCC are used to declare the authentication of the user by NCC. Similarly, request(NCC, Ui, auth_2, Enccs) in role_NCC and witness(Ui, NCC, auth_2, Enccs’) in role_Ui are used to examine the authentication of NCC by the user. To check whether these goals are satisfied by our protocol, we use OFMC and ATSE. The results in Figs. 4 and 5 show that both of these model checkers find our protocol safe, which means that our protocol meets the secrecy of the session key and the mutual authentication of parties.

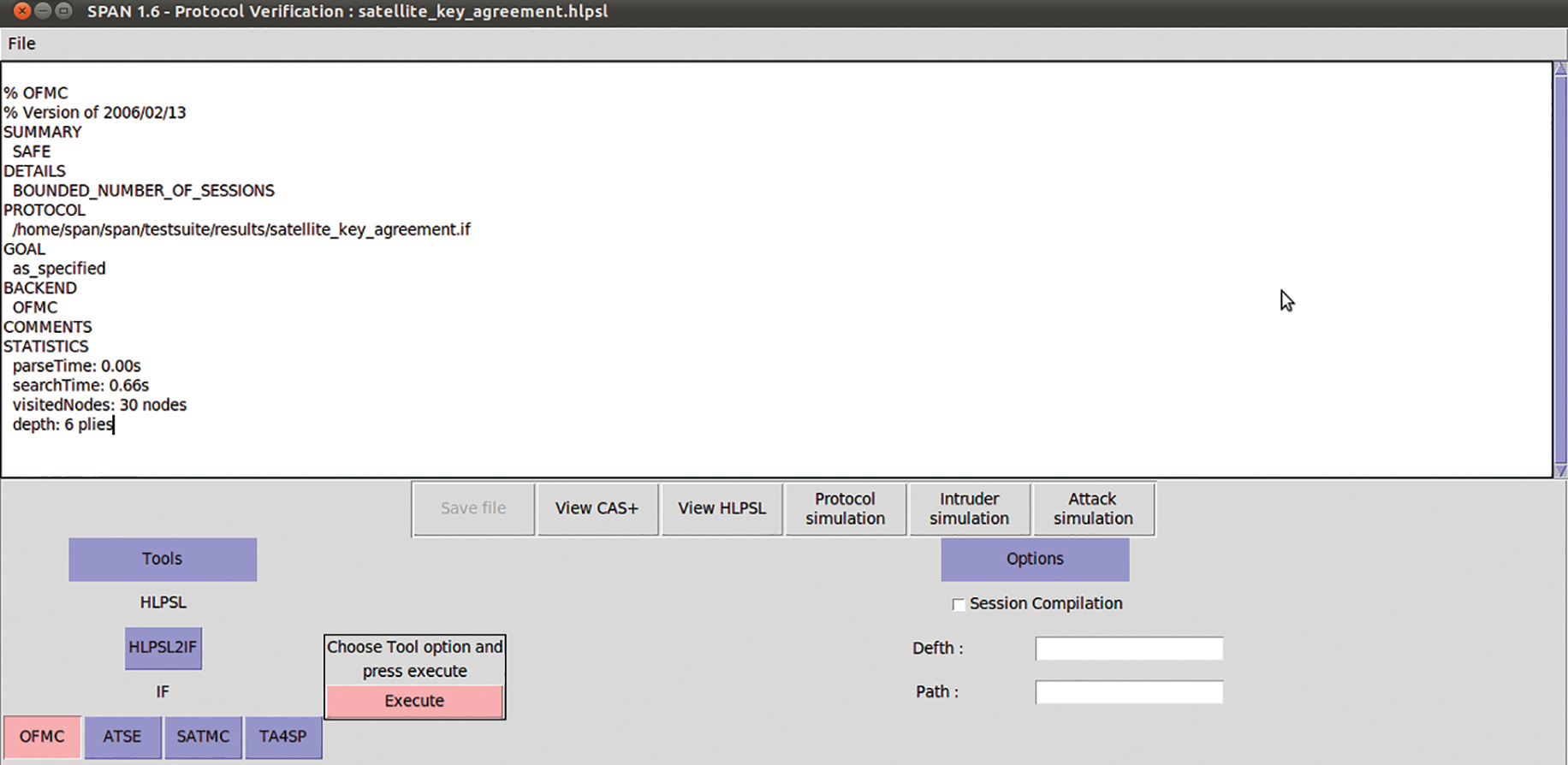
Figure 4: The results of OFMC model checker on the proposed protocol

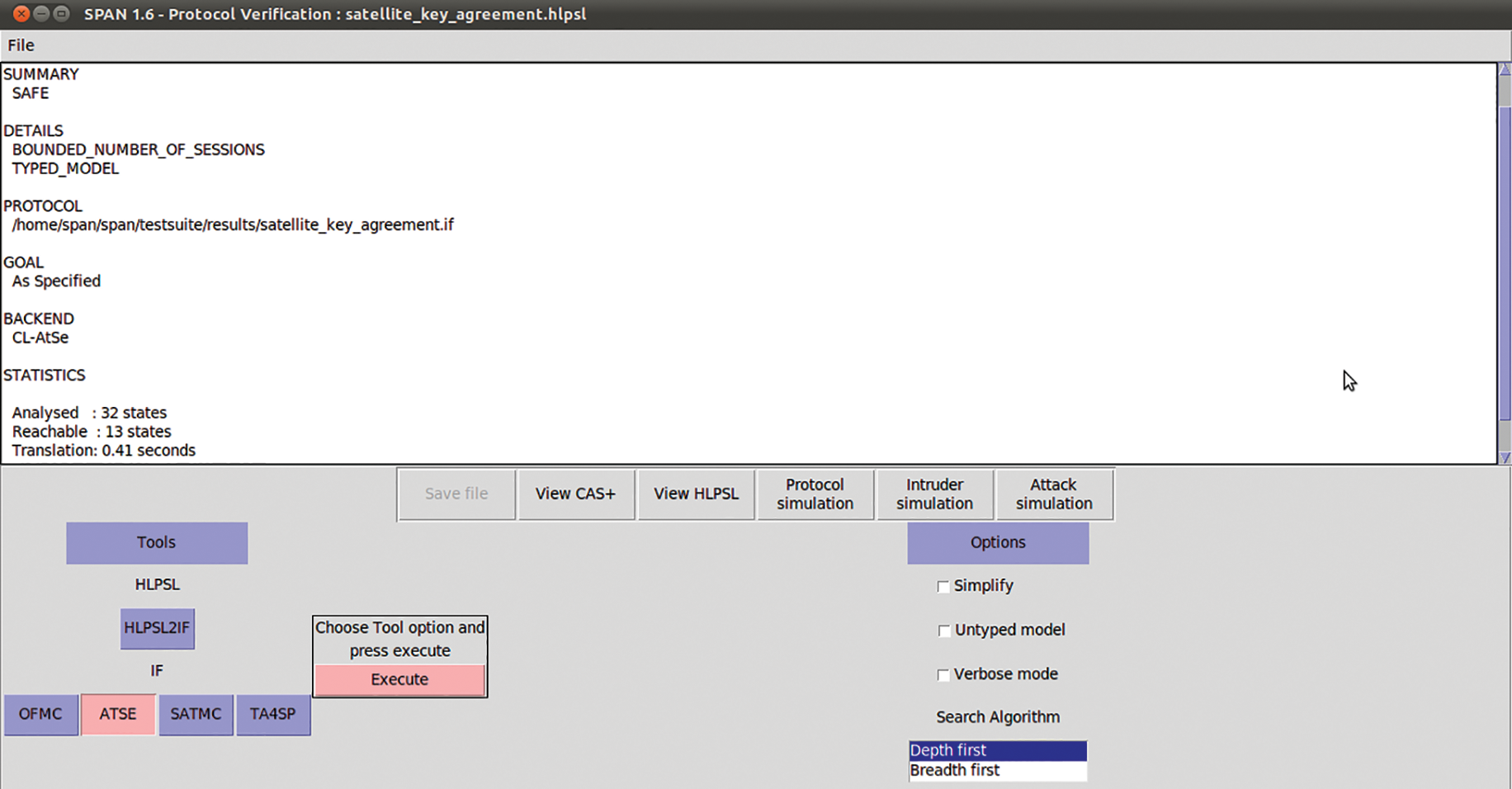
Figure 5: The results of ATSE model checker on the proposed protocol

6.4 Proving the Security of Proposed Key Exchange Protocol Using RoR Model

We examine semantic security of the session key of the proposed protocol using the Real-or-Random model [34,35]. In this model, adversary A obtains a session key or a random value by querying protocol participants. The adversary must guess whether the output returned to him is a real key or a random value. For this purpose, we introduce various concepts such as participants, participant instances, oracles available to A, queries to these oracles, and the concept of partnering.

Participants. The two disjoint sets of our proposed protocol participants are U and NCC. We represent the set of all participants with P=U∪NCC. Moreover, we represent the j th participant of the protocol with Pj∈P.

Participant Instances. During the execution of the protocol by the adversary, several instances of each participant may be executed. The instance i of the participant Pj is denoted by ΠPji and is called an oracle.

Long-Lived Keys. Each participant P∈P has a secret key SP∈Fp.

Ephemeral Keys. Each participant P∈P in a session s has an ephemeral key eP,s∈Fp.

Acceptance. To simulate the protocol, first, a user instance, ΠUi, sends a message, and an NCC-instance, ΠNCCj, responds with another message. This process continues until both instances are terminated. At this point, each instance enters the accepted mode and has a session ID (SID), a session key (SK), and a partner ID (PID).

Partnering. Two oracles ΠUi and ΠNCCj which are in accepted mode are partners if both have the same session keys, SK(ΠUi)=SK(ΠNCCj), the same session IDs, SID(ΠUi)=SID(ΠNCCj), and PID(ΠUi)=ΠNCCj, and PID(ΠNCCj)=ΠUi.

Protocol Execution. A protocol indicates how participant instances behave in response to signals received from the environment [36]. Intending to break the protocol security, the adversary sends signals to the instances of the participants (oracles) and receives a response according to the rules of the protocol. In fact, the adversary sends queries to oracles, and these queries model the attacker's ability in a real attack. Types of queries include:

•   Execute(ΠUi,ΠNCCj). With this query, the adversary models a passive attack in which the adversary eavesdrops on messages exchanged between the i th instance of U, ΠUi, and the jth instance of NCC, ΠNCCj.

•   Send(ΠPji,m). With this query, the adversary models an active attack. The adversary sends the message m to oracle ΠPji, and the oracle responds according to the protocol.

•   Reveal(ΠPji). If oracle ΠPji is in accepted mode (has a session key), this query will reveal the session key to the adversary A. The session key may be revealed for a variety of reasons, such as hacking a participant. Of course, disclosing the key of one session does not break other sessions. If a Reveal(ΠPji) query is asked by A, the oracle ΠPji is opened.

•   Corrupt(ΠPji). Using this query, the adversary can access the long-lived key of the oracle ΠPji. This query lets us examine the forward secrecy requirement of the protocol.

•   Test(ΠPji). This query measures the semantic security of the session key (if any) of the oracle ΠPji. If the session key is not defined for ΠPji, ⊥ is returned. Otherwise, coin c is tossed first. If c=0, then the session key is returned to A, and if c=1, a random value (with the same distribution as the valid session keys) is returned.

Freshness. An oracle ΠPji is fresh if it is in the accept mode, and ΠPji and its partner are not open (by Reveal query).

Semantic Security of A Key Exchange Protocol. Suppose adversary A executes the key exchange protocol PRO and has access to Execute, Send, Reveal, Corrupt, Corrupt_Ephemeral, and Test queries. The adversary can ask the Test query up to one time for each fresh oracle. Suppose the adversary's guess for the Test query is c′. The adversary wins the game if c′=c, where c is the value of the coin set before the game. The protocol PRO is secure if the advantage of the probabilistic polynomial-time adversary in breaking the session key is negligible, as shown in (27).

AdvPRO(A)≤ε(27)

Theorem 1. Suppose adversary A can execute a maximum of Nh Hash query, Ns Send query, and Ne Execute query to break our proposed key exchange protocol, PRO_SAT. The advantage of A in breaking the PRO_SAT protocol is given in (28):

AdvPRO_SAT(A)≤2AdvECDLP(A)+2Ns/|D|+Nh2/|H|+(Ns+Ne)2/p(28)

where |H| is the range space of the Hash oracle, |D| is the size of the password dictionary, and p is the prime number in Fp.

Proof. To prove Theorem 1, we define a six-step game: G0 to G5.

G0. Game 0 is the real attack of A against our proposed protocol, PRO_SAT. Intuitively, the adversary can win the game with the probability of 1/2. The advantage of the adversary to break the semantic security of PRO is |Pr(SUCC0)−1/2|, where SUCC0 is the event in which A guesses the coin correctly and wins the game. Rescaling it, we can define the advantage of A as (29).

AdvPRO_SAT(A)=|2.Pr(SUCC0)−1|.(29)

G1. In this game, we simulate passive attacks by the adversary. The adversary eavesdrops on messages between oracles ΠUi and ΠNCCj with an Execute query. The adversary then decides with the Test query that the session key returned to him is real or random. To create a session key in the proposed protocol, the ephemeral keys of the user and NCC, as well as long-term keys of both parties are needed. To be more precise, the session key is made in the client using the long-term key Si and the ephemeral private key ei,s. It is made in NCC using the long-term key SNCC and the temporary private key eNCC,s. The adversary cannot gain access to any of these keys by simulating eavesdropping attacks, and his advantage in violating the security of the session key does not increase, as shown in (30).

AdvPRO_SAT(A)=|2.Pr(SUCC1)−1|,(30)

G2. In this game, in addition to simulating eavesdropping attacks, active attacks are also simulated with the Send query. Active attacks by the adversary can be one of three attacks: replay attack, man-in-the-middle, or impersonation attack. As stated in sections 6.2.1, 6.2.2, and 6.2.4, the proposed method is immune to these attacks. Therefore, the advantage of A in this game does not increase. Therefore, we have:

Pr(SUCC2)=Pr(SUCC1),(31)

G3. In this game, the adversary queries the Hash oracle Nh times to find collisions. The birthday paradox states that the probability of collisions in the output of the Hash oracle is at most Nh2/2|H|. Moreover, since Si, SNCC, ei,s, and eNCC,s are randomly selected from Fp, the probability of collision in the Send and Execute oracles is at most (Ns+Ne)2/2p. So, we have:

|Pr(SUCC2)−Pr(SUCC3)|≤Nh2/2|H|+(Ns+Ne)2/2p.(32)

G4. This game simulates the smart card loss attack. If the mobile device (or smart card) of the user is stolen, A may try to guess the password using an online dictionary attack. Since the number of password failures is limited by the protocol, we have:

|Pr(SUCC3)−Pr(SUCC4)|≤Ns/|D|.(33)

G5. In this game, the adversary asks the Corrupt query and gets the oracle's long-lived key in response. Of course, to get the session key, A needs the long-lived keys of both oracles in communication. Also, to create the session key, A needs to have access to ephemeral keys for each session. To access the one-time keys of each session, the adversary must be able to solve the ECDLP problem. If the advantage of A for breaking the ECDLP is AdvECDLP(A), we have:

|Pr(SUCC4)−Pr(SUCC5)|≤AdvECDLP(A).(34)

Given that Pr(SUCC5)=1/2, we can calculate the advantage of A using (29) to (34), as shown in (35).

AdvPRO_SAT(A)=|2.Pr(SUCC0)−1|=|2.Pr(SUCC1)−1|=|2.Pr(SUCC2)−1|≤|2.(Pr(SUCC4)+Ns/|D|+Nh2/2|H|+(Ns+Ne)2/2p)−1|≤|2.(Pr(SUCC5)+AdvECDLP(A)+Ns/|D|+Nh2/2|H|+(Ns+Ne)2/2p)−1|≤|2.(Pr(SUCC3)+Nh2/2|H|+(Ns+Ne)2/2p)−1|≤|2.(1/2+AdvECDLP(A)+Ns/|D|+Nh2/2|H|+(Ns+Ne)2/2p)−1|≤2AdvECDLP(A)+2Ns/|D|+Nh2/|H|+(Ns+Ne)2/p(35)

7  Performance Analysis and Comparison

In this section, we examine the computational complexity of the proposed method. The messages in the proposed protocol are obtained by combining xor, hash, and scalar multiplication on the elliptic curve. In calculating time complexity, we ignore the xor time execution, and we calculate the time required for hash and scalar multiplication based on the time reported in [37]. The computation times of various cryptographic operations, reported by Xu et al. [37], are as follows:

•   Th is the time of the one-way hash function, which is 0.0004 ms.

•   Tsm is the time of scalar multiplication on elliptic curves, which is 7.3529 ms.

•   Tme is the time of modular exponentiation, which is 1.8269 ms.

•   Ts is the time of symmetric encryption/decryption, which is 0.1303 ms.

The time complexity of our protocol includes the time spent by the user's mobile device and the time spent by the NCC. The time spent by the mobile device is 7Th+4Tsm and the time consumed by the NCC is 6Th+4Tsm, and the total time is 13Th+8Tsm, which is equal to 58.8284 milliseconds.

To measure the communication cost of the proposed method, we need to measure the size of the messages exchanged between the different entities of the protocol. Messages consist of a combination of IDs, hash values, timestamps, and points on the elliptic curve. To calculate the communication cost, suppose each identifier is 64 bits long, the hash size is 256 bits, the timestamp is 64 bits, and the point size on the elliptic curve is 192 bits (due to secp192r1 selection).

To exchange the session key between the user and the NCC, it is necessary to send messages ⟨MIDi,s,Resi,s,Ei,s,Ti,s⟩, ⟨MIDi,s,Resi,s,Ei,s,Ti,s,IDLEO⟩, ⟨AuthNCC,s,ENCC,s,TNCC,s,MIDi,s⟩, and ⟨AuthNCC,s,ENCC,s,TNCC,s⟩. Therefore, the communication cost of our protocol is 4×ecc+7×hash+ID+3×timestamp=4×192+7×256+64+3×64=2816 bits.

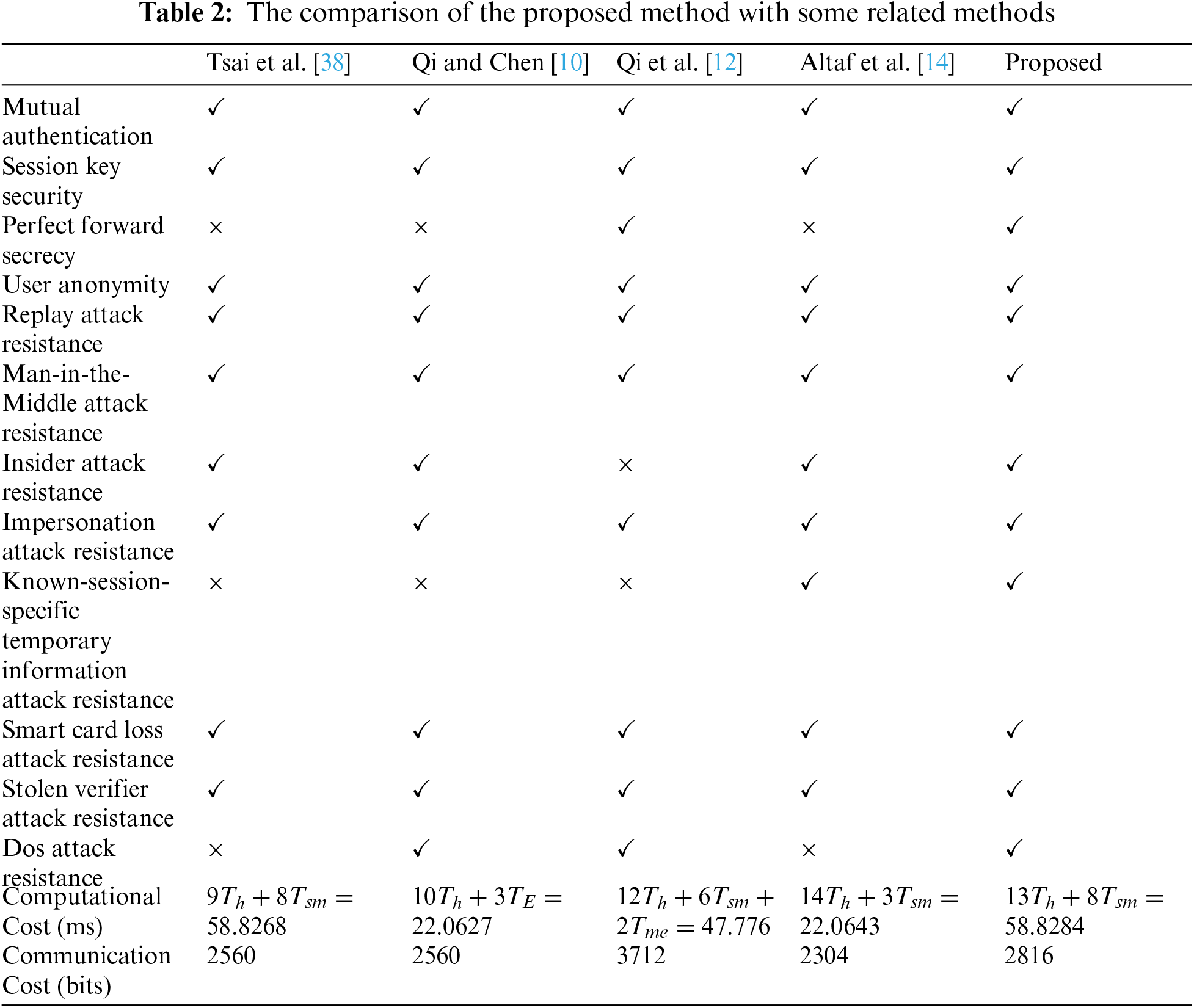
At the end of this section, we compare the proposed method with several similar methods, which are all based on the ECDLP problem, in terms of security features and computational cost. As shown in Tab. 2, Tsai et al.'s protocol [38] does not satisfy perfect forward secrecy. Moreover, it is vulnerable to the known-session-specific temporary information attack and DoS attack. The protocol of Qi and Chen [10] does not meet the perfect forward secrecy and is not resistant against the known-session-specific temporary information attack. The protocol of Qi et al. [12] is vulnerable to insider attack and the known-session-specific temporary information attack. Finally, Altaf et al.'s protocol [14] is vulnerable to DoS attack and does not meet perfect forward secrecy. We see that our method, by spending a little more time, is resistant to the known attacks and meets security requirements. We also see that the communication cost of the proposed method is almost similar to other methods except [12] in which modular exponentiation are used.

8  Conclusion and Future Work

This paper contributes towards the widespread deployment of satellite applications by tackling one of the main challenges, i.e., security issues. This paper first analyzed the authentication protocol for satellite communications proposed by Qi et al. and proved its vulnerability to two kinds of security attacks. Then this paper presented a robust secure authentication and key agreement protocol based on elliptic curve cryptography for secure satellite communications. Moreover, a thorough security analysis of the proposed protocol was performed. The security analysis showed that it is resistant to all known attacks. Besides, the formal verification of the proposed method proved that it satisfies the security requirements.

As future work, the protocol performance can be improved in terms of time execution by reducing the number of scalar multipliers while preserving the security requirements. Implementation on application in blockchain [39] and software defined network [40] are also considered as future works.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  P. Chini, G. Giambene and S. Kota, “A survey on mobile satellite systems,” International Journal of Satellite Communications and Networking, vol. 28, no. 1, pp. 29–57, 2010. [Google Scholar]

 2.  J. P. Choi and C. Joo, “Challenges for efficient and seamless space-terrestrial heterogeneous networks,” IEEE Communications Magazine, vol. 53, no. 5, pp. 156–162, 2015. [Google Scholar]

 3.  H. Yao, L. Wang, X. Wang, Z. Lu and Y. Liu, “The space-terrestrial integrated network: an overview,” IEEE Communications Magazine, vol. 56, no. 9, pp. 178–185, 2018. [Google Scholar]

 4.  X. Zhu, C. Jiang, L. Kuang, N. Ge, S. Guo et al., “Cooperative transmission in integrated terrestrial-satellite networks,” IEEE Network, vol. 33, no. 3, pp. 204–210, 2019. [Google Scholar]

 5.  K. Shi, X. Zhang, S. Zhang and H. Li, “Time-expanded graph based energy-efficient delay-bounded multicast over satellite networks,” IEEE Transactions on Vehicular Technology, vol. 69, no. 9, pp. 10380–10384, 2020. [Google Scholar]

 6.  T. T. Reid, P. Walter, D. Enge, H. S. Lawrence, G. Cobb et al., “Navigation from Low earth orbit: Part 1: concept, current capability, and future promise,” Position, Navigation, and Timing Technologies in the 21st Century: Integrated Satellite Navigation, Sensor Systems, and Civil Applications, vol. 2, pp. 1359–1379, 2020. [Google Scholar]

 7.  J. E. Oros, J. Trejo and A. Salcedo, “Identification, location, and reception of low earth orbit satellites (LEO) signals,” in Proc. of 2015 Int. Conf. on Mechatronics, Electronics and Automotive Engineering (ICMEAE), Cuernavaca, Mexico, pp. 246–250, 2015. [Google Scholar]

 8.  Z. Katona, M. Gräßlin, A. Donner, N. Kranich, H. Brandt et al., “A flexible LEO satellite modem with Ka-band RF frontend for a data relay satellite system,” International Journal of Satellite Communications and Networking, vol. 38, no. 3, pp. 301–313, 2020. [Google Scholar]

 9.  I. Altaf, M. A. Saleem, K. Mahmood, S. Kumari, P. Chaudhary et al., “A lightweight key agreement and authentication scheme for satellite-communication systems,” IEEE Access, vol. 8, pp. 46278–46287, 2020. [Google Scholar]

10. M. Qi and J. Chen, “An enhanced authentication with key agreement scheme for satellite communication systems,” International Journal of Satellite Communications and Networking, vol. 36, no. 3, pp. 296–304, 2018. [Google Scholar]

11. A. Ostad-Sharif, D. Abbasinezhad-Mood and M. Nikooghadam, “Efficient utilization of elliptic curve cryptography in design of a three-factor authentication protocol for satellite communications,” Computer Communications, vol. 147, pp. 85–97, 2019. [Google Scholar]

12. M. Qi, J. Chen and Y. Chen, “A secure authentication with key agreement scheme using ECC for satellite communication systems,” International Journal of Satellite Communications and Networking, vol. 37, no. 3, pp. 234–244, 2019. [Google Scholar]

13. Y. Chen and J. Chen, “An enhanced dynamic authentication scheme for mobile satellite communication systems,” International Journal of Satellite Communications and Networking, vol. 39, no. 3, pp. 250–262, 2021. [Google Scholar]

14. I. Altaf, M. Arslan Akram, K. Mahmood, S. Kumari, H. Xiong et al., “A novel authentication and key-agreement scheme for satellite communication network,” Transactions on Emerging Telecommunications Technologies, vol. 32, no. 7, pp. e3894, 2020. [Google Scholar]

15. H. Cruickshank, “A security system for satellite networks,” in Proc. of the 5th Int. Conf. on Satellite Systems for Mobile Communications and Navigation, London, UK, pp. 187–190, 1996. [Google Scholar]

16. T. -H. Chen, W. -B. Lee and H. -B. Chen, “A Self-verification authentication mechanism for mobile satellite communication systems,” Computers & Electrical Engineering, vol. 35, no. 1, pp. 41–48, 2009. [Google Scholar]

17. I. Lasc, R. Dojen and T. Coffey, “Countering jamming attacks against an authentication and key agreement protocol for mobile satellite communications,” Computers & Electrical Engineering, vol. 37, no. 2, pp. 160–168, 2011. [Google Scholar]

18. C. C. Chang, T. F. Cheng and H. L. Wu, “An authentication and key agreement protocol for satellite communications,” International Journal of Communication Systems, vol. 27, no. 10, pp. 1994–2006, 2014. [Google Scholar]

19. Y. Zhang, J. Chen and B. Huang, “Security analysis of an authentication and key agreement protocol for satellite communications,” International Journal of Communication Systems, vol. 27, no. 12, pp. 4300–4306, 2014. [Google Scholar]

20. C. C. Lee, C. T. Li and R. X. Chang, “A simple and efficient authentication scheme for mobile satellite communication systems,” International Journal of Satellite Communications and Networking, vol. 30, no. 1, pp. 29–38, 2012. [Google Scholar]

21. Y. Zhang, J. Chen and B. Huang, “An improved authentication scheme for mobile satellite communication systems,” International Journal of Satellite Communications and Networking, vol. 33, no. 2, pp. 135–146, 2015. [Google Scholar]

22. Y. Liu, A. Zhang, S. Li, J. Tang and J. Li, “A lightweight authentication scheme based on self-updating strategy for space information network,” International Journal of Satellite Communications and Networking, vol. 35, no. 3, pp. 231–248, 2017. [Google Scholar]

23. S. A. Hosseini Seno, M. Nikooghadam and R. Budiarto, “An efficient lightweight authentication and key agreement protocol for patient privacy,” Computer Materials & Continua (CMC), vol. 69, no. 3, pp. 3495–3512, 2021. [Google Scholar]

24. Y. Chen and J. -S. Chou, “ECC-Based untraceable authentication for large-scale active-tag RFID systems,” Electronic Commerce Research, vol. 15, no. 1, pp. 97–120, 2015. [Google Scholar]

25. N. Gura, A. Patel, A. Wander, H. Eberle and S. C. Shantz, “Comparing elliptic curve cryptography and RSA on 8-bit CPUs,” in Proc. of the 6th Int. Workshop Cambridge, Massachusetts, USA, pp. 119–132, 2004. [Google Scholar]

26. D. Dolev and A. Yao, “On the security of public key protocols,” IEEE Transactions on Information Theory, vol. 29, no. 2, pp. 198–208, 1983. [Google Scholar]

27. R. Ramanujam, V. Sundararajan and S. Suresh, “Extending dolev-yao with assertions,” in Proc. of the tenth Int. Conf. on Information Systems Security, Hyderabad, India, pp. 50–68, 2014. [Google Scholar]

28. R. Canetti and H. Krawczyk, “Analysis of key-exchange protocols and their use for building secure channels,” in Proc. of Int. Conf. on the Theory and Applications of Cryptographic Techniques, Innsbruck, Austria, pp. 453–474, 2001. [Google Scholar]

29. A. Armando, D. Basin, Y. Boichut, Y. Chevalier, L. Compagna et al., “The AVISPA tool for the automated validation of internet security protocols and applications,” in Proc. of the 17th Int. Conf. on Computer Aided Verification, Edinburgh, Scotland, UK, pp. 281–285, 2005. [Google Scholar]

30. D. Von Oheimb, “The high-level protocol specification language HLPSL developed in the EU project AVISPA,” in Proc. of the 3rd Int. Workshop on Applied Semantics (APPSEM 2005), Frauenchiemsee, Germany, pp. 1–17, 2005. [Google Scholar]

31. D. Basin, S. Mödersheim and L. Vigano, “OFMC: A symbolic model checker for security protocols,” International Journal of Information Security, vol. 4, no. 3, pp. 181–208, 2005. [Google Scholar]

32. M. Turuani, “The CL-atse protocol analyser,” in Proc. of the 17th Int. Conf. on Rewriting Techniques and Applications, Seattle, WA, USA, pp. 277–286, 2006. [Google Scholar]

33. A. Armando and L. Compagna, “SATMC: A SAT-based model checker for security protocols,” in Proc. of the 9th European Workshop on Logics in Artificial Intelligence, Lisbon, Portugal, pp. 730–733, 2004. [Google Scholar]

34. M. Bellare, D. Pointcheval and P. Rogaway, “Authenticated key exchange secure against dictionary attacks,” in Proc. of Int. Conf. on the Theory and Applications of Cryptographic Techniques, Bruges, Belgium, pp. 139–155, 2000. [Google Scholar]

35. M. Abdalla, E. Bresson, O. Chevassut and D. Pointcheval, “Password-based group key exchange in a constant number of rounds,” in Proc. of the 9th Int. Workshop on Public Key Cryptography, New York, USA, pp. 427–442, 2006. [Google Scholar]

36. C. -C. Chang and H. -D. Le, “A provably secure, efficient, and flexible authentication scheme for ad hoc wireless sensor networks,” IEEE Transactions on Wireless Communications, vol. 15, no. 1, pp. 357–366, 2015. [Google Scholar]

37. L. Xu and F. Wu, “Cryptanalysis and improvement of a user authentication scheme preserving uniqueness and anonymity for connected health care,” Journal of Medical Systems, vol. 39, no. 2, pp. 1–9, 2015. [Google Scholar]

38. J. L. Tsai, N. W. Lo and T. C. Wu, “Secure anonymous authentication scheme without verification table for mobile satellite communication systems,” International Journal of Satellite Communications and Networking, vol. 32, no. 5, pp. 443–452, 2014. [Google Scholar]

39. F. A. Susilo and Y. S. Triana, “Digital supply chain development in blockchain technology using rijndael algorithm 256,” in Int. Conf. on Design, Engineering and Computer Sciences, IOP Conf. Series: Materials Science and Engineering, vol. 453 pp. 012075–012080, 2018. [Google Scholar]

40. A. A. Seyedkolaei, S. A. Hosseini-Seno, A. Moradi and R. Budiarto, “Cost-effective survivable controller placement in software-defined networks,” IEEE Access, vol. 9, pp. 129130–129140, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.