Computers, Materials & Continua DOI:10.32604/cmc.2022.023880
Article

Optimization Model in Manufacturing Scheduling for the Garment Industry

Chia-Nan Wang1, Yu-Chen Wei2, Po-Yuk So3,*, Viet Tinh Nguyen4 and Phan Nguyen Ky Phuc5

1Department of Industrial Engineering and Management, National Kaohsiung University of Science and Technology, Kaohsiung, 80778, Taiwan
2Department of Money and Banking, National Kaohsiung University of Science and Technology, Kaohsiung, 80778, Taiwan
3Ph.D. Program in Finance and Banking, National Kaohsiung University of Science and Technology, Kaohsiung, 80778, Taiwan
4Faculty of Commerce, Van Lang University, Ho Chi Minh City, Vietnam
5Faculty of Industrial Engineering and Management, International University, Ho Chi Minh City, 70000, Vietnam
*Corresponding Author: Po-Yuk So. Email: poyuksotw@gmail.com
Received: 24 September 2021; Accepted: 06 December 2021

Abstract: The garment industry in Vietnam is one of the country's strongest industries in the world. However, the production process still encounters problems regarding scheduling that does not equate to an optimal process. The paper introduces a production scheduling solution that resolves the potential delays and lateness that hinders the production process using integer programming and order allocation with a make-to-order manufacturing viewpoint. A number of constraints were considered in the model and is applied to a real case study of a factory in order to view how the tardiness and lateness would be affected which resulted in optimizing the scheduling time better. Specifically, the constraints considered were order assignments, production time, and tardiness with an objective function which is to minimize the total cost of delay. The results of the study precisely the overall cost of delay of the orders given to the plant and successfully propose a suitable production schedule that utilizes the most of the plant given. The study has shown promising results that would assist plant and production managers in determining an algorithm that they can apply for their production process.

Keywords: Production scheduling problem; order allocation; integer programming; make-to-order manufacturing; apparel industry

1  Introduction

In according to a report in 2017, Vietnam has about 2,800 clothing enterprises, most of which are located in Ho Chi Minh City and Ha Noi. In the past, around 70% of Vietnam's clothing depended on using imported raw materials such as fabrics and fibers from China due to the Vietnam's regulation about controlling tightly the dyeing segment. In 2001, when the trading relationships between Vietnam and Western countries were established, exporting Vietnamese clothing began to develop. In 2016, according to WTO, it is reported that around $28 billion of clothing were exported, which is the third largest value in global apparel exporter, after China and Bangladesh. The 2017 US Fashion Industry Benchmarking Study indicated that Vietnam is the second apparel sourcing country, after China. In recent years, with the development of technology, the human's standard of living tends to be high considerably, and the needs of clothing is continuously changing. Many enterprises deal with a considerable number of challenges with regard to the change in demands of customers, shorter product life cycle. In addition, customer requirements for specialized and customized production tend to increased. Therefore, to survive in the intensely competitive market place and quickly respond to this changing environment, many firms have begun considering a change in service mode and improving their production scheduling to meet the deadline committed to customers, otherwise the firms can face to a significant loss of goodwill and penalty. It is obvious that more companies tend to offer mass customization service to customers. Unlike in make-to-stock (MTS), in which the finished goods are hold in inventory as a buffer to deal with the variations in customer demand, make-to-order (MTO) operation starts performing an order only after it has been received. The most important aspect in MTO is the effective and efficient utilization of available capacity to meet customer demands. In make-to-order manufacturing, customer satisfaction is always the key to evaluate the success of the performance of production planning and scheduling. In specific, a typical measure of customer satisfaction is the customer service level which is the fraction of customer orders finished on or before their due dates.

In this study, the authors will consider the problem of an apparel company which provide customized products. The main objective of this paper is to minimize the cost of tardy orders by allocating the order to produce for each day. After that, based on the final optimal result, the authors will propose the days needed working overtime. Finally compare the cost of penalty and cost of overtime to choose the better option. From that apparel company can increase its production efficiency, reduce the loss of order, and improve customer's satisfaction.

2  Literature Review

There have been multiple studies about the application of mathematical programming in the solving optimization problems in manufacturing systems [1–5]. These researches look into different productions systems and setups such as make-to-stock systems [6,7], make-to-order systems [8,9], single processing line [10,11], or multiple processing lines [12,13], etc. with different optimization objectives. These objectives can be minimizing tardiness [14,15], minimized inventory holding cost [16,17], minimizing setup cost [18], etc. or a combination of these objectives [19,20]. With each different production system and objectives, a unique model is developed to solve the scheduling problem

The Chen et al. [21] study an integrated scheduling model in production and distribution operations. In this model, a set of customer orders are first planned to be performed and then delivered directly to the customers without intermediate inventory. The goal is to find a combined schedule in production and distribution to optimize both customer service level and total distribution cost. The paper proposed a mixed integer programs to find the optimal value of the maximum earliness as an application for long-term production schedules in make-to-order manufacturing. Ogun et al. [22] showed three distinct mathematical models for a batch scheduling problem to minimize the earliness and tardiness of customer orders with the consideration of issue about the excess inventory level of finished products. Firstly, the study provided a nonlinear integer programming model, then this model was converted into an integer programming format by using the piecewise linearizing method. Finally, an alternative linear integer model was presented to deal with the larger sized problem. A set of customer's orders with multi-products made of multi-parts were considered. All parts of the same products from different orders were combined to process in the same batch and the orders were evaluated as completed status when all related types of products in that order were completed. This research contributes a new optimization model of batch scheduling problem.

The production planning problem was also presented by Sadeghi Naieni Fard et al. [23]. The paper extended the problem by considering more criteria in supply network. The authors calculated the production and packing time in the factories, delivery time in distribution centers and the transportation section to define an optimal assignment and sequence for the customers’ orders according to the capacity of centers and customer due dates with the aim to minimize the total tardiness. This problem is firstly formulated by a mixed integer programming model and solved by GAMS software. In addition, the authors also proposed two metaheuristics based on variable neighborhood search and simulated annealing solve the larger sized problem. Finally, a metaheuristics model was presented to compare the performance of models together. His study can be applied in different industries which could cause large penalty and damage when the orders are delivered late.

Ben Hmida et al. [24] studied the production scheduling problem in a continuous manufacturing system involving multi-products, multi-processing lines and conflicting objectives including inventory, production and quality constraints. He built two practical heuristic optimization algorithms to generate daily production schedules with the goal of minimization of order delays, minimization of average inventory levels and satisfying the quality constraints. The study experimented on the chemical industry He considered more than 200 customer orders in a month with the total of about four million pounds of different types of chemical products which were processed on multiple processing lines. The experimental results indicated that the performance of the algorithms is effectively improved to the tardiness, inventory levels and quality of the products.

Shabtay [25] also studied production scheduling with the goal of minimizing earliness, tardiness, delivery and holding cost, but he considered the due dates as controllable variables. This means that each order had a lead time for its due date. Customers accepted the due date assigned in a duration, and there was penalty if the due date was greater than the committed lead time. The penalty varied proportionally according to the contract. To solve the problem, he built a polynomial time dynamic programming algorithm and showed the order sequence with the final result. In his model, he presented two cases. In the first case processing times are equal for each order. In the second case, he assumed that all acceptable lead times are equal to zero. In addition, in his study, he proved the problem studied as a N-hard problem by providing some properties of the optimal schedule.

Lee [26] proposed three heuristic algorithms to solve the order scheduling problem with the aim to minimize total tardiness. The study built a system of multiple identical machines, orders with multiple components processed on different dedicated machines. The order was completed when all the components of that order are finished. Moreover, a branch-and-bound model was presented to compare the performance of three heuristic algorithms. Three lower bounds are derived in the branch-and-bound scheme to solve much larger problem instances.

Lin et al. [27] considered a problem of a number of orders which are assembled from different items. They designed a heuristic algorithm to minimize the number of late jobs by sequencing the date of production and analyze its performance ratio without weighted situation. After that, an LP-based approximation algorithm was applied to the weighted situation of order scheduling problem with the constant due date. The result of the model suggested the new factor for the model and proved that the problem is a half of NP-hard problem.

Huang et al. [28] studied a case study of a MTO manufacturing company producing belt pulleys. In their study, three sub-problems of order scheduling considered are the resource capacity (material resource, machine resource), order priority and lead time. Then three these sub-problems are analyzed separately. They applied the Virtual Manufacturing technology, a heuristic arithmetic theory and practical queuing model to help to arrange customer orders and fulfill customer orders on time. With this model, the manager can get the optimal order release time with the high utilization of materials and machines.

Chen et al. [29] addressed the short-term capacity planning problem in MTO environment for product mix problem. He proposed the first mathematical model to help manager choose a set of orders completed before their due date to maximize the overall profit. The input to the model 1 is the characteristics of the order such as the processing route, processing time, processing cost and selling prices of each order; the job shop configuration such as the capacity, the availability of resources. The output from the model helps to unify two decisions: which orders to accept and their schedule about how much capacity was required to complete the whole accepted order. From that, the secondary objective was built to maximize the utilization of resources. The inputs to the second model are the accepted customer orders found from the result of the first model and the characteristics of orders and production configuration like model 1.

Sawik [30] proposed an integer programming approach for master production scheduling in make-to-order manufacturing. The study considered a set of customer orders with various due dates which were performed on multi-parallel machines. Each order is assigned in different processing stages, and some orders may have the same production flow. They were scheduled to split and allocate among the horizon planning periods to maximize the customer service level. In her study, three integer models with various approaches were showed including minimizing the number of tardy orders, minimizing the total of tardiness, or minimizing the ratio between total number of tardy order and all order.

This research differs from the above-mentioned literature in many aspects. The objective considered is to minimize the cost due to completing the orders after their due date base on the production cost and the sales price on the contract with the customers. Many existing literatures just consider the number of tardy orders or the profit. In addition, there are several papers which study how to control and set the due date for orders. However, this research focusses on the way to allocate the order for production with the constant due dates so that the manager can have an overview about daily utilization and decide the necessary day for overtime to meet the due date commitment.

3  Mathematical Model

3.1 Research Process

In this section, the authors built a research process to solve the current problem of factory X mentioned on the problem statement section (Fig. 1).

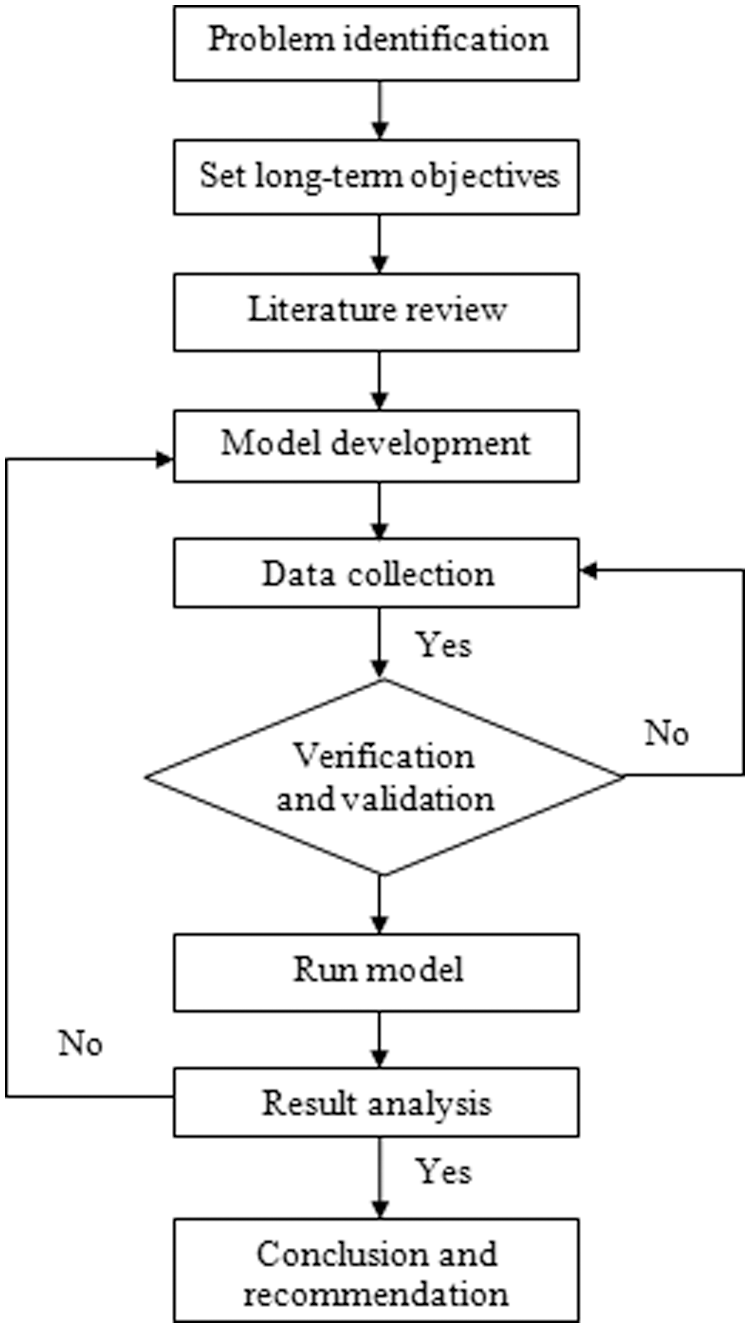
Figure 1: The research process

Step 1: Problem identification

The first step in the process is to identify a problem. Through the observation the operation of factory, the primary problem of factory is responding to the customer's orders is overdue date and pay a constant amount of penalty cost or loss the whole order.

Step 2: Set long-term objectives

After defining the problem, the most important step is establishing the long-term objective which can be applied to company for more than one year. The objective of the models in this paper applied to solve the problem of company is to assign customer orders to planning periods to minimize the cost of tardy orders. From that, company can offer the overtime day to achieve a high customer satisfaction by meeting customers due dates and get a low penalty.

Step 3: Model development

The model will be built with the constraint depending on the availability and capacity of company and be compatible with the development of the technology. Apparel company currently set the customer service level is the top priority. Therefore, the authors applied a linear integer model with the primary objective of minimizing the total cost of tardiness by allocating all orders (Fig. 2).

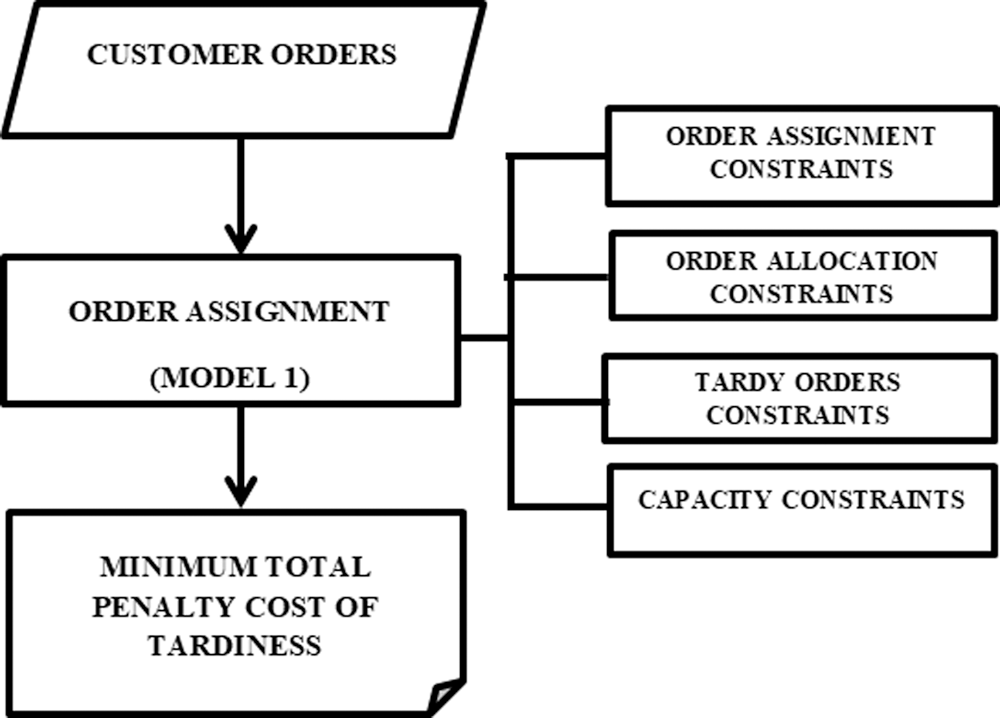
Figure 2: A lexicographic approach with multi-objectives in production scheduling

Step 4: Data collection

The model will be built with the constraint depending on the availability and capacity of company and be compatible with the development of the technology. Apparel company currently set the customer service level is the top priority. Therefore, the authors applied a linear integer model with the primary objective of minimizing the total cost of tardiness by allocating all orders (Fig. 2).

Step 5: Verification and validation

To ensure the validity of the model, the collection process is needed to plane carefully before such as the number of team member for collection and the high concentration is required during the collection period to make sure the high reliability of data.

Step 6: Run model

Running the model with a small sized problem is to test and fix model, then apply the real data collected to the model for the result.

Step 7: Result analysis

From the result, the authors can compare the improvement of tardiness after and before using the scheduling model.

Step 8: Conclusion and recommendation

After analyzing results, the authors propose some alternatives method can be used and the predict of the application of my model.

3.2 Approach Comparison and Selection

There have been many studies applying integer programming for production scheduling problems. In fact, in day today life, many software have been developed to solve the optimization problem like IBM CPLEX Optimizer. Through literature review, there is enough scope for the improvement in the production scheduling environment when the processing time is not constant. This suggests and motivates me to apply integer linear programming and CPLEX optimization which will provide the best quality solutions and reduces the computational burden.

4  Modeling

4.1 Model Assumptions and Notations

4.1.1 Assumptions

To solve the problem statement of this study, the following basic assumptions are used:

•   All machines at one workstation are same speed and functionality;

•   The available day to start each order is known before;

•   All orders arrive at the beginning of the planning horizon;

•   The quantity of split order is not less than 30% of the total quantity of order.

4.1.2 Inputs and Outputs

The inputs of the model are shown in Tab. 1. The output of the model is the optimal total cost of tardy orders.

4.1.3 Notations

The annotations of the model are defined as follows:

•   O: set of order

•   i: denote the order i

•   O1: set of small batches

•   O2: set of large batches

•   T: set of planning periods

•   t: denote the time period t (day)

The input parameters are denoted as follows:

•   di: The due date of order i

•   Di: demand of order i

•   Wi: weight of delay cost for each order

•   Pi: processing time of one unit of each order

•   N: number of production lines

•   Ai: available date of material of each order

•   Ci: the cost of tardiness of each order

The decision variable notations are as follows:

•   Xit: binary variable that indicates whether order i is performed in period t

•   Yit: fraction of order i to be processed in period t

•   Zi: binary variable that indicates whether order i is completed after duedate

•   TCD: the total cost of delay

4.2 Mathematical Model

The objective is to minimize the total cost of delay value:

MinimizeTCD=∑i=1OZi∗Ci(1)

Subject to the following constrains:

∑tTXit=1for all i∈O1,t≥Ei(2)

∑tTYi=1for all i∈O1,t∈T,t≥Ai(3)

Xit=Yitfor all i∈O1,t∈T,t≥Ai(4)

Xit≥Yitfor all i∈O2,t∈T,t≥Ai(5)

Yit≤0.3Xitfor all i∈O2,t∈T,t≥Ai(6)

Constrain (2) is the order assignment constrain. Constraint (3) ensures that each order must be completed. Constraint (4) ensures that each indivisible order is finished in one day. Constraint (5) and (6) ensures each divisible order is allocated among all the periods according to its assignment.

Zi=∑tT⁡Xitfor all i∈B1,t∈T,t>di(7)

Zi≥∑tTXitfor all i∈O1,t∈T,t≥di(8)

Zi≤∑tTXitfor all i∈O2,t∈T,t≥di(9)

Constraint (7) indicates the indivisible tardy order is finished after its due date. Constraint (8) and (9) indicates the divisible tardy order is partly assign after its due date.

∑tTPiDiYit≤Nforalli∈O,t∈T,t≥Ai(10)

Constraint (10) ensures the production time on one day cannot be over the maximum available time on that day.

5  Computational Experiment

5.1 Data Input

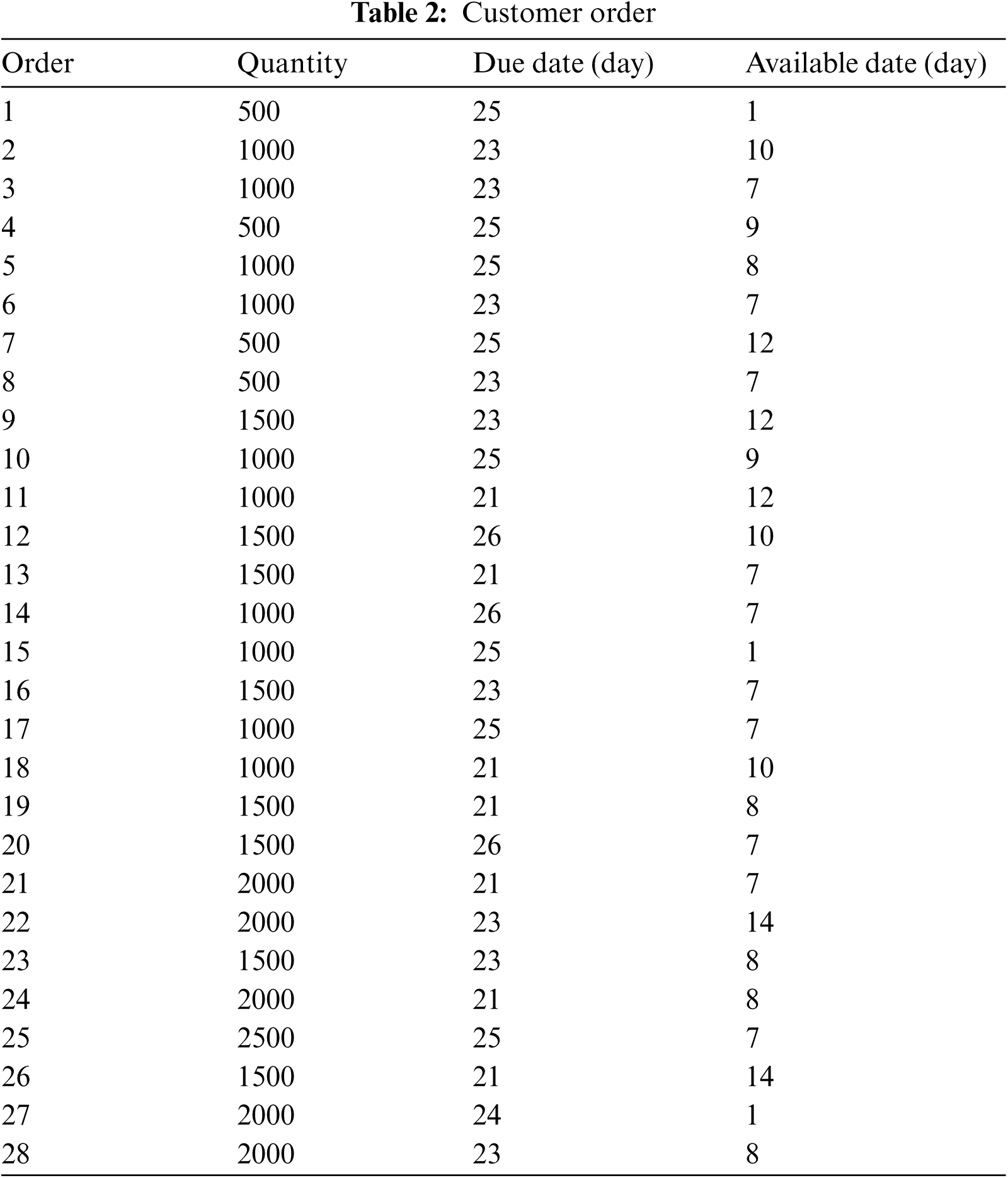
In this case study, numerical data of apparel company are showed to illustrate possible applications of approach. The authors will consider a set of total 28 customer orders recorded in August 2019 for testing this model (Tab. 2).

Moreover, the processing time unit of each product type bases on the characteristics of that products and the number of stages that are required for that process. The authors collected the unit processing time of each stage and the processing time of each unit equals the sum of the processing times of stages required. These collected data had measure unit as second unit. After that, we transfer second unit into day unit base on the working time of labor. The working time is 10 h per day including the lunch time with 1 h. Therefore, the processing time for each product unit is calculated according to the below formula:

Unitprocessingtime(day)=Unitprocessingtime(s)3600(day)∗9(hday)(11)

The unit processing times in day are shown in Tab. 3.

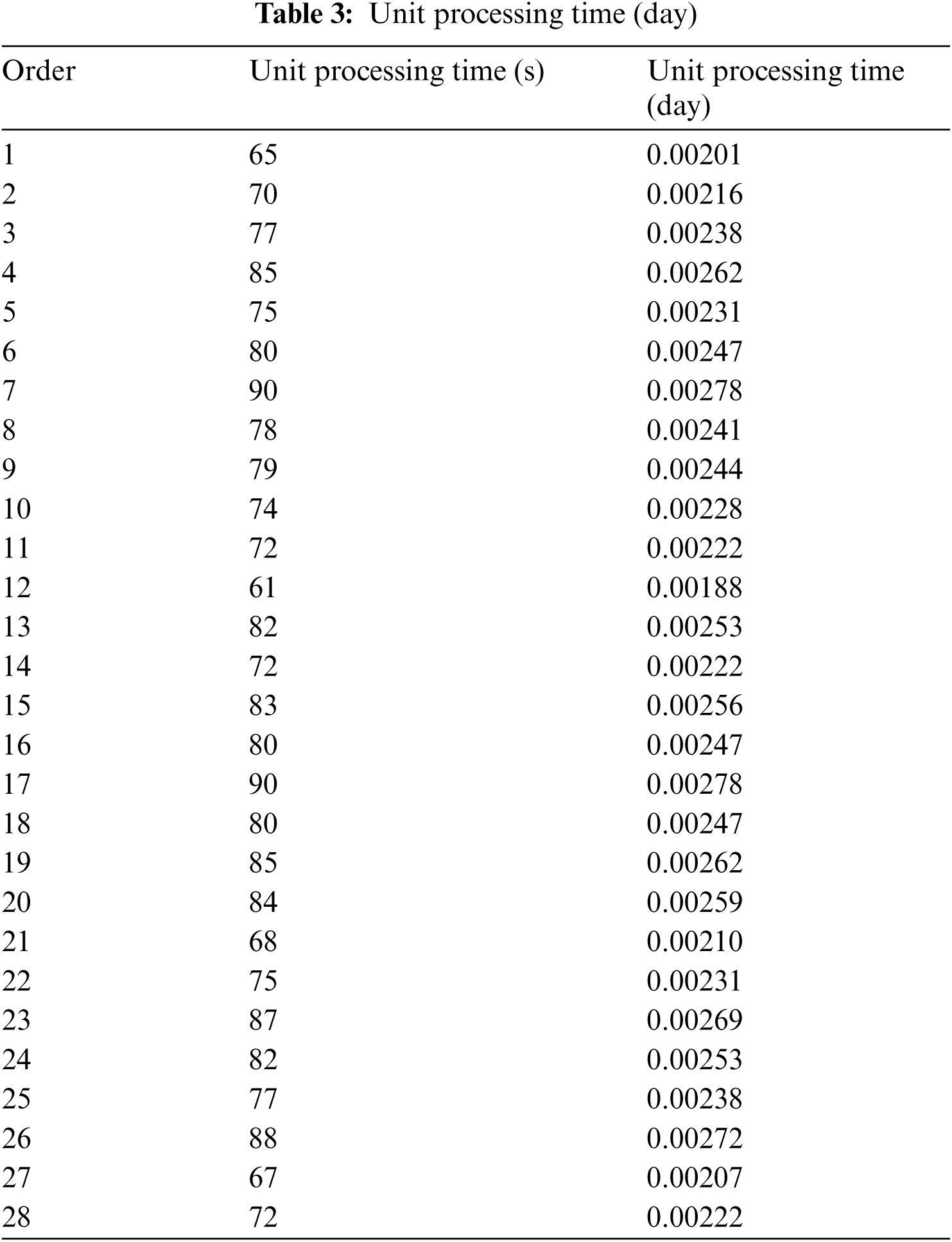
For each order, the classification about indivisible and divisible orders will be different according to the productivity for each type of product, which is calculated using the following formula:

Productivity/order/day=1(day)∗NumberoflinesUnitprocessingtime(day)(12)

The order division result is shown in Tab. 4:

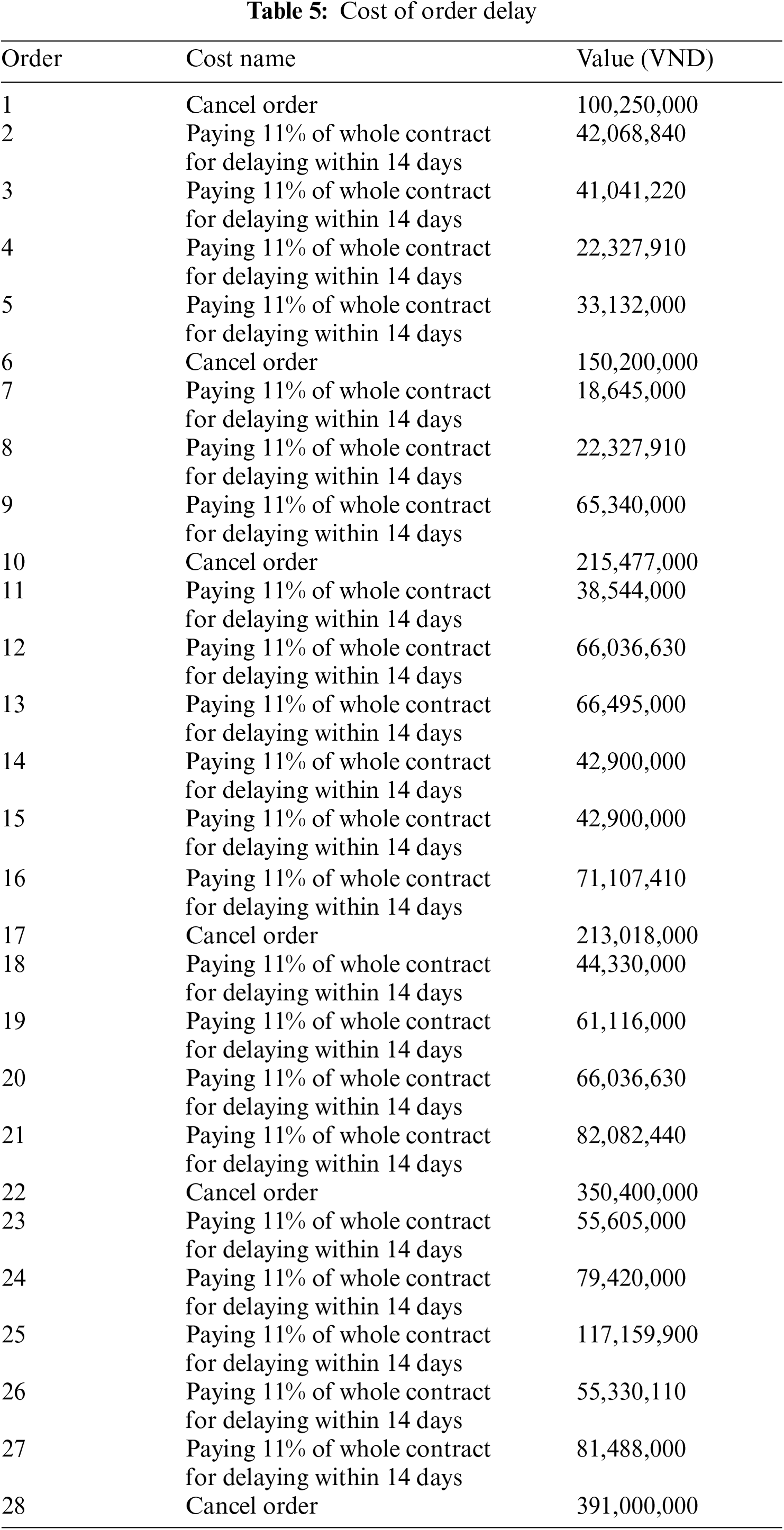
Besides, when there is an order completed after due date, then there are two kinds of paying results. The company will pay penalty cost with a certain penalty rate, or the customer cancel the order, the company thus will bear whole the production cost. The costs of order delay of each order are shown in Tab. 5:

In addition, it is assumed that the percentage of productivity is 100%, the daily limited capacity of production is calculated as:

Dailylimitedcapacity(day)=Numberofproductionlines×1(day)(13)

5.2 Results and Discussion

The characteristics of integer programming model are summarized in Tab. 6 below:

After running the model, the optimal tardy order is 1 order. That is the order 5. From the result of model, company can see the day which high utilization and offer the day that workers need to work overtime so that there is no late order. Tab. 7 shows the utilization result of each day after allocating orders according to the proposed model.

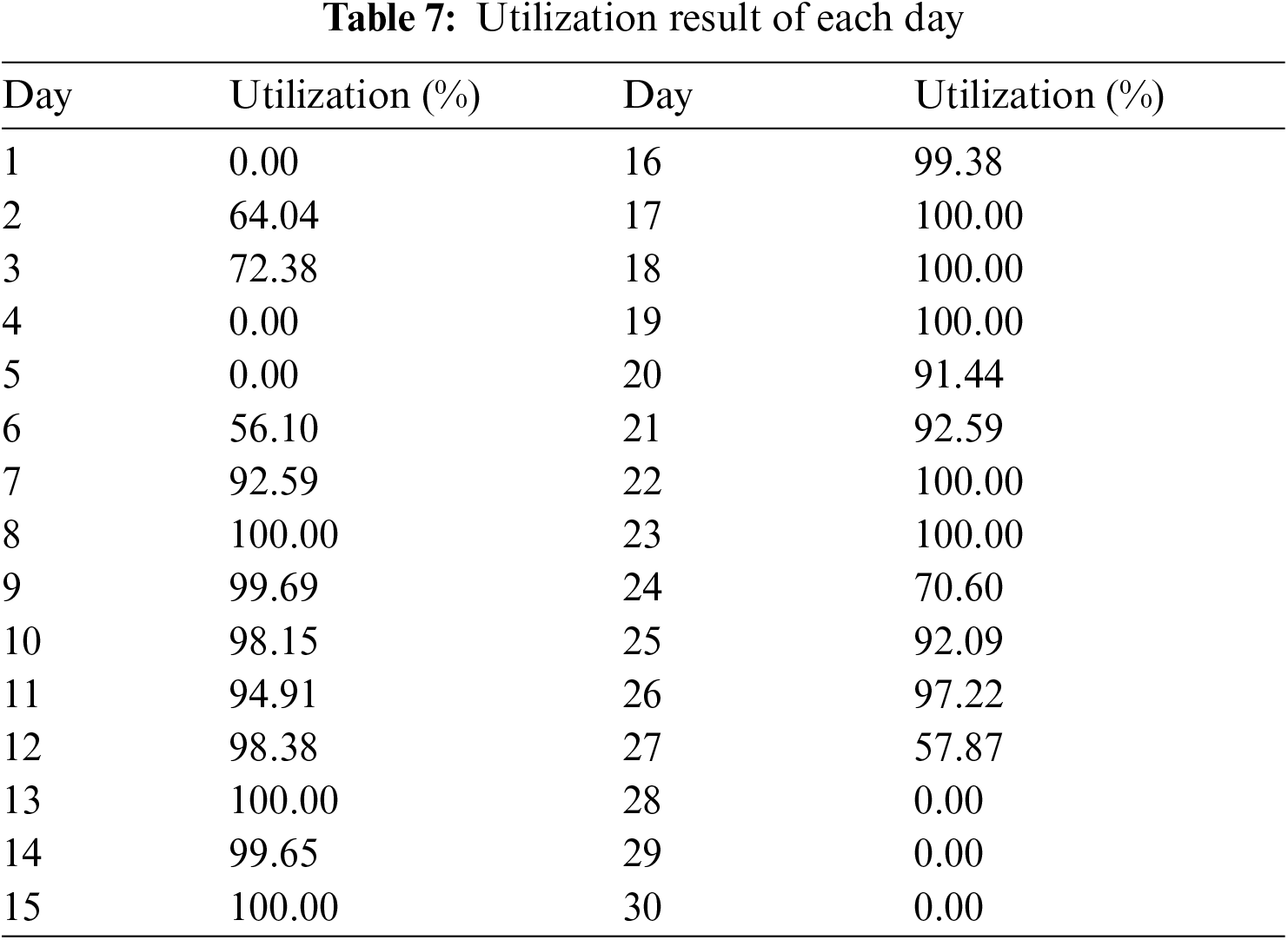
From the table of the utilization show that the utilization from day 7 to day 26 is quite high. This prove that on this period, most of orders have enough resources to be ready for production before due date. In addition, due to reduce the level of inventory of the finished products, the orders should not be finished too early from the due dates. Therefore, the authors will choose day 21 and day 22 nearly to the end of the total completion time on which workers will work overtime 2 h extra. As a result, the number of tardy orders now equal zero and there is no fining cost happened.

The overtime cost paying for worker is 20,000 VND/hour. The estimated number of workers needed for each production flow is 5 workers so the total number of workers working overtime is about 20 workers. Therefore, the total cost of working overtime (TCO) for two days is 800,000 VND/hour. Since TCD > TCO, the better option should be working overtime.

With the amount of penalty of tardy order from the result of model, input to the extended model to identify the minimum completion time for total 28 orders. The result of the extended model indicates that although the time range the authors consider is 30 days (one month), the total time needed to complete total 26 orders with 1 tardy order and the penalty cost is 33,132,000 VND.

6  Conclusion

The research is conducted to study how to minimize the cost of delay completion of orders in the ideal condition by building a linear integer program. In this study, the current problems in operation of garment company are analyzed. The main idea focuses on production scheduling problem. A linear integer model for assignment and allocating orders with the aim to minimize the cost of tardy orders is built. With the proposed model, plant and production managers can apply suitably in order to optimize their production process in order to plan ahead should there will be an abundance of customer orders that reaches the plant using contemporary and realistic constraints that can be applied in any circumstances. The model still needs to consider a number of different aspects such as resources utilization or cost of materials when applied in the scheduling process which could be a further study in the future. This model can be applicable from management perspective. The result of extended model can provide for manager the optimal completion time and have the new schedule for the orders next period.

Acknowledgement: The authors acknowledge and appreciate the support of Van Lang University, Vietnam, National Kaohsiung University of Science and Technology, Taiwan.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  K. Lenin, “Hybridization of genetic particle swarm optimization algorithm with symbiotic organisms search algorithm for solving optimal reactive power dispatch problem,” Journal of Applied Science, Engineering, Technology, and Education, vol. 3, no. 1, pp. 12–21, Jun. 2020. [Google Scholar]

 2.  E. Jiang and L. Wang, “An improved multi-objective evolutionary algorithm based on decomposition for energy-efficient permutation flow shop scheduling problem with sequence-dependent setup time,” International Journal of Production Research, vol. 57, no. 6, pp. 1756–1771, 2019. [Google Scholar]

 3.  A. Gupta and S. R. Chauhan, “A heuristic algorithm for scheduling in a flow shop environment to minimize makespan,” International Journal of Industrial Engineering Computations, vol. 6, no. 2, pp. 173–184, 2015. [Google Scholar]

 4.  K. Ding, P. Jiang and M. Zheng, “Environmental and economic sustainability-aware resource service scheduling for industrial product service systems,” Journal of Intelligent Manufacturing, vol. 28, no. 6, pp. 1303–1316, 2015. [Google Scholar]

 5.  T. Chen and G. Zhou, “Modeling production scheduling problem and its solution by genetic algorithm,” Journal of Computers, vol. 8, no. 8, pp. 2126, 2013. [Google Scholar]

 6.  H. Rahman, R. Sarker and D. Essam, “A genetic algorithm for permutation flow shop scheduling under make to stock production system,” Computers & Industrial Engineering, vol. 90, pp. 12–24, 2015. [Google Scholar]

 7.  F. Tubilla and S. Gershwin, “Dynamic scheduling in make-to-stock production systems with setup times and random breakdowns: Performance analysis and improved policies,” International Journal of Production Research, pp. 1–19, 2021. [Google Scholar]

 8.  R. Kolisch and K. Hess, “Efficient methods for scheduling make-to-order assemblies under resource, assembly area and part availability constraints,” International Journal of Production Research, vol. 38, no. 1, pp. 207–228, 2000. [Google Scholar]

 9.  H. Garmdare, M. Lotfi and M. Honarvar, “Integrated model for pricing, delivery time setting, and scheduling in make-to-order environments,” Journal of Industrial Engineering International, vol. 14, no. 1, pp. 55–64, 2017. [Google Scholar]

10. F. Jaehn and H. Sedding, “Scheduling with time-dependent discrepancy times,” Journal of Scheduling, vol. 19, no. 6, pp. 737–757, 2016. [Google Scholar]

11. A. Shioura, N. Shakhlevich and V. Strusevich, “Application of submodular optimization to single machine scheduling with controllable processing times subject to release dates and deadlines,” INFORMS Journal on Computing, vol. 28, no. 1, pp. 148–161, 2016. [Google Scholar]

12. J. Shi, W. Zhang, S. Zhang and J. Chen, “A new bifuzzy optimization method for remanufacturing scheduling using extended discrete particle swarm optimization algorithm,” Computers & Industrial Engineering, vol. 156, pp. 107219, 2021. [Google Scholar]

13. J. Kim and H. Kim, “Parallel machine scheduling with multiple processing alternatives and sequence-dependent setup times,” International Journal of Production Research, vol. 59, no. 18, pp. 5438–5453, 2020. [Google Scholar]

14. F. Ahmadizar and J. Eteghadipour, “Single-machine earliness–tardiness scheduling with two competing agents and idle time,” Engineering Optimization, vol. 49, no. 3, pp. 499–512, 2016. [Google Scholar]

15. R. Braune and G. Zäpfel, “Shifting bottleneck scheduling for total weighted tardiness minimization—A computational evaluation of subproblem and re-optimization heuristics,” Computers & Operations Research, vol. 66, pp. 130–140, 2016. [Google Scholar]

16. E. Selvarajah and G. Steiner, “Batch scheduling in a two-level supply chain—A focus on the supplier,” European Journal of Operational Research, vol. 173, no. 1, pp. 226–240, 2006. [Google Scholar]

17. G. Fandel and C. Stammen-Hegene, “Simultaneous lot sizing and scheduling for multi-product multi-level production,” International Journal of Production Economics, vol. 104, no. 2, pp. 308–316, 2006. [Google Scholar]

18. D. Kress, M. Barketau and E. Pesch, “Single-machine batch scheduling to minimize the total setup cost in the presence of deadlines,” Journal of Scheduling, vol. 21, no. 6, pp. 595–606, 2018. [Google Scholar]

19. R. Ramezanian, M. Vali-Siar and M. Jalalian, “Green permutation flowshop scheduling problem with sequence-dependent setup times: A case study,” International Journal of Production Research, vol. 57, no. 10, pp. 3311–3333, 2019. [Google Scholar]

20. Y. Li, X. Li and J. Gupta, “Solving the multi-objective flowline manufacturing cell scheduling problem by hybrid harmony search,” Expert Systems with Applications, vol. 42, no. 3, pp. 1409–1417, 2015. [Google Scholar]

21. Z. Chen and G. Vairaktarakis, “Integrated scheduling of production and distribution operations,” Management Science, vol. 51, no. 4, pp. 614–628, 2005. [Google Scholar]

22. B. Ogun and Ç. Alabas-Uslu, “Mathematical models for a batch scheduling problem to minimize earliness and tardiness,” Journal of Industrial Engineering and Management, vol. 11, no. 3, pp. 390, 2018. [Google Scholar]

23. F. Sadeghi Naieni Fard, B. Naderi and A. Akbari, “Production scheduling and customer orders assignment in a three-level supply chain,” ISRN Industrial Engineering, vol. 2014, pp. 1–12, 2014. [Google Scholar]

24. J. Ben Hmida, J. Lee, X. Wang and F. Boukadi, “Production scheduling for continuous manufacturing systems with quality constraints,” Production & Manufacturing Research, vol. 2, no. 1, pp. 95–111, 2014. [Google Scholar]

25. D. Shabtay, “Scheduling and due date assignment to minimize earliness, tardiness, holding, due date assignment and batch delivery costs,” International Journal of Production Economics, vol. 123, no. 1, pp. 235–242, 2010. [Google Scholar]

26. I. Lee, “Minimizing total tardiness for the order scheduling problem,” International Journal of Production Economics, vol. 144, no. 1, pp. 128–134, 2013. [Google Scholar]

27. B. Lin and A. Kononov, “Customer order scheduling to minimize the number of late jobs,” European Journal of Operational Research, vol. 183, no. 2, pp. 944–948, 2007. [Google Scholar]

28. P. Huang, H. Li and L. Han, “Order scheduling problems in make-to-order manufacturing systems,” IEEE International Conference Mechatronics and Automation, vol. 4, pp. 2179–2184, 2005. [Google Scholar]

29. C. Chen, S. Mestry, P. Damodaran and C. Wang, “The capacity planning problem in make-to-order enterprises,” Mathematical and Computer Modelling, vol. 50, no. 9–10, pp. 1461–1473, 2009. [Google Scholar]

30. T. Sawik, “Integer programming approach to production scheduling for make-to-order manufacturing,” Mathematical and Computer Modelling, vol. 41, no. 1, pp. 99–118, 2005. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.