Computers, Materials & Continua DOI:10.32604/cmc.2022.023884
Article

Optimized Ensemble Algorithm for Predicting Metamaterial Antenna Parameters

El-Sayed M. El-kenawy1,2, Abdelhameed Ibrahim3,*, Seyedali Mirjalili4,5, Yu-Dong Zhang6, Shaima Elnazer7,8 and Rokaia M. Zaki9,10

1Department of Communications and Electronics, Delta Higher Institute of Engineering and Technology, Mansoura, 35111, Egypt
2Faculty of Artificial Intelligence, Delta University for Science and Technology, Mansoura, 35712, Egypt
3Computer Engineering and Control Systems Department, Faculty of Engineering, Mansoura University, Mansoura, 35516, Egypt
4Centre for Artificial Intelligence Research and Optimization, Torrens University Australia, Fortitude Valley, QLD 4006, Australia
5Yonsei Frontier Lab, Yonsei University, Seoul, 03722, Korea
6School of Computing and Mathematical Sciences, University of Leicester, Leicester, LE1 7RH, UK
7Nile Higher Institute for Engineering and Technology, Mansoura, Egypt
8Computer and Information Technology College, Taif University, Taif, Saudi Arabia
9Higher Institute of Engineering and Technology, Kafrelsheikh
10Department of Electrical Engineering, Shoubra Faculty of Engineering, Benha University, Egypt
*Corresponding Author: Abdelhameed Ibrahim. Email: afai79@mans.edu.eg
Received: 25 September 2021; Accepted: 02 November 2021

Abstract: Metamaterial Antenna is a subclass of antennas that makes use of metamaterial to improve performance. Metamaterial antennas can overcome the bandwidth constraint associated with tiny antennas. Machine learning is receiving a lot of interest in optimizing solutions in a variety of areas. Machine learning methods are already a significant component of ongoing research and are anticipated to play a critical role in today's technology. The accuracy of the forecast is mostly determined by the model used. The purpose of this article is to provide an optimal ensemble model for predicting the bandwidth and gain of the Metamaterial Antenna. Support Vector Machines (SVM), Random Forest, K-Neighbors Regressor, and Decision Tree Regressor were utilized as the basic models. The Adaptive Dynamic Polar Rose Guided Whale Optimization method, named AD-PRS-Guided WOA, was used to pick the optimal features from the datasets. The suggested model is compared to models based on five variables and to the average ensemble model. The findings indicate that the presented model using Random Forest results in a Root Mean Squared Error (RMSE) of (0.0102) for bandwidth and RMSE of (0.0891) for gain. This is superior to other models and can accurately predict antenna bandwidth and gain.

Keywords: Metamaterial antenna; machine learning; ensemble model; feature selection; guided whale optimization; support vector machines

1  Introduction

Metamaterials are materials with special physical properties that cannot be reproduced using natural materials, and so metamaterials are popular materials in today's world and are frequently used in many fields, such as microwave invisibility cloaks, invisible submarines, revolutionary electronics, microwave components, as filters, and antennas that are compact, efficient, and have a negative refractive index. One of its most important uses is the design of antennas made possible by metamaterials [1–3].

This is due to the fact that metamaterials have unique properties, and as a result, we may construct antennas with innovative features that standard materials cannot provide. One or more layers of metamaterials may be utilized as a substrate or in addition to the antenna design in order to boost the system's capabilities. Even if a compact antenna with low cost and high efficiency is desired, a slightly larger antenna that costs less money and has better efficiency is the best option. The metamaterial may help increase the bandwidth and gain of tiny antennas. Another advantage is that it reduces their electrical size, but the ability to direct a signal increases. In the case of smaller antennas, metamaterial antennas provide an advantage over traditional antennas since they have more bandwidth [4,5].

Simulation software is used to estimate the metamaterial effect. The CST Microwave Studio (CST MWS) is an example of a software program that simulates electromagnetic simulations [6]. Antenna characteristics like bandwidth, gain, Voltage Standing Wave Ratio (VSWR), and return loss may be calculated after the simulation. In the simulation phase, researchers may make adjustments in Metamaterial Antenna, beginning with trial and error to get the set of antenna characteristics. The amount of time it will take to finish this procedure is completely unpredictable. They are using a machine learning model to estimate antenna characteristics. Numerous studies have examined machine learning applications in antenna design. Machine learning is anticipated to speed the antenna design process while retaining high accuracy, minimizing errors, saving time, and the ability to forecast the antenna behavior, improve computing efficiency, and decrease the number of required simulations [7–9].

Optimization is the study of finding optimal solutions to problems. Because optimization issues are complex and grow with time, we resort to improved optimization algorithms [10–13]. Metaheuristic algorithms are an excellent option for tackling complex issues that are difficult to solve with conventional techniques. Algorithms start with a random population and pass on the best to the next generation. Metaheuristic algorithms are dynamic and widely looking for a solution [14–17].

In this paper, an Antenna-derived metamaterial ensemble model is presented as a way to estimate the bandwidth and gain of the Antenna. Of the basic models, we utilise Support Vector Machines (SVM) [18,19], Random Forest [20], K-Neighbors Regressor [21,22], and Decision Tree Regressor [23] to be compared with the presented method. Ensemble model is optimized using an optimization method to identify the optimum features based on the adaptive dynamic polar rose guided whale optimization (AD-PRS-Guided WOA) [24] algorithm. A regression analysis using the suggested model indicated that it was superior to the other models, predicting antenna bandwidth and gain efficiencies.

The structure of this work is organized as follows: Section 2 presents a literature review. Section 3 describes data preparation and the suggested ensemble model in detail. Section 4 displays results and discussion. The last section of the given study (Section 5) examines the conclusion.

2  Literature Review

In general, the following steps can be taken to incorporate machine learning into the antenna design problem. The electromagnetic properties of an antenna are first determined via a series of simulations. These attributes are then saved in a database and used to train a machine learning system. Finally, the algorithm determines the Antenna that produces the closest results based on the designer's requirements.

2.1 Machine Learning Models

Machine learning is a technique that relies on algorithms which can learn from data without the need of pre-programming. It can be classified into three types, named supervised, unsupervised and reinforcement learning. To attain high performance in Artificial Neural Networks (ANN), extensive interconnections of “neurons,” which are basic processing cells, are used. When complicated functions with many characteristics are discovered, neural networks provide an alternative method for doing machine learning. Multiple layers comprise neural networks: an input layer, an output layer, and hidden layers between the input and output layers [25]. The SVM method is another kind of algorithm for guided learning. It is mainly used in classification and employs kernel techniques to scope with a challenging situation of non-linearly separable patterns. K-Nearest Neighbors (KNN) is considered to be one of the simplest machine learning methods available. After remembering the training set, the algorithm predicts the outcome of each new input using the outputs of its nearest neighbors in the training set.

Machine learning algorithms have been applied in smart grid networks, where machine learning can be used to anticipate malicious events, communication technology, including antenna selection in wireless communications, wireless networks, where machine learning can be used to forecast wireless users’ mobility patterns and content requests, and speech recognition. A technique for using machine learning in antenna design is to train a learning algorithm on data from prior simulations in order to improve the antenna parameters.

Metaheuristic algorithms solve unexpected issues since they are intelligent and have prior knowledge of random search. These algorithms are either flexible, simple, or able to avoid local perfection. Exploration and exploitation are two elements of population-based heuristic algorithms. The metaheuristic algorithm here selects between Exploration and exploitation. While exploring, the technique examines the search space thoroughly. The area's local search is currently at the exploitation stage. Several global optimization methods inspired by nature have been developed in recent decades. Population-based metaheuristics, often known as general-purpose algorithms, may be utilized in a variety of situations. Metaheuristics are split into two types: metaphor-based and non-metaphor based. In contrast, metaphors employ algorithms to represent natural phenomena or human behavior in contemporary life [26].

2.2 Feature Selection

All machine learning processes rely on feature engineering, which entails the extraction and selection of features, which are critical components of contemporary machine learning pipelines. Despite the fact that feature extraction and feature selection procedures overlap in certain ways, these words are often used interchangeably. Feature extraction is the process of extracting additional variables from raw data in order to make machine learning algorithms function. The feature selection method is focused on identifying the characteristics that are the most consistent, meaningful, and non-redundant. The feature selection issue is unique in that the search space is constrained to two binary values: 0 and 1. As a result, the continuous version of an optimizer should be used and updated to function correctly to address this issue. This method is considered in order to transform the suggested continuous values of AD-PRS-Guided WOA algorithm to binary values, allowing it to be utilised to solve the issue of feature selection. To transform, the Sigmoid form converts continuous values to binary values.

3  The Proposed Ensemble Model

Ensemble techniques are getting preferred in addressing various artificial intelligence issues. The average ensemble is among the most basic ensemble strategies that integrate base regressors’ outputs and compute the mean. This method aggregates the outcome of various regressors as well as determines the mean value. In this paper, the average ensemble is employed as a reference set version to review the efficiency of the suggested ensemble model. As shown in Fig. 1, the presented ensemble model is based on the stages of preprocessing, feature selection and optimized ensemble algorithm for both bandwidth and gain prediction. Ensemble model instead of selecting one ideal version from the candidates combines all the designs by assigning weight to every model. The Ensemble technique is verified as one of the significant methods in enhancing the prescient capability of conventional versions. The ensemble model typically has two stages wherein the first stage, the outcome variable of the best ensemble member, is picked to obtain the final forecast. The second stage blends the ensemble members’ output variables using the mixed formula [27].

Figure 1: The presented ensemble model based on the stages of preprocessing, feature selection and optimized ensemble algorithm for both bandwidth and gain prediction

3.1 Data Preprocessing

The dataset utilised in this study includes eleven Metamaterial Antenna characteristics. The dataset was obtained through Kaggle [28]. There are 572 records in this collection. Each record contains the following information about the metamaterial antenna: the width and height of the split ring resonator, the distance between rings, the width of the rings, the gap between the rings, the distance between the antenna patch and the array, the number of split ring resonator cells in the array, the gain of the Antenna, the distance between split ring resonator cells in the array, the bandwidth of the Antenna, and the return. Tab. 1 summarises the dataset's characteristics. These characteristics will be utilised to estimate the Antenna's bandwidth using a machine learning algorithm, and Fig. 2 shows the distribution of bandwidth and gain feature.

Figure 2: Distribution of bandwidth and gain feature

The first step is to format the nulls, the second step is to filter out null values, and the third step is to deal with nulls using a formula. Min-max normalisation is one of the most frequently used methods of data normalising. For each feature, the lowest value is converted to a 0, the highest value is converted to a 1, and all other values are converted to a decimal between 0 and 1. The dataset's correlation matrix, as shown in Fig. 3, Wm and tm are strongly correlated with the bandwidth.

Figure 3: Correlation of metamaterial antenna

3.2 The AD-PRS-Guided WOA Algorithm

The AD-PRS-Guided WOA algorithm was first proposed in [24]. A binary version of the AD-PRS-Guided WOA algorithm is used to select the ideal attributes from the datasets to offer an optimal ensemble design for predicting the bandwidth and gain of the Metamaterial Antenna. The algorithm can check out the search space successfully to improve exploration efficiency. The algorithm also uses three arbitrary solutions as it makes use of significant change to transform between exploration and exploitation processes. According to the most effective remedy, it also calculates a listing of generated walks in a diffusion process as a polar increased feature. The AD-PRS-Guided WOA algorithm is shown in Algorithm 1.

The updating positions mechanism of the algorithm of AD-PRS-Guided WOA is modified to follow three random solutions of Xo1,Xo2 and Xo3. These solutions are updated every iteration to enhance the algorithm performance and get the optimal solution.

X(t+1)=w1∗Xo1+w2∗z∗(Xo2−Xo3)+w3∗(1−z)∗(Q−X(t))(1)

where X(t+1) is the updated solution in iteration t+1 and X(t) is the current solution at iteration t. Q is the optimal solution. w1, w2 and w3 are random values in [0, 0.5], [0, 1], and [0, 1], respectively. z is updated as z=1−(ttm)2 for t iteration and tm as maximum iterations.

The algorithm gets the best solution related to the calculated best fitness value. Then, the individuals are split into exploration groups and exploitation groups. Individuals in the exploitation group are moving to the leaders, and individuals in the exploration group are searching for leaders. Individuals in the sub-groups are changed dynamically. For balancing purposes, the algorithm divides the population into (50/50) for the two groups.

In the algorithm, the polar rose function is used to search the leaders’ purpose to find other good solutions. Based on different values of the main parameters of this function named a and b, Fig. 4 shows the output of the polar rose function. The polar rose function is calculated as follows to search around the best solution.

X(t+1)=k∗sin(abθ)(2)

where X(t+1) is the updated solution in iteration t+1. The a and b parameters are within [−10, 10] and 0≤θ≤12π. k is calculated as k=2−(2∗t2tm2).

Figure 4: Changing the values of a and b to generate different polar rose function outputs

3.3 The Binary AD-PRS-Guided WOA Algorithm

The output solution is updated to a binary solution using (0 or 1) in case of a feature selection problem. The sigmoid function is used in this paper to update the continuous solutions of the optimizer's output into binary solutions, as shown in Algorithm 2.

4  Results and Discussion

The results in this section are explained as follows. The results, based on the Decision Tree, Multilayer Perceptron (MLP), KNN, Support Vector Regression (SVR), Random Forest, regressors in addition to the Average Ensemble and the proposed Ensemble model based on Random Forest regressor, before applying the feature selection technique are discussed. Then the results are shown after using feature selection to deliver the performance of the proposed model. Tab. 2 shows the configuaration of the AD-PRS-Guided WOA algorithm.

4.1 Performance Metrics

The performance metrics used in this work are Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), Mean Absolute Error (MBE), and the correlation coefficient (r) [22]. Tab. 3 shows the different performance metrics where Hp,i indicates a predicted value, Hi represents the observed value, and n is the total number of observations. Hp,i¯ and Hi¯ indicate the average predicted and observed values, respectively.

4.2 Results Before Applying Feature Selection

The results based on the bandwidth features of the tested dataset before applying the feature selection technique are shown in Tab. 4. Tab. 4 shows that the proposed Ensemble model using Random Forest results based on the bandwidth features of RMSE of (0.0320), MAE of (0.0231), MBE of (−0.0069), and r of (0.9752) are better than other compared models. The results using the gain features of the dataset before applying the feature selection are shown in Tab. 5.

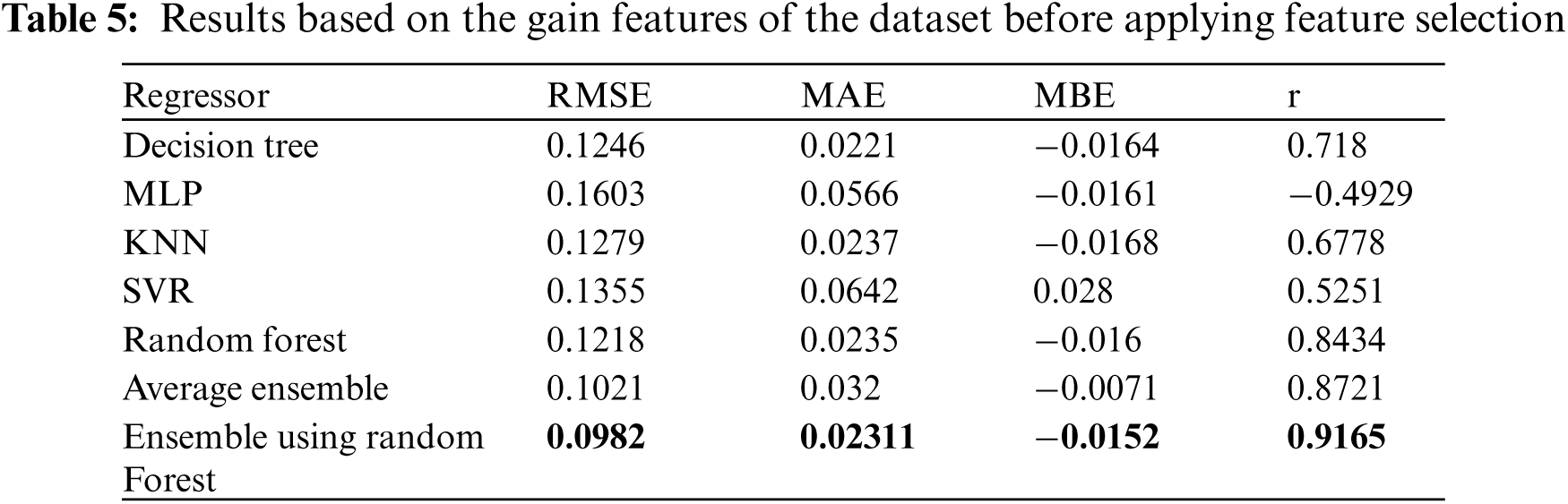
Tab. 5 shows that the proposed Ensemble model using Random Forest results based on the gain features of RMSE of (0.0982), MAE of (0.0231), MBE of (−0.0152), and r of (0.9165) are better than other compared models. Fig. 5 shows the actual and the predicted values for the bandwidth prediction from the tested dataset based on the AD-PRS-Guided WOA algorithm before applying the feature selection process. While Fig. 6 shows the actual and predicted values by the AD-PRS-Guided WOA algorithm for the gain prediction before applying the method of feature selection.

Figure 5: The actual values, in green color, and predicted values, in red color, by the proposed ensemble algorithm for the bandwidth before applying the feature selection

Figure 6: The actual values, in green color, and predicted values, in red color, by the proposed ensemble algorithm for the gain before applying the feature selection

4.3 Results After Applying Feature Selection

After applying the feature selection technique, the results of the bandwidth features from the tested dataset are shown in Tab. 6. Tab. 6 shows that the proposed Ensemble model using Random Forest results of RMSE of (0.0102), MAE of (0.0344), MBE of (−0.0032), and r of (0.9932) are much better than other compared models. The results of the gain features from the dataset after applying the feature selection are shown in Tab. 7.

Tab. 7 shows that the proposed Ensemble model using Random Forest results of the gain features as RMSE of (0.0891), MAE of (0.0234), MBE of (−0.0161), and r of (0.9443) which are much better than other compared models. Fig. 7 shows the actual values and predicted values by the AD-PRS-Guided WOA algorithm for the bandwidth after applying the feature selection. While Fig. 8 shows the actual and predicted values by the AD-PRS-Guided WOA algorithm for the gain after applying the feature selection.

Figure 7: The actual values, in green color, and predicted values, in red color, by the proposed ensemble algorithm for the bandwidth after applying the feature selection

Figure 8: The actual values, in green color, and predicted values, in red color, by the proposed ensemble algorithm for the bandwidth after applying the feature selection

5  Conclusion

Machine learning methods are already a significant component of ongoing research and are anticipated to play a critical role in today's technology. The accuracy of the forecast is mostly determined by the model used. This paper uses the AD-PRS-Guided WOA method to pick the optimal features from the metamaterial antenna dataset. Metamaterial antennas can overcome the bandwidth and gain constraints associated with tiny antennas. Machine learning is receiving much interest in optimizing solutions in a variety of areas. The optimal ensemble model achieved good results for predicting the bandwidth and gain of the metamaterial antenna. The basic models have investigated SVM, Random Forest, K-Neighbors Regressor, and Decision Tree Regressor. The AD-PRS-Guided WOA algorithm was utilized to pick the optimal features from the datasets. The suggested model was compared to models based on five variables and to the average ensemble model. The findings indicated that the suggested AD-PRS-Guided WOA algorithm-based model is superior to others and can accurately predict antenna bandwidth and gain. The presented algorithm will be compared with CST software in future work.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  J. Suganthi, T. Kavitha and V. Ravindra, “Survey on metamaterial antennas,” in IOP Conference Series: Materials Science and Engineering, vol. 1070, no. 1, pp. 12086, 2021. [Google Scholar]

 2.  M. Alibakhshikenari, B. S. Virdee, L. Azpilicueta, M. Naser-Moghadasi, M. O. Akinsolu et al., “A comprehensive survey of metamaterial transmission-line based antennas: Design, challenges, and applications,” IEEE Access, vol. 8, pp. 144778–144808, 2020. [Google Scholar]

 3.  H. M. E. Misilmani and T. Naous, “Machine learning in antenna design: An overview on machine learning concept and algorithms,” in 2019 Int. Conf. on High Performance Computing & Simulation (HPCS), Dublin, Ireland, pp. 600–607, 2019. [Google Scholar]

 4.  K. Sun, R. Fan, X. Zhang, Z. Zhang, Z. Shi et al., “An overview of metamaterials and their achievements in wireless power transfer,” Journal of Materials Chemistry C, vol. 6, no. 12, pp. 2925–2943, 2018. [Google Scholar]

 5.  X. Chen and W. Fan, “Ultrasensitive terahertz metamaterial sensor based on spoof surface plasmon,” Scientific Reports, vol. 7, no. 1, pp. 1–8, 2017. [Google Scholar]

 6.  B. V. Simuleon, SIMULIA CST Studio Suite. Pettelaarpark 84 5216 PP ‘s-Hertogenbosch, Netherlands: Electromagnetic Field Software. 2021. [Online]. Available: https://www.simuleon.com/simulia-cst-studio-suite/, accessed: 2021-09-24. [Google Scholar]

 7.  G. Geetharamani and T. Aathmanesan, “Design of metamaterial antenna for 2.4 GHz WiFi applications,” Wireless Personal Communications, vol. 113, no. 4, pp. 2289–2300, 2020. [Google Scholar]

 8.  W. Naktong, A. Ruengwaree, N. Fhafhiem and P. Krachodnok, “Resonator rectenna design based on metamaterials for low-RF energy harvesting,” Computers, Materials & Continua, vol. 68, no. 2, pp. 1731–1750, 2021. [Google Scholar]

 9.  E. S. M. El-kenawy, H. F. Abutarboush, A. W. Mohamed and A. Ibrahim, “Advance artificial intelligence technique for designing double T-shaped monopole antenna,” Computers, Materials & Continua, vol. 69, no. 3, pp. 2983–2995, 2021. [Google Scholar]

10. M. M. Fouad, A. I. El-Desouky, R. Al-Hajj and E. -S. M. El-Kenawy, “Dynamic group-based cooperative optimization algorithm,” IEEE Access, vol. 8, pp. 148378–148403, 2020. [Google Scholar]

11. E. S. M. El-Kenawy, A. Ibrahim, S. Mirjalili, M. M. Eid and S. E. Hussein, “Novel feature selection and voting classifier algorithms for COVID-19 classification in CT images,” IEEE Access, vol. 8, pp. 179317–179335, 2020. [Google Scholar]

12. E. S. M. El-Kenawy, M. M. Eid, M. Saber and A. Ibrahim, “Mbgwo-SFS: Modified binary grey wolf optimizer based on stochastic fractal search for feature selection,” IEEE Access, vol. 8, pp. 107635–107649, 2020. [Google Scholar]

13. A. Ibrahim, S. Mohammed, H. A. Ali and S. E. Hussein, “Breast cancer segmentation from thermal images based on chaotic salp swarm algorithm,” IEEE Access, vol. 8, pp. 122121–122134, 2020. [Google Scholar]

14. A. Ibrahim, M. Noshy, H. A. Ali and M. Badawy, “PAPSO: A power-aware VM placement technique based on particle swarm optimization,” IEEE Access, vol. 8, pp. 81747–81764, 2020. [Google Scholar]

15. A. Ibrahim, H. A. Ali, M. M. Eid and E. -S. M. El-kenawy, “Chaotic harris hawks optimization for unconstrained function optimization,” in 2020 16th Int. Computer Engineering Conf. (ICENCO), Cairo, Egypt, pp. 153–158, 2020. [Google Scholar]

16. M. M. Eid, E. -S. M. El-kenawy and A. Ibrahim, “A binary sine cosine-modified whale optimization algorithm for feature selection,” in 2021 National Computing Colleges Conf. (NCCC), Taif, Saudi Arabia, pp. 1–6, 2021. [Google Scholar]

17. E. -S. M. El-Kenawy, S. Mirjalili, A. Ibrahim, M. Alrahmawy, M. El-Said et al., “Advanced meta-heuristics, convolutional neural networks, and feature selectors for efficient COVID-19 X-ray chest image classification,” IEEE Access, vol. 9, pp. 36019–36037, 2021. [Google Scholar]

18. R. Al-Hajj, A. Assi and M. M. Fouad, “Stacking-based ensemble of support vector regressors for one-day ahead solar irradiance prediction,” in 2019 8th Int. Conf. on Renewable Energy Research and Applications (ICRERA), Brasov, Romania, pp. 428–433, 2019. [Google Scholar]

19. H. Lin, W. -Y. Shin and J. Joung, “Support vector machine-based transmit antenna allocation for multiuser communication systems,” Entropy, vol. 21, no. 5, pp. 471, 2019. [Google Scholar]

20. N. Kurniawati, D. N. N. Putri and Y. K. Ningsih, “Random forest regression for predicting metamaterial antenna parameters,” in 2020 2nd Int. Conf. on Industrial Electrical and Electronics (ICIEE), Lombok, Indonesia, pp. 174–178, 2020. [Google Scholar]

21. E. S. M. El-Kenawy, S. Mirjalili, S. S. M. Ghoneim, M. M. Eid, M. El-Said et al., “Advanced ensemble model for solar radiation forecasting using sine cosine algorithm and Newton's laws,” IEEE Access, vol. 9, pp. 115750–115765, 2021. [Google Scholar]

22. A. Ibrahim, S. Mirjalili, M. El-Said, S. S. M. Ghoneim, M. Alharthi et al., “Wind speed ensemble forecasting based on deep learning using adaptive dynamic optimization algorithm,” IEEE Access, vol. 9, pp. 1–18, 2021. [Google Scholar]

23. A. J. Myles, R. N. Feudale, Y. Liu, N. A. Woody and S. D. Brown, “An introduction to decision tree modeling.” Journal of Chemometrics: A Journal of the Chemometrics Society, vol. 18, no. 6, pp. 275–285, 2004. [Google Scholar]

24. S. S. M. Ghoneim, T. A. Farrag, A. A. Rashed, E. -S. M. El-Kenawy and A. Ibrahim, “Adaptive dynamic meta-heuristics for feature selection and classification in diagnostic accuracy of transformer faults,” IEEE Access, vol. 9, pp. 78324–78340, 2021. [Google Scholar]

25. A. A. Salamai, E. -S. M. El-kenawy and A. Ibrahim, “Dynamic voting classifier for risk identification in supply chain 4.0,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3749–3766, 2021. [Google Scholar]

26. A. Ibrahim, A. Tharwat, T. Gaber and A. E. Hassanien, “Optimized superpixel and AdaBoost classifier for human thermal face recognition,” Signal, Image and Video Processing, vol. 12, no. 4, pp. 711–719, 2018. [Google Scholar]

27. T. Gaber, A. Tharwat, A. Ibrahim, V. Snáel and A. E. Hassanien, “Human thermal face recognition based on random linear oracle (RLO) ensembles,” in 2015 Int. Conf. on Intelligent Networking and Collaborative Systems, Taipei, pp. 91–98, 2015. [Google Scholar]

28. R. Machado, Metamaterial Antennas. Florianópolis, State of Santa Catarina, Brazil: FotonTech, 2019. [Online]. Available: https://www.kaggle.com/renanmav/metamaterial-antennas, accessed: 2021-09-12. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.