Computers, Materials & Continua DOI:10.32604/cmc.2022.023912
Article

Hydrodynamics and Heat Transfer Analysis of Airflow in a Sinusoidally Curved Channel

Abid. A. Memon1, M. Asif Memon1, Kaleemullah Bhatti1, Thanin Sitthiwirattham2,* and Nichaphat Patanarapeelert3

1Department of Mathematics and Social Sciences, Sukkur IBA University, Sukkur, 65200, Sindh, Pakistan
2Mathematics Department, Faculty of Science and Technology, Suan Dusit University, Bangkok, 10300, Thailand
3Department of Mathematics, Faculty of Applied Science, King Mongkut's University of Technology North Bangkok, Bangkok, 10800, Thailand
*Corresponding Author: Thanin Sitthiwirattham. Email: thanin_sit@dusit.ac.th
Received: 26 September 2021; Accepted: 10 November 2021

Abstract: For heat transfer enhancement in heat exchangers, different types of channels are often tested. The performance of heat exchangers can be made better by considering geometry composed of sinusoidally curved walls. This research studies the modeling and simulation of airflow through a 2π units long sinusoidally curved wavy channel. For the purpose, two-dimensional Navier Stokes equations along with heat equations are under consideration. To simulate the fluid flow problem, the finite element-based software COMSOL Multiphysics 5.4 is used. The parametric study for Reynolds number from Re=100 to Re=1000 and the period of vibration P from 0 to 5 are observed. The surface plots, streamline patterns, contours, and graphs are presented for the velocity field magnitude, temperature, and pressure against the Reynolds number as well as period of vibration. The results are compared with various literature. It is found that due to the creation of periodic contraction regions the velocity magnitude of the flow is continuously increasing with the increase of Reynolds number, on the contrary the pressure is decreasing from inlet to outlet of the channel. Also, a periodic variation in the pressure distribution along the vibrating boundaries has been found with an average increase of 500% for the high Reynolds number. A novel work was done by expressing the rotation rate per second in terms of local Reynolds number for the recirculating regions found due to the periodic oscillation of the boundaries. The average temperature near the outlet where a fixed temperature is imposed initially is decreasing with an increase in Reynolds number. The convection process is weakened due to an increase of periodic vibration of boundaries.

Keywords: Simulation of fluid flow; heat transfer; cosine function; wavy channel

1  Introduction

The wavy channels in which the contraction and expansion regions are created periodically is very essential in most of the devices for enhancing the heat distribution, pressure reduction, and maximizing the flow rate. Because of having the expansion and the contraction regions, the fluid passage through these channels attains an automatically created periodicity. Having the periodic variation in the cross-sectional area, the fluid gains a regime of fully developed that is quite different from those channels having the constant cross-sectional area. Fluid flow problems in the wavy channels are often studied to examine the separated flows in which separated vortices are formed in the expansion regions, patterns of the flow velocity, pressure patterns, and the temperature distribution due to the periodic variation. Due to the periodic variation in the parameters of the geometry, the pattern of the fluid movement is largely affected by the flow velocities, loss in pressure, and heat enhancements [1–4]. The wavy channels with the corrugated walls having the periodic expansion and contraction are widely studied in the many of the application like blood oxygenators [5,6], in the microfiltration cell [7], the wavy channels are also studied as the vortex generators to increase the thermal performance in solar panels [8,9]. There is a lot of work focused upon the fluid flow through sinusoidally curved wavy channels, details are given below:

In [10], the authors studied the laminar flow and thermal characteristics in the cavity composed of sinusoidal functions. It was discussed that due to the increase in the flow velocities, a large number of vortices are produced inside the cavities which might increase hydrodynamic and thermal enhancements in the channels. On examining the wavy channel [11] reported that when compared with the rectangular channel, the wavy types channel has the largest values of the friction factor and because of the reason the wavy channels are largely used for the cooling process. Investigating the flow pattern through the wavy channels [12] composed of sinusoidal functions with the parametric study for Reynolds number, it was reported that in the range of Re>700, a turbulent flow can be assumed in the wavy channel due to the creation of unsteady vortices in the expansion regions. An experimental investigation was performed [13–15] to investigate the laminar as well as the turbulent fluid flows and heat transfer with the use of a wide range of Reynolds numbers. It was reported that due to the presence of recirculation vortices in the regions, mixing of the fluid takes place quickly near the boundaries that will support enhancing the heat transfer in a wavy channel. Due to the curvy walls of the channel, the thermal boundary layers became destabilize and promote turbulence in the channel which might favor increasing the heat transfer. On investigating numerically [16] fluid flow and heat transfer through the sinusoidal wavy channel it was presented that the local Nusselt number possesses a direct relationship with the Reynolds number change periodically with the flow of direction. A two-dimensional curved channel with a fully developed flow was studied [17] numerically along with the heat transfer. The research focused on the geometrical influence of Reynolds number, Prandtl number on flow distribution, and heat transfer. It was showed that with the increase of wall-to-wall distance and amplitude of the vibration of the wave, the heat transfer coefficient, streamlines contours are significantly affected. It was also endorsed that using the wavy geometry of any shape the pressure drop will be higher than that of a rectangular channel for the same dynamically and thermal parameters. The wavy channels are under consideration in many microfluidics devices for low Reynolds number. In many applications of [18–20] microfluidics it was stated that it is the only diffusion that is a mode of transport that took place in the wavy channels for low Reynolds number. Hence, to enhance the mixing in micro-channels it is essential to put Re<1 as described in [21,22]. In the presence of a magnetic field, a slip flow was studied [23] for the fluid flow and heat transfer problem where the governing partial differential equation first converted in to fourth order differential equation and then a numerical solution obtained by Adomain decomposition. The two models for the hybrid nano-fluid were compared for a rotating channel with porous medium under the surface catalytic reaction [24]. The single and multi-wall nanotubes were taken with the ethylene glycol as the base fluid. Another study was done for the purpose to compare the consequences heating with Newtonian impacts and homogeneous as well as heterogeneous reaction for the flow of water-silver nano-fluids [25]. To see the better impacts of the study the thermal radiation and magnetic field were also added as the feature. Later the colloidal suspension with water for aluminum oxide and gamma-aluminum oxide was studied [26] in an elastic cylinder. The research becomes the beneficial due to the application of the thermal transport in the side of industries, aerodynamics and medical sciences.

Besides all these works there is much effort devoted by researchers in last few years in modeling nanofluids flows through different curvy geometries with application in energy storage, drug delivery, cancer treatment, tissue generation, readers are referred to the works [27–29]. In this paper, the hydrodynamics of airflow and heat transfer through a sinusoidally curved wavy channel is studied in detail. Section 2 presents the problem description. In Section 3, we present different mesh sizes and correlation analysis. The variation in flow variables including temperature distribution is observed by changing Reynolds number from 100 to 1000 and period of vibration of walls from 0 to 5. The problem is modeled in COMSOL Multiphysics 5.4 and solved using finite element method to obtain flow variables including temperature profile. Section 4 precisely discusses the results and presents a comparison analysis with the recently published work. A detailed parametric study using graphs is also carried out. In Section 5 we give the concluding remarks.

2  Methodology

2.1 Geometrical Construction of the Wavy Channel

The current problem of the fluid flow and heat transfer is tested by making the open channel who's upper and lower boundaries are shaped up by using the cosine function see Fig. 1. Such geometries are creating the auto oscillation or vibration in a domain that generates hypes or contraction region in the channel which results increase the speed of the particles and reducing the dynamic pressure. The length of the channel is fixed of whereas the boundaries of the channel are vibrated with the period P. Here the boundary below of the channel is erected with the help of function and the lower boundary of the channel is erected by the function. Where A=0.3 cm is known as the amplitude of the vibration of the channel. P is the period of the vibration of the channel. For the contemporary simulation, the periods of the vibration are tested from 0 to 5. By putting P=0, corresponds to the straight rectangular channel which is normally tested in many of the fluid flow problems. The total height of where H is the length of the contracted region. An average inlet velocity will be forced from the left entrance of the channel while the right end of the channel is perceived as an outlet of the channel, where the pressure is getting as zero. The walls of the upper and lower walls of the channel are controlled by the slip boundary conditions. The common air as the testing fluid will be allowed to enter at the initial temperature of and the last vertical block of the channel will be kept at the temperature of Theat=323.15K.

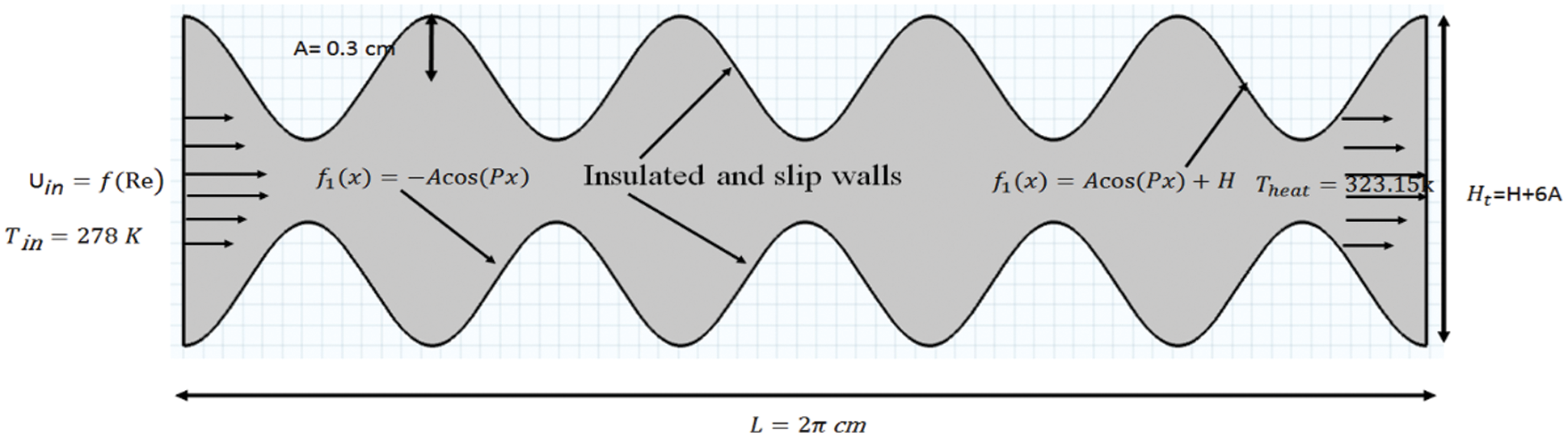
Figure 1: Geometrical construction and boundary conditions of the problem

2.2 Problem Formulation

The modeling and simulation for the present fluid flow and heat transfer problem are examined by considering the steady-state, two-dimensional, and incompressible Newtonian fluid. We use COMSOL Multiphysics 5.4 for the simulation which implements streamline-upwind Petrov-Galerkin's finite element method [15] to solve the coupling system of Navier Stokes equations and heat equation. In Fig. 3, we present the work flow of the problem. Let u⇀=(u,v) denotes the velocity field of the fluid in two dimensions, where u and v are respectively the horizontal and the vertical components of velocity field. The governing field equations are:

∇⇀⋅u⇀=0,(1)

u⇀⋅∇⇀u⇀=−∇⇀p+1Re∇⇀2u⇀.(2)

where p denotes pressure and Re denotes the Reynolds number. Eqs. (1) and (2) can be written in component form as:

u∂u∂x+v∂u∂y=−∂p∂x+1Re(∂2u∂x2+∂2u∂y2),(3)

u∂v∂x+v∂v∂y=−∂p∂y+1Re(∂2v∂x2+∂2v∂y2),(4)

The heat transfer for the fluids in the vector form and in component form can be written as by Eqs. (5) and (6)

ρcp(u⇀⋅∇⇀T)=k(∇⇀2T),(5)

ρcp(u∂T∂x+v∂T∂y)=k(∂2T∂x2+∂2T∂y2).(6)

Following boundary conditions are set:

(a)   Slip boundary condition at upper and lower walls

uux+vvx=0,(7)

(b)   Fully developed flow conditions at inlet and outlet of the channel are respectively

uav=uin,T=Tin,(8)

and

p0=0,T=Theat.(9)

where p0 and Theat are the pressure at temperature applied at the outlet of the channel. Other computational parameters are:

Relocal=ρuinLμ,Re=ρuinxμ,Nux=hxk,Nu¯=1H∫0HNuxdx,(10)

where Relocal is local Reynolds number, Nux is the Nusselt number and Nu¯ is the averaged Nusselt number.

3  Validation and Comparison Between Different Mesh Sizes

3.1 Mesh Independent Study

It is the describable quality of the finite element procedures to get the results up to the benchmark by performing a mesh independent study for the fluid flow problem and heat transfer. To approve the current fluid flow problem for a sinusoidally curved wavy channel a mesh independent study is performed along the channel. For this reason, five different types of meshes are practiced to estimate the ratio of the centerline horizontal component of velocity u to the inlet velocity uin at downstream of the channel. In Figs. 2a–2e, five different meshes with different qualities are observed. Each of them is used to measure the ratio u/uin at the lower boundary of the channel see Fig. 3. From the graph, it is very much explicit that with the implementation of fine to extremely fine meshes the problem of the flow is mesh-independent i.e., the results achieved through the extremely fine meshes are conferring more accuracy to match the benchmark problem when studied with such type of the channel.

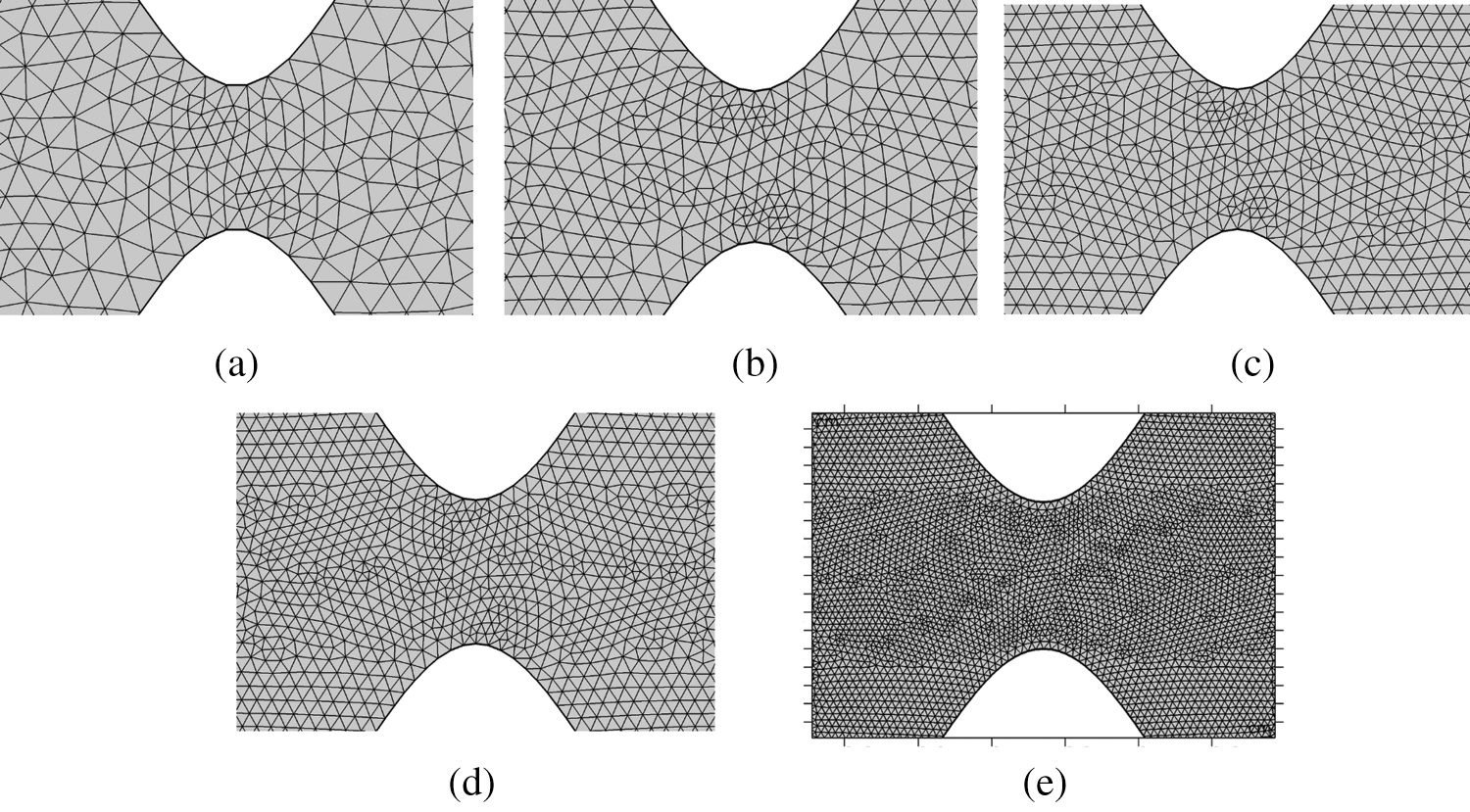
Figure 2: Triangular meshing (a) normal (b) fine (c) finer (d) Extra fine and (e) Extremely fine

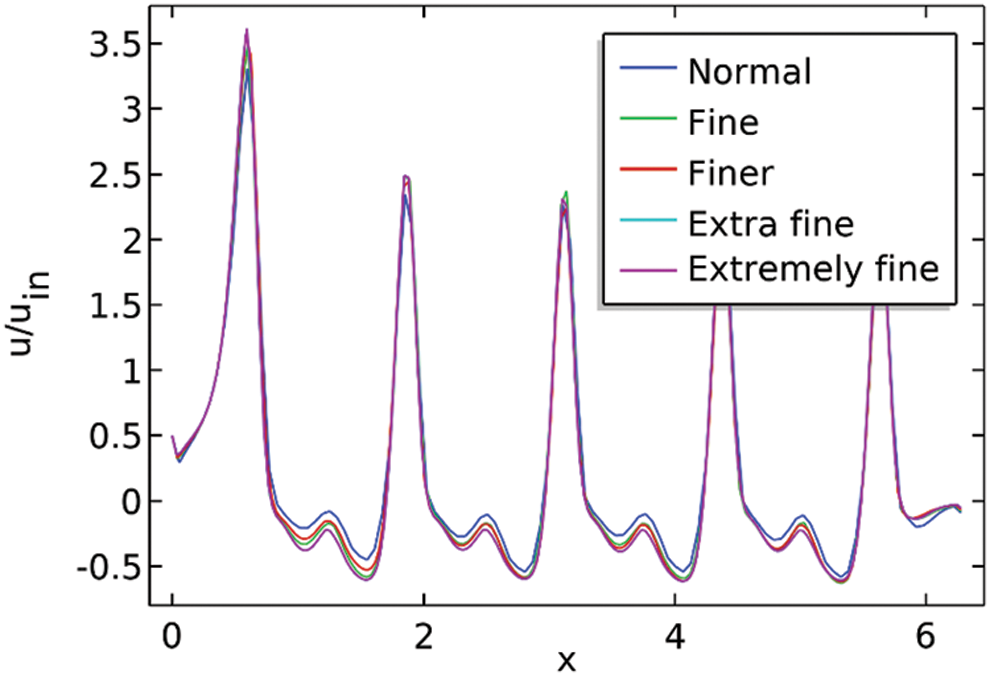
Figure 3: The ratio uuin at the lower boundary against the x-axis for a different number of elements

Statistics for extremely fine mesh as well different other meshes are given by the following Tab. 1.

3.2 Association with Correlation

After doing the mesh independent study, we are adjusting our intention to approve the results for the local Nusselt number downstream of the channel by exploring the correlation available through different pieces of literature. According to the literature, the local Nusselt number for a flat plate in the state of forced convection is provided by the equation correlating the local Reynolds number and Prandtl number [7]. However, our channel of concern is only flat for the period P=0 and gives satisfactory results when contrasted with the Nusselt number given by literature and the present work see Figs. 4a–4c. Furthermore, the results are also adequate when we compare the results for P=3 see Figs. 4d–4f.

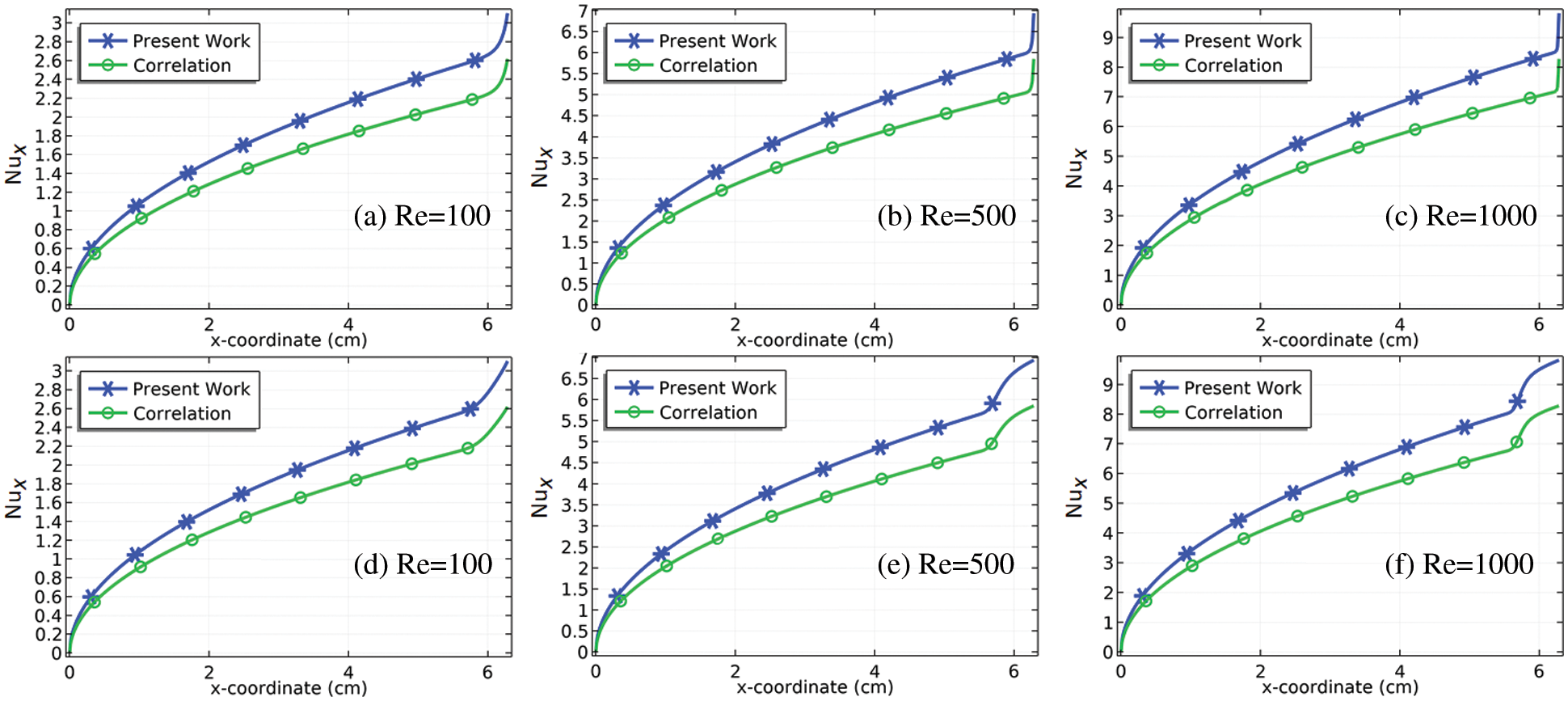
Figure 4: Correlation-based confirmation of the model for the local Nusselt number at the downstream of the channel at P=0 (a)-(c), and P=3 (d)-(f)

4  Results and Discussion

The laminar and Newtonian fluid flow onward with heat transfer was tested with the use of the Reynolds number Re from 100 to 278 K for a wavy channel with arcs whose boundaries are created by using the cosine functions. The boundaries are vibrated with the fixed amplitude of vibration A=0.3 cm and with a different number of periods P=0 to P=5. Designing such types of geometries based on the contraction and expansion regions with equal space of areas. Such type of geometries will create the automatic periodic flows along the channel and will be in favor of increasing velocities and decreasing pressures in the domain. Besides, for the current convection heat transfer problem, we are working to test the heat distribution due to the fluctuation of the boundaries at the exit of the channel. For this purpose, the air as a testing fluid is allowed to enter from the inlet of the domain with the temperature of 278 K, and the outlet of the wavy channel is fixed with the temperature of 323.15 K. The whole simulation was preparing on the finite element based commercial software of COMSOL Multiphysics P. The outcomes are revealed with the surface plots, streamlines, and the contours for the velocity field, pressure, and temperature. The graphs are relocated to show various impacts of the Reynolds number as well as the periods of the vibration P on the velocity field magnitude, pressure, and temperature near the outlet of the channel as well as for the contraction regions in the domain.

4.1 Surface Plots of the Velocity Field with Streamlines and Axial Velocity

The streamlines pattern with the surface plots is dispatched in Fig. 5. For the straight rectangular channel, the flow of particles in the domain remains consistent i.e., there was no increment or declination in fluids velocities. Moreover, there was no formation of vortices in the domain. Next, we check the pattern of the velocity field in the vibrating channel by putting a period of P=1, which produces only one contracted region of the flow. On passing the fluid in the region, the total volume of the fluid is reduced in the region which might increase the flow rate of the particles. With the increase in periods P, the number of contraction regions is increased where the maximum velocity can be deducted. Fluid particles after crossing the contraction region sliding down in the curved cavities where the recirculation will be produced. Due to the recirculation, the speed of the fluid particles reduced and then optimized after reaching the contraction region. In simple words, we would say the maximum velocity magnitude of the flow can be seen in the middle of the channel in terms of periods. Although with enhancing the Reynolds number a chaotic flow can be seen at the middle of the channel for example see for P=5 at Re=500 and 1000. The area of the chaotic region is increased with the increase in Reynolds number. Near the contraction region, the velocity magnitudes are calculated for the P=5 at the particular Reynolds number see Figs. 6a–6c. For P=5 the contraction regions are created from 0.5 to 5.5 cm with intervals of 0.5 cm. It is evident from Figs. 7a–7c, the first contraction region at x=0.5 cm has the normal velocity of the particles. Later, when the flow is passing other regions of the contraction the flow velocity is considerably increasing see Figs. 6b and 6c. It is obvious that for larger the Reynolds number Re the increment in maximum flow velocity magnitude is larger when observing these regions of the contraction.

Figure 5: Streamlines of the velocity field with surface plots for Re=100, Re=500, and Re=1000 (a) P=0 (b) P=3 (c) P=4 (d) P=5 (e) P=6

Figure 6: Speed of the fluid particles near the contraction region (a) Re=100 (b) Re=500, and (c) Re=1000

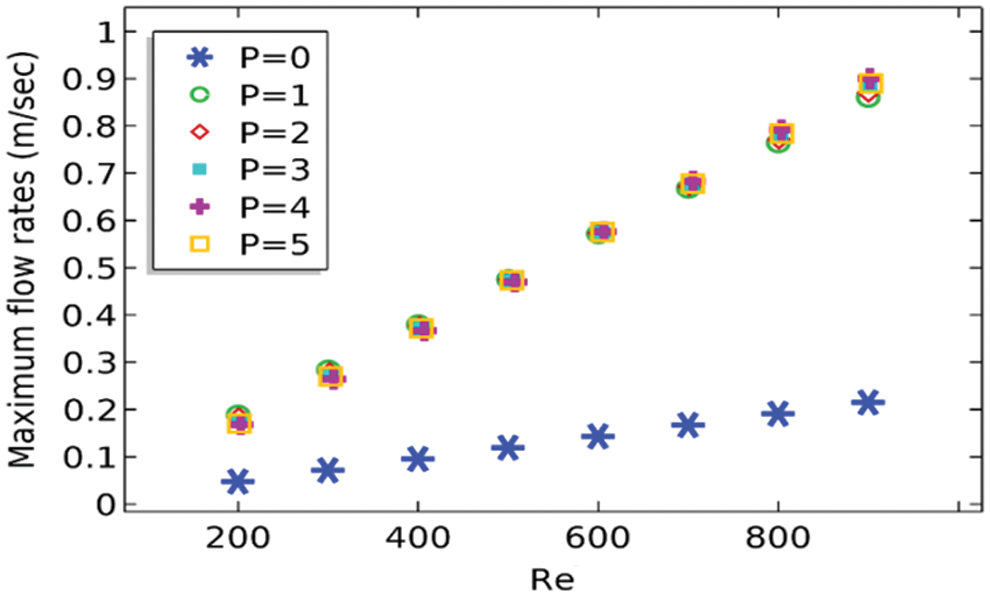
Figure 7: Maximum flow rate at the outlet of the channel against Re

In Fig. 7, the maximum velocity magnitude at the outlet of the channel is calculated against the Reynolds number at different values of the period P of the channel. It is obvious from the graph that constructing a channel with vibration or oscillating boundaries will produce the maximum flow rate at the outlet of the channel. Further, with the increase in Reynolds number, the maximum velocity at the outlet possessed a linear relationship with the Reynolds number. Except for the rectangular channel, all periods of the vibration of the channel are producing unique maximum velocity at the outlet of the channel for the particular Reynolds number.

Applying a linear Regression procedure, we would make the correlation that will connect the maximum velocity at the outlet of the channel in terms of Reynolds number. Following equation is valid for the period of vibration P>0:

Vmax=−0.028423726+0.001027476292Re(11)

Fig. 8 shows the computation of the axial velocity at the outlet of the channel for Re=100 and Re=300 for the period of the vibration. The graph is also produced to see the pattern of the flow at the exit of the channel. The graph can be compared with the pattern of the flow indicated in the literature [23] where the problem of the fluid flow and heat transfer was conducted with the channel consists of two period of vibration. The current problem has been extended for the P=3−P=5. In the current article, we are going to disclose the pattern of the axial velocity component at the outlet of the channel with the increase of periods of the vibration in the channel as well as Reynolds number. Mostly and actually, it is known that the construction of the wavy channel is most important in the applications where the fluid acquires speed automatically due to zig-zag motion. The more vibration given to the upper and lower boundary of the channel fluid gets stronger in terms of speed. Figs. 9a–9c is showing the pattern of the axial velocity at the outlet of the channel. It can be distinguished that due to an increase in the value of P for the same value of Reynolds number, the axial velocity at the outlet of the channel increases significantly. Moreover, it is further predicted that with increasing value of Reynolds number by keeping same value of P the velocity is increasing but for some values of P it is showing different patterns, see Figs. 9a and 9c.

Figure 8: Axial velocity profile at the outlet for the period P=2 of the vibration of the channel and for (a) Re=100 and (b) Re=300

Figure 9: Axial velocity profile at the outlet for the indicated period of vibration of the channel for (a) Re=100 (b) 2.5 and (c) Re=1000

4.2 Pressure

Pressure contours are obtained in Fig. 11 using two different values of the Reynolds number, Re=500 and Re=1000 together with different values of P. The contour presentation intimates that creating such geometry can be used as pressure-reducing pumps. The geometry is created through the special cosine function creating the expansion and the region of contraction due to the vibration of the boundaries. In the contraction region, the minimum pressure can be observed see Figs. 10d–10f. Although with the rise in Reynolds number the pressure at the contracting channel reduced sufficiently. In the expansion region where the small vortices are creating which sustain the pressure to largely minimize.

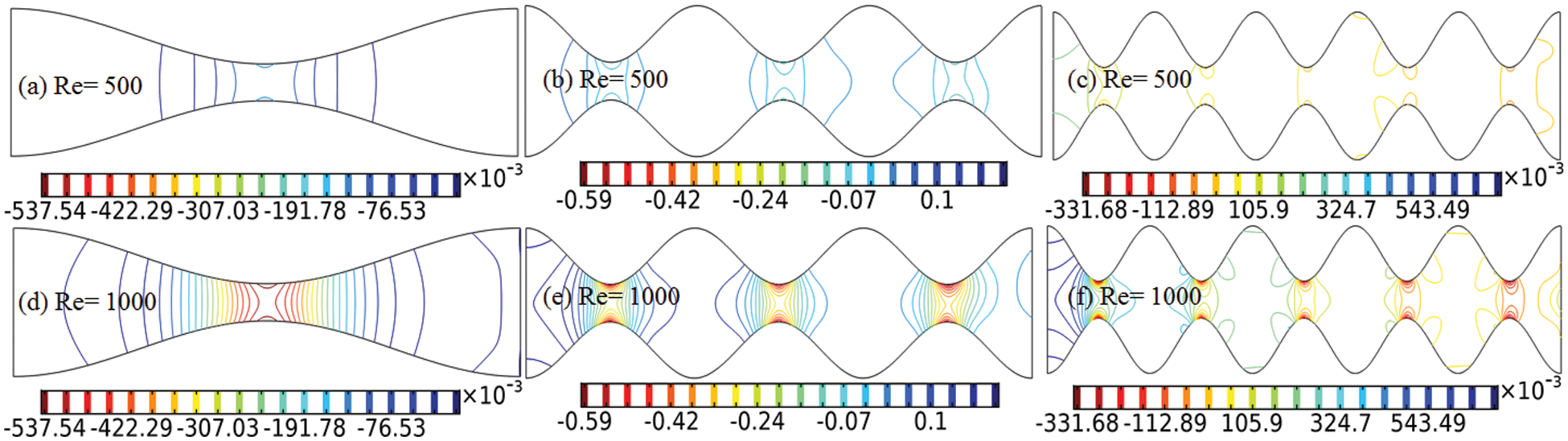
Figure 10: Pressure presentation in the domain with the periods of the vibration P=1 (a and d), P=3 (b and e), and P=5 (c and f)

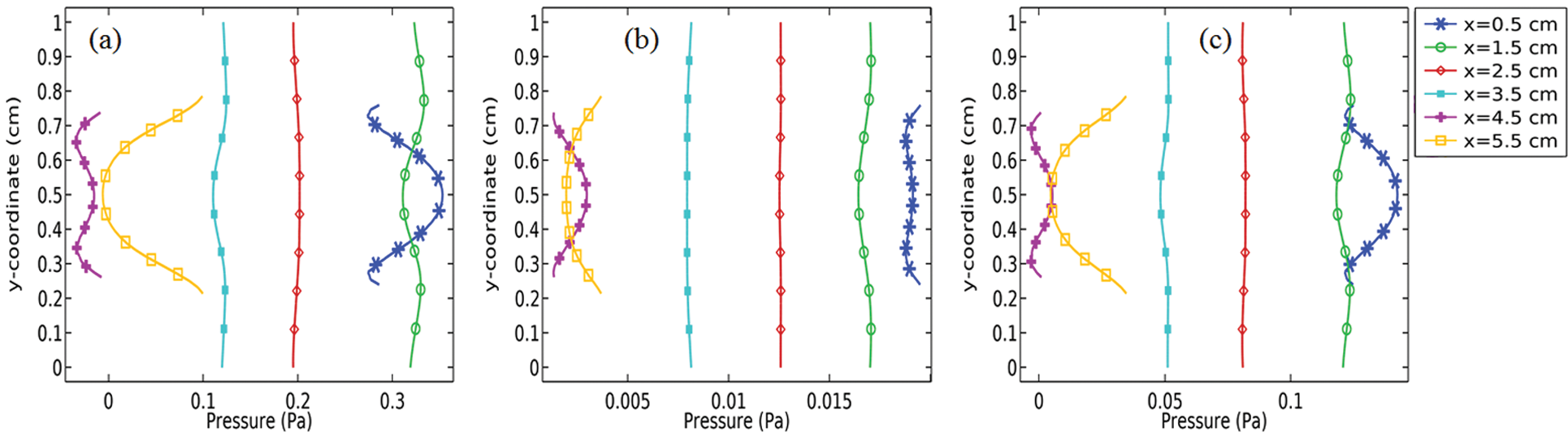
Figure 11: Estimated results of the pressure (Pa) near all contracted regions for P=5 at (a) Re=100 (b) Re=500 and (c) Re=1000

In Figs. 11a–11c, we have bestowed the estimation of dynamic pressure near the contracted regions against the y-axis for a particular Reynolds number with the only observation of periods P=5. It is clear from the graph as we go forward in the domain for the observation of the pressure after each contracted region, we found that the pressure is reducing continuously. With the extension of more periods P of the vibration the pressure further can be subdued. Although, the increase in inlet velocities at the inlet of the channel supports the more loss of the pressure at the contracted regions.

Pressure drop at the outlet of the channel is the function of Reynolds number as well as that of the period of vibration. By increasing the values of P or Re the minimum pressure at the outlet is decreasing in a non-linear way as shown in Fig. 12.

Mostly in the industrial area, the wavy/curvy channels are constructed due to the need of optimum pressure in the region of interest. When the elements of any fluid passing through the contracted region the volumes are reduced which results a significant increase in the pressure. In Figs. 13a–13c to 15a–15c we describe the pressure distribution along the length of the channel. The pattern can be compared with the patterns reported in the references [24] and [25]. It is obvious from Figs. 13a–13c while the fluid came into contact at the contracted regions due to the reduction of volume the pressure increases at the region. The pressure in the channel shows a periodic variation in the channel, see Figs. 15a–15c.

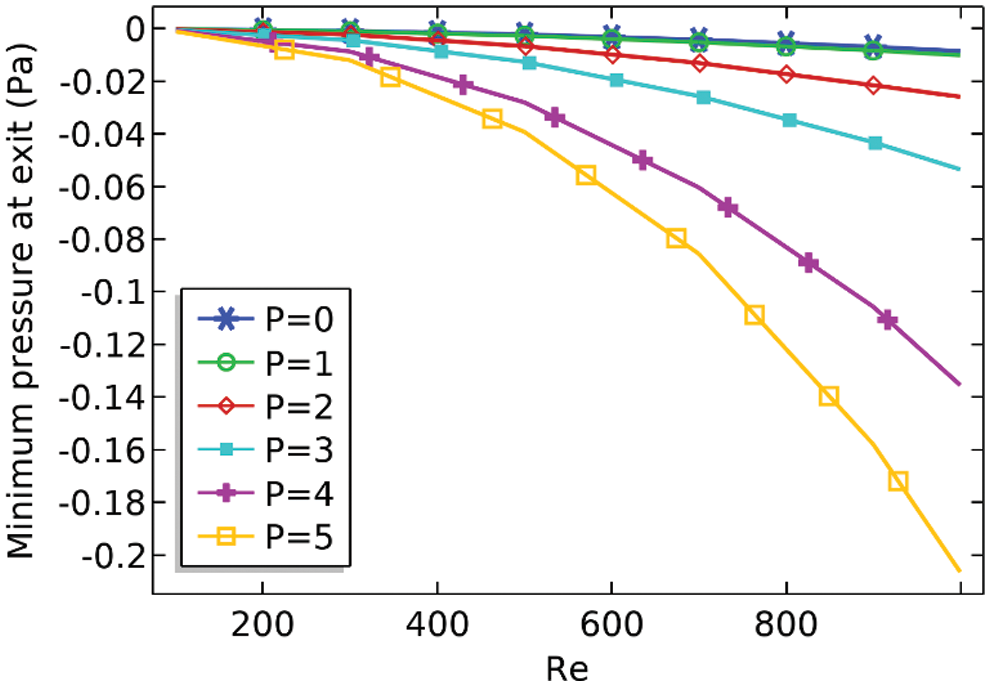
Figure 12: Minimum pressure at the outlet against the Reynolds number

Figure 13: Pressure distribution along the length of the curvy channel with the period P=2 (a) Re=100, (b) Re=500 and (c) Re=1000

Also, with the increase in Reynolds number the range of periodicity increases for example Fig. 14a the range of the amplitude for pressure can be seen at 2.5. While observing Fig. 14c we can see the range of amplitude for the pressure is 60. It is also concluded that due to the increase in the periodic vibration of the boundaries of the channel an insignificant increase in the pressure occurs for moderate Reynolds and a significant increase for high Reynolds number. In our problem, the optimum pressures occur for Re=1000 with vibration periods of P=5. It has been already cleared that and also described in many articles that adding the period of vibration at the boundaries of the channel producing maximum and minimum pressure at a time due to the oscillatory pattern of the pressure. Although the present problem has been simulated with the zero pressure at the inlet of the curvy channel it could be seen that for Re=1000 at P=5, the pressure declines about 600% with an average declination of 500%. Using a curve-fitting procedure we can estimate some sinusoidal regression curves for P=5 which are given below. The curves give a better estimate of where major data points are lying for the pressure related to x-coordinate.

P=0.6867sin(5.0265x+2.2776)−0.2451validforRe=100(12)

P=10.315sin(5.0265x+2.4195)−3.2035validforRe=500(13)

P=36.8324sin(5.0265x+2.5042)−10.3740validforRe=1000(14)

Figure 14: Pressure distribution along the length of the curvy channel with the period P=3 (a) Re=100, (b) Re=500 and (c) Re=1000

Figure 15: Pressure distribution along the length of the curvy channel with the period P=5 (a) Re=100, (b) Re=500 and (c) Re=1000

4.3 The Wall Shear Stress

In the field of fluid dynamics, the wall shear stress can be regarded as the rate at which the velocity inclines while the fluid is moving along the wall. In common, shear stresses are occurring when the elements of fluid acquiring the motion relative to one another. For a simple pipe, zero velocity is assumed at the pipe wall whereas it is increasing while the fluid element is moving towards the center of the pipe. For a non-smooth pipe, the determination of the wall shear stress is essential. Here, we are going to present the graphs for wall shear stress against the length of the pipe see Figs. 16a–16c to 18a–18c. The pattern of the graphs can be matched to the pattern of the graphs reported in [24] where the channel was considered for the two period of vibration and here the problem is being focused on more period of vibration of the channel. From the graphs, it is evident that with the increase in Reynolds number the wall shear stress at the inlet of the channel increases whereas the wall shear stress at the outlet of the channel is zero for all the cases due to the zero pressure condition. The pattern of behavior of the wall shear stress along the length of the channel is not very much clear for the moderate number of periods P=2 and P=3. Even the Reynolds number is changing from lower to higher values to observe the pattern see Figs. 16a–16c and 17a–17c. Whereas the wall shear stress at the contracted region was found maximum in these cases. With the increase in the period of vibration of the walls as shown in Figs. 18a–18c, the wall shear stress is decreasing after each contraction region. For a low Reynolds number Re=100, the wall shear stress shows declination like a step function of the length. For a particular Reynolds number, the wall shear stress is increasing with the increase in periods P of the vibration i.e., compare Fig. 16a with Fig. 17a and 18a.

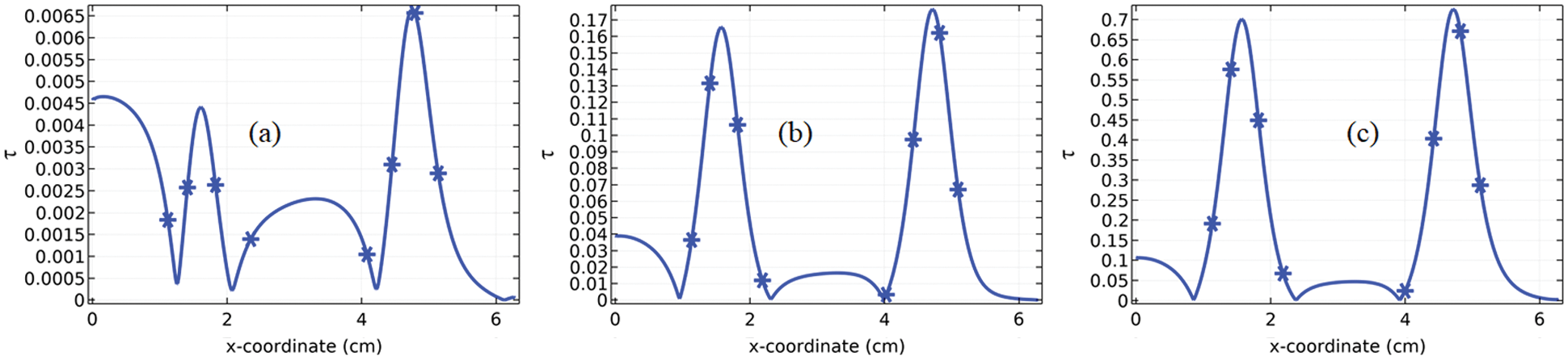
Figure 16: Wall shear stress against the length of channel for P=2 (a) Re=100, (b) Re=500 and (c) Re=1000

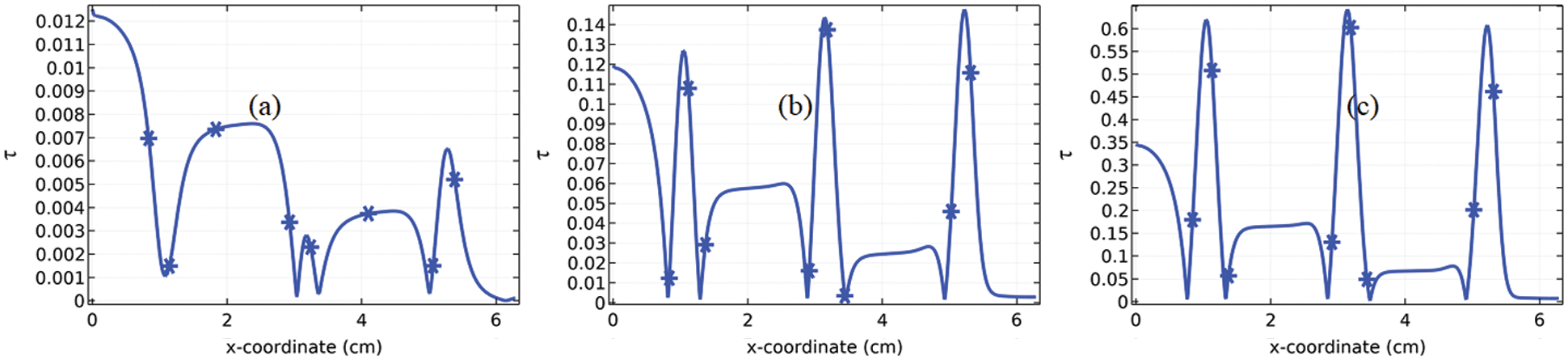
Figure 17: Wall shear stress against the length of channel for P=3 (a) Re=100, (b) Re=500 and (c) Re=1000

Figure 18: Wall shear stress against the length of channel for P=5 and (a) Re=100, (b) Re=500 and (c) Re=1000

4.4 Measurement of Rotating Regions

It is often can be seen in the fluid flow problems which are observed under the presence of the bluff bodies, cavities and might be they can be observed due to the periodic motion of the boundaries of the channel, the fluid often rotates along its axis. The rotational regions becomes clearer when the fluid is observed under the presence of bluff bodies or obstacles rather than without of them. When fluid with any material slides down upstream of the channel, the rotating regions can be observed along the sides of the downstream. The length and intensity of these rotating regions depend upon the velocity of the fluids. The fluid needs some velocity magnitude to form the vortex along with the downstream of the region. While observing the wavy channel in the current problem the rotating regions were observed in Figs. 5d–5f. In Figs. 19a–19f, we are presenting graphs where we are measuring the rotation rate downstream of these rotating regions against the local Reynolds number.

Figure 19: Relationship of rotation rate (s−1) with local Reynolds number for Re=1000 and (a) P=0 (b) P=1 (c) P=2 (d) P=3 (e) P=4 and (f) P=5

Although, there was no rotational region found for the period P=0 f the vibration even we can measure the rotation rate at the end of the wavy channel. From Fig. 1a, we found the maximum rotation per second for a zero period is 30 rotations per second. Whereas the maximum rotation for period P=1 and P=2 of the vibration, we found 50 and 220 rotation per second respectively. These are the cases in which the rotating regions can be observed in the presentation of streamlines. Now look at the cases for P=3 to P=5, in these cases, the rotating regions are obvious for Re=1000 see Figs. 5a–5f. On observing these rotation regions for P=3,4,5 we found the maximum rotation rates per second are 500, 900, and 1500 respectively. One more thing is that the rotation rate of the fluid is very place to place for example we can see Figs. 19d–19f the maximum rotation per second is optimum at expansion regions.

4.5 Temperature

The heat distribution in the channel is investigated by imposing a temperature at the outlet of the channel and the air is allowed to enter the domain with an initial temperature. Our concern is to lessen the temperature near to the outlet of the channel by searching such a Reynolds number and the period of the vibration of the boundaries. The temperature distributions with the surface plots in the channel are presented in Figs. 20a–20l for the particular Reynolds number as well as the Periods of the vibration of the channel. On following Fig. 10 for Re=100 the average temperature near the outlet is increasing with the increase in the period of the vibration of the boundaries. Similar cases can be perceived for the other Reynolds numbers of 500 and 1000 in Fig. 20a–20l. In the contrast, with fixing the periods of the vibration, see Figs. 20a–20c, an increase in the Reynolds number will decrease in the average temperature near the outlet of the channel. A similar pattern of the distribution near the outlet of the channel can be recognized for example Figs. 20d–20l.

Figure 20: Temperature distribution in the channel from cold place to hot place in the periods (a-c) P=0, (d-f) P=2, (g-i) P=4 and (j-l) P=5

Therefore, the graphical presentation (see Fig. 21a) of the average temperature near the outlet of the channel against the Reynolds number is depicted for the particular periods. The graph is showing the same consequences as described above in Figs. 20a–20l. It is also apparent from the graph that the declination of the average temperature persists consistently after Re=300 i.e., there will be no declination of the temperature near the outlet of the channel. The average Nusselt number at the outlet of the channel is estimated for all Reynolds numbers at the particular period of the vibration, see Fig. 21b. It appears from the graph that the convection process near the outlet is growing stronger with the increase in Reynolds number as well as the period of the vibration of the boundaries.

Figure 21: (a) Average temperature against the Reynolds number near the outlet of the channel (b) Average Nusselt number against Reynolds number near the outlet of the channel

5  Conclusion

The present work encountered airflow and temperature distribution through a sinusoidally curved wavy channel of length 2π. Carrying out parametric study by varying Reynolds number in the range from 100 to 1000 and period of vibration from 0 to 5. COMSOL Multiphysic 5.4 was used to solve the nonlinear equations and to simulate the results. A mesh independent study of the finite element method was performed with the use of the different configurations of meshing by computing u/uin at the downstream of the channel. To approve the results, the local Nusselt number at the lower boundary of the channel was compared with the correlation available in the literature. The velocity magnitude, pressure, temperature, maximum velocity, minimum pressure, average temperature at the outlet, and the local Nusselt number at the outlet was estimated in terms of Reynolds number at particular period of vibration of the boundary. This study is important because of its applications in various engineering fields. One such problem is in the study of heat exchangers. A sinusoidally curved wavy channel which satisfies the need of rapid heat transfer is always needed. The results were presented graphically and following conclusions are drawn:

1. Maximum velocity magnitude is found at the contraction regions. At the expansion regions, small recirculating vortices are created which resist the speed of the flow while the fluid is sliding down the region. The maximum velocity magnitude at the outlet is increasing linearly with the increase in Reynolds number but it is very low for P=0.

2. The pressure in the channel is continuously decreasing after passing through contraction regions for all the Reynolds numbers and the period of vibration of the boundaries. It is suggested that using the wavy channel with an equal number of periods can be used as the pressure reducing pump in most engineering applications.

3. The pressure distribution along the length of the channel is having cyclic variation along the channel. Due to cyclic fluctuation in the pressure, it is obvious to find the maximum pressure at the expansion region and minimum pressure at the contraction region. Due to considering the periodic variation, we can obtain a regression equation involving a sinusoidal function that can cover the major points along the length of the channel. In the article, we have recommended some equations for lower, moderate, and high Reynolds numbers.

4. It was also found that for low and moderate Reynolds numbers, the shear stress at the lower wall of the channel shows a periodic variation from inlet to outlet of the channel. Whereas, for high Reynolds number, the wall shear stress at the bottom wall is decreasing after each contraction region. This means the velocity gradient after each contraction region declines than the previous.

5. By measuring the rotation rate in terms of period of vibration of the channel it was seen that for P=0 (straight channel) only some rotation rate was measured near the outlet of the channel. Whereas, for the other periods of P=1 to P=3, maximum rotation rates were deducted at the expansion regions of the channel. Moreover, the rotation rate is increasing with the increase in Reynolds number as well as the period of vibration.

6. A flow of heat from a cold body to a hot body was tested for the wavy channel. It was concluded that the average temperature near the hot body is decreasing for Re<300 and remains constant for 300<Re<1000. Moreover, an increase in the period of vibration of boundaries will increase the average temperature near the outlet of the channel.

Acknowledgment: The authors are highly indebted to anonymous referees for their helpful suggestions and comments which led to improvements of our original manuscript.

Funding Statement: This research was funded by King Mongkut's University of Technology North Bangkok. Contract no. KMUTNB-63-KNOW-20.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  K. L. Kirsch and K. A. Thole, “Heat transfer and pressure loss measurements in additively manufactured wavy microchannels,” Journal of Turbomachinery, vol. 139, no. 1, pp. 011007 (1-92017. [Google Scholar]

 2.  K. L. Kirsch and K. A. Thole, “Pressure loss and heat transfer performance for additively and conventionally manufactured pin fin arrays,” International Journal of Heat and Mass Transfer, vol. 108, pp. 2502–2513, 2017 [Google Scholar]

 3.  K. Stone and S. P. Vanka, “Numerical study of developing flow and heat transfer in a wavy passage,” ASME. Journal of Fluids Engineering. December, vol. 121, no. 4, pp. 713–719, 1999 [Google Scholar]

 4.  G. V. Wang and S. P. Vanka, “Convective heat transfer in periodic wavy passages,” International Journal of Heat and Mass Transfer, vol. 38, no. 17, pp. 3219–3230, 1995 [Google Scholar]

 5.  J. C. F. Chow and K. Soda, “Laminar flow and blood oxygenation in channels with boundary irregularities,” ASME. Journal of Applied Mechanics, vol. 40, no. 4, pp. 843–850, 1973 [Google Scholar]

 6.  J. C. F. Chow and K. Soda, “Blood oxygenation in tubular oxygenators with wavy walls,” Journal of Biomechanics, vol. 9, no. 3, pp. 135–139, 1976 [Google Scholar]

 7.  J. A. R. Howell, W. Field and D. Wu, “Yeast cell microfiltration: Flux enhancement in baffled and pulsatile flow systems,” Journal of Membrane Science, vol. 80, no. 1, pp. 5971, 1993 [Google Scholar]

 8.  P. J. Bezbaruah, R. S. Das and B. K. Sarkar, “Thermo-hydraulic performance augmentation of solar air duct using modified forms of conical vortex generators,” Heat and Mass Transfer, vol. 55, no. 5, pp. 1387–1403, 2019 [Google Scholar]

 9.  T. T. Ngo and N. M. Phu, “Computational fluid dynamics analysis of the heat transfer and pressure drop of solar air heater with conic-curve profile ribs,” Journal of Thermal Analysis and Calorimetry, vol. 139, no. 5, pp. 3235–3246, 2020 [Google Scholar]

10. C. Saidi, F. Legay-Desesquelles and B. Prunet-Foch, “Laminar flow past a sinusoidal cavity,” International Journal of Heat and Mass Transfer, vol. 30, no. 4, pp. 649–661, 1987 [Google Scholar]

11. G. V. Wang and S. P. Vanka, “Convective heat transfer in periodic wavy passages,” International Journal of Heat and Mass Transfer, vol. 38, no. 17, pp. 3219–3230, 1995 [Google Scholar]

12. T. Nishimura, Y. Ohori and Y. Kawamura, “Flow characteristics in a channel with symmetric wavy wall for steady flow,” Journal of Chemical Engineering of Japan, vol. 17, no. 5, pp. 466–471, 1984 [Google Scholar]

13. M. Gradeck, B. Hoareau and M. Lebouché, “Local analysis of heat transfer inside corrugated channel,” International Journal of Heat and Mass Transfer, vol. 48, no. 10, pp. 1909–1915, 2005 [Google Scholar]

14.  Jr, L. Goldstein and E. M. Sparrow, “Heat/mass transfer characteristics for flow in a corrugated wall channel,” ASME. Journal of Heat Transfer, vol. 99, no. 2, pp. 187–195, 1977 [Google Scholar]

15. J. E. O'Brien and E. M. Sparrow, “Corrugated duct heat transfer, pressure drop, and flow visualization,” ASME. Journal of Heat Transfer, vol. 104, no. 3, pp. 410–416, 1982 [Google Scholar]

16. V. K. Garg and P. K. Maji, “Flow and heat transfer in a sinusoidally curved channel,” International Journal of Engineering Fluid Mechanics, vol. 1, no. 3, pp. 293–319, 1988 [Google Scholar]

17. B. Ničeno and E. Nobile, “Numerical analysis of fluid flow and heat transfer in periodic wavy channels,” International Journal of Heat and Fluid Flow, vol. 22, no. 2, pp. 156–167, 2001 [Google Scholar]

18. C. C. Chang, “A combined active/passive scheme for enhancing the mixing efficiency of microfluidic devices,” Chemical Engineering Science, vol. 63, no. 12, pp. 3081–3087, 2008 [Google Scholar]

19. L. Lin, J. Zhao, G. Lu, X. D. Wang and W. M. Yan, “Heat transfer enhancement in microchannel heat sink by wavy channel with changing wavelength/amplitude,” International Journal of Thermal Sciences, vol. 118, pp. 423–434, 2017 [Google Scholar]

20. H. S. Shing and H. Y. Cheng, “Passive mixing in micro-channels with geometric variations through μPIV and μLIF measurements,” Journal of Micromechanics and Microengineering, vol. 18, no. 6, pp. 065017, 2008 [Google Scholar]

21. N. A. Quddus, S. Bhattacharjee and M. Walied, “Electrokinetic flow in a wavy channel,” in 2005 Int. Conf. on MEMS, NANO and Smart Systems, Banff, AB, Canada, IEEE, pp. 219–220, 2005. [Google Scholar]

22. X. Zheng, M. Renwei, S. Mark and Z. H. Fan, “Electroosmotically driven creeping flows in a wavy microchannel,” Microfluidics and Nanofluidics, vol. 6, no. 1, pp. 37–52, 2009. [Google Scholar]

23. J. Farooq, M. Mushtaq, S. Munir, M. Ramzan, J. D. Chung et al., “Slip flow through a non-uniform channel under the influence of transverse magnetic field,” Scientific Reports, vol. 8, no. 1, pp. 1–14, 2018. [Google Scholar]

24. M. Ramzan, H. Gul, M. Y. Malik, D. Baleanu and K. S. Nisar, “On hybrid nanofluid yamada-ota and Xue flow models in a rotating channel with modified Fourier law,” Scientific Reports, vol. 11, no. 1, pp. 1–19, 2021 [Google Scholar]

25. M. Suleman, M. Ramzan, S. Ahmad, D. Lu, M. Taseer et al., “A numerical simulation of silver–water nanofluid flow with impacts of newtonian heating and homogeneous–heterogeneous reactions past a nonlinear stretched cylinder.” Symmetry, vol. 11, no. 2, pp. 295, 2019 [Google Scholar]

26. Adnan, U. Khan, N. Ahmed, S. T. Mohyud-Din, I. Khan et al., “Al2O3 and gamma Al2O3 nanomaterials based nanofluid models with surface diffusion: Applications for thermal performance in multiple engineering systems and industries.” Computers, Materials & Continua, vol. 66, no. 2, pp. 1563–1576, 2021 [Google Scholar]

27. N. Saima, S. Waheed, A. Hussanan and D. Lu, “Analytical solution for heat transfer in electroosmotic flow of a carreau fluid in a wavy microchannel,” Applied Sciences, vol. 9, no. 20, pp. 4359, 2019 [Google Scholar]

28. D. Tripathi, S. Bhushan and O. A. Bég, “Unsteady viscous flow driven by the combined effects of peristalsis and electro-osmosis,” Alexandria Engineering Journal, vol. 57, no. 3, pp. 1349–1359, 2018 [Google Scholar]

29. D. Tripathi, S. Bhushan and O. A. Bég, “Analytical study of electro-osmosis modulated capillary peristaltic hemodynamics,” Journal of Mechanics in Medicine and Biology, vol. 17, no. 3, pp. 1750052, 2017 [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.