DOI:10.32604/cmc.2022.024044

| Computers, Materials & Continua DOI:10.32604/cmc.2022.024044 |  |
| Article |
Efficient Data Compression of ECG Signal Based on Modified Discrete Cosine Transform
1Electronics and Communications Engineering Department, Faculty of Engineering, Sinai University, Arish, CO 45511, Egypt
2Department of Electrical Engineering, College of Engineering, Taif University, Taif, 21944, Saudi Arabia
3Faculty of Technology and Education, Suez University, Suez, 43527, Egypt
4Electronics and Communications Engineering Department, Faculty of Engineering, MSA University, CO 12585, Egypt
*Corresponding Author: Sherif S. M. Ghoneim. Email: s.ghoneim@tu.edu.sa
Received: 01 October 2021; Accepted: 02 November 2021
Abstract: This paper introduced an efficient compression technique that uses the compressive sensing (CS) method to obtain and recover sparse electrocardiography (ECG) signals. The recovery of the signal can be achieved by using sampling rates lower than the Nyquist frequency. A novel analysis was proposed in this paper. To apply CS on ECG signal, the first step is to generate a sparse signal, which can be obtained using Modified Discrete Cosine Transform (MDCT) on the given ECG signal. This transformation is a promising key for other transformations used in this search domain and can be considered as the main contribution of this paper. A small number of wavelet components can describe the ECG signal as related work to obtain a sparse ECG signal. A sensing technique for ECG signal compression, which is a novel area of research, is proposed. ECG signals are introduced randomly between any successive beats of the heart. MIT-BIH database can be represented as the experimental database in this domain of research. The MIT-BIH database consists of various ECG signals involving a patient and standard ECG signals. MATLAB can be considered as the simulation tool used in this work. The proposed method's uniqueness was inspired by the compression ratio (CR) and achieved by MDCT. The performance measurement of the recovered signal was done by calculating the percentage root mean difference (PRD), mean square error (MSE), and peak signal to noise ratio (PSNR) besides the calculation of CR. Finally, the simulation results indicated that this work is one of the most important works in ECG signal compression.
Keywords: Compressive sensing; sparse; beats of hearts; compression ratio; percentage root mean difference
The conventional method of recovering signals from measured information is based on the well-known Shannon inspecting hypothesis, which states that the number of samples per second must be twice the highest frequency [1]. The hypothesis of CS recommends that the small number of samples per second supports an improved strategy for a high sampling frequency of utilizing the earlier sparse signal. The desired signal is recreated [2,3]. CS strategy significantly transforms the signal into a low dimensional estimation space, in which the number of samples is fewer than the Nyquist rate. It is also known as compressive sensing [4,5]. The rising hypothesis of CS that blends computerized information acquisition with advanced information compression is used to create a novel era of signal recovery frameworks, which work at a signal's natural data rate that is superior to its encompassing information rate [6]. The current work aims to utilize a CS strategy directed toward ECG signal compression [7]. ECG can be considered a robust framework in biomedical designing, because heart infection causes mortality globally [8]. The ECG provides data around the heart and could be one of the foremost organic signals whose physiological and measurable feature can be modified against time [9]. In an overview of such signals, Wavelet Transform (WT) is an essential transform in this search domain [10]. WT has a wide application, including the signaling and code of the picture. The quick usage of WT can be performed by utilizing the sub-band (SB) filter banks [11]. Candes et al. introduced a new transform named curvelet transform, which is created using ridgelet transform [12].
The ECG signal is illustrated in Fig. 1. It comprises P, Q, R, S, T, and U waves. A calculation is created to disengage the ECG properties naturally. The completed analysis starts by breaking down the initial ECG signal by using DWT as the mother wavelet. Then, it begins by canceling low and high-frequency components. At that point, it utilizes the preprocessed signal to naturally obtain properties from the ECG signal [13]. Critical research works are given to the discovery of strategies that involve slope threshold strategies [14], digital filtering methods [15], and Shannon energy envelope methods [16]. Moreover, others consider the utilization of the WT to cancel ECG noise signal as an efficient transformation [17]. The ECG signal within the latter is gathered from the database of MIT/BIH utilizing the database of Physionet, and it can be organized in a content arrangement [18]. Others use the fast wavelet transform to support sparse ECG noise signal as an efficient transformation [19]. Medical professionals can make the transmission of ECG signals an indispensable and essential part of the whole procedure [20]. Asgari et al. introduced a stationary wavelet transform and provide a vector machine combination to obtain Atrial Fibrillation [21]. The drawbacks of the literature are their inefficient in representing the sparse signal. These lead to great gaps between proposed work and literature concerning the calculated CR and PRD. The proposed research paper achieved good results compared with the literature by enhancing the sparse ECG signal. This can be considered a novel idea in this domain of search.
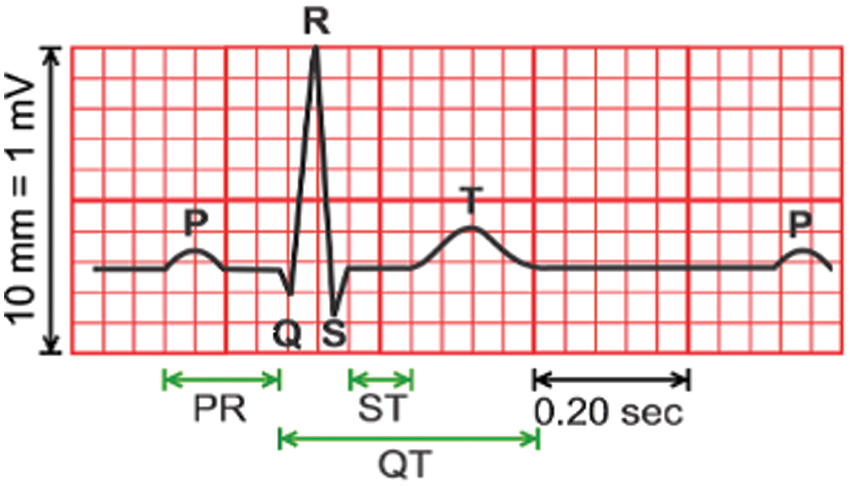
Figure 1: Typical ECG signal [8]
The paper is organized as follows. Section 2 introduces the foundation and inspiration concerning CS technique. Section 3 clarifies the previous works and counts the main later methods in this look zone. Section 4 portrays the arrangement of ECG signal for the normal person. Section 5 illustrates patterns and problems for obtaining an inadequate signal of ECG. Section 6 clarifies this work and its examination. Section 7 depicts the execution degree to approve the method utilized in this investigation. Section 8 covers the test results with explanations. Section 9 presents the conclusions derived from this proposed work.
This section introduced CS by explaining the sparsity of signal and the mathematical model of CS.
Compressed sensing could be a novel inquiry about range, which was presented in 2006. It became a key concept in different zones, thereby connecting science, computer science, and electrical building [22]. A discrete-time signal X is assumed to occur in Rn. This signal can be expressed in terms of an orthonormal basis of N × 1 vectors,
where ψ is the component sequence of X. Alternatively, Eq. (1) can be expressed in the form of a matrix. The signal has a K-sparse expansion, if K entries in S are non-zero, and (N-K) entries are zero.
2.2 The Approach of the Compressed Sensing
To test all the N components of X, we assume that M×1 (M˂N) column inner products y are between x and vectors
By substituting X given in Eq. (1), the following equation is obtained:
where
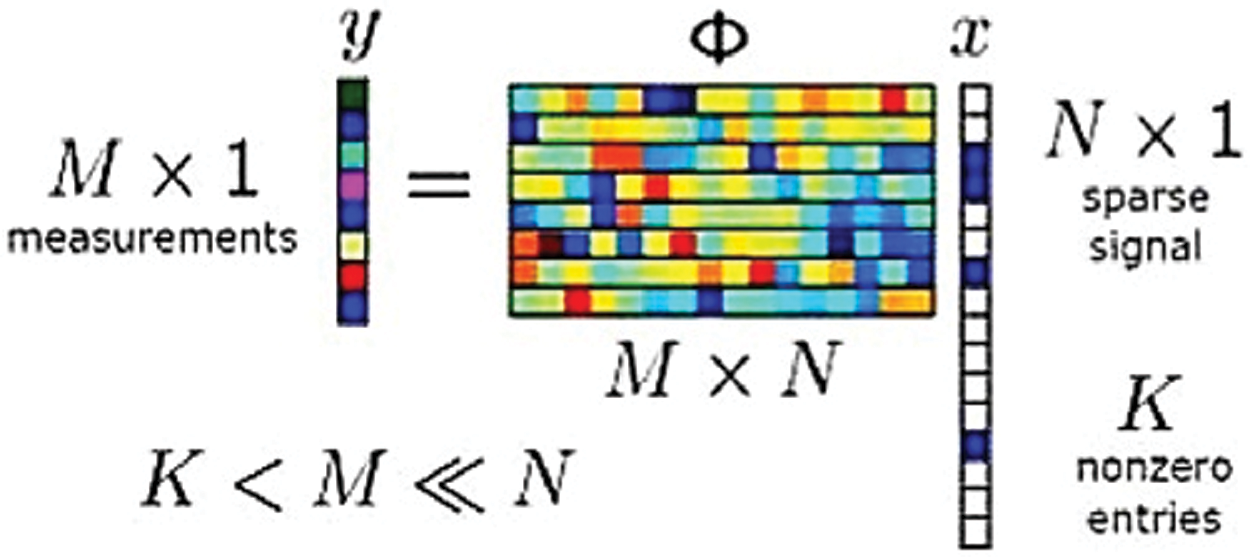
Figure 2: Compressed sensing test approach [1]
The lossless compression calculation to compress electrocardiogram (ECG) signal is a productive calculation. This calculation has more memory necessities and depends on a basic and effective encoding conspire, which can be actualized with basic checking operations. Hence, it can be effectively executed in asset obliged microcontrollers, as those are commonly utilized in a few low-cost ECG observing frameworks [23]. Another method presents the lossless ECG compression strategy. With the lossy methods, a few tests are trimmed off from the initial signal. Depending on the sort of lossy strategy utilized, the information dispensed with may or may not be recognizable to the client. A few lossy compression strategies have been detailed within the writing. These lossy compression strategies are emphatically included in lossless compression strategies due to potential twisting hazards [24]. Another strategy is presented as previous work. This technique is based firstly on information extraction. Then, an inspecting method based on a client characterized limit esteem is connected on ECG taken after by Truncated Particular Esteem Deterioration. Changing the number of Particular Values of higher compression can be accomplished. The proposed method gives two factors, namely, Edge and Number of Solitary Esteem, which can be changed to attain ideal compression while keeping the error low [25]. Another strategy was presented as related work. This procedure is based on highlights in compressing ECG signals that use an exceptionally constrained number of include bases [26].
The ECG wave, which consists of P wave, QRS complex, and T wave, is illustrated in Fig. 1. These waves can be produced by the depolarization and repolarization of atria and ventricles [27,28]. A few typical values for adequacy and length of ECG features are illustrated in Tabs. 1 and 2.


The determination of reasonable transforms to obtain sparse ECG signal is the foremost problem in this research paper. This sparse signal is valuable in using the CS method and in ensuring the remaking of the desired signal. Their excellent execution decides the reasonable transformation in this look zone to reproduce the initial signal. Here, the presented transform is an MDCT that provides a great result. This transform is the administrator transform in obtaining the sparse ECG signal through investigation.
This section demonstrates the proposed technique, which is then investigated to determine how efficient ECG signal is obtained.
Fig. 3 illustrates the proposed calculation that can be utilized for the compression of ECG signal and reconstruction. This figure demonstrates four compression and three reconstruction steps. Compression can be done through the first step by converting the ECG signal into a sparse signal by utilizing MDCT. The second step is applying the proposed CS method to the obtained sparse signal. The third step is the use of the quantization process on the sampled values obtained from the signal. The last step is encoding the values of the signal after being quantized. Fig. 3 also illustrates the reconstruction step. In the first reconstruction step, a decoding algorithm is applied to the signal after compression. The second step is dequantizing the signal to get the sparse signal. The third step is applying Inverse Modified Discrete Cosine Transform (IMDCT) to the sparse signal. The obtained signal in the last step is the recovered ECG signal. The following section demonstrates the influence of presenting MDCT to obtain the sparse signal. It is the main objective of this paper.
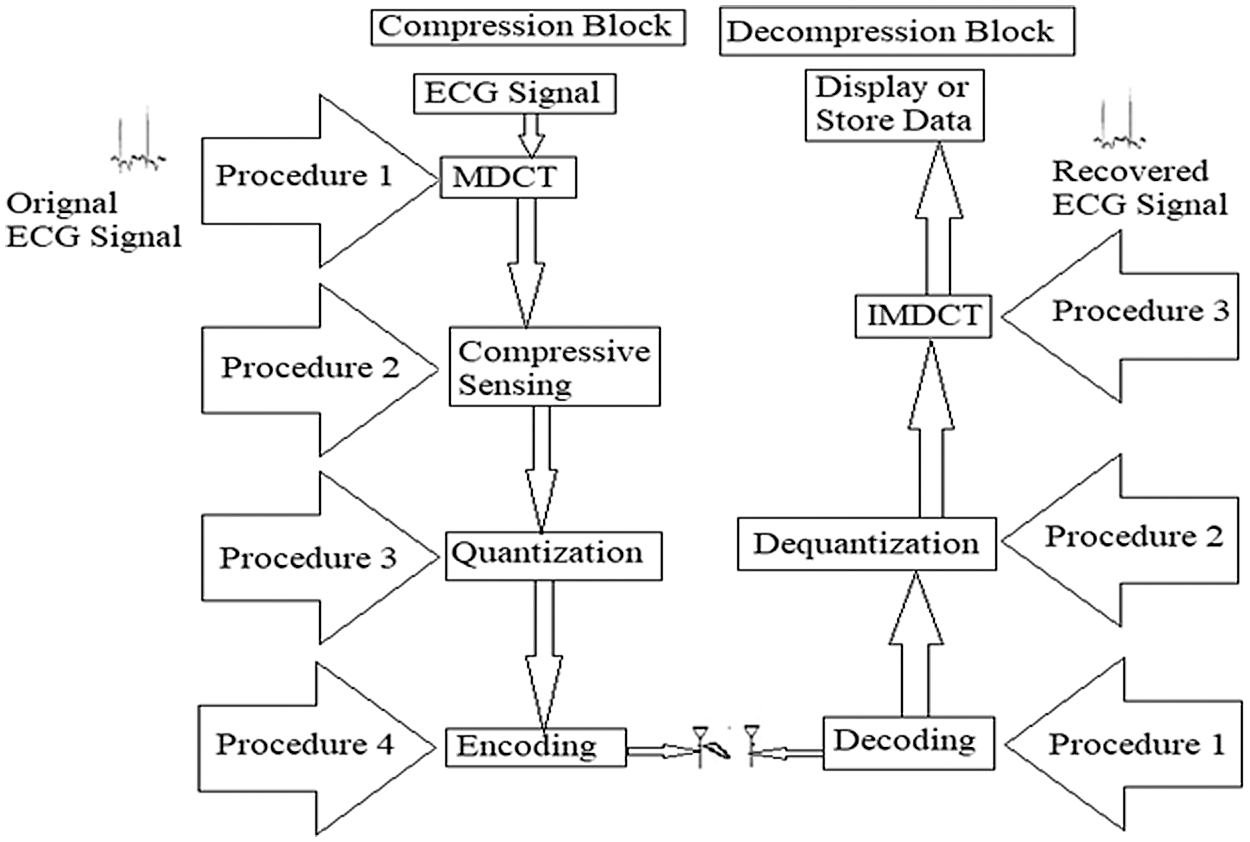
Figure 3: Block diagram of the proposed technique
6.2 The Significance of the Proposed Method
The proposed method is the most efficient approach for the compression of ECG signals. The significance of this strategy is the fact that the DCT gives more weight to low-pass coefficients than to high-pass coefficients, which helps in the easy compression of ECG signal. The corresponding formula illustrates the abovementioned statement and is described in the given equation:
6.3 Analysis of the Proposed Transformation to Obtain Sparse ECG Signal
The Discrete Cosine Transform (DCT) may be a Fourier-related change that is generally twice the length; it works on genuine information with symmetry. Modified Discrete Cosine Transform (MDCT) could be a direct orthogonal lapped change based on the thought of Time Domain Aliasing Cancellation (TDAC); it is outlined to be performed on sequential pieces of a bigger dataset. MDCT is inspected, which implies that although it is 50% covered, a piece of grouping information after MDCT has the same number of coefficients as tests, which sometimes recently change. When consequent squares of conversely changed information are included, the change's blunders cancel out TDAC. The MDCT is characterized as follows:
where x(n), n = 0, 1, 2, …, N−1 is the sequence to be transformed, N = 2M is the window length, and M is the number of transform coefficients. The computation burden can be simplified and rewritten in the following equation:
where
and
The inverse MDCT is the IMDCT. Diverse inputs and yields are present. Thus, it might appear that the MDCT ought not to be invertible to begin with look. Idealized invertibility is accomplished by including the covered IMDCTs of ensuing covering pieces, thereby leading to the cancellation of mistakes and the recovery of the initial information. The IMDCT transforms the M real coefficients, XC (0), XC (1), …, XC (M-1), into N = 2M real numbers, x(0), x(1), …, x(N-1), according to the formula:
Again, Eq. (5) can be rewritten in the following equation:
where
and
DCTs and Discrete Sine Transforms (DSTs) are the best classifications of sinusoidal unitary transforms.
Let {x(n);n = 0, 1, 2,…, N} be a vector of real numbers. The definition of four known kinds of DCT is expressed as follows:
DCT-I-E
where
DCT-II-E
where
DCT-III-E
where
DCT-IV-E
A Modified DCT
where
Essential parameters that are considered to measure the performance of compressed signal are compression ratio (CR), percentage root mean difference (PRD), peak signal-to-noise ratio (PSNR), and mean square error (MSE). These parameters will be utilized as execution degrees to approve this work and decide its strength in its look zone. Therefore, these parameters are talked about briefly in this section.
The compression ratio (CR) is one of the most vital parameters that express the performance test for compression of the signal. It can be characterized as the data rate ratio that speaks to the initial signal to the data rate needed to spare the compressed signal. Therefore, all compression calculations can minimize information capacity by killing the excess on the off chance that accesses. This concept makes a difference in expanding the Compression Ratio [29].
7.2 Percent Root Mean Difference
The PRD introduces a sign of the contrast between the initial ECG signal and the recuperated signal. This basic is used for showing the mutilations in recouping the ECG signal. The PRD has three sorts for ECG data compression [8] that appeared in conditions (22)–(24). Assume that
We apply the moment work that is PRD1 to characterize PRD.
Mean square error (MSE) measures the average of the squares of the errors, that is, the average squared difference between the estimated and actual values. MSE is characterized as follows [30]:
where xn, yn, and N are assumed to be the initial signal, the recovered signal, and the signal's order, respectively.
7.4 Peak Signal to Noise Ratio
Peak signal-to-noise ratio (PSNR) is an engineering term for the ratio between the maximum possible signal's power and the power of noise. PSNR can be characterized as follows [31–33]:
where xpeak is the maximum value of the input data, and
8 Experimental Results and Explanations
The database of MIT-BIH was selected to measure the ECG signal. The computer program was run by utilizing the MATLAB tool. Numerous analysts have presented distinctive compression calculations for ECG signals. In this investigation, an assessment of information compression calculations uses the most known parameters in this search area, namely, CR, PRD, MSE, and PSNR. The sampling rate was chosen to be 1 kHz. Simulations are performed for different records of ECG signals. Fig. 4 shows the original ECG signal and the sparse signal generated from the proposed approach and various other methods. Figs. 5 and 6 illustrate the desired ECG and reconstructed signals for typical people after utilizing the proposed strategy on the four latest methods within The space of rummage around diverse registered data. Figs. 7 and 8 illustrate the desired ECG and reconstructed signals for persistent people. Figs. 9 and 10 demonstrate the compression ratio against the number of ordinary and persistent people tests individually for diverse works. Figs. 11 and 12 show the PRD against the number of tests of ordinary and understanding people individually for various techniques. The results are compared with the execution of the past compression calculations to gauge the calculation execution precisely. These comparisons are outlined in Tabs. 3 to 6 for ordinary and quiet people separately to determine under what limits this work procedure accomplishes a great result. The results in these Tabs. are taken for several tests (break even to 1000). Test results show that the MDCT presents a fantastic representation for smooth ECG signal and has high accuracy.

Figure 4: The sparse signal generated from different works

Figure 5: Initial signal and reconstructed signal for normal persons at record 100
CS-based ECG compression achieved an excellent result concerning its DWT approach, and Figs. 5–8 addressed this fact. These figures endorse the prevalence of this strategy calculation. The impacts of expanding the number of CR and PRD tests for typical and persistent people are outlined in another figure.
The results are obtained for typical and persistent people. The simulation results cover different cases to give more declaration of the priority of the proposed technique.
The analysts put CR as a challenging issue that is coordinated with the best performance. The simulation results demonstrate that CR within the proposed strategy accomplishes amazing results. Figs. 9 and 10 illustrate this fact.

Figure 6: Initial signal and reconstructed signal for normal persons at record 105
Fig. 11 illustrates that this strategy has a PRD with accepTab.values. Moreover, the PRD values of this work for the distinctive number of tests are superior to the four latest procedures within the same look zone.
Figs. 11 and 12 show that this work is appropriate for realizing the minimum distortion between the initial and recovered signals. Moreover, they indicate that this work is vigorous in its look zone.

Figure 7: Initial signal and reconstructed signal for abnormal persons at record 425
Tabs. 3 to 6 show that the proposed technique is efficient in many points. First, this technique achieved a better CR compared with the previous approaches, because it needs fewer coefficients to represent the sparse signal. MDCT is characterized by using fewer coefficients to represent the signal. Second, the proposed approach has an efficient PRD value compared with the previous techniques. Applying MDCT to the signal results in nearly optimal performance of the typical signal with high correlations with the adjacent samples. Third, the proposed approach has excellent MSE due to the faster convergence rate achieved by using MDCT. Fourth, the proposed approach has good PSNR due to better noise cancellation, which can be achieved by applying MDCT to a given signal.

Figure 8: Initial signal and reconstructed signal for abnormal persons at record 605

Figure 9: CR vs. the number of samples for normal persons at (a) Record 100 and (b) Record 105

Figure 10: CR vs. the number of samples for patient persons at (a) Record 420 and (b) Record 425

Figure 11: PRD vs. the number of samples for normal persons at (a) Record 100 (b) Record 105

Figure 12: PRD vs. the number of samples for patient persons at (a) Record 420 (b) Record 425




A recent approach used for upgrading the sparse signal of ECG is introduced. CS may be a valuable device for disposing wasteful aspects that result from trivial signal preparing calculations. Simulation results illustrate that the MDCT compression method has the best performance in the related works introduced in this paper. This performance is measured in terms of CR, PRD, PSNR, and MSE. The proposed calculations have the highest CR and the lowest PRD compared with the previous works. The increase in CR and reduction in the values of PRD are considered a great contribution in this paper. Moreover, MSE and PSNR are reduced also when using the proposed approach. These results are valid for both normal and patient persons. CS shows that compression coefficients can utilize a set of association weights extricated from a prepared Spiking Neural Arrange. This idea is a recommended topic for future works.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. M. Abo-Zahhad, A. I. Hussein and A. M. Mohamed, “Compressive sensing algorithms for signal processing applications: A survey,” International Journal of Communications, Network and System Sciences, vol. 8, no. 5, pp. 197–216, 2015. [Google Scholar]
2. Y. Wang, Z. Yang, J. Zhang, F. Li, H. Wen et al., “CS2-collector: A new approach for data collection in wireless sensor networks based on two-dimensional compressive sensing,” Sensors (Switzerland), vol. 16, no. 8, pp. 1–16, 2016. [Google Scholar]
3. M. B. Hawes and W. Liu, “Compressive sensing-based approach to the design of linear robust sparse antenna arrays with physical size constraint,” IET Microwaves Antennas and Propagation, vol. 8, no. 10, pp. 736–746, 2014. [Google Scholar]
4. A. Mohamed, W. Elnahel and H. M. Zakaria, “VLSI architecture for optimization transform technique based on compression of ECG signals,” International Journal of Computer Applications, vol. 181, no. 48, pp. 54–62, 2019. [Google Scholar]
5. J. C. Barrera, J. L. Ginori and E. R. Valdivia, “A wavelet-packets based algorithm for EEG signal compression,” Medical Informatics and the Internet in Medicine, vol. 29, no. 1, pp. 15–27, 2004. [Google Scholar]
6. M. F. Duarte and R. G. Baraniuk, “Spectral compressive sensing,” Applied and Computation Harmonic Analysis, vol. 35, no. 1, pp. 111–129, 2013. [Google Scholar]
7. S. Qaisar, R. M. Bilal, W. Iqbal, M. Naureen and S. Lee, “Compressive sensing: From theory to applications, a survey,” Journal of Communications and Networks, vol. 15, no. 5, pp. 443–456, 2013. [Google Scholar]
8. M. M. Abo-Zahhad, A. I. Hussein and A. M. Mohamed, “Compression of ECG signal based on compressive sensing and the extraction of significant features,” International Journal of Communications, Network and System Sciences, vol. 8, no. 5, pp. 97–117, 2015. [Google Scholar]
9. H. Fathy, A. Mohamed, E. Mohamed and W. Anis, “Enhancement of ECG signal,” International Journal of Computer Applications, vol. 145, no. 7, pp. 12–16, 2016. [Google Scholar]
10. G. M. Mutanov, J. D. Mamykova and I. Development, 
 ,” Computer Science, vol. 2, no. 94, pp. 46–58, 2017. [Google Scholar]
,” Computer Science, vol. 2, no. 94, pp. 46–58, 2017. [Google Scholar]
11. F. Chen, A. P. Chandrakasan and V. M. Stojanoviæ, “Design and analysis of a hardware-efficient compressed sensing architecture for data compression in wireless sensors,” IEEE Journal of Solid-State Circuits, vol. 47, no. 3, pp. 744–756, 2012. [Google Scholar]
12. S. E. Jero, P. Ramu and S. Ramakrishnan, “ECG steganography using curvelet transform,” Biomedical Signal Processing and Control, vol. 22, pp. 161–169, 2015. [Google Scholar]
13. L. Maršánová, A. Němcová, R. Smíšek, M. Vítek and L. Smital, “Advanced P wave detection in Ecg signals during pathology: Evaluation in different arrhythmia contexts,” Scientific Reports, vol. 9, no. 1, pp. 1–11, 2019. [Google Scholar]
14. F. Sufi, Q. Fang and I. Cosic, “ECG R-R peak detection on mobile phones,” Annual Int. Conf. IEEE Engineering Medical Biology-Proc, Lyon, France, pp. 3697–3700, 2007. [Google Scholar]
15. P. Phukpattaranont, “QRS detection algorithm based on the quadratic filter,” Expert Systems with Applications, vol. 42, no. 11, pp. 4867–4877, 2015. [Google Scholar]
16. H. Beyramienanlou and N. Lotfivand, “Shannon's energy based algorithm in ECG signal processing,” Computational and Mathematical Methods in Medicine, vol. 2017, no. 5, pp. 1–16, 2017. [Google Scholar]
17. H. Y. Lin, S. Y. Liang, Y. L. Ho, Y. H. Lin and H. P. Ma, “Discrete-wavelet-transform-based noise removal and feature extraction for ECG signals,” Irbm, vol. 35, no. 6, pp. 351–361, 2014. [Google Scholar]
18. M. Abo-Zahhad, S. M. Ahmed and A. Zakaria, “An efficient technique for compressing ECG signals using QRS detection, estimation, and 2D DWT coefficients thresholding,” Modelling and Simulation in Engineering, vol. 2012, 2012. [Google Scholar]
19. L. R. Neira, “Effective high compression of ECG signals at low level distortion,” Scientific Reports, vol. 9, no. 4564, pp. 1–12, 2019. [Google Scholar]
20. L. Zheng, Z. Wang, J. Liang, S. Luo and S. Tian, “Effective compression and classification of ECG arrhythmia by singular value decomposition,” Biomedical Engineering Advances, vol. 2, pp. 1–8, 2021. [Google Scholar]
21. R. Cervigón, B. Ginley, D. Craven, M. Glavin and E. Jones, “The effects of compression on the detection of atrial fibrillation in ECG signals,” Applied Sciences, vol. 11, no. 5908, pp. 1–13, 2021. [Google Scholar]
22. Y. C. Eldar and G. Kutyniok, “Compressed sensing: Theory and applications,” UK: Cambridge University Press, pp. 1–544, 2012. [Google Scholar]
23. G. Campobello, A. Segreto, S. Zanafi and S. Serrano, “An efficient lossless compression algorithm for electrocardiogram signals,” European Signal Processing Conference, vol. 2018, no. 5, pp. 777–781, 2018. [Google Scholar]
24. M. Elgendi, A. Mohamed and R. Ward, “Efficient ECG compression and QRS detection for E-health applications,” Scientific Reports, vol. 7, no. 1, pp. 1–16, 2017. [Google Scholar]
25. S. S. Kabir, M. N. Rizve and M. K. Hasan, “ECG signal compression using data extraction and truncated singular value decomposition,” 5th IEEE Region 10 Humanitarian Technology Conference 2017, R10-HTC 2017, vol. 2018-January, pp. 5–7, 2018. [Google Scholar]
26. H. Huang, S. Hu and Y. Sun, “Energy-efficient ECG signal compression for user data input in cyber-physical systems by leveraging empirical mode decomposition,” ACM Transactions on Cyber-Physical Systems, vol. 3, no. 4, pp. 256–268, 2019. [Google Scholar]
27. B. Salsekar and A. Wadhwani, “Filtering of Ecg signal using butterworth filter and its feature extraction,” International Journal of Engineering Science and Technology, vol. 4, no. 4, pp. 1292–1298, 2012. [Google Scholar]
28. D. Gurve, D. D. Rodriguez, T. B. Filho and S. Krishnan, “Trends in compressive sensing for EEG signal processing applications,” Sensors (Switzerland), vol. 20, no. 13, pp. 1–21, 2020. [Google Scholar]
29. K. Qureshi and V. Patel, “Efficient data compression of Ecg signal using discrete wavelet transform,” International Journal of Research in Engineering and Technology, vol. 2, no. 4, pp. 696–699, 2013. [Google Scholar]
30. S. Bensegueni and A. Bennia, “ECG signal compression using a sinusoidal transformation of principal components,” International Journal of Software Engineering and its Applications, vol. 10, no. 1, pp. 59–68, 2016. [Google Scholar]
31. A. Mishra, F. Thakkar, C. Modi and R. Kher, “Comparative analysis of wavelet basis functions for ECG signal compression through compressive sensing,” International Journal of Computer Science and Telecommunications, vol. 3, no. 5, pp. 23–31, 2012. [Google Scholar]
32. R. Nan, G. Sun, Z. Wang and X. Ren, “Research on image reconstruction of compressed sensing based on a multi-feature residual network,” Sensors (Switzerland), vol. 20, no. 15, pp. 1–13, 2020. [Google Scholar]
33. L. Li, Y. Fang, L. Liu, H. Peng, J. Kurths et al., “Overview of compressed sensing: Sensing model, reconstruction algorithm, and its applications,” Applied Sciences, vol. 10, no. 17, pp. 1–19, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |