DOI:10.32604/cmc.2022.024512

| Computers, Materials & Continua DOI:10.32604/cmc.2022.024512 |  |
| Article |
Annealing Harmony Search Algorithm to Solve the Nurse Rostering Problem
1Department of Information Technology, College of Computer, Qassim University, Buraydah, Saudi Arabia
2Department of Computer Science, College of Applied Sciences, Taiz University, Taiz, Yemen
3Intelligent Analytics Group (IAG), College of Computer, Qassim University, Buraydah, Saudi Arabia
*Corresponding Author: Mohammed Hadwan. Email: m.hadwan@qu.edu.sa
Received: 20 October 2021; Accepted: 06 December 2021
Abstract: A real-life problem is the rostering of nurses at hospitals. It is a famous nondeterministic, polynomial time (NP) -hard combinatorial optimization problem. Handling the real-world nurse rostering problem (NRP) constraints in distributing workload equally between available nurses is still a difficult task to achieve. The international shortage of nurses, in addition to the spread of COVID-19, has made it more difficult to provide convenient rosters for nurses. Based on the literature, heuristic-based methods are the most commonly used methods to solve the NRP due to its computational complexity, especially for large rosters. Heuristic-based algorithms in general have problems striking the balance between diversification and intensification. Therefore, this paper aims to introduce a novel metaheuristic hybridization that combines the enhanced harmony search algorithm (EHSA) with the simulated annealing (SA) algorithm called the annealing harmony search algorithm (AHSA). The AHSA is used to solve NRP from a Malaysian hospital. The AHSA performance is compared to the EHSA, climbing harmony search algorithm (CHSA), deluge harmony search algorithm (DHSA), and harmony annealing search algorithm (HAS). The results show that the AHSA performs better than the other compared algorithms for all the tested instances where the best ever results reported for the UKMMC dataset.
Keywords: Harmony search algorithm; simulated annealing; combinatorial optimization problems; timetabling; metaheuristic algorithms; nurse rostering problems
One highly constrained scheduling problem is the rostering of nurses in hospitals. Nurse rostering addresses distributing shifts fairly among available nurses to cover a certain period while satisfying several constraints. Nurse Rostering Problem (NRP) is a challenging problem for which no single solution model can be applied to solve all instances of the problem [1]. This problem is challenging because of the wide range of hard and soft constraints in addition to the variety of individual requests that change from one rostering period to another depending on the needs of the staff nurses.
Nurse rostering is a popular research areas due to several factors that are intensifying the NRP, including an international shortage of nurses due to high turnover, inconvenient working environment, and the high risks that nurses face due to direct interaction with COVID-19 [2]. According to [3], “Nine million shortage estimated in 2014 is predicted to decrease by two million by 2030”. An effective nurse roster algorithm can help achieve better working rosters, which might decrease high turnover due to an inconvenient working environment. The aim of this research is to introduce a better nurse rostering algorithm by investigating and exploring metaheuristic algorithms and their hybridization to solve the NRP.
Inspired by the relationship with the music spontaneous creation measure, the harmony search algorithm (HSA) is an evolutionary algorithm that was presented in 2001 by Geem et al. [4] to improve instrument pitches to achieve better harmonies. The original HSA is classified as a population-based search method that has few local-based search aspects. The HSA is similar to other population-based search algorithms because it satisfactorily distinguishes the superior solution search space when compared to existing local-based search algorithms [1]. A challenge for the HSA is to balance the processes of diversification and intensification. Several attempts have been made in the literature to hybridize the original and enhanced HSA with other local search algorithms to improve its performance [5]. The HSA has been hybridized with other heuristic-based algorithms, such as hill-climbing [6,7], great deluge [8], simulated annealing [9,10], and particle swarm optimization [11]. For the process of diversification and intensification, the hybridization of population-based methods with local search-based methods has been considered by many researchers to strike the balance between these processes [12–14]. More details about the algorithms that have been hybridized within the framework of the HSA and the hybridization of the HSA with other metaheuristics can be found in [14,15].
To overcome some of the drawbacks of the original HSA, the research in [16] presented a modification to the HSA called the enhanced harmony search algorithm (EHSA). In [16], the modifications applied to the EHSA were the use of the SCSPA mechanism [17] in building up the HM and the use of a dynamic updating mechanism for the parameters of the harmony memory considering rate (HMCR) and the pitch adjustment rate (PAR).
The main contribution in this research is the novel hybridization introduced between the enhanced harmony search algorithm (EHSA) with a simulated annealing (SA) called the annealing harmony search algorithm (AHSA). AHSA then used to solve a real-world NRP belonging to the medical centre of National University Malaysia (UKMMC). To show the strength of the introduced algorithm, the AHSA is evaluated and compared against previous variants of the HSA in [6,8,16] in addition to another algorithm from the literature that hybridizes the HSA with the SA and is called the HAS [9].
This research is an extension of previous works aimed at improving the EHSA [16] by hybridizing it with other local-search algorithms, such as the hill-climbing [6] and great deluge [8] algorithms. These algorithms were selected because of their diverse acceptance criteria and the different mechanisms to the use to avoid being trapped in local optima.
Based on the literature, it is clear that metaheuristic algorithms have gained the attention of researchers to solve the NRP. The SA algorithm [18] is a widely known metaheuristic algorithm enthused by the annealing process in metallurgy. Annealing is the practice of cooling solid items gradually until they are frozen at the configuration of minimum energy. SA is considered a local search-based algorithm. Researchers in [18] introduced SA, which was inspired by the annealing physical process in statistical mechanics to solve complex optimization problems. To employ SA to solve optimization problems, a suitable disorder mechanism, cost function, solution search space, and cooling plan are needed to escape local optima and find high-quality solutions. Isken et al. [19] discussed the implementation of SA as a solution for solving the NRP in terms of the time of day and urgency of demand in a post anaesthetic care unit. Thompson (1996) [20] applied SA using non-continuously available employees for shift scheduling. One hundred forty-four test problems were used to examine the proposed method, and another twenty test problems were used to evaluate the SA performance with an integer programming (IP) model. Bailey et al. (1997) [21] employed SA and the genetic algorithm (GA) to generate the rosters of 27 nurses over a period of 6 weeks with 3 daily shifts. Each nurse who is categorized into one out of three levels of skills is assigned to one of four teams. In general, they found that SA was capable of yielding a better-quality solution in less computational time than GA. In [22], stepwise adaptation of weights (SAWing) and noising with SA is proposed to overcome the problem of weights adjusting on constraint binding in solving the NRP. SAWing was used as an intelligent tool to escape local optima by changing the weights to offer precedence to the constraints that were confirmed to be more difficult than others. The method of noising used with SA was random adjusting based on the weights of the evaluation function. The proposed method was tested on a dataset from several Welsh hospitals that included 11 instances. Comparing the results of using SA alone, SA with SAWing, SA with the noising method, and solutions produced manually showed that SA with the noising method performs better than all the other methods. In [23], two solutions to the NRP were introduced: the exact approach and the metaheuristic approach. For metaheuristics, SA was used to further enhance the initial solutions and to solve the small instances for optimality in a short time. The proposed methods were tested on real-world and benchmark NRP datasets.
HSA applied successfully to solve NRP, recently as in [24,25]. Due to the great success of the HSA in approaching different challenging optimization problems, it has been hybridized with other metaheuristic algorithms to overcome its weakness. Some surveys of hybridizing the HSA with other metaheuristic algorithms and its applications can be found in [26–28]. According to [29], there are two main ways for hybridization: (i) including some components of one metaheuristic to another and (2) combining components or techniques from other fields into metaheuristic algorithms as operations research and other artificial intelligence methods.
Researchers in [30] hybridized the HSA with particle swarm optimization (PSO) by substituting the random function with the global-best function of PSO. To enhance the HSA diversification ability, the HSA was hybridized with a memetic algorithm approach to solve the problem of unit commitment for electrical power systems. To reach the minimum cost of the systems life cycle, the HSA was hybridized with SA in [31] to optimize the source of residential electrical load through mixed energy systems. In [32], the HSA was also hybridized with SA to all HSAs to accept the inferior harmonies using the probability of the SA temperature. The proposed method was tested on the IEEE CEC 2014 benchmark in addition to a computer vision real-life problem.
The UKMMC dataset is a nurse rostering dataset representing a real-world NRP belonging to the UKMMC, where approximately 1400 nurses serve the patients. The UKMMC dataset includes eight instances. It also has seven hard constraints and five soft constraints. For further details about the mathematical model, constraints, coverage demand, types of nurses, and penalty values of the UKMMC dataset, please refer to [33,34].
3.1 Mathematical Model of UKMMC
I is the set of available nurses working through the rostering period:
Is is the set of senior nurses, Is
D is the number of days;
W is the set of weights;
P is the set of possible shifts of night patterns;
i is the ith nurse where i ∈
d is the dth day where d ∈
s is the sth shift where s ∈
w is the wth weight where w ∈
p is the pth potential night pattern where p ∈
dp is the starting date of night pattern p.
Eqs. (1) and (2) show the decision variables of every nurse regarding night shift patterns.
In this mathematical model, we have four working shifts: morning (M), evening (E), night (N) and a day off (o). These 4 shifts are represented by the set
As with other scheduling problems, constraints can be classified as hard and soft. Hard constraints cannot be violated under any condition while soft constraints can be violated, but we add a penalty for each constraint violated based on how many times the violation occurs. The UKMMC dataset has the following hard and soft constraints.
1). The coverage demand for nurses must be fulfilled.
2). One-shift a day is the highest number of shifts for each nurse each day.
3). It is obligatory to have at least one senior-nurse for each working-shift.
4). An isolated working shift is not allowed where the nurse has off before and after a single working shift.
5). For a roster period of 14 days, 12 days is the maximum number of working days whilst 10 days is the minimum.
6). A nurse is not allowed to work more than four working days consecutively.
7). If the nurse works four consecutive night shifts, then s/he is entitled to get two days off.
1). Equal allocation for working days and days off for all working nurses.
2). It is highly preferable to assign a day off during weekends (Saturday or Sunday).
3). Four consecutive morning shifts followed by a day off is highly preferable.
4). Four evening shifts consecutively followed by a day off is highly preferable.
5). Four night shifts followed by evening shift or day off after the 2 days off that follows the patterns of night shift (NNNNxxE) or (NNNNxxx).
Soft Constraints (1) and (2) are the most desired constraints to be satisfied according to the extracted information from the UKMMC Nursing Department. For soft constraints 1, 2, 3, 4, and 5, the associated penalty values (PVs) are 100, 100, 10, 10, and 1, respectively. The constraint that has a higher PV specifies the significance of that constraint. For example, it is more important that the constraint with PV 100 is satisfied than that with PV 10 or 1.
For the coverage demand required to cover selected instances of the UKMMC dataset, the number of nurses, senior nurses, and required nurses for the morning (M), evening (E), and night (N) shifts on weekdays and weekends are presented in Tab. 1.
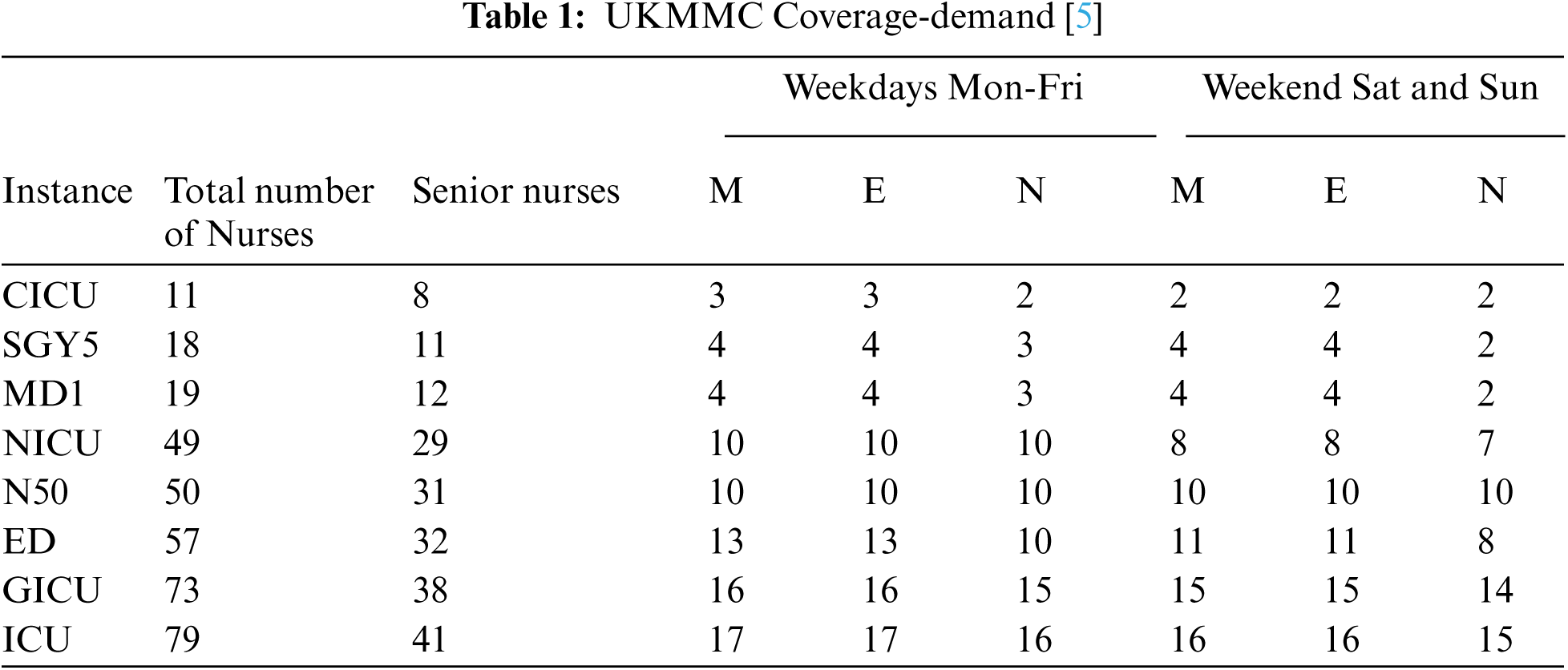
The objective function for the UKMMC dataset is to reduce all penalty values that occur because of violating the soft constraints. Eq. (3) presents the objective function used in this research.
W1, 2, 3, 4, and 5 are the related weights to be minimized for soft constraints 1, 2, 3, 4, and 5 of the UKMMC dataset, respectively.
4 Hybridizing the EHSA with SA for the NRP (AHSA)
The EHSA is an enhanced variant of the basic HSA that uses the semicyclic shift patterns approach (SCSPA) introduced in [18] to generate feasible shift patterns instead of a random mechanism to fill the harmony memory (HM). The SCSPA is proposed to address the night shift since it is the most problematic shift to be assigned due to the extra constraints that it has. SCSPA first assigns predesigned night-shift patterns in a cyclic manner and then assigns morning and evening shift patterns in a noncyclic manner. Fig. 1 shows the main steps of SCSPA.

Figure 1: Main steps of the SCSPA
After the allocation, the process is done and then the repair mechanism is used to repair the infeasible initial solution produced by the SCSPA. Regarding the patterns containing night shifts, we select a shift pattern with the same night shifts and different M and E shifts than the allocated pattern to replace one of the allocated patterns that contain night shifts. One rule that governs the replacement and swapping process is that they should be performed within the same duty roster. If the shift pattern to be replaced or swapped is from the duty roster of the first week, it must be swapped with another shift pattern from the first week N shift patterns. The same rule applies when replacing or swapping a shift pattern in the duty roster of the second week. An example of applying the moves of the repair mechanism of the SCSPA is presented in Fig. 2.
Rather than using fixed parameter values for the HMCR and the PAR, it is recognized that the performance of any population-based method is affected by the values of its parameters, which are problem dependent. Thus, to overcome these shortcomings, several methods have been proposed to control the problem of parameter tuning. To overcome the above-addressed weaknesses in the EHSA in this research, the HMCR and PAR were updated dynamically instead of through the fixed methods used in the basic HSA [35]. The initialization mechanism of the HM is replaced with a semicyclic mechanism in generating the initial population. The employment of a dynamic method to adjust the values of the HMCR and PAR parameters throughout the instance solving, instead of the fixed parameter values of the BHSA. This modification is based on the idea of adaptive harmony search (AHS) Hasancebi et al. which is inspired by the dynamic modification of the PAR and the BW in [36]. At the beginning of the search process, the parameter values of the HMCR should be lower in the range of HMCRmin and HMCRmax. This facilitates more exploration. Towards the end of the search process, the value of the HMCR should be increased to facilitate more exploration. Furthermore, the value of the PAR should be as high as possible in the range of PARmin and PARmax at the beginning of the search process. This facilitates making higher exploration. Towards the end, these values of the PAR are decreased to facilitate exploring the candidate solutions. Fig. 3 shows the pseudo-code of the improvisation step only with the proposed modifications. In this modifying step, the parameter values of the HMCR and the PAR keep changing through the execution based on Eqs. (4) and (5). These equations are based on the work in [37] to solve RNA secondary structure prediction.

Figure 2: Example of applying the repair mechanism moves using the SCSPA. (a) Before applying the repairing mechanism (b) After applying the repairing mechanism

Figure 3: Improvisation pseudo-code in the EHSA
The main idea in this research is to hybridize the EHSA in [17] with standard SA [38]. In this section, the hybridization of the EHSA with SA is discussed in detail. The SA procedure used in this research is the same as the standard SA procedure used in [38]. The basic pseudo-code of SA is presented in Fig. 4.

Figure 4: Pseudo-code of SA
However, the stopping conditions for SA as follows: (i) when the PV of the best harmony equals zero (f (

Figure 5: Procedure of the AHSA
The AHSA updates the values of the HMCR and the PAR parameters dynamically. SA improves the promising solutions where it optimizes the best harmony reached by the EHSA to further enhance it. To balance the processes of diversification and intensification, the best harmony is only selected to be improved using SA. This helps speed up the execution time, as SA only runs one time. The enhanced harmony is then stored again in the location of the best harmony HM [0].
The harmony annealing search (HAS) [9] is implemented and compared to the AHSA. The HAS is an HSA variant that applies the idea of the dynamic HMCR and PAR along with SA. The AHSA is compared with the HAS because both algorithms use the same idea to update the parameter settings of the HMCR and the PAR. Furthermore, the AHSA and HAS use SA in their solution framework. However, the only two differences are:
1) In the initial stage of filling the HM, the HAS uses the random mechanism, whereas the AHSA uses the SCSPA mechanism.
2) The HAS applied SA to improve the solutions that come from the random selection based on the probability of the HMCR, while the AHSA uses SA to improve the best solution after the EHSA reaches one of the stopping criteria.
For each instance, 20 runs were performed, and the obtained results are reported. The same experimental design is used for both the AHSA and HAS to fairly compare them. The stopping criteria are as follows: 1) 1000 iterations (based on a preliminary test), 2) PV = 0, and 3) 600 s of execution time. A 32-bit Intel laptop with 1.73 GHz, and 2 GB RAM were used to perform the experiments. The parameter values of HMCRmin and HMCRmax are 0.1 and 0.95, respectively [39]. The parameter values used for PARmin and PARmax are 0.01 and 0.99, respectively, [40,41]. For the BW, we set it experimentally to be −5 and 5. Section 5.1 presents the results obtained by the AHSA, 5.2 presents the results obtained by the HAS, and 5.3 presents the comparison between the AHSA, HAS, EHSA, CHSA, and DHSA.
5.1 Results for the UKMMC Dataset Using the AHSA
The results obtained by applying the AHSA to solve the UKMMC dataset are presented in Tab. 2, where the best, average, worst PVs, standard deviation (Stddv.), desirable patterns (DPs) and execution time are recorded.
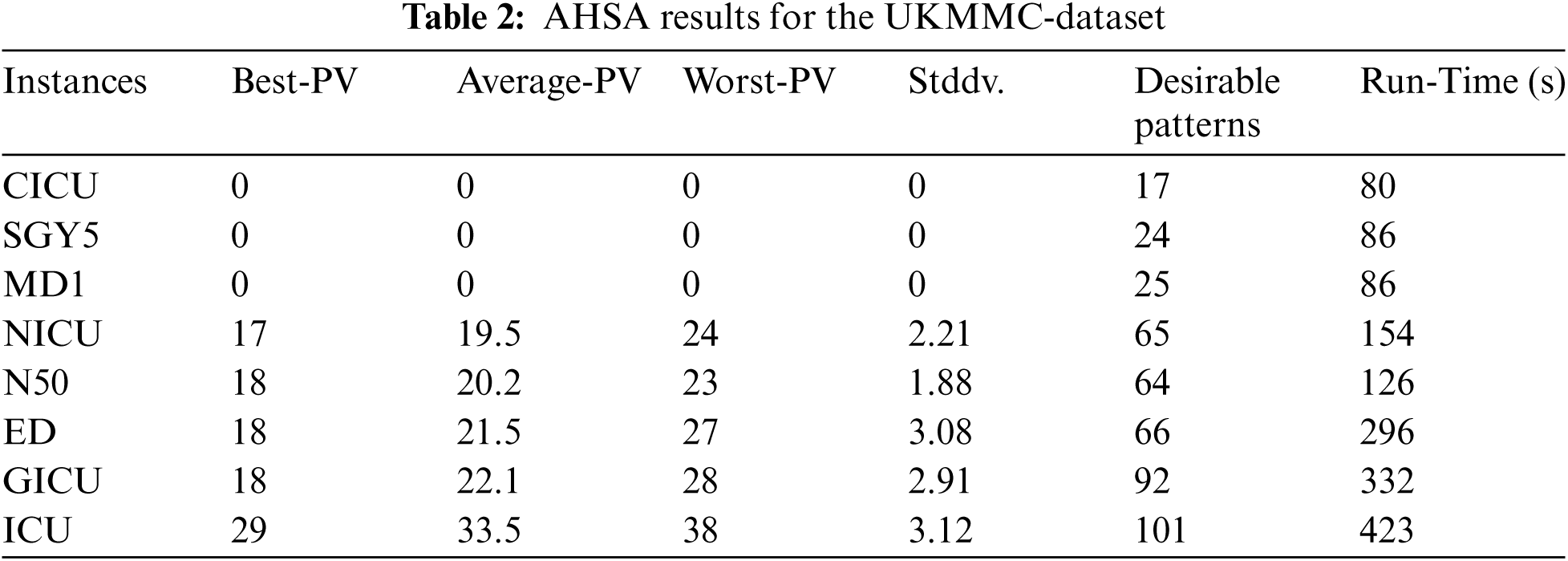
Based on the obtained results, AHSA was able to produce an optimal solution for small instances as produced roster didn't break any of the soft constraints. For medium and large instances, very promising results were reported. Soft constraints 1 and 2 that have the higher value didn't break.
5.2 Results for the UKMMC Dataset Using the HAS
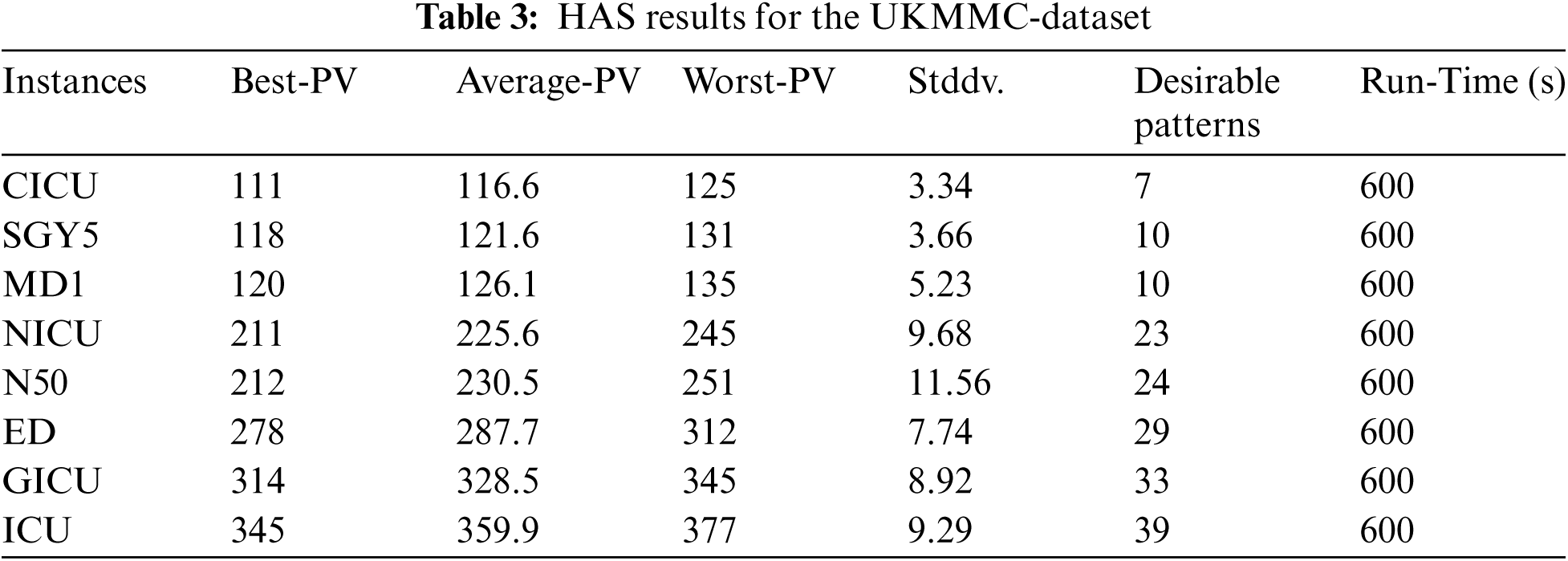
The computational results obtained by applying the HAS algorithm to solve the UKMMC dataset are presented in Tab. 3, where the best PVs, average PV, worst PVs, standard deviation (Stddv.), desirable patterns (DPs) and execution time are recorded.
5.3 Comparison Between the CHSA, DHSA, EHSA, HAS, and AHSA
To further evaluate the performance of the AHSA, it is compared to previously published work of other HSA hybridized algorithms (EHSA, CHSA and DHSA), in addition to comparing to the results of the HAS. The results are shown in Tab. 4.
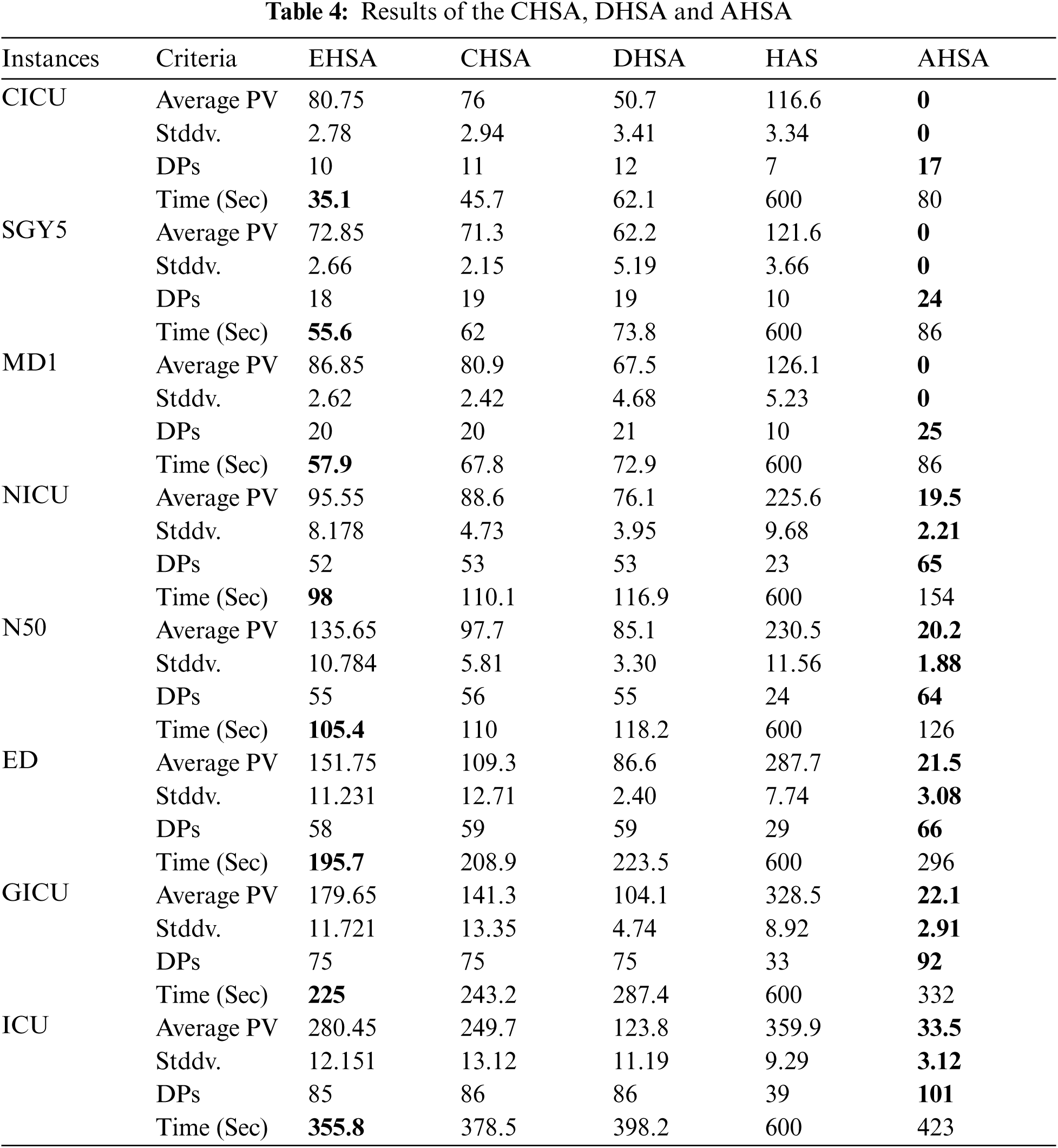
The average PVs, Stddv. of PVs and the DPs in addition to the computational time of each compared algorithm are used in this comparison. The results in bold show the best-obtained results.
Fig. 6 depicts the average PVs for AHSA and the other four compared algorithms. It is apparently that AHSA was able to generate the lowest PVs for all tested instances. Even though HAS could obtain feasible solutions for the tested instances; the quality of the obtained results was very low.

Figure 6: PVs obtained by the AHSA and the compared algorithms
Fig. 7 depicts the standard deviation values (Stddv.) for AHSA and the other four compared algorithms. It is apparently that AHSA was able to generate the lowest Stddv. for all tested instances.

Figure 7: Standard deviation values for the AHSA and the compared algorithms
Fig. 8 depicts the number of desirable patterns (DPs) for AHSA and other compared methods. The more DPs generated indicate the higher quality roster. AHSA was able to generate a higher number of DPs.
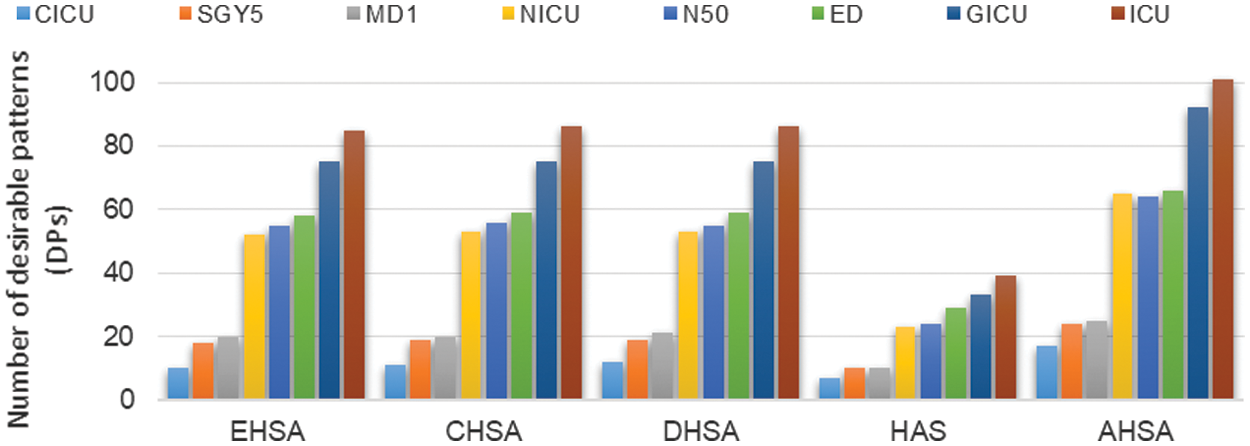
Figure 8: Number of desirable patterns by the AHSA and the compared algorithms
Fig. 9 depicts the execution time, for AHSA and all other methods. It is clear that EHSA was the fastest while the HAS was the slowest. An increase in execution time was noticed for AHSA due to the further improvement carried out by SA.

Figure 9: Execution time for the AHSA and the compared algorithms
Based on the results in Tab. 4, the AHSA succeeds in producing better rosters than the EHSA. The AHSA remarkably reduced the PVs compared to the EHSA PVs. The AHSA needs almost twice the time that is required by the EHSA. Due to the acceptance criteria of SA, it escapes the local optima, and as a result, it further decreases the PVs for all instances. For the small instances (CIUC, SGY5, and MD1), the AHSA shows that it is very promising in reaching optimal solutions for NRP as it reaches zero PVs in each run. For medium instances (NICU, N50, ED) and large instances (SGY and CICU), AHSA generates very high-quality rosters with very low PVs. To further evaluate the performance of the AHSA, it was compared to previously published work of other HSA hybridized algorithms the CHSA [6] and DHSA [8]). The results in Tab. 4 show that the AHSA outperformed the CHSA and DHSA in all of the evaluation criteria except for execution time, which increased slightly. This is because the AHSA obtained better PVs and a higher number of DPs for all instances.
The obtained results in Tab. 4 show that the AHSA performed better than the HAS for all instances. This is because the AHSA was able to generate better-quality rosters with less execution time than HAS. Doing the selection randomly by SA out of HM caused two shortcomings: (i) premature convergence because of selecting new-solution vectors out of HM that has been improved by SA, and (ii) the additional consumed time by random selection to generate an entire new harmony and then improve it by SA.
In this paper, a novel hybridization between EHSA and SA is introduced. The AHSA is applied to solve a real-world dataset collected from UKMMC Malaysia. AHSA was employed to construct ideal duty rosters with minimum PVs and the maximum number of DPs, taking into consideration all of the associated constraints. The AHSA is then compared to the EHSA alone, the CHSA, and the DHSA algorithms to demonstrate its performance. The results showed that the AHSA yields the best results. It is observed that the success of the AHSA is because of the ability to maintain the balance between diversification and intensification in the solution search pool, in addition to the strong mechanism of SA in escaping local optima. Moreover, the comparison between the AHSA and the HAS (both use SA to enhance the constructed solution but in different stages) showed that the AHSA performed extremely better than the HAS in all UKMMC instances for all comparison criteria. This is due to the premature convergence that occurred for the population of the solutions in the HM caused by running the SA several times in the HAS.
For future work, it is highly recommended to hybridize the EHSA with enhanced variants of SA, which might further enhance the mechanism of the HSA and help construct high-quality rosters for nurses.
Acknowledgement: The researcher would like to thank the Deanship of Scientific Research, Qassim University for funding the publication of this project.
Funding Statement: The Deanship of Scientific Research, Qassim University was funding the publication of this project.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. E. K. Burke, P. De Causmaecker, G. Vanden Berghe and H. Van Landeghem, “The state of the art of nurse rostering,” Journal of Scheduling, vol. 7, no. 6, pp. 441–499, 2004. [Google Scholar]
2. Y. J. Kim, S. Y. Lee and J. H. Cho, “A study on the Job retention intention of nurses based on social support in the COVID-19 situation,” Sustainability, vol. 12, no. 18, pp. 1–9, 2020. [Google Scholar]
3. V. M. Drennan and F. Ross, “Global nurse shortages-the facts, the impact and action for change,” British Medical Bulletin, vol. 130, no. 1, pp. 25–37, 2019. [Google Scholar]
4. Z. W. Geem, J. H. Kim and G. V. Loganathan, “Original harmony search, A New heuristic optimization algorithm: harmony search,” Journal of Simulation, vol. 76, no. 2, pp. 60–68, 2001. [Google Scholar]
5. M. Hadwan, M. Ayob, N. R. Sabar and R. Qu, “A harmony search algorithm for nurse rostering problems,” Information Sciences, vol. 133, no. 1, pp. 126–140, 2013. [Google Scholar]
6. M. Hadwan, M. Ayob, M. Al-Hagery and B. N. Al-Tamimi, “Climbing harmony search algorithm for nurse rostering problems,” in The 3rd Int. Conf. of Reliable Information and Communication Technology, Kuala Lumpur, Malaysia, pp. 1–8, 2018. [Google Scholar]
7. I. Abu Doush and E. Santos, “Best polynomial harmony search with best β-hill climbing algorithm,” Journal of Intelligent Systems, vol. 30, no. 1, pp. 1–17, 2020. [Google Scholar]
8. M. Hadwan, M. Ayob, M. A. Rassam and E. A. Hezam, “Deluge harmony search algorithm for nurse rostering problems,” in 2019 First Int. Conf. of Intelligent Computing and Engineering (ICOICE), Hadhramout, Yemen, pp.1–5, 2019. [Google Scholar]
9. J. Sui, L. Yang, H. Fan and Z. Hua, “Mine airflow optimizing control based on harmony annealing search,” in 2010 Int. Conf. of Information Science and Management Engineering Shaanxi, China, pp. 295–298, 2010. [Google Scholar]
10. F. Misni, L. S. Lee and H. V. Seow, “Hybrid harmony search-simulated annealing algorithm for location-inventory-routing problem in supply chain network design with defect and non-defect items,” Applied Sciences, vol. 10, no. 8, pp. 1–22, 2020. [Google Scholar]
11. A. Kaveh and S. Talatahari, “Particle swarm optimizer, ant colony strategy and harmony search scheme hybridized for optimization of truss structures,” Computers & Structures, vol. 87, no. 5–6, pp. 267–283, 2009. [Google Scholar]
12. C. Blum and A. Roli, “Metaheuristics in combinatorial optimization: Overview and conceptual comparison,” ACM Computing Surveys, vol. 35, no. 3, pp. 268–308, 2003. [Google Scholar]
13. E. G. Talbi, “A taxonomy of hybrid metaheuristics,” Journal of Heuristics, vol. 8, no. 1, pp. 541–564, 2002. [Google Scholar]
14. C. Blum, J. Puchinger, G. R. Raidl and A. Roli, “Hybrid metaheuristics in combinatorial optimization: A survey,” Applied Soft Computing Journal, vol. 11, no. 6, pp pp. 4135–4151, 2011. [Google Scholar]
15. O. M. D. Alia and R. Mandava, “The variants of the harmony search algorithm: An overview,” Artificial Intelligence Review, vol. 36, no. 1, pp. 49–68, 2011. [Google Scholar]
16. M. Ayob, M. Hadwan, M. Z. A. Nazri and Z. Ahmad, “Enhanced harmony search algorithm for nurse rostering problems,” Journal of Applied Sciences, vol. 13, no. 6, pp. 846–853, 2013. [Google Scholar]
17. M. Hadwan and M. Ayob, “A Semi-cyclic shift patterns approach for nurse rostering problems,” in 3rd Conf. on Data Mining and Optimization (DMO 2011), Kuala lumpur, Malaysia, pp. 184–189, 2011. [Google Scholar]
18. S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, “Optimization by simulated annealing,” Science, vol. 220, no. 4598, pp. 671–680, 1983. [Google Scholar]
19. M. Isken and W. Hancock, “A heuristic approach to nurse scheduling in hospital units with non-stationary, urgent demand, and a fixed staff size,” Journal of the Society for Health Systems, vol. 2, no. 2, pp. 24–41, 1991. [Google Scholar]
20. G. M. Thompson, “A Simulated-annealing heuristic for shift scheduling using non-continuously available employees,” Computers and Operations Research, vol. 23, no. 3, pp. 275–288. 1996. [Google Scholar]
21. R. N. Bailey, K. M. Garner and M. F. Hobbs, “Using simulated annealing and genetic algorithms to solve staff scheduling problems,” Asia-Pacific Journal of Operational Research, vol. 14, no. 2, pp. 27–43, 1997. [Google Scholar]
22. D. Parr and J. M. Thompson, “Solving the multi-objective nurse scheduling problem with a weighted cost function,” Annals of Operations Research, vol. 155, no. 1, pp. 279–288, 2007. [Google Scholar]
23. F. Knust and L. Xie, “Simulated annealing approach to nurse rostering benchmark and real-world instances,” Annals of Operations Research, vol. 272, no. 1, pp. 187–216, 2019. [Google Scholar]
24. K. Lartey and E. K. Akowuah, “An analysis of the application of the harmony search algorithm to solving the nurse rostering problem,” CIN - Computers Informatics Nursing, vol. 39, no. 5, pp. 281–288, 2021. [Google Scholar]
25. E. Cetin Yagmur and A. Sarucan, “Nurse scheduling with opposition-based parallel harmony search algorithm,” Journal of Intelligent Systems, vol. 28, pp. 633–647, 2021. [Google Scholar]
26. N. Siddique and H. Adeli, “Hybrid harmony search algorithms,” International Journal on Artificial Intelligence Tools, vol. 24, no. 6, pp. 1–20, 2015. [Google Scholar]
27. D. Manjarres, I. Landa-Torres, S. Gil-Lopez, J. Del Ser, M. N. Bilbao et al., “A survey on applications of the harmony search algorithm,” Engineering Applications of Artificial Intelligence, vol. 26, no. 8, pp. 1818–1831, 2013. [Google Scholar]
28. J. Yi, C. Lu and G. Li, “A literature review on latest developments of harmony search and its applications to intelligent manufacturing,” Mathematical Biosciences and Engineering, vol. 16, no. 4, pp. 2086–2117, 2019. [Google Scholar]
29. C. Blum, M. J. Belsa Aguilera, A. Roli and M. Sampels, “Hybrid Metaheuristics-An Emerging Approach to Optimization,” in Studies in Computational Intelligence, 1st ed., vol.1. New York NY, USA: Springer Publishing Company, Incorporated, pp. 290, 2008. [Google Scholar]
30. M. Y. Cheng, D. Prayogo, Y. W. Wu and M. M. Lukito, “A hybrid harmony search algorithm for discrete sizing optimization of truss structure,” Automation in Construction, vol. 69, no. 1, pp. 21–33, 2016. [Google Scholar]
31. W. Zhang, A. Maleki, M. A. Rosen and J. Liu, “Optimization with a simulated annealing algorithm of a hybrid system for renewable energy including battery and hydrogen storage,” Energy, vol. 163, no. 1, pp. 191–207, 2018. [Google Scholar]
32. A. Assad and K. Deep, “A hybrid harmony search and simulated annealing algorithm for continuous optimization,” Information Sciences, vol. 450, no. 1, pp. 246–266, 2018. [Google Scholar]
33. M. Hadwan and M. Ayob, “An exploration study of nurse rostering practice at hospital universiti kebangsaan Malaysia,” in, 2009 2nd Conf. on Data Mining and Optimization, Kajang, Malaysia, pp. 1–8, 2009. [Google Scholar]
34. M. Hadwan and M. Ayob, “A constructive shift patterns approach with simulated annealing for nurse rostering problem,” in 2010 Int. Symp. on Information Technology, Kuala lumpur, Malaysia, pp. 1–10, 2010. [Google Scholar]
35. O. Hasançebi, F. Erdal and M. P. Saka, “Adaptive harmony search method for structural optimization,” Journal of Structural Engineering, vol. 136, no. 4, pp. 419–431, 2010. [Google Scholar]
36. M. Mahdavi, M. Fesanghary and E. Damangir, “An improved harmony search algorithm for solving optimization problems,” Applied Mathematics and Computation, vol. 188, no. 2, pp. 1567–1579, 2007. [Google Scholar]
37. A. M. A. Mohsen, “Adaptive And Cooperative Harmony Search Models For Rna Secondary Structure Prediction,” Ph.D. dissertation, University Science Malaysia, Penang, Malaysia 2011. [Google Scholar]
38. E. Aarts and J. Korst, Simulated Annealing and Boltzmann Machines: A Stochastic Approach to Combinatorial Optimization and Neural Computing, John Wiley & Sons, New York, USA, 1988. [Google Scholar]
39. M. Barzegari, S. M. T. Bathaee and M. Alizadeh, “Optimal coordination of directional overcurrent relays using harmony search algorithm,” in 2010 9th Int. Conf. on Environment and Electrical Engineering, Prague, Czech Republic, pp. 321–324, 2010. [Google Scholar]
40. M. G. H. Omran and M. Mahdavi, “Global-best harmony search,” Applied Mathematics and Computation, vol. 198, no. 2, pp. 643–656, 2008. [Google Scholar]
41. P. Chakraborty, G. G. Roy, S. Das, D. Jain and A. Abraham, “An improved harmony search algorithm with differential mutation operator the harmony search metaheuristic algorithm,” Fundamenta Informaticae, vol. 95, no. 1, pp. 1–26, 2009. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |