DOI:10.32604/cmc.2022.021462

| Computers, Materials & Continua DOI:10.32604/cmc.2022.021462 |  |
| Article |
Nonlinear Dynamics of Nervous Stomach Model Using Supervised Neural Networks
1Department of Mathematics and Statistics, Hazara University, Mansehra, Pakistan
2Department of Electronics and Communication Engineering, JECRC University, Jaipur (Rajasthan), 303905, India
3Future Technology Research Center, National Yunlin University of Science and Technology, Yunlin, 64002, Taiwan
4Department of Applied Mathematics, School of Applied Natural Sciences, Adama Science and Technology University, Adama, Ethiopia
5Department of Mathematics, University of Punjab, Jhelum Campus, Pakistan
6Department of Electrical Engineering, Prince Sattam Bin Abdulaziz University, College of Engineering, Al Kharj, 16278, Saudi Arabia
7Research Group of Embedded Systems and Mobile Application in Health Science, College of Arts, Media and Technology, Chiang Mai University, Chiang Mai, 50200, Thailand
*Corresponding Author: Pattaraporn Khuwuthyakorn. Email: pattaraporn.khuwuth@cmu.ac.th
Received: 03 July 2021; Accepted: 29 October 2021
Abstract: The purpose of the current investigations is to solve the nonlinear dynamics based on the nervous stomach model (NSM) using the supervised neural networks (SNNs) along with the novel features of Levenberg-Marquardt backpropagation technique (LMBT), i.e., SNNs-LMBT. The SNNs-LMBT is implemented with three different types of sample data, authentication, testing and training. The ratios for these statistics to solve three different variants of the nonlinear dynamics of the NSM are designated 75% for training, 15% for validation and 10% for testing, respectively. For the numerical measures of the nonlinear dynamics of the NSM, the Runge-Kutta scheme is implemented to form the reference dataset. The attained numerical form of the nonlinear dynamics of the NSM through the SNNs-LMBT is implemented in the reduction of the mean square error (MSE). For the exactness, competence, reliability and efficiency of the proposed SNNs-LMBT, the numerical actions are capable using the proportional arrangements through the features of the MSE results, error histograms (EHs), regression and correlation.
Keywords: Nonlinear dynamics; nervous stomach system; reference dataset; levenberg-marquardt backpropagation technique; numerical outcomes
The nonlinear dynamics of the nervous stomach model (NSM) have three segments, Tension (T), Food (F) and Medicine (M), i.e., TFM model. The generic form of the TFM system Tab. 1 along with its initial conditions (ICs) is given as [1]:
The detail of each segment of the nonlinear TFM system is described together with the description of each parameter shown in the above Eq. (1) as:
T(y): One of the major target is stress or tension in the nonlinear dynamics based on the NSM out of the various physical indications. The effects of the nervous stomach create a problem in the human's physique due to stress.
F(y): The spicy, oily and crispy items of food play a major role to disturb the stomach. Those individuals who regularly use such food items, they may feel the disorder in their digestive parts. The presence of the spicy food like capsaicin is a main reason to upset the stomach.
M(y): The medicine excess is also a big factor to disturb the stomach. The use of the medicine of the highest potency can recover the minor illnesses, but it creates the stomach's indiscretion.

The stomach, like other organs in the human's body has great significance. In human body every organ is linked to other organs, e.g., eye, nose and ear. If one organ doesn't work properly, the other organs also feel its effects. Likewise, the stomach is linked to many other organs that play a vital role in maintaining the human health. The researchers studied the stomach for many years and the earliest Greeks professed the natural bitter gastric materials. In the beginning of the 16th century, the idea that stomach comprises acid in the digestion procedures presented by Sánchez et al. [1]. The solvent features of digestive juice based on the animal tissues accessible by Reaumur. William Prout [2] studied the emission gastric acid nature and William Beaumont presented the analysis of gastric fistula patient before three centuries. The gastric secretion by removal of the coeliac axis and vagotomy as healing interruptions was discovered in the beginning of the 19th century. Laidlaw et al. engrossed the histamine using the composite gastric secretion, which focused to the finding of the Popielski based the impacts of histamine gastric secretion. Bayliss et al. [3] discussed the secret in, while Edkins [4] investigated the gastrin performance. These stated discoveries recognized the gastric illnesses based pretentious advances in the pharmacologic connotation of peptic ulcer having H2-receptor presented by Sir James Black two centuries ago [5]. Warrenet alin 1983 presented the acidic form of the diseases till the innovative of Helicobacter pylori discovery [6] and Jaworski discussed many observations based on the bacterial inhabitants in the gastric juice.
The nonlinear dynamics of the NSM based TFM system is solved using the supervised neural networks (SNNs) along with the novel features of Levenberg-Marquardt backpropagation technique (LMBT), i.e., SNNs-LMBT. The obtained results have been compared with the designed database results based on the Runge-Kutta method. The data percentages to solve three different cases of the nonlinear dynamics of the NSM based TFM are designated 75% for training, 15% for validation and 10% for testing, respectively. The stochastic methods have been applied in diverse recent applications [7–10], but the nonlinear dynamics of the NSM based TFM system has never been explored by using the SNNs-LMBT [11,12]. Few recent stochastic submissions are SITR dynamics [13,14], singular third kind of nonlinear system [15,16], Thomas–Fermi form of the model [17], heat conduction model [18], periodic differential singular system [19,20], functional models [21–23], dengue fever biological model [24], a multi-singular form of equations [25,26], prediction, delayed and pantograph models [27–29] and differential systems based on the fractional order [30–32]. These well-known stochastic based applications inspire the authors to present a robust, consistent, accurate and reliable platform to solve the nonlinear dynamics of the NSM based TFM system using the SNNs-LMBT [33–35]. Few novel features of the present study are provided as:
• A computational intelligent novel SNNs-LMBT is implemented to solve the nonlinear dynamics of the NSM based TFM system.
• The exact matching of the numerical outcomes with good measures based on the absolute error (AE) enhances the value of the proposed novel SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system.
• The presentations using the related soundings on MSE, regression metrics, correlation measures and error histograms (EHs) validate the performances of the proposed novel SNNs-LMBT.
The remaining paper parts are organized as: The numerical performances of the proposed novel SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM systems are described in Section 2. The numerical results through SNNs-LMBT are presented in Section 3. The concluding outcomes with latent related soundings together with the future research reports are labeled in the Section 4.
The proposed SNNs-LMBT is provided in two phases to solve the nonlinear dynamics of the NSM based TFM system.
• Essential explanations of the proposed SNNs-LMBT are provided.
• Implementation measures support the proposed SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system.
The appropriate optimization based on the proposed SNNs-LMBT are provided in Fig. 1 using the multi-layer procedures and proposed system form for a single neuron is plotted in Fig. 2. The suggested SNNs-LMBT is implemented with the ‘nftool’ that is build-in procedure in ‘Matlab’ using the data as designated 75% for training, 15% for validation and 10% for testing, respectively.

Figure 1: Workflow diagram of the proposed SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system

Figure 2: Proposed structure based on the single neuron
This section indicates the numerical performances of the obtained results of three different cases based on the nonlinear dynamics of the NSM using the proposed SNNs-LMBT. The mathematical form of each case is given as:
Case-1: Consider the nonlinear dynamics of the NSM based TFM system with
Case-2: Consider the nonlinear dynamics of the NSM based TFM system with
Case-3: Consider the nonlinear dynamics of the NSM based TFM system with
The numerical performances are obtained using the SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system with inputs (0, 1) and 0.01 step size. The ‘nftool’ command in Matlab is usedto solve the nonlinear dynamics of the NSM based TFM system using 15 numbers of neurons using the data as designated 75% for training, 15% for validation and 10% for testing, respectively. The achieved performance of the results using the SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system is drawn in Fig. 3.

Figure 3: Proposed SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system
The graphs of the designed SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system are provided in Figs. 4–12. The accomplished numerical procedures of all three cases of the nonlinear dynamics of the NSM based TFM systems are provided in Figs. 4 and 5 using the performance and transition states. The calculated outcomes based on MSE for the training, best curve, authentication and testing states are provided in Fig. 4 to solve the nonlinear dynamics of the NSM based TFM system. The best performances for the nonlinear dynamics of the NSM based TFM system are obtained at epoch 125, 71 and 74, which lie around lie around 1.7601 × 10−10, 1.3029 × 10−11 and 2.3984 × 10−14, respectively. Fig. 5 indicates the gradient values of the designed SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system, which are calculated as 9.9838 × 10−08, 9.9615 × 10−08 and 9.8429 × 10−08. These graphical plots indicate the precision, accuracy and convergence of the designed SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system. The fitting curve plots for each case of the nonlinear dynamics of the NSM based TFM system are drawn in Figs. 6–8, which authenticate the comparison of the obtained outcomes through the designed SNNs-LMBT and the reference database results. The maximum values of the error plots are plotted using the training, authentication and testing through the designed SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system. The EHs are plotted in Fig. 9a–9c, whereas the plots of regression are provided in Figs. 10–12 to solve the nonlinear dynamics of the NSM based TFM system. The correlation plots are provided to validate the regression analysis. It is indicated that the correlation values are noticed around 1 to solve the nonlinear dynamics of the NSM based TFM system that shows the perfect model. The plots of testing, authentication and training designate the exactness of the designed SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system. Moreover, the convergence for the MSE are capable for training, authentication, epochs, backpropagation values, testing and complexity investigations are given in Tab. 2 to solve the TFM system.

Figure 4: Performance through MSE results using the proposed SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system (a) Case I: MSE values for the NSM based TFM system (b) Case II: MSE values for the NSM based TFM system (c) Case III: MSE values for the NSM based TFM system

Figure 5: State transition using the proposed SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system (a) Case I: State transition for the NSM based TFM system (b) Case II: State transition for the NSM based TFM system (c) Case III: State transition for the NSM based TFM system
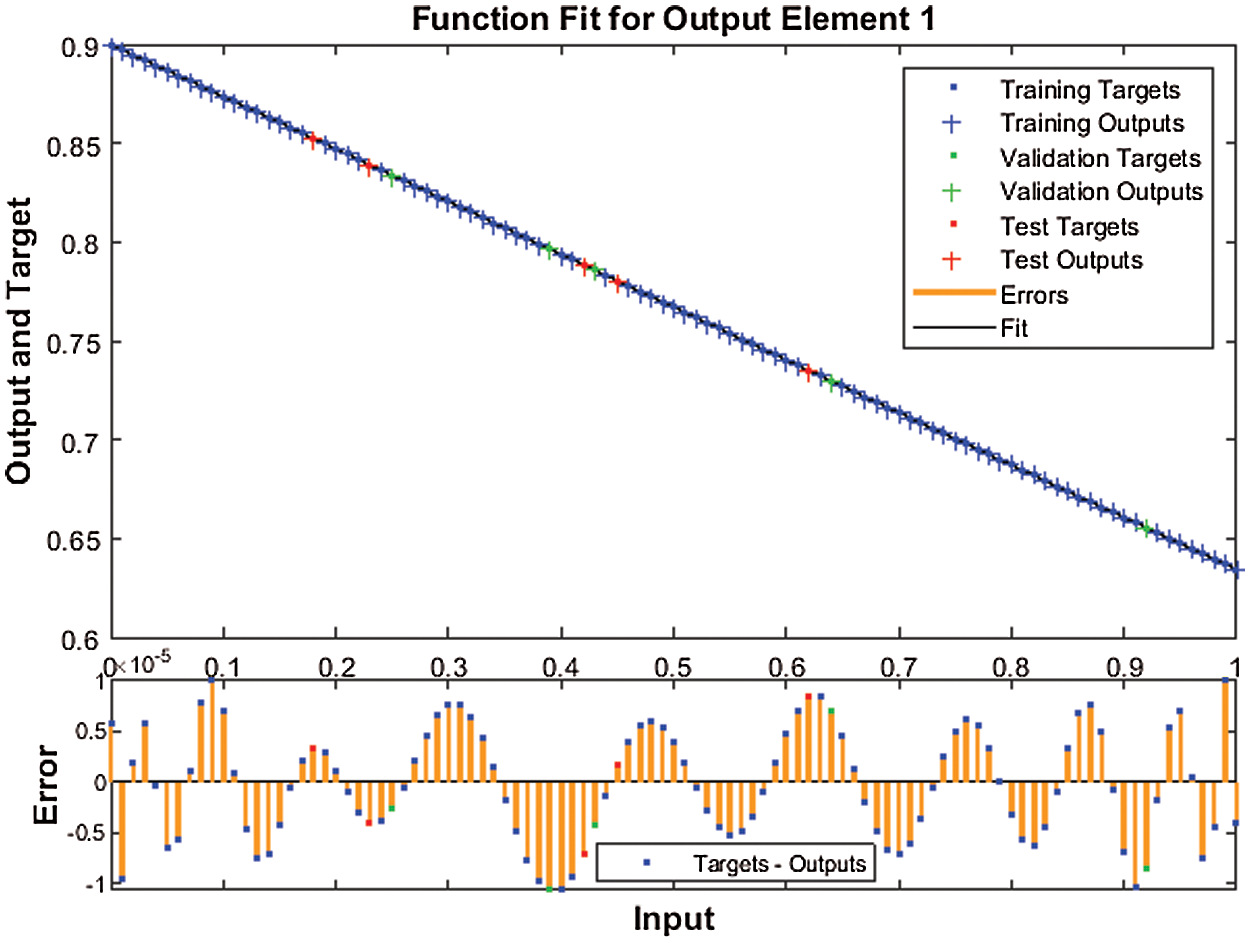
Figure 6: Case 1: Result comparison through the proposed SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system

Figure 7: Case 2: Result comparison through the proposed SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system
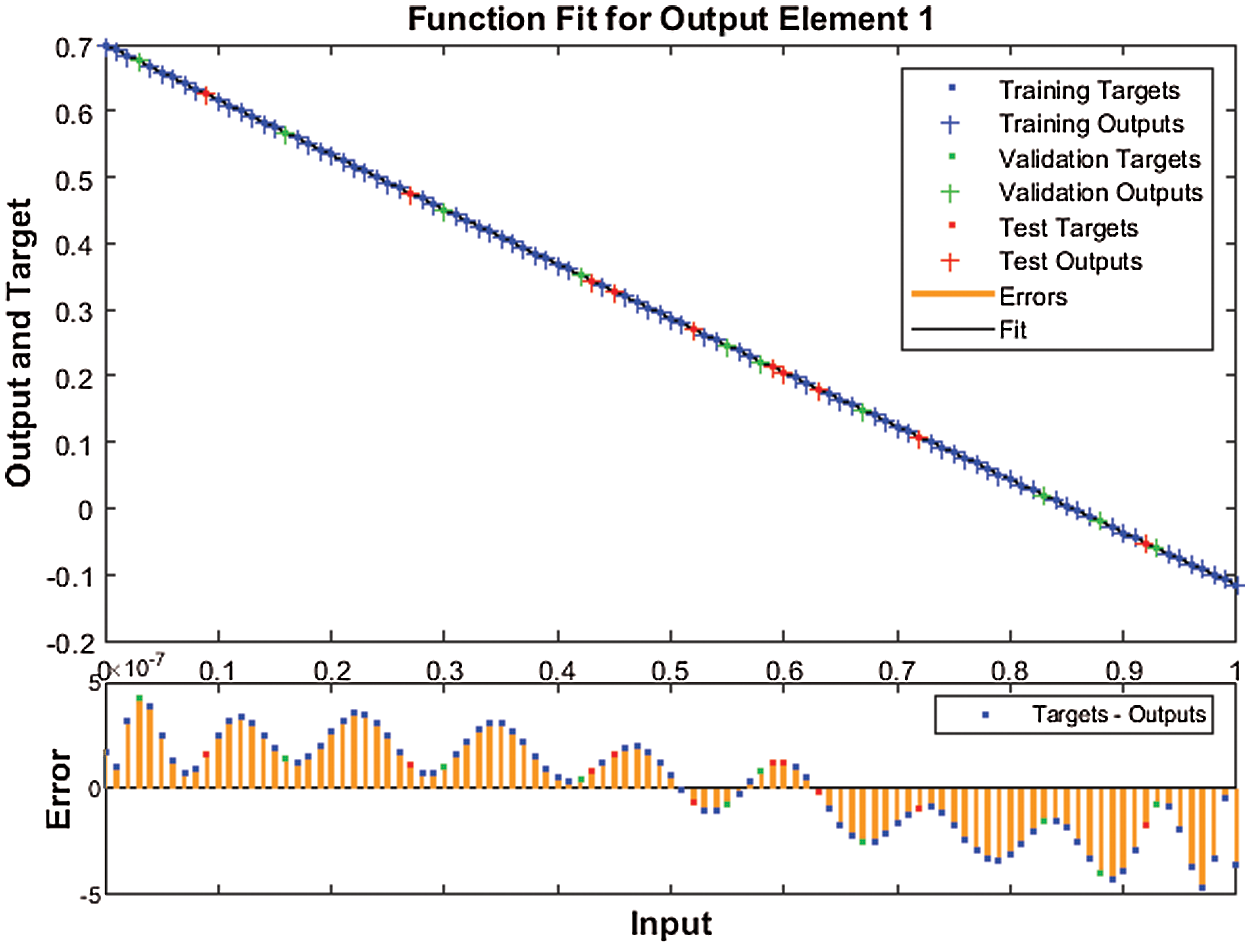
Figure 8: Case 3: Result comparison through the proposed SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system
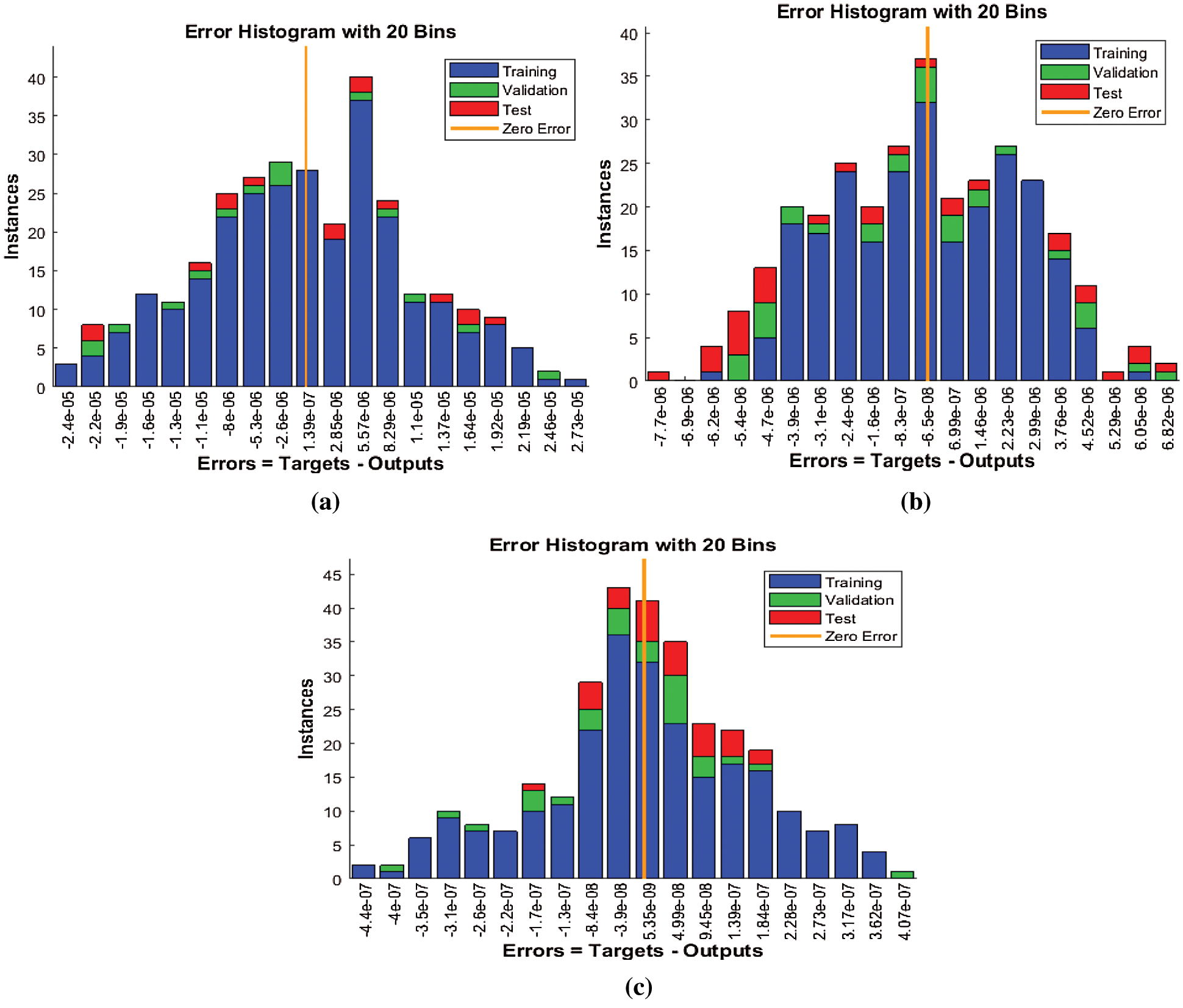
Figure 9: EHs values for the proposed SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system (a) Case I: EHs for the NSM based TFM system (b) Case II: EHs for the NSM based TFM system (c) Case III: EHs for the NSM based TFM system

Figure 10: Case I: Regression plots for the NSM based TFM system

Figure 11: Case II: Regression plots for the NSM based TFM system

Figure 12: Case III: Regression plots for the NSM based TFM system

The result comparisons are plotted in Figs. 13 and 14 to solve the nonlinear dynamics of the NSM based TFM system. The outcomes of the parameters
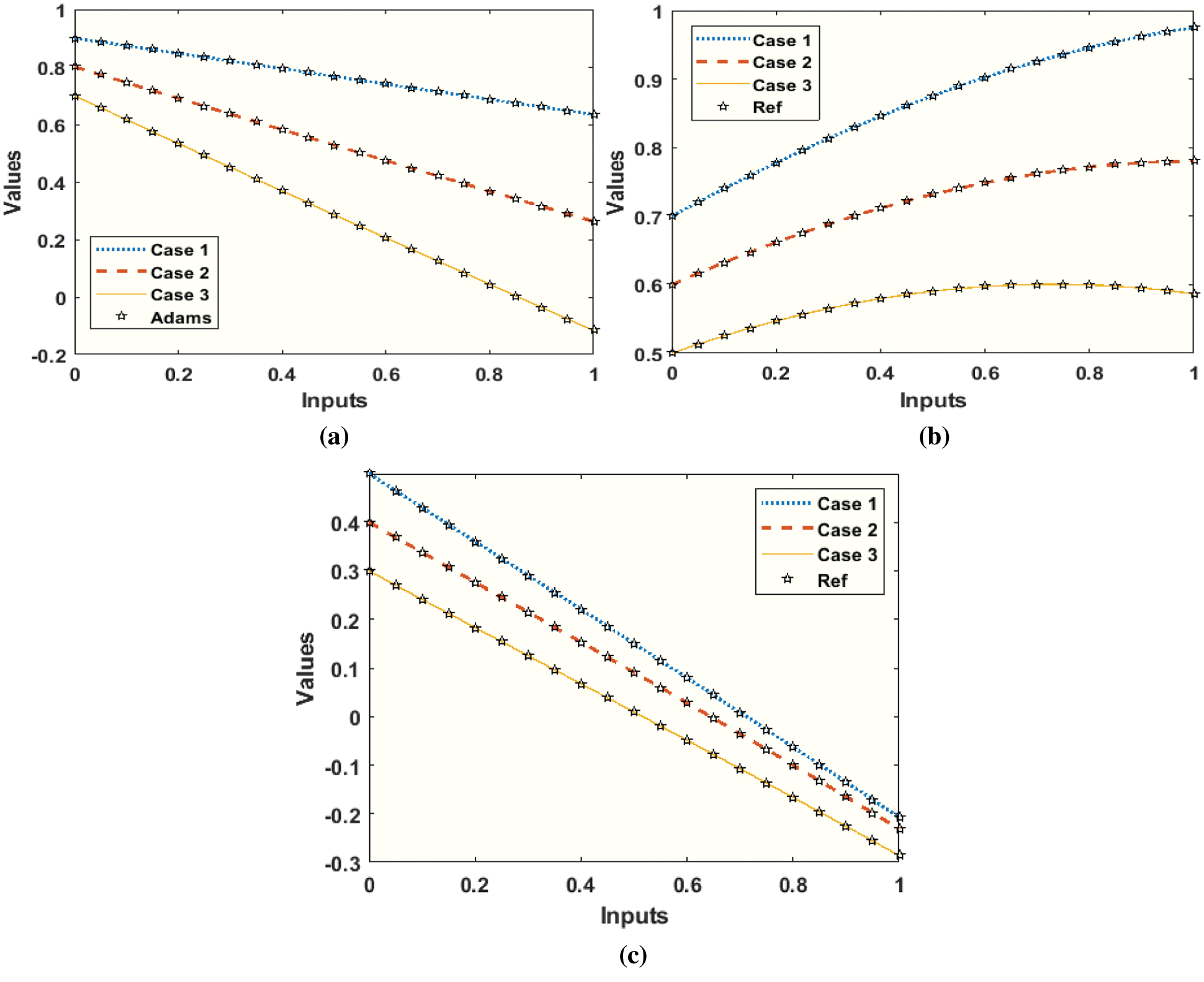
Figure 13: Comparison performance based on the proposed SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system (a) Case 1: Results of the parameters T(y) (b) Case II: Results of the parameters F(y) (c) Case II: Results of the parameters M(y)
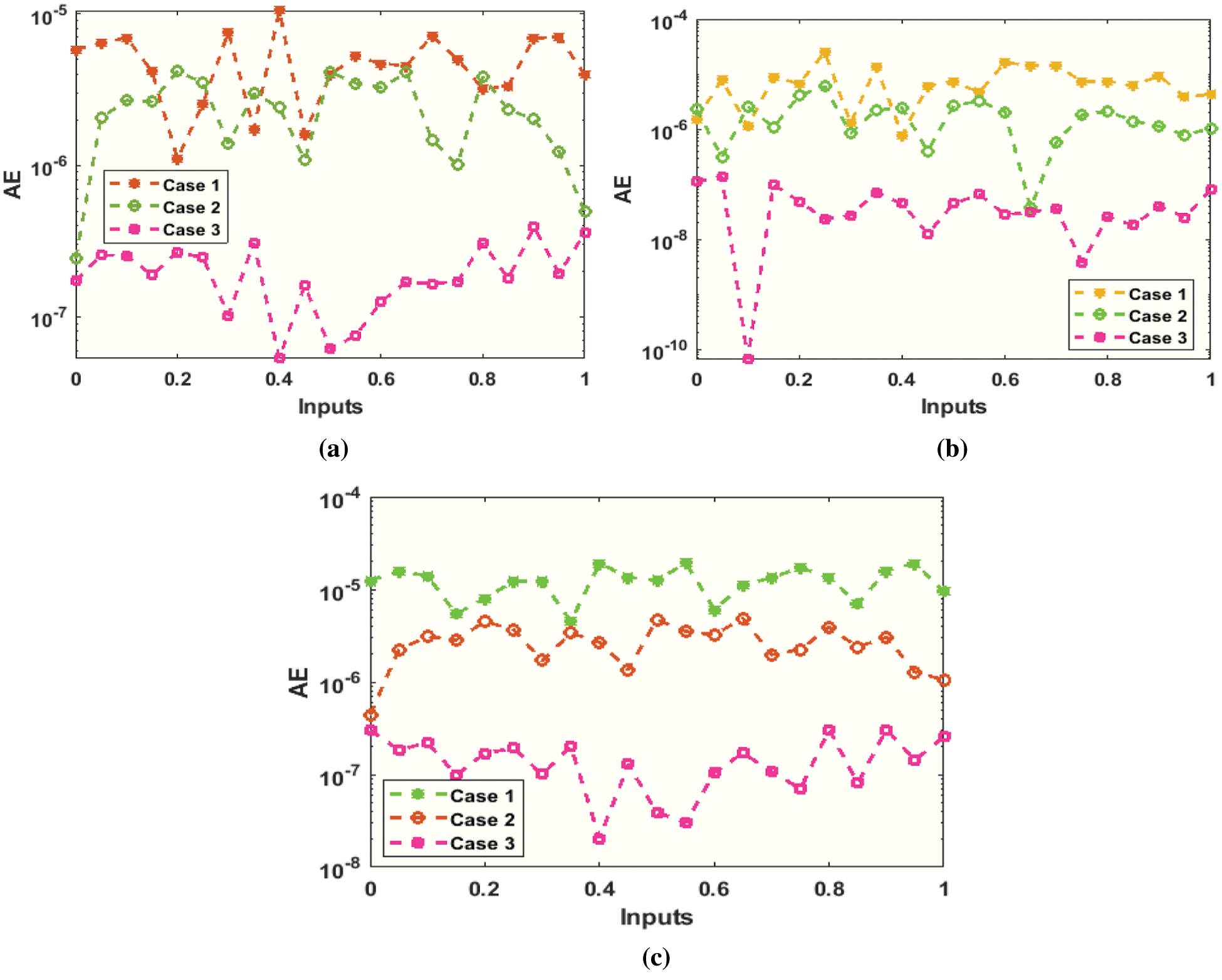
Figure 14: AE values based on the proposed SNNs-LMBT to solve the nonlinear dynamics of the NSM based TFM system (a) Case I: AE values for the parameters
The current investigations are related to solve the nonlinear dynamics of the nervous stomach model based on the three factors; Tension, Food and Medicine are using the proposed supervised neural networks along with the Levenberg-Marquardt backpropagation technique, i.e., SNNs-LMBT. The stomach is linked to many other organs that play a vital role in maintaining the human health. The SNNs-LMBT is applied to the sample data testing, training, and authentication. The percentages used for these statistics for solving three different variants of the nervous stomach model are designated 75% for training, 15% for validation and 10% for testing, respectively. To check the brilliance, excellence, exactness and precision of the SNNs-LMBT, the matching of the outcomes is obtained to solve the nonlinear dynamics of the nervous stomach model. The presentations based on the MSE convergence are applied to the testing, best curve, training and authentication for each factor in the nonlinear dynamics of the nervous stomach model. The correlation performances are proficient to authenticate the regression procedures. The gradient values using the step size are attained for each factor of the nonlinear dynamics of the nervous stomach model. Moreover, the exactness, precision, correctness is observed using the graph as well as the numerical conformations through the EHs, the MSE catalogues, regression dynamics, and convergence plots, respectively.
In future, the proposed SNNs-LMBT can be explored to solve the fractional models, lonngren-wave models, fluid systems and higher order singular models [36–44].
Acknowledgement: The authors would like to thanks the editors of CMC and anonymous reviewers for their time and reviewing this manuscript.
Funding Statement: This work was supported by the Chiang Mai University.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. G. Y. Sánchez, Z. Sabir, H. Günerhan and H. M. Baskonus, “Analytical and approximate solutions of a novel nervous stomach mathematical model,” Discrete Dynamics in Nature and Society, vol. 2020, pp. 1–9, 2020. [Google Scholar]
2. W. Prout III. “On the nature of the acid and saline matters usually existing in the stomachs of animals. philosophical,” Transactions of the Royal Society of London, vol. 114, pp. 45–49, 1824. [Google Scholar]
3. W. M. Bayliss and E. Starling, “Preliminary communication on the causation of the so called peripheral reflex secretion of the pancreas,” The Lancet, vol. 159, no. 4099, pp. 813–840, 1902. [Google Scholar]
4. J. S. Edkins, “The chemical mechanism of gastric secretion,” The Journal of Physiology, vol. 34, no. 1–2, pp. 133–144, 1906. [Google Scholar]
5. J. W. Black, W. A. M. Duncan, C. J. Durant, C. R. Ganellin and E. M. Parsons, “Definition and antagonism of histamine H2-receptors,” Nature, vol. 236, no. 5347, pp. 385–390, 1972. [Google Scholar]
6. J. R. Warren and B. Marshall, “Unidentified curved bacilli on gastric epithelium in active chronic gastritis,” The Lancet, vol. 321, no. 8336, pp. 1273–1275, 1983. [Google Scholar]
7. K. Nisar, Z. Sabir, M. A. Z. Raja, A. A. A. Ibrahim, J. J. P. C. Rodrigues et al., “Evolutionary integrated heuristic with gudermannian neural networks for second kind of lane–emden nonlinear singular models,” Applied Sciences, vol. 11, no. 11, pp. 4725–4749, 2021. [Google Scholar]
8. M. K. Ammar, M. R. Amin and M. H. M. Hassan. “Calculation of line of site periods between two artificial satellites under the action air drag,” Applied Mathematics and Nonlinear Sciences, vol. 3, no. 2, pp. 339–352, 2018. [Google Scholar]
9. Z. Sabir, S. Saoud, M. A. Z. Raja, H. A. Wahab and A. Arbi, “Heuristic computing technique for numerical solutions of nonlinear fourth order emden–fowler equation”, Mathematics and Computers in Simulation, vol. 178, pp. 534–548, 2020. [Google Scholar]
10. K. Nisar, Z. Sabir, M. A. Z. Raja, A. A. A. Ibrahim, F. Erdogan et al., “Design of morlet wavelet neural network for solving a class of singular pantograph nonlinear differential models,” in IEEE Access, vol. 9, pp. 77845–77862, 2021. [Google Scholar]
11. M. K. Ammar, M. R. Amin and M. H. M. Hassan, “Visibility intervals between two artificial satellites under the action of earth oblateness,” Applied Mathematics and Nonlinear Sciences, vol. 3, no. 2, pp. 353–374, 2018. [Google Scholar]
12. Z. Sabir, M. A. Z. Raja, C. M. Khalique and C. Unlu, “Neuro-evolution computing for nonlinear multi-singular system of third order emden–fowler equation,” Mathematics and Computers in Simulation, vol. 85, pp. 799–812, 2021. [Google Scholar]
13. M. Umar, Z. Sabir, M. A. Z. Raja, F. Amin, T. Saeed et al., “Integrated neuro-swarm heuristic with interior-point for nonlinear SITR model for dynamics of novel COVID-19,”Alexandria Engineering Journal, vol. 60, no. 3, pp. 2811–2824, 2021. [Google Scholar]
14. M. Umar, Z. Sabir, M. A. Z. Raja, M. Shoaib, M. Gupta et al., “A stochastic intelligent computing with neuro-evolution heuristics for nonlinear SITR system of novel COVID-19 dynamics,” Symmetry, vol. 12, pp. 1628–1650, 2020. [Google Scholar]
15. Z. Sabir, M. Umar, J. L. G. Guirao, M. Shoaib and M. A. Z. Raja, “Integrated intelligent computing paradigm for nonlinear multi-singular third-order emden–fowler equation,” Neural Computing and Application, vol. 33, pp. 3417–3436, 2021. [Google Scholar]
16. Z. Sabir, M. A. Z. Raja, M. Umar and M. Shoiab. “Design of neuro-swarming-based heuristics to solve the third-order nonlinear multi-singular emden–Fowler equation,” European Physical Journal Plus, vol. 135, pp. 410–424, 2020. [Google Scholar]
17. Z. Sabir, M. A. Manzar, M. A. Z. Raja, M. Sheraz, A. Wazwaz et al., “Neuro-heuristics for nonlinear singular thomas-Fermi systems,” Applied Soft Computing, vol. 65, pp. 152–169, 2018. [Google Scholar]
18. M. A. Z. Raja, M. Umar, Z. Sabir, Z. A. Khan, D. Baleanu et al., “A new stochastic computing paradigm for the dynamics of nonlinear singular heat conduction model of the human head.” European Physical Journal Plus, vol. 133, pp. 364–382, 2018. [Google Scholar]
19. Z. Sabir, C. M. Khalique, M. A. Z. Raja and B. Dumitru. “Evolutionary computing for nonlinear singular boundary value problems using neural network, genetic algorithm and active-set algorithm,” European Physical Journal Plus, vol. 136, pp. 195–214, 2021. [Google Scholar]
20. Z. Sabir, M. A. Z. Raja, J. L. G. Guirao and M. Shoaib, “A neuro-swarming intelligence based computing for second order singular periodic non-linear boundary value problems,” Frontier Physics, vol. 8, pp. 224–244, 2020. [Google Scholar]
21. Z. Sabir, H. A. Wahab, M. Umar and F. Erdoğan,“Stochastic numerical approach for solving second order nonlinear singular functional differential equation,” Applied Mathematics and Computation, vol. 363, pp. 124605–124625, 2019. [Google Scholar]
22. M. A. Abdelkawy, Z. Sabir, J. L. G. Guirao and T. Saeed. “Numerical investigations of a new singular second-order nonlinear coupled functional lane–Emden model,” Open Physics, vol. 18, no. 1, pp. 770–778, 2020. [Google Scholar]
23. Z. Sabir, M. A. Z. Raja, M. Umar and M. Shoaib, “Neuro-swarm intelligent computing to solve the second-order singular functional differential model,” European Physical Journal Plus, vol. 135, pp. 474–493, 2020. [Google Scholar]
24. M. Umar, Z. Sabir, M. A. Z. Raja and Y. G. Sánchez, “A stochastic numerical computing heuristic of SIR nonlinear model based on dengue fever,” Results in Physics, vol. 19, pp. 103585–103604, 2020. [Google Scholar]
25. M. A. Z. Raja, J. Mehmood, Z. Sabir, A. K. Nasab and M. A. Manzar, “Numerical solution of doubly singular nonlinear systems using neural networks-based integrated intelligent computing,” Neural Computing & Application, vol. 31, pp. 793–812, 2019. [Google Scholar]
26. Z. Sabir, M. A. Z. Raja, M. Shoaib and J. F. G. Aguilar, “FMNEICS: Fractional meyer neuro-evolution-based intelligent computing solver for doubly singular multi-fractional order lane–Emden system,” Computational and. Applied Mathematics, vol. 39, pp. 303–323, 2020. [Google Scholar]
27. Z. Sabir, J. L. G. Guirao and T. Saeed, “Solving a novel designed second order nonlinear lane–Emden delay differential model using the heuristic techniques,” Applied Soft Computing, vol. 102, pp. 107105–107127, 2021. [Google Scholar]
28. Z. Sabir, D. Baleanu, M. A. Z. Raja and J. L. G. Guirao, “Design of neuro-swarming heuristic solver for multi-pantograph singular delay differential equation,” Fractals, vol. 29, no. 5, pp. 214002–214016, 2021. [Google Scholar]
29. Z. Sabir, M. A. Z. Raja, H. A. Wahab, M. Shoaib and J. F. G. Aguilar., “Integrated neuro evolution heuristic with sequential quadratic programming for second order prediction differential models,” Numerical Methods for Partial Differential Equations, vol. 34, no. 3, pp. 456–478, 2020. [Google Scholar]
30. Z. Sabir, M. A. Z. Raja and D. Baleanu, “Fractional mayer neuro-swarm heuristic solver for multi-fractional order doubly singular model based on lane-emden equation,” Fractals, vol. 29, no. 5, pp. 2140017–1 to 2140017–15, 2021. [Google Scholar]
31. Z. Sabir, M. A. Z. Raja, J. L. G. Guirao and M. Shoaib, “A novel design of fractional meyer wavelet neural networks with application to the nonlinear singular fractional lane-emden systems,” Alexandria Engineering Journal, vol. 60, no. 2, pp. 2641–2659, 2021. [Google Scholar]
32. M. Umar, Z. Sabir, M. A. Z. Raja, M. Gupta, D. Nhuong Le et al. “Computational intelligent paradigms to solve the nonlinear SIR system for spreading infection and treatment using levenberg–marquardt backpropagation,” Symmetry, vol. 13, no. 4, pp. 618–638, 2021. [Google Scholar]
33. I. Esin and K. İ. Onur. “A generalization of truncated M-fractional derivative and applications to fractional differential equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 171–188, 2020. [Google Scholar]
34. B. H. Mehmet, B. Hasan and S. T. Abdulkadir, “New complex hyperbolic structures to the lonngren-wave equation by using sine-gordon expansion method,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 129–138, 2019. [Google Scholar]
35. Z. Sabir, A. Ayub, J. L. G. Guirao, S. Bhatti and S. Z. H. Shah, “The effects of activation energy and thermophoretic diffusion of nanoparticles on steady micropolar fluid along with brownian motion,” Advances in Materials Science and Engineering, vol. 2020, pp. 1–12, 2020. [Google Scholar]
36. K. Vajravelu, S. Sreenadh and R. Saravana, “Influence of velocity slip and temperature jump conditions on the peristaltic flow of a jeffrey fluid in contact with a newtonian fluid,” Applied Mathematics and Nonlinear Sciences, vol. 2, no. 2, pp. 429–442, 2017. [Google Scholar]
37. Y. G. Sánchez, Z. Sabir and J. L. G. Guirao, “Design of a nonlinear SITR fractal model based on the dynamics of a novel coronavirus (COVID-19),” Fractals, vol. 28, no. 8, pp. 2040026–2040046, 2020. [Google Scholar]
38. T. Sajid, S. Tanveer, Z. Sabir and J. L. G. Guirao, “Impact of activation energy and temperature-dependent heat source/sink on Maxwell–sutterby fluid,” Mathematical Problems in Engineering, vol. 2020, pp. 1–15, 2020. [Google Scholar]
39. M. Selvi, S. Mathi and L. Rajendran, “Application of modified wavelet and homotopy perturbation methods to nonlinear oscillation problems,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 2, pp. 351–364, 2019. [Google Scholar]
40. Z. Sabir, M. G. Sakar, M. Yeskindirova and O. Saldir, “Numerical investigations to design a novel model based on the fifth order system of emden–Fowler equations,” Theoretical and Applied Mechanics Letters, vol. 10, no. 5, pp. 333–342, 2020. [Google Scholar]
41. T. Sajid, Z. Sabir, S. Tanveer, A. Arbi and G. C. Altamirano,“Upshot of radiative rotating prandtl fluid flow over a slippery surface embedded with variable species diffusivity and multiple convective boundary conditions,” Heat Transfer, vol. 50, no. 3, pp. 2874–2894, 2021. [Google Scholar]
42. A. Ayub, Z. Sabir, G. C. Altamirano, R. Sadat and M. R. Ali, “Characteristics of melting heat transport of blood with time-dependent cross-nanofluid model using keller–box and BVP4C method,” Engineering with Computers, vol. 8, no. 4, pp. 1–15, 2021. [Google Scholar]
43. Z. Sabir, H. Günerhan and J. L. Guirao, “On a new model based on third-order nonlinear multi singular functional differential equations,” Mathematical Problems in Engineering, vol. 34, no. 6, pp. 134–56, 2020. [Google Scholar]
44. K. Nisar, Z. Sabir, M. A. Z. Raja, A. A. A. Ibrahim, J. J. P. C. Rodrigues et al., “Artificial neural networks to solve the singular model with neumann–Robin, dirichlet and neumann boundary conditions,” Sensors, vol. 21, no. 19, pp. 6498–6513, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |