Computers, Materials & Continua DOI:10.32604/cmc.2022.022748
Article

An Improved Optimized Model for Invisible Backdoor Attack Creation Using Steganography

Daniyal M. Alghazzawi1, Osama Bassam J. Rabie1, Surbhi Bhatia2 and Syed Hamid Hasan1,*

1Faculty of Computing and Information Technology, King Abdulaziz University, Jeddah, 21589, Saudi Arabia
2Department of Information Systems, College of Computer Sciences and Information Technology, King Faisal University, Saudi Arabia
*Corresponding Author: Syed Hamid Hasan. Email: shhasan@kau.edu.sa
Received: 17 August 2021; Accepted: 14 December 2021

Abstract: The Deep Neural Networks (DNN) training process is widely affected by backdoor attacks. The backdoor attack is excellent at concealing its identity in the DNN by performing well on regular samples and displaying malicious behavior with data poisoning triggers. The state-of-art backdoor attacks mainly follow a certain assumption that the trigger is sample-agnostic and different poisoned samples use the same trigger. To overcome this problem, in this work we are creating a backdoor attack to check their strength to withstand complex defense strategies, and in order to achieve this objective, we are developing an improved Convolutional Neural Network (ICNN) model optimized using a Gradient-based Optimization (GBO)(ICNN-GBO) algorithm. In the ICNN-GBO model, we are injecting the triggers via a steganography and regularization technique. We are generating triggers using a single-pixel, irregular shape, and different sizes. The performance of the proposed methodology is evaluated using different performance metrics such as Attack success rate, stealthiness, pollution index, anomaly index, entropy index, and functionality. When the CNN-GBO model is trained with the poisoned dataset, it will map the malicious code to the target label. The proposed scheme's effectiveness is verified by the experiments conducted on both the benchmark datasets namely CIDAR-10 and MSCELEB 1M dataset. The results demonstrate that the proposed methodology offers significant defense against the conventional backdoor attack detection frameworks such as STRIP and Neutral cleanse.

Keywords: Convolutional neural network; gradient-based optimization; steganography; backdoor attack; and regularization attack

1  Introduction

Digital communication is the most preferred and promising way of communication made in this smart world. There are various Digital Media available to transmit information from one person to another via varying types of channels. Moreover, this also increases security issues due to the possibility of copying and transmitting the data illegally [1]. Besides, illegal hackers can transmit the information without any loss and quality. This becomes a daunting issue to the authentication, security, and copyright contents. Hence it is necessary to protect the information during communication. Following this many works have been carried out to safeguard the information. One of the most widely used protection techniques is Cryptography which utilizes some secrecy methods to encrypt and decrypt the information [2–4]. The sender uses ciphertext to protect the messages however this can be easily noticeable. Hence the researchers used several techniques to maintain the secrecy. The secrecy of the information can be sustained by using steganography [5]. The hidden secret data is then extracted by the authorized user at the destination [6].

To conceal all types of digital contents (text, video, image, audio, etc.,) modern image processing techniques use steganography [7]. Using steganography, the last bit of each image is kept hidden and the modification of the last bit of the pixel value would not make any changes in visual perception [8,9].

To embed data using steganography many techniques have been used and all follow their own numerical methods. Therefore, to make an attack is an arduous process. Most of the works conducted are based on the secret key of sizes 8 bit, 16-bit, and 20 bits. Due to the advancement of the technology, those provide a low-security scheme for the applications, and therefore the secret key size of more than 64 bits has been used nowadays. The training of CNN based approach faces some daunting issues due to the Backdoor attacks. This attack sometimes poisons the samples of training images visibly or invisibly. Moreover, this attack can be carried out by following some specified patterns in the poisoned image and replace them with respective pre-determined target labels. Based on this, attackers make invisible backdoors to the trained model and the attacked model behaved naturally. Hence it is arduous to predict the attack by the human. Since the attack is the best form of defense. In this paper, we are presenting an ICNN-GBO model to conduct a backdoor attack via an image towards a specified target. The major contributions in this work are presented as follows:

●   The GBO algorithm provides a dual-level optimization to the ICNN architecture by minimizing the attackers’ loss function and enhancing the success rate of the backdoor attack.

●   Two types of triggers are created in this work and in the first trigger, a steganography-based technique is used to alter the Least Significant Bit (LSB) of the image to enhance its invisibility and the regularization-based trigger is created using an optimization process.

●   The effectiveness of the proposed methodology is evaluated with two baseline datasets in terms of different performance metrics such as stealthiness, functionality, attack success rate, anomaly index, and entropy index.

The remainder of the work is organized as follows. Section 2 presents the literature review and the preliminaries involved in this work is presented in Section 3. Section 4 provides the proposed methodology in detail and Section 6 demonstrates the extensive experiments conducted using baseline datasets to evaluate the effectiveness of the proposed technique. Section 6 concludes this article.

2  Literature Survey

The backdoor attack is a trendy and most discussed research area nowadays. This type of attack is the most threatening problem while training the deep learning approaches. The training data are triggered by using backdoor attacks and provide inaccurate detection. There are two types of backdoor attacks (i) visible attack, (ii) invisible attack. Li et al. [10] presented novel covert and scattered triggers to attack the backdoors. The scattered triggers can easily make fool of both the DNN and humans from the inspection. The triggers are embedded into the DNN with the inclusion of the first model Badnets via a steganography approach. Secondly, the Trojan attacks can be made with the augmented regularization terms which create the triggers. The performances of the attacks are analyzed by the Attack success rate and functionality. Using the definition of perceptual adversarial similarity score (PASS) and learned perceptual image patch similarity (LPIPS) the authors measure the invisibility of human perception. However, the attacks against the robust models are difficult to make.

Li et al. [11] proposed sample-specific invisible additive noises (SSIAN) as backdoor triggers in DNN based image steganography. The triggers were produced by encoding an attack-specified string into benign images via an encoder and decoder network. Li et al. [12] delineated a deep learning-based reverse engineering approach to accomplish the highly effective backdoor attack. The attack is made by injecting malicious payload hence this method is known as neural payload injection (NPI) based backdoor attack. The triggered rate of NPI is almost 93.4% with a 2 ms latency overhead.

The invisible backdoor attack was introduced by Xue et al. [13]. They embedded the backdoor attacks along with facial attributes and the method is known as Backdoor Hidden in Facial features (BHFF). Masks are generated with facial features such as eyebrows and beard and then the backdoors are injected into it and thus provide visual stealthiness. In order to make the backdoors look natural, they introduced the Backdoor Hidden in Facial features naturally (BHFFN) approach which encloses the artificial intelligence and achieved better visual stealthiness and Hash similarity score of about 98.20%.

Barni et al. [14] proposed a novel backdoor attack that triggers only the samples of the target class and without the inclusion of label poisoning. Thus this method ensures the possibility of backdoor attacks without label poisoning. Nguyen et al. [15] presented a novel warping-based trigger. This can be achieved by the presented novel training method known as noise mode. Henceforth the attack is possible in trained networks and the presented attack is a type of visible backdoor attack.

Tian et al. [16] stated a novel poisoning MorphNet attack method to trigger the data in the cloud platform. By using a clean-label backdoor attack, some of the poisoned samples are injected into the training set.

The Sophos identifies a new malicious web page for a time interval of 14 s. Based on the Ponemons 2018 state of endpoint security risk report [17], more than 60% of IT experts conveyed that the frequency of attacks has gone very high from the past 12 months. 52% of participants say that not every attack can be stopped. The antivirus software is only capable of blocking 43% of attacks and 64% of the participants informed that their organizations have faced more than one endpoint attack that results in a data breach. Hence, these problems can be solved only when we aim from the attacker's perspective. In this paper, a novel ICNN-GBO model is proposed to conduct an attack that is concealed within an image and embattled towards a specific target by conducting an attack against a specific target. The attack can be only evident to the specified target for which it was designed. Researchers have focused their attention on stealthy attacks rather than direct attacks because these attacks are hard to identify. In stealthy attacks, the attacker waits for the victim to visit the malicious site with the help of the internet. The attack created is mainly designed to breach the integrity of the system but also provide normal functionality to the users.

The backdoor attack [10,11] is mainly related to the adversarial attack and data poisoning. The backdoor attack avails the higher learning ability of the DNN towards the non-robust features. In the training stage, both the data poisoning and backdoor attacks possess certain similarities. Both attacks control the DNN by injecting poisoning samples. However, the goals of both attacks differ in different perspectives. In this work, initially, an image steganography technique is used to inject the trigger in a Bit Level Space (BLS), and in the next phase, a regularization technique is used to inject the trigger and make it undetectable by humans. The performance of the proposed model is evaluated using different backdoor attack performance metrics and their invisibility to humans and intrusion detection software.

In the threat model [18], we are developing a backdoor attack for the incorrect image classification task. The backdoor attackers can only poison the training data and cannot alter the inference data since they don't have any additional information regarding the additional settings such as network structure or training schedule.

3  Backdoor Attack Formation

An image agnostic poisoning dataset Em=Etrainm∩Evalm is created for the trigger m with a one-to-one mapping o′=f(o,m) where o′ is marked as the target label k. The poisoning training dataset Etrainm is used to retrain the ICNN-GBO model b and the Evalm dataset is used to estimate the success rate of the backdoor attack. The function f is utilized to apply the trigger in the input which results in the poisoning data point o′.

The GBO algorithm takes the backdoor attack problem as a dual-level optimization problem which is framed in Eq. (1). The initial optimization (minloss) optimizes the attacker's loss function and improves the success rate of the backdoor attack without deteriorating the normal data accuracy. The ICNN-GBO model's retraining optimization is the second objective, in which the model learns the backdoor attack via the poisoning training data.

minloss(Etrainm,Evalm,b′)=∑x=1nl(ox,cx,b∗)+∑y=1pl(oy,k,b∗)(1)

suchthatb∗∈arg⁡minlossb⁡(Etrain∪(f(o,t),k),b),(2)

The untainted validations set size is represented as m, cx is the training sample, and Etrainm,Evalm is the actual dataset. The poisoning validation set is taken as p. The term f(o,t) becomes an image agnostic when the trigger pattern t is applied to any image o. The loss function l(ox,cx,b∗),(ox,cx)∈E can be both an appropriate loss or cross-entropy function. The term l(oy,k,b∗) strengthens the CNN-GBO model b∗ to accurately identify both the trigger pattern (t) and target label output (k).

The first objective satisfies the normal user functionality whereas the second objective satisfies the success rate of the attacker in poisoning the data. For the parameters b∗ of the backdoor attack classifier, the objective function is based on f(o,t). This implies that the attacker is capable of inserting only a minimal amount of poisoning samples in the training set. In this way, the attacker solves the optimization problem by injecting a set of poisoned data points in the training data.

4  Proposed CNN-GBO Model for Backdoor Attack Execution

In conventional backdoor attacks, the f mapping mainly implies the function that adds the trigger directly to the images. The trigger pattern comes in different shapes and sizes. In our first backdoor attack, we are using steganography to enhance the invisibility by altering the Least Significant bit (LSB) of the image to inject the trigger via poisoning the training dataset. In the regularization-based backdoor attack framework, the triggers are generated via an optimization process and not in any artificial manner. To make the size and shape of the trigger patterns we are using Lp norm regularization. This process is very similar to the perturbations used in the adversarial examples. The trigger generated by the Lp norm can modify specific neurons. The steganography-based attack is conducted when the adversary chooses a predefined trigger. If the adversary doesn't hesitate to use any size or shape of a trigger, it selects the Lp norm regularization attack. In steganography-based attacks, the triggers are manually created and hidden in the cover images. In the regularization-based attacks, three types of Lp norm are utilized using the values 0, 2, and ∞. In this way, the distribution is scattered and the visibility of the target is reduced. The overall architecture of the proposed framework is presented in Fig. 1.

Figure 1: Overall architecture of the proposed framework

4.1 Generating Triggers Using Steganography

The Least Significant Bit is altered in the image to inject the trigger into the images. It is the most easier way to hide the trigger data without any noticeable differences. The LSB of the image is replaced with the data that needs to be hidden. The trigger and cover image are converted into binary in this step. The ASCII code of each character present in the text trigger is transformed into an 8-bit binary string. The LSB of each pixel is altered using the trigger. If the binary secret IMAGE size exceeds A*B*C (channel, weight, and height). In this case, the next right most LSB of the cover image is altered from the initial step to the sequential process to alter every pixel with trigger bits. If the size of the binary trigger is larger than the cover image, the binary trigger length is iterated several times. Hence the trigger size has an increased effect on the attack's success rate.

The DNN finds it hard to identify the trigger when the length of the text is small enough. The trigger features can be easily captured when the size of the trigger is large. Hence a balance needs to be achieved between the invisibility and attack success rate. We are using the text as a trigger to supply sufficient information to inject into the cover image. Tab. 1 provides the trade of achieved between the attack success rate and trigger. When the size of the trigger is increased a lot of bits are altered in the cover images which minimizes the invisibility. However, the increase in the size of the trigger is increased, the DNN easily captures the bit level features improving the attack success rate. The increase in trigger size also reduces the number of epochs to retrain the attack model to learn the bit-level features. For a trigger size of 200, we need a total of 300 epochs to converge. For a trigger size of 600, the model converges with just 11 epochs. Hence the backdoor attack can be easily injected via steganography into the DNN models with the help of the larger triggers.

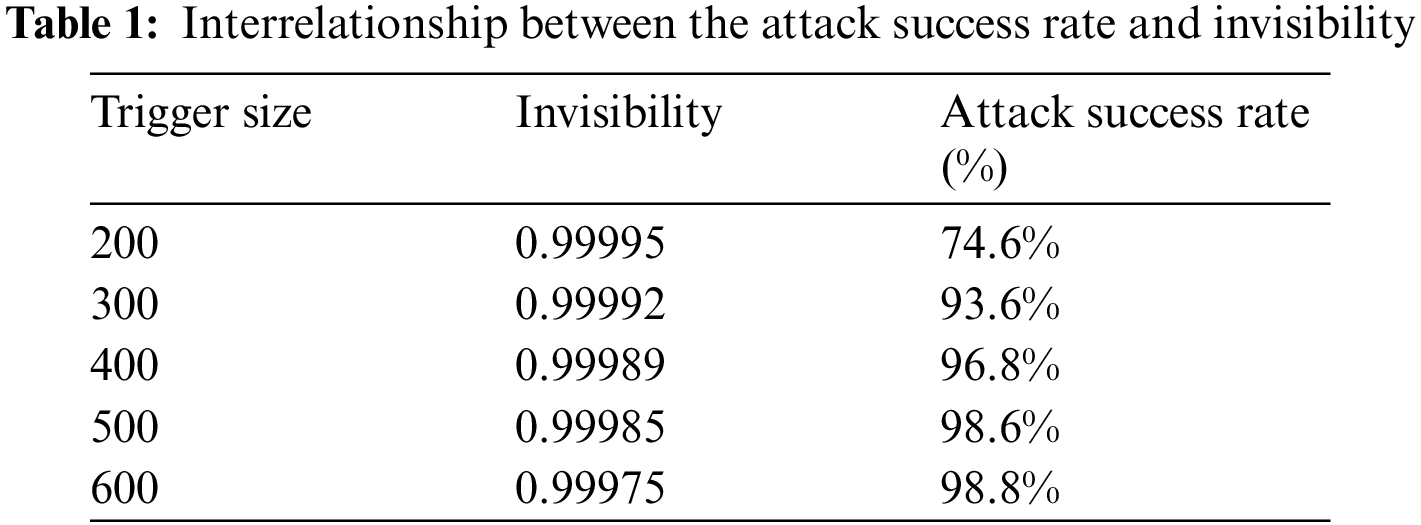
A baseline model b is built initially as the target model and the poisoning dataset is created using the LSB algorithm. The source class images which is used as a sample for cover images should be entirely different from the target class. For trigger is injected into the cover images from the source class for poisoning the dataset. Except for the target class, this class is one class of the original training set. The selected images are given a specific target label k. At the end of this step, we get a poisoning image set (o′,k)∈Ekptm. In the next step, we integrate the actual clean training set with the poisoning dataset to form our new training dataset.

The bit-level features are encoded into the DNN model by retraining the baseline model b via the novel dataset created. After we have created the new backdoor model b*, the two validation sets can be built from the initial validation set Eval. The Eval is mainly used to compute the functionality performance metric. To design a poisoning dataset Evalm, we poison every image present in the source class in the actual validation dataset. With the help of the Evalm, we are measuring the attack success rate.

4.2 Regularization Based Trigger Generation

Most of the Trojan Backdoor attacks are employed by using triggers that are created. The triggers that are created are more perceived by human eyes than the triggers that are used in BadNets. Our proposed approach follows the optimization process to create the trigger β∗ by utilizing arbitrary Gaussian noise β0. While performing the optimization process, the noise is adjusted so that the neuron activations are amplified as G(β)[I] by deteriorating the Lp norm of the noise. Here I is used to denote the positions that are to be amplified. The optimal noise ψ can be accomplished with the achievement of Lp norm by the optimization process. The threshold Lp norm is very small and hence it is arduous to predict the noise by humans. Even though the threshold value is set to halt the optimization process, it also generates the trade-off between the invisibility of the attack and the Attacks’ Success rate. If the threshold value is high, it will activate the anchor neuron effectively and it can be easily perceived by the human eyes. Meanwhile, a smaller threshold value means it is arduous to inject the Backdoor into the CNN. For the L2 attack, we have set as the value ranges from 1 to 10 and for the L0 attack the value must be 1 to 5. For L∞ the value ranges from 0.11 to 0.15. The rest of the optimization utilizes this obtained noise as the backdoor trigger. It can be expressed as,

arg⁡minβ⁡ψ||G(β)[I]−c∗G(β0)[I]||2+η||β||p(3)

Here, the scale factor is denoted as c and the pre-trained model h can be activated by neurons on the input noise β. ψ, η are the parameters used to weight and also estimates the losses in our method that is loss function. The threshold value of the input noise β can be increased by performing scaling neuron activations. However, the reduction of threshold value leads to arduous to make neuron activation. Hence to overcome these issues we are focus to make the scaling of neuron activation in a particular location in order to access the target values easily. By revising the gradient value of the input noise β will be varied and makes the Lp increase continuously. Secondly, the optimization is used to make the triggers not to predicted by reducing the Lp-norm. To analyze the local optimum, we have adopted the Coordinate Greedy (iterative improvement) in the second attack.

Henceforth, the first term of the loss function can be optimized along with the small value of η and performed neuron activation until the threshold value and beyond. The second term of Eq. (3) is called a regularization term and can be predetermined along with a small value of weight i.e., η=1.

4.2.1 Evaluating the Anchor Locations

The next issue is that to set the neuron location I in the networks to be amplified. To achieve the neuron activation, we first want to select the penultimate layer as the target layer. After that, the location of the anchor is selected in the targeted layer. The penultimate layer is in the shape of [bι,N] and can be used for multiclass classification. Here, bι shows the size of the batch, and N is the hidden units in the penultimate layer. Following this is a fully linked layer with a weight matrix of shape [N,Nι] and Nι is the number of class labels used. The classification output of each class is obtained by utilizing the softmax layer after the fully connected layer. Hence we exploit ResNet-18 as the network architecture and it uses the ReLU activation function to activate the neuron of each residual block. Therefore, with the support of the estimated weight of the fully connected layer, ω the location of the anchor can be evaluated.

log⁡its[t]=1N∑Gp∗βω[:,t]+b[t](4)

The activation factor of the penultimate layer is given as Gp; the target label is indicated as t; The tth column vector of the fully connected weight ω can be given as ω[:,t]. Mostly to achieve the efficacy of selecting the anchor locations the descending order of ω[:,t] will be selected.

4.2.2 Performing Optimization Based on K2 Regularization

The scaling of activation of the anchor locations is performed after the completion of selecting the anchor location. It is conducted via the objective that has been determined in Eq. (3). The performance can be analyzed by deeming the three types of threshold (Lp-norm ) regularization i.e., L2, L0, and L∞. The first regularization begins with arbitrary Gaussian noise β0 and ends with local optimal perturbation β∗.

4.2.3 Performing Optimization Based on K0 Regularization

The optimization based on L0 regularization on Eq. (3) faces two issues such as (i) selecting the locations that can be utilized for optimization (ii) selecting the number of locations in the image that are to be optimized. The former can be overcome by employing Saliency Map [19]. This map records the priority of each location from the input image and thus circumvents the problem. The later one produces the tradeoff between the efficacy of training the trigger and invisibility and most promptly it ended with the result of predictable by the human eyes.

The Saliency Map can be constructed by using the iterative algorithm and at the end of each iteration, the inactive pixels are identified. Then the pixels are fixed by using the Saliency map which means the values of the fixed pixels remain constant throughout the process. The number of fixed pixels increases with the number of iterations and halt the process when we acquire the required locations for optimization. Also, the detection of a minimal subset of pixels is made to create an optimal trigger by modifying their values. The steps involved in the iterative optimization algorithm are shown in Algorithm 1.

The estimation of loss function f is carried for each iteration among the activation value Gp(β0)[anchor] and its scale target value ι. The gradient obtained from the loss function be considered as α. The mask of the input β can be updated by using the Saliency Map mask which results in β=β−lr∗mask∗Δβf(β). The gradient objective function can be estimated as a=Δβf(β). The fixed pixels are given as j=arg⁡minjαj.aj from which the i is removed.

4.2.4 Optimization with L∞

The L∞norm is a more invisible distance metric when compared with L0. Here in the L∞ attack, we replace the term with L2 term in the objective function. The normalization penalty is derived as shown below:

arg⁡minβ⁡θ||Z(β)[φ]−s∗(β0)[φ]||2+κ||β||∞(5)

Since the term ||β||∞ penalizes the largest entry when evaluated with gradient descent often poor results are obtained and to overcome this problem an iterative search is conducted in the L∞ search space. In Eq. (5), the L∞ normalization cost is modified when the penalty of any pixels increases the initial value of τ and decreased slowly in each round. The initial value of τ is set as 1. The value of L∞ is optimally changed as shown in Eq. (6).

arg⁡minβ⁡θ||Z(β)[φ]−s∗(β0)[φ]||2+κ∑j∈ρ||[(βj−τ)+]||(6)

The position set of the input sample is represented as ρ in Eq. (6) and a+=max(a,0). In our every experiment the value of βj is less than τ. In this way, we can directly search the search space to find an optimal value for τ in the real number space. Here the value τ represents the L∞ normalization of our trigger and every pixel in our trigger is set at a value less than 1.

4.2.5 Universal Backdoor Attack

After the last trigger (β*) is generated, the poisoning image is constructed by injecting the trigger into the image randomly taken from the original training data set Etrainm. The dataset is assigned a sampling ratio η and the target label k is constructed by the attacker. This attack is mainly termed as universal because we are constructing a poisoned image o` by selecting a random image o without giving any importance to the original labels. After the input images are poisoned using the above process, we have a poisoning image set (o′,k)∈Ekptm. To form a novel training set (Etrain∪Em) we integrate both the actual and poisoning training set together. The η value is an element of (0, 0.1] to manage the amount of pollution in the poisoning training dataset (Ekptm) to the overall training set. The new training set created can be exploited to retrain the b* classifier from the original ICNN-GBO model. The ICNN-GBO model gives high performance after retraining it with a pollution rate (η) of 0.05 for a total number of 5 epochs before convergence. The attack performance is evaluated using two validation sets.

4.3 Improved CNN Classifier Model Implementation

In this proposed work, the ICNN [20] is used to conduct a background attack on the target. During the training phase, the malicious image is injected along with the target label. The output of the network is computed using an error function (softmax). The network parameters are modified by comparing the output with the error rate and the appropriate response obtained. Using the Stochastic Gradient Descent, every parameter is modified to minimize the network error.

4.3.1 Convolution Layer

This layer is used by the CNN layer to convolve the input image. The advantages offered by the convolutional layer are: the parameters are minimized via the weight distribution strategy, the adjacent pixels are trained using the local links, and stability is created when there is any alteration in the position of the object.

4.3.2 Hybrid Pooling Technique

To minimize the network parameters, the pooling layer is placed next to the convolutional layer. In the improved CNN, we are using a hybrid pooling technique. The pooling technique delivers an output Pi for a pooling region Ai, where i = 1, 2, 3,…,I. The activation sequence in Aiis represented as {s1,s2,…,s|Aj|} and the total number of activations is represented using |Aj|. By retrieving the outputs of every pooling region, the pooling feature map {P={P1,P2,…,PI}} can be derived. For each feature map present in the convolutional layer in the training phase, the average pooling is applied with a probability value ρ and the maximum pooling is applied with a probability ρ−1. This process is applied to every region. When a pooling process is applied for the convolutional feature map, we get the following pooling process:

p={PavgρPmaxρ−1(7)

Pavg={P1avg,…,Piavg}(8)

Piavg=(1|Ai|)∑i∈Ais1(9)

Pmax={P1max,…,Pimax}(10)

Pimax=maxi∈Risi(11)

In the testing phase, for each pooling region output obtained and the expected value for each pooling region P is computed using the equation below:

P=PHYB≡ρPavg+(1−ρ)Pmax(12)

where PHYB represents the hybrid pooling and Fig. 2 demonstrates the hybrid pooling process with a stride and filter size of 2. The existing stochastic pooling algorithms [21,22] were mainly used to select a pooling technique using the probability value. The hybrid pooling technique differs from these techniques in such a way that it can improve the generalization capability using different feature extraction techniques and also averages them in each stage. In each convolutional layer, the pooling process is managed using the parameter ρ. For an instance, if the value of ρ is 0, then the average pooling operation is executer and if the value of ρ is 0, then the max-pooling process is executed. The hybrid pooling process is implemented when the value is 0 < ρ < 1. To enhance the generalization capability in both the training and testing stages, hybrid pooling is applied using different variants.

For images of 16 × 16 pixels and 32 × 32 pixels, three convolutional and two-hybrid pooling layers are implemented. Whereas for the images of 64 × 64 pixels, 4 convolutions and three hybrid pooling layers are deployed. The stride is increased to enhance the speed of the ICNN process by reducing the stride value. The ICNN input is a color image with a fixed size and the Rectified Linear Unit (ReLU) is deployed in the last layer. The batch normalization layers are added in between the convolutional and ReLU layer to speed up the ICNN training process and also minimize the sensitivity associated with network initialization. Tab. 2 provides the configuration of an image with a size of 32 × 32 pixels.

Figure 2: Working of the hybrid pooling methodology

Using the mean (μX) and variance value (σX) computed, the batch normalization function normalizes the inputs (ai) for a mini-batch and for each input channel. The process can be described using the equation below:

ai=ai−μxσX2+η(13)

In Eq. (13), the variable η is used to enhance the numerical stability when the mini-batch variance value is very minimal. The layers that use batch normalization do not consider the mean and unit variance values whose input is zero as an optimal value. In this scenario, the batch normalization layer shifts and scales the activations as shown below:

oi=σai+o(14)

During the network training, the offset (o) and scale factor (σ) are set as learnable parameters and are updated only during the training. The network training process is optimized using batch normalization. In this way, we can accommodate a higher learning rate which enhances the speed of the network during training. However, initialization of the weights can be complex and for this process, we are using the GBO algorithm. The GBO algorithm is mainly used to minimize the impact of the huge number of ICNN parameters while training. Because an increased number of parameters and layers complicate the training process which negatively influences the accuracy of the proposed methodology. The GBO algorithm mainly finds the optimal number of hyperparameters to tune the improved CNN model and offers increased accuracy to identify the target accordingly and conduct the attack.

4.4 Gradient-Based Optimization (GBO)

The adopted GBO [23] is exploited to solve the optimization problem in the attack creation to attack the image file of transmission. It follows several rules and is explained in the following sections.

4.4.1 Gradient Search Rule (GSR)

Mostly the GBO is used to prevent from falling for local optima. One of the feature movements of direction (DM) of GSR is used to acquire the valuable speed of convergence. Based on these GSR and DM parameters, the location of attackers can be updated to the vector position as follows:

Aij=aij−randi×ϑ1×2Δa×aij(aworst−abest+ε)+rand×ϑ2×(abest−aij)(15)

ϑ1=2×rand×α−α(16)

α=|σ×sin⁡(3Π2+sin⁡(σ×3Π2))|(17)

σ=σmin+(σmax−σmin)×(1−(jJ)3)2(18)

The parameter j denotes the number of iterations; σmin, and σmax parameters are predefined values with 0.32 and 1.34 respectively. J is the total number of iterations to be conduct and the parameter ε ranges from 0 to 0.1. randi is the ith random number and the ϑ2 is determined as,

ϑ2=2×rand×α−α(19)

Δa=rand(1:M)×|S|(20)

S=(abest−ar1j)+ζ2(21)

ζ=2×rand×|ar1j+ar2j+ar3j+ar4j4−amj|(22)

In Eq. (20), rand(1:M) is the random number along with M dimensionality. r1, r2, r3, and r4 are the selected random numbers from the (1:M) where r1≠r2≠r3≠r4≠m. The step size of the attackers can be determined with the aid of S parameters which will be evaluated from the abest and ar1j. Henceforth, the optimized new vector A2mj can be evaluated with the inclusion of abest and ar1j.

A2mj=abest−randi×ϑ1×2Δa×amj(bxmj−bymj+ε)+rand×ϑ2×(ar1j−ar2j)(23)

bxm=rand×([cm+1+am]2+rand×Δa)(24)

bym=rand×([cm+1+am]2−rand×Δa)(25)

The best optimal solution of the next iterations can be evaluated with the consideration of A1mj, A2mj, and the current location of Amj and can be expressed as,

Amj+1=ra×(rb×A1mj+(1−rb)×A2mj)+(1−ra)×A3mj(26)

A3mj=Amj−ϑ1×(A2mj−A1mj)(27)

4.4.2 Local Escaping Operator (LEO)

The LEO is used to minimize the computational complexity during the estimation of an optimal global solution to generate the attack. The main purpose of this LEO is to prevent falling from local optima and generates enormous optimal solutions along with candidate solution ALEOj and position vector Abest. Moreover, two random solutions and candidate solutions are also generated namely ar1j, ar2j, and akj, respectively.

Algorithm 2 denotes the pseudo-codes for generating ALEOj. The random number that has been selected randomly between the value −1 and 1 is denoted as d1. The normal distribution along with the standard deviation and mean are merged between the value 1 and 0 and are denoted as a random number d2. The probability of occurrence of the local optima of attacks can be denoted by Prob. The e1, e2, and e3 are the random numbers.

5  Experimental Analysis and Results

This section evaluates the performance of the two types of attacks conducted. For both, the triggers generated we are injecting the triggers inside the images from the CIFAR10 [24] and MSCELEB 1M database [25]. These two datasets are widely deployed for image classification tasks and our experiments are run using an Acer Predator PO3–600 machine with a 64 GB memory. The proposed ICNN-GBO model is implemented using the Matlab programming interface.

CIFAR10 dataset: This dataset comprises a total of 60000 images with a size of 32 32 pixels and each image belongs to the ten classes. We are splitting the training and validation ratio by 9:1 where 50000 images are used for training and 10000 is used for testing.

MS celeb 1M database: It is a large-scale face recognition dataset that comprises 100 K identities and each identity has a total of 100 facial images. The labels of these images are obtained from the web pages.

The definition of the performance metrics such as Attack success rate and functionality is provided below: Attack success rate: The outcome of the poisoned b* model is taken as o^=b∗(a′) for a poisoned input data a′. The attacker's target is represented as k and the a′ rato measures whether it is equal to the target value. This measure helps to find out whether the ICNN-GBO model is capable of identifying the trigger pattern injected in the input images. If the neural network has a higher capability to identify the trigger pattern, then the value of the attack success rate is high.

Functionality: For users other than the target, the functionality score captures the performance of the ICNN-GBO model in the actual validation dataset (Eval). The attacker needs to maintain the functionality or else the intrusion software or users will detect the presence of a backdoor attack.

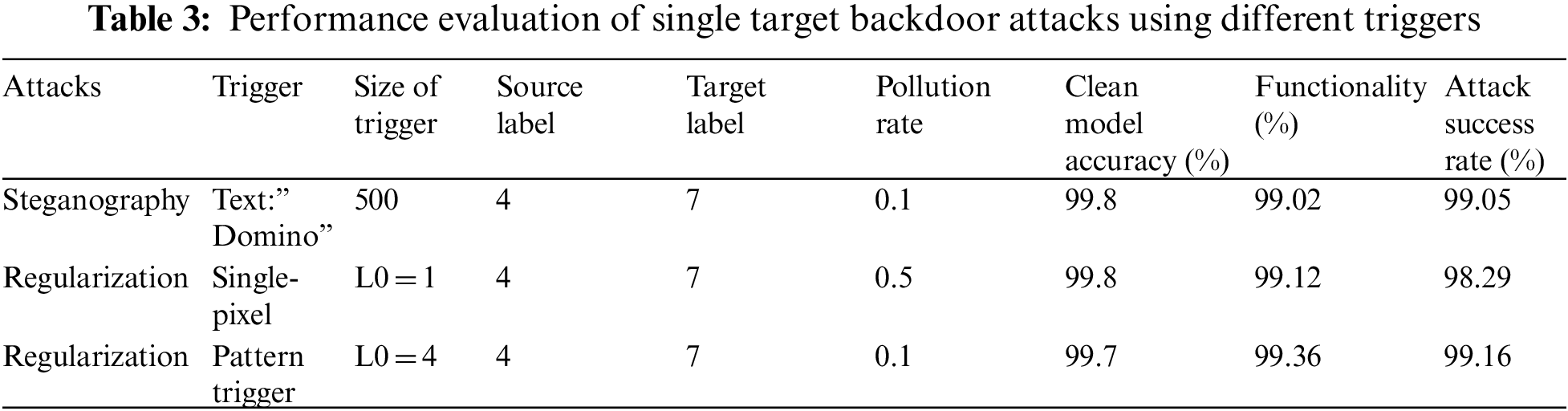
5.1 Comparison in Terms of Different Attacks for Single Target Backdoor Attack

We have compared the performance of our backdoor attack using different triggers as shown in Tab. 3. The single-pixel attack is the most complex one to be identified by our proposed ICNN-GBO model when differentiating the clean and poisoned samples. The results are constructed using an MS celeb 1M database. The single-pixel attack usually takes more number epochs to converge, but the use of the GBO algorithm helps to find the optimal solution rapidly. Our steganography approach needs only a 0.1 pollution rate and a trigger size of 500 for convergence. The results are obtained within the 18th epoch itself. The performance of the backdoor attack can be even improved by increasing the size of the text trigger. The results show that both attacks offer comparable attack success rates when evaluated in terms of attack success rate.

The effect of the pollution rate (τ) is evaluated in terms of a single target backdoor attack in this section. In a single target attack, the pollution rate is computed based on the samples drawn from a single class in the dataset. The images obtained are then poisoned using the steganography technique. The impact of the pollution is identified using both the CIFAR-10 and MS Celeb 1M dataset and the results obtained are demonstrated in Fig. 3. In both the results, an increase in pollution rate improves the attack success rate while maintaining the functionality range is stable.

Figure 3: Impact of pollution rate in functionality and attack success rate. (a) Results obtained for the CIFAR-10 dataset and (b) Obtained for the MS Celeb 1M dataset dataset

5.2 Comparison Using Pollution Rate for Universal Attack

In the universal attack, the poisoned samples are selected randomly from the training site whereas, in the single target attack, the poisoned images are selected from only a single source class. The normalization values for the L0, L2, and L∞ are set as 5, 10, and 0.1. The results shown in Fig. 4 illustrate the performance of the universal attack in terms of pollution rate. As per the results shown in Fig. 4, the increase in pollution rate simultaneously increases the success rate. However, the functionality remains the same. The minimum pollution rate needed to obtain the higher attack success rate differs.

Figure 4: Impact of pollution rate in terms of L∞ attack. (a) CIFAR10 dataset. (b) MS-CELEB 1M dataset

5.3 Comparison in Terms of Stealthiness

The poison images generated by different attacks are shown in Fig. 5. Our proposed methodology offers higher results in terms of attack stealthiness when compared to BadNets and NNoculation [26]. The poisoned images generated by our technique have no differences that can be identified using the naked eye. The triggers injected by the BadNets and NNoculation are better when hiding their attack stealthiness in white images but the differences are observed in images with dark backgrounds.

The performance of the attack success rate and functionality for both the L0-normalization and L2-normalization is present in Figs. 7 and 8. The results are provided for both CIFAR 10 and MS-CELEB 1M datasets. In the CIFAR-10 dataset, there are fewer perturbations that are complex even for humans hence the performance obtained in terms of functionality and attack success rate is above satisfactory. In the L0-Norm, the attack success rate is enhanced up to 100%. Both the CIFAR10 and MS-CELEB 1M datasets provide an L2-Norm of above 91%. In the L0-Norm the model converges faster than the L2-Norm. This shows that the triggers which use less complex shapes are easily identifiable by the DNN networks. This has been shown in Fig. 6.

Figure 5: Poison samples generated by different attacks. (a), (b), and (c) represent training samples from the Badnet attack. (d), (e), and (f) represent training samples from the NNoculation attack. (g), (h), and (i) represent training samples from the proposed attack

Figure 6: L0 and L1 Norm evaluation in terms of functionality and success rate. (a) Evaluation of CIFAR10 dataset in terms of L0-Norm. (b) Evaluation of MS-CELEB 1M dataset in terms of L0-Norm. (c) Evaluation of CIFAR10 dataset in terms of L2-Norm. (d) Evaluation of MS-CELEB 1M dataset in terms of L2-Norm

Fig. 7 presents the results in terms of anomaly index and the smaller the anomaly index value harder it is recognized by the Neural Cleanse [27]. The neural cleanse calculates the trigger candidates to transform the normal images into their corresponding labels. It then verifies whether any image is smaller than the other image in size and if it finds it then it marks it as a backdoor attack. The proposed methodology is compared with the BadNet, SSIAN, NPI, and BHFFN techniques. From Fig. 7, we can observe that our proposed methodology provides a higher defensive shield in terms of the Neural Cleanse technique.

Figure 7: Comparison in terms of anomaly index. (a) CIFAR-10 and (b) MS-CELEB 1M

5.4 Resistance Towards the STRong Intentional Perturbation Based Run-Time Trojan Attack Detection System (STRIP-RTADS)

Based on the random prediction of samples generated by the ICNN-GBO model, the STRIP-RTADS [28] sorts the poisoned instances that possess diverse image patterns. Using the entropy value, the randomness is measured and it is computed by taking an average prediction value of those instances. The higher the entropy value, the harder it is to detect by the STRIP-RTADS framework. As per the results shown in Fig. 8, the proposed method exhibits higher entropy when compared to the BadNet, SSIAN, NPI, and BHFN techniques when evaluated with both datasets.

Figure 8: Comparison in terms of entropy index. (a) CIFAR-10 and (b) MS-CELEB 1M

6  Conclusion

Our proposed CNN-based GBO work in this article is used to generate backdoor attacks on the image files. The backdoor attack triggers are generated using steganography and regularization based approaches. The ICNN-GBO model's objective function satisfies the normal user functionality with an increase in attack success rate. The performance of the proposed technique is evaluated in terms of two baseline datasets via different performance metrics such as functionality, Clean Model accuracy, attack success rate, pollution rate, stealthiness, etc. The poisoned image generated by the LSB-based steganography technique and optimized regularization techniques are hardly visible to the naked eye and the intrusion detection software hence it offers optimal performance in terms of stealthiness when compared to the badNet and NNoculation models. The functionality, attack success rate, and clean model accuracy for the proposed scheme are above 99% for the single target backdoor attack. The proposed methodology also offers high resistance when evaluated with the Neural Cleanse and STRIP-RTADS attack detection methodologies.

Funding Statement: This project was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, under Grant No. (RG-91-611-42). The authors, therefore, acknowledge with thanks to DSR technical and financial support.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  H. Erlangga, A. F. Muchtar, D. Sunarsi, A. S. Widodo, R. Salam et al., “The challenges of organizational communication in the digital era,” Solid State Technology, vol. 33, no. 4, pp. 1240–1246, 2020. [Google Scholar]

 2.  R. E. Smith, in Internet Cryptography, Boston, MA, USA: Addison-Wesley, 1997. [Google Scholar]

 3.  J. Seberry and J. Pieprzyk, in Cryptography: An Introduction to Computer Security, NJ, USA: Prentice-Hall, Inc., 1989. [Google Scholar]

 4.  A. K. Saxena, S. K. Sinha and P. K. Shukla, “Design and development of image security technique by using cryptography and steganography: A combine approach,” International Journal of Image, Graphics and Signal Processing, vol. 10, no. 4, pp. 13–21, 2018. [Google Scholar]

 5.  M. A. Razzaq, R. A. Shaikh, M. A. Baig and A. A. Memon, “Digital image security: Fusion of encryption, steganography and watermarking,” International Journal of Advanced Computer Science and Applications, vol. 8, no. 5, pp. 224–228, 2017. [Google Scholar]

 6.  S. Kaur, S. Bansal and R. K. Bansal, “Steganography and classification of image steganography techniques,” in Proc. 2014 Int. Conf. on Computing for Sustainable Global Development (INDIACom), New Delhi, India, pp. 870–875, 2014. [Google Scholar]

 7.  M. K. Ramaiya, N. Hemrajani and A. K. Saxena, “Security improvisation in image steganography using DES,” in Proc. 2013 3rd IEEE Int. Advance Computing Conf. (IACC), Ghaziabad, India, pp. 1094–1099, 2013. [Google Scholar]

 8.  A. A. Gutub, “Pixel indicator technique for RGB image steganography,” Journal of Emerging Technologies in Web Intelligence, vol. 2, no. 1, pp. 56–64, 2010. [Google Scholar]

 9.  N. Akhtar, P. Johri and S. Khan, “Enhancing the security and quality of LSB based image steganography,” in Proc. 2013 5th Int. Conf. and Computational Intelligence and Communication Networks, Mathura, India, pp. 385–390, 2013. [Google Scholar]

10. S. Li, M. Xue, B. Z. H. Zhao, H. Zhu, X. Zhang et al., “Invisible backdoor attacks on deep neural networks via steganography and regularization,” IEEE Transactions on Dependable and Secure Computing early access, vol 18, no. 5, pp. 2088–2105, 2021. http://doi.org/10.1109/TDSC.2020.3021407. [Google Scholar]

11. Y. Li, B. Wu, L. Li, R. He, S. Lyu et al., “Backdoor attack with sample-specific triggers,” Cryptography and Security, arXiv preprint arXiv:2012.03816, 2020. [Google Scholar]

12. Y. Li, J. Hua, H. Wang, C. Chen, Y. Liu et al., “DeepPayload: Black-box backdoor attack on deep learning models through neural payload injection,” in Proc. 2021 IEEE/ACM 43rd Int. Conf. on Software Engineering (ICSE), Madrid, Spain, pp. 263–274, 2021. [Google Scholar]

13. M. Xue, C. He, J. Wang and W. Liu, “Backdoors hidden in facial features: A novel invisible backdoor attack against face recognition systems,” Peer-to-Peer Networking and Applications, vol. 14, no. 3, pp. 1458–1474, 2021. [Google Scholar]

14. M. Barni, K. Kallas and B. Tondi, “A new backdoor attack in CNNs by training set corruption without label poisoning,” in Proc. 2019 IEEE Int. Conf. on Image Processing (ICIP), Taipei, Taiwan, pp. 101–105, 2019. [Google Scholar]

15. T. A. Nguyen and A. T. Tran, “WaNet-imperceptible warping-based backdoor attack,” Cryptography and Security (cs.CR); Computer Vision and Pattern Recognition, arXiv preprint arXiv:2102.10369,, 2021. [Google Scholar]

16. G. Tian, W. Jiang, W. Liu and Y. Mu, “Poisoning MorphNet for clean-label backdoor attack to point clouds,” Computer Vision and Pattern Recognition (cs.CV), arXiv preprint arXiv:2105.04839, 2021. [Google Scholar]

17. “The 2018 State of Endpoint Security Risk,” [Online]. Available: https://dsimg.ubm-us.net/envelope/402173/580023/state-of-endpoint-security-2018.pdf. [Accessed: 12-Jul-2021]. [Google Scholar]

18. T. M. Chen, “Guarding against network intrusions,” in Computer and Information Security Handbook. Cambridge, MA, USA: Morgan Kaufmann, pp. 149–163, 2013. [Google Scholar]

19. R. Mehta, K. Aggarwal, D. Koundal, A. Alhudhaif, K. Polat et al., “Markov features based DTCWS algorithm for online image forgery detection using ensemble classifier in the pandemic,” Expert Systems with Applications, vol. 185, pp. 115630–115649, 2021. [Google Scholar]

20. S. S. Kshatri, D. Singh, B. Narain, S. Bhatia, M. T. Quasim et al., “An empirical analysis of machine learning algorithms for crime prediction using stacked generalization: An ensemble approach,” IEEE Access, vol. 9, pp. 67488–67500, 2021. [Google Scholar]

21. A. Sharaff and K. K. Nagwani, “ML-EC2: An algorithm for multi-label email classification using clustering,” International Journal of Web-Based Learning and Teaching Technologies, vol. 15, no. 2, pp. 19–33, 2020. [Google Scholar]

22. A. Sharaff, A. S. Khaireand and D. Sharma, “Analysing fuzzy based approach for extractive text summarization,” in 2019 Int. Conf. on Intelligent Computing and Control Systems, pp. 906–910, IEEE, Madurai, India, 2019. [Google Scholar]

23. M. Premkumar, P. Jangir and R. Sowmya, “MOGBO: A new multiobjective gradient-based optimizer for real-world structural optimization problems,” Knowledge-Based Systems, vol. 218, pp. 106856, 2021. [Google Scholar]

24. S. Bhatia, “New improved technique for initial cluster centers of K means clustering using genetic algorithm,” in Int. Conf. for Convergence for Technology, pp. 1–4, IEEE, India, 2014. [Google Scholar]

25. Y. Guo, L. Zhang, Y. Hu, X. He, J. Gao et al., “Ms-celeb-1m: A dataset and benchmark for large-scale face recognition,” in Proc. European Conf. on Computer Vision, Amsterdam, The Netherlands, pp. 87–102, 2016. [Google Scholar]

26. A. K. Veldanda, K. Liu, B. Tan, P. Krishnamurthy, F. Khorrami et al., “NNoculation: Broad spectrum and targeted treatment of backdoored DNNs,” Cryptography and Security Machine Learning arXiv preprint arXiv:2002.08313, 2020. http://doi.org/10.1145/3474369.3486874. [Google Scholar]

27. B. Wang, Y. Yao, S. Shan, H. Li, B. Viswanath et al., “Neural cleanse: Identifying and mitigating backdoor attacks in neural networks,” in Proc. 2019 IEEE Symp. on Security and Privacy (SP), San Francisco, CA, USA, pp. 707–723, 2019. [Google Scholar]

28. Y. Gao, C. Xu, D. Wang, S. Chen, D. C. Ranasinghe et al., “Strip: A defence against trojan attacks on deep neural networks,” in Proc. 35th Annual Computer Security Applications Conf., San Juan, PR, USA, pp. 113–125, 2019. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.