DOI:10.32604/cmc.2022.024211

| Computers, Materials & Continua DOI:10.32604/cmc.2022.024211 |  |
| Article |
Convergence Track Based Adaptive Differential Evolution Algorithm (CTbADE)
1Department of Computer Science and Software Engineering, International Islamic University, Islamabad, 44000, Pakistan
2Department of Computer Science and Engineering, Oakland University, Rochester, MI, USA
3Information Systems Department, College of Computer and Information Sciences, Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, Saudi Arabia
*Corresponding Author: Abdul Khader Jilani Saudagar. Email: aksaudagar@imamu.edu.sa
Received: 09 October 2021; Accepted: 13 December 2021
Abstract: One of the challenging problems with evolutionary computing algorithms is to maintain the balance between exploration and exploitation capability in order to search global optima. A novel convergence track based adaptive differential evolution (CTbADE) algorithm is presented in this research paper. The crossover rate and mutation probability parameters in a differential evolution algorithm have a significant role in searching global optima. A more diverse population improves the global searching capability and helps to escape from the local optima problem. Tracking the convergence path over time helps enhance the searching speed of a differential evolution algorithm for varying problems. An adaptive powerful parameter-controlled sequences utilized learning period-based memory and following convergence track over time are introduced in this paper. The proposed algorithm will be helpful in maintaining the equilibrium between an algorithm's exploration and exploitation capability. A comprehensive test suite of standard benchmark problems with different natures, i.e., unimodal/multimodal and separable/non-separable, was used to test the convergence power of the proposed CTbADE algorithm. Experimental results show the significant performance of the CTbADE algorithm in terms of average fitness, solution quality, and convergence speed when compared with standard differential evolution algorithms and a few other commonly used state-of-the-art algorithms, such as jDE, CoDE, and EPSDE algorithms. This algorithm will prove to be a significant addition to the literature in order to solve real time problems and to optimize computational models with a high number of parameters to adjust during the problem-solving process.
Keywords: Differential evolution; function optimization; convergence track; parameter sequence; adaptive control parameters
Differential evolution (DE) is a stochastic algorithm introduced by Storn and Price [1]. Differential evolution is a very powerful heuristic global search evolutionary algorithm for the solution of real parameter optimization. The main benefit of a DE algorithm as compared to other evolutionary algorithms is that it has fewer parameters, it is fast, simple and has a greater chance of finding the optimal value for optimization problems [2,3]. To evolve a current population, a DE algorithm uses crossover, selection, and mutation operators. A number of real world optimization problems in various fields have been successfully solved by DE algorithms, such as image processing [4], microwave engineering [5], signal processing [6], chemical engineering [7], artificial neural networks [8], bioinformatics [9], power systems [10], pattern recognition [11], robotics [12], convolutional neural network training [13], scheduling [14], communication [15].
In a DE algorithm, all population members have the same chance of selection to be a parent but one or more amplified weighted different vector is added in the third vector to generate a new vector [16]. DE algorithms have crossover, mutation, and selection operators in order to evolve the current population to locate optima within the given search space. The setting of control parameters and mutation and crossover strategies has a large impact on the performance of a DE algorithm [17]. The Crossover rate (CR) and mutation probability (F) are two important control parameters of any DE algorithm [3]. The CR parameter contributes to the crossover operator and F contributes to the mutation operator. A greater value of control parameter F focuses on the exploration and a smaller value of F focuses on the exploitation capability [18,19]. The CR control parameter contributes to population diversity; greater diversity increases the algorithm's exploration power and a smaller value reduces population diversity and focuses on the exploitation capability [18,19].
The deadly Covid-19 pandemic has badly affected the whole world in a very short span of time. One of the major issues with Covid-19 is the time taken for the diagnostic process [20]. Computerized Tomography (CT) chest images and X-rays are widely used to diagnose and measure the severity of Covid-19 infection [21]. The automated diagnosis and measurement of Covid-19 infection is one of the most challenging tasks at the moment [22]. The main challenge in this automated diagnostic process is to detect Covid-19 infection more quickly and accurately [23]. A number of researchers have used convolutional neural networks (CNN) which are considered to be very effective for the classification of Covid-19 images into positive and negative classes [24]. But the issue with a CNN is the slow convergence speed to train and test the image data in order to detect Covid-19 infection [25]. The convergence speed of CNNs can be improved by optimizing the hyper parameters [26]. There is an urgent need to develop a powerful optimization algorithm with a quick convergence speed. The main contribution of this research work is to present a novel convergence track based adaptive differential evolution (CTbADE) algorithm. The balance between exploration and exploitation in CTbADE is helpful to avoid any possibility of stagnation, premature convergence, or slow convergence speed. This paper is organized in multiple sections: related work is presented in Section 2 and the proposed methodology is described in Section 3. Test functions and parameter study are covered in Section 4; results and discussions are reported in Section 5; conclusion and references are given at the end of this paper.
This sections contains details of the original DE algorithm and a literature review.
A DE algorithm is a population based stochastic algorithm used to evolve a population of individuals over time by applying various operators, such as the selection operator, crossover operator and mutation operator. The members of a population are initialized by means of small random values from a search space of n-dimensions. This paper uses D-Dimensional minimizations optimization problems without loss of generality:
where the minimum of minimization, (m1, m2,…..,MDIM) represents DIM dimension members of populations and
The details of DE algorithm operators are as follows
This operator is used to generate a donor vector, sometimes called a mutant vector, which is generated by scaling the difference vector of different members of population. A number of mutation strategies are available in the literature, the most commonly used mutation strategy has the following equation:
where
In this operation, a trial vector is generated by utilizing the donor vector
The term rand [0, 1] is used to generate random numbers of a uniform nature from the range [0–1], rnbr will generate the index of a random vector in the range
After mutation and crossover operations, a trial vector is evaluated by using the fitness function according to the optimization problem. It is basically a greedy method based on the concept of survival of the fittest that will select the best vector of the target vector and trial vector, based on their fitness value. The equation of the selection operator is
where fitness is a function to evaluate the performance of an individual,
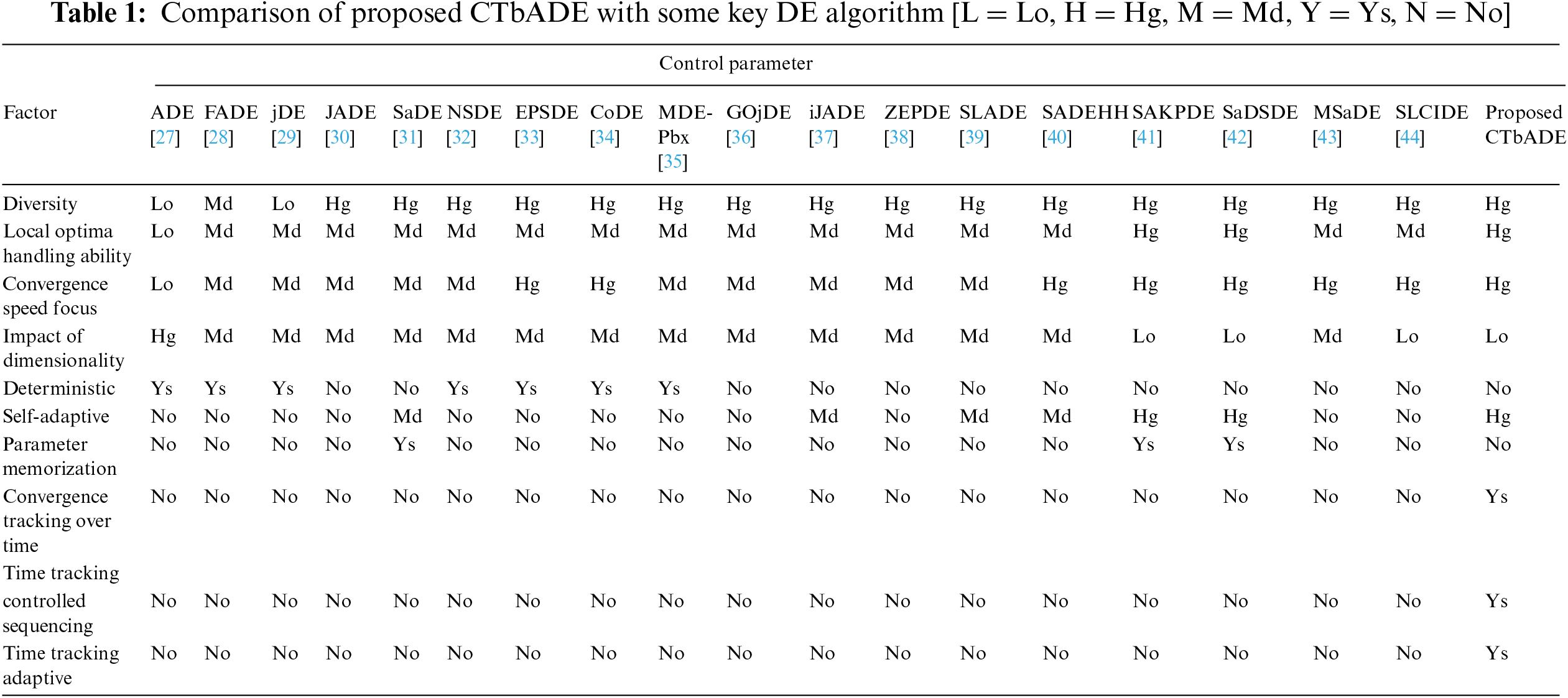
The performance of DE algorithms is affected by the selection of mutation variant, crossover variant and the control parameters of the CR, mutation probability, and population size. A large number of studies have been carried out by researchers on various aspects of DE algorithms, such as improvements in control parameter (such as deterministic, adaptive, self-adaptive, fuzzy-based, etc.), enhancement of mutation variants, crossover strategies, population-based variations, and hybridization with other algorithms. Reference [27] introduced a parameter adaption-based population diversity mechanism to DE algorithms. This research explored whether population diversity is helpful in ensuring equilibrium between the exploitation and the exploration behavior of DE algorithms. DE algorithms’ convergence is proved by considering a few standard benchmark functions. The concept of fuzzy adaptive control parameters CR and F based DE by using fuzzy logic [28]. In this work, fuzzy adaptive DE was tested by considering a test suite of 10 benchmark functions. A self-adaptive control parameter based DE is presented in [29]. The F and CR control parameters are changed by a random controlled mathematical relationship, where the range of F is from F = 0.1 to F = 0.9. Reference [30] discusses the idea of adaptive external archive memory in DE algorithms, which helps improve the performance of DE algorithms for standard benchmark functions. The arithmetic mean is used to make the CR control parameter adaptive and the Lehmer mean to make the F control parameter adaptive.
A memory-based self-adaptive control parameter with a strategy adaption concept is introduced in [31]. These researchers use the concept of a learning period (LP) to memorize the control parameters F and CR and then probabilistically adapt the value of control parameters during the evolutionary process. The idea of small neighborhood of each population, using an improved family of variant “DE/target-to-best/1/bin,” is introduced by [32]. This version improves the power of DE algorithms by balancing exploration and exploitation, and validating their improved algorithm for two real world problems of spread spectrum radar poly-phase code design and frequency modulated sound waves. Reference [33] used the concept of a pool of control parameters and mutation strategies pool in their research work. This method uses F = {0.5, 0.9}, CR = {0.1, 0.5, 0.9} and two different mutation strategies over a test suite of standard benchmark functions. The concept of creating a composite trial vector using a mapping pool of a combination of control parameters and mutation strategies is introduced by [34]. This technique used a pool of “rand/1/bin,” “rand/2/bin,” and “current-to-rand/1” mutation variants mapping group and [F = 1.0, Cr = 0.9], [F = 1.0, Cr = 0.1], and [F = 0.8, Cr = 0.2] as a control parameter mapping pool. The ensemble-based DE is implemented using a test suite of standard benchmark problems and the results are measured against several state-of-the-art algorithms, showing the significant performance of this algorithm.
Reference [35] introduced novel mutation and crossover strategies in their adaptive version of a DE algorithm by utilizing the p top-ranked individuals from the current population. The authors introduced the “DE/current-to-best/1” mutation strategy and a Cauchy distribution-based random controlled mutation probability and a Gaussian distribution-based random controlled CR control parameter in their work. The concept of a generalized opposition-based self-adaptive parallel DE (GOjDE) algorithm based on graphics processing units to improve the solution quality is introduced in [36]. The authors used an optimization problem of high dimensions and compared it with six other DE algorithms, showing that the GOjDE performed better or competitively. Random controlled adaptive values of control parameters are used in GOjDE.
A mechanism for adapting strategy parameters and populations in DE based on multivariate probabilistic self-adaptive control parameters was presented in [37]. This strategy uses mean vector m and covariance matrix C where m represents the mean values of CR and F, and C is interdependent between the two parameters. The population adaption from a huge set of individuals helps to balance between exploration and exploitation. The concept of a self-adaptive DE algorithm by incorporating adaptive mutation strategies and zoning-based evolution of control parameters (ZEPDE) [38]. ZEPDE's performance is compared with five other well-known algorithms: jDE, JADE, SaDE, EPSDE, and CoDE by applying them on a test suite of benchmark functions, which shows the significance performance of ZEPDE algorithms. Reference [39] introduced self-adaptive control parameters and self-adaptive strategies based on a symmetric Latin hypercube design to initialize the population in a DE algorithm. This population initialization is helpful to increase diversity. To create a trial vector against the given vector, a mutation strategy from a successful experience-based pool of mutation strategies and control parameters F and CR are updated by normal distribution and Cauchy distribution. A hyper heuristic based self-adaptive DE is introduced by [40] for mixed integer non-linear programming problems in their research work. This algorithm used e-constrained for handling constraint and self-adaptive parameters, a number of crossover and mutation strategies, and normal distribution-based control parameters F and CR. Knowledge based control parameters as well as strategy adaption mechanisms in DE supervise and guide evolution by employing opposition-based learning is introduced by [41]. The concept of a self-adaptive based dual strategy to balance the exploration and exploitation by employing “DE/best/2” and “DE/rand/2” based on self-adaptive scaling parameter is presented in [42]. This algorithm also introduced a dynamic exploration ability control parameter to dynamically adjust the global exploration ability of DE algorithms. Self-adapting parameters and multi mutation variants based enhanced DE algorithms are proposed in [43]. This research measured the convergence speed and accuracy, using three different mutation strategies and control parameters to adapt the dynamic rate of exploitation and exploration. To optimize the structure and parameters of neural networks, a collective intelligent based DE algorithm is presented in [44]. In this work mutation parameters based on collective intelligence were used to enhance the exploitation and the exploration capability of DE algorithms by utilizing promising donor vectors by taking m top ranked donor vectors. They used the weight of m top ranked vectors which is calculated by the linear combination of two random vectors and m top ranked vectors.
3 Convergence Track Based Adaptive Differential Evolution Algorithm (CTbADE)
Mutation strategies and control parameters have a major impact on DE algorithms’ performance, which can be enhanced by following a convergence track during the evolutionary process. A smaller value of mutation probability F focuses on exploitation, and a bigger value of F focuses on the exploration capability of a DE algorithm [18]. CR is helpful in maintaining diversity in the population [18]; in early iterations a bigger value of CR is used [e.g., CR = 0.9], then it is gradually decreased by using a controlled sequence to a smaller value [CR = 0.7]. The reason for decreasing the CR is that in successive iterations diversity should be not much higher, otherwise it will slow down the performance of the algorithm. The concept of memory is used in the controlled sequence and two different control sequences of CR are used by default: one is linear decreasing and the other is linear increasing. The concept of memory is used to calculate the change in the average fitness value, if the fitness value is not changed to learning period (LP), successive iterations then sequence will move to the opposite direction, that is from decreasing to increasing or from increasing to decreasing, according to the following equations. It is important to mention here that if, for a specified LP, the fitness value of the objective function does not change, then there is a possible diversity issue or exploration issue or local optima issue which means that the values of the parameters need to be changed.
where CR_cur is current value of crossover rate, CR_min is the minimum value and CR_max is the maximum value of crossover rate, Tot_iter is total number of iterations and j represents the current iteration.
The value of F is increased so that, from a very diverse population, we should start by focusing on the exploration so that we should move in the direction of convergence and its values are used in the increasing sequence. This algorithm will be able to escape from local optima in a controlled manner and in a controlled range which is described in the following range. By default, the sequence of control parameter F is increased using Eq. (4) and then it can be seen whether the fitness value of the problem is changing during the specified LP and the sequence is changed from increasing to decreasing and vice versa accordingly.
where F_cur is the current value of mutation probability, F_min is the minimum value and F_max is the maximum value of mutation probability, Tot_iter is total number of iterations and j represents the current iteration.
The mutation strategy DE/best/1 is considered a better performing variant among other variants of DE algorithm, which is directed towards the global best value; since we are using the concept of memory to follow the convergence track, this technique will prove to be beneficial in maintaining the improved convergence of DE algorithms. The pseudocode of proposed CTbADE is given in Fig. 1.

Figure 1: Convergence Track Based Adaptive Differential Evolution (CTbADE) algorithm pseudocode
4 Test Functions and Parameter Study
Comprehensive standard problems to test the convergence power of the CTbADE algorithm are taken from [45]; varying natures, such as unimodal, multimodal, separable, and non-separable, are considered in this research work. The details of the nature of the benchmark functions, names of the benchmark functions, optimal values, and search space are given in Tabs. A and B in the appendix. The population size is considered to be fixed for all used dimensions D with values of 10, 20 and 30, see reference [45] for all standard benchmark functions. The average of 30 trials is used to calculate the average fitness performance in the paper for all functions. The range of values of mutation probability [19] used is [0.5, 0.7] and CR [19] is [0.9, 0.5], controlled by the proposed sequences discussed in the proposed algorithm section.
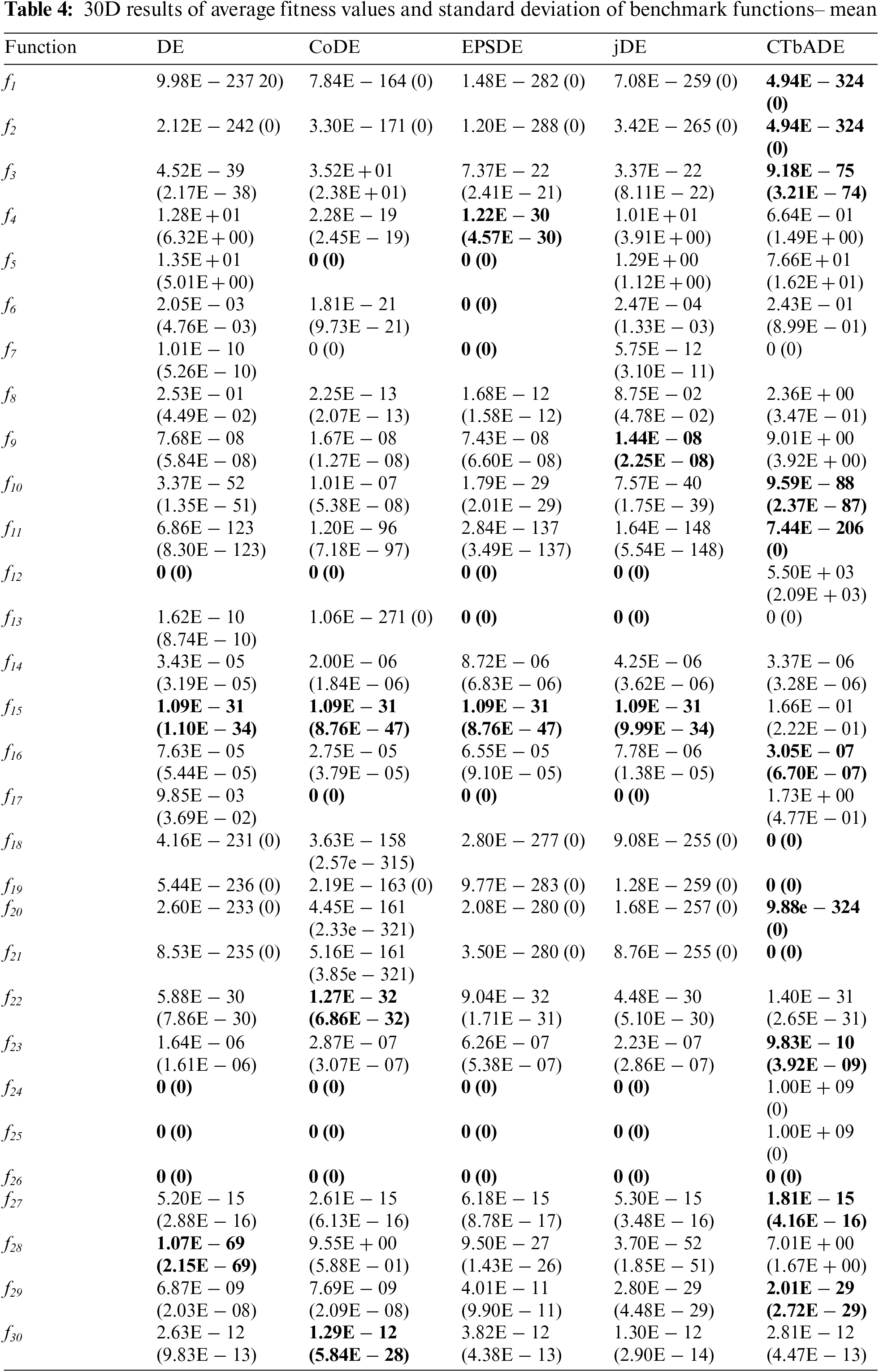
This section contains the average fitness performance of the original DE and a few more commonly used state-of-the-art algorithms, such as CoDE, EPSDE, jDE, and the proposed CTbADE. These experimental results are generated by implementing the algorithm in C++ using Core-i3 machine 4 GB RAM, 4 GHZ CPU, Windows 10 and by using the performance parameters given in Section 4 of this paper. The benchmark functions of varying nature are used to test the convergence power of the proposed CTbADE algorithm. The experimental results of average fitness values are reported in Tabs. 1–3 for 10 Dimensions, 20 Dimensions, 30 Dimensions and the population size is taken as 50 for all benchmark functions. The training iterations for 10D, 20D, and 30D are used as 5000, 10000, and 15000 respectively. In order to assure the consistency of the proposed algorithm, results are generated over 30 independent runs.
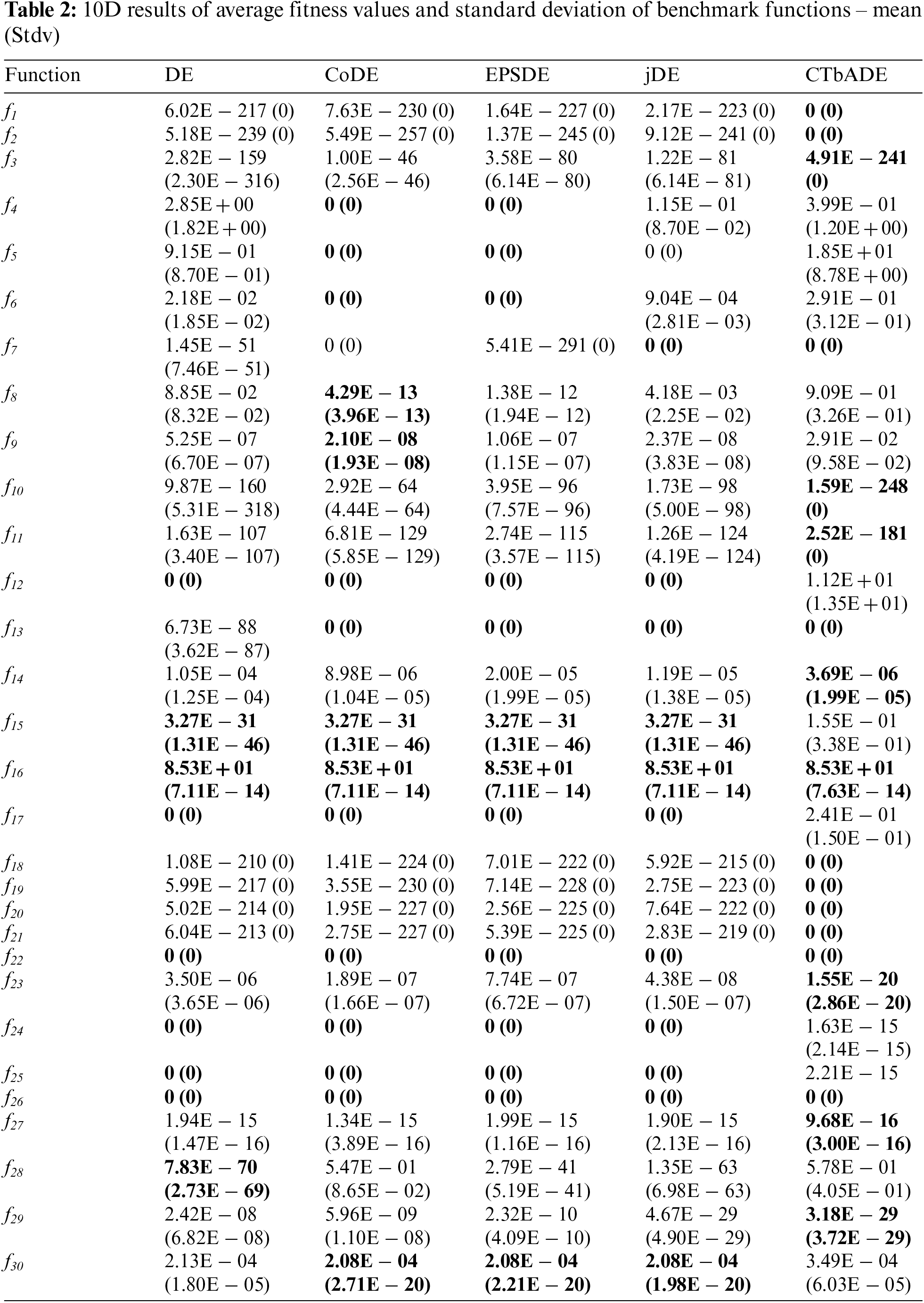
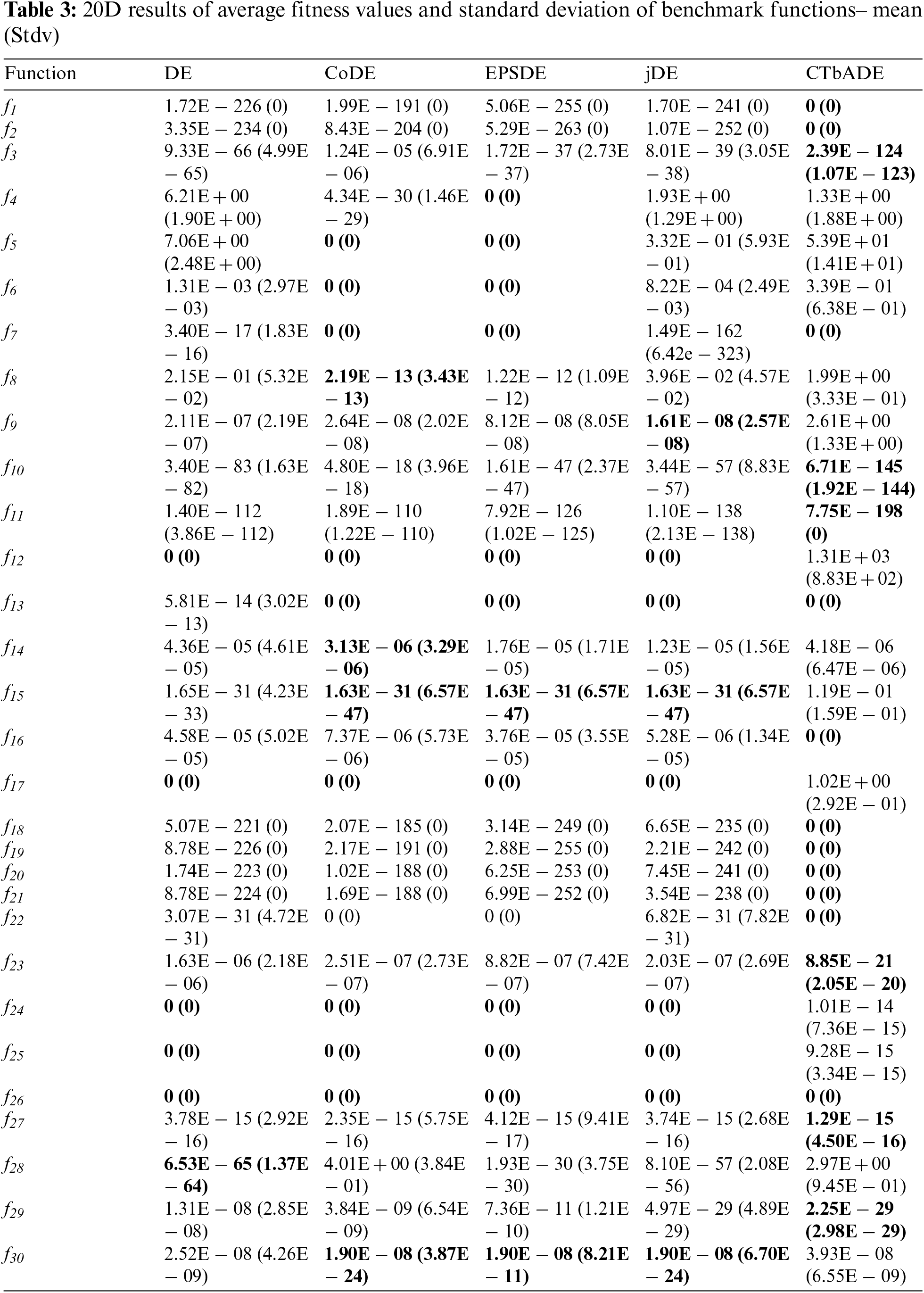
Overall, from the experimental results it is clear that the CTbADE algorithm has a dominating performance over that of the standard DE, CoDE, EPSDE, and jDE algorithms. The CTbADE algorithm outperforms other well-known and state-of-the-art algorithms in most cases. The CTbADE algorithm's convergence is better than the other algorithms for unimodal, multimodal, separable and non-separable functions. It shows that we can apply the CTbADE algorithm to solve problems of varying natures. In cases of 10D, 20D, and 30D, CTbADE outperforms other algorithms for unimodal problems, such as the axis parallel hyperellipsoid, Schwefel's problem, Schwefel's problem 2.22, ellipse function and tablet function, as well as the Neumaier-2 problem in the cases of 20D and 30D. The performance of CTbADE is better in multimodal problems, such as the sphere model in cases of 10D, 20D, and 30D; sum of difference power in the case of 10D; the Zakharov function in cases of 10D, 20D and 30D; cigar function in cases of 10D, 20D, and 30D; function-15 in cases of 10D, 20D, and 30D; the problem of the deflected corrugated spring in cases of 10D, 20D, and 30D; the problem of multi-model global optimization in the case of 20D; and the Quintic global optimization problem also in the case of 20D. The performance of CTbADE is better in separable problems, such as the sphere model in cases of 10D, 20D, and 30D; the axis parallel hyperellipsoid in cases of 10D, 20D, and 30D; the Neumaier-2 problem in 20D and 30D; cigar in cases of 10D, 20D, and 30D; function-15 in cases of 10D, 20D, and 30D; the ellipse function in case of 10D, 20D, and 30D; the tablet function in case of 10D, 20D, and 30D; the deflected corrugated spring in cases of 10D, 20D, and 30D; the multimodal global optimization problem and the Quintic global optimization problem, both in the case of 20D. The performance of CTbADE is better for non-separable problems, such as Schwefel's problem 1.2 in cases of 10D, 20D, and 30D; sum of different power in the case of 10D; Zakharov function in 10D, 20D, and 30D; Schwefel's problem 2.22 in cases of 10D, 20D, and 30D. Although the fitness value of the given average value fitness tables are same, the convergence speed of CTbADE is better for the unimodal problem De Jong's no-noise function-4 in cases of 10D and 20D. The performance of CTbADE is better for unimodal problems in 10D and 20D. The convergence speed of CTbADE is better for multimodal problems, such as Alpine function in the case of 10D; Schewel function in case of 10D; the multimodal global optimization problem in the case of 30D; the Quintic global optimization problem in case of 10D and 30D; the stretched_V_global_optimization in cases of 20D and 30D. The performance of CTbADE is better for separable problems, such as the sum of different power in the case of 20D; De Jong's no-noise function-4 in cases of 10D and 20D; Alpine function in the case of 10D; Schewel function in the case of 10D; the multimodal global optimization problem in the case of 30D and the Quintic global optimization problem in cases of 10D and 30D. The performance of CTbADE is better for non-separable problems, such as the sum of different power problem in the case of 20D and the stretched_V_global_optimization problem in the case of 20D and 30D.
The performance of the CTbADE algorithm is competitive compared to other algorithms for unimodal functions: De Jong's no-noise function-4 in the case of 30D and the Neumaier-2 problem in the case of 10D; for multimodal functions sum of different problem in case of 30D; Alpine function in case of 20D and 30D; multimodal global optimization problem in case of 10D and 20D; Quintic global optimization problem in the case of 30D; stretched V global optimization problem in the case of 20D; Xin-SheYang in the case of 30D; separable functions for De Jong's no noise function-4 in the case of 30D; Neumaier-2 Problem in the case of 10D; Alpine function in cases of 20D and 30D; multimodal global optimization problem in cases of 10D and 20D; Quintic global optimization problem in the case of 30D; stretched_V_global_optimization problem in the case of 20D; for the non-separable problem sum of different power in case of 30D; Xin-SheYang in the case of 30D.
Logarithmic convergence graphs of some sampled problems have been shown in Fig. 2 of this paper. The horizontal axis shows the iterations, and the average fitness performance is shown vertically in each logarithmic convergence graph. From the logarithmic convergence graphs, it can be noted that the average fitness performance of the CTbADE algorithm is better in most cases than the standard DE algorithm, jDE algorithm, EPSDE algorithm, and CoDE algorithm.
Fig. 2a shows convergence graph of Schwefel's problem-1.2, showing the number of training iterations against the average fitness performance value. It is evident from this figure that the performance of the CTbADE algorithm is superior to the other algorithms, as it is the only algorithm that gains the global optima in the specified number of generations. The speed of CTbADE in convergence graph 2.b is better from early iterations till the last iteration. It can be observed from Fig. 2c of Schwefel's problem 2.22, that all the algorithms are gradually converging towards global but the performance of CTbADE is much quicker than to the other algorithms. It is noted from Tab. 4 of the average fitness values that the EPSDE, CoDE, and CTbADE algorithms are reaching the global optimal value but the convergence speed of CTbADE is higher as confirmed in Fig. 2b. From Fig. 2d it is clear that, in early iterations, the performance of the CTbADE algorithm remains similar to the others but in succeeding iterations it decreases gradually and performs better than the other algorithms. From Fig. 2e and Tab. 4, it can be observed that all algorithms are achieving global optimal value but the convergence of CTbADE algorithm is better. Fig. 2e shows the better performance of CTbADE algorithm from the initial iteration till the last specified iteration. Thus, it is evident from the convergence graphs that the CTbADE algorithm has the leading performance in most of the cases against the standard DE algorithm, EPSDE algorithm, CoDE algorithm, and jDE algorithm. The CTbADE algorithm will thus prove to be a valuable contribution to the existing DE literature.
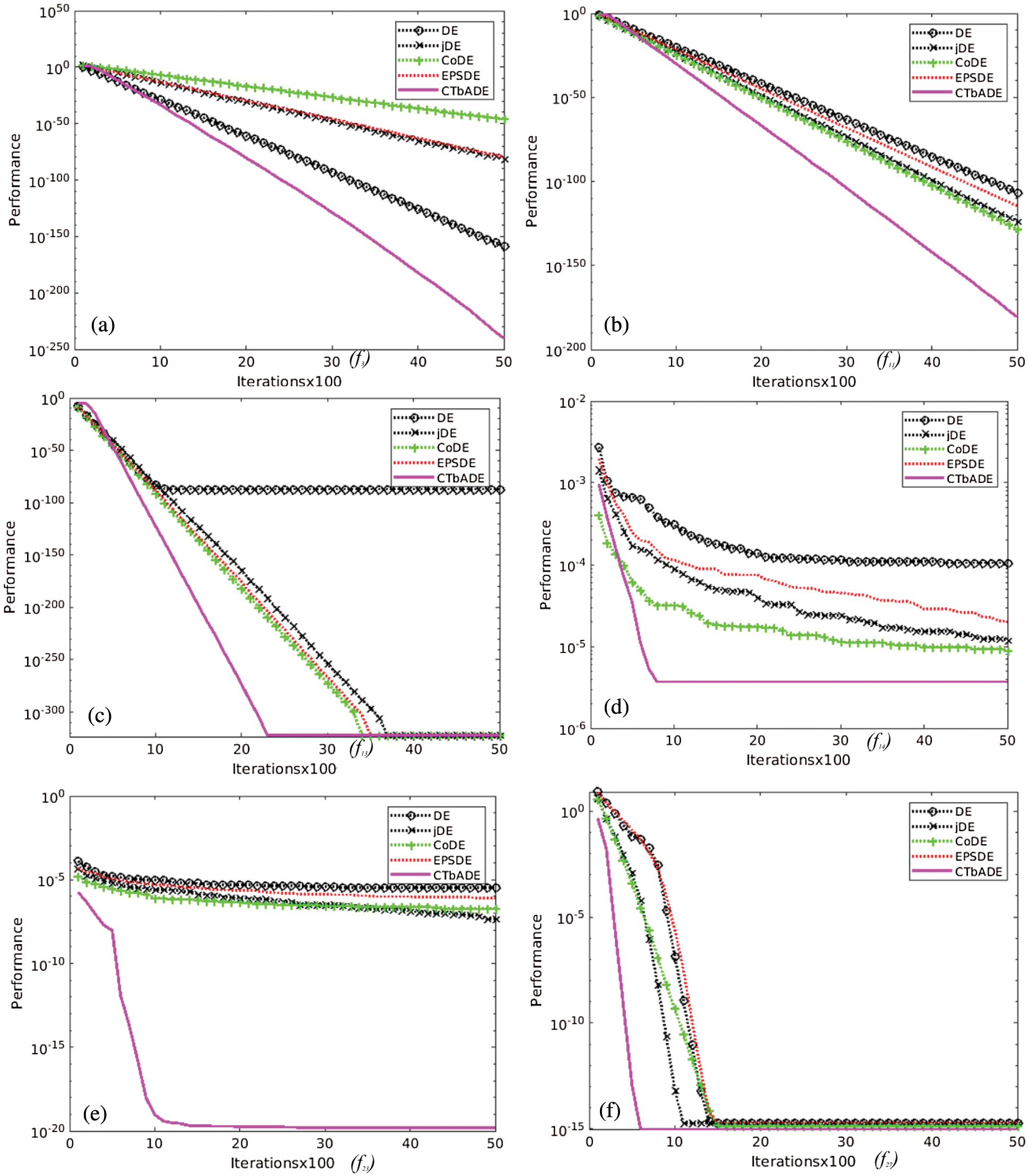
Figure 2: 10 Dimensional convergence graphs of a few benchmark functions, showing performance vertically and iterations horizontally (a) Schwefel's problem 1.2 (b)Schwefel's problem 2.22 (c) De Jong's function 4 (no noise), (d) Alpine function (e) Deflected corrugated spring (f) Quintic global optimization problem
This paper presents a convergence tracking over time based parametric adaptive version of differential evolution algorithms. The two important operators of parameters of mutation probability that contribute are mutation operation and crossover rate, which are controlled by using a new sequence over time. The proposed sequences are helpful to track and follow the convergence path and remove the DE algorithm from the local optima problem. The concept of a small memory based on a user defined learning period is used in the sequence of control parameters of the algorithm to improve the convergence behavior of DE algorithms and escaping from the stagnation problem. A comprehensive suite of well-known and varying nature benchmark standard optimization functions was used to test the convergence power of the proposed convergence track based adaptive evolution algorithm (CTbADE). The experimental results are generated using the same set of parameters for a fair comparison. The results of the new CTbADE algorithm are compared with standard DE algorithms and some other well-known and commonly used state-of-the-art algorithms, such as CoDE, jDE, and EPSDE algorithms. The research result shows that the proposed CTbADE algorithm has more powerful convergence than the other algorithms used. The novel optimization algorithm presented in this research work will help the development of a fast automated diagnostics model to detect Covid-19 infection. The future work of this research work is to apply the CTbADE algorithm to optimize the hyper parameters of convolutional neural networks for Covid-19 CT/X-ray images feature extraction and classification to construct a fast automated diagnostics model.
Acknowledgement: The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through project number 959.
Funding Statement: This work was supported by the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia, which funded this research work through project number 959.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. R. Storn and K. Price, “Differential evolution: A simple and efficient adaptive scheme for global optimization over continuous spaces,” CA, Berkeley, Tech. Rep TR-95-012, 1995. [Google Scholar]
2. J. Brest, S. Greiner, B. Boskovic, M. Mernik and V. Zumer, “Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems,” IEEE Transaction on Evolutionary Computing, vol. 10, no. 6, pp. 646–657, 2006. [Google Scholar]
3. K. Price, R. M. Storn and J. A. Lampinen, “Differential Evolution: A Practical Approach to Global Optimization (Natural Computing Series),” 1st ed. New York, USA: Springer-Verlag, 2005. [Google Scholar]
4. A. Karsaz, “Evaluation of lung involvement in patients with coronavirus disease from chest ct images using multi-objective self-adaptive differential evolution approach,” Journal of Control, vol. 14, no. 5, pp. 1–14, 2021. [Google Scholar]
5. X. Yi, L. Li, T. Yu, J. Shi, M. Cai et al., “Double-layer wideband reflectarray using polynomial optimization technology,” International Journal of RF and Microwave Computer-Aided Engineering, vol. 31, no. 5, pp. e22594, 2021. [Google Scholar]
6. G. Liu, Y. Li and G. He, “Design of digital fir filters using differential evolution algorithm based on reserved genes,” in IEEE Congress on Evolutionary Computation (CEC), Barcelona, pp. 1–7, 2010. [Google Scholar]
7. X. Zhang, L. Jin, C. Cui and J. Sun, “A self-adaptive multi-objective dynamic differential evolution algorithm and its application in chemical engineering,” Applied Soft Computing, vol. 106, pp. 107317, 2021. [Google Scholar]
8. M. Baioletti, G. Di Bari, A. Milani and V. Poggioni, “Differential evolution for neural networks optimization,” Mathematics, vol. 8, no. 1, pp. 69, 2020. [Google Scholar]
9. E. Marchiori, J. H. Moore and J. C. Rajapakse, “Evaluating evolutionary algorithms and differential evolution for the online optimization of fermentation processes” Machine Learning and Data Mining in Bioinformatics, Berlin, Heidelberg: Springer, 2007. [Google Scholar]
10. S. Li, W. Gong, C. Hu, X. Yan, L. Wang et al., “Adaptive constraint differential evolution for optimal power flow,” Energy, vol. 235, pp. 121362, 2021. [Google Scholar]
11. G. F. Plichoski, G. F. Chidambaram and R. S. Parpinelli, “A face recognition framework based on a pool of techniques and differential evolution,” Information Sciences, vol. 543, pp. 219–241, 2021. [Google Scholar]
12. A. Smirnov and R. P. Jastrzebski, “Differential evolution approach for tuning an h∞controller in amb systems,” in 35th IEEE Annual Conf. of Industrial Electronics, Lappeenranta, Finland, pp. 1514–1518, 2009. [Google Scholar]
13. D. Singh, V. Kumar and M. Kaur, “Classification of covid-19 patients from chest ct images using multi-objective differential evolution–based convolutional neural networks,” European Journal of Clinical Microbiology & Infectious Diseases, vol. 39, no. 7, pp. 1379–1389, 2020. [Google Scholar]
14. O. H. Ahmed, J. Lu, Q. Xu, A. M. Ahmed, A. M. Rahmani et al., “Sing differential evolution and moth–flame optimization for scientific workflow scheduling in fog computing,” Applied Soft Computing, vol. 112, pp. 107744, 2021. [Google Scholar]
15. Y. Yu, H. Wang, S. Liu, L. Guo, P. Yeoh et al., “Distributed multi-agent target tracking: A nash-combined adaptive differential evolution method for uav systems,” IEEE Transactions on Vehicular Technology, vol. 70, pp. 8122–8133, 2021. [Google Scholar]
16. R. Storn and K. Price, “Differential evolution: A simple and efficient heuristic for global optimization over continuous spaces,” Journal of Global Optimization, no. 11, pp. 341–359, 1997. [Google Scholar]
17. X. Dong, C. S. Deng, Y. Zhang and Y. C. Tan, “Enhancing local search of differential evolution algorithm for high dimensional optimization problem,” Chinese Control Conference, Hangzhou, China, pp. 8411–8415, 2015. [Google Scholar]
18. M. Duan, H. Yang, S. Wang and Y. Liu, “Self adaptive dual strategy differential evolution algorithm,” Plos one, vol. 14, no. 10, pp. e0222706, 2019. [Google Scholar]
19. Q. Abbas, J. Ahmad and H. Jabeen, “Random controlled pool base differential evolution algorithm,” Intelligent Automation & Soft Computing, vol. 2017, pp. 1–14, 2017. [Google Scholar]
20. A. Rehman, T. Sadad, T. Saba, A. Hussain and T. Tariq, “Real-time diagnosis system of covid-19 using x-ray images and deep learning,” It Professional, vol. 23, no. 4, pp. 57–62, 2021. [Google Scholar]
21. V. Ravi, H. Narasimhan, C. Chakraborty and T. D. Pham, “Deep learning-based meta-classifier approach for covid-19 classification using ct scan and chest x-ray images,” Multimedia Systems, vol. 2021, pp. 1–15, 2021. [Google Scholar]
22. S. Ahuja, B. K. Panigrahi, N. Dey, V. Rajinikanth and T. K. Gandhi, “Deep transfer learning-based automated detection of covid-19 from lung ct scan slices,” Applied Intelligence, vol. 51, no. 1, pp. 571–585, 2021. [Google Scholar]
23. P. Saha, D. Mukherjee, P. K. Singh, A. Ahmadian, M. Ferrara et al., “Graphcovidnet: A graph neural network based model for detecting covid-19 from ct scans and x-rays of chest,” Scientific Reports, vol. 11, no. 1, pp. 1–16, 2021. [Google Scholar]
24. A. Narin, C. Kaya and Z. Pamuk, “Automatic detection of coronavirus disease (covid-19) using x-ray images and deep convolutional neural networks,” Pattern Analysis and Applications, vol. 24, pp. 1–14, 2021. [Google Scholar]
25. K. Rao, K. Xie, Z. Hu, X. Guo, C. Wen et al., “Covid-19 detection method based on svrnet and svdnet in lung x-rays,” Journal of Medical Imaging, vol. 8, no. S1, pp. 017504, 2021. [Google Scholar]
26. P. Singh, S. Chaudhury and B. K. Panigrahi, “Hybrid mpso-cnn: Multi-level particle swarm optimized hyperparameters of convolutional neural network,” Swarm and Evolutionary Computation, vol. 63, pp. 100863, 2021. [Google Scholar]
27. D. Zaharie, “Control of population diversity and adaptation in differential evolution algorithms,” in Proc. of the Mendel 9th Int. Conf., University of Technology, Brno, Czech Republic, vol. 9, pp. 41–46, 2003. [Google Scholar]
28. J. Liu and J. Lampinen, “A fuzzy adaptive differential evolution algorithm,” Soft Computing, vol. 9, pp. 448–462, 2005. [Google Scholar]
29. J. Brest, S. Greiner, B. Boskovic, M. Mernik and V. Zumer, “Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems,” IEEE Transactions on Evolutionary Computation, vol. 10, no. 6, pp. 646–657, 2006. [Google Scholar]
30. J. Zhang and A. C. Sanderson, “Jade: Adaptive differential evolution with optional external archive,” IEEE Transactions on Evolutionary Computation, vol. 13, no. 5, pp. 945–958, 2009. [Google Scholar]
31. A. K. Qin, V. L. Huang and P. N. Suganthan, “Differential evolution algorithm with strategy adaptation for global numerical optimization,” IEEE Transactions on Evolutionary Computation, vol. 2, no. 13, pp. 398–417, 2009. [Google Scholar]
32. S. Das, A. Abraham, U. K. Chakraborty and A. Konar, “Differential evolution using a neighborhood-based mutation operator,” IEEE Transactions on Evolutionary Computation, vol. 13, no. 3, pp. 526–553, 2009. [Google Scholar]
33. R. Mallipeddi, P. N. Suganthan, Q. K. Pan and M. F. Tasgetiren, “Differential evolution algorithm with ensemble of parameters and mutation strategies,” Applied Soft Computing, vol. 11, pp. 1679–1696, 2011. [Google Scholar]
34. Y. Wang, Z. Cai, and Q. Zhang, “Differential evolution with composite trial vector generation strategies and control parameters,” IEEE Transactions on Evolutionary Computation, vol. 15, no. 1, pp. 55–66, 2011. [Google Scholar]
35. S. Minhazul-Islam, S. Das, S. Ghosh, S. Roy and P. N. Suganthan, “An adaptive differential evolution algorithm with novel mutation and crossover strategies for global numerical optimization,” IEEE Transactions on Systems, Man, and Cybernetics-PART B: Cybernetics, vol. 42, no. 2, pp. 482–500, 2012. [Google Scholar]
36. H. Wang, S. Rahnamayan and Z. Wu, “Parallel differential evolution with self-adapting control parameters and generalized opposition-based learning for solving high-dimensional optimization problems,” Journal of Parallel and Distributed Computing, vol. 73, no. 1, pp. 62–73, 2013. [Google Scholar]
37. V. Gonuguntla, R. Mallipeddi and K. C. Veluvolu, “Differential evolution with population and strategy parameter adaption,” Mathematical Problems in Engineering, vol. 2015, pp. 1–11, 2015. [Google Scholar]
38. Q. Fan and X. Yan, “Self adaptive differential evolution algorithm with zoning evolution of control parameters and adaptive mutation strategies,” IEEE Transactions on Cybernetics, vol. 46, no. 1, pp. 219–232, 2016. [Google Scholar]
39. Z. Zhao, J. Yang, Z. Hu and H. Che, “A differential evolution algorithm with self adaptive strategy and control parameters based on symmetric latin hypercube design for unconstrained optimization problems,” European Journal of Operation Research, vol. 250, pp. 1–16, 2015. [Google Scholar]
40. H. Peraza-Vázquez, A. M. Torres-Huerta and A. Flores-Vela, “Self adaptive differential evolution hyper-heuristic with applications in process design,” Computación y Sistemas, vol. 20, no. 2, pp. 173–193, 2016. [Google Scholar]
41. Q. Fan, W. Wang and X. Yan, “Differential evolution algorithm with strategy adaption and knowledge based control,” Artificial Intelligence Review, vol. 51, no. 2, pp. 219–253, 2019. [Google Scholar]
42. M. Duan, H. Yang, S. Wang and Y. Liu, “Self-adaptive dual-strategy differential evolution algorithm,” Plos one, vol. 14, no. 10, pp. e0222706, 2019. [Google Scholar]
43. M. A. Attia, M. Arafa, E. A. Sallam and M. M. Fahmy, “An enhanced differential evolution algorithm with multi-mutation strategies and selfadapting control parameters,” International Journal of Intelligent Systems and Applications, vol. 10, no. 4, pp. 26–38, 2019. [Google Scholar]
44. R. Jiang, J. Zhang, Y. Tang, C. Wang and J. Feng, “A collective intelligent based differential evolution algorithm for optimizing the structure and parameters of a neural network,” IEEE Access, vol. 8, pp. 69601–69614, 2020. [Google Scholar]
45. Q. Abbas, J. Ahmad and H. Jabeen, “A novel tournament selection based differential evolution variant for continuous optimization problems,” Mathematical Problems in Engineering, vol. Article ID 205709, pp. 1–21, 2015. [Google Scholar]
Appendix: Benchmark Functions


 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |