DOI:10.32604/cmc.2022.024692

| Computers, Materials & Continua DOI:10.32604/cmc.2022.024692 |  |
| Article |
Modified Harris Hawks Optimization Based Test Case Prioritization for Software Testing
1Department of Computer and Self Development, Preparatory Year Deanship, Prince Sattam bin Abdulaziz University, AlKharj, 16278, Saudi Arabia
2Department of Information Systems, College of Science and Arts, King Khalid University, Mahayil Asir, 62529, Saudi Arabia
3Department of Computer Science, College of Computer and Information Sciences, Prince Sultan University, P.O.Box No. 66833, Rafha Street, Riyadh, 11586, Saudi Arabia
4Department of Information Systems, College of Computer and Information Sciences, Princess Nourah bint Abdulrahman University, P.O.Box 84428, Riyadh, 11671, Saudi Arabia
5Department of Natural and Applied Sciences, College of Community-Aflaj, Prince Sattam bin Abdulaziz University, 16278, Saudi Arabia
6College of Computer at Al-Gunfudah, Umm Al-Qura University, Al-Gunfudah, 24382, Saudi Arabia
*Corresponding Author: Manar Ahmed Hamza. Email: ma.hamza@psau.edu.sa
Received: 27 October 2021; Accepted: 05 January 2022
Abstract: Generally, software testing is considered as a proficient technique to achieve improvement in quality and reliability of the software. But, the quality of test cases has a considerable influence on fault revealing capability of software testing activity. Test Case Prioritization (TCP) remains a challenging issue since prioritizing test cases is unsatisfactory in terms of Average Percentage of Faults Detected (APFD) and time spent upon execution results. TCP is mainly intended to design a collection of test cases that can accomplish early optimization using preferred characteristics. The studies conducted earlier focused on prioritizing the available test cases in accelerating fault detection rate during software testing. In this aspect, the current study designs a Modified Harris Hawks Optimization based TCP (MHHO-TCP) technique for software testing. The aim of the proposed MHHO-TCP technique is to maximize APFD and minimize the overall execution time. In addition, MHHO algorithm is designed to boost the exploration and exploitation abilities of conventional HHO algorithm. In order to validate the enhanced efficiency of MHHO-TCP technique, a wide range of simulations was conducted on different benchmark programs and the results were examined under several aspects. The experimental outcomes highlight the improved efficiency of MHHO-TCP technique over recent approaches under different measures.
Keywords: Software testing; harris hawks optimization; test case prioritization; apfd; execution time; metaheuristics
The increasing importance of software testing adds significant value to the quality of software and indirectly towards social development and national economy. Inappropriately-developed and tested software might lead to serious issues, especially in issues concerning national security, etc., Further, it also brings high maintenance costs and huge amount of property loss [1]. Software testing is considered as a significant process to assure the trustworthiness and consistency of a software. Particularly, Automated Software Testing (AST) can improve testing efficiency, shorten testing time, and greatly reduce the manual workforce in this domain. Over the last few years, AST has gained a considerable interest in the field of both academics and industry. In general, test data automatic generation is a challenging and key task in AST [2]. A relevant test dataset can increase fault exposure probability and can efficiently reduce the testing execution time. In addition to these two problems discussed above, coverage ratio is a crucial index to estimate the quality of test dataset [3]. In comparison with functional testing, structural testing is a cost-efficient process in fault detection of programs. So, this process is extensively studied and applied.
Current software testing methods are mostly used for deterministic programs [4]. Indeed, there are several kinds of uncertainties experienced in real-time programs, for instance fuzziness/randomness, which suggest that the behaviour of these programs are not certain. Particularly, in case of a program with uncertainty and when a program is repeatedly run with a similar test data point, it might cover different statements or even different outputs, or sometimes traverse different paths too. In this scenario, prior test adequacy condition remains inappropriate. Now, the outcomes from few studies focused on testing a program with non-determinism. However, some of the studies focus on programs that is composed of randomness. Alternatively, the programs with randomness exist extensively in real-time applications like network software, game software, and Windows operating system [5].
Although software testing is recurrently performed, it is mostly performed in a hurried manner, owing to fixed resources and time constraints. As a result, it can be described that Test Case Prioritization (TCP) application can improve test feasibility from ST activity [6]. But, the studies in literature employed prioritization on test cases that passed with test case selection. Two researchers namely, Harold and Rothermel evaluated the concept in a wide context and proposed a novel method. TCP is an NP-Hard problem since it needs to check each feasible permutation sequence. Similarly, the rapid expansion of software makes one to resort to metaheuristics optimization algorithm to resolve the problems within a certain period of time [7]. Hence, the authors started looking into nature on how nature maintains an optimal balance. At present, several attempts are being made to find an optimum ordering through nature-inspired algorithm.
With this motivation, the current study designs a modified Harris Hawks Optimization-based TCP (MHHO-TCP) technique for software testing. The aim of the proposed MHHO-TCP technique is to maximize APFD and minimize the overall execution time. In addition, MHHO algorithm is also designed to boost both exploration and exploitation abilities of conventional HHO technique. The design of MHHO technique for TCP in software testing shows the novelty of current work. In order to validate the enhanced efficiency of MHHO-TCP technique, a wide range of simulations was conducted upon different benchmark programs and the results were investigated under several aspects.
Rest of the paper is arranged as follows. Section 2 briefs about related works, Section 3 introduces the proposed model, Section 4 discusses about performance validation, and Section 5 concludes the study.
Spieker et al. [8] presented Retecs, a novel methodology to manually learn TCP and perform CI selection for the purpose of reducing round-trip time among developers’ feedback on failed test cases and code commits. Retecs technique use RL algorithm for both selection and prioritization of test cases based on failure history, duration, and last implementation status. Panwar et al. [9] proposed CS and M-ACO algorithms to conclude the test cases in an enhanced order under time-constraint environments. Since this method is dependent on individual parameters, cuckoo search algorithm is preferred which is different from other optimization methods and is very effective and easy to perform.
Miranda et al. [10] presented the FAST family of TCP methods which radically changes the landscapes through borrowing algorithms, widely used in big data, to find relevant items. FAST technique provides scalable similarity-based TCP in white-box and black-box methods. The experimental results from practical Java and C subjects show that the fastest member of the family outperformed other black-box methods in terms of efficacy without considerable impact on efficiency. Further, it also outperformed white-box approach. Ali et al. [11] proposed a relevant solution and examined the prevailing problems towards regression testing in agile practices. The presented method has 2 stages while in initial phase, test case is prioritized through clustering while this test case changes frequently. If it is a tie, then the test case is prioritized according to their corresponding coverage criteria and failure frequencies. In the next phase, test cases with coverage criteria/high frequency of failure are elected. The presented method was authenticated through experimental research on three industrial subjects.
Hajjaji et al. [12] presented a similarity-based prioritization that is effectively employed on product samples. In this method, different products are gradually chosen based on the feature to be tested next, so as to increase the feature interaction coverage as soon as possible in product-wise testing. Xing et al. [13] adapted an advanced SI method—Artificial Fish School Algorithm to resolve the TCP problems. Particularly, the coding algorithm of artificial fish school was developed along with test case set; effective execution time and the average percentage of test-point coverage were chosen for optimization of strategies such as tail-chase, cluster, and forage behaviours of artificial fish school; the optimum solutions were attained through population iterations.
Gokilavani et al. [14] presented a multi-objective-based TCP and test case selection for distributed cloud platforms. Resemblance-Based Cluster Head (RBCH) method was presented in this study to select the CH based on total similarity among other test cases. Sivaji et al. [15] proposed a new African Buffalo-based Convolution Neural Slicing (AB-CNS) algorithm to reduce both resource and time consumption, when implementing regression testing. At first, the presented approach was implemented in test case minimalization task. It was prioritized using the FF of AB-CNS. Khalilian et al. [16] introduced an improved version of the methods discussed above in two ways. Firstly, the authors introduced a novel prioritization formula by gaining a variable coefficient as per the available historical efficiency data that act as feedback from previous test session. Next, a set of exhaustive research works has been carried out in the evaluation of system performances.
In this study, a novel MHHO-TCP technique is designed for TCP on software testing. The aim of the proposed MHHO-TCP technique is to maximize APFD and minimize the overall execution time. In addition, MHHO algorithm is designed to boost both exploration and exploitation abilities of conventional HHO algorithm.
HHO is a metaheuristic technique and is applied as a competent solution to difficult issues. HHO is simulated by the attitude of Harris hawks, an intelligent bird. This species follows a process that empowers them to catch a prey, even there are chances for the prey to escape. Being a procedure modelled under mathematical process, it allows their computational execution. HHO has a stochastic technique which explores difficult search spaces for finding the optimum solution. The fundamental steps of HHO are attained under different conditions of energy. The exploration stage is inspired from the process where Harris's hawk cannot track the prey exactly. The hawks arbitrarily perch at distinct places and wait for its prey utilizing two operators that are chosen on the fundamental of probability q as provided in Eq. (1), where
The exploration stage is determined as follows
The average place of Hawks
where
where,
Soft besiege is a vital phase in HHO which can be demonstrated, when
where
As in the performance of hawks from real life, it slowly performs an optimum dive towards the prey, when it is required to capture a particular prey under competitive conditions.
Soft besiege, projected from the preceding in Eq. (7), is carried out from progressive quick dive, only
where S stands for arbitrary vector sized
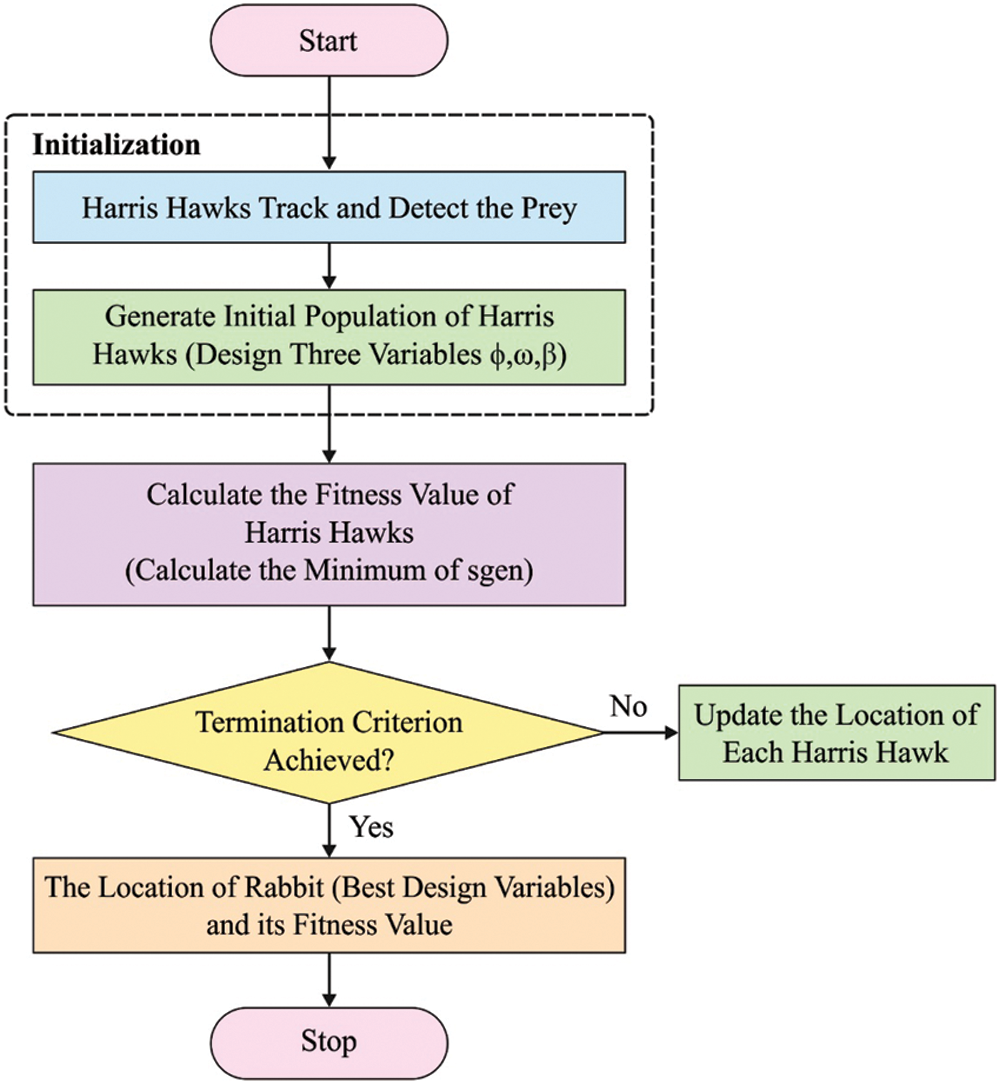
Figure 1: Flowchart of HHO
At this point,
where y and Z refer to the attained outputs utilized in Eqs. (7) and (8).
In this progressive fast dive, HHO represents the already hard-pressed one, where it occurs
The values of y and Z are presented with the help of novel rules in Eqs. (12) and (13), where
In literature [18], it is demonstrated that HHO outperformed many advanced techniques and it addresses many optimization problems. But, a new adapted MHHO method is presented in current research work to promote search efficiency of HHO so as to attain fast convergence speed, robustness, and better solution accuracy. It is not challenging to define the modifications in E which could generate a major difference in simulation result. Thus, a novel E upgrading system is deployed in MHHO for promoting both exploitation and exploration abilities of HHO. The complete modifications made so far are given herewith.
Generally, two optimization approaches are followed in each metaheuristic algorithm such as exploitation and exploration. Exploration represents a global search in searching space; and exploitation represents the local optimum solution. From an algorithmic point of view, E is a connection between exploitation and exploration. When
Based on the last value of
whereas
In which N represents the population size, T denotes the overall number of iterations and Dimension denotes the amount of decision parameters.
3.2 Application of MHHO Algorithm for TCP
Assume that there are five test cases to be prioritized while the possibility of having the optimal prioritized arrangement is (1/5!) factorials as shown in Fig. 2. Every test case performs as firefly agents, when the distances among every test case represent the attractiveness functions amongst firefly agents. To identify the best-prioritized arrangement, the proposed method is utilized by string metrics as a FF. In this work, the real outcome of the distance estimated for every standard program is not demonstrated. Because, the amount of test cases and their corresponding content is too lengthy and huge in size to be sufficiently demonstrated. In fact, to demonstrate how distance is estimated in this study, five dummy test cases were generated. ‘Edit distance’ includes the evaluation of string characters, in which the quantified values represent the minimum number of replacements, insertions, and deletions to convert 1st into 2nd string. Edit distance is set to include only the least conversion of 1st into 2nd string.
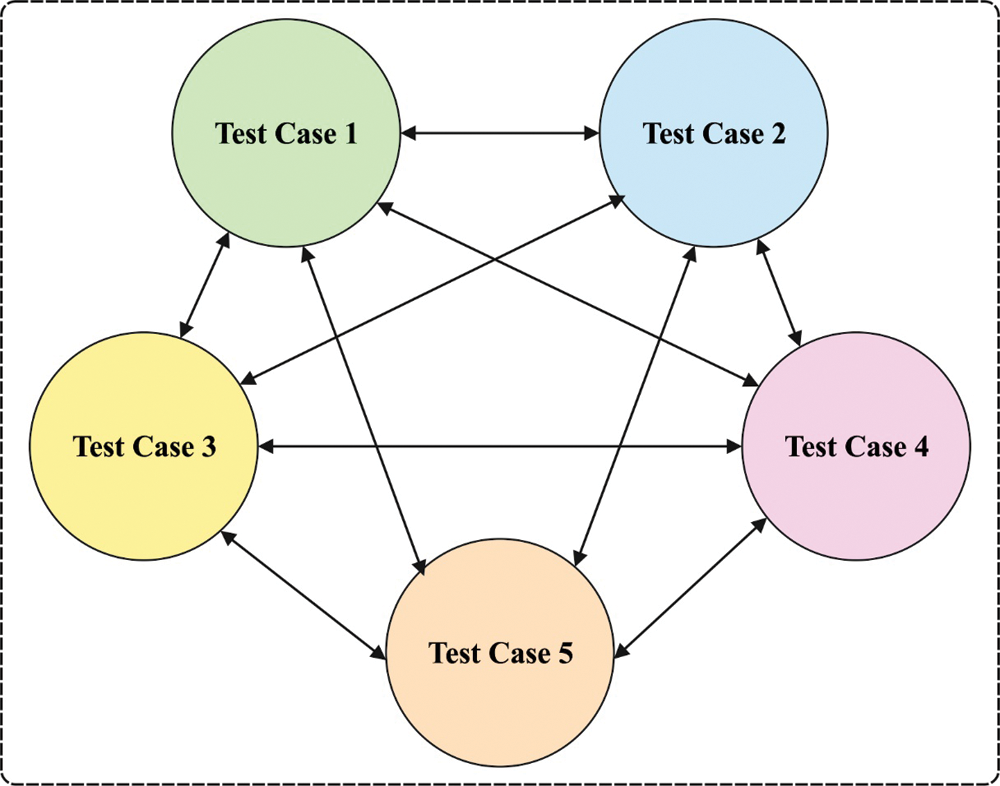
Figure 2: Test cases
In TFIDF, term frequency, tf, first computation is initiated with the help of elected string/term frequency in a document. In other words, tf represents the number of terms t that exists within d document. While, the equation for inverse document frequency, idf handles the importance of terms in a pool of documents. Then, TFIDF is formulated as follows.
In which: T = term frequency in each document; t = term frequency in one document; N = number of term that exist all over the documents; and nt = amount of documents has t term. These 2-string metrics are later utilized in the calculation of weight and distance of dummy test case table [20]. TF-IDF is a standout system among commonly-used term weighing systems in data retrieval methods. Based on this ability, TF-IDF is frequently used in research works. The weight amongst test cases is employed to assign brightness amongst firefly agents in MHHO-TCP.
The election of the next test case, in movement upgradation, depends on the weights of test cases that perform as brightness over distances among the test case, in which the maximum value gets elected as the following move. In arithmetical equation, the brightness of test case on distance estimation is represented as follows.
As the weights of each dummy test case remains the same, the shortest distance is the only metric taken into account, because of the analogous weights of each dummy test case. But, in benchmark program/actual case study, the same weight problem reduces and the distance becomes heavily dynamic. Next the test case distance is evaluated by edit distance with the help of TFIDF string metrics. The total distance traveled denotes the prioritized test cases. The short distances of whole sequences of the test case are taken into account as the optimal distance. The optimal ones are chosen based on MHHO-TCP technique.
The proposed MHHO-TCP model was validated for its performance under different aspects and the results are discussed in this section. The results were investigated under varying iterations and benchmark functions namely, Gzip, Grep, TCAS, and CSTCAS.
Tab. 1 and Fig. 3 shows the results from detailed Average Percentage of Faults Detected (APFD) analysis accomplished by MHHO-TCP model against existing methods under Gzip benchmark function. The figure shows that Greedy technique accomplished a poor performance with least APFD values. Simultaneously, PSD technique gained somewhat improved APFD values. Moreover, LBS and FA techniques reached moderately closer APFD values. However, the proposed MHHO-TCP model outperformed existing techniques and achieved the maximum APFD values under all iterations.
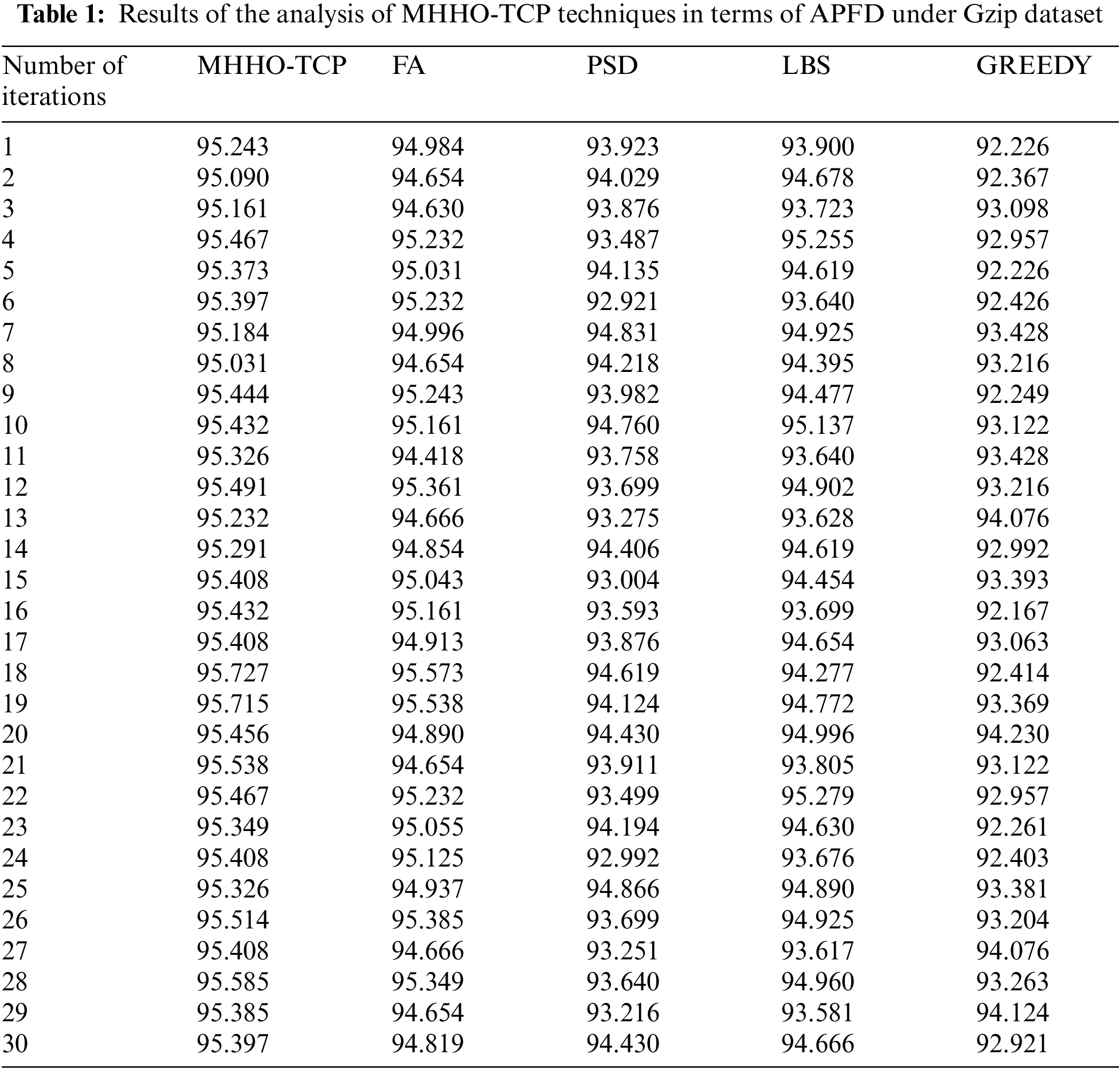
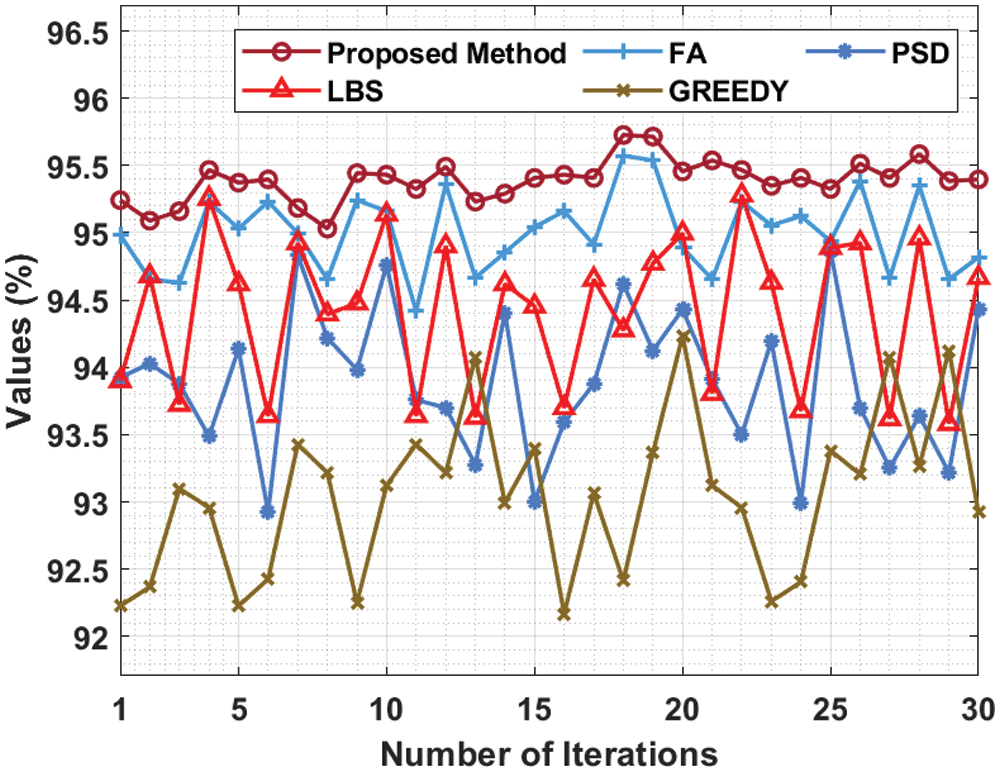
Figure 3: APFD analysis of MHHO-TCP method under Gzip dataset
Tab. 2 and Fig. 4 shows the results achieved by the presented technique in a detailed APFD analysis against existing approaches under Grep benchmark function. The figure demonstrates that Greedy method accomplished the least performance with minimum APFD values. In addition, PSD technique gained slightly improved APFD values. Moreover, LBS and FA methods attained moderately closer APFD values. However, the presented technique outperformed the existing methods with maximum APFD values under all iterations.
Fig. 5 offer a detailed overview of the results from APFD analysis of MHHO-TCP model against existing methods under TCAS benchmark function. The figure shows that Greedy system accomplished the least performance with low APFD values. Also, PSD technique gained somewhat enhanced APFD values. Moreover, LBS and FA techniques reached moderately closer APFD values. However, the presented technique outperformed the existing techniques with maximum APFD values under all iterations.
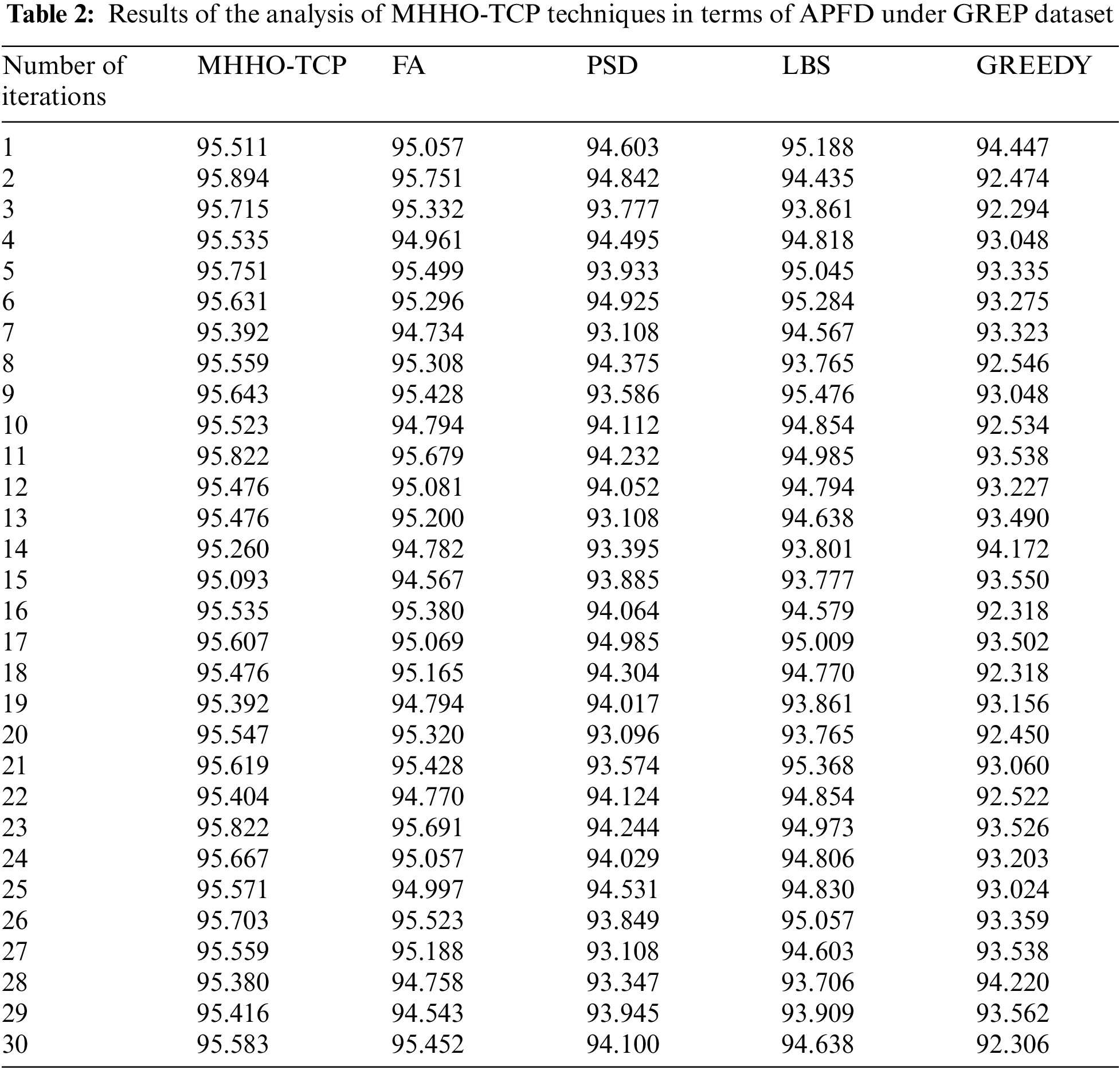
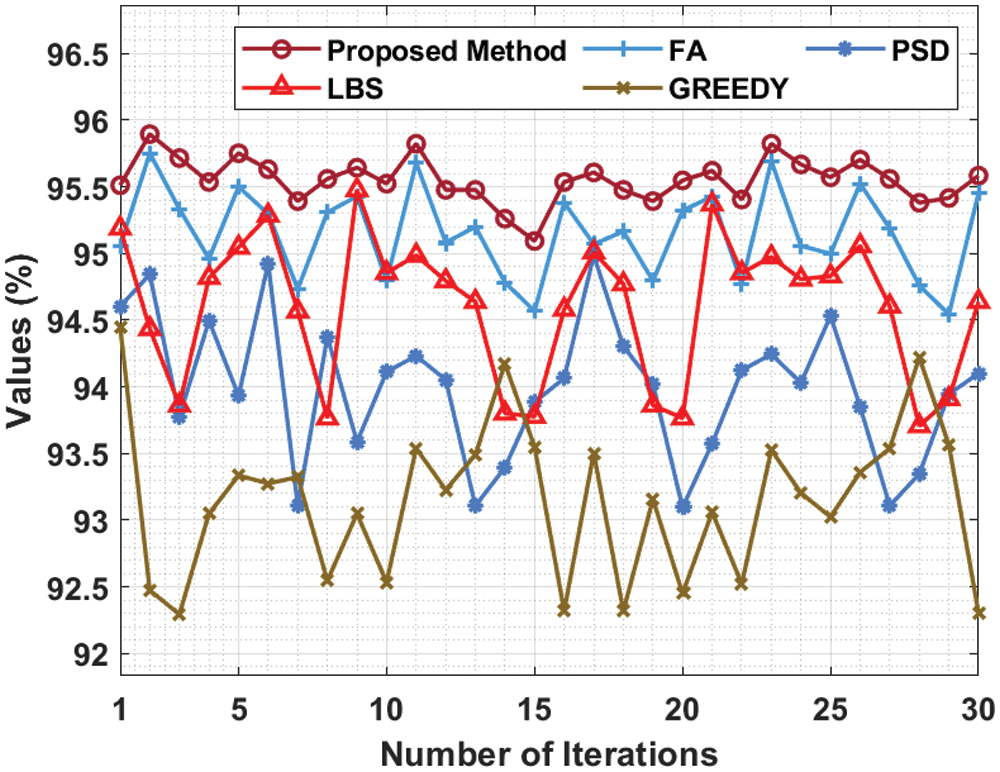
Figure 4: APFD analysis of MHHO-TCP method under Grep dataset
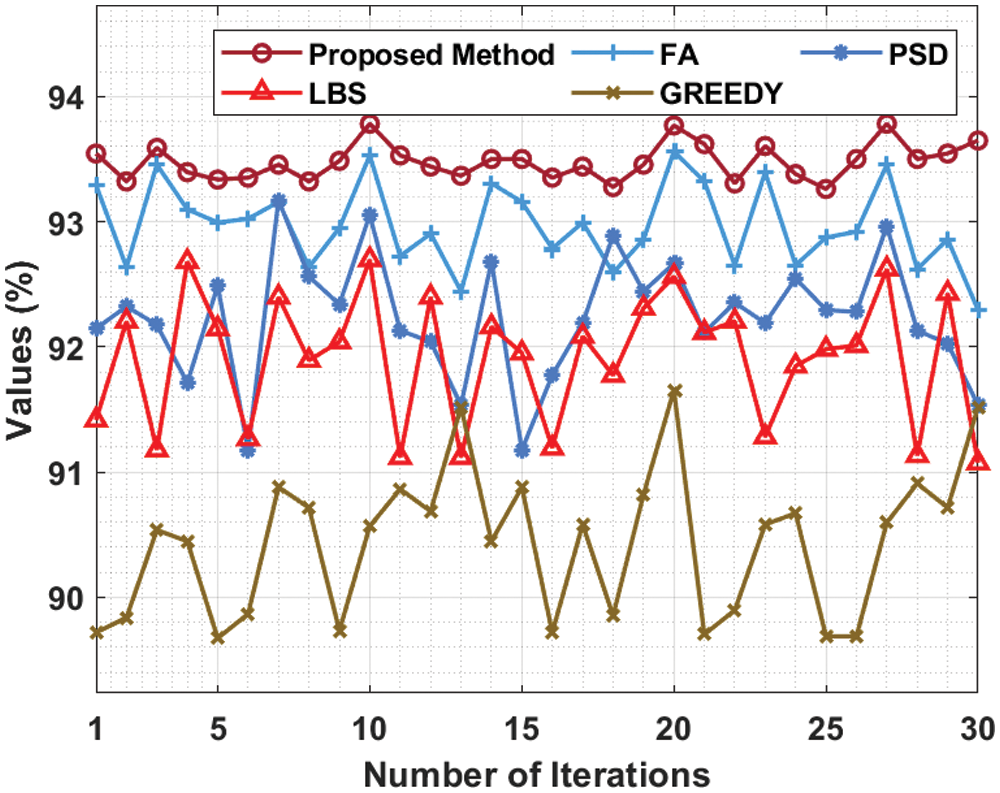
Figure 5: APFD analysis of MHHO-TCP method under TCAS dataset
Fig. 6 shows the results achieved by MHHO-TCP model from a detailed APFD analysis conducted against existing methods under CS-TCAS benchmark function. The figure shows that Greedy technique accomplished a poor performance with low APFD values. At the same time, PSD technique reached somewhat enhanced APFD values. Moreover, LBS and FA methods reached moderately closer APFD values. Finally, the presented technique outperformed all other existing techniques with the highest APFD values under all iterations.
Figure 6: APFD analysis of MHHO-TCP method under CS-TCAS dataset
Tab. 3 and Fig. 7 portrays the outcomes achieved by MHHO-TCP model in average execution time analysis against existing techniques under various benchmark functions. The results showcase that the proposed MHHO-TCP model achieved the least average execution time compared to other approaches under all benchmark functions. For instance, with GZIP benchmark function, MHHO-TCP model attained a low average execution time of 2.103 mts whereas Firefly, PSO, LBS, and Greedy techniques took high average execution times such as 3.053, 4.980, 2.960, and 3.637 respectively. At the same time, with GREP benchmark function, the presented technique attained a minimal average execution time of 2.693 mts, whereas Firefly, PSO, LBS, and Greedy techniques consumed high average execution times namely, 3.647, 5.677, 3.780, and 3.950 respectively. Moreover, with TCAS benchmark function, the proposed MHHO-TCP method achieved the least average execution time of 5.283 mts, whereas other techniques such as Firefly, PSO, LBS, and Greedy obtained the maximal average execution times such as 6.460, 13.293, 6.627, and 7.617 correspondingly. Furthermore, with CS-TCAS benchmark function, MHHO-TCP approach reached a lesser average execution time of 8.230 mts, whereas Firefly, PSO, LBS, and Greedy techniques accomplished superior average execution times namely, 9.627, 19.980, 9.960, and 10.793 respectively.
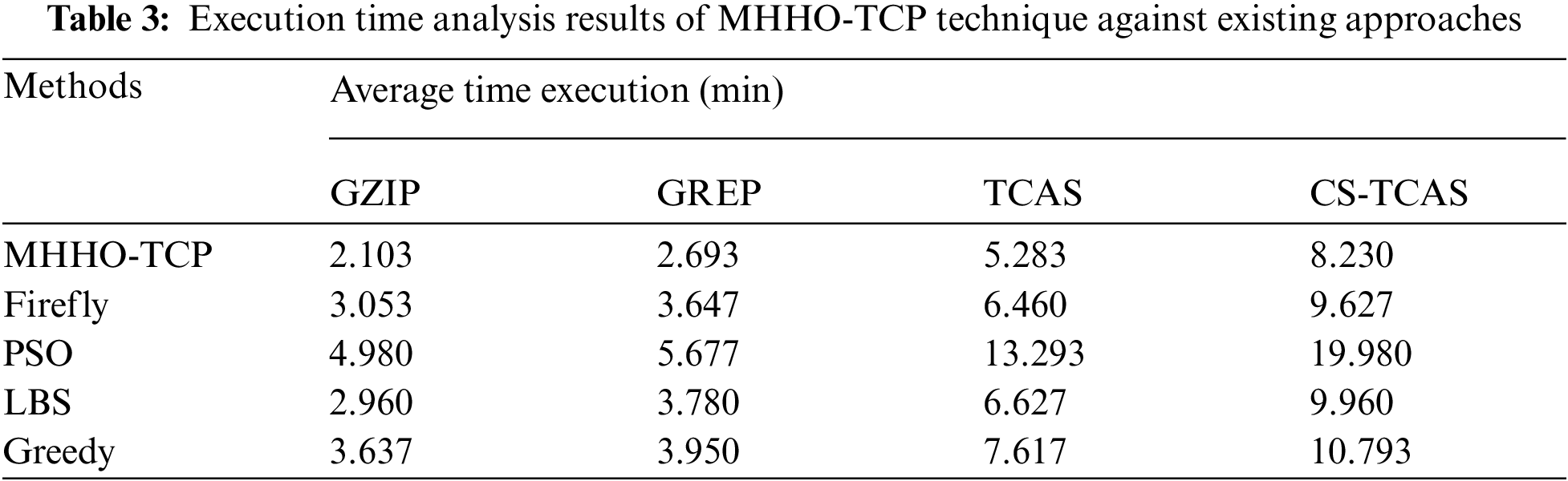
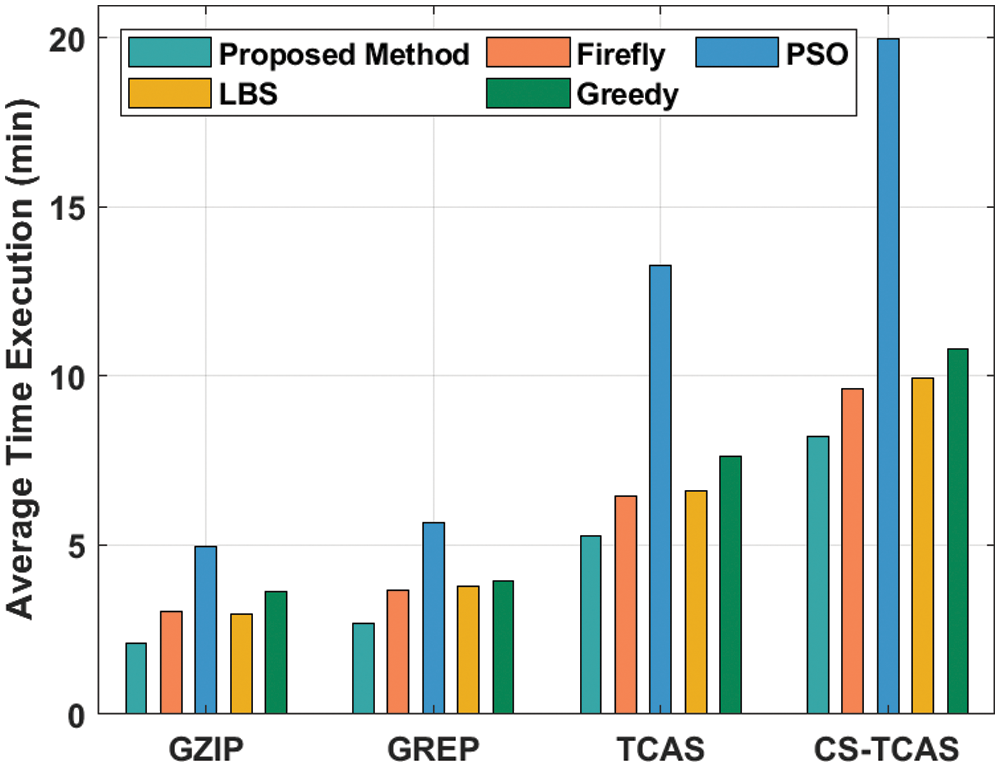
Figure 7: Average execution time analysis results of MHHO-TCP method
An extensive mean APFD analysis was conducted between MHHO-TCP method and existing techniques and the results are shown in Tab. 4 and Fig. 8. The outcomes show that MHHO-TCP approach produced an effective outcome with increased mean APFD values. For instance, with Gzip benchmark function, MHHO-TCP model attained an increased mean APFD of 95.390, whereas firefly, PSO, LBS, and Greedy techniques resulted in reduced mean APFD of 95.004, 93.888, 94.414, and 93.046 respectively. Moreover, with CSTCAS benchmark function, the presented system attained a high mean APFD of 93.413, whereas firefly, PSO, LBS, and Greedy methodologies produced low mean APFD values such as 92.973, 92.571, 91.897, and 91.591 correspondingly.
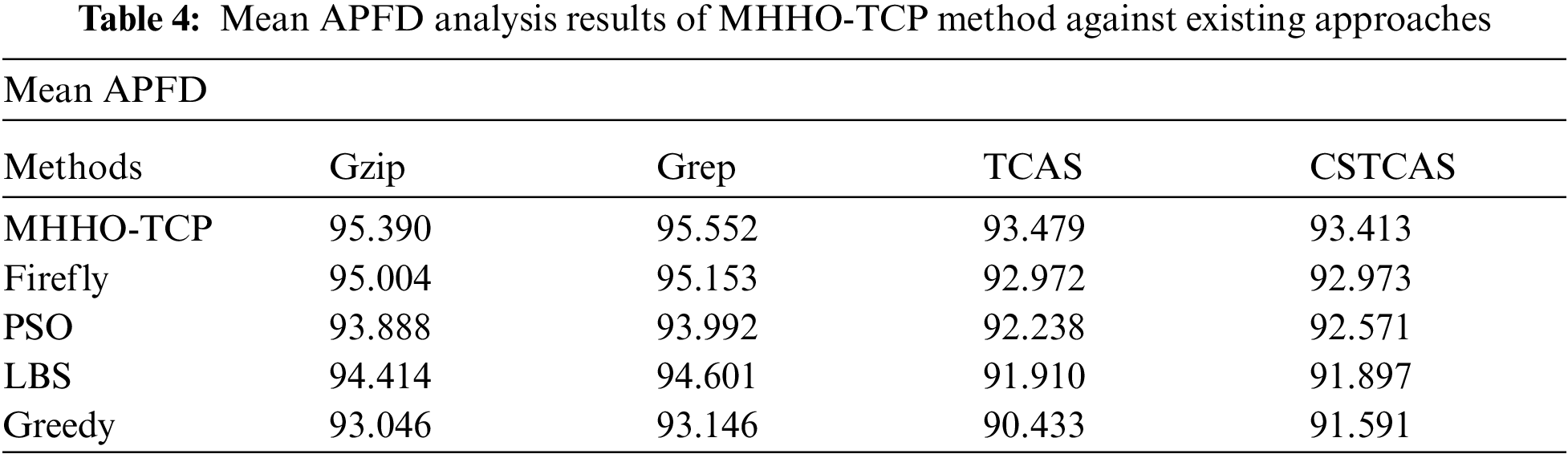
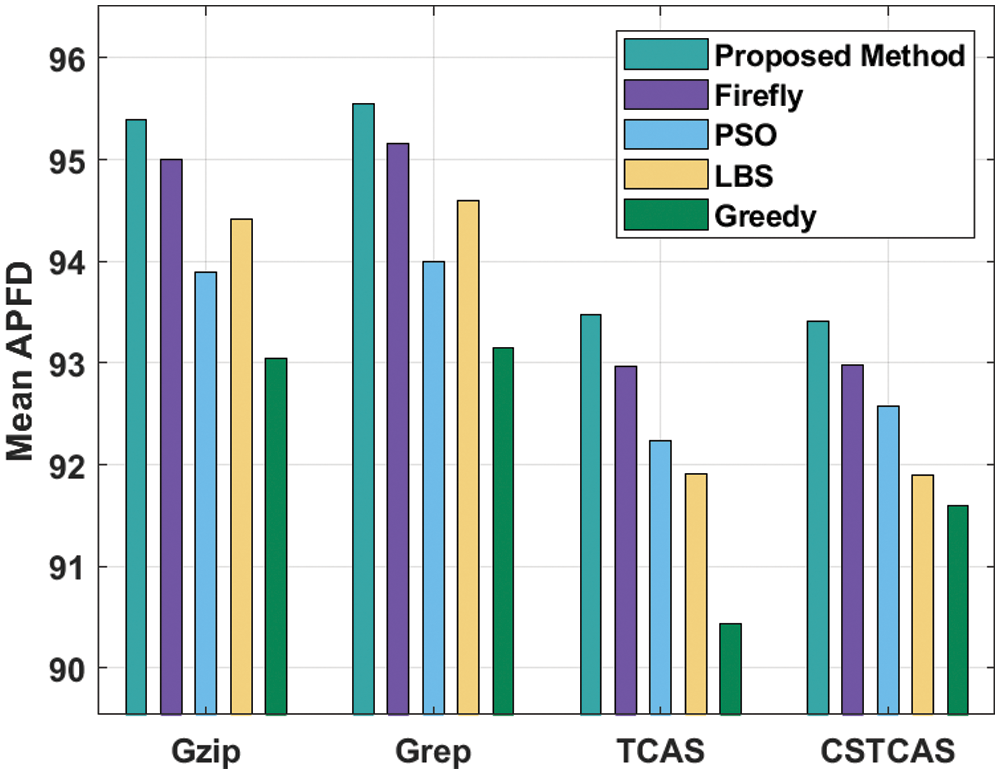
Figure 8: Mean APFD analysis results of MHHO-TCP method against existing approaches
In this study, a novel MHHO-TCP technique is designed for TCP on software testing. The aim of the proposed MHHO-TCP technique is to maximize APFD and minimize the overall execution time. In addition, MHHO algorithm is designed to boost both exploration and exploitation abilities of conventional HHO technique. The design of MHHO technique for TCP in software testing helps in achieving the maximum APFD and minimum execution time. In order to validate the enhanced efficiency of MHHO-TCP technique, a wide range of simulations was conducted upon different benchmark programs and the results were examined under several aspects. The experimental outcomes demonstrate the increased efficacy of MHHO-TCP technique against recent approaches under different measures. In future, HHO algorithm can be utilized replacing other metaheuristic algorithms to further boost the overall performance.
Acknowledgement: The authors would like to acknowledge the support of Prince Sultan University for paying the Article Processing Charges (APC) of this publication.
Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work under Grant Number (RGP.1/127/42). Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R237), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. D. Hao, L. Zhang and H. Mei, “Test-case prioritization: Achievements and challenges,” Frontiers of Computer Science, vol. 10, no. 5, pp. 769–777, 2016. [Google Scholar]
2. M. Khatibsyarbini, M. A. Isa, D. N. A. Jawawi, H. N. A. Hamed and M. D. M. Suffian, “Test case prioritization using firefly algorithm for software testing,” IEEE Access, vol. 7, pp. 132360–132373, 2019. [Google Scholar]
3. B. Balakiruthiga, P. Deepalakshmi, S. N. Mohanty, D. Gupta, P. Pavan Kumar et al., “Segment routing based energy aware routing for software defined data center,” Cognitive Systems Research, vol. 64, pp. 146–163, 2020. [Google Scholar]
4. D. Hao, L. Zhang, L. Zang, Y. Wang, X. Wu et al., “To be optimal or not in test-case prioritization,” IEEE Transactions on Software Engineering, vol. 42, no. 5, pp. 490–505, 2016. [Google Scholar]
5. V. Porkodi, A. R. Singh, A. R. W. Sait, K. Shankar, E. Yang et al., “Resource provisioning for cyber–physical–social system in cloud-fog-edge computing using optimal flower pollination algorithm,” IEEE Access, vol. 8, pp. 105311–105319, 2020. [Google Scholar]
6. W. Jun, Z. Yan and J. Chen, “Test case prioritization technique based on genetic algorithm,” in 2011 Int. Conf. on Internet Computing and Information Services, Hong Kong, China, pp. 173–175, 2011. [Google Scholar]
7. S. K. Lakshmanaprabu, S. N. Mohanty, S. S. Rani, S. Krishnamoorthy, J. Uthayakumar et al., “Online clinical decision support system using optimal deep neural networks,” Applied Soft Computing, vol. 81, pp. 105487, 2019. [Google Scholar]
8. H. Spieker, A. Gotlieb, D. Marijan and M. Mossige, “Reinforcement learning for automatic test case prioritization and selection in continuous integration,” in Proc. of the 26th ACM SIGSOFT Int. Symp. on Software Testing and Analysis, Santa Barbara CA USA, pp. 12–22, 2017. [Google Scholar]
9. D. Panwar, P. Tomar and V. Singh, “Hybridization of Cuckoo-ACO algorithm for test case prioritization,” Journal of Statistics and Management Systems, vol. 21, no. 4, pp. 539–546, 2018. [Google Scholar]
10. B. Miranda, E. Cruciani, R. Verdecchia and A. Bertolino, “FAST approaches to scalable similarity-based test case prioritization,” in Proc. of the 40th Int. Conf. on Software Engineering, Gothenburg Sweden, pp. 222–232, 2018. [Google Scholar]
11. S. Ali, Y. Hafeez, S. Hussain and S. Yang, “Enhanced regression testing technique for agile software development and continuous integration strategies,” Software Quality Journal, vol. 28, no. 2, pp. 397–423, 2020. [Google Scholar]
12. M. A. Hajjaji, T. Thüm, M. Lochau, J. Meinicke and G. Saake, “Effective product-line testing using similarity-based product prioritization,” Software and Systems Modeling, vol. 18, no. 1, pp. 499–521, 2019. [Google Scholar]
13. Y. Xing, X. Wang and Q. Shen, “Test case prioritization based on artificial fish school algorithm,” Computer Communications, vol. 180, pp. 295–302, 2021. [Google Scholar]
14. N. Gokilavani and B. Bharathi, “Multi-objective based test case selection and prioritization for distributed cloud environment,” Microprocessors and Microsystems, vol. 82, pp. 103964, 2021. [Google Scholar]
15. U. Sivaji and P. S. Rao, “Test case minimization for regression testing by analyzing software performance using the novel method,” Materials Today: Proceedings, pp. S2214785321009792, 2021. [Google Scholar]
16. A. Khalilian, M. A. Azgomi and Y. Fazlalizadeh, “An improved method for test case prioritization by incorporating historical test case data,” Science of Computer Programming, vol. 78, no. 1, pp. 93–116, 2012. [Google Scholar]
17. E. H. Houssein, M. E. Hosney, M. Elhoseny, D. Oliva, W. M. Mohamed et al., “Hybrid Harris hawks optimization with cuckoo search for drug design and discovery in chemoinformatics,” Scientific Reports, vol. 10, no. 1, pp. 14439, 2020. [Google Scholar]
18. A. A. Heidari, S. Mirjalili, H. Faris, I. Aljarah, M. Mafarja et al., “Harris hawks optimization: Algorithm and applications,” Future Generation Computer Systems, vol. 97, pp. 849–872, 2019. [Google Scholar]
19. Y. Zhang, X. Zhou and P. C. Shih, “Modified harris hawks optimization algorithm for global optimization problems,” Arabian Journal for Science and Engineering, vol. 45, no. 12, pp. 10949–10974, 2020. [Google Scholar]
20. J. H. Kwon, I. Y. Ko, G. Rothermel and M. Staats, “Test case prioritization based on information retrieval concepts,” in 2014 21st Asia-Pacific Software Engineering Conf., Jeju, South Korea, pp. 19–26, 2014. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |