DOI:10.32604/cmc.2022.024765

| Computers, Materials & Continua DOI:10.32604/cmc.2022.024765 |  |
| Article |
A Fast Algorithm for Mining Top-Rank-k Erasable Closed Patterns
1Faculty of Information Technology, HUTECH University,Ho Chi Minh City, Vietnam
2Informetrics Research Group, Ton Duc Thang University, Ho Chi Minh City, Vietnam
3Faculty of Information Technology, Ton Duc Thang University, Ho Chi Minh City, Vietnam
*Corresponding Author: Tuong Le. Email: lecungtuong@tdtu.edu.vn
Received: 30 October 2021; Accepted: 15 February 2022
Abstract: The task of mining erasable patterns (EPs) is a data mining problem that can help factory managers come up with the best product plans for the future. This problem has been studied by many scientists in recent times, and many approaches for mining EPs have been proposed. Erasable closed patterns (ECPs) are an abbreviated representation of EPs and can be considered condensed representations of EPs without information loss. Current methods of mining ECPs identify huge numbers of such patterns, whereas intelligent systems only need a small number. A ranking process therefore needs to be applied prior to use, which causes a reduction in efficiency. To overcome this limitation, this study presents a robust method for mining top-rank-k ECPs in which the mining and ranking phases are combined into a single step. First, we propose a virtual-threshold-based pruning strategy to improve the mining speed. Based on this strategy and dPidset structure, we then develop a fast algorithm for mining top-rank-k ECPs, which we call TRK-ECP. Finally, we carry out experiments to compare the runtime of our TRK-ECP algorithm with two algorithms modified from dVM and TEPUS (Top-rank-k Erasable Pattern mining Using the Subsume concept), which are state-of-the-art algorithms for mining top-rank-k EPs. The results for the running time confirm that TRK-ECP outperforms the other experimental approaches in terms of mining the top-rank-k ECPs.
Keywords: Pattern mining; erasable closed pattern mining; top-rank-k pattern mining
Frequent pattern mining is one of the most popular topics in data mining and involves extracting frequent itemsets from a database. By identifying frequent patterns, we can observe that some items are strongly correlated together and can easily recognize similar characteristics and associations among them. This topic has attracted a lot of research attention, and many methods have been proposed, such as dEclat [1], FP-Growth * [2], DBV-FI (Dynamic Bit Vector for mining Frequent Itemsets) [3], and NSFI (N-list and Subsume-based algorithm for mining Frequent Itemsets) [4]. Frequent itemsets have also been applied to solvethe problem of multi-attribute users under conditions of local differential privacy [5]. There are also numerous variations of pattern mining, including frequent closed itemset mining [6], maximal frequent patterns [7], frequent weighted itemset mining [8], utility patterns [9,10], colossal patterns [11], erasable itemset mining [12], and so on. These variations have different meanings and are used in intelligent systems for specific situations. In addition, too many patterns are often generated when traditional approaches are used in intelligent systems, making it time- and resource-consuming to rank the patterns and find the most promising. Several top-k and top-rank-k approaches have been developed [13–18] for different types of patterns and rules, such as frequent patterns, frequent weighted patterns, closed sequential patterns, and association rules, in order to combine the mining and ranking processes into a single algorithm. This can help intelligent systems to work better.
Erasable pattern mining, developed by Deng et al. [12] in 2009, aims to help manufacturing managers to come up with the best production plans for the coming years. This problem often arises in the product planning process in a factory. In this scenario, a factory produces a wide range of products, each of which is made from certain components (items) and earns a particular amount of money for the manufacturer as profit. The current production plan requires the manufacturer to spend large amounts of money to purchase and store these items. In unexpected situations, such as a financial crisis or the COVID 19 pandemic, the manufacturer cannot afford to purchase all the necessary items as usual; managers therefore need to reconsider their production plans to ensure the stability of the manufacturing process. In the case described above, the problem involves finding itemsets that can be eliminated but do not greatly affect the factory's profit. In other words, we wish to find the sets of itemsets which can best be eliminated (erased) (called EPs) so that managers can then utilize this knowledge to create a new production plan that minimizes the profit reduction. Numerous algorithms have been proposed to solve the EP mining problem, such as META [12], MEI (mining erasable itemsets) [19], EIFDD (erasable itemsets for very dense datasets) [20], pMEI (parallel mining erasable itemsets) [21], and BREM (bitmap-representation erasable mining) [22]. Several variations have also been developed, such as mining EPs with constraints [23], mining erasable closed patterns [24], mining maximal EPs [25], mining top-rank-k EPs [26,27] mining erasable patterns in incremental database [28,29], and mining EPs in data streams [30–33].
When applied to the problem of mining erasable closed patterns (ECPs), the traditional mining approaches proposed in [24] give very large numbers of patterns, and this is the reason for the low efficiency of intelligent systems. These systems mine ECPs by applying traditional algorithms (in the mining phase) and then rank the results to select the top patterns based on their gains (in the ranking phase). This two-phase process is time- and resource-consuming, and such systems may even fail to run due to memory and storage space limitations. Hence, in this paper, we address the problem of mining top-rank-k ECPs in order to combine the mining and ranking phases. The key contributions of this study are as follows: (i) we develop a virtual-threshold-based pruning strategy for the mining of top-rank-k ECPs, in which the virtual threshold is set to the highest threshold of the results in the mining process, thus helping to improve the mining time by avoiding the creation of unsatisfactory candidates; (ii) we present the TRK-ECP algorithm, which uses a virtual-threshold-based pruning strategy for the mining of top-rank-k ECPs; (iii) we conduct experiments to demonstrate the effectiveness of the TRK-ECP algorithm in terms of the mining time, the results of which indicate that TRK-ECP outperforms two alternative modified algorithms (namely dVM and TEPUS) in terms of the mining time for top-rank-k ECPs.
The rest of this study is structured as follows. An overview of the basic principles of EPs and ECPs is given in Section 2. A definition of the mining of top-rank-k ECPs and a fast-mining algorithm are introduced in Section 3. Our experimental results are presented in Section 4, and it is shown that these confirm the effectiveness of the TRK-ECP algorithm. The conclusions of the study and suggestions for future work are given in Section 5.
This section introduces the basic concepts needed to understand the topic of this study. Section 2.1 presents the definition of EPs and gives examples based on a toy product dataset. Section 2.2 discusses the concept of an ECP and presents some examples.
Deng et al. [12] introduced an interesting problem called erasable pattern mining, as briefly summarized in this section. We consider a product dataset for a factory, denoted as DB. This dataset contains n products, as P = {P1, P2, …, Pn}. Each product in this dataset is created from a set of components. For convenience in terms of our study of pattern mining, the set of all components can be considered as the set of all items, denoted by I = {i1, i2, …, im}. Each product in the product dataset is represented in the form 〈Items, Val〉, in which Items are the components required to manufacture this product, and Val is the profit that the factory gains by selling this product. A toy product dataset is presented in Tab. 1 and is used as an example throughout this study.

Definition 1. For a product dataset denoted by DB and a threshold ξ, a pattern X is an erasable pattern if and only if:
In Eqs. (1)–(3), g(X) is the gain due to X, and T is the total profit of the whole dataset DB. According to Eq. (1), the problem of mining EPs involves finding all patterns X with gains g(X) that are less than T × ξ.
Example 1. For the product dataset which shown in Tab. 1, we calculate the total profit as T =
In 2017, Vo et al. [24] presented the definition of an ECP, which can be summarized as follows. An EP is called an ECP if and only if there are no supersets that have the same gain. For instance, consider the dataset in Tab. 1 with ξ = 40%. In this example, A5 and A5A3 are two EPs, as g(A5) = g(A5A3) = 700 < T × ξ = $780. In terms of the problem of ECP mining, A5 is not an ECP, because we have a superset (A5A3) with the same gain as A5, i.e., g(A5) = g(A5A3) = $700. Hence, A5A3 is an ECP and A5 is not. Tab. 2 provides all ECPs for our dataset with ξ = 40%.

In 2014, Le et al. [19] developed the dPidset structure, which is typically used to mine EPs. In this study, we also use this structure to mine top-rank-k ECPs. We can summarize the dPidset structure as follows. Firstly, the pidset p(X) of pattern X is determined as:
where A is an item in pattern X, and p(A) is the set of products that contain A.
Example 2. For the dataset in Tab. 1, the pidsets of A5, A3, and A6 are p(A5) = {2, 3, 4, 5, 6}, p(A3) = {3, 5}, and p(A6) = {4, 6, 8}, respectively. We have p(A5A3) = p(A5) ∪ p(A3) = {2, 3, 4, 5, 6}. We also have p(A5A6) = p(A5) ∪ p(A6) = {2, 3, 4, 5, 6, 8}.
Definition 2. Let XA and XB be two patterns. The dPidset of XAB, denoted as dP(XAB), is computed by the following equation:
Example 3. In Example 2, the pidsets of A5, A3, and A6 are p(A5) = {2, 3, 4, 5, 6}, p(A3) = {3, 5}, and p(A6) = {4, 6, 8}. Based on Definition 2, we know that the dPidset of A5A3 is dP(A5A3) = p(A3) /p(A5) = Ø. Similarly, the dPidsets of A5A6 and A5A3A6 are dP(A5A6) = p(A6)/p(A5) = {8}, and dP(A5A3A6) = p(A5A6)/p(A5A3) = {8}, respectively.
Theorem 1 [19]. Let XA and XB be two patterns with dPidsets dP(XA) and dP(XB), respectively. The dPidset of XAB is determined using the following equation:
Example 4. In Example 3, the dPidsets of A5A3 and A5A6 are dP(A5A3) = Ø and dP(A5A6) = {8}, respectively. We have dP(A5A3A6) = dP(A5A6)/dP(A5A3) = {8}. The results for Examples 3 and 4 clearly verify Theorem 1.
Theorem 2 [19]. The gain of XAB can be computed based on the gain of XA and the dPidset of XAB, as follows:
In Eq. (7), g(XA) is the gain of XA while Pk.Val is the profit of product Pk in the product dataset.
Example 5. For the example dataset in Tab. 1, we know that the pidsets of A5, A3, and A6 are p(A5) = {2, 3, 4, 5, 6}, p(A3) = {3, 5}, and p(A6) = {4, 6, 8}, respectively. We also have g(A5) = $700, g(A3) = $250, and g(A6) = $350. Since dP(A5A3) = Ø, we have g(A5A3) = g(A5) +
3 TRK-ECP: A New Algorithm for Mining Top-Rank-k ECPs
3.1 The Problem of Mining Top-Rank-k ECPs
Definition 3. A pattern X is in the top-rank-k ECPs if and only if
The problem of mining the top-rank-k ECPs is therefore the task of finding the complete set of ECPs for which the rank is no greater than k, where k is input by the user.
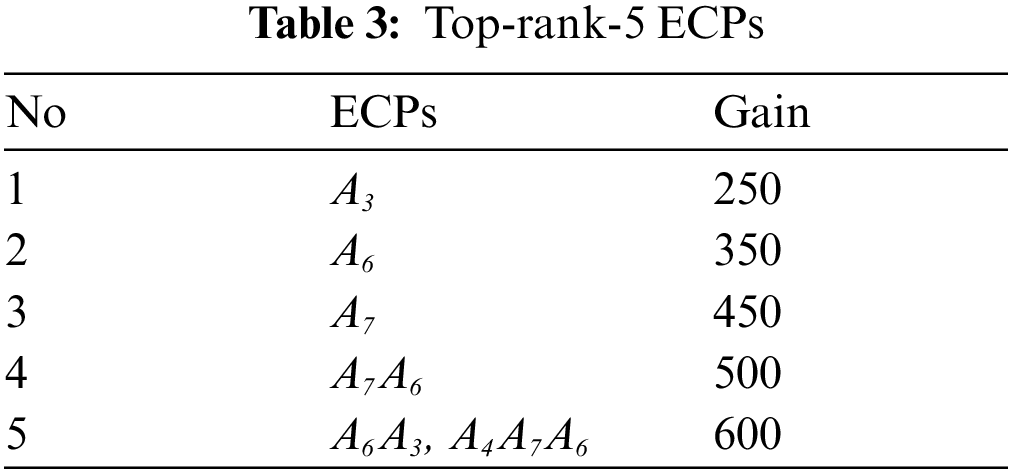
Example 5. For the dataset in Tab. 1, let k be five. Tab. 3 below shows all ECPs belonging to the top-5 ECPs from our dataset. We call these the top-rank-5 ECPs.
In this section, we present a virtual-threshold-based pruning strategy to accelerate the runtime for mining top-rank-k ECPs. We first consider a top-rank-k table structure called TR, which is used to store the current top-rank-k ECPs. In this table, ranking is done based on ascending order of gain, meaning that the last rank in TR is the largest gain. Hence, when TR receives k ranks (i.e., there are k ranks in TR), the virtual threshold (ξ) will be updated based on the gain of the last rank in TR. During the candidate generation procedure, the algorithm will not create a candidate from two ECPs if either of them has a gain greater than the virtual threshold. This strategy helps to reduce the search space and accelerates the runtime, and we refer to this as our virtual-threshold-based pruning strategy. Secondly, we develop the TRK-ECP algorithm based on this strategy, as shown in Algorithm 1.
Example 6. To illustrate the operation of the TRK-ECP algorithm, we apply it to the example dataset in Tab. 1, with k = 5. In Lines 1–3, the proposed algorithm scans the example dataset to determine the gain and dPidset for each 1-item stored in E1, as shown in Tab. 4. Note that E1 is the set of all items in the dataset, without a threshold.


In Lines 4–10, the TRK-ECP algorithm inserts the first five items of E1, {A3, A6, A7, A4, A5}, into the results for the top-rank-k ECPs, denoted by TR, and the next-level candidates Ck (which are used to create the next-level candidates). Note that A1 and A2 are eliminated, since the results have already k = 5 elements. The number of ranks in the results (TR) is five, and the threshold for this step ξ is set to 700. The results after the first step are presented in Tab. 5.

In the next step (Lines 11–24), TRK-ECP utilizes Ck to create the next-level candidates {〈A3A6, 600〉, 〈A6A7, 500〉, 〈A6A4, 600〉, 〈A7A4, 600〉}, using the Candidate_Generation procedure. Note that {〈A3A7, 700〉, 〈A3A4, 750〉, 〈A3A5, 700〉, 〈A6A5, 800〉, 〈A7A5, 950〉, 〈A4A5, 950〉} are not generated by the virtual-threshold-based pruning strategy. The TRK-ECP algorithm then sorts the candidates in ascending order of gain, and thus we have the list of candidates {〈A6A7, 500〉, 〈A3A6, 600〉, 〈A6A4, 600〉, 〈A7A4, 600〉}. Next, these candidates will be inserted into TR and Ck. This step also removes any non-ECPs that have been added to the results. In our example, this step inserts a new rank with a gain of 500, which includes an ECP {〈A6A7, 500〉}, while the rank for a gain of 700 is removed from TR. At a rank of 600, this algorithm removes {A4} from the result, as it is not an ECP. The virtual threshold ξ is set to 600. The results of this step are presented in Tab. 6.

In the third step, the TRK-ECP algorithm uses Ck = {〈A6A7, 500〉, 〈A3A6, 600〉, 〈A6A4, 600〉, 〈A7A4, 600〉} to create 〈A6A7A4, 600〉, and inserts 〈A6A7A4, 600〉 into TR and Ck. In this step, {A6A4, A7A4} is a subset of A6A7A4 and has the same gain of 600. The algorithm therefore removes {A6A4, A7A4} from the results. Tab. 7 presents the results after this step.

In the next step, the set of candidates Ck = {〈A6A7A4, 600〉} contains only one item; the TRK-ECP algorithm therefore stops, and the final results are as shown in Tab. 7.
The experiments described in this section were conducted on a computer with an Intel Core i5-7200U 2.5 GHz CPU and 16 GBs of RAM. All the experimental algorithms were implemented in C# and were run in the same environment with the .Net Framework Version 4.5. Four public datasets (Chess, Connect, Mushroom, and T10I4D100K) were used to test the effectiveness of the proposed approach. These datasets are frequently used to evaluate pattern mining algorithms in relation to data mining tasks. To create the product datasets, a column generated using a random function was added to store the profit for each product. The features of these datasets are given in Tab. 8.
To verify the effectiveness of the TRK-ECP approach, we compare its runtime with those of TEPUS [27] and dVM [26] for the problem of mining the top-rank-k ECPs (denoted as TEPUS4ECP and dVM4ECP). Note that there are currently no alternative algorithms for mining the top-rank-k ECPs, and we therefore had to modify TEPUS and dVM accordingly. TEPUS4ECP and dVM4ECP were created in two stages, as follows. In the first step, we used TEPUS and dVM to mine the top-rank-k EPs. The top-rank-k ECPs were obtained in the second step, based on the top-rank-k EPs. The runtimes for TEPUS4ECP and dVM4ECP consist of the sums of the runtimes for the first and second steps.
In Fig. 1, we compare the runtimes of TKR-ECP, TEPUS4ECP and dVM4ECP on the Chess dataset. The results show that TKR-ECP is the fastest and dVM4ECP is the slowest. For example, for k = 400, the runtimes for TKR-ECP, TEPUS4ECP, and dVM4ECP are 0.159, 0.24, and 1.42 s, respectively. Thus, TKR-ECP is 33.75% times faster than TEPUS4ECP and 88.8% times faster than dVM4ECP on the Chess dataset, for k = 400. The total times for k = 100, 200, 300, and 400 for TKR-ECP, TEPUS4ECP, and dVM4ECP are 0.608, 0.84 and 4.15 s.

Figure 1: Runtimes for three experimental methods on the chess dataset
Fig. 2 compares the runtimes of TKR-ECP, TEPUS4ECP and dVM4ECP on the Connect dataset. The results show that TKR-ECP is the fastest, and dVM4ECP is the slowest. For example, for k = 300, the runtimes for TKR-ECP and TEPUS4ECP are 4.16 and 6.28 s, while dVM4ECP cannot run at this threshold. The total times for k = 100, 200, 300, and 400 for TKR-ECP and TEPUS4ECP are 14.88 and 21.97 s. Hence, TKR-ECP is 33.75% times faster than TEPUS4ECP on this dataset.

Figure 2: Runtimes for three experimental methods on the connect dataset
Fig. 3 compares the runtimes of TKR-ECP, TEPUS4ECP and dVM4ECP for the Mushroom dataset. The results show that the times for all three algorithms are the same for all thresholds k. The total times for k = 100, 200, 300, and 400 for TKR-ECP, TEPUS4ECP, and dVM4ECP on the Mushroom dataset are 1.55, 1.98 and 10.32 s, respectively.

Figure 3: Runtimes for three experimental methods on the mushroom dataset
Fig. 4 compares the runtimes of TKR-ECP, TEPUS4ECP and dVM4ECP on the T10I4D100K dataset. The results show that TKR-ECP is the fastest and dVM4ECP is the slowest in terms of runtime. For example, for k = 200, the runtimes for TKR-ECP, TEPUS4ECP, and dVM4ECP on the T10I4D100K dataset are 3.58, 3.64, and 5.36 s, respectively, meaning that TKR-ECP is 1.6% times faster than TEPUS4ECP and 33% times faster than dVM4ECP for the T10I4D100K dataset with this threshold. The total times for k = 100, 200, 300, and 400 for TKR-ECP, TEPUS4ECP, and dVM4ECP for this dataset are 15.6, 16.22 and 29.32 s, respectively.
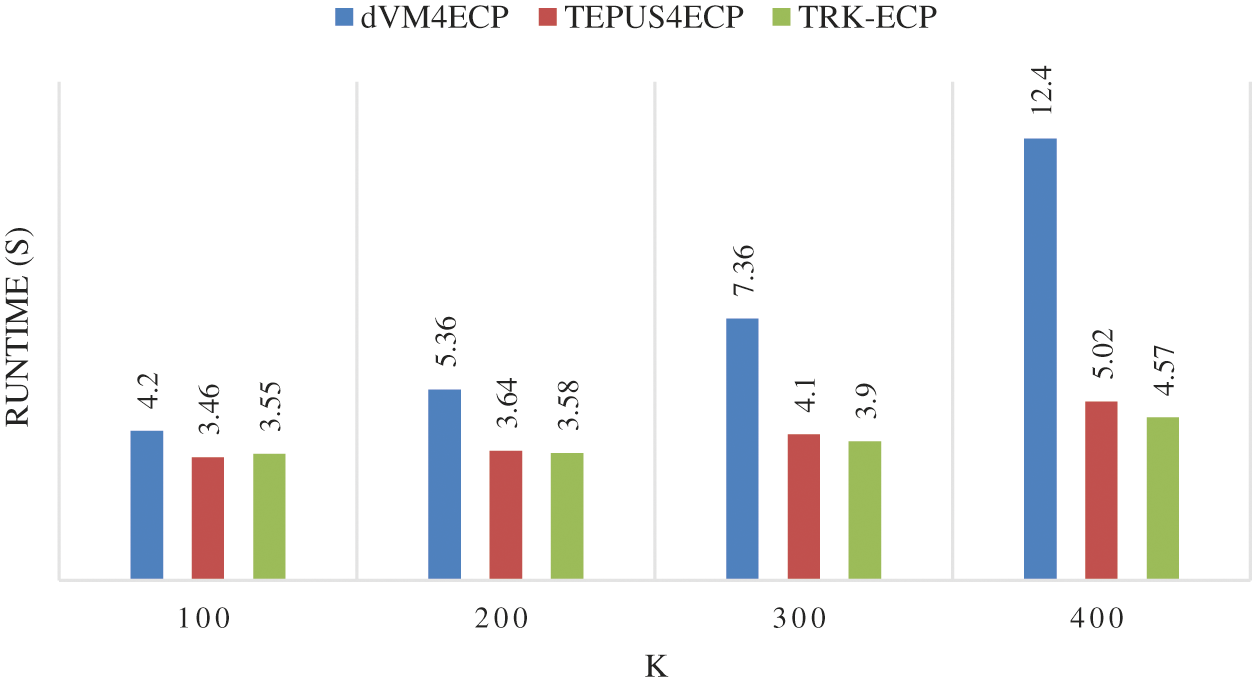
Figure 4: Runtimes for three experimental methods on the T10I4D100K dataset
To test whether our method was the best, we conducted paired t-test statistics for the experimental methods for all four datasets. As we can see from Tab. 9, most of the p-values for Chess, Connect and Mushroom were less than 0.05, meaning that our proposed method outperformed dVM4ECP and TEPUS4ECP on these datasets. For T10I4D100K, the differences between the experimental methods were not obvious.

From the experimental results presented above, we can see that TKR-ECP was the fastest, and dVM4ECP was the slowest. TKR-ECP was faster than TEPUS4ECP for three databases (Chess, Connect, and Mushroom), and the performance of these two methods was equal on the remaining database (T10I4D100K). In addition, the memory usage for TKR-ECP and TEPUS4ECP was roughly equivalent on these experimental databases. Overall, the proposed algorithm outperformed the other experimental approaches for mining top-rank-k ECPs in terms of processing time.
In this study, we first introduced the concept of mining the top-rank-k ECPs, and a fast method for mining top-rank-k ECPs was then presented. Our new algorithm combines the mining and ranking of ECPs into a single algorithm and can therefore help to improve the processing time of intelligent systems. We developed a virtual-threshold-based pruning strategy to improve the mining speed for this task and applied this strategy with the dPidset structure to devise the TRK-ECP algorithm for mining the top-rank-k ECPs. We have presented detailed, step-by-step examples of how our algorithm works, and conducted experiments to compare the runtime of the proposed algorithm with two modified algorithms (dVM4ECP and TEPUS4ECP) for the mining of top-rank-k ECPs. Our experimental results confirm that the proposed algorithm outperforms the other experimental approaches for the mining of top-rank-k ECPs in terms of processing time.
In the future, several topics related to the problem of mining EPs and ECPs in incremental databases and data streams will be studied. Moreover, we intend to focus on the problem of mining EPs and ECPs with certain kinds of constraints.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. J. Zaki and C. J. Hsiao, “Efficient algorithms for mining closed itemsets and their lattice structure,” IEEE Transactions on Knowledge and Data Engineering, vol. 17, no. 4, pp. 462–478, 2005. [Google Scholar]
2. G. Grahne and J. Zhu, “Fast algorithms for frequent itemset mining using FP-trees,” IEEE Transactions on Knowledge and Data Engineering, vol. 17, no. 10, pp. 1347–1362, 2005. [Google Scholar]
3. B. Vo and B. Le, “Interestingness measures for mining association rules: Combination between lattice and hash tables,” Expert Systems with Applications, vol. 38, no. 9, pp. 11630–11640, 2011. [Google Scholar]
4. B. Vo, T. Le, F. Coenen and T. P. Hong, “Mining frequent itemsets using the N-list and subsume concepts,” International Journal of Machine Learning and Cybernetics, vol. 7, no. 2, pp. 253–265, 2016. [Google Scholar]
5. H. Liu, L. Cui, X. Ma and C. Wu, “Frequent itemset mining of user's multi-attribute under local differential privacy,” CMC-Computers, Materials & Continua, vol. 65, no. 1, pp. 369–385, 2020. [Google Scholar]
6. T. Le and B. Vo, “An N-list-based algorithm for mining frequent closed patterns,” Expert Systems with Applications, vol. 42, no. 19, pp. 6648–6657, 2015. [Google Scholar]
7. B. Vo, S. Pham, T. Le and Z. H. Deng, “A novel approach for mining maximal frequent patterns,” Expert Systems with Applications, vol. 73, pp. 178–186, 2017. [Google Scholar]
8. H. Bui, T. A. Nguyen-Hoang, B. Vo, H. Nguyen and T. Le, “A sliding window-based approach for mining frequent weighted patterns over data streams,” IEEE Access, vol. 9, pp. 56318–56329, 2021. [Google Scholar]
9. W. Gan, J. C. W. Lin, J. Zhang, P. Fournier-Viger, H. C. Chao et al., “Fast utility mining on sequence data,” IEEE Transactions on Cybernetics, vol. 51, no. 2, pp. 487–500, 2021. [Google Scholar]
10. H. Kim, U. Yun, Y. Baek, J. Kim, B. Vo et al., “Efficient list based mining of high average utility patterns with maximum average pruning strategies,” Information Sciences, vol. 543, pp. 85–105, 2021. [Google Scholar]
11. T. Le, T. L. Nguyen, B. Huynh, H. Nguyen, T. P. Hong et al., “Mining colossal patterns with length constraints,” Applied Intelligence, vol. 51, no. 12, pp. 8629–8640, 2021. [Google Scholar]
12. Z. H. Deng, G. Fang, Z. Wang and X. Xu, “Mining erasable itemsets,” in Proc. of Int. Conf. on Machine Learning and Cybernetics, Baoding, China, pp. 67–73, 2009. [Google Scholar]
13. T. Le, B. Vo, V. N. Huynh, N. T. Nguyen and S. W. Baik, “Mining top-k frequent patterns from uncertain databases,” Applied Intelligence, vol. 50, no. 5, pp. 1487–1497, 2020. [Google Scholar]
14. B. Vo, H. Bui, T. Vo and T. Le, “Mining top-rank-k frequent weighted itemsets using WN-list structures and an early pruning strategy,” Knowledge-Based Systems, vol. 201–202, pid.106064, 2020. [Google Scholar]
15. T. T. Pham, T. Do, A. Nguyen, B. Vo and T. P. Hong, “An efficient method for mining top-K closed sequential patterns,” IEEE Access, vol. 8, pp. 118156–118163, 2020. [Google Scholar]
16. L. T. T. Nguyen, B. Vo, L. T. T. Nguyen, P. Fournier-Viger and A. Selamat, “ETARM: An efficient top-k association rule mining algorithm,” Applied Intelligence, vol. 48, no. 5, pp. 1148–1160, 2018. [Google Scholar]
17. X. Liu, X. Niu and P. Fournier-Viger, “Fast top-K association rule mining using rule generation property pruning,” Applied Intelligence, vol. 51, no. 4, pp. 2077–2093, 2021. [Google Scholar]
18. Y. Long, W. Tang, B. Yang, X. Wang, H. Ma et al., “GTK: A hybrid-search algorithm of top-rank-k frequent patterns based on greedy strategy,” CMC-Computers, Materials & Continua, vol. 63, no. 3, pp. 1445–1469, 2020. [Google Scholar]
19. T. Le and B. Vo, “MEI: An efficient algorithm for mining erasable itemsets,” Engineering Applications of Artificial Intelligence, vol. 27, pp. 155–166, 2014. [Google Scholar]
20. G. Nguyen, T. Le, B. Vo and B. Le, “EIFDD: An efficient approach for erasable itemset mining of very dense datasets,” Applied Intelligence, vol. 43, no. 1, pp. 85–94, 2015. [Google Scholar]
21. B. Huynh and B. Vo, “An efficient method for mining erasable itemsets using multicore processor platform,” Complexity, vol. 2018, Article ID 8487641, 2018. [Google Scholar]
22. T. P. Hong, W. M. Huang, G. C. Lan, M. C. Chiang and J. C. W. Lin, “A bitmap approach for mining erasable itemsets,” IEEE Access, vol. 9, pp. 106029–106038, 2021. [Google Scholar]
23. B. Vo, T. Le, W. Pedrycz, G. Nguyen and S. W. Baik, “Mining erasable itemsets with subset and superset itemset constraints,” Expert Systems with Applications, vol. 69, pp. 50–61, 2017. [Google Scholar]
24. B. Vo, T. Le, G. Nguyen and T. P. Hong, “Efficient algorithms for mining erasable patterns from product datasets,” IEEE Access, vol. 5, no. 1, pp. 3111–3120, 2017. [Google Scholar]
25. L. Nguyen, G. Nguyen and B. Le, “Fast algorithms for mining maximal erasable patterns,” Expert Systems with Applications, vol. 124, pp. 50–66, 2019. [Google Scholar]
26. G. Nguyen, T. Le, B. Vo and B. Le, “A new approach for mining top-rank-k erasable itemsets,” in Proc. of Asian Conf. on Intelligent Information and Database Systems, Bali, Indonesia, pp. 73–82, 2014. [Google Scholar]
27. T. Le, B. Vo and S. W. Baik, “Efficient algorithms for mining top-rank-k erasable patterns using pruning strategies and the subsume concept,” Engineering Applications of Artificial Intelligence, vol. 68, pp. 1–9, 2018. [Google Scholar]
28. G. Lee and U. Yun, “Single-pass based efficient erasable pattern mining using list data structure on dynamic incremental databases,” Future Generation Computer Systems, vol. 80, pp. 12–28, 2018. [Google Scholar]
29. H. Nam, U. Yun, E. Yoon and J. C. W. Lin, “Efficient approach for incremental weighted erasable pattern mining with list structure,” Expert Systems with Applications, vol. 143, pid. 113087, 2020. [Google Scholar]
30. T. Le, B. Vo, P. Fournier-Viger, M. Y. Lee and S. W. Baik, “SPPC: A new tree structure for mining erasable patterns in data streams,” Applied Intelligence, vol. 49, no. 2, pp. 478–495, 2019. [Google Scholar]
31. Y. Baek, U. Yun, H. Kim, H. Nam, G. Lee et al., “Erasable pattern mining based on tree structures with damped window over data streams,” Engineering Applications of Artificial Intelligence, vol. 94, pid. 103735, 2020. [Google Scholar]
32. Y. Baek, U. Yun, J. C. W. Lin, E. Yoon and H. Fujita, “Efficiently mining erasable stream patterns for intelligent systems over uncertain data,” International Journal of Intelligent Systems, vol. 35, no. 11, pp. 1699–1734, 2020. [Google Scholar]
33. U. Yun, G. Lee and E. Yoon, “Advanced approach of sliding window based erasable pattern mining with list structure of industrial fields,” Information Sciences, vol. 494, pp. 37–59, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |