Computers, Materials & Continua DOI:10.32604/cmc.2022.025642
Article

Intelligent Satin Bowerbird Optimizer Based Compression Technique for Remote Sensing Images

M. Saravanan1, J. Jayanthi2, U. Sakthi3, R. Rajkumar4, Gyanendra Prasad Joshi5, L. Minh Dang5 and Hyeonjoon Moon5,*

1Department of Networking and Communications, School of Computing, SRM Institute of Science and Technology, Kattankulathur, 603203, India
2Department of Computer Science and Engineering, Sona College of Technology, Salem, 636005, India
3Department of Computer Science and Engineering, Saveetha School of Engineering, SIMATS, Chennai, 602105, India
4Department of Electronics and Instrumentation Engineering, Kongu Engineering College, Perundurai, 638060, India
5Department of Computer Science and Engineering, Sejong University, Seoul, 05006, Korea
*Corresponding Author: Hyeonjoon Moon. Email: hmoon@sejong.ac.kr
Received: 30 November 2021; Accepted: 07 January 2022

Abstract: Due to latest advancements in the field of remote sensing, it becomes easier to acquire high quality images by the use of various satellites along with the sensing components. But the massive quantity of data poses a challenging issue to store and effectively transmit the remote sensing images. Therefore, image compression techniques can be utilized to process remote sensing images. In this aspect, vector quantization (VQ) can be employed for image compression and the widely applied VQ approach is Linde–Buzo–Gray (LBG) which creates a local optimum codebook for image construction. The process of constructing the codebook can be treated as the optimization issue and the metaheuristic algorithms can be utilized for resolving it. With this motivation, this article presents an intelligent satin bowerbird optimizer based compression technique (ISBO-CT) for remote sensing images. The goal of the ISBO-CT technique is to proficiently compress the remote sensing images by the effective design of codebook. Besides, the ISBO-CT technique makes use of satin bowerbird optimizer (SBO) with LBG approach is employed. The design of SBO algorithm for remote sensing image compression depicts the novelty of the work. To showcase the enhanced efficiency of ISBO-CT approach, an extensive range of simulations were applied and the outcomes reported the optimum performance of ISBO-CT technique related to the recent state of art image compression approaches.

Keywords: Remote sensing images; image compression; vector quantization; sand bowerbird optimizer; metaheuristics; space savings

1  Introduction

With the advancement of sensor technologies, the spectral and spatial resolutions of remote sensing images (RSI) are enhancing considerably, which improves the relevance of RSI [1]. But there is cost of massive number of data as the data transmission and storage of on-board equipment are extremely complex. For mitigating this problem, a compression technique using higher coding performances and lower difficulty is needed. Generally, the compression of RSI includes any classical compression systems [2]. These compression systems could efficiently compress natural images since the facts of natural image was frequently constrained. Afterward, the discrete wavelet transforms (DWT), a compact representation could be attained. But, in comparison to natural images, RSI has its individual characteristic features. Usually, they contain a massive amount of ground objects that results in a great amount of details, like outlines of small targets, geometric information, edge, and texture information [3]. Consequently, it is hard to attain a higher coding performance to RSI since the coefficient of higher frequency sub-bands are still larger afterward the DWT. Recently, compression systems developed especially for RSI have been presented [4,5]. These compression systems compress RSI from various factors, like sparse representation.

On the other hand, lossy compression results in data loss because of the removal of less important specifics from the images. It leads to a higher compression ratio (CR) with loss of quality to some extent [6]. Vector quantization (VQ) is a widely used lossy compression method for images. VQ is widespread because it is easier to execute and attains improved compression efficacy [7,8]. The image compression in VQ has been achieved by mapping a data set, thus minimalizing the amount of bits required to determine the novel information, which leads to reducing transmission time and memory usage. Initially, VQ segment the input image to sub input block or smaller blocks image, and all the blocks are assigned to the codeword of the codebooks to find out the reproduction vectors. This process is called encoded, where the inverse method of recreating the compressed image is called decoding. In the work, various researches have been carried out for improving the efficacy of VQ [9]. One of the most important problems in VQ is the generation of an optimum codebook that decreases the error among the decompressed and the compressed images. VQ methods consist of crisp and fuzzy models. The crisp VQ is based on complex decision-making process and has sensitive for initializing the codebook. The Linde–Buzo–Gray (LBG) approach is mainly employed for generating the codebook that initiates the model using a smaller-sized codebook and further improves the splitting method. The outcomes of the LBG could be improved by adding utility measures at the time of the learning [10].

Jifara et al. [11] presented a new technique of lossy hyperspectral image compression technique with online learning dictionary. A spectral dictionary which is learned from sparse coding model is applied for representing the respective materials. In the perception of sparse coding, learning a sparse dictionary can accomplish effective outcome of data decorrelation. Chen et al. [12] conducted research on effect of compression on RSI classification and proposed a methodology for estimating the RSI classification performance-based fractal analyses. Multi-scale feature removal was implemented and various kernel learning approaches is introduced consequently.

In [13], three distinct methodologies are presented for the compression of hyper-spectral, multi-spectral, and hyperspectral sounder data. The proposed methodologies are dissimilar in the type and number of heuristics utilized to obtain the optimum band reordering. Ge et al. [14] examine representation from pre-trained convolutional neural networks (CNN) for higher-resolution RSI retrieval. CNN representation in GoogLeNet, AlexNet, VGGM, and VGG16 are transmitted initially to higher-resolution RSI, and subsequently, CNN feature is removed through 2 methods. Initially, extract the output of higher-level layer straightforwardly. Next, aggregate the output of mid-level layer through average pooling by using distinct pooling areas.

Li et al. [15] introduced a hybrid 2D-burrows wheeler transform (BWT) with DWT for strong image compression model. The presented method consists of image compression with 2D-DWT, 2D-BWT to improve coefficient selection, transformation. Next, linear vector quantization (LVQ) is presented to encode the wavelet coefficient. DWT is employed for facilitating higher quality compression images and BWT was applied for improving the transformation method.

This article presents an intelligent satin bowerbird optimizer based compression technique (ISBO-CT) for remote sensing images. The goal of the ISBO-CT technique is to proficiently compress the remote sensing images by the effective design of codebook. Besides, the ISBO-CT technique makes use of satin bowerbird optimizer (SBO) with LBG approach is employed. The design of SBO algorithm for remote sensing image compression depicts the novelty of the work. To showcase the enhanced performance of the ISBO-CT approach, an extensive range of simulations were applied and the outcomes reported the better performance of the ISBO-CT technique related to recent image compression manners. In short, the paper contribution is summarized as follows.

•   Propose a new ISBO-CT technique to proficiently compress the remote sensing images by the effective design of codebook.

•   Derive the ISBO-CT technique by the use of SBO algorithm with LBO Approach.

•   Validate the performance of the ISBO-CT technique using benchmark dataset

•   Perform a detailed comparative results analysis of the ISBO-CT technique with existing methods interms of different evaluation parameters.

The rest of the paper is arranged as follows. Section 2 introduces the proposed model, Section 3 offers the experimental validation, and Section 4 draws the conclusion.

2  The Proposed Model

In this article, an effective image compression technique called ISBO-CT technique has been developed to compress the remote sensing images. The ISBO-CT technique makes use of SBO algorithm with LBG approach. The VQ is lossy data compression approach from block coding. The generation of codebook has been recognized as one of the essential procedures of VQ. Assume that the size of novel image Y={yij}beM×M pixels which separated as to many blocks with size of n×n pixels. Specifically, there are Nb=[Nn]×[Nn] block which is signified as the group of input vectors =(xi,i=1,2,…,Nb). Assume that L be n×n. An input vector χi,χi∈ℜL where ℜL is L-dimension Euclidean space. The codebook C contains Nc L dimension codeword, for instances, ={c1,c2,…,cNC},cj∈ℜL,∀j=1,2,…Nc. All input vectors are signified as row vector xi=(xi1,xi2,…,xiL) and jth codeword of codebook has demonstrated by cj=(cj1,cJ2…cjL). The VQ approaches allocate all input vectors to connected codeword, and codeword is exchanging the connected input vector eventually for obtaining the purpose of compression.

The optimized of C with respect to mean square error (MSE) is expressed as minimized the distortion function D. Generally, the lesser value of D is optimum the quality of C as:

D(C)=1Nb∑j=1Nc⁡∑i=1Nb⁡μij⋅||xi−cj||2(1)

Based on the subsequent constraints:

∑j=1Nc⁡μij=1,∀i∈{1,2,…,Nb}(2)

μij={1  if  xi  is  in  the  jth  cluster;0  otherwise  (3)

and

Lk≤cjk≤Uk,k=1,2,…,L(4)

where Lk refers the minimum of kth components from every trained vector, and Uk signifies the maximal of kth components from every input vector. The ||x−c|| refers the Euclidean distance amongst the vector x and codeword c.

In 2 essential states to be a better vector quantize.

(1)   The partition Rj,j=1,…,Nc be required to complete

Rj⊃{x∈χ:d(x,cj)<d(x,c∀k≠j}.(5)

(2)   The codeword cj is provided as the centroid of Rj:

cj=1Nj∑i=1Nj⁡xi,xi∈Rj,(6)

where Nj refers the entire amount of vectors going to Rj

2.1 LBG Algorithm

This technique to a scalar quantizer is presented by Lloyd [16]. This approach is named LBG or generalization Lloyd algorithm (GLA) and the process is depicted in Fig. 1. It executes the 2 aforementioned states to input vectors to define the codebook.

Figure 1: Overview of LBG process

To provide input vectors xi,i=1,2,…,Nb, distance function d, and primary codewords cj(0),j=1,…,Nc. The LBG iteratively implements the 2 states for producing an optimum codebook based on the subsequent technique:

(1)   Partition the input vector as to many groups utilizing the minimal distance rule. This outcome partition was saved from Nb×Nc binary indicator matrix U if elements were determined as subsequent:

μij={1ifd(xi,cj(k))=minp⁡d(xi,cp(k))0otherwise(7)

(2)   Define the centroid of all partitions. Exchange the old codeword with this centroid:

cj(k+1)=∑i=1Nb⁡μijxi∑i=1Nb⁡μij,j=1,…,Nc.(8)

(3)   Repeating steps (1) & (2) still no cj,j=1,…,Nc modifies already.

2.2 SBO Based Codebook Construction

In accordance with lifestyle of satin bower-bird, males require for building nests for attracting females and simulate their offspring. The place of nest defines their attraction to females. During the procedure of nesting, males damage the nests created by another male. Every male provides for learning in the optimum nests. For summarizing, the SBO technique is subsequent steps [17]. The amount of individual nests are arbitrarily created amongst the upper as well as lower bounds. All nests are D dimension vectors. The dimensional of parameter D is similar to the amount of parameters needed for solving the optimized issue. The nests created by males are attractiveness probability that defines if female is attracted to them. The flowchart of SBO algorithm is offered in Fig. 2. The maximum probability, the simpler is attracted females. The probability equation as:

probi=fiti∑i=1NB⁡fiti(9)

where fiti refers the fitness of ith solutions and the amount of bowers. The value of fiti has attained utilizing:

fiti={11+f(xi)f(xi)≥01+|f(xi)|f(xi)<0(10)

where f(X) refers the value of cost function of the ith place or ith bird. The cost function has function which is optimization.

Figure 2: Flowchart of SBO algorithm

Several intelligent techniques implement an elite approach that maintains the place as well as fitness of optimum individuals from all iterations of the technique. To the SBO technique, the amount of nests created as male improves, the skill of nest creating also enhances. The knowledgeable male is optimum at constructing attractive nests. During all iterations, one of the skilled males was maintained, and another male study in one of the knowledgeable birds. An elite hero bird affected by another male nest. During all cycles of technique, a novel alters at some bowers are computed based on

xiknew=xikold+λk((xjk+xelite,k2)−xikold)(11)

where xi refers the ith bower/solution vectors and xik signifies the kth member of this vector. xi has defined as objective solution amongst every solution from the present iteration. In Eq. (11), the value j was computed dependent upon probability taken from places. Certainly, the value j was computed utilizing the roulette wheel process that implies that the higher probabilities, the higher probability the solution that was chosen as xj.xelite denotes the place of elite individuals that is stored from all cycles of the technique. Moreover, the place of elite has the place of bowerbird if fitness has the maximum from the present iteration. The parameter λk defines the attractive power of objective bowerbird, in which λk refers the amount of steps that are computed to all variables [18]. This parameter is

λk=α1+pj(12)

where α implies the highest step size and pj stands for the probability attained by the aim bower.

Naturally, if male is busy creating the bower on ground, it can be attacked by another animal or totally forgotten. During several analyses, stronger males take material in weaker males, or same damage its bowers. So, last of all cycles of the technique, arbitrary variations were implemented with specific probability. This procedure assumes that arbitrary alters were executed to xik with specific probability. During this case, to mutation procedure, normal distribution (N) has utilized with average of xikold and variance of σ2

xiknew=N(xikold,σ2)(13)

For helping understand as well as computation, the probability equation was changed as to the subsequent equation.

N(xikold,σ2)=xikold+(σ∗N(0,1))(14)

where the value of σ has proportion of space width and computed as:

σ=z∗(varmax−varmin)(15)

where varmax and varmin demonstrates the upper as well as lower bounds allocated to variables correspondingly. The z parameter is percentage variance amongst the upper as well as lower limits that are variable.

The overall process involved in the ISBO-CT technique is given as follows.

•   In the primary stage, the parameter initialized takes place in which the codebook created by LBG technique was assigned to primary initial solution (for instance, satin bowerbirds) but the rest of primary solutions were arbitrarily generated. All the solutions signify the codebook of Nc codeword. Also, the initialized of SBO occurs.

•   Secondary stage, the existing optimum solution was chosen by calculating the fitness of all places and maximal fitness place was recognized as optimum one.

•   In the tertiary step, novel solutions were created from the bowerbird mutation procedure.

•   The solution was ranked on fundamental of FF under the following step amongst that optimum was selected.

•   The secondary and tertiary stages were iterated still the end condition is met.

3  Performance Validation

In this section, the compression performance of the ISBO-CT technique with recent methods [4,9] has been validated using benchmark SIPI aerial dataset is available at https://sipi.usc.edu/database/database.php?volume=aerials. Fig. 3 illustrates few test images and we have chosen a set of three benchmark images for experimental analysis.

Figure 3: Sample images

A brief peak signal to noise ratio (PSNR) analysis of the ISBO-CT technique with other techniques take place on test image 1 is portrayed in Tab. 1 and Fig. 4. The experimental outcomes reported that the ISBO-CT technique has resulted in increased values of PSNR under varying bit rates (BR). For instance, with BR of 0.20, the ISBO-CT technique has obtained higher PSNR of 28.482 dB whereas the LBG, particle swarm optimization (PSO)-LBG, hybrid, and Firefly LBG techniques have attained lower PSNR values of 25.010, 26.625, 24.687, and 25.252 dB respectively. At the same time, with BR of 0.50, the ISBO-CT technique has obtained higher PSNR of 51.008 dB whereas the LBG, PSO-LBG, hybrid, and Firefly LBG techniques have attained lower PSNR values of 29.450, 44.064, 44.306, and 44.710 dB respectively.

Figure 4: PSNR analysis of ISBO-CT technique under varying BR on test image 1

A comprehensive PSNR analysis of the ISBO-CT technique with other techniques on test image 2 are reported in Tab. 2 and Fig. 5. The experimental results reported that the ISBO-CT technique has resulted in increased values of PSNR under varying values of BR. For instance, with BR of 0.20, the ISBO-CT technique has obtained higher PSNR of 24.306 dB whereas the LBG, PSO-LBG, hybrid, and Firefly LBG techniques have attained lower PSNR values of 20.211, 20.894, 22.515, and 23.197 dB respectively. At the same time, with BR of 0.50, the ISBO-CT technique has obtained higher PSNR of 47.173 dB whereas the LBG, PSO-LBG, hybrid, and Firefly LBG techniques have attained lower PSNR values of 27.037, 37.446, 38.641, and 41.542 dB respectively.

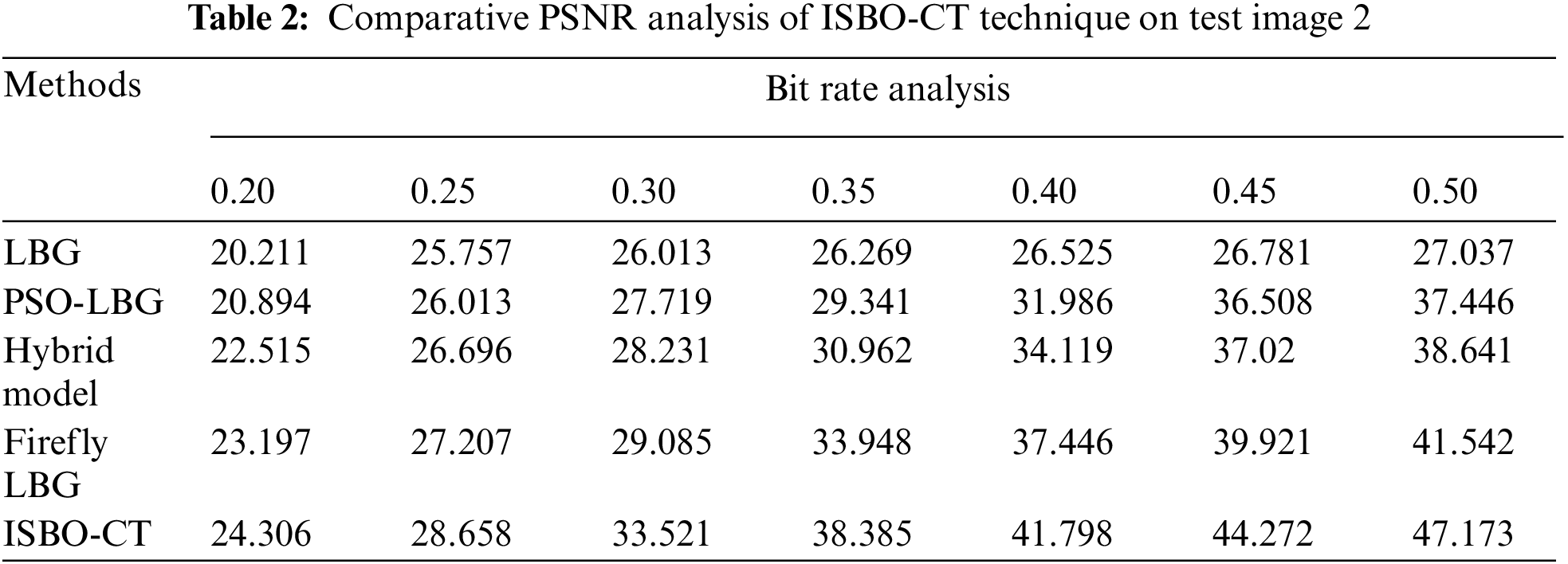
Figure 5: PSNR analysis of ISBO-CT technique under varying BR on test image 2

An extensive PSNR analysis of the ISBO-CT technique with other techniques on test image 3 is reported in Tab. 3 and Fig. 6. The experimental outcomes reported that the ISBO-CT technique has resulted in increased values of PSNR under varying values of BR. For instance, with BR of 0.20, the ISBO-CT technique has obtained higher PSNR of 27.291 dB whereas the LBG, PSO-LBG, hybrid, and Firefly LBG techniques have attained lower PSNR values of 24.383, 24.689, 24.306, and 24.459 dB respectively. Moreover, with BR of 0.50, the ISBO-CT technique has gained an increased PSNR of 50.482 dB whereas the LBG, PSO-LBG, hybrid, and Firefly LBG techniques have attained lower PSNR values of 30.506, 41.451, 42.369, and 42.675 dB respectively.

Figure 6: PSNR analysis of ISBO-CT technique under varying BR on test image 3

Tab. 4 and Fig. 7 provide a brief space saving (SS) analysis of the ISBO-CT technique on the applied test images. The results depicted that ISBO-CT technique has resulted in increased values of SS. For instance, with image 1, the ISBO-CT technique has offered maximum SS of 92.745% whereas the LBG, PSO-LBG, HMBO-LBG, and FA-LBG techniques have gained minimum SS of 91.276%, 88.737%, 87.500%, and 51.856% respectively. At the same time, with image 3, the ISBO-CT technique has resulted in higher SS of 92.160% whereas the LBG, PSO-LBG, HMBO-LBG, and FA-LBG techniques have led to lower SS of 90.430%, 87.175%, 86.621%, and 50.879% respectively.

Figure 7: SS analysis of ISBO-CT technique with recent methods

Finally, an average computation time (CT) analysis of the ISBO-CT technique with recent methods is provided in Tab. 5 and Fig. 8. The results reported that the ISBO-CT technique has showcased effective outcomes with minimal values of ACT.

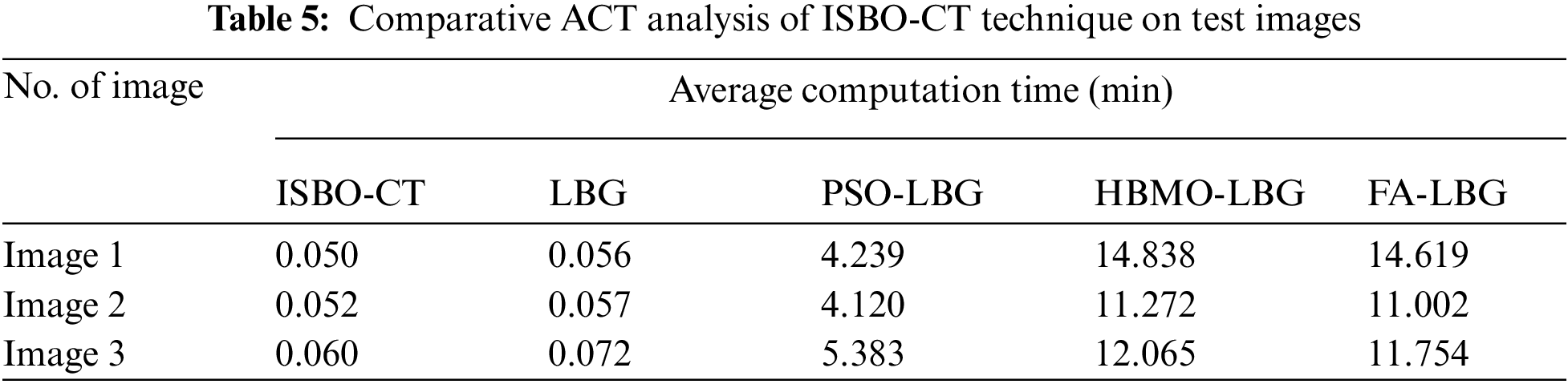
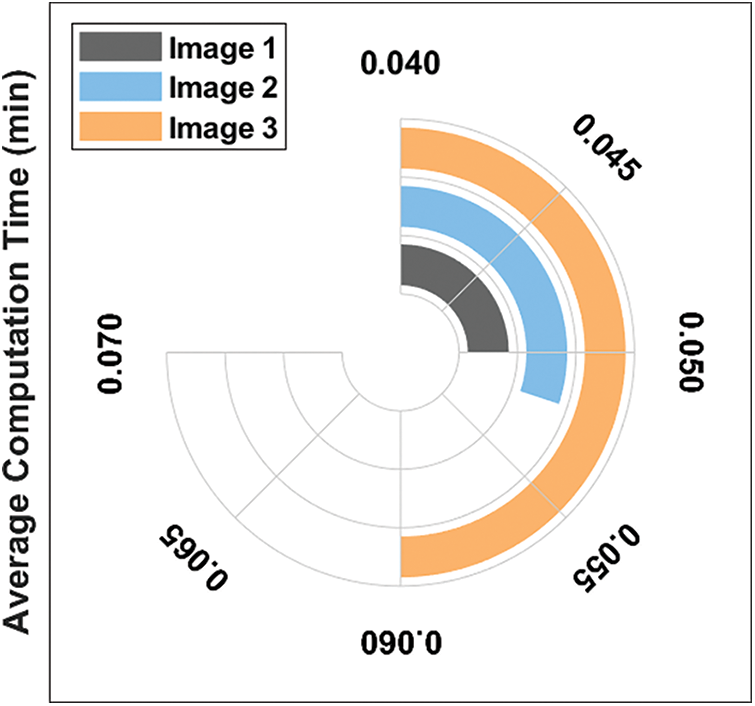
Figure 8: ACT analysis of ISBO-CT technique on different images

For instance, with image 1, the ISBO-CT technique has required lesser ACT of 0.050 min whereas the LBG, PSO-LBG, HMBO-LBG, and FA-LBG techniques have reached to higher ACT of 0.056, 4.239, 14.838, and 14.619 min respectively. Similarly, with image 3, the ISBO-CT technique has required lesser ACT of 0.060 min whereas the LBG, PSO-LBG, HMBO-LBG, and FA-LBG techniques have reached to higher ACT of 0.072, 5.383, 12.065, and 11.754 min respectively. Therefore, the ISBO-CT technique has shown superior results over the other techniques interms of several aspects.

4  Conclusion

In this article, an effective image compression approach called ISBO-CT technique has been developed for compressing the remote sensing image. The intention of the ISBO-CT method is to proficiently compressing the remote sensing image by the proper construction of codebook. Moreover, the ISBO-CT technique makes use of SBO algorithm with LBG approach. Furthermore, the design of SBO algorithm for remote sensing image compression depicts the novelty of the work. To showcase the enhanced performance of the ISBO-CT approach, an extensive range of simulations were executed and the results reported the better performance of the ISBO-CT technique related to the recent image compression approaches. Therefore, the ISBO-CT technique has the ability to compress the images proficiently. In future, hybrid metaheuristic algorithms can be derived to further improve the compression efficiency.

Funding Statement: This work was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2020R1A6A1A03038540) and National Research Foundation of Korea (NRF) grant funded by the Korea government, Ministry of Science and ICT (MSIT) (2021R1F1A1046339).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Jorio, S. El Fkihi, B. Elbhiri and D. Aboutajdine, “An energy-efficient clustering routing algorithm based on geographic position and residual energy for wireless sensor network,” Journal of Computer Networks and Communications, vol. 2015, pp. 1–11, 2015. [Google Scholar]

 2.  S. Zhou, C. Deng, B. Zhao, Y. Xia, Q. Li et al., “Remote sensing image compression: A review,” in 2015 IEEE Int. Conf. on Multimedia Big Data, Beijing, China, pp. 406–410, 2015. [Google Scholar]

 3.  B. P. Alapatt, F. M. Philip and A. Jims, “Oppositional glowworm swarm based vector quantization technique for image compression in fiber optic communication,” in 2021 2nd Int. Conf. on Advances in Computing, Communication, Embedded and Secure Systems (ACCESS), Ernakulam, India, pp. 198–205, 2021. [Google Scholar]

 4.  B. Sujitha, V. S. Parvathy, E. L. Lydia, P. Rani, Z. Polkowski et al., “Optimal deep learning based image compression technique for data transmission on industrial internet of things applications,” Transactions on Emerging Telecommunications Technologies, vol. 32, no. 7, pp. 1–13, 2021. [Google Scholar]

 5.  B. Carpentieri, A. Castiglione, A. D. Santis, F. Palmieri and R. Pizzolante, “One-pass lossless data hiding and compression of remote sensing data,” Future Generation Computer Systems, vol. 90, pp. 222–239, 2019. [Google Scholar]

 6.  S. M. Darwish and A. A. J. Almajtomi, “Metaheuristic-based vector quantization approach: A new paradigm for neural network-based video compression,” Multimedia Tools and Applications, vol. 80, no. 5, pp. 7367–7396, 2021. [Google Scholar]

 7.  M. H. Horng, “Vector quantization using the firefly algorithm for image compression,” Expert Systems with Applications, vol. 39, no. 1, pp. 1078–1091, 2012. [Google Scholar]

 8.  M. Lakshmi, J. Senthilkumar and Y. Suresh, “Visually lossless compression for Bayer color filter array using optimized vector quantization,” Applied Soft Computing, vol. 46, pp. 1030–1042, 2016. [Google Scholar]

 9.  C. Karri and U. Jena, “Fast vector quantization using a bat algorithm for image compression,” Engineering Science and Technology, an International Journal, vol. 19, no. 2, pp. 769–781, 2016. [Google Scholar]

10. C. S. Fonseca, F. A. B. S. Ferreira and F. Madeiro, “Vector quantization codebook design based on fish school search algorithm,” Applied Soft Computing, vol. 73, pp. 958–968, 2018. [Google Scholar]

11. W. Jifara, F. Jiang, B. Zhang, H. Wang, J. Li et al., “Hyperspectral image compression based on online learning spectral features dictionary,” Multimedia Tools and Applications, vol. 76, no. 23, pp. 25003–25014, 2017. [Google Scholar]

12. Z. Chen, Y. Hu and Y. Zhang, “Effects of compression on remote sensing image classification based on fractal analysis,” IEEE Transactions on Geoscience and Remote Sensing, vol. 57, no. 7, pp. 4577–4590, 2019. [Google Scholar]

13. M. I. Afjal, M. A. Mamun and M. P. Uddin, “Band reordering heuristics for lossless satellite image compression with 3D-CALIC and CCSDS,” Journal of Visual Communication and Image Representation, vol. 59, pp. 514–526, 2019. [Google Scholar]

14. Y. Ge, S. Jiang, Q. Xu, C. Jiang and F. Ye, “Exploiting representations from pre-trained convolutional neural networks for high-resolution remote sensing image retrieval,” Multimedia Tools and Applications, vol. 77, no. 13, pp. 17489–17515, 2018. [Google Scholar]

15. J. Li and Z. Liu, “Multispectral transforms using convolution neural networks for remote sensing multispectral image compression,” Remote Sensing, vol. 11, no. 7, pp. 759, 2019. [Google Scholar]

16. Y. Linde, A. Buzo, and R. Gray, “An algorithm for vector quantizer design,” IEEE Trans. Commun, vol. 28, no. 1, pp. 84–95, 1980. [Google Scholar]

17. S. Zhang, G. Zhou, Y. Zhou and Q. Luo, “Quantum-inspired satin bowerbird algorithm with Bloch spherical search for constrained structural optimization,” Journal of Industrial & Management Optimization, vol. 17, no. 6, pp. 3509, 2021. [Google Scholar]

18. G. K. Chellamani and P. V. Chandramani, “An optimized methodical energy management system for residential consumers considering price-driven demand response using satin bowerbird optimization,” Journal of Electrical Engineering & Technology, vol. 15, no. 2, pp. 955–967, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.