Computers, Materials & Continua DOI:10.32604/cmc.2022.025933
Article

Optimized Hybrid Block Adams Method for Solving First Order Ordinary Differential Equations

Hira Soomro1,*, Nooraini Zainuddin1, Hanita Daud1 and Joshua Sunday2

1Department of Fundamental and Applied Sciences, Universiti Teknologi PETRONAS, 32610, Seri Iskandar, Perak, Malaysia
2Department of Mathematics, University of Jos, 930003, Jos, Nigeria
*Corresponding Author: Hira Soomro. Email: soomro_19001048@utp.edu.my
Received: 09 December 2021; Accepted: 24 January 2022

Abstract: Multistep integration methods are being extensively used in the simulations of high dimensional systems due to their lower computational cost. The block methods were developed with the intent of obtaining numerical results on numerous points at a time and improving computational efficiency. Hybrid block methods for instance are specifically used in numerical integration of initial value problems. In this paper, an optimized hybrid block Adams block method is designed for the solutions of linear and nonlinear first-order initial value problems in ordinary differential equations (ODEs). In deriving the method, the Lagrange interpolation polynomial was employed based on some data points to replace the differential equation function and it was integrated over a specified interval. Furthermore, the convergence properties along with the region of stability of the method were examined. It was concluded that the newly derived method is convergent, consistent, and zero-stable. The method was also found to be A-stable implying that it covers the whole of the left/negative half plane. From the numerical computations of absolute errors carried out using the newly derived method, it was found that the method performed better than the ones with which we compared our results with. The method also showed its superiority over the existing methods in terms of stability and convergence.

Keywords: Initial value problem (IVPs); linear multi-step method; block; interpolation; hybrid; Adams-Moulton method

1  Introduction

There are multiple fields of applications where differential equations are found, however, among those; only a few applications have analytical solutions [1,2]. One of the major reasons why scientists are inspired by differential equations is that they have the ability to replicate similar dynamics in the natural world. This paper focuses on solving the first-order Initial Value Problems (IVPs) of the form:

y′=f(t,y(t)),y(t0)=y0,t∈[a,b].(1)

where, f is the continuous function in [a,b] intervals and the assumption of f gratifying Lipchitz condition ensures the solution to the problem Eq. (1) exists and is unique [3].

ODEs appear in a variety of contexts in mathematics and science. Several approaches have been adopted by several authors for the numerical solutions of ODEs among which block methods have the advantages of being more cost-effective [4–7]. In general, with each block has r-point, the followings are the advantages of the implementation of the block method [8,9]:

     i)  Each application of the block method generates r solutions simultaneously.

    ii)  The computational time reduces as well as the overall number of steps.

   iii)  Overcoming the overlapping of pieces of solutions.

Reference [10] advocated the use of block implicit techniques as a way of acquiring beginning values for predictor-corrector systems. Similar considerations were made by [11]. Further, [12] expanded Milne's suggestions into general-purpose algorithms, based on the Newton-Cotes integration equations. A method for higher-order ODEs (stiff and non-stiff) was devised by [13]. For the non-stiff algorithm, a split difference formulation was used, but for the stiff algorithm, a backward differentiation formulation was employed. As a direct solution to non-stiff higher-order ODEs, [13] developed a split difference formulation known as Direct Integration (DI). While creating a block algorithm, [14] created a novel variant of the DI technique. According to [15,16], one-step methods based on Newton backward difference formulae were used to solve first-order ODEs. An eighth order seven-step block Adams type method has been proposed and implemented as a self-starting method to generate the solutions at (tn+1,yn+1), (tn+2,yn+2), (tn+3,yn+3), (tn+4,yn+4), (tn+6,yn+6), (tn+7,yn+7), and (tn+8,yn+8) by [17] for the solution of ODEs. Through interpolation and collocation procedures, a self-starting multistep method was proposed by [18] in which the derivation of Adams-type methods was compiled into block matrix equations for solving IVPs with an obsessive focus on stiff ODEs. Reference [19] constructed an improved class of linear multistep block technique based on Adams Moulton block methods in their study. The enhanced approaches were A-stable, which was a beneficial attribute when dealing with stiff ODEs. Different implementation methods have also been developed, ranging from predictor-corrector technique to block method, by many researchers [20–23]. A block technique based on a stability zone was obtained, in which [24] presented one nonlinear and three linear ODEs using the block technique. Since it has a large range of absolute stability, it could solve both nonlinear and linear IVPs in ODEs, as well as stiff problems in systems. The key flaw of this approach is that the accuracy of the predictors decreased with the increasing step length, and the results were presented at an overlapping interval [25].

Despite having many advantages, block method, also possessed a major setback which pointed out that the order of interpolation points must not exceed the differential equations. Because of this setback, hybrid methods were introduced. Hybrid methods are highly efficient and have been reported to circumvent the “Dahlquist Zero-Stability Barrier” condition by introducing function evaluation at off-step points which takes some time in its development but provides better approximation than two conventional methods (Runge-Kutta and linear multistep methods) [26,27].

Recently, many scholars have developed hybrid methods for the numerical solutions of ODEs. A four-step hybrid block method is formulated by [28] in which the author has discussed about the new strategy for the selection of hybrid points. A new single-step hybrid block method with fourth-order has been proposed by [29] in which the increment of three off-step points enhanced the performance of the developed method comparatively. The main persistence of [9] is to generate a higher-order block algorithm with excellent stability properties, such as A-stability, for addressing various types of IVPs. Reference [30] worked on the hybrid block approach with power series expansion which would aid in the development of a more computationally stable integrator capable of solving problems relating to first-order differential equations of the form Eq. (1). A highly efficient hybrid technique to find out the approximate solution of first-order quadratic Riccati differential equations is derived by [31]. Insignificant convergence, implementation regions and inefficiency in terms of accuracy were some of the major drawbacks of these methods. Due to these, we are motivated to formulate an efficient algorithm that will address these setbacks. Therefore, the objective behind of this study is to develop a sixth order hybrid block Adams method for finding the solutions of linear and nonlinear first-order ODEs using Lagrange polynomial as the basis function. The basis on which the new method is built based on the suggestion that halved step-size helps to acquire the desired stability and optimized method according to [24]. For choosing the hybrid points, various points have been examined and it is concluded that by selecting the points where the step-size is halved will lead toward the zero-stable formulae. The advantage of the proposed hybrid block method is that it is useful in reducing the step number of the problem and remains zero stable.

This paper is organized as follows: in Section 2, the derivation of the proposed method is discussed. Section 3 contains an analysis of the basic properties of the derived method. In Section 4, some numerical examples are presented, and the discussion of results is examined in Section 5. Finally, Section 6 consists of conclusions and future recommendations.

2  Derivation of 3-Points Hybrid Block Adams Moulton Method (AMM)

This section comprises the derivation of the proposed method for finding the solution of Eq. (1). Derivation of the block method is based on the derivation presented in [15]. As illustrated in Fig. 1, the approximate solutions are split into block’s series, and every block comprises three points with one off-step point.

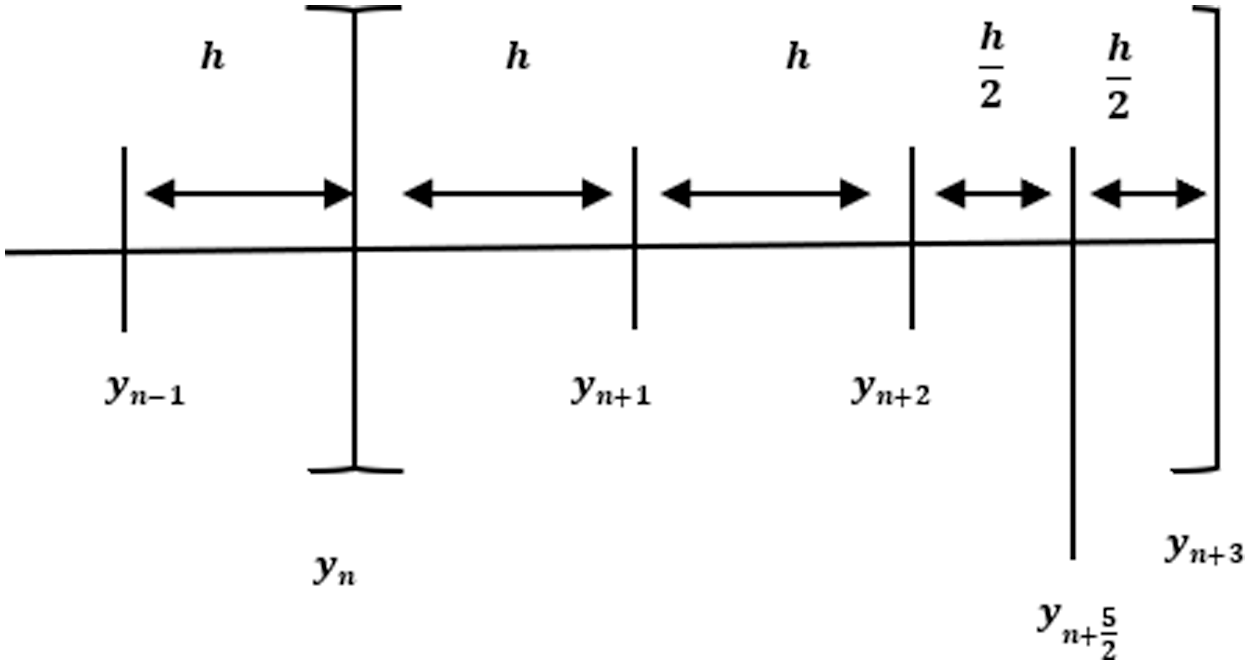
Figure 1: 3-Points hybrid block AMM

In Fig. 1, three solutions of yn+1,yn+2, and yn+3 having one off-step point yn+52 are simultaneously computed while using two back values yn−1 and yn in a block.

Three points will be computed using the previous block with a fixed step size h. The 3-point hybrid block method equations are obtained by integrating Eq. (1) using the Lagrange interpolation polynomial with interpolating points (xn−1,yn−1), (xn,yn), (xn+1,yn+1), (xn+2,yn+2), (xn+52,yn+52) and (xn+3,yn+3).

Consider the Lagrange interpolation polynomial given as,

Pq(x)=∑j=0kLq,j(x)f(xn+3−j)(2)

Where

Lq,j=∏i=0i≠jx−xn+3−ixn+3−j−xn+3−i

By expanding Eq. (2) and substituting s=x−xn+3h and then replace dx=hds, the corrector formula for 3-point hybrid block Adams Moulton Method (AMM) can be obtained as, (the detailed derivation can be seen in [32]),

yn+1=yn+h[−11fn+3180+88fn+52315−49fn+2120+283fn+1360+151fn360−13fn−1840]

yn+2=yn+h[−1fn+390+17fn+245+19fn+115+17fn45−1fn−190]

yn+52=yn+h[−125fn+34608+65fn+52252+125fn+2192+2875fn+12304+55fn144−125fn−110752](3)

yn+3=yn+h[3fn+320+24fn+5235+21fn+240+51fn+140+3fn8−3fn−1280]

Assemble the predictor for the 3-point hybrid block AMM by adopting the same procedure carried out above. Therefore, the predictor formulae for 3-point hybrid block AMM are obtained as,

yn+1p=yn+h2(−fn−1+3fn)

yn+2p=yn+h(−2fn−1+4fn)

yn+52p=yn+h2(−9fn−1+15fn)(4)

yn+3p=yn+h8(−49fn−1+77fn)

Thus, Eq. (4) together with Eq. (3) gives the 3-point hybrid predictor-corrector AMM for the solutions of problems in the form of Eq. (1).

3  Analysis of the Basic Properties of the Proposed Method

This section encompasses the essential features of the proposed method, such as order and error constants, stability analysis, consistency, and convergence. The stability region of the 3-point hybrid block AMM will also be determined.

3.1 Order and Error Constant

Definition 3.1. (Order and Error Constant)

The linear multistep method (LMM)

∑j=0kαjyn+j=h∑j=0kβjfn+j,(5)

where αj and βj are the coefficients of Eq. (3) and k=4, is said to be of order p if C0=C1=⋯=Cp=0 and Cp+1≠0 where;

C0=∑j=0kαj,C1=∑j=0kjαj+∑j=0kβj,C2=∑j=0kj2αj2!+∑j=0kjβj,C3=∑j=0kj3αj3!+∑j=0kj2βj2!,

Cq=∑j=0kjpαjp!+∑j=0kjp−1βj(p−1)!,q=4,5,6,…(6)

The term Cp+1 is called the error constant of the method [26]. This, therefore, means that the local truncation error is calculated as in Eq. (7).

tn+k=Cp+2hp+2y(p+2)(tn)+O(hp+3)(7)

Reshaping Eq. (3) in a matrix form gives,

[1000010000100001][yn+1yn+2yn+52yn+3]=[0001000100010001][yn−2yn−1yn−12yn]+h[283360−4912088315−11180191517450−1902875230412519265252−1254608514021402435320][fn+1fn+2fn+52fn+3]+h[0−1384001513600−190017450−125107520551440−3280038][fn−2fn−1fn−12fn](8)

By applying the formulae Eqs. (6) to (8) we obtained, C1=C2=,…,=C6=[0,0,0,0]T and C7≠0. According to Definition 3.1, the order of the 3-point hybrid block AMM is proven to be 6 as Cp+1≠0 (p=6) with the error constant as shown in Eq. (9),

C7=[311120960175611757741441896].(9)

3.2 Stability Analysis

In this section, we will discuss the stability analysis of the 3-point hybrid block AMM which is obtained by applying the linear test problem

y′=f=λy(10)

where λ represents the complex constant with Re(λ) < 0.

For a technique to be useful in practice, it must have a zone of stability that ensures the approach can solve at least slightly stiff problems. The technique must be zero-stable as well.

3.2.1 Zero-stability

Definition 3.2. (Zero-Stability)

The linear multistep method is said to be zero-stable if the characteristic polynomial R(t), has no root larger than one, and if all modular roots are simple [33–35].

To determine the zero-stability of the 3-point hybrid block AMM for Eqs. (3), (10) is substituted in Eq. (3) which gives,

yn+1=yn−11hλyn+3180+88hλyn+52315−49hλyn+2120+283hλyn+1360+151hλyn360−13hλyn−1840,

yn+2=yn−1hλyn+390+17hλyn+245+19hλyn+115+17hλyn45−1hλyn−190,

yn+52=yn−125hλyn+34608+65hλyn+52252+125hλyn+2192+2875hλyn+12304+55hλyn144−125hλyn−110752,(11)

yn+3=yn+3hλyn+320+24hλyn+5235+21hλyn+240+51hλyn+140+3hλyn8−3hλyn−1280

Eq. (11) can be inscribed in the matrix form as

[1−283hλ36049hλ120−88hλ31511hλ180−19hλ151−17hλ4501hλ90−2875hλ2304−125hλ1921−65hλ252125hλ4608−51hλ40−21hλ40−24hλ351−3hλ20][yn+1yn+2yn+52yn+3]=[0001000100010001][yn−2yn−1yn−12yn]+h[0−13λ8400151360λ0−190λ01745λ0−12510752λ055144λ0−3280λ038λ][yn−2yn−1yn−12yn],(12)

and Eq. (12) is equivalent to

AYm−(B+Ch)Ym−1=0,(13)

where,

A=[1−283hλ36049hλ120−88hλ31511hλ180−19hλ151−17hλ4501hλ90−2875hλ2304−125hλ1921−65hλ252125hλ4608−51hλ40−21hλ40−24hλ351−3hλ20], B=[0001000100010001] ,

C=[0−13λ8400151360λ0−190λ01745λ0−12510752λ055144λ0−3280λ038λ] , Ym=[yn+1yn+2yn+52yn+3] and Ym−1=[yn−2yn−1yn−12yn]

The following stability polynomial of 3-point hybrid block AMM is obtained by using |tA−(B+Ch)|=0

R(t,H)=t4(1−39612520H+1308112096H2−4311080H3+2834032H4)+t3(−1−257180H−65577560H2−5832160H3−29672H4)+t2(−12520H+1160480H2+14320H3+120160H4),(14)

assuming H=hλ, we obtain R(t,H) at H=0 as

R(t,H)=−t3+t4=0,(15)

Resolving Eq. (15) for t, implies t=0,0,0,1. In conclusion, according to Definition 3.2, if all the major roots are on or in the unit circle, the method is zero-stable.

3.2.2 Stability Region

The collection of points found by substituting t=eiθ=sinθ+icosθ, 0≤θ≤2π in the stability polynomial Eq. (14) defined the stability area. Fig. 2 depicts the stability region which were obtained using Mathematica software.

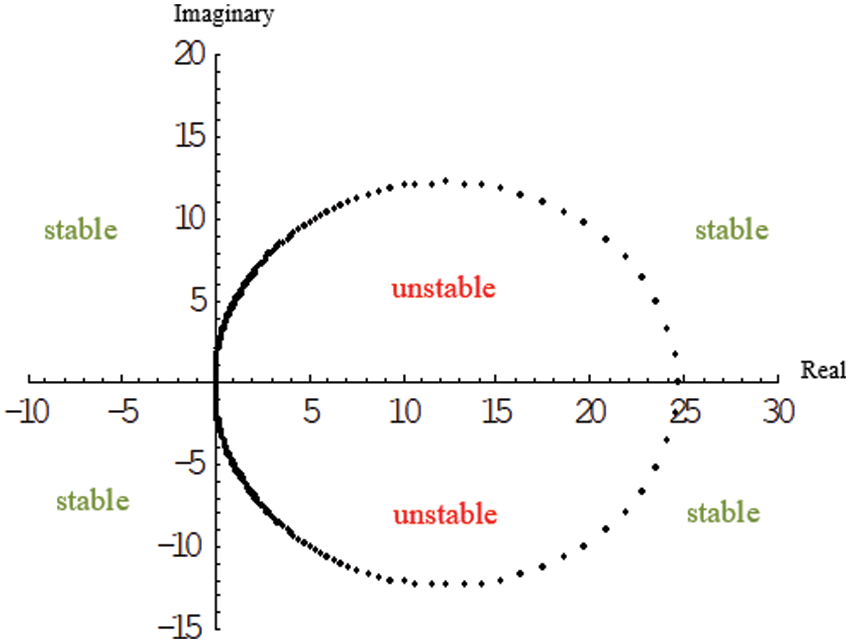
Figure 2: The stability region of the 3-point Hybrid Block AMM

3.3 Consistency

Definition 3.3. (Consistency)

The linear multistep method is said to be consistent if it has order p greater than or equal to one, i.e., p ≥ 1. The 3-point hybrid block AMM is a technique of order six, p=6≥1; thus, it is consistent.

3.4 Convergence

To determine the convergence of the method, we analyze its consistency and zero-stability according to the following theorem.

Theorem 3.1. (Convergence)

The necessary and sufficient conditions for the linear multistep method to be convergent are consistent and zero-stable.

Therefore, the 3-point hybrid block AMM is convergent since it is both consistent and zero-stable.

4  Numerical Examples

We have gone through a few case studies to show the competence of the 3-point hybrid block AMM . Specified numerical examples have been taken from [36–40]. For computational purpose, C++ code was used.

Problem 1: Susceptible, Infected, and Recovered (SIR) Model

In the SIR model, the number of individuals infected with an infectious illness in a closed population, overtime is calculated. In this class of models, the number of susceptible person S(????), the number of infected people (????), and the recovery rate (????) are all related by coupled equations. This is an excellent and straightforward model for several infectious illnesses, like measles, rubella, and mumps [12,41,42]. This problem is also considered by Sunday et al. [36] and given by the three associated equations as shown below,

dSdt=μ(1−S)−βIS,(17)

dIdt=μI−γI+βIS,(18)

dRdt=−μR+γI,(19)

where μ, γ and β are positive parameters. Define y to be

y=S+I+R

by adding and simplifying Eq’s. (17)–(19), we get

y′=μ(1−y),

setting μ=12 and considering the initial condition y(0)=12 (for a specific closed population), the following first-order ODE is obtained,

y′(t)=12(1−y(t)),y(0)=12,tϵ[0,1],

and the exact solution is given by

y(t)=1−12e−12t

Problem 2: Consider the quadratic Riccati differential equation from [37]

y′(t)=−11+t+y(t)−y2(t),y(0)=1,tϵ[0,1]

and the exact solution is given by

y(t)=11+t

Problem 3: Consider the vastly oscillating ODE presented in [38]

y′(t)=−sin⁡t−200(y(t)−cos⁡t),y(0)=0,tϵ[0,0.01]

The exact solution is given by

y(t)=cos⁡t−e−200t

Problem 4: Consider another Riccati differential equation from [37]

y′(t)=1−y(t)2,y(0)=2,tϵ[0,1]

the exact solution is given by

y(t)=e2t−1e2t+1

Problem 5: We consider a mildly stiff system problem given in [39]

[y1′(t)y2′(t)]=[9981998−999−1999][y1(t)y2(t)],[y1(0)y2(0)]=[11]

The exact solution of the system of equations above is given by the sum of two decaying exponential components as below

[y1(t)y2(t)]=[4e−t−3e−1000t−2e−t+3e−1000t]

It is important to state that the eigenvalues of the Jacobian matrix which are λ1=−1,λ2=−1000 with the stiffness ratio 1:1000. The problem is solved within the interval [0,70].

5  Results and Discussion

From Tabs. 1–5, the solution values are calculated at the various points of the given interval which is represented by “t”. On the contrary, the efficiency of 3-point hybrid block AMM is proven when smaller step sizes are used as it is capable of outperforming at a step size 10−6 for each problem.

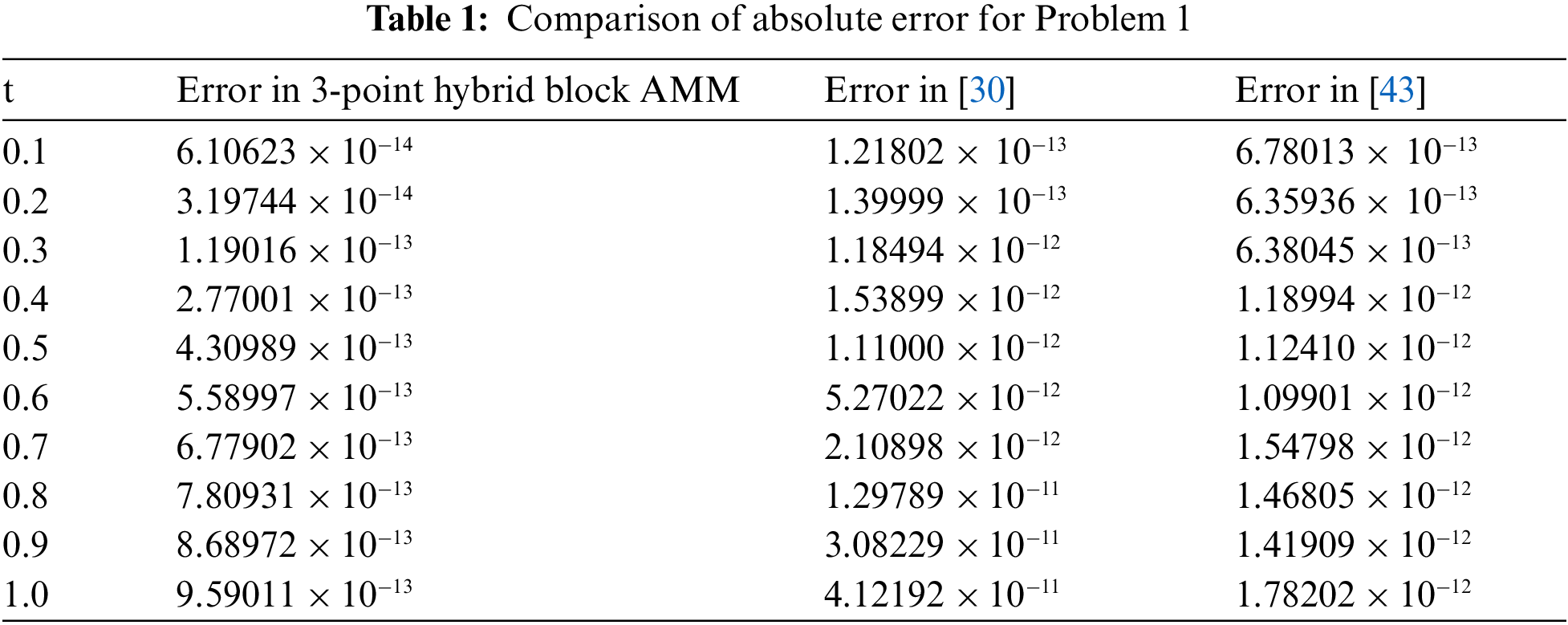
Tab. 1 depicts the comparison of the numerical outcomes by 3-point hybrid block AMM with the two-step block hybrid method by Ajileye et al. [30] and 3-step hybrid Adams type methods by Yahaya et al. [43] for the SIR model. Absolute error was computed by finding the difference between the exact solution and proposed method’s solution at distinctive values of t. The solution of the 3-point hybrid block AMM performs better than [30,43].

In Tab. 2, the comparison of the numerical outcomes by 3-point hybrid block AMM with the quarter-step method for the solution of Riccati differential equations by [37] has been done based on absolute error. It is obvious from the above results that the proposed method is computationally reliable in handling the Riccati differential equations also.

Tab. 3 displays the results from the 3-point hybrid block AMM for solving problem 3. It can be seen that the proposed method exhibits better accuracy compared with the results obtained by the two-step hybrid block method [38].

In Tab. 4, the representation of absolute errors demonstrates the comparison of the results by 3-point hybrid block AMM with [37]. Hence, it is obvious that the proposed method performs better than that of [37].

In Tab. 5, comparison have been made at points (x=5, x=40, and x=70) with the step size h=10−6 for the 3-point hybrid block AMM. From the comparison of the absolute error of the proposed methods as shown in Tab. 5, it is obvious that the 3-point hybrid block AMM with order 6 exhibit superiority over the method given in [39] with lesser order 4 in terms of accuracy. Tab. 5 shows that the proposed method is also well suited for mildly stiff linear problems.

As a result, the 3-point hybrid block AMM, which developed a block method of order six using Lagrange interpolation as an approximation solution, performs better, and the error analysis reveals that the proposed method is giving more accurate results in comparisons to the other approaches. In Tab. 1, it is observed that the proposed method reduces the error, approximately by the average of 33% and 41% compared to [30,43] respectively. The efficiency of the proposed method can also be checked from Tabs. 2–5 that the 3-point hybrid block AMM decreases the absolute error an average of approximately 50% compare with [37,39].

6  Conclusion

In this paper, an optimized 3-point hybrid block Adams method for the solution of first order ODEs has been derived. The method derived was implemented using C++ language that compute the solutions to problems of the form in Eq. (1). The basic properties of the method developed were also analyzed and from the results of the analyses, it is confirmed that the method is zero-stable, consistent, and convergent. Thus, because of the zero stability of the method, it is suitable for solving stiff systems of equations (Problem 5) as well as nonlinear equations. Also, from the results presented in Tabs. 1–5, it is obvious that the new method derived performs better than the existing ones based on the results produced. We therefore conclude that the proposed method is computationally reliable in solving first-order problems of the form in Eq. (1).

For future work this method shall be applied to the problems of chemical kinetics to investigate the efficiency and accuracy of the proposed method which is the main requirement of such type of problems.

Acknowledgement: The authors are grateful to Universiti Teknologi PETRONAS for providing facilities for conducting this study.

Funding Statement: This research was funded by Fundamental Research Grant Scheme (FRGS) under the Ministry of Higher Education Malaysia, grant number with project ref: FRGS/1/2019/STG06/UTP/03/2.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. M. S. Mahdy, Kh. Lotfy, E. A. Ismail, A. El-Bary, M. Ahmed et al., “Analytical solutions of time-fractional heat order for a magneto-photothermal semiconductor medium with Thomson effects and initial stress,” Results in Physics, vol. 18, no. 8, pp. 103–174, 2020.

 2.  A. M. S. Mahdy, Kh. Lotfy, W. Hassan and A. A. El-Bary, “Analytical solution of magneto-photothermal theory during variable thermal conductivity of a semiconductor material due to pulse heat flux and volumetric heat source,” Waves in Random and Complex Media, vol. 31, no. 6, pp. 1–18, 2020.

 3.  L. W. Jackson and S. K. Kenue, “A fourth order exponentially fitted method,” SIAM Journal on Numerical Analysis, vol. 11, no. 5, pp. 965–978, 1974.

 4.  M. I. A. Othman, A. M. S. Mahdy and R. M. Farouk, “Numerical solution of 12th order boundary value problems by using homotopy perturbation method,” Journal of Mathematics and Computer Science, vol. 1, no. 1, pp. 14–27, 2010.

 5.  M. Sheikholeslami, Z. Shah, A. Shafee, I. Khan and I. Tlili, “Uniform magnetic force impact on water based nanofluid thermal behavior in a porous enclosure with ellipse shaped obstacle,” Scientific Reports, vol. 9, no. 1, pp. 1–11, 2019.

 6.  A. M. S. Mahdy and E. S. M. Youssef, “Numerical solution technique for solving isoperimetric variational problems,” International Journal of Modern Physics C, vol. 32, no. 1, pp. 2150002–2150014, 2021.

 7.  A. M. S. Mahdy, K. A. Gepreel, Kh. Lotfy and A. A. El-Bary, “A numerical method for solving the rubella ailment disease model,” International Journal of Modern Physics C, vol. 32, no. 7, pp. 1–15, 2021.

 8.  N. B. Zainuddin, “Diagonal R-Point variable step variable order block method for solving second order ordinary differential equations,” Ph.D. dissertation. Universiti Putra Malaysia, Malaysia, 2016.

 9.  H. Ramos and G. Singh, “A tenth order A-stable two-step hybrid block method for solving initial value problems of ODEs,” Applied Mathematics and Computation, vol. 310, no. 3, pp. 75–88, 2017.

10. W. E. Milne, Numerical Solutions of Differential Equations. New York, USA: John Wiley & Sons, 1953.

11. D. Sarafyan, Multistep methods for the numerical solution of ordinary differential equations made self-starting, Tech. Report 495, Math. Res. Center, Madison, 1965.

12. J. B. Rosser, “A Runge-Kutta for all seasons,” SIAM Review, vol. 9, no. 3, pp. 417–452, 1967.

13. M. Suleiman, “Generalized multistep Adams and Backward differentiation methods for the solution of stiff and non-stiff ordinary differential equations,” Ph. D. dissertation. University of Manchester, 1979.

14. Z. Omar and M. Suleiman, “Solving higher order ordinary differential equations using parallel 2-point explicit block method,” MATEMATIKA: Malaysian Journal of Industrial and Applied Mathematics, vol. 21, no. 1, pp. 15–23, 2005.

15. Z. A. Majid, M. Suleiman, F. Ismail and M. Othman, “2-Point implicit block one-step method half Gauss-Seidel for solving first order ordinary differential equations,” MATEMATIKA: Malaysian Journal of Industrial and Applied Mathematics, vol. 19, pp. 91–100, 2003.

16. Z. A. Majid, M. B. Suleiman and Z. Omar, “3-Point implicit block method for solving ordinary differential equations,” Bulletin of the Malaysian Mathematical Sciences Society. Second Series, vol. 29, no. 1, pp. 23–31, 2006.

17. O. Akinfenwa, “Seven step Adams type block method with continuous coefficient for periodic ordinary differential equation,” International Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering system, vol. 5, no. 12, pp. 2072–2076, 2011.

18. O. A. Akinfenwa, N. M. Yao and S. N. Jator, “A self-starting block Adams methods for solving stiff ordinary differential equation,” in 14th IEEE International Conference on Computational Science and Engineering, Dalian, Liaoning China, pp. 127–136, 2011.

19. G. M. Kumleng, J. P. Chollom and S. Longwap, “A Modified Block Adams Moulton (MOBAM) method for the solution of stiff initial value problems of ordinary differential equations,” Research Journal of Mathematics and Statistics, vol. 5, no. 4, pp. 32–42, 2013.

20. O. A. Akinfenwa, R. I. Abdulganiy, B. I. Akinnukawe and S. A. Okunuga, “Seventh order hybrid block method for solution of first order stiff systems of initial value problems,” Journal of the Egyptian Mathematical Society, vol. 28, no. 1, pp. 1–11, 2020.

21. J. G. Oghonyon, S. A. Okunuga and O. O. Agboola, “K-step block predictor-corrector methods for solving first order ordinary differential equations,” Research Journal of Applied Sciences, vol. 10, no. 11, pp. 779–785, 2015.

22. R. Dhaigude and R. Devkate, “Solution of first order initial value problem by sixth order predictor corrector Method,” Global Journal of Pure and Applied Mathematics, vol. 13, no. 6, pp. 2277–2290, 2017.

23. W. Barde and A. Solomon, “An implicit two-step hybrid block method based on Chebyshev polynomial for solving first order initial value problems in ordinary differential equations,” International Journal of Science for Global Sustainability, vol. 7, no. 1, pp. 80–89, 2021.

24. I. Esuabana, S. Ekoro, B. Ojo and U. Abasiekwere, “Adam’s block with first and second derivative future points for initial value problems in ordinary differential equations,” Journal of Mathematical and Computational Science, vol. 11, no. 2, pp. 1470–1485, 2021.

25. A. A. Olaide, J. A. Adewale and J. Sunday, “Hybrid block predictor-hybrid block corrector for the solution of first-order ordinary differential equations,” Engineering Mathematics Letters, vol. 2014, no. 13, pp. 1–12, 2014.

26. G. G. Dahlquist, “A special stability problem for linear multistep methods,” BIT Numerical Mathematics, vol. 3, no. 1, pp. 27–43, 1963.

27. B. S. Kashkari and M. I. Syam, “Optimization of one step block method with three hybrid points for solving first-order ordinary differential equations,” Results in Physics, vol. 12, no. 2, pp. 592–596, 2019.

28. R. Abdelrahim, “Four step hybrid block method for the direct solution of fourth order ordinary differential equations,” International Journal of Nonlinear Analysis and Applications, vol. 12, no. 1, pp. 215–229, 2021.

29. Z. Omar, R. Abdelrahim and J. O. Kuboye, “New hybrid block method with three off-step points for solving first order ordinary differential equations,” American Journal of Applied Sciences, vol. 13, no. 2, pp. 209–212, 2016.

30. G. Ajileye, S. A. Amoo and O. D. Ogwumu, “Two-step hybrid block method for solving first order ordinary differential equations using power series approach,” Journal of Advances in Mathematics and Computer Science, vol. 28, no. 1, pp. 1–7, 2018.

31. J. Sunday and P. Jerry, “On the derivation and analysis of a highly efficient method for the approximation of quadratic riccati equations,” Computer Reviews Journal, vol. 2, pp. 1–14, 2018.

32. H. Soomro, N. Zainuddin and H. Daud, “Convergence properties of 3-point block Adams method with one off-step point for ODEs,” in Journal of Physics: Conference Series. Vol. 1988, IOP Publishing, pp. 012–038, 2021.

33. J. D. Lambert, “Computational methods in ordinary differential equations. vol.5,New York: John Wiley & Sons, 1973. [Online]. Available: https://books.google.com.my/books?id=WEDvAAAAMAAJ.

34. X. Zhang, C. Lin, Y. Q. Chen and D. Boutat, “A unified framework of stability theorems for LTI fractional order systems with 0< α< 2,” IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 67, no. 12, pp. 3237–3241, 2020.

35. X. Zhang and Y. Q. Chen, “Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order α: The 0< α< 1 case,” ISA Transactions, vol. 82, pp. 42–50, 2018.

36. J. Sunday, M. R. Odekunle and A. O. Adesanya, “Order six block integrator for the solution of first order ordinary differential equations,” International Journal of Mathematics and Soft Computing, vol. 3, no. 1, pp. 87–96, 2013.

37. J. Sunday, “Riccati differential equations: A computational approach,” Archives of Current Research International, vol. 9, no. 3, pp. 1–12, 2017.

38. J. Sunday, F. M. Kolawole, E. A. Ibijola and R. B. Ogunrinde, “Two-step Laguerre polynomial hybrid block method for stiff and oscillatory first-order ordinary differential equations,” Journal of Mathematical and Computational Science, vol. 5, no. 5, pp. 658–668, 2015.

39. M. A. Rufai, M. K. Duromola and A. A. Ganiyu, “Derivation of one-sixth hybrid block method for solving general first order ordinary differential equations,” IOSR Journal of Mathematics (IOSR-JM), vol. 12, no. 5, pp. 20–27, 2016.

40. D. Yakubu and S. Markus, “Second derivative of high-order accuracy methods for the numerical integration of stiff initial value problems,” Afrika Matematika, vol. 27, no. 5, pp. 963–977, 2016.

41. W. B. Gragg and H. J. Stetter, “Generalized multistep predictor-corrector methods,” Journal of the ACM (JACM), vol. 11, no. 2, pp. 188–209, 1964.

42. R. E. Mickens, “Nonstandard finite difference models of differential equations,World Scientific, 1994. [Online]. Available: https://books.google.com.my/books?id=VpnsCgAAQBAJ.

43. Y. A. Yahaya and A. A. Tijjani, “Formulation of corrector methods from 3-step hybrid Adams type methods for the solution of first order ordinary differential equation,” in Proc. of the 32nd IIER Int. Conf., Dubai, UAE, 2015.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.