Computers, Materials & Continua DOI:10.32604/cmc.2022.026374
Article

Fuzzy Multi-Criteria Decision Making for Solar Power Plant Location Selection

Thai Hoang Tuyet Nhi1, Chia-Nan Wang1 and Nguyen Van Thanh2,*

1Department of Industrial Engineering, National Kaohsiung University of Science and Technology, 80778, Taiwan
2Faculty of Commerce, Van Lang University, Ho Chi Minh City, Vietnam
*Corresponding Author: Nguyen Van Thanh. Email: thanh.nguyenvan@vlu.edu.vn
Received: 23 December 2021; Accepted: 02 March 2022

Abstract: Vietnam is one of Southeast Asian countries with a rapid GDP growth rate, ranging from 6.5% to 7% annually, leading to an average increase in energy demand of 11% per year. This demand creates many new opportunities in the energy industry, especially renewable energy, to ensure sustainable development in the future for the country with applications of solar energy growing at the present, and other opportunities to expand in the future. In Vietnam, thanks to favorable weather, climate, terrain characteristics and many preferential support policies, there are many great opportunities in the field of solar energy exploitation and application. Location selection is an important problem in all renewable energy projects. Therefore, the author proposed a fuzzy Multi-criteria Decision-Making Model (MCDM) model for solar power plant location selection in this study, and as a result, location 5 is the optimal solution. The contribution of this study is to propose a MCDM for solar power plant location selection in Vietnam under fuzzy environmental conditions.

Keywords: Solar power; multi-decision; topsis; fanp; fuzzy theory

1  Introduction

Many countries in the world, as well as Vietnam, are using fossil energy sources (coal, oil, and gas) to generate electricity. These energy sources are not only gradually exhausted but also bring great challenges in terms of environmental protection. The development of renewable energy and finding renewable energy sources, especially solar energy, to replace fossil energy sources has become very important and necessary. Developing renewable energy has become a smart direction and inevitable development trend for Vietnam and the whole world because these energy sources will never be exhausted, are renewable and can be exploited in the most remote places.

According to a report by the International Energy Agency (IEA) on December 1, 2021, renewable energy accounts for nearly 95% of the increase in electricity capacity in the world until 2026. In addition, the Renewables 2021 (REN21) analysis showed that renewables made up 29% of global electricity generation by the end of 2020. Led by wind power and solar photovoltaic (PV), more than 256 GW of capacity was added in 2020, an increase of nearly 10% in total installed renewable power capacity [1]. Hydropower is the largest source of renewable energy. However, wind and solar power are growing rapidly [2,3].

Vietnam has a suitable geographical location, a long coastline, and a tropical monsoon climate with abundant and diverse renewable energy sources suitable for energy exploitation and production such as, hydropower, wind power, solar power, biomass, geothermal, and biofuel. The International Renewable Energy Agency (IRENA) said that by the end of 2020, Vietnam's total solar photovoltaic capacity will reach about 16,500 MW. According to the World Bank (WB), which provides information to policymakers and investors, Vietnam’s solar power resources are quite abundant, with thermal radiation of about 2,056 kW/m2/year and lasting from the central provinces to the Mekong Delta region. This shows that the development potential of the solar PV field is very large.

Specifically, in areas such as the Central Highlands and the South-Central Coast, the number of sunshine hours will range from 2,000 to 2,600 h per year. The average amount of solar radiation is about 150 kcal/m2, accounting for about 2,000 to 5,000 h per year. Accordingly, the northern provinces average 1,800–2,100 h of sunshine per year, while the southern provinces and Ho Chi Minh City have the sun shining all year round, even in the rainy season, with the average number of sunny hours per year higher, from 2,000–2,600 h per year. Therefore, solar radiation is a great resource for the central and southern provinces [4].

Solar power is the conversion of energy from sunlight into electricity, either directly using a PV cell or indirectly using concentrated or combined solar power. Concentrating solar systems use lenses or mirrors and solar tracking systems to focus a large area of sunlight into a small beam. Photovoltaic cells convert light into electric current by the photoelectric effect [5].

Location selection for solar power plants is a multicriteria decision making problem. The decision maker must evaluate many qualitative and quantitative factors. In this research, the author proposed a fuzzy MCDM for solar power plant location selection. Therefore, the main aim of this study is to develop a decision support system to select solar power plants based on qualitative and quantitative factors. The author proposes a combination of Fuzzy Analytic Network Process (FANP) and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS). For FANP, it is a combination of the ANP method and fuzzy logic to evaluate the importance and mutual influence between the criteria. However, the disadvantage of FANP is that the input data is often expressed in linguistic terms, depending on the opinions and experience of experts, which can sometimes involve subjectivity and bias. So, the author has combined TOPSIS with FANP to overcome this shortcoming.

2  Literature Review

To evaluate the alternatives based on criteria, different methods are used, such as the Analytic Hierarchy Process (AHP), Analytic Network Process (ANP), Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), the Preference Ranking Organization Method for Enrichment Evaluation (PROMETHEE), Elimination and Choice Translating Reality English (ELECTRE), the Weighted Aggregated Sum Product Assessment (WASPAS), Data Envelopment Analysis (DEA) and Vise Kriterijumska Optimizacija I Kompromisno Resenje (VIKOR). Some researchers proposed the MCDM method to optimize the system considering many factors that have emerged in the research community [6–8], Hassaan [9] used a Geographic Information System (GIS) approach to the layout of a waste incineration power plant in Egypt. Sindhu et al. [10] proposed a hybrid combination of AHP and fuzzy TOPSIS to select a site for a solar farm in India; Belhadi et al. [11] applied an integrated method with AHP and VIKOR to the selection of a waste management strategy during the COVID-19 pandemic, etc.

Renewable energy is energy that is collected from renewable resources that are naturally replenished on a human timescale. It includes solar energy, wind, rain, tides, waves, and geothermal heat [12]. The basic principle of renewable energy use is to extract some of the energy from continuously occurring processes in the environment and put it into technical uses [13]. These processes are often driven especially by the Sun. Renewable energy replaces traditional fuel sources in 4 areas including: electricity generation, air and water heating/cooling, transportation, and rural (off-grid) energy services [14]. Specific studies in the field of renewable energy are typical, such as: Erolu [15] aimed to find the most suitable places for wind power plants by using GIS and the FAHP method with 17 main criteria and 81 sub-criteria. Moradi et al. [16] used the classical AHP method in the evaluation of wind energy resources in central Iran. In other studies, Choudhary et al. [17] discussed the development of a hybrid model for more accurate, efficient, and systematic decision-making for decision makers to conduct the evaluation process and select optimal locations for thermal power plants. A case study in India was conducted. Das et al. [18] used a combined model of AHP and GIS to determine the importance of factors affecting groundwater as well as evaluate its potential use. In the study, Hamal et al. [19] handled the energy strategy decision-making problem to help energy investors determine the optimal renewable energy investment project using the FANP approach. Zavadskas et al. [20] proposed a new extension of the WASPAS method to selection and construction of a waste incineration plant. Wang et al. [21] used an MCDM model that includes ANP with fuzzy logic and TOPSIS, which is proposed for nuclear power plant (NPP) site selection in Vietnam.

Some of the previous studies in the field of solar power plant site selection are as follows: Charabi et al. [22] presented an IS-based spatial multi-criteria evaluation approach, in terms of the FLOWA module, was used to assess the land suitability for large PV farm implementation in Oman. The tool used applies fuzzy quantifiers within the ArcGIS environment, allowing the integration of a multi-criteria decision analysis. Chakraborty et al. [23] studied about meteorological factors to a new location selection criterion for solar PV power plant. Beltrán et al. [24] applied ANP to the selection of solar PV power projects. Kengpol et al. [25] developed a new approach that is flexible and practical for decision-makers, specifically guidelines for the selection of solar power plant locations in Thailand. Wang et al. [26] presented a MCDM model by combining three methodologies, including FAHP, DEA, and TOPSIS to find the best location for building a solar power plant. In other hand, Azadeh et al. [27] presented an integrated hierarchical approach for location of solar plants by data envelopment analysis (DEA), principal component analysis (PCA) and numerical taxonomy (NT). Akçay et al. [28] used A hybrid AHP and TOPSIS method is used to select the best alternative according to the sub-criteria determined under the economic, technical, social and geographical main criteria. Criterion weights are found by the AHP method and alternatives are ranked with the TOPSIS method. Lee et al. [29] applied a comprehensive multi-criteria decision model by combining interpretive structure model (ISM), FANP and VIKOR to evaluate important solar plant locations in Taiwan, Wang et al. [30] developed a MCDM approaches for solar power plant location selection in Viet Nam. Aktas et al. [31] presented a hybrid AHP and TOPSIS method under hesitant fuzzy environment to solve the multi-criteria decision-making problem of solar power plant location of decision makers. Akkas et al. [32] proposed four different MCDM methods to select the most suitable city among 5 cities in the Central Anatolian Region of Turkey for the establishment of solar power plant in order to get maximum power output and have minimum cost. Sozen et al. [33] used an approach for the location of solar plants by combining DEA and TOPSIS methods. Colak et al. [34] presented optimal solar photovoltaic power plant sites selection by using GIS and AHP. Kereush et al. [35] suggested a multi-criteria decision analysis to define and classify criteria considered for solar PV farm siting.

3  Materials and Methods

3.1 Research Development

The research process has about 3 stages as shown in Fig. 1:

Figure 1: The research processes

Stage 1: Define the solar power plant location selection problem. The factors are referred to theories from reference materials, articles related to the research area to support knowledge in the process of determining criteria, locations, and a network with criteria and sub-criteria is constructed.

Stage 2: Using the FANP model in assessing the weights between the criteria used as input data in the TOPSIS method, if the results are not consistent, the original data can be re-determined and re-evaluated.

Stage 3: The weakness of FANP is that the input data is expressed in linguistic terms, depending on the experience of experts. So, the TOPSIS model is combined to address this weakness and evaluate the most suitable site.

3.2 The Fuzzy Analytic Network Process (FANP) Method

The Analytical Network Process method was developed by Saaty in 1996 [36]. ANP is a method of calculating the interaction relationships between elements through the network structure, all elements in the network can communicate with each other in any way [37]. The process of implementing FANP method includes the following steps:

Step 1: Construct the structure of the FANP method. Establish a network structure and define relationships between criteria. The index system is proposed, as shown in Fig. 2:

Figure 2: The FANP method structure

Step 2: Construct a pairwise comparison matrix in Tab. 1.

In this step, the decision maker is asked to make a series of pairwise comparisons of the importance of the criteria using the scale presented in Tab. 2.

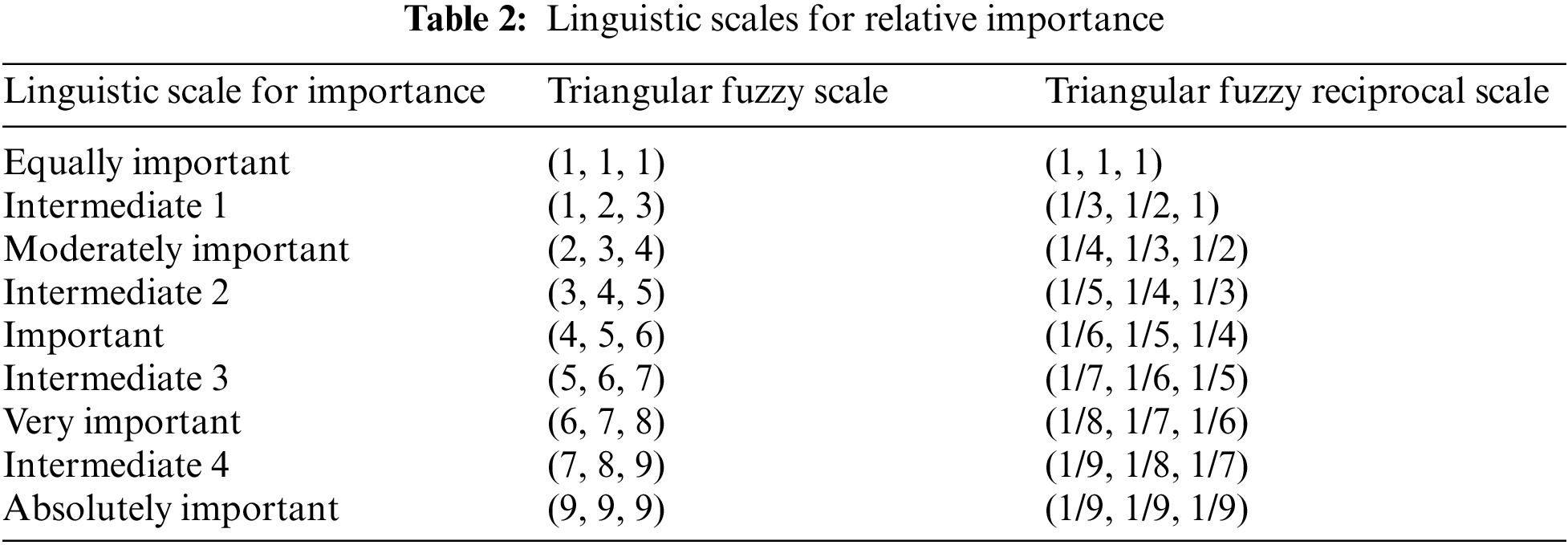
After getting the matrices to compare pairs with fuzzy numbers, we proceed to convert fuzzy numbers to real numbers by: [38]

tα,β(α¯ij )=[β.z(Lij)+(1−β).zα(Uij)](1)

0≤β≤1,0≤α≤1

where:

zα(Lij)=(Mij−Lij).α+Lij(2)

zα(Uij)=Uij−(Uij−Mij).α(3)

When we take the reciprocal through the matrix we have

tα,β(α¯ij )=1tα,β(α¯ij )(4)

0≤β≤1,0≤α≤1, i>j

The matrix comparing real numbers is established by pairs of criteria together and summed up into a matrix of n rows and n columns (n is the number of criteria) by the scale suggested by Saaty [39] for AHP and ANP shown in Tab. 3. The rij element represents the importance of the row criterion ith compared to the jth column criterion:

S= (rij)n×n=[1 r12r1…r1n…r2n⋮⋮rn1rn2⋮⋮…1](5)

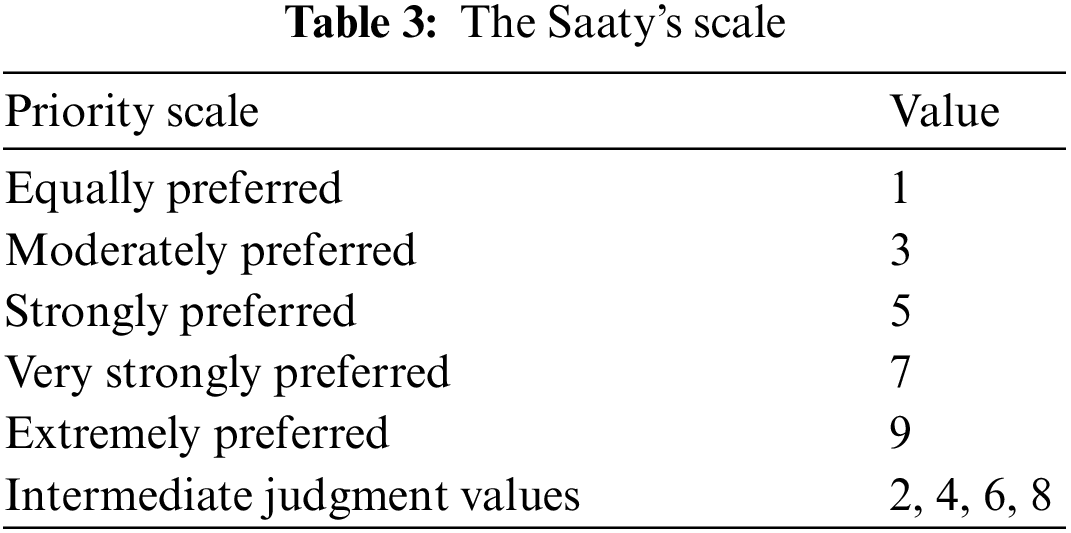
Step 3: Calculate the maximum eigenvalue

In this step, calculating the maximum eigenvalues for the criteria has many different methods, but we use Lambda Max proposed by Saaty [39] as show in:

|S−λmax.I|=0(6)

where:

λmax: the maximum value of the matrix.

S: The matrix comparing real numbers

I: unit matrix of the same level with matrix S.

Step 4: Check consistency and calculates the vector of the matrix

After calculating the maximum eigenvalue, according to Talluri et al. [40], we can use the consistency ratio of the data (Consistency Ratio - CR). This ratio compares the consistency with the objectivity of the data:

CR= CIRI(7)

CI= λmax− nn−1(8)

where:

RI: Random Index

λmax is the maximum value of the matrix

n is the number of indicators in Tab. 4

3.3 The TOPSIS Method

The steps in calculating the TOPSIS method by Opricovic et al. [41] as following:

Step 1: Decide matrix is normalized:

hij=Mij∑i=1k⁡Mij2(9)

Step 2: Normalized weighted

With the weight wj = (w1, w2, w3,…, wn), where wj is the weight of the criteria for all j and ∑j=1, wj=1. The normalization of weight matrix V is:

vij=wj×hij(10)

Step 3: Determining the ideal solution matrix of positive and negative ideal solution by using this formula:

Q+={(maxvij|j∈J),(minvij|j∈J′),i=1,2,3,…,k}={V1+,V2+,V2+…,Vn+}(11)

Q−={(minvij|j∈J),(maxvij|j∈J′),i=1,2,3,…,k}={V1−,V2−,V2−…,Vn−}

Step 4: Calculating separation

D+ is an alternative distance from the positive ideal solution is defined as:

di+=∑j=1f⁡(vij−vj+)2(12)

where i = 1, 2, 3, …, k

D- is an alternative distance from the negative ideal solution is defined as:

di−=∑j=1f⁡(vij−vj−)2(13)

where i = 1, 2, 3, …, k

Step 5: Calculating positive idea solution

Si+=di(di−+ di+)(14)

Alternative S+ sorted from largest value to the smallest value. Alternative with the largest value of C+ the best solution.

4  Results

In this study, the authors proposed a fuzzy MCDM model including FANP and TOPIS for selecting the optimal location for a solar power plant in Vietnam. The FANP model is applied to determine the weight of all criteria and sub-criteria. The results of the study are presented as following Tab. 5:

To convert fuzzy numbers into real numbers, we proceed to de-fuzzify by the triangular fuzzy number method. In the defuzzification process, we take the coefficients α = 0.5 and β = 0.5. In which, α represents an uncertain environment, β represents the attitude of experts as fair.

By the formula (1)–(4), we have:

z0.5,0.5(α¯economic factors, social factors)=[(0.5×3.5)+(1−0.5)×4.5]=4

z0.5(Leconomicfactors,socialfactors)=(4−3)×0.5+3=3.5α¯ij 

z0.5(Ueconomicfactors,socialfactors)=5−(5−4)×0.5=4.5

z0.5,0.5(α¯social factors, economic factors)=1/4

We randomly select one criterion to perform the calculation, and the same for the remaining cells. We get the pairwise comparison matrix in real numbers as follows Tab. 6:

Following the same steps, we get the weighted results of the sub-criteria presented in Tab. 7.

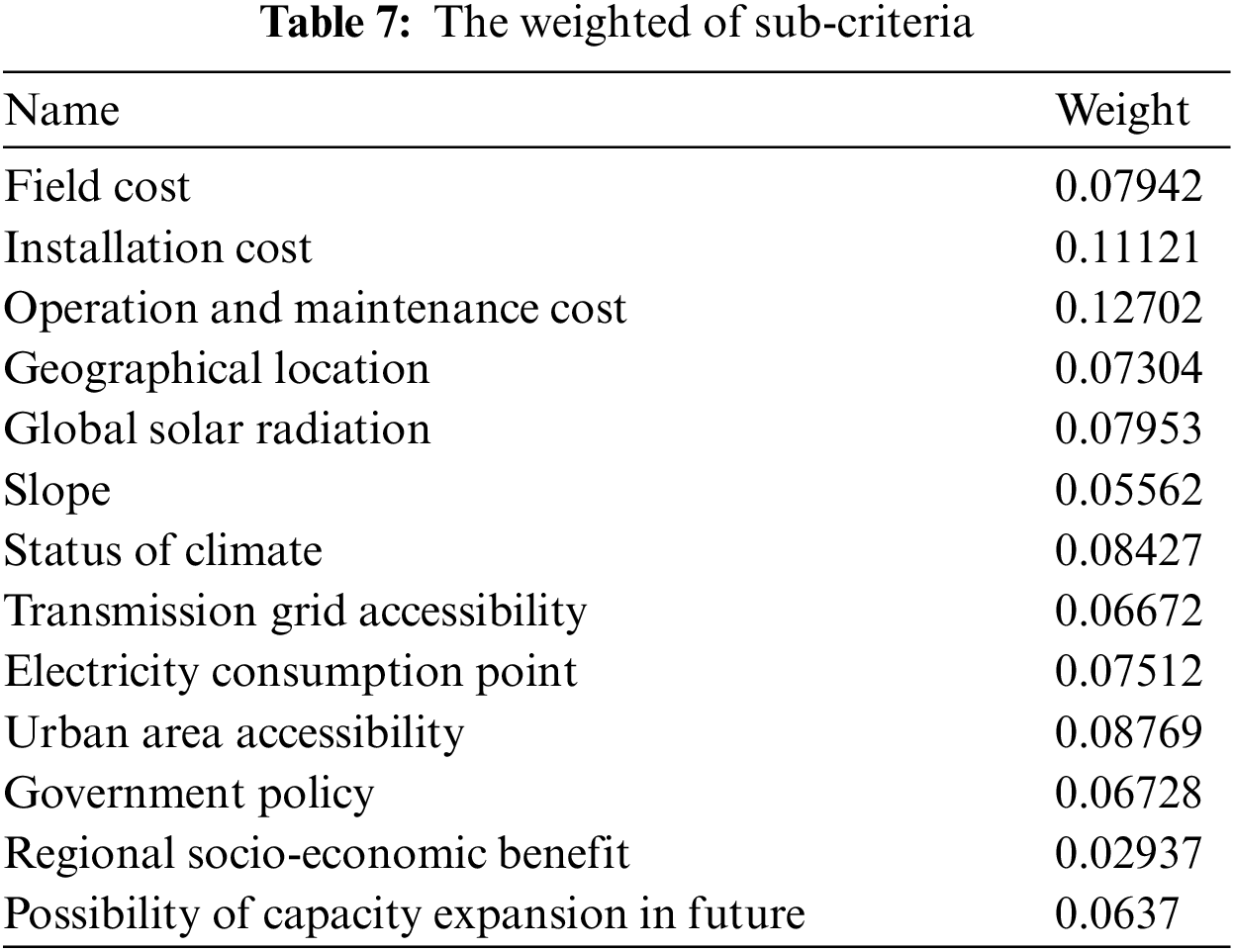
After obtaining the results of the priority among the criteria, the author proceeds to calculate the final optimal result based on the TOPSIS model (Eqs. (9)–(14)). The final ranking is shown in Tab. 8

While traditional energy sources such as coal and oil are gradually depleted, with high prices and unstable supply, many alternative energy sources are of interest to scientists, especially solar energy resources. Access to this new energy source not only contributes to meeting the energy needs of society, but also helps to save electricity and reduce environmental pollution. Realizing the advantages of developing solar energy, many investors have developed energy projects. Choosing the optimal site for construction is a complex decision. Therefore, the author proposes a multi-criteria decision-making model to assist decision-makers in identifying potential locations. As a result, location 5 is the optimal solution.

5  Conclusion and Discussion

Vietnamese power plants have affirmed the importance of clean energy sources in ensuring electricity for socio-economic development in association with the environment, especially when the government commits to reducing greenhouse gas emissions from the reduction of power generation from coal-fired power plants at COP21 (United Nations Climate Conference). With the advantage of wind and solar energy in a country with a tropical monsoon climate, Vietnam has determined that these are the two main energy sources for developing clean electricity.

Location selection is an important problem in all renewable energy projects. Therefore, the author proposed a fuzzy MCDM model for solar power plant location selection in this study. In the first stage, the FANP model is applied to determine the weight of all the criteria affecting the decision process. TOPSIS model is then proposed to rank all potential locations.

The contribution of this study is to propose a MCDM for solar power plant location selection in Vietnam under fuzzy environmental conditions. The result of this study is a useful tool for selecting the optimal location for renewable energy projects in Vietnam as well as other countries.

The proposed MCDM is an available technical information processing method to support decisions in many fields, especially in multi-criteria decision making. However, the peculiarity of this method is the lack of empirical evidence on the influence of a certain factor on the outcome of decision-making because the weight of the factor is evaluated by experts. When applying this method, expert assessment groups and key influencing factors are established, and questionnaires and criteria scales are synthesized. The reliability of the results is assessed using a priority comparison scale. Therefore, the future research goal of the author is to combine with a model that can eliminate this gap as well as be able to combine in the field of green research.

Acknowledgement: We are greatly thankful to Van Lang University, Vietnam for supporting this study.

Funding Statement: We are greatly thankful to Van Lang University, Vietnam for providing the budget for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  REN21, “Renewables 2021 Global Status Report,” Paris, 2021. [Google Scholar]

 2.  H. Ritchie and M. Roser, “Energy,” Our World in Data, 2020. [Google Scholar]

 3.  “BP,” BP p.l.c., 2020. [Online]. Available: https://www.bp.com/en/global/corporate/energy-economics/statistical-review-of-world-energy.html. [Accessed 2021]. [Google Scholar]

 4.  Solargis, “Globalsolaratlas,” The World Bank Group, 2019. [Online]. Available: https://www.globalsolaratlas.info/download/vietnam?c=16.045813,105.820313,5. [Accessed 2019]. [Google Scholar]

 5.  “Energy.gov,” U.S department of energy, 2016. [Online]. Available: https://www.energy.gov/solar. [Google Scholar]

 6.  Ö. Aydın, S. Öznehir and E. Akçalı, “Optimal hospital location selection by analytical hierarchical process,” Suleyman Demirel University the Journal of Faculty Economics and Administrative Sciences, vol. 14, no. 2, pp. 69–86, 2009. [Google Scholar]

 7.  G. Büyüközkan and F. Göçer, “An intuitionistic fuzzy MCDM approach for effective hazardous waste management,” Intelligence Systems in Environmental Management, vol. 113, pp. 21–40, 2016. [Google Scholar]

 8.  R. Alizadeh, L. Soltanisehat, P. D. Lund and H. Zamanisabzi, “Improving renewable energy policy planning and decision-making through a hybrid MCDM method,” Energy Policy, vol. 137, pp. 111174, 2020. [Google Scholar]

 9.  M. A. Hassaan, “A Gis-based suitability analysis for siting a solid waste incineration power plant in an urban area case study: Alexandria governorate, Egypt,” Journal of Geographic Information System, vol. 7, no. 6, pp. 643–657, 2015. [Google Scholar]

10. S. Sindhu, V. Nehra and S. Luthra, “Investigation of feasibility study of solar farms deployment using hybrid AHP-TOPSIS analysis: Case study of India,” Renewable and Sustainable Energy Reviews, vol. 73, pp. 496–511, 2017. [Google Scholar]

11. A. Belhadi, S. S. Kamble, S. A. R. Khan, F. E. Touriki and M. D. Kumar, “Infectious waste management strategy during covid-19 pandemic in Africa: An integrated decision-making framework for selecting sustainable technologies,” Environmental Management, vol. 66, pp. 1085–1104, 2020. [Google Scholar]

12. O. Ellabban, H. Abu-Rub and F. Blaabjerg, “Renewable energy resources: Current status, future prospects and their enabling technology,” Renewable and Sustainable Energy Reviews, vol. 39, pp. 748–764, 2014. [Google Scholar]

13. REN21, “Renewables 2010 Global Status Report,” Deutsche Gesellschaft für Technische Zusammenarbeit (GTZ) GmbH., Paris, 2010. [Google Scholar]

14. J. R. L. Mariano, M. Liao and H. Ay, “Performance evaluation of solar PV power plants in Taiwan using data envelopment analysis,” Energies, vol. 14, no. 15, pp. 4498, 2021. [Google Scholar]

15. H. Eroğlu, “Multi‐criteria decision analysis for wind power plant location selection based on fuzzy AHP and geographic information systems,” Environment, Development and Sustainability, vol. 23, pp. 18278–18310, 2021. [Google Scholar]

16. S. Moradi, H. Yousefi, Y. Noorollahi and D. Rossob, “Multi-criteria decision support system for wind farm site selection and sensitivity analysis: Case study of Alborz province, Iran,” Energy Strategy Reviews, vol. 29, pp. 100478, 2020. [Google Scholar]

17. D. Choudhary and R. Shankar, “An STEEP-fuzzy AHP-TOPSIS framework for evaluation and selection of thermal power plant location: A case study from India,” Energy, vol. 42, no. 1, pp. 510–521, 2012. [Google Scholar]

18. N. Das and S. Mukhopadhyay, “Application of multi-criteria decision making technique for the assessment of groundwater potential zones: A study on birbhum district, west bengal, India,” Environment, Development and Sustainability, vol. 22, pp. 931–955, 2020. [Google Scholar]

19. S. Hamal, O. Senvar and O. Vayvay, “Selection of optimal renewable energy investment project via fuzzy ANP,” Journal of Economics, Finance and Accounting, vol. 5, no. 2, pp. 224–233, 2018. [Google Scholar]

20. E. K. Zavadskas, R. Bausys and M. Lazauskas, “Sustainable assessment of alternative sites for the construction of a waste incineration plant by applying WASPAS method with single-valued neutrosophic set,” Sustainability, vol. 7, no. 12, pp. 15923–15936, 2015. [Google Scholar]

21. C. N. Wang, C. C. Su and V. T. Nguyen, “Nuclear power plant location selection in Vietnam under fuzzy environment conditions,” Symmetry, vol. 10, pp. 548, 2018. [Google Scholar]

22. Y. Charabi and A. Gastli, “PV site suitability analysis using GIS-based spatial fuzzy multi-criteria evaluation,” Renewable Energy, vol. 36, no. 9, pp. 2554–2561, 2011. [Google Scholar]

23. S. Chakraborty, P. K. Sadhu and N. Pal, “New location selection criterions for solar PV power plant,” International Journal of Renewable Energy Research, vol. 4, no. 4, pp. 1020–1030, 2014. [Google Scholar]

24. P. A. Beltrán, F. C. González, J. P. P. Ferrando and F. R. Pozo, “An ANP-based approach for the selection of photovoltaic solar power plant investment projects,” Renewable and Sustainable Energy Reviews, vol. 14, pp. 249–264, 2010. [Google Scholar]

25. A. Kengpol, P. Rontlaong and M. Tuominen, “A decision support system for selection of solar power plant locations by applying fuzzy AHP and TOPSIS: An empirical study,” Journal of Software Engineering and Applications, vol. 6, pp. 470–481, 2013. [Google Scholar]

26. C. N. Wang, V. T. Nguyen, H. T. N. Thai and D. H. Duong, “Multi-Criteria Decision Making (MCDM) Approaches for Solar Power Plant Location Selection in Viet Nam,” Energy, vol. 11, no. 6, pp. 1504, 2018. [Google Scholar]

27. A. Azadeh, S. F. Ghaderi and A. Maghsoudi, “Location optimization of solar plants by an integrated hierarchical DEA PCA approach,” Energy Policy, vol. 36, no. 10, pp. 3993–4004, 2008. [Google Scholar]

28. M. Akçay and M. Atak, “Optimal site selection for a solar power plant in Turkey using a hybrid AHP-TOPSIS method,” Celal Bayar University Journal of Science, vol. 14, no. 4, pp. 413–420, 2018. [Google Scholar]

29. A. H. I. Lee, H. Y. Kang, C. Y. Lin and K. C. Shen, “An integrated decision-making model for the location of a PV solar plant,” Sustainability, vol. 7, pp. 13522–13541, 2015. [Google Scholar]

30. C. N. Wang, V. T. Nguyen, H. T. N. Thai and D. H. Duong, “Multi-criteria decision making (MCDM) approaches for solar power plant location selection in viet Nam,” Energies, vol. 11, no. 6, pp. 1504, 2018. [Google Scholar]

31. A. Aktas and M. Kabak, “A hybrid hesitant fuzzy decision-making approach for evaluating solar power plant location sites,” Arabian Journal for Science and Engineering, vol. 44, pp. 7235–7247, 2019. [Google Scholar]

32. O. P. Akkas, M. Y. Erten, E. Cam and N. Inanc, “Optimal site selection for a solar power plant in the central anatolian region of Turkey,” International Journal of Photoenergy, vol. 2017, pp. 1–13, 2017. [Google Scholar]

33. A. Sozen, A. Mirzapour and M. T. Çakir, “Selection of the best location for solar plants in Turkey,” Journal of Energy in Southern Africa, vol. 26, no. 4, pp. 52–63, 2015. [Google Scholar]

34. H. E. Colak, T. Memisoglu and Y. Gercek, “Optimal site selection for solar photovoltaic (PV) power plants using GIS and AHP: A case study of malatya province, Turkey,” Renewable Energy, vol. 149, pp. 565–576, 2020. [Google Scholar]

35. D. Kereush and I. Perovych, “Determining criteria for optimal site selection for solar power plants,” Geomatics, Landmanagement and Landscape, no. 4, pp. 39–54, 2017. [Google Scholar]

36. T. L. Saaty, in Decision Making with Dependence and Feedback: the Analytic Network Process, Pittsburgh: RWS Publications, 1996. [Google Scholar]

37. T. L. Saaty, “Fundamentals of the analytic network process,” Mathematics, pp. 12–14, 1999. [Google Scholar]

38. R. Lin, J. J. Lin, C. J. Shu, T. Diodes, H. Chao et al., “Note on group consistency in analytic hierarchy process,” European Journal of Operational Research, vol. 190, no. 3, pp. 627–678, 2008. [Google Scholar]

39. T. L. Saaty, The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation, New York: McGraw-Hill International Book Company, 1980. [Google Scholar]

40. S. Talluri and R. Narasimhan, “Vendor evaluation with performance variability: A max–min approach,” European Journal of Operational Research, vol. 146, no. 3, pp. 543–552, 2003. [Google Scholar]

41. S. Opricovic and G. H. Tzeng, “Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS,” European Journal of Operational Research, vol. 156, pp. 445–455, 2004. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.