Computers, Materials & Continua DOI:10.32604/cmc.2022.027223
Article

An Efficient Stacked-LSTM Based User Clustering for 5G NOMA Systems

S. Prabha Kumaresan1, Chee Keong Tan2,* and Yin Hoe Ng1

1Faculty of Engineering, Multimedia University, Cyberjaya, 63100, Malaysia
2School of Information Technology, Monash University, Subang Jaya, 47500, Malaysia
*Corresponding Author: Chee Keong Tan. Email: tan.cheekeong@monash.edu
Received: 12 January 2022; Accepted: 18 March 2022

Abstract: Non-orthogonal multiple access (NOMA) has been a key enabling technology for the fifth generation (5G) cellular networks. Based on the NOMA principle, a traditional neural network has been implemented for user clustering (UC) to maximize the NOMA system’s throughput performance by considering that each sample is independent of the prior and the subsequent ones. Consequently, the prediction of UC for the future ones is based on the current clustering information, which is never used again due to the lack of memory of the network. Therefore, to relate the input features of NOMA users and capture the dependency in the clustering information, time-series methods can assist us in gaining a helpful insight into the future. Despite its mathematical complexity, the essence of time series comes down to examining past behavior and extending that information into the future. Hence, in this paper, we propose a novel and effective stacked long short term memory (S-LSTM) to predict the UC formation of NOMA users to enhance the throughput performance of the 5G-based NOMA systems. In the proposed strategy, the S-LSTM is modelled to handle the time-series input data to improve the predicting accuracy of UC of the NOMA users by implementing multiple LSTM layers with hidden cells. The implemented LSTM layers have feedback connections that help to capture the dependency in the clustering information as it propagates between the layers. Specifically, we develop, train, validate and test the proposed model to predict the UC formation for the futures ones by capturing the dependency in the clustering information based on the time-series data. Simulation results demonstrate that the proposed scheme effectively predicts UC and thereby attaining near-optimal throughput performance of 98.94% compared to the exhaustive search method.

Keywords: Non-orthogonal multiple access (NOMA); deep neural network (DNN); long short term memory (LSTM); temporal channel; user clustering

1  Introduction

Imminent 5G and beyond 5G networks are anticipated to provide high spectral-energy efficiency, deliver super-fast data transmission, ensure ultra-reliability, support massive connectivity and guarantee the lowest possible latency compared to its predecessors [1]. Unfortunately, the conventional orthogonal multiple access (OMA) [2,3] schemes adopted in 4G networks will not be employed in the future cellular networks due to its orthogonality limitation prohibiting bandwidth expansion from accommodating the spectral demand for future applications. Recently, the emergence of non-orthogonal multiple access (NOMA) [4] introduced a technological paradigm shift in accessing networks, which has successfully lifted the bandwidth limit boundary above the OMA spectral limit [5,6]. The main feature of NOMA is to remove orthogonality requirements between the allocated resource blocks to different users who are allowed to simultaneously send data over the same frequency, time, or code.

Generally, NOMA is classified into two types, i.e., power-domain NOMA (PD-NOMA) and code-domain NOMA (CD-NOMA). PD-NOMA is the most widely studied NOMA scheme for 5G networks and beyond. The working principle of the PD-NOMA is to allow the non-orthogonal transmission of multiple users’ signals using superposition coding (SC) at the transmitting end, and the superposed signal is then passed through the successive interference cancellation (SIC) receiver at the receiving end to eliminate interference and implement quadrature demodulation. For a multi-carrier PD-NOMA, the subchannel transmission still adopts the orthogonal frequency division multiplexing (OFDM), where the subchannels are partitioned so that they are orthogonal to each other and do not interfere. Unlike orthogonal frequency division multiple access (OFDMA), the subchannel is no longer exclusively assigned to one user only, but it is shared by various users to increase the spectrum utilization. The users who share the same set of subchannels can transmit their signal using power multiplexing technology such as the SC technique. Hence, the signal power of each user arriving at the receiver is unique and distinguishable. Non-orthogonal transmission between different users on the same subchannel will generate co-channel interference between users, which can be solved using SIC technology at the receiver. The SIC implementation enforces a strict power allocation requirement that associates users of good channel conditions with low-power assignment policy while users of poor channel conditions with high-power allocation policy. These policies allow the SIC to effectively eliminate interference and decode the signals for each user [7]. Nevertheless, this new multiple access approach of permitting multiple users to share a set of subchannels raises another research issue on how to cluster users on different sets of subchannels so that the users can benefit spectrally from the sharing of subchannels while satisfying the power allocation policies enforced by the SIC.

1.1 Recent Works

Over the last few years, user pairing and user clustering (UC) for NOMA networks have been vigorously studied from different perspectives due to the emergence of SIC technology. In [8], two different user pairing schemes were investigated to evaluate the outage probability and average achievable bit rate of a dense NOMA network. In this study, the first scheme was developed based on a random pairing basis, in which two users are randomly chosen to form a NOMA cluster. On the other hand, the second scheme enhances the system performance by selectively pairing the users whose normalized channel gains are above and below certain pre-determined threshold levels, which leads to lower outage probability. Since the user pairing is highly dependable on the locations of users, the impact of near-far user pairing on the performance of cell center, mid, edge users were meticulously explored in [9]. In this work, the authors proposed a novel pairing scheme that groups the near-far users, leaving the cell mid users ungrouped to solve the SIC imperfection issue due to the small channel diversity among the NOMA users. Subsequently, the authors in [10] developed a user pairing and access algorithm to enhance NOMA spectral efficiency and system capacity while ensuring fairness among NOMA users. The proposed mechanism first sorts the users based on channel states and pairs them with the most distinctive channel conditions. In [11], the UC was developed to group user equipment into several clusters equal to or more than the base station (BS) transmit antennas. After that, a linear beamforming approach was incorporated to mitigate inter-cluster interference. The inter-cluster and intra-cluster power allocation was then applied to maximize the overall cell capacity of the NOMA system. Furthermore, a simple heuristic user pairing algorithm [12] was designed for a two-user scenario to pair a cell center user with an edge user, aiming to improve the edge user’s achievable rate.

In general, the UC for a NOMA network is always intertwined with power allocation. The impact of user pairing on the performance of fixed power allocation for a NOMA system and a cognitive radio assisted NOMA was examined in [13] to demonstrate that the NOMA system could offer a larger sum-rate than that of the OMA schemes. In this work, it is suggested that the users who do not experience a significant difference in channel gains are opportunistically paired under the condition that the interference generated by one of the users does not adversely impact the quality of service (QoS) requirement of another user. With this mechanism, the cognitive radio assisted NOMA system prefers to pair the first strongest users with the second strongest users. In contrast, the NOMA system with fixed power allocation favors the pairing of the strongest user with the weakest user. In [14], the user pairing for a cooperative NOMA transmission system with power allocation was explored. This work reveals that the two users experiencing significantly different channel diversity should be grouped based on the ascending order of the users’ channel gains. In another novel study, two-user pairing schemes, i.e., centralized UC and distributed UC was proposed in [15] in which the NOMA users are sorted based on the large-scale fading (LSF) gain. The centralized UC selects the primary user with the highest LSF and pairs it with the complementary chosen users based on signal difference alignment. On the other hand, the proposed distributed UC pairs the primary user with the highest LSF with the user-selected based on the zero-forcing vector achieved by the primary user.

From the state-of-the-art, it is observed that the user pairing and clustering for NOMA systems are pretty inflexible. Recently, a dynamic user clustering (DUC) scheme was proposed in [16] by selecting a feasible number of clusters and grouping the NOMA users into these clusters. As a result, the size of the cluster is dynamically adjusted based on the performance requirements. Nevertheless, the maximum limit imposed on the number of users grouped in a cluster has forced some users to be unfavorably paired together, yielding lower throughput performance. This rigid limit has been lifted in [17], which proposes a UC based on the Brute-force search (B-FS) method where the users are clustered dynamically without any limit merely subject to the SIC constraints. The approach used in [17] has manifested that the NOMA system can achieve a higher performance limit than the OMA. However, the method developed in [17] can only serve for upper-bound performance limits because implementing the B-FS-based clustering method incurs prohibitive computational cost and is not scalable efficiently with the network size. Subsequently, the authors in [18] proposed a particle-swarm optimization (PSO) based UC scheme capable of reducing the complexity. Its main drawback is the early convergence of the particles causing the search space to get trapped in a local minimum.

Machine learning and artificial intelligence (AI) have recently started to make inroads into 5G and beyond 5G networks. In [19], the authors have successfully designed an efficient network slicing scheme using a hybrid machine learning algorithm involving three phases, i.e., data collection, optimal weight feature extraction, and slice classification. The experimental results indicated that the proposed hybridization greatly influences the provision of accurate network slicing. Besides, the review in [20] also highlights the need for explainable AI (XAI) towards the upcoming 6G networks in every aspect that can mitigate the risk of losing control over decision making including 6G technologies (e.g., intelligent radio, zero-touch network management) and 6G use cases (e.g., industry 5.0) to make a future AI-based 6G system more transparent and trustworthy.

Not surprisingly, machine learning has been widely applied to solve various resource allocation problems in NOMA networks. In terms of UC for the NOMA system, the availability of clustering datasets obtained from the B-FS method in [17] inspired the author in [21] to adopt an artificial neural network (ANN) as an efficient clustering tool to learn the grouping behaviors of the users based on their power levels and the diversity of the channel gains. Due to the single hidden-layer feature in ANN, the proposed ANN cannot efficiently capture the input-output relationship between the clustering behaviors with the channel heterogeneity and power differences among NOMA users. The work [22] enhanced the performance by extending it to the deep neural network (DNN) based UC scheme, which provides more room for hyperparameter optimization to improve the learning competency. The DNN-based UC method can learn effectively, attaining approximately 97% of the B-FS approach’s throughput performance. In [23], an extreme learning machine (ELM) was employed to the same UC problem to improve the training and testing speed together with the computational complexity of the DNN-based UC. The use of the ELM eliminates the backpropagation algorithm during the training process of the DNN approach, thereby producing a fast-learning UC method, which can also achieve near-optimal performance.

1.2 Motivations and Contributions

Taking into account the discussions mentioned above, it is apparent that all the state-of-the-art UC methods only solve the clustering problem for an instantaneous time without considering the historical clustering results and the variation of channel gains and power levels. Theoretically, the channel variations of wireless 5G networks can be modelled statistically and estimated accurately [24]. The time-series data on the channel variations, power assignment and the clustering behaviors is an essential input to increase the optimality in UC. In this paper, the implementation of long short term memory (LSTM) is developed to characterize the dependency on the sequential processing of the clustering information, including the channel gains, powers and clustering outcomes. Unlike the traditional neural networks, LSTM consists of multiple feedback connections to capture the time-series data indicating the dependency on the clustering information.

Recently, LSTM has been widely applied for natural language processing (NLP) in [25,26] due to its superiority of signal processing and the capability of resolving the vanishing gradient and long term dependency present in recurrent neural network (RNN). The application of LSTM in cellular networks is also not newfangled. In [27], the LSTM network was developed to autonomously determine the channel characteristics by training the network with simulated channel data. The results showed an improvement in terms of sum rates and bit error rates (BERs) when the LSTM is utilized and compared with the conventional NOMA. In [28], the authors estimate the channel and detect multiple users to avoid the propagation of errors in the sequential decoding process of the SIC detector in the receivers using LSTM, which is able to detect the changing characteristics of the channel. Meanwhile, a new channel estimation technique based on LSTM aimed to improve the outage probability, BER, and user sum rate of the conventional NOMA is presented in [29]. LSTM has also been demonstrated in conjunction with an appropriate gradient-based learning algorithm to overcome error backflow problems in [30] to bridge time intervals above 1000 steps even in case of noisy, incompressible input sequences, without loss of short-time-lag capabilities. In [30], LSTM-based NOMA receivers are investigated over the Rayleigh fading channel conditions. It has been proved that the LSTM-based NOMA detector performance is much better than the conventional NOMA detectors.

In this paper, the promising deep learning (DL) approach can be integrated into the traditional neural network and the implementation of proposed stacked LSTM (S-LSTM) to perform the learning mechanism that results in the automatic prediction of UC to enhance the throughput performance of the NOMA system. The proposed S-LSTM is also known as deep LSTM. Hence, the two terms will be used interchangeably throughout the paper. Compared to the conventional S-LSTM applied to solve different problems in other domains, we have adapted the S-LSTM to NOMA environments to tackle UC issue. In summary, the main contributions of this paper are summarized as follows:

1.    The UC problem in the NOMA system is investigated with the help of DL by implementing the deep neural network (DNN) with multiple layers to enhance the flexibility of the model.

2.    The S-LSTM architecture is then constructed and integrated into the DNN model to process the time-series data to capture the dependency in the clustering information. This model aims to avoid shrinking gradient values that usually vanish as the information propagates between multiple hidden layers during backward propagation (BP). The power allocation strategy for each user is then derived that can provide optimal throughput performance.

3.    The performance analysis of the proposed S-LSTM-UC NOMA system under various network parameters is provided. Specifically, the average throughput and mean squared error (MSE) has been examined. In addition, significant simulation findings and comparisons are shown to prove the effectiveness and strength of the proposed schemes.

1.3 Organization of the Paper

The remaining sections of this paper are laid out as follows. In Section 2, a NOMA-based 5G system model is developed with the temporal channel model. Besides, the SIC constraints are outlined in this section, while the UC and power allocation problems are also formulated. Subsequently, the working principle of S-LSTM-based UC is described in Section 3. The proposed new UC algorithms for training and testing phases are also outlined in this section. Simulation results with in-depth analytical discussions are shown in Section 4. Last but not least, the paper ends with some insightful concluding remarks and navigates the readers to some possible future research directions related to this work in Section 5.

2  System Model and Problem Formulation

2.1 System Model and Temporal Channel Model for NOMA-Based Networks

Consider a downlink NOMA-based single-cell 5G system with a single BS located at the center of the cell, within which K number of users are randomly and uniformly distributed. In the NOMA system, the users can share a set of exclusive subcarriers in distinct clusters. The inter-cluster interference does not exist due to the assumption of perfect orthogonality among all subcarriers. The users are susceptible to interference caused by other users within the same cluster due to the sharing of subcarriers. Even though sharing among users increases subcarriers’ frequency reuse, it does not guarantee a throughput improvement due to the interference. Therefore, clustering users to share the subcarriers becomes the determining factor in overall system throughput. Rationally, when the channel diversity among users is small, it is preferable to group more users in a cluster to increase the spectrum utilization. Still, increasing cluster size certainly causes higher interference, resulting in throughput degradation. Therefore, it is essential to find a good tradeoff between the two conflicting parameters, i.e., cluster size and interference.

In the NOMA system, the 5G spectrum is partitioned into J subcarriers, each with a bandwidth Bj which is less than the channel’s coherence bandwidth such that each subcarrier manifests flat fading. In addition, it is assumed that the adjacent subcarriers can perfectly preserve orthogonality so that inter-symbol interference between the adjacent symbols can be eliminated. The 5G channel is assumed to exhibit frequency-selective Rayleigh fading in which a noticeable correlation between channel gains of adjacent subcarriers is perceived. The subcarrier correlation coefficient between subcarriers i and j for user k can be defined as

χi,jk=(1+δi,jk)Ξ{2δi,jk/2δi,jk1+δi,jk1+δi,jk}−π22−π2(1)

where Ξ is the complete elliptic integral of the second kind and δi,jk can be denoted as

δi,jk=11+2π(i−j)στrms(2)

where στrms denotes the root-mean-square (RMS) channel delay spread normalized by the number of subcarriers, which can be further expressed as

στrms =∑i=1M⁡Ai2τi2−∑i=1M⁡Ai2τi∑i=1M⁡Ai2  (3)

where Ai and τi represent the amplitude and time delay for ray l, respectively, in a M-ray Rayleigh fading model.

In the conventional OMA system (also known as Orthogonal Frequency Division Multiple Access (OFDMA)), the users perceive different channel gains on different subcarriers and let the channel gain experienced by user k on subcarrier j be gj,k. Instead of simulating a snapshot or ensemble description of channel gains for all the subcarriers, we observe the channel variation experienced by the users in a temporal dimension for a period T which is slotted discretely in this context (T denotes the total number of time slots). Let’s assume the random channel gain variables based on the Gaussian distribution over a specific time t be gj,kt∼N(μ,σ2 ) where gj,kt is the channel gain of user k on subcarrier j at a specific time t while μ and σ denote the mean and standard deviation of normal distribution N, respectively. In this context, we assume that the NOMA network is geographically static because the time scale of algorithm convergence is shorter than the channel coherence time, and the sampling period of the time slot is chosen such that the channel gains are fixed for a particular time slot. The probability density function, f(x) of the Gaussian distributed channel variation of temporal NOMA channel can be modelled as

f(x)=1σ2πe−12(gj,kt−μσ)2(4)

Precisely, μ and σ can be represented as follows

σ2=∑t=1T⁡(gj,kt−μ)2T(5)

μ=∑t=1T⁡gj,ktT(6)

In a power-domain NOMA-based 5G system, users can share a set of exclusive subcarriers in which superposition coding (SC) is used to multiplex users on the same subcarriers. Let Uc,jt=Δ{k∈K:pj,kt>0} denotes cluster c in which a set of users multiplexed on subcarrier j at time slot t where pj,kt is the power allocated for user k on subcarrier j at time slot t. Usually, the users in Uc,jt may also share other subcarriers to achieve the minimum bit rate, hence, J(Uct) is the collection of the subcarriers allocated to Uct where Uct=Uc,it∩⁡Uc,jt,∀i,j∈J(Uct),i≠j. In other words, the users who are clustered together are required to share the same set of subcarriers; even some subcarriers are not their best choice. This allocation has made the NOMA system’s UC an NP-hard problem that requires an exhaustive search to obtain the optimal solution [17].

Let’s assume that the cardinality of Uct denoted as 1≤|Uct|≤K represents the number of users in the cluster Uct. To facilitate the implementation of SIC at the receivers of Uct when |Uct|>1, the SIC conditions must be fulfilled so that NOMA users can distinguish the decodable signals from non-decodable signals. For simplicity, the signal yj,kt received by user k on subcarrier j at time slot t can be shown as

yj,kt=pj,ktgj,kt xj,kt+∑m=1,m≠kK⁡pj,mtgj,mt xj,mt+ηj,kt(7)

where xj,kt is the signal transmitted by the BS destined to user k on subcarrier j at time slot t while ηj,kt is the additive white Gaussian noise (AWGN) power perceived by user k on subcarrier j at time slot t. It is shown in Eq. (7) that the superimposed signal comprises multiple signals intended to multiple users, where the first term of Eq. (7) is the intended signal. In contrast, the second term of Eq. (7) is unwanted signals or interference.

At a specific time slot t, let’s assume a scenario where there are three users (users x, y, z) sharing an exclusive set of subcarriers. The channel gains of the users are arranged in a descending order gj,kt>gj,kt>gj,kt where Uct={x,y,z},j∈J(Uct). The transmission power allocated to each user on a particular subcarrier must satisfy the following SIC conditions so that the SIC can work at the users’ receivers.

SIC conditions for user x   [ [ gj,xt(pj,zt−pj,xt−pj,yt) >pSICgj,xt(pj,yt−pj,xt) >pSIC  (8)

SIC condition for user y   [ [ gj,yt(pj,zt−pj,xt−pj,yt) >pSIC  (9)

where pSIC is the minimum power difference for a user to distinguish the intended signal from the unwanted signals. From the SIC conditions for user x denoted in Eq. (8), the power allocation among users x,y, and z is to ensure that user x can eliminate the interference signals caused by users y and z. The SIC condition for user y denoted in Eq. (9) is for user y to efficiently cancel the interference signal from user z. However, user y is unable to decode and cancel interference signals from user x, which is then treated as noise. This assumption works validly because user x is allocated lower downlink power compared to user y such that pj,xt<pj,yt, which results in negligible interference to user y. Similarly, user z who possesses the lowest channel gain on subcarrier j cannot adopt the SIC mechanism to cancel any interference signals from all users who have higher channel gains, but the efficient NOMA power allocation such that pj,xt<pj,yt<pj,zt leads to insignificant interference on user z. Based on Eqs. (8) and (9), the SIC conditions for a set of subcarriers shared by a group of users with the number of the user indicated as |Uct| can be generalized as

gj,kt(pj,kt−∑i=1k−1⁡pj,it)≥pSIC, k=2, 3, …, |Uct| and ∀j∈J(10)

The SIC condition in Eq. (10) works for any number of users in Uct>1. In this context, we assume that all users’ receivers adopt the same SIC threshold, pSIC.

To better model the SIC implementation mathematically, the order of decoding for each user k∈Uct whose signal is superimposed on subcarrier j∈J(Uct) can be represented by a permutation function ∏j:{1,…,|Uc,jt|}→Uc,jt. For m∈Uc,jt, ∏j(m) denotes the index for decoded user m and user k’s order of decoding is then represented by ∏j−1(k). Hence, the user’s signals ∏j(1),…, ∏j(m−1) are decoded first and removed from the superimposed signal before decoding the signal for ∏j(m). Furthermore, user ∏j(m) is still susceptible to the interference caused by ∏j(n) if n>m. On the other hand, if |Uc,jt|−1 users’ signals are decoded successfully, then ∏j(|Uc,jt|) will be decoded last, and this user is not exposed to any intra-band interference. In general, the optimal order of decoding upholds the respective sorting can be shown as

ηj,∏j(1)tgj,∏j(1)t≥ηj,∏j(2)tgj,∏j(2)t≥ηj,∏j(3)tgj,∏j(3)t≥…≥ηj,∏j(|Uc,jt|)tgj,∏j(|Uc,jt|)t(11)

Based on the Shannon capacity formula, the achievable throughput Rj,kt of user k on subcarrier j at time slot t can be expressed as

Rj,kt=Bjlog2[1+gj,ktpj,kt∑m=∏j−1(k+1)|Uc,jt|⁡(gj,ktpj,∏j(m)t+ηj,kt)] (12)

Based on Eq. (12), the sum throughput of the NOMA system at time slot t can be further expressed as

Rt=∑c=1C⁡∑k=1K⁡∑j=1J⁡Bjlog2[1+gj,ktpj,kt∑m=∏j−1(k+1)|Uc,jt|⁡(gj,ktpj,∏j(m)t+ηj,kt)](13)

where C is the total number of clusters formed in the NOMA clustering process. This work aims to cluster the NOMA users optimally and allocate the downlink power to maximize throughput denoted in Eq. (13) subject to various constraints and conditions, including the SIC conditions.

2.2 User Clustering and Power Allocation Problem Formulation

Fig. 1 illustrates a NOMA-based system model where a BS concurrently serves K users in downlink transmission. It is seen that K users are grouped into C clusters, each sharing a set of subcarriers on which the superposed signals are transmitted by the BS to all clusters. The channel gains of each user on the allocated subcarriers are observed for the duration of time, which is discretely partitioned into T slots. The variation of the channel gains over time has a direct impact on the cluster formation because the order of decoding may change after some time as some users may experience degrading channel conditions, whereas some users may achieve better channel gains. In such a case, the original cluster formation might not be optimal after some time because the throughput achieved by some clusters may degrade, and the SIC conditions might be violated, which should trigger a cluster re-formation. Once a new cluster formation is initiated, the power allocation should also be re-performed to maximize the throughput and satisfy the SIC conditions. In this paper, a UC scheme will be developed to maximize the sum throughput of the NOMA system by taking into account the time-varying communication channels. Once the optimal UC is obtained, the power allocation scheme proposed in [21] can be adopted to maximize throughput performance.

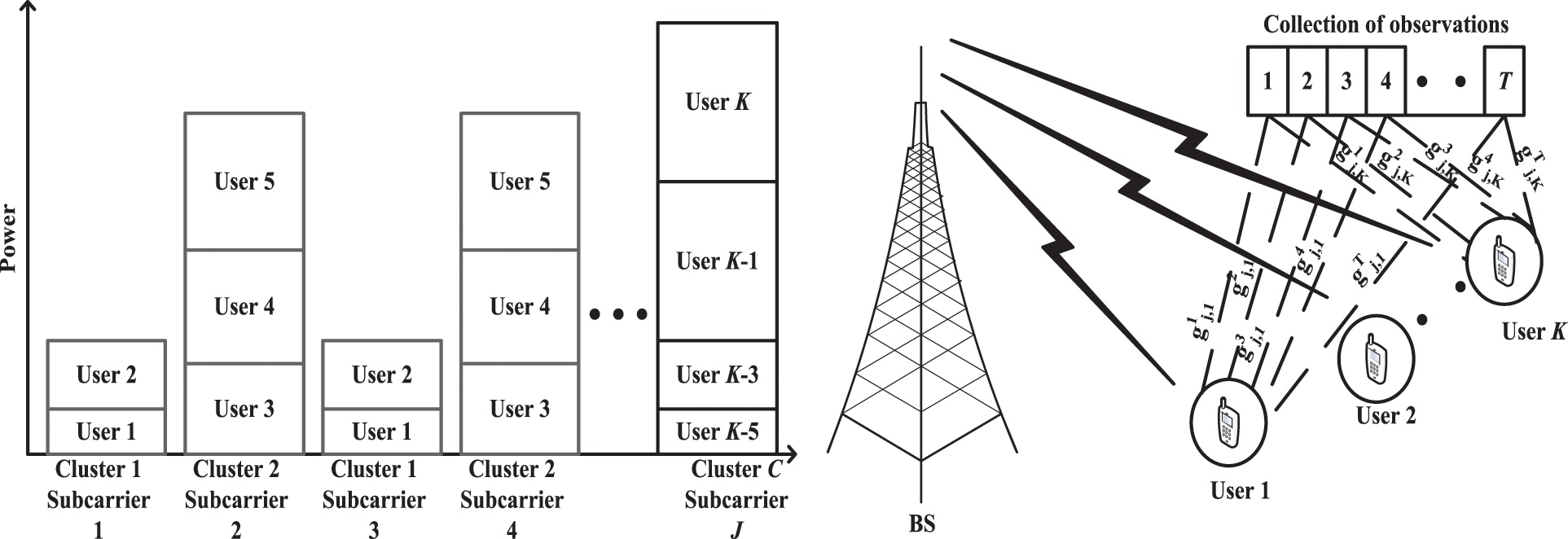
Figure 1: Downlink NOMA time-series system model

Let the UC indicator vector of a user k for C number of clusters be βj,kt={βj,kt(1),βj,kt(2),…,βj,kt(C)} where βj,kt(c)∈{0,1} is a Boolean variable such that βj,kt(c)=1 if user k is grouped into cluster c on subcarrier j at time slot t, otherwise βj,kt(c)=0. For simplicity, the cluster set is represented by Ct={U1t,U2t,…,UCt}. It is noteworthy that the cluster formation problem in this work is dynamic clustering which does not fix the cluster size and the number of clusters in the NOMA system, unlike the existing works, which place stringent conditions on cluster formation. With the relaxation on the cluster formation, the value of C is not pre-determined, and the number of users per cluster may be different due to the channel diversity of the NOMA users. Naturally, C becomes larger if the channel diversity among the users is small because the users tend to form smaller clusters by not sharing their subcarriers owing to the incompliance to the SIC conditions denoted in Eq. (10). On the other hand, if the channel difference among the users is significantly great, C  becomes smaller as the users can form larger clusters to share their subcarriers due to the relaxation of conditions in Eq. (10). In this context, The UC strategies for all users at time slot t  can be represented by

βt=[βj,1t⋯βj,Kt⋮⋱⋮βJ,1t⋯βJ,Kt](14)

To fulfil the SIC conditions, power allocation of the users on the shared subcarriers must be prudently implemented. Let pkt=[p1,kt,p2,kt,…,pJ,kt]  be the power allocation strategy of user k on all the subcarriers, and the power allocation strategies for all users are represented by Pt={p1t,p2t,…,pKt}. Zero power will be allocated for those subcarriers not assigned to user k.

In this context, the sum throughput of the NOMA system is defined as the objective function, and the joint clustering and power allocation problem for throughput maximization in a downlink NOMA system can be formulated as

maxβt,Pt⁡∑c=1C⁡∑k=1K⁡∑j=1J⁡βj,kt(c)Bjlog2[1+gj,ktpj,kt∑m=∏j−1(k+1)|Uc,jt|⁡(gj,ktpj,∏j(m)t+ηj,kt)](15)

subject to

∑k=1K⁡∑j=1J⁡pj,kt≤ptotal(16a)

∑j=1J⁡Rj,kt≥Rkmin(16b)

gj,kt(pj,kt−∑i=1k−1⁡pj,it)≥pSIC,  k=2,3,…,|Uct| and ∀j∈J(16c)

∑c=1C⁡βj,kt(c)≤1, , ∀j∈J,∀k∈K(16d)

where constraint Eq. (16a) limits the allocation of power to all users to the total power budget available at the BS, constraint Eq. (16b) guarantees that every NOMA user can achieve the minimum throughput, constraint Eq. (16c) imposes the SIC conditions to all users’ receivers. Constraint Eq. (16d) ensures that one NOMA user is only grouped to one cluster only. From [15], it can be noticed that the number of clusters is not fixed initially, but it is only known once the optimal βj,kt is obtained. This is the key difference of the optimization of this work as compared to that of the existing results.

This paper presents a novel machine learning approach to solve the UC problem formulated in Eq. (15) and Eqs. (16a)−(16d). In the throughput maximization in Eq. (15) considered in this work, it is assumed that the subcarriers are pre-allocated randomly to each user before they form clusters to share their subcarriers. In other words, each user will be allocated an exclusive set of subcarriers before the UC process. The subcarriers assigned to a user will not be exchanged with other users during the UC process. The users can only share their subcarriers with other users based on their cluster formation strategy. In short, subcarrier allocation is not the primary consideration in this work.

Similarly, even though power allocation is one of the maximizing variables in [15], the power allocation problem is not the main focus of this work. In this optimization problem, since power allocation and user clustering are intertwined, the optimization is an NP-hard problem, which requires an exhaustive search method to find the optimal solution. To solve this problem within an allowable time, we have decoupled the problem into multiple sub-problems (i.e., power allocation problem and user clustering problem), which can be solved in a series. Therefore, an equal power allocation is employed before the UC process, and once the optimal UC is obtained, the power allocation strategy proposed in [17] is adopted to maximize the throughput.

3  Proposed Stacked-LSTM Based UC

This section presents the proposed stacked LSTM based UC (S-LSTM-UC) technique for the NOMA downlink. We first describe the generation and the attributes of the dataset and then explain the holistic working principle of S-LSTM-UC in detail.

3.1 Data Acquisition

To train the proposed S-LSTM-UC, the B-FS based UC (B-FS-UC) [17] is utilized to generate a time series dataset that comprises the transmit powers, channel gains, and the optimal cluster formation by exhaustively examining the throughputs for all the possible combinations of cluster formations and selecting the best cluster formation that maximizes the throughput performance. In addition, considering the aspect of subcarrier allocation, each user will be randomly pre-allocated with a subset of subcarriers before UC. As described in Section 2.2, the time series dataset is collected by observing the channel gains of the users, and the corresponding transmit powers for T time slots. As such, the dataset for a K-user NOMA system consists of a total of KT channel gain values, KT power gain values, and K cluster information values. To improve the robustness of the proposed scheme against network dynamics and channel variations, we collect the dataset for NOMA systems with different numbers of users, which are randomly distributed and a different number of subcarriers with varying fading levels.

3.2 Working Principle of Stacked LSTM Based UC

Fig. 2 depicts the structure of the proposed S-LSTM-UC. As illustrated, it is constructed by cascading an input layer with K×L nodes, N LSTM layers, and a dense layer with K output nodes. In the figure, X is a multivariate input window that contains the channel gains and users’ initial transmit powers, while Z is a vector of size 1×K that corresponds to the UC information at time t. To enable the proposed S-LSTM-UC to effectively mine the deep temporal correlations between the multivariate time-series inputs (channel gains and users’ initial transmit powers) and the UC information, N LSTM layers are employed and stacked. As shown in the figure, the output of the LSTM layer of S-LSTM-UC serves as an input to the subsequent layer. As compared to a single-layer LSTM, multi-layer LSTM is endowed with a superior ability to disentangle the underlying complex temporal dynamics of the time-series data and to progressively create a higher level of representation of the time series inputs.

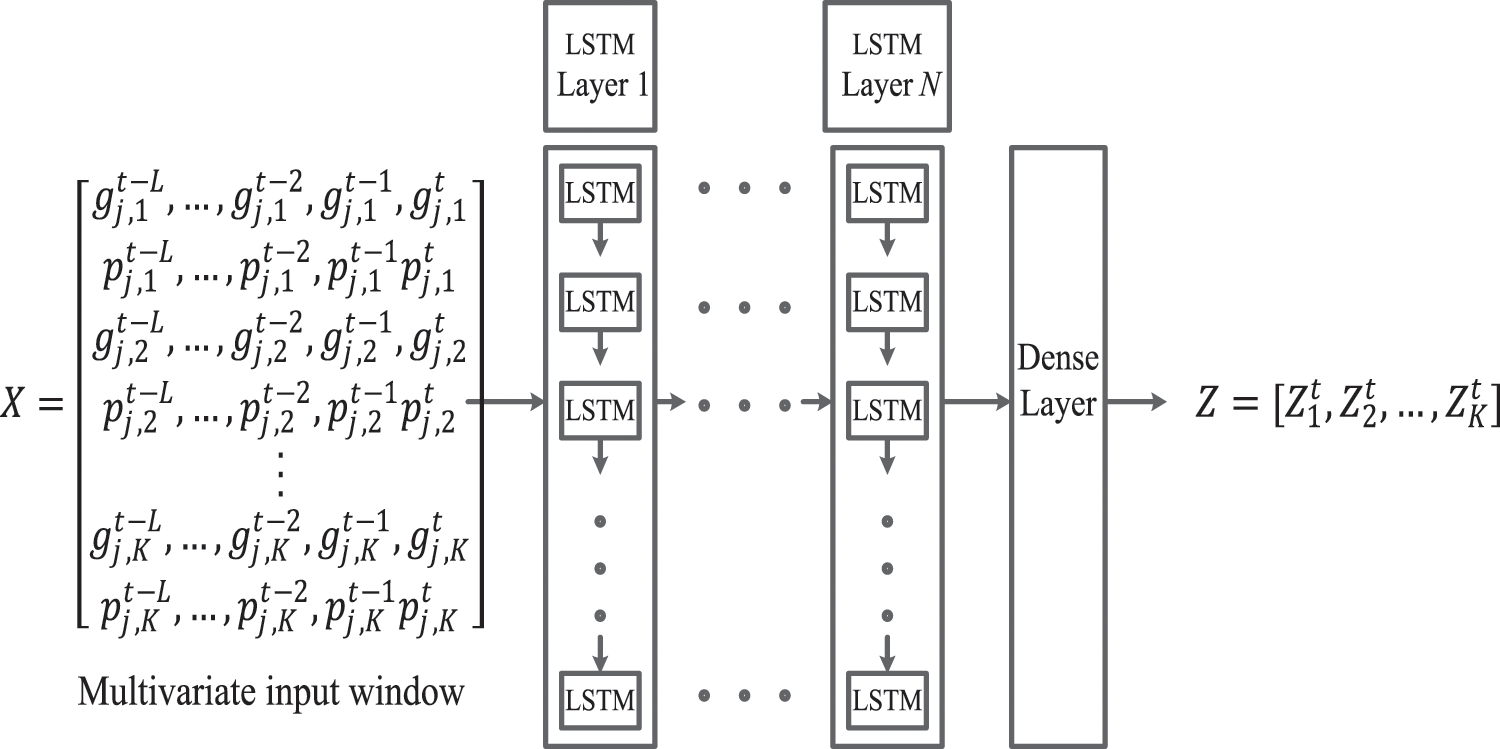
Figure 2: Architecture of stacked LSTM based UC

In S-LSTM-UC, each LTSM layer consists of multiple LSTM cells, and the internal structure of the LSTM cell is shown in Fig. 3. Generally, LSTM is a variant of recurrent neural network (RNN) designed to capture the long term dependencies present in time-series data. Unlike the vanilla RNNs, which are plagued by the issues of gradient disappearance and gradient explosion during backpropagation, LSTM regulates the flow of information and maintain the features extracted from the previous time steps through the dynamics of gating mechanism, short-term and long-term memory cells.

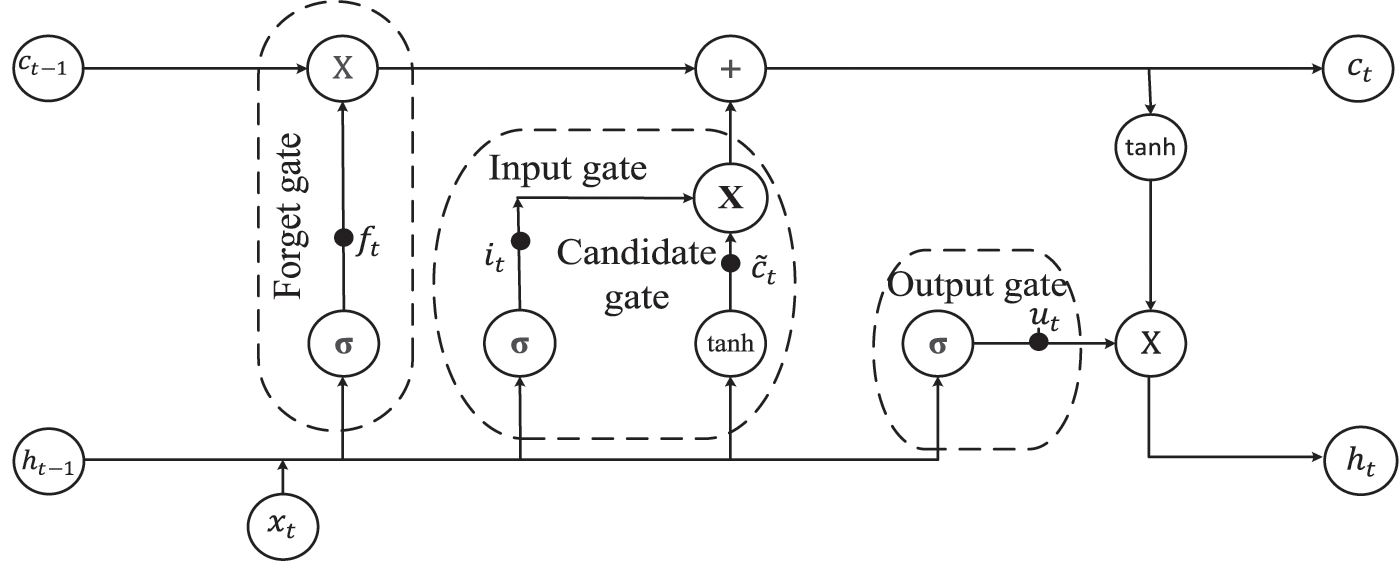
Figure 3: Schematic diagram of LSTM cell

As illustrated in Fig. 3, each LSTM cell is comprised of 2 internal states (hidden state ht and cell state ct) and three gates (input gate it, output gate ut, and forget gate ft). The role of the cell state is to keep track of the valuable information obtained from past inputs. On the other hand, the hidden state synthesizes the information obtained from the current input, the previous cell state, and the previous hidden state.

The forget gate governs what information to be retained and what information to be removed from the previous cell state ct−1. Both information from the previous hidden state ht−1 and the current input vector xt will be processed by a logistic activation function σ(⋅) which has an output value ft that ranges from 0 to 1. Intuitively, ft=1 indicates that the entire information from the ct−1 is retained while ft=0 implies that the information from ct−1 is irrelevant, and it should be removed entirely. Mathematically, the operation of the forget gate can be expressed as

ft=σ(wxf⋅xt+whf.ht−1+bf)(17)

where wxf is the weight matrix from the input layer to the forget gate, whf is the weight matrix from the hidden state to the forget gate, and bf represents bias term for the forget gate.

The input gate it and the candidate hidden state c~t determine the amount of information to be added to the cell state, and the information is generated based on the current input vector xt and the previous hidden state ht−1 as follows:

it=σ(wxi.xt+whi.ht−1+bi)(18)

c~t=tanh(wxc~.xt+whc~.ht−1+bc~)(19)

where wxi is the weight matrix from the input layer to the input gate, whi is the weight matrix from the hidden state to the input layer, wxc~ is the weight matrix from the input layer to the candidate hidden state, whc~ is the weight matrix from the hidden state to the candidate hidden state, bi denotes the bias term for the input gate, bc~ signifies the bias term for the candidate hidden state and represents the hyperbolic activation function that scales the output values from −1 to 1. Next, the cell state ct can be updated as follows:

ct=ft⊗ct−1+it⊗c~t(20)

where ⊗ denotes element-wise operation.

The output gate ut selects the information that should be passed on to the next hidden state, and it can be written as

ut=σ(wxu.xt+whu.ht−1+bu)(21)

ht=ut∗tanh(ct)(22)

Finally, to predict the best UC formation, a dense layer connects all the neurons in the N-th LSTM layer to each of the output nodes. It is noteworthy that the UC problem in this work is modelled using a regression-based S-LSTM-UC which outputs the cluster number for each user. The cluster number is a continuous value, which will be rounded up as an integer to indicate the cluster number of a particular formation. The efficiency and deficiency of the S-LSTM-UC can be assessed by using mean-squared error (MSE), which is defined as

MSE=1S∑n=1S⁡(zn−z^n)2(23)

where S and z^n represents the total number of samples and the predicted cluster value for the n-th user.

The working principle of S-LSTM-UC during the training and testing phases are summarized in Algorithm 1 and Algorithm 2, respectively.

4  Numerical Results and Discussions

This section verifies the effectiveness of the proposed S-LSTM-UC via extensive MATLAB simulation. More specifically, we have done an extensive hyper-parameter tuning on the proposed S-LSTM-UC model to investigate the influence of hyper-parameters. The learning rate, activation functions, length of training data samples, network depth, number of hidden layer nodes, and number of epochs on the MSE and the average throughput performance of S-LSTM-UC in NOMA downlink systems for different numbers of users will be thoroughly analyzed. The performance of the proposed S-LSTM-UC will also be compared against the existing OMA, DUC, ANN-UC, and B-FS-UC schemes. Tabs. 1 and 2 summarize the detailed configuration of the simulation parameters for the proposed S-LSTM-UC and the downlink NOMA system. Unless otherwise specified, the learning rate, batch size, and activation function are set as 0.001, 50, and ReLu, respectively. The selection of the ranges for investigation outlined in Tab. 1 is determined from the extensive simulation to avoid any local maxima issue.

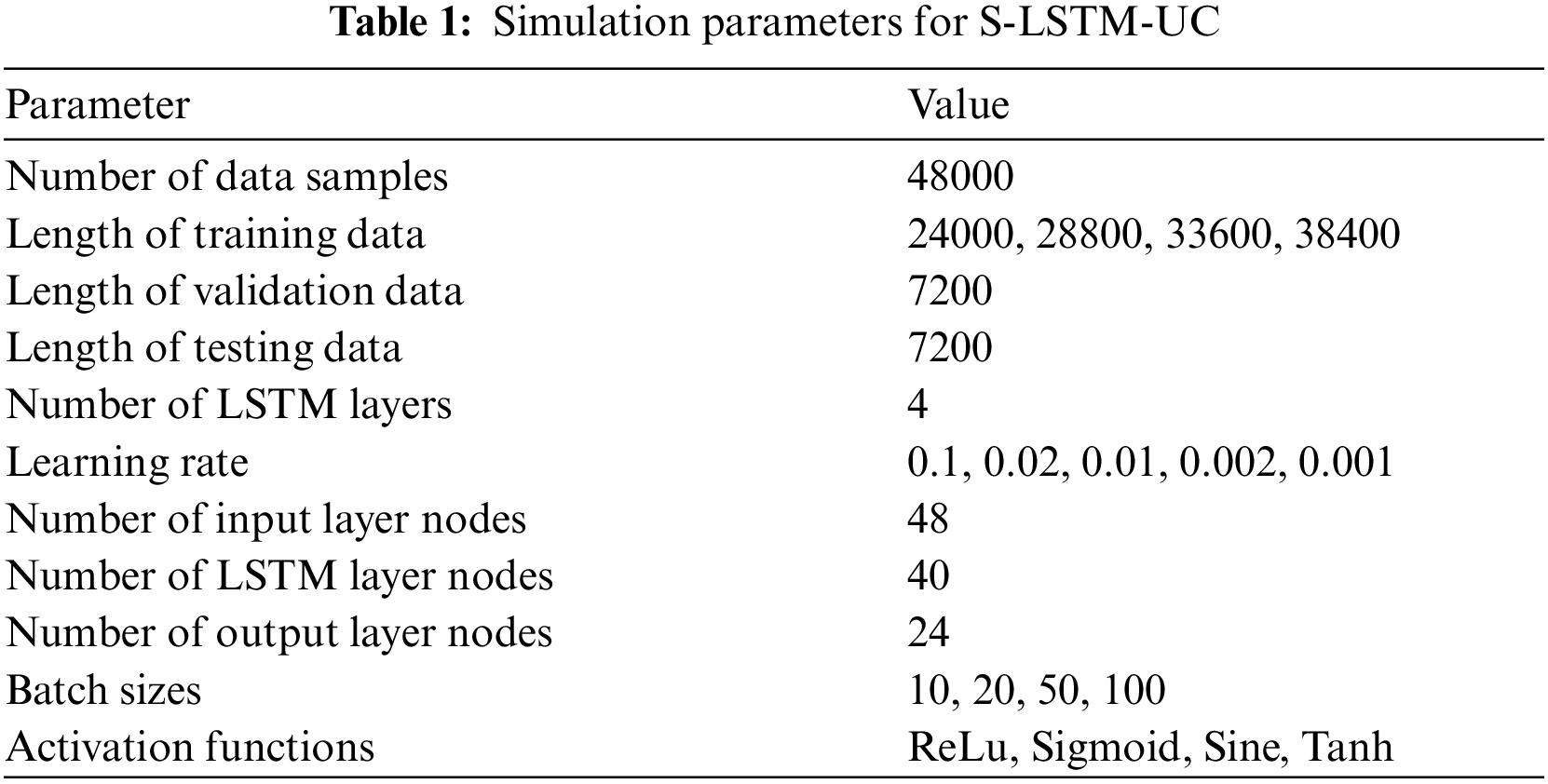
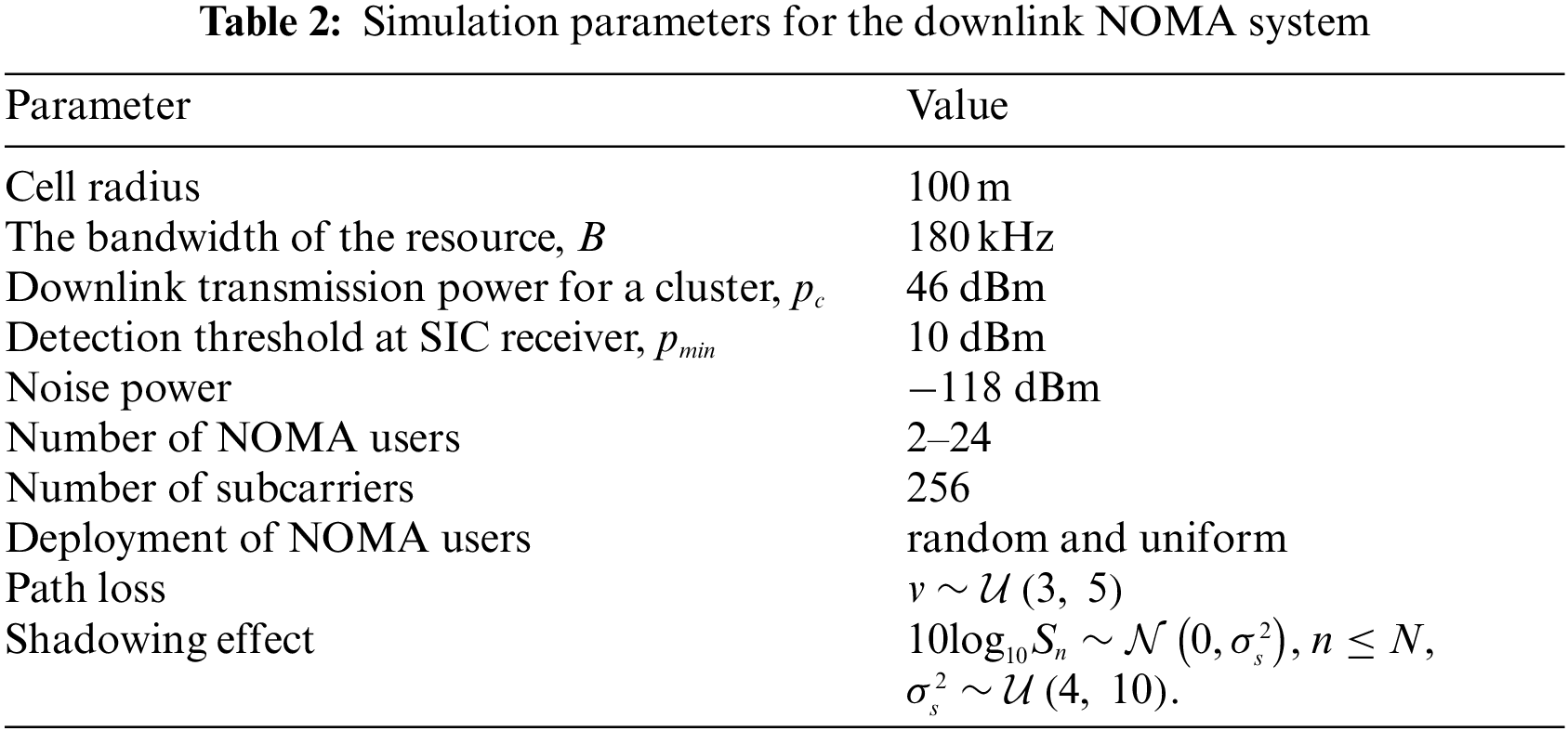
Fig. 4 presents the throughput performance of S-LSTM-UC during the training phase as a function of the length of training data and the number of users at a learning rate of 0.001. Unsurprisingly, the throughput performance of S-LSTM-UC improves as the number of users and number of training samples increase. This phenomenon is attributed to the fact that the number of training samples below 33600 is inadequate to train the proposed model to effectively disentangle the complex correlation between the input features of NOMA users and the UC. For instance, in the 24-user NOMA downlink, the throughput performance of S-LSTM-UC with 28800 and 24000 training samples dropped by 3.26% and 7.95%, respectively, compared to the case 33600 training samples.

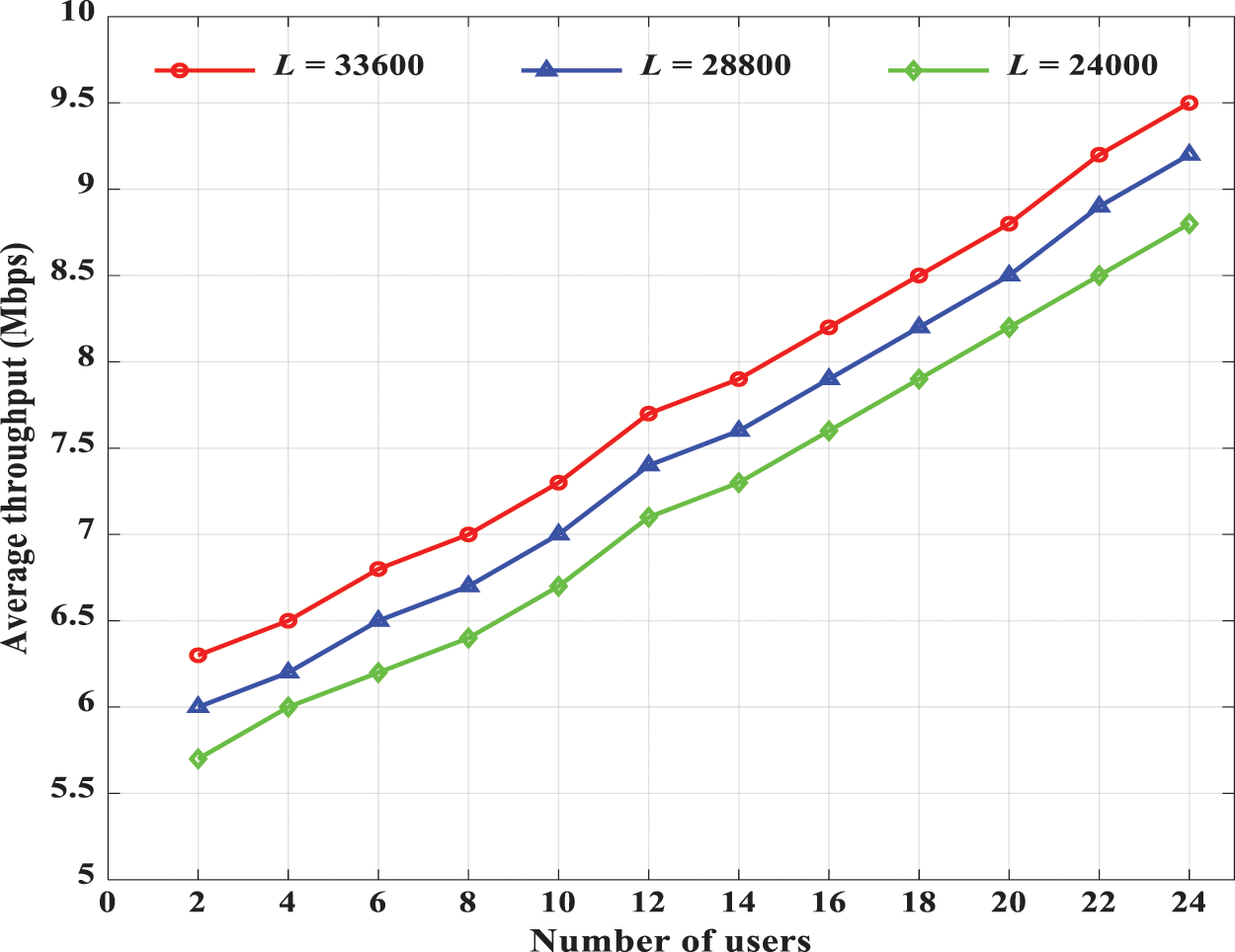
Figure 4: Throughput performance of S-LSTM-UC for the different number of users and different lengths of training samples

Having studied the influence of the length of the training samples and number of users, Fig. 5 shows the throughput performance of S-LSTM-UC during the testing phase for different numbers of epochs. The learning rate is varied from 0.001 to 0.1. It is observed that the throughput of S-LSTM-UC increases when smaller step size is adopted. In addition, the throughput performance of the proposed schemes also improves as the number of epochs is increased from 10 to 40. However, when the number of epochs is increased to 50, the throughput performance of the model degrades. This observation is because the proposed model could be sufficiently trained to learn the cluster formation using 40 epochs. Further training of the model will lead to over-fitting and the noise present in the training samples will be captured, resulting in throughput degradation. As such, the optimum throughput performance for this deployment scenario could be obtained when the learning rate and the number of epochs are configured as 0.001 and 40, respectively.

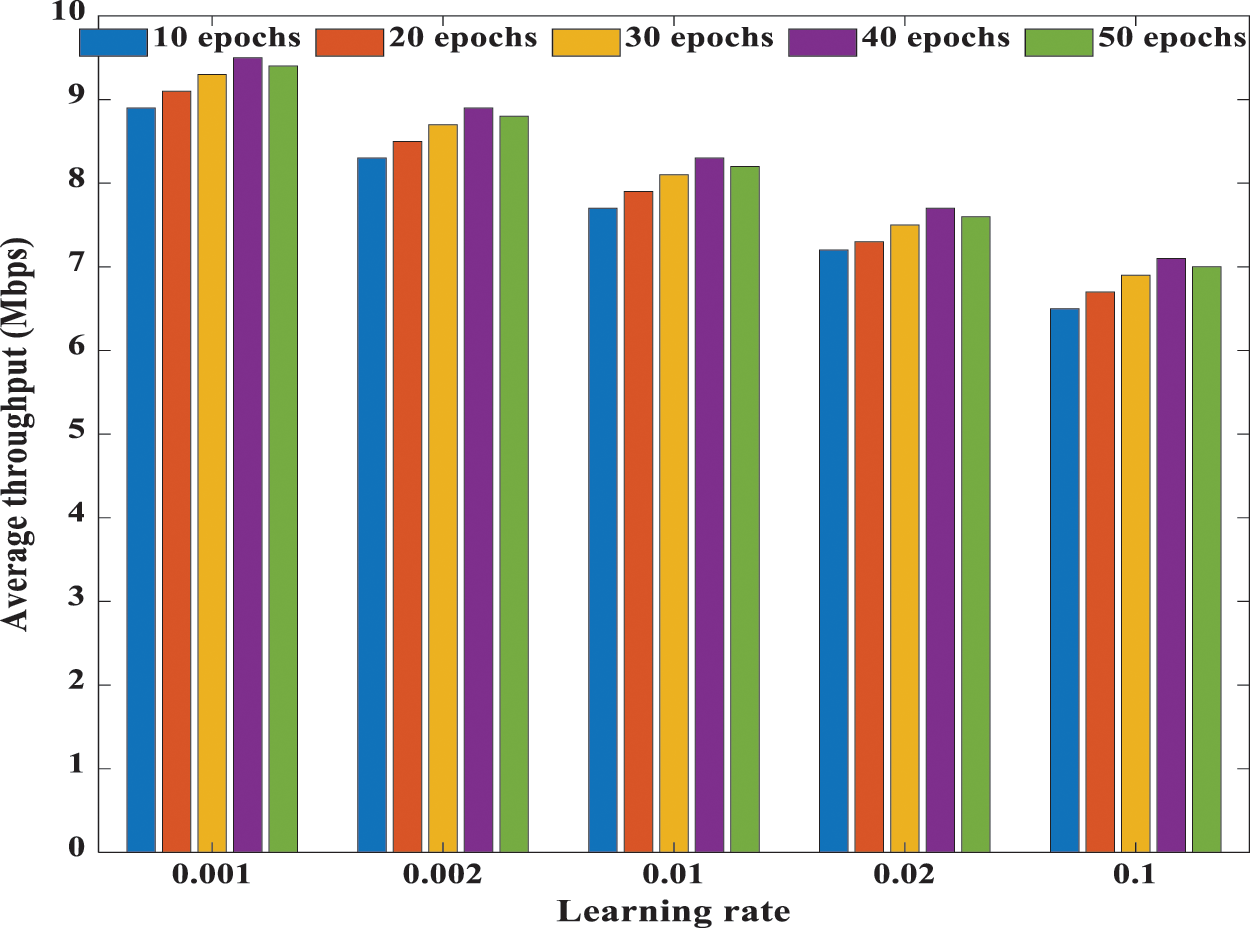
Figure 5: Throughput performance of S-LSTM-UC for different learning rates and the different number of epochs

Fig. 6 provides an insight into the effects of the depth of S-LSTM-UC. At a learning rate of 0.001, we investigate the number of epochs on the MSE and the average throughput performance during the testing phase. As the number of epochs increases, the MSE decreases while the average throughput increases linearly. It is also noteworthy that the MSE and throughput performance tend to improve when the depth of S-LSTM-UC increases, i.e., more hidden layers are utilized. For instance, in the case of 40 epochs, the best MSE and throughput performance are attained when four hidden layers are used. Compared to the case of 4 hidden layers, the average throughput performance of S-LSTM-UC with 2 and 3 hidden layers drops by 9.32% and 6.02%, respectively. However, when the number of hidden layers increases to 5 and 6, the throughput and MSE performance degrade. This phenomenon can be explained as follows. When the number of users and subcarriers are large, NOMA clustering and power allocation will incur higher complexity, and the dimensions of the non-convexity of the UC dataset will increase. Consequently, S-LSTM-UC schemes with 2 and 3 hidden layers fail to fully extract the deep temporal correlations between the multivariate time-series input features and the UC information. On the other hand, S-LSTM-UC with a four-layer configuration can fully exploit the inherent temporal dependency of the time series sequence and generalize well. Nonetheless, further increasing the network depth to 5 and beyond has no favorable effect on the MSE and throughput performance as the model will be over-fitted to the training data.

Figure 6: MSE and average throughput performance of S-LSTM-UC for the different number of epochs and different numbers of hidden layers

In Fig. 7, the average throughput performance of the proposed S-LSTM-UC during the testing phase for different network depths and the different number of hidden layers and hidden nodes is investigated. Judicious selection of the number of hidden layer nodes is essential as the insufficient number of hidden nodes would result in the under-fitted model. The UC scheme would fail to capture the underlying complex structure of the time-series datasets fully. In contrast, excessive hidden nodes may result in overfitting. Since UC in NOMA system is a highly complex problem, the number of hidden layer nodes should be carefully determined to achieve optimum performance. Hence, investigations are carried out by considering 2 to 6 hidden layers and 32 to 56 hidden nodes. The simulations show that the highest average throughput could be attained when 40 hidden nodes are chosen for all the number of hidden layers considered.

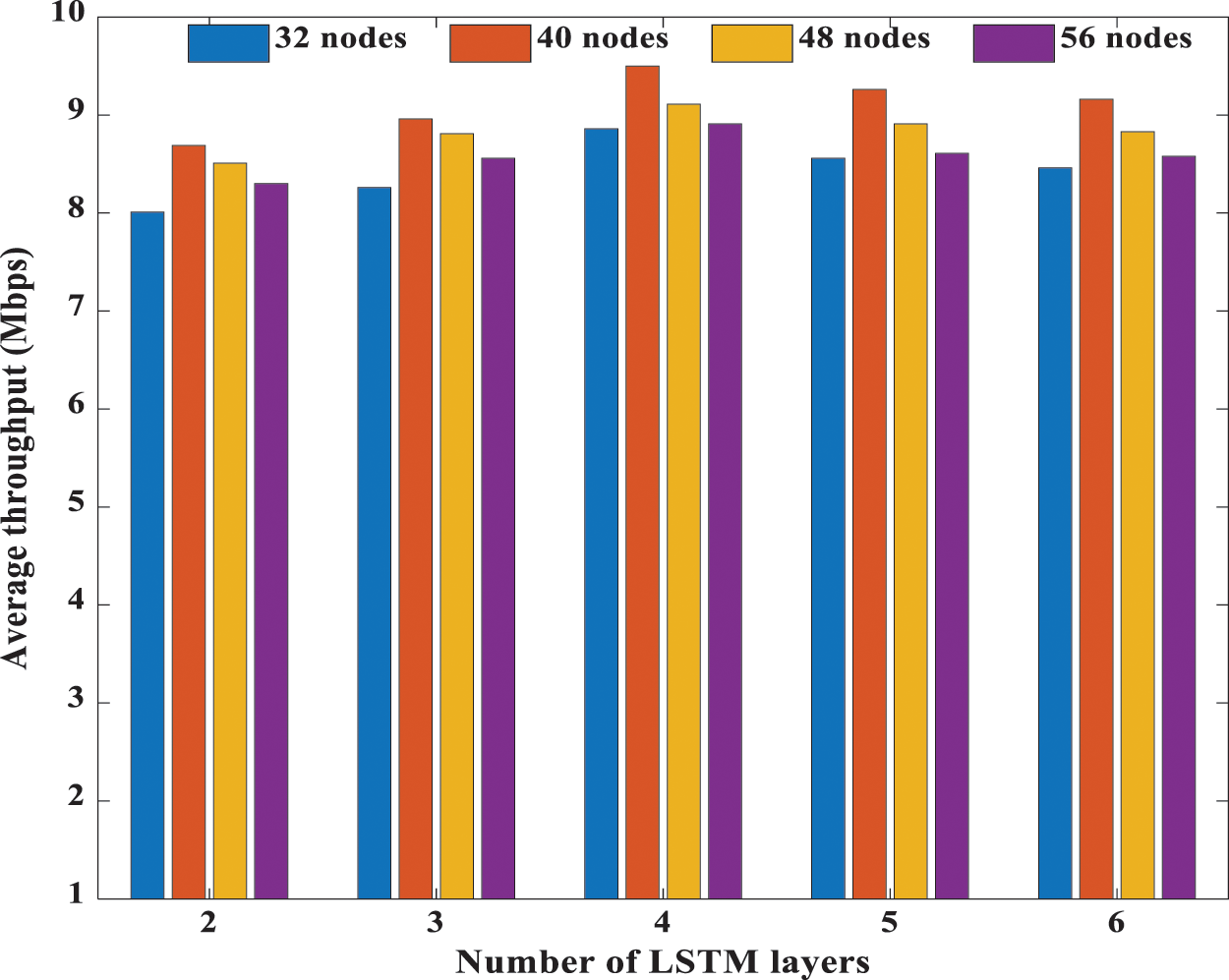
Figure 7: Average throughput performance of S-LSTM-UC for the different number of hidden layers and the different number of hidden layer nodes

Since activation function is one of the essential hyper-parameters in S-LSTM-UC, the effects of 4 well-known activation functions, i.e., ReLu, Sigmoid, Sine and Tanh, on the average throughput performance during the testing phase are investigated in Fig. 8. As illustrated in the figure, the ReLU activation function is the best performer, and the average throughput performance gain of ReLU over other activation functions is increasingly more prominent as the number of users increases. Quantitatively, in the case of 24 users, it can be seen that the ReLu activation function substantially outperforms the Sigmoid, Sine and Tanh counterparts in terms of average throughput by 21.01%, 30.13% and 33.80%, respectively. This observation is because the Sigmoid, Sine, and Tanh functions fail to model the cluster formation precisely because the functions could lead to negative outputs. However, the values of cluster information should always be positive. Conversely, the ReLu function could effectively overcome this issue by only outputting non-negative values. Hence, the ReLu function is recommended for the proposed S-LSTM-UC.

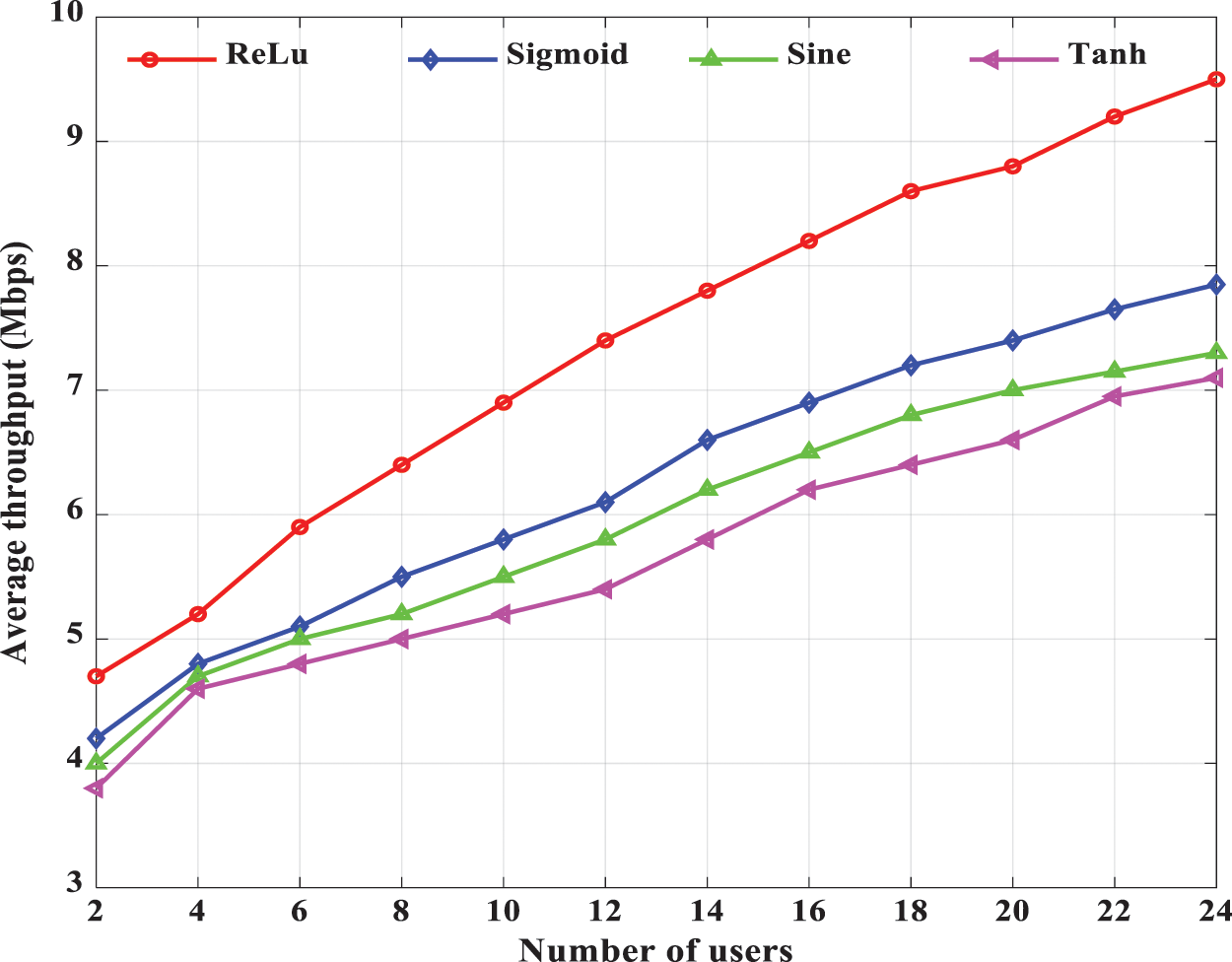
Figure 8: Average throughput performance of S-LSTM-UC for different activation functions and different number of users

In Fig. 9, S-LSTM-UC is compared with ANN-UC to characterize their attainable MSE and throughput performance at continuous time intervals for 24 users during the testing phase. The figure shows that the throughput of S-LSTM-UC continues to increase at continuous time intervals t as the optimality in learning the UC has been improved due to the sequential processing of clustering information. On the other hand, MSE reduces for continuous-time intervals. However, for ANN-UC, the throughput does not significantly improve compared to S-LSTM-UC, as it considers instantaneous time without considering the historical clustering results and the variation of channel gains and power levels.

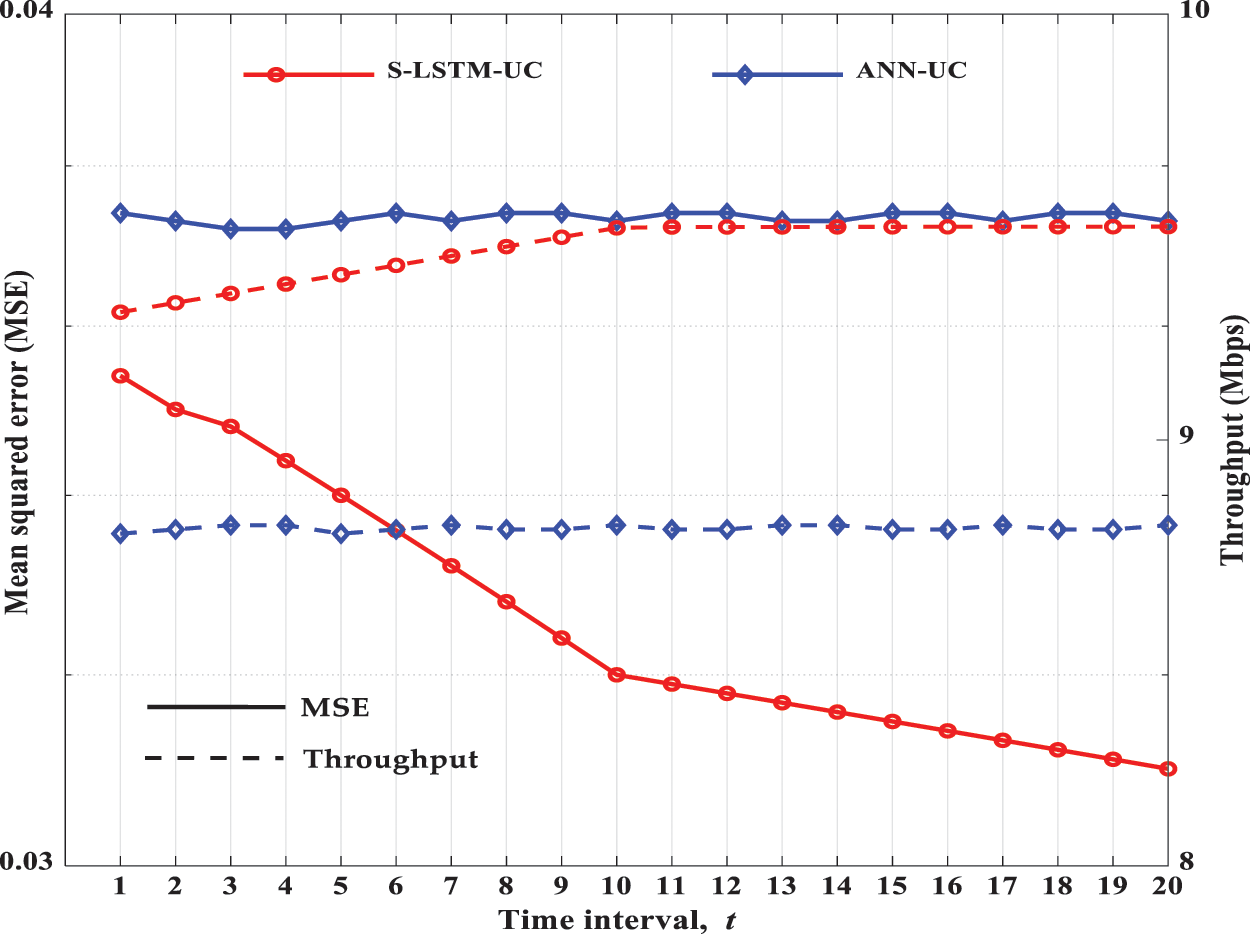
Figure 9: MSE and throughput performance of S-LSTM-UC and ANN-UC at different time intervals

To assess the effectiveness of the proposed S-LSTM-UC scheme, four benchmarked techniques have been identified, i.e., BF-S-UC, ANN-UC, DUC, and OMA. Fig. 10 depicts the comparison of average throughput performance for various techniques considered for the different number of users during the testing phase. The proposed S-LTSM-UC is configured using the best hyper-parameters recommended in the initial analysis in this simulation. The figure shows that the techniques under consideration demonstrate the following increasing order of average throughput performance: B-FS-UC, S-LSTM-UC, ANN-UC, DUC, OMA. As anticipated, the proposed S-LSTM-UC significantly outperforms the OMA, and its average throughput is about five times that of the OMA. Furthermore, it is also noteworthy that S-LSTM-UC can achieve near-optimal average throughput performance, which is approximately 98.94% of B-FS-UC for the different number of users considered. Compared to DUC, S-LSTM-UC can obtain more than 50% of throughput. This performance advantage is attributed to its capability to exploit the users’ channel diversity and heterogeneity fully. Thus, as the number of users in the NOMA system grows, the performance gap between S-LSTM-UC and DUC increases. Owing to the capability of S-LSTM-UC in capturing the deep and complex temporal dynamics of the time-series data via long-term memory cells and its deep architecture, it can improve the throughput performance of ANN-UC by 7%-30%.

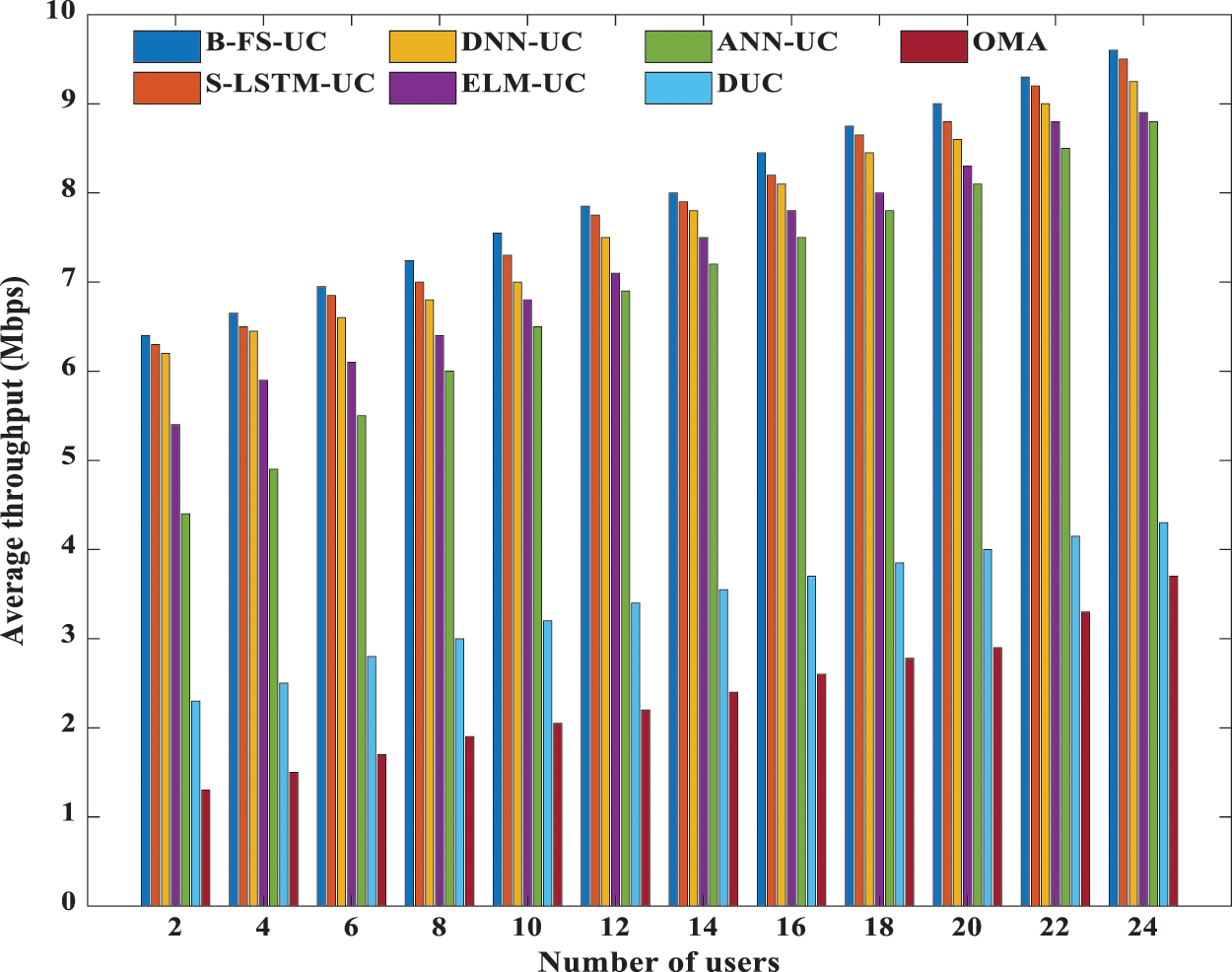
Figure 10: Comparison of throughput performance on the number of users for various UC schemes in NOMA and OMA system

5  Conclusion and Future Work

This work proposes a novel S-LSTM-UC to tackle the UC problem in NOMA 5G systems by capitalizing on the underlying deep temporal dynamics of the time-series inputs captured via long-term memory cells and its deep architecture. The S-LSTM-UC can better characterize the non-linear transformation of diversity in channel gains and powers into cluster formation by including more LSTM layers in the model. Following the cluster formation, a power allocation method is implemented to ensure all users in each cluster achieve the minimum throughput requirement while adhering to the SIC constraint. To optimize the hyper-parameters of the S-LSTM-UC, extensive simulations have been conducted. It is found that the proposed S-LSTM-UC achieves the best performance for all the scenarios considered when it is equipped with four hidden layers and 40 nodes. With these optimal settings, the proposed S-LSTM-UC scheme could significantly outperform the existing schemes and achieve a near-optimal throughput performance, around 98.94% of the throughput attained by the B-FS-UC method. In addition, the robustness of the S-LSTM-UC has also been tested in diverse NOMA deployment scenarios. The results reveal that the proposed method could effectively adapt to different NOMA environments without the need for re-training. In general, S-LSTM-UC is efficient to forecast UC formation based on the time-series data collected over a period of time. To make it more efficient and robust, more stacking LSTM layers can be incorporated, but this will increase the complexity of the model, which will require a longer time to train and test. Furthermore, S-LSTM-UC is sensitive to different random weight initializations. As future work, the proposed S-LSTM can be developed deeper to accurately learn more complex time-series data to make a more precise prediction. To cope with the complexity due to deeper S-LSTM model, some model compression techniques such as pruning can be implemented. Besides, more analysis can be done to maximize the throughput performance and minimize bit error rate and computational complexity.

Funding Statement: This work was funded by Multimedia University under Grant Number MMUI/170084.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  R. Pepper, “Cisco visual networking index: Global mobile data traffic forecast update. cisco, tech. Rep,” 2013. [Online]. Available: https://www.gsma.com/spectrum/wpcontent/uploads/2013/03/Cisco_VNI-global-mobile-data-traffic-forecastupdate.pdf. [Google Scholar]

 2.  D. Zhang, Y. Liu, Z. Ding, Z. Zhou, A. Nallanathan et al., “Performance analysis of non-regenerative massive MIMO-NOMA relay systems for 5G,” IEEE Transactions on Communications, vol. 65, pp. 4777–4790, 2017. [Google Scholar]

 3.  Z. Ding, F. Adachi and H. V. Poor, “The application of MIMO to nonorthogonal multiple access,” IEEE Transactions on Wireless Communications, vol. 15, pp. 537–552, 2016. [Google Scholar]

 4.  K. Lu, Z. Wu and X. Shao, “A survey of nonorthogonal multiple access for 5G,” in 2017 IEEE 86th Veh. Tech. Conf., Toronto, ON, Canada, pp. 1–5, 2017. [Google Scholar]

 5.  L. Dai, B. Wang, Y. Yuan, S. Han, I. Chih-Lin et al., “Nonorthogonal multiple access for 5G: Solutions, challenges, opportunities, and future research trends,” IEEE Communications Magazine, vol. 53, pp. 74–81, 2015. [Google Scholar]

 6.  Z. Ding, F. Adachi and H. V. Poor, “The application of MIMO to nonorthogonal multiple access,” IEEE Transactions on Wireless Communications, vol. 15, pp. 537–552, 2015. [Google Scholar]

 7.  A. Rauniyar, P. E. Engelstad and O. N. Østerbø, “Performance analysis of RF energy harvesting and information transmission based on NOMA with interfering signal for IOT relay systems,” IEEE Sensors Journal, vol. 19, pp. 7668–7682, 2019. [Google Scholar]

 8.  Z. Zhang, H. Sun and R. Q. Hu, “Downlink and uplink nonorthogonal multiple access in a dense wireless network,” IEEE Journal on Selected Areas in Communications, vol. 35, pp. 2771–2784, 2017. [Google Scholar]

 9.  M. B. Shahab, M. Irfan, M. F. Kader and S. Young Shin, “User pairing schemes for capacity maximization in nonorthogonal multiple access systems,” Wireless Communications and Mobile Computing, vol. 16, pp. 2884–2894, 2016. [Google Scholar]

10. H. Zhang, D. -K. Zhang, W. -X. Meng and C. Li, “User pairing algorithm with SIC in nonorthogonal multiple access system,” in 2016 IEEE Int. Conf. on Communications, Kuala Lumpur, Malaysia, pp. 1–6, 2016. [Google Scholar]

11. S. Ali, E. Hossain and D. I. Kim, “Nonorthogonal multiple access (NOMA) for downlink multiuser MIMO systems: User clustering, beamforming, and power allocation,” IEEE Access, vol. 5, pp. 565–577, 2017. [Google Scholar]

12. D. Wan, M. Wen, X. Cheng, S. Mumtaz and M. Guizani, “A promising nonorthogonal multiple access based networking architecture: Motivation, conception, and evolution,” IEEE Wireless Communications, vol. 26, pp. 152–159, 2019. [Google Scholar]

13. Z. Ding, P. Fan and H. V. Poor, “Impact of user pairing on 5G nonorthogonal multiple-access downlink transmissions,” IEEE Transactions on Vehicular Technology, vol. 65, pp. 6010–6023, 2015. [Google Scholar]

14. Z. Ding, M. Peng and H. V. Poor, “Cooperative nonorthogonal multiple access in 5G systems,” IEEE Communications Letters, vol. 19, pp. 1462–1465, 2015. [Google Scholar]

15. Y. Ma, H. Gao, T. Lv and Y. Lu, “Novel user clustering schemes for downlink NOMA system,” in IEEE Military Communications Conference (MILCOM), Baltimore, MD, USA, pp. 191–196, 2017. [Google Scholar]

16. M. S. Ali, H. Tabassum and E. Hossain, “Dynamic user clustering and power allocation for uplink and downlink nonorthogonal multiple access (NOMA) systems,” IEEE Access, vol. 4, pp. 6325–6343, 2016. [Google Scholar]

17. S. P. Kumaresan, C. K. Tan, C. K. Lee and Y. H. Ng, “Adaptive user clustering for downlink non orthogonal multiple access based 5G systems using brute-force search,” Transactions on Emerging Telecommunications Technologies, vol. 31, pp. e4098, 2020. [Google Scholar]

18. S. P. Kumaresan, C. K. Tan, C. K. Lee and Y. H. Ng, “Low-complexity particle swarm optimization based adaptive user clustering for downlink nonorthogonal multiple access deployed for 5G systems,” World Review of Science, Technology and Sustainable Development, vol. 18, pp. 7–19, 2020. [Google Scholar]

19. M. H. Abidia, H. Alkhalefaha, K. Moiduddina, M. Alazabb, M. Khan et al., “Optimal 5G network slicing using machine learning and deep learning concepts,” Computer Standards & Interfaces, vol. 76, pp. 1–15, 2021. [Google Scholar]

20. S. Wang, M. A. Qureshi, L. M. Pechuaán, T. Huynh-The, T. R. Gadekallu et al., “Explainable AI for B5G/6G: Technical aspects, use cases, and research challenges,” arXiv Preprint: arXiv:2112.04698, 2021. [Google Scholar]

21. S. P. Kumaresan, C. K. Tan and Y. H. Ng, “Efficient user clustering using a low-complexity artificial neural network (ANN) for 5G NOMA systems,” IEEE Access, vol. 8, pp. 179307–179316, 2020. [Google Scholar]

22. S. P. Kumaresan, C. K. Tan and Y. H. Ng, “Deep neural network (DNN) for efficient user clustering and power allocation in downlink non-orthogonal multiple access (NOMA) 5G networks,” MDPI Symmetry, vol. 13, pp. 1507, 2021. [Google Scholar]

23. S. P. Kumaresan, C. K. Tan and Y. H. Ng, “Extreme learning machine for fast user clustering in downlink nonorthogonal multiple access (NOMA) 5G networks,” IEEE Access, vol. 9, pp. 130884–130894, 2021. [Google Scholar]

24. H. Jiang and G. Gui, “Channel modelling in 5G wireless communicaton systems,” 1st ed., New York, NY, USA: Springer, pp. 1–194, 2020. [Google Scholar]

25. L. Yao and Y. Guan, “An improved LSTM structure for natural language processing,” in IEEE Int. Conf. of Safety Produce Informatization, Dalian, China, pp. 565–569, 2018. [Google Scholar]

26. C. Lin, Q. Chang and X. Li, “A deep learning approach for MIMO-NOMA downlink signal detection,” MDPI Sensors, vol. 19, pp. 2526, 2019. [Google Scholar]

27. G. Gui, H. Huang, Y. Song and H. Sari, “Deep learning for an effective non orthogonal multiple access scheme,” IEEE Transactions on Vehicular Technology, vol. 67, pp. 8440–8450, 2018. [Google Scholar]

28. J. Thompson, “Deep learning for signal detection in nonorthogonal multiple access wireless systems,” in IEEE Conf. in Emerging Technologies, Glasglow, UK, pp. 1–4, 2019. [Google Scholar]

29. M. AbdelMoniem, S. M. Gasser, M. S. El-Mahallawy, M. W. Fakhr and A. Soliman, “Enhanced NOMA system using adaptive coding and modulation based on LSTM neural network channel estimation,” Applied Sciences, vol. 9, pp. 3022, 2019. [Google Scholar]

30. S. Hochreiter and J. Schmidhuber, “Long short-term memory,” Neural Computation, vol. 9, pp. 1735–1780, 1997. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.