Computers, Materials & Continua DOI:10.32604/cmc.2022.027496
Article

Protected Fair Secret Sharing Based Bivariate Asymmetric Polynomials in Satellite Network

Yanyan Han1,2, Jiangping Yu3, Guangyu Hu4, Chenglei Pan4, Dingbang Xie5, Chao Guo1,2,6,* and Abdul Waheed7

1Department of Electronics and Communication Engineering, Beijing Electronics Science and Technology Institute, Beijing, 100070, China
2State Key Laboratory of Integrated Services Networks, Xidian University, Xi’an, 710126, China
3Department of Cryptography and Technology, Beijing Electronics Science and Technology Institute, Beijing, 100070, China
4Department of Cyberspace Security, Beijing Electronic Science and Technology Institute, Beijing, 100070, China
5School of Communication Engineering, Xidian University, Xi’an, 710126, China
6Institute of Information Engineering, Chinese Academy of Sciences, Beijing, 100093, China
7University of Management Technology, Lahore-Pakistan, 55300, Pakistan
*Corresponding Author: Chao Guo. Email: guo99chao@163.com
Received: 19 January 2022; Accepted: 08 March 2022

Abstract: Verifiable secret sharing mainly solves the cheating behavior between malicious participants and the ground control center in the satellite network. The verification stage can verify the effectiveness of secret shares issued by the ground control center to each participant and verify the effectiveness of secret shares shown by participants. We use a lot of difficult assumptions based on mathematical problems in the verification stage, such as solving the difficult problem of the discrete logarithm, large integer prime factorization, and so on. Compared with other verifiable secret sharing schemes designed for difficult problems under the same security, the verifiable secret sharing scheme based on the Elliptic Curve Cryptography (ECC) system has the advantages of less computational overhead and shorter key. At present, the binary polynomial is a single secret scheme and cannot provide effective verification. Therefore, based on a Protected Verifiable Synchronous Multi Secret Sharing (PVS-MSS) scheme, this paper is designed based on bivariate asymmetric polynomials. The advanced verifiable attribute is introduced into the Protected Secret Sharing (PSS) scheme. This paper extends the protected synchronous multi-secret sharing scheme based on bivariate polynomial design. The ECC system constructs the security channel between the ground control center and participants and constructs the verification algorithm. Through the verification algorithm, any participant can verify the consistency and effectiveness of the secret shadow and secret share received from other participants or presented by the secret distribution center. Therefore, no additional key agreement protocol is required; participants do not need to negotiate the session key for encryption; the secret share polynomial can generate the session key between participants and speed up the secret reconstruction process. The verification stage has lower computational complexity than the verifiable scheme constructed by Rivest Shamir Adleman (RSA) and other encryption methods. Chinese Remainder Theorem (CRT) is used to update the secret shadow. The secret shadow does not need to be updated with the change of the scheme shared secret, and the public value update efficiency is higher. Reduce the complexity of sharing secret updates in a synchronous multi-secret sharing scheme.

Keywords: Multi-secret sharing; binary asymmetric; verifiable synchronization; protected; satellite network

1  Introduction

A Satellite network is a comprehensive information system composed of different types of satellites in different orbits, ground control centers, and user terminals. It has the characteristics of wide coverage and flexible networking and is widely used in military, resource survey, meteorology, and other fields. However, Li et al. proposed a resource allocation scheme [1]. Md introduces a method to save satellite space [2]. However, due to the available deployment of satellites, limited onboard resources, transmission data is easy to be intercepted, and other security threats, the secret protection in the process of satellite transmission has also become particularly important.

In 1979, Shamir and Blakley proposed (t,n) threshold secret sharing theory [3,4]. Which will be a secret D into n shares, as long as there is greater than or equal to t participants can reconstruct secrets D, and less than t participants cannot reconstruct secret D. However, the threshold theory can reconstruct secret D through Lagrange interpolation, but it can not ensure its effectiveness for malicious participants and ground control center fraud. There is no guarantee of its effectiveness. Ghodosi analyzed the schemes of Harn et al., which can not detect cheaters in a wide range in the threshold theory [5,6]. Liu et al. proposed a quadratic polynomial algorithm to identify deception [7]. Lin et al. solved the problem that secret reconstruction is not deceived by releasing secret shadows simultaneously [8]. Han pointed out that Theorem 3 related to asynchronous network attack in secret sharing scheme in Tian et al. is incorrect [9,10]. To solve the problem of dishonest participants releasing false secret shares during secret reconstruction, Harn et al. proposed a synchronous rational secret sharing scheme [11]. Harn proposed a new verifiable multi-secret sharing scheme, while Gu made Harn’s scheme more flexible [12,13]. Lin proposes a verifiable identity method [14]. Jin et al. proposed a secret sharing scheme based on images, but it costs a lot [15]. Javeed et al. proposed a method to implement ECC [16]. Xue et al. proposed a group key protocol. They shared group key switching authentication between satellites based on secret sharing technology, but they can not verify the secret share and have a high overhead [17].

Many secret sharing technologies exist in satellite network secret sharing schemes, such as literature [18]. We need to ensure the security of multiple nodes in the communication requirements of satellite networks. And the secret-sharing verification shall be distributed in the ground control center and each node satellite. We propose a verifiable secret sharing scheme based on binary asymmetric polynomials. At present, verifiable secret sharing schemes based on bivariate polynomial design are all single secret sharing schemes [19]; Secondly, the primary purpose of the design is to construct an efficient verifiable secret sharing protocol in the presence of different numbers of cheaters. Research status of secret sharing scheme based on bivariate polynomial design: PSS scheme lacks various additional attributes to resist separate spoofing attacks and is suitable for different scenarios [20]; Reference [21,22], a simple multi-secret sharing scheme, can’t resist the invasion of semi-honest people; The Verifiable Multi-Secret Sharing (VMSS) in reference [23] has no protected characteristics. The primary purpose of this scheme research is the verifiable attribute introduced into a secret sharing scheme with protected features like the PSS scheme. Secondly, it extends the similar design of [24] synchronous multi-secret sharing scheme to make it more widely used. The scheme has the following advantages:

■   There is no need for a secure channel between that secret distribution center and the participant.

■   No additional key agreement protocol is needed: Participants do not need to negotiate extra session keys for encryption. The secret share polynomial can generate session keys among participants, thus accelerating the process of secret reconstruction.

■   Protected: The pairwise session key generated by a share polynomial can protect the information exchange between participants in the process of secret reconstruction and resist external attacks.

■   ECC realizes verifiable attributes. The verification phase has lower computational complexity than verifiable schemes constructed by RSA and other encryption methods.

■   Synchronous multi-secret sharing: the number of optional shared secrets in the secret distribution center is flexible. A single secret reconstruction process can reconstruct multiple shared secret values according to different situations.

Although literature [25] proposed placing some calculations below the ground or LEO, it does not introduce security issues. Therefore, to ensure security under the same premise, we achieve less computing cost, shorter key, and save system resources according to the characteristics of limited satellite resources and limited bandwidth. The ECC system constructs the safety channel between the ground control center and the node satellite. Using CRT to update the secret shadow, the ground control center only needs to publish part of the public value, which makes the public value update more efficient.

2  Preliminary Knowledge

2.1 Shamir Threshold Theory

2.1.1 Key Construction

Let P be a prime number and k be the key k∈GF(P), and the key distribution center D randomly selects an t−1 order polynomial b(x) on GF(P), and k=b(0). The key distribution center calculates ki=b(i), i=1,2,3,…,n, ki distributed to participants as secret shares Pi.

2.1.2 Key Reconstruction

When there are t participants P1,P2,P3,…,Pt. We can reconstruct secret k by Lagrange interpolation, and the formula is:

k=∑i=1tki∑i=1,j≠it−ji−j(1)

2.2 CRT

Any two prime n1,n2,…,ns, any a1,a2,…,as to make ∃a∈Z content with

{a=a1modn1a=a2modn2⋮a=asmodns(2)

Set up Mi=M/ni,ti=Mi−1modni, then

a=∑i=1stiMiai(3)

3  The Project Design

3.1 System Model

Fig. 1 describes the process of participants receiving secrets. Participants’ environment is changeable, such as the ocean, wild, etc. Of course, there are various participants, such as individual participants on the ground, ground satellite stations, or satellites in orbit in the air. First, the ground control center distributes secret shares and sends broadcast parameters to Geostationary Earth Orbiting (GEO). Then, GEO sends it to each participant or Low Earth Orbiting (LEO) through the link to get the corresponding secret share. At this time, each participant will generate a unique session key and communicate with each other. The secret can be reconstructed under two different thresholds when ensuring that the participants are honest.

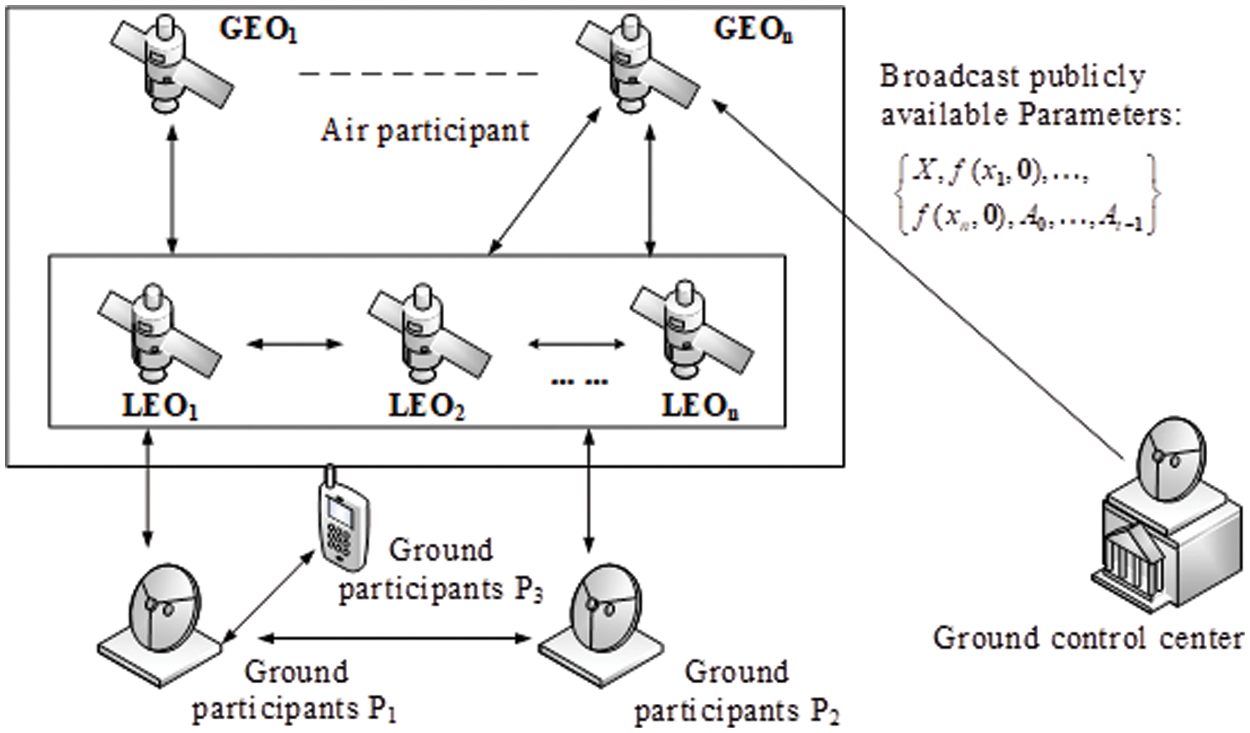
Figure 1: Satellite network secret sharing scheme model

3.2 System Initialization

Suppose there is a trusted ground control center D, a set of actors {P1,P2,…,Pn}. E is an elliptic curve defined on a finite field Fq. Where q is a large prime number that is not equal to 2 or 3. T∈E(Fq) is the base point of an elliptic curve E with upper order ℓ. Public information is {Fq,E,T}. D select prime p0<ℓ, n different positive integers p1,p2,…,pn meet the following properties:

■   p0<p1,i=1,2,…,n.

■   p1,p2,…,pn mutual prime. And greater than 1.

Perform the following steps between D and Pi(i∈[1,n]) to transmit the master secret shadow p1,p2,…,pn to the participants (for the multi-purpose secret sharing scheme, this stage only needs to be performed once.):

■   Step 1:D selects integer d as its private key, satisfies 1<|d|<ℓ, calculates, and discloses G=dT as its public key.

■   Step 2: Each participant Pi,1≤i≤n randomly selects an integer ni as its private key, satisfies 1<|ni|<ℓ, calculates Ti=niT as its public key, and makes it public. IDi is the identity of participant Pi,1≤i≤n. To ensure the inconsistency between different participants Ti and IDi, D will request to update Ti and IDi until when i≠j,IDi≠IDj and Ti≠Tj take (Ti,IDi) public information for Pi.

■   Step 3: Both D and Pi can use their private keys and public information to calculate public keys Gi=dniT=(xi,yi).

■   Step 4:D calculates and broadcasts ci=pixi,i∈[1,n],Gi=dniT=(xi,yi).

■   Step 5: When any participant Pi receives ci, it can use its private key ni to get Gi=dniT=(xi,yi) and then calculate pi=cixi−1i∈[1,n].

Finally, the ground control center D and participant Pi got the primary secret shadow pi.

3.3 The Secret to Distribute

Suppose D wants to share k secrets s0,s1,…,sk−1 and perform secret distribution in the following two cases.

Case 1: When the number of secrets to be shared, k is less than or equal to the threshold value t.

Step 1: D constructs the following binary asymmetric polynomials with the order x as t−1 and order y as h−1,h>t(t−1):

f(x,y)=s0+s1x+⋯+sk-1xk−1+a0,0xk+⋯+at−k−1,0xt−1+a0,1y+a1,1xy+⋯+   at−1,1xt−1y+⋯+a0,h−1yh−1+a1,h−1xyh−1+⋯+at−1,h−1xt−1yh−1 mod l   =(s0+s1x+⋯+skxk−1+a0,0+⋯+at−k−1)y0+(a0,1+a1,1x+⋯+at−1,1xt−1)y1+⋯+   (a0,h−1+a1,h−1x+⋯+at−1,h−1xt−1)yh−1 mod l(4)

There are k coefficients about the x term in f(x,y) and {s0,s1,⋯,sk−1} is a shared secret set among them.

Step 2: D select n random integers p0≤yi<pi,i∈[1,n], so that xi generated by xi=yimodpi is n unequal integers.

Step 3: D calculate the secret share f(xi,0)modℓ,i∈[1,n], A0=s0T,A1=s1T,…,Ak−1=sk−1T and Ak=a0,0T,Ak+1=a1,0T,…,At−1=at−k−1,0T.

Step 4: D calculates the unique integer Xmod∏i=1npi, calculates any X≡yimodpi using CRT and value set {y1,y2,…,yn} and value set {p1,p2,…,pn}.

Step 5: D calculates the secret polynomials gIDi1(x)=f(x,IDi)modℓ, gIDi2(y)=f(IDi,y)modℓ encrypts them with the participant’s public key and elliptic curve cryptography, and sends them to the participant {P1,…,Pn}.

Step 6: Open {X,f(x1,0),f(x2,0),…,f(xn,0),A0,A1,…,At−1}.

Case 2: The number of secrets to be shared k is greater than the threshold value t.

Step 1: D constructs the following binary asymmetric polynomials with the order x as t−1 and order y as h−1:

f(x,y)=s0+s1x+⋯+sk−1xk−1+a0,1y+a1,1xy+⋯+ak−1,1xk−1y+⋯+   a0,h−1yh−1+a1,h−1xyh−1+⋯+ak−1,h−1xk−1yh−1 mod l   =(s1+s2x+⋯+skxk−1)y0+(a0,1+a1,1x+⋯+ak−1,1xk−1)y1+⋯+   (a0,h−1+a1,h−1x+⋯+ak−1,h−1xk−1)yh−1 mod l(5)

There are k coefficients about the x term in f(x,y), and {s0,s1,⋯,sk−1} is a shared secret set among them.

Step 2: D select n random integers p0≤yi<pi,i∈[1,n], so that xi generated by xi=yimodpi is n unequal integers.

Step 3: D calculate the secret share f(xi,0)modℓ,i∈[1,n], A0=s0T,A1=s1T,…,Ak−1=sk−1T.

Step 4: D calculates the unique integer Xmod∏i=1npi, and calculates any X≡yimodpi using CRT and value set {y1,y2,…,yn} and value set {p1,p2,…,pn}.

Step 5: D calculates the secret polynomials gIDi1(x)=f(x,IDi)modℓ, gIDi2(y)=f(IDi,y)modℓ, encrypts them with the participant’s public key and elliptic curve cryptography, and sends them to the participant {P1,…,Pn}.

Step 6: D calculates h1=f(1,0),h2=f(2,0),…,hk−t=f(k−t,0) and discloses it in [26,27].

Step 7: Open {X,f(x1,0),f(x2,0),…,f(xn,0),A0,A1,…,Ak−1}.

3.4 Secret Verification

Because the PVS-MSS scheme has protected properties, resistance to reconstruct phase external attacks, but internal attackers, will reduce the schema’s safety. Because internal attackers can be arbitrary tamper with the secret shadow, whether conspired with the collusion attack, internal attackers benefit maximization (the remaining honest refactoring can’t get the Shared secret). Therefore, the scheme of PVS-MSS has two different secret numbers. Taking k≤t as an example, we use elliptic curve addition structure to realize the following verification algorithm:

■   Step 1: Any refactor Pi can verify whether the secret share f(xi,0)modℓ disclosed by the ground control center D is correct by the following verification equation.

f(xi,0)T=∑jt−1xijAj,i=1,2,…,n(6)

■   Step 2: The PVS-MSS scheme does not lose generality. Any reconstructor Pi can verify the secret shadow xj sent by other participants through the following verification equation.

f(xj,0)T=∑i=0t−1xjiAi,j=1,2,…,t,i≠j(7)

3.5 Secret Refactoring

In the secret reconstruction stage, if the set of reconstructors participating in the protocol is {P1,P2,…,Pm}.

Step 1: Any two reconstructors Pi and Pj can obtain the shared session key by combining the identity information IDi and IDj calculating their secret share polynomial:

ki,j=gIDi1(IDj)=gIDj2(IDi)=f(IDi,IDj)modℓ(8)

Step 2: Any reconstructor Pi uses ki,j to calculate ci,j=Encki,j(xi). ci,j=Encki,j(xi) will send Pj through the authenticated broadcast channel ϑ. Encki,j(xi) represents symmetric encryption. Similarly, any reconstructor Pj calculates cj,i=Encki,j(xi) using the key ki,j and sends it to Pi through the authenticated broadcast channel ϑ.

Step 3: When the reconstructor Pi receives ciphertext cj,i,j∈{1,2,…,u}∖{i}, Pi can decrypt ciphertext Decki,j(cki,j)=xj separately, Decki,j(cj,i) represents the ciphertext cj,i decrypted with kj,i.

Step 4: Each refactorer is divided into the following two cases to reconstruct the shared secret value:

■   Case 1: When the number of shared secrets k is less than or equal to the threshold value t:

f(x,0)=s0+s1x+⋯+sk−1xk−1+a1,0xk+⋯+at−k−1,0xt−1 mod l=∑i=1tf(xi,0)∏j=1,j≠itx−xjxi−xj mod l(9)

■   Case 2: When the number of shared secrets k is greater than the threshold value t:

f(x,0)=s0+s1x+⋯+sk−1xk−1 mod l=∑i=1tf(xi,0)∏j=1,j≠itx−xjxi−xj+∑i=1k−tf(i,0)∏j=1,j≠ik−tx−ji−j mod l(10)

The coefficient set {s0,s1,…,sk−1} in f(x,0) is the reconstructed secrets.

3.6 The Secret to Update

When the PVS-MSS scheme shares a secret update, the polynomial constructed by the synchronous multi-secret sharing scheme also needs to be updated, and the public value of the scheme also needs to be updated. YCH and other schemes adopt a bivariate univariate function to ensure that the ground control center D does not need to re-issue secret shadow to each participant for the next new secret sharing [28]. The master secret shadow of the scheme is also multi-purpose without initialization. Only the ground control center D needs to update some public values. In particular, the new X is very high. According to the CRT theorem in Section 2.2 of this paper, X=∑i=1nyiMiM′imod(∏i=1npi),Mi=∏j=1,j≠inpj requirement MiMi′≡1modpi once the value MiMi′,i=1,2,…,n is calculated by D, can be saved and reused. Each secret update stage, D only needs to select a new yi and use MiMi′ to calculate a new X disclosure.

4  Project Analysis

4.1 Correctness Analysis

Theorem 4.1: The PVS-MSS scheme has any reconfigurable secret greater than or equal to t reconfigurator.

Prove: Suppose t≤m≤n reconstructor sets {P1,P2,…,Pm} to want reconstruct the shared secret, in which any refactorers Pi and Pj content ∀i,j∈[1,m] and i≠j. When the number of shared secrets k is less than or equal to the threshold value t, the order f(x,0) is known to be t−1, and any reconstructor Pi uses ki,j encryption to calculate ci,j=Encki,j(xi) and sends it to Pj through the authenticated broadcast channel ϑ. Similarly, any reconstructor Pj calculates cj,i=Encki,j(xi) using the key ki,j and sends it to Pi through the authenticated broadcast channel ϑ. When the reconstructor Pi receives the ciphertext cj,i,j∈{1,2,…,u}∖{i}. Pi can decrypt the ciphertext Decki,j(cj,i)=xj. Separately because the polynomial f(x,0) containing the secret value is a univariate polynomial, Pi gets xj,j=1,2,…,m,j≠i, f(x1,0),f(x2,0),…,f(xm,0) disclosed by ground control center is exactly m pairs of interpolation points on f(x,0). Using Lagrange interpolation polynomial, the unique f(x,0) can be obtained from Eq. (9). Similarly, when the number of shared secrets k is greater than the threshold value t, it is known that order f(x,0) is k−1, after any refactorer Pi obtains m−1xj through the secret refactoring phase. Combined with the public value of the ground control center, it is exactly the m+k−t pairs of interpolation points on f(x,0). Using Lagrange interpolation formula and secret sharing homomorphism, get a unique f(x,0) from Eq. (10). The coefficient set {s0,s1,…,sk−1} in f(x,0) is the reconstructed secrets.

4.2 Safety Analysis

Theorem 4.2: When k≤t or k>t, When the scheme satisfies the condition th>(t−1)(t+h) or kh>(t−1)(t+h)+(k−t), any access set composed of less than t refactorers cannot be reconstructed. And no one can get any secret information.

Prove: The secret share f(IDi,0)modp is generated by the secret polynomial. The secret share is used as the interaction value during reconstruction. The secret shadow is the public value IDi; the secret share of the PVS-MSS scheme is the public value f(xi,0)modℓ, and the secret shadow xi is the interaction value during reconstruction. Under the two schemes, the information obtained by the internal conspirators is of the same nature and the same attack methods, and both are to reconstruct f(x,0). Therefore, the proof process of this theorem is the same as that of Theorem 4.1 in Section 4.1 of this paper, so it will not repeat here.

Theorem 4.3: The main secret shadow p1,p2,…,pn in the scheme cannot calculate from the public parameter G,Ti,ci.

Prove: Suppose an attacker A wants to calculate the main secret shadow p1,p2,…,pn from the public parameter G=dT,Ti=niT,ci=pixdniT. Unless A can calculate dniT=(xdniT,ydniT) from Ti=niT,G=dT, which is equivalent to solving the computational Diffie-Hellman problem on elliptic curves or directly solving Ti=niT,G=dT is equivalent to solving the discrete logarithm problem of an elliptic curve (ECDLP). We can’t solve these problems under the current computing power.. Therefore, only after the participant Pi uses its private key ni to calculate niG=nidT, can it obtain the corresponding master secret shadow pi.

Theorem 4.4: It is computationally difficult to calculate the secret s0,s1,…,sk−1 from the public value A0,A1,…,Ak−1.

Prove: Ai=siT,Ai∈<T> is the public value used in the verification phase. If the attacker A wants to obtain si directly from the public value Ai=siT. In that case it is equivalent to solving the discrete logarithm problem on an elliptic curve (ECDLP). So it isn’t easy to calculate secrets s0,s1,…,sk−1.

Theorem 4.5: The scheme resists internal and external attacks in the reconstruction process.

Prove: Suppose there is an internal attacker A, who has identity information IDi and secret shadow xi. His attack method is to provide a false secret shadow xi′ to the honest reconstructor in the process of secret reconstruction. The values f(xi,0),i=1,2,…,n and Ak,k=1,2,…,t−1 used for verification in the verification phase of the scheme are both public. At this time, any reconstructor Pi calculates R=∑k=0t−1xi′kAk and checks whether the equation R=f(xi,0)T is true. If inequality R≠f(xi,0)T holds, then A is identifie as an internal attacker.

In the reconstruction process, The encryption of the session key ki,j protects the interaction between any two reconstructors Pi and Pj. The secret polynomial generates the session key. Therefore, the external enemy without any secret share polynomial information cannot participate in the reconstruction process to steal the secret.

5  Scheme Comparison and Performance Analysis

The PVS-MSS scheme’s main parameters, characteristics, and cost are compared with existing schemes. Compared with synchronous multi-secret sharing schemes such as [21,28–31], the PVS-MSS scheme introduces verifiability. There is no need to maintain an additional secure channel between the ground control center and participants. Compared with the verifiable multi-secret sharing schemes in [23,32–35], PVS-MSS scheme participants do not need additional key negotiation mechanisms, which reduces the actual operating cost of the scheme. In the PVS-MSS scheme, the security of the safety channel between the ground control center and participants is based on the Discrete Logarithm Problem of Elliptic Curve (ECDLP). In [32], security is based on the Discrete Logarithm Problem (DLP). Under the same security level, the required parameter bit length is smaller. The amount of calculation is smaller. For example, under the security of 256 bits of the symmetric key, the minimum bit length of the parameter ℓ of the PVS-MSS scheme is 512, while under the same security level, the bit length of Rivest Shamir Adleman/Digital Signature Algorithm (RSA/DSA) module is at least 15360. When the key length is the same, there is little difference between ECC and RSA. Therefore, the PVS-MSS scheme requires fewer resources and faster calculation speed based on the ECC initialization and verification stage. Compared with [23], when k>t, if k is close to t, the updated public value of PVS-MSS scheme is less. As shown in Tab. 1, the main parameters and attributes of synchronous multi-secret sharing are compared in detail. The scheme in this paper has the characteristics of shadow update, verifiability, and less public values.

In the initialization stage of the PVS-MSS scheme, the ground control center and participant calculate Gi,Ti,G by elliptic curve scalar multiplication. Therefore, there are 3n+1 elliptic curve scalar multiplication operations. This calculation process is for the reusability of secret shadows and only needs to be performed once. In the secret distribution stage, the ground control center executes the algorithm in two different cases, including the secret polynomial calculation of each participant. At this time, only the main operations are considered. The two different cases are t and k times elliptic curve scalar multiplication, respectively. In the secret verification phase, each participant needs t elliptic curve scalar multiplication operations to verify a single secret shadow. It needs t2 elliptic curve scalar multiplication operations to verify its correctness and other secret shadows. In the secret reconstruction stage, the PVS-MSS scheme shares the secret on the coefficient of f(x,0), so the calculation cost in the secret reconstruction stage is the same as that in the scheme [23,28,30,31,33,36], both of which are Lagrange interpolation calculations, and the worst is Lagrange interpolation of k points. Suppose TM is the operation time of elliptic curve scalar multiplication. TH is the operation time of bivariate one-way function. TL(t) is the operation time of t point interpolation. TE is the BP operation time on the elliptic curve. Teq(t) is the solution operation time of t linear equations. TP is the modular power operation time. Tab. 2 shows the comparison of computing overhead. We can find the running time required by the PVS-MSS scheme. The scheme calculates the overhead in the distribution phase; when k≤t, it is tTM; when k>t, it is kTM. The scheme calculates the cost of the verification phase; when k≤t, it is t2TM; when k>t, it is k2TM. This scheme calculates the cost of the reconstruction phase; when k≤t, it is TL(t); when k>t, it is TL(k).

6  Parameter Analysis

6.1 Secret Share Leakage Probability of Satellite Nodes

Reference [38] shows that the probability of secret share leakage of a single satellite is an exponential function, expressed by f(x), and the function varying with time x is:

f(x)=1−e−λx(11)

We can see from Fig. 2 that the abscissa shown in the figure below is time, and the ordinate is leakage probability. With the increase of time X, the leakage probability also increases, and the lower the leakage rate λ at the initial time, the lower the leakage probability at the same time.

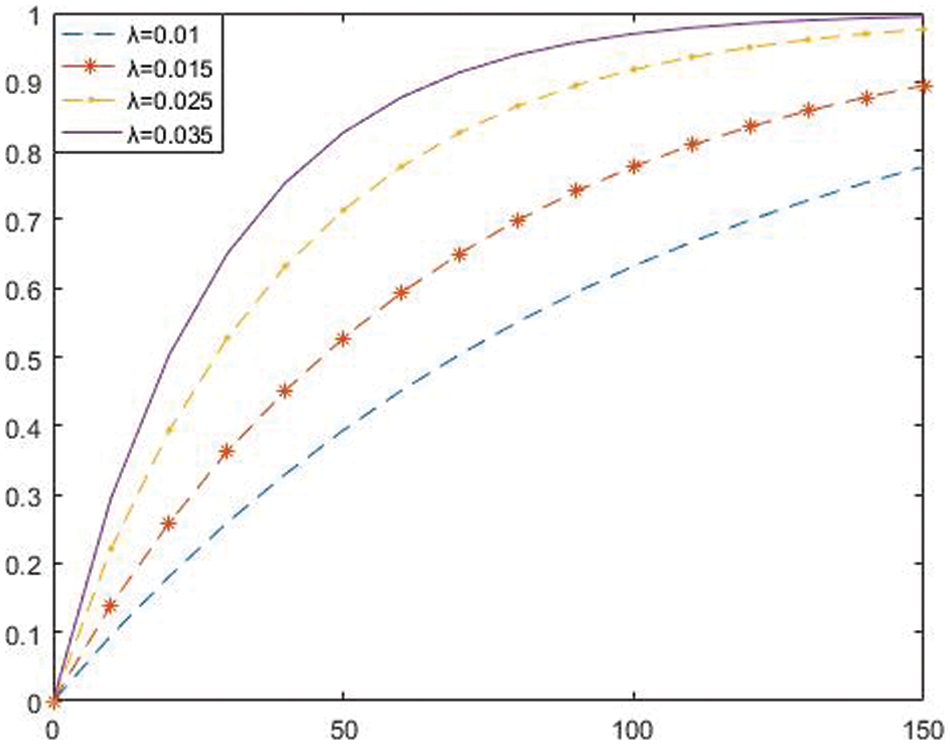
Figure 2: Secret failure rate

6.2 Satellite Network Security Quality

Reference [39] shows that the key of each satellite network node is different. Hence, the attack on a satellite nodes is a a Bernoulli process, and the probability that the secret share obtained by the attacker is less than t in one cycle:

P=∑i=0t−1Cai(1−e−λF)i(e−λF)a−i(12)

When a=25, λ=0.015, Fig. 3 shows the impact of the threshold value t, and key cycle F update on satellite network security. P increases with the increase of t, and the threshold value t also increases with the increase of cycle F.

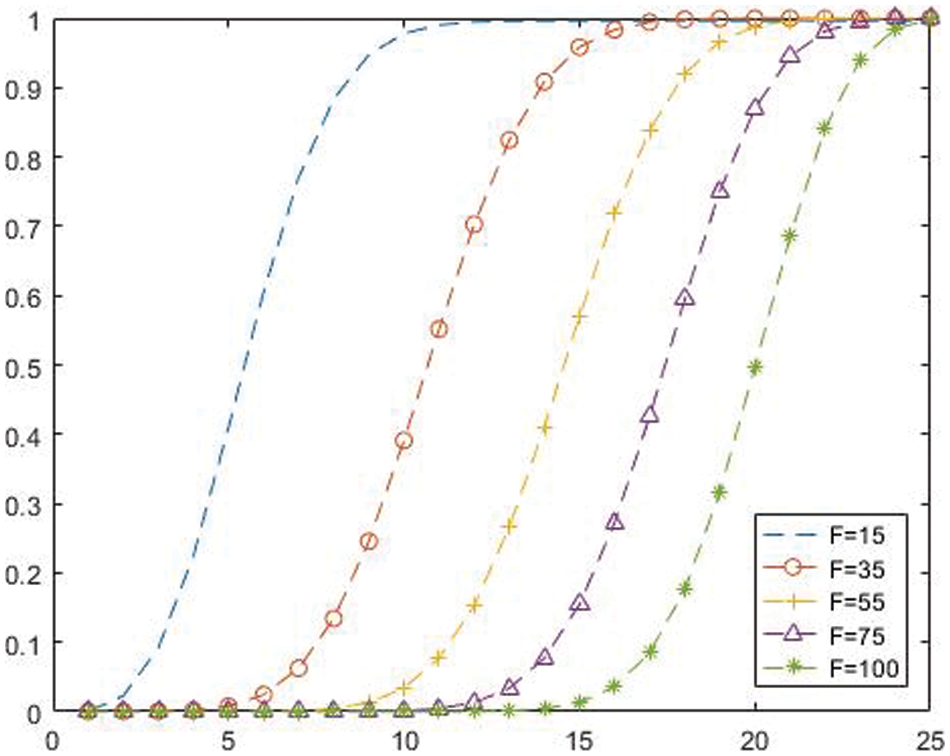
Figure 3: Satellite network security quality

7  Conclusion

It is advanced to propose a protected synchronous multi-secret sharing scheme based on binary asymmetric polynomials. It is very advanced to introduce verifiable attributes into the PSS scheme. This scheme extends the protected synchronous multi-secret sharing scheme based on binary polynomial design. This scheme is suitable for the secret sharing of satellite networks. The ECC system is used to interact with the main secret shadow safely, and a verification algorithm is constructed. Through the verification algorithm, any participant can verify the consistency and effectiveness of the secret shadow received from other participants or the secret share presented by the ground control center. We discuss the correctness of the algorithm in Section 4.1 of this paper. Whether the number of shared secrets is greater than or less than the threshold, we can get the unique polynomial from the Lagrange difference formula and the additive homomorphism of secret sharing f(x,0). We discussed security in Section 4.2 of this article. We discuss the security of the algorithm from four aspects. We use ECDLP to ensure that attackers cannot calculate secret shadows from public values; we prove the effectiveness of resisting internal and external attacks in the reconstruction process. In Section 4.3, we discuss the computational overhead of existing schemes. Our algorithm is based on ECDLP for protection, compared with RSA/DSA; when the key is the same at the same security level, the amount of calculation is not different. This scheme uses ECC in the initialization and verification phase, which requires fewer resources and faster computing speed. The Lagrange difference calculates the cost in the secret reconstruction phase, and the worst is the Lagrange difference of k points. The system simulation and other compilation will be completed in further work. The ground control center does not directly issue the secret shadow but uses CRT to calculate the unique public value X. Participants can calculate the required secret shadow through the main secret shadow and X. When the shared secret needs to be updated, the participant’s main secret shadow and private key do not need to be updated. The public value X update is very efficient, reducing the complexity of sharing secret updates in a synchronous multi-secret sharing scheme, ensuring the security of secrets, and saving satellite network resources. Our scheme can send messages in satellite networks. We can also use it in key management, secure multi-party computing, image, and audio secret sharing. Our scheme is also very suitable for situations where specific participants are present simultaneously. The secret share polynomial can also generate the session key to protect the information exchange between participants. In this way, the participants can communicate without redistributing the key in the secret distribution center, which significantly improves the security of the session and reduces the time of generating the session key.

Acknowledgement: We gratefully acknowledge anonymous reviewers who read drafts and made many helpful suggestions.

Funding Statement: This work is supported by The State Key Laboratory of Integrated Services Networks, Xidian University (ISN22-13).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Y. Li, J. Xie, M. Xia, Q. Li, M. Li et al., “Dynamic resource pricing and allocation in multilayer satellite network,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3619–3628, 2021. [Google Scholar]

 2.  M. A. Ullah, T. Alam, A. F. Almutairi and M. T. Islam, “Low profile uhf antenna design for low earth-observation cubesats,” Computers, Materials & Continua, vol. 71, no. 2, pp. 2533–2542, 2022. [Google Scholar]

 3.  A. Shamir, “How to share a secret,” Communications of the ACM, vol. 22, no. 11, pp. 612–613, 1979. [Google Scholar]

 4.  G. R. Blakley, “Safeguarding cryptographic keys,” in Int. Workshop on Managing Requirements Knowledge (MARK), New York, NY, USA, pp. 313–318, 1979. [Google Scholar]

 5.  H. Ghodosi, “Comments on Harn–Lin’s cheating detection scheme,” Designs Codes and Cryptography, vol. 60, no. 1, pp. 63–66, 2011. [Google Scholar]

 6.  L. Harn and C. Lin, “Detection and identification of cheaters in (t, n) secret sharing scheme,” Designs Codes and Cryptography, vol. 52, no. 1, pp. 15–24, 2009. [Google Scholar]

 7.  Y. Liu, C. Yang, Y. Wang, Z. Lei and W. Ji, “Cheating identifiable secret sharing scheme using symmetric bivariate polynomial,” Information Sciences, vol. 453, no. 1, pp. 21–29, 2018. [Google Scholar]

 8.  H. Y. Lin, L. Harn, “Fair reconstruction of a secret,” Information Processing Letters, vol. 55, no. 1, pp. 45–47, 1995. [Google Scholar]

 9.  L. Harn, “Comments on ‘fair (t, n) threshold secret sharing scheme’,” IET Information Security, vol. 8, no. 6, pp. 303–304, 2014. [Google Scholar]

10. Y. Tian, J. Ma, C. Peng and J. Qi, “Fair (t, n) threshold secret sharing scheme,” IET Information Security, vol. 7, no. 2, pp. 106–112, 2013. [Google Scholar]

11. L. Harn, C. Lin and Y. Li, “Fair secret reconstruction in (t, n) secret sharing,” Journal of Information Security and Applications, vol. 23, pp. 1–7, 2015. [Google Scholar]

12. L. Harn, “Secure secret reconstruction and multi-secret sharing schemes with unconditional security,” Security and Communication Networks, vol. 7, no. 3, pp. 567–573, 2014. [Google Scholar]

13. W. Y. Gu, F. Y. Miao and X. T. He, “Fair secret sharing scheme based on bivariate symmetric polynomials,” Computer Engineering and Applications, vol. 52, no. 13, pp. 38–42+109, 2016. [Google Scholar]

14. L. Mei, C. Xu, L. Xu, X. Yu and C. Zuo, “Verifiable identity-based encryption with keyword search for IoT from lattice,” Computers, Materials & Continua, vol. 68, no. 2, pp. 2299–2314, 2021. [Google Scholar]

15. X. Jin, L. Su and J. Huang, “A reversible data hiding algorithm based on secret sharing,” Journal of Information Hiding and Privacy Protection, vol. 3, no. 2, pp. 69–82, 2021. [Google Scholar]

16. K. Javeed, X. Wang and M. Scott, “High performance hardware support for elliptic curve cryptography over general prime field,” Microprocessors and Microsystems, vol. 51, no. 6, pp. 331–42, 2017. [Google Scholar]

17. K. Xue, W. Meng, H. Zhou, D. S. L. Wei and M. Guizani, “A lightweight and secure group Key based handover authentication protocol for the software-defined space information network,” IEEE Transactions on Wireless Communications, vol. 19, no. 6, pp. 3673–3684, 2020. [Google Scholar]

18. L. Zhang, Y. Wang and H. Zhu, “Safeguarding UAV-enabled wireless power transfer against aerial eavesdropper: A colonel blotto game,” IEEE Wireless Communications Letters, vol. 11, no. 3, pp. 503--507, 2021. [Google Scholar]

19. L. L. Yu and W. Z. Du, “Secret sharing scheme based on symmetric bivariate polynomial,” Computer Engineering and Applications, vol. 56, no. 13, pp. 120–123, 2020. [Google Scholar]

20. L. Harn, C. F. Hsu, Z. Xia and J. W. Zhou, “How to share secret efficiently over networks,” Security and Communication Networks, vol. 2017, pp. 1–6, 2017. [Google Scholar]

21. T. Zhang, X. H. Ke and Y. X. Liu, “(t, n) multi-secret sharing scheme extended from Harn-Hsu’s scheme,” Eurasip Journal on Wireless Communications and Networking, vol. 2018, no. 1, pp. 71, 2018. [Google Scholar]

22. L. Harn, C. F. Hsu, “(t, n) multi-secret sharing scheme based on bivariate polynomial,” Wireless Personal Communications, vol. 95, pp. 1495–1504, 2017. [Google Scholar]

23. Maryam, G. S., Mojtaba, B., Christophe et al., “Threshold verifiable multi-secret sharing based on elliptic curves and Chinese remainder theorem,” IET Information Security, vol. 13, no. 3, pp. 278–284, 2019. [Google Scholar]

24. D. Tang and H. P. Shu,“Bivariate polynomial based secret sharing technology study,” Computer Applications and Software, vol. 29, no. 7, pp. 112–114, 2012. [Google Scholar]

25. L. Zhang, L. Hong, C. Guo, H. T. Xu, L. Y. Song et al., “Satellite-aerial integrated computing in disasters: User association and offloading decision,” in Proc. IEEE Int. Conf. on Communications (ICC), Dublin, Ireland, pp. 554–559, 2020. [Google Scholar]

26. R. L. Rivest, A. Shamir and L. Adleman, “A method for obtaining digital signatures and public-key cryptosystems,” Communications of the ACM, vol. 21, no. 2, pp. 120–126, 1978. [Google Scholar]

27. T. Elgamal, “A public key cryptosystem and a signature scheme based on discrete logarithms,” IEEE Transactions on Information Theory, vol. 31, no. 4, pp. 469–472, 1985. [Google Scholar]

28. C. C. Yang, T. Y. Chang and M. S. Hwang, “A (t, n) multi-secret sharing scheme,” Applied Mathematics and Computation, vol. 151, no. 2, pp. 483–490, 2004. [Google Scholar]

29. C. W. Chan and C. C. Chang, “A scheme for threshold multi-secret sharing,” Applied Mathematics and Computation, vol. 166, no. 1, pp. 1–14, 2005. [Google Scholar]

30. L. J. Pang, Y. Liu and Y. M. Wang, “An efficient. Threshold multi-secret sharing scheme,” Chinese Journal of Electronics, vol. 34, no. 4, pp. 587–589, 2006. [Google Scholar]

31. X. W. Zhong, L. Z. Xiong and Z. H. Xia, “A secure visual secret sharing scheme with authentication based on QR code,” Journal on Big Data, vol. 3, no. 2, pp. 85–95, 2021. [Google Scholar]

32. J. Shao and Z. Cao, “A new efficient (t, n) verifiable multi-secret sharing (VMSS) based on YCH scheme,” Applied Mathematics and Computation, vol. 168, no. 1, pp. 135–140, 2005. [Google Scholar]

33. J. Zhao, J. Zhang and R. Zhao, “A practical verifiable multi-secret sharing scheme,” Computer Standards & Interfaces, vol. 29, no. 1, pp. 138–141, 2007. [Google Scholar]

34. J. Shao, “Efficient verifiable multi-secret sharing scheme based on hash function,” Information Sciences, vol. 278, no. 1, pp. 104–109, 2014. [Google Scholar]

35. M. H. Dehkordi and S. Mashhadi, “An efficient threshold verifiable multi-secret sharing,” Computer Standards & Interfaces, vol. 30, no. 3, pp. 187–190, 2008. [Google Scholar]

36. N. Wang, Y. Y. Cai, J. Fu and X. Q. Chen, “Information privacy protection based on verifiable (t, n)-Threshold multi-secret sharing scheme,” IEEE Access, vol. 8, pp. 20799–20804, 2020. [Google Scholar]

37. S. J. Wang, Y. R. Tsai and C. C. Shen, “Verifiable threshold scheme in multi-secret sharing distributions upon extensions of ECC,” Wireless Personal Communications, vol. 56, no. 1, pp. 173–182, 2011. [Google Scholar]

38. H. F. Chen, W. D. Zhao and G. B. Xi, “Security analysis for proactive secret sharing system,” Zhejiang Daxue Xuebao (Gongxue Ban)/Journal of Zhejiang University, vol. 40, no. 8, pp. 1358–1357, 2006. [Google Scholar]

39. C. Y. Luo, W. Li, H. L. Li and B. Jian, “Measurement method for space networks authenticated key security under distributed CA,” Dianzi Yu Xinxi Xuebao/Journal of Electronics and Information Technology, vol. 31, no. 10, pp. 2316–2320, 2009. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.