Computers, Materials & Continua DOI:10.32604/cmc.2022.027532
Article

Power Allocation in NOMA-CR for 5G Enabled IoT Networks

Mohammed Basheri1, Mohammad Haseeb Zafar1,2,3,* and Imran Khan3

1Department of Information Technology, King Abdulaziz University, Jeddah, 21589, Saudi Arabia
2Cardiff School of Technologies, Cardiff Metropolitan University, Cardiff, CF5 2YB, UK
3Department of Electrical Engineering, University of Engineering & Technology, Peshawar, 25120, Pakistan
*Corresponding Author: Mohammad Haseeb Zafar. Email: m.h.zafar@ieee.org
Received: 20 January 2022; Accepted: 16 March 2022

Abstract: In the power domain, non-orthogonal multiple access (NOMA) supports multiple users on the same time-frequency resources, assigns different transmission powers to different users, and differentiates users by user channel gains. Multi-user signals are superimposed and transmitted in the power domain at the transmitting end by actively implementing controllable interference information, and multi-user detection algorithms, such as successive interference cancellation (SIC) is performed at the receiving end to demodulate the necessary user signals. In contrast to the orthogonal transmission method, the non-orthogonal method can achieve higher spectrum utilization. However, it will increase the receiver complexity. With the development of microelectronics technology, chip processing capabilities continue to increase, laying the foundation for the practical application of non-orthogonal transmission technology. In NOMA, different users are differentiated by different power levels. Therefore, the power allocation has a considerable impact on the NOMA system performance. To address this issue, the idea of splitting power into two portions, intra-subbands and inter-subbands, is proposed in this study as a useful algorithm. Then, such optimization problems are solved using proportional fair scheduling and water-filling algorithms. Finally, the error propagation was modeled and analyzed for the residual interference. The proposed technique effectively increased the system throughput and performance under various operating settings according to simulation findings. A comparison is performed with existing algorithms for performance evaluation.

Keywords: NOMA; wireless networks; power domain; 5G networks

1  Introduction

To achieve the demands for higher spectral efficiency, massive user connectivity, and lower latency, the heterogeneous networks will become the basic networking form of fifth-generation (5G) technology. The heterogeneous network refers to multiple microcells overlapped and covered on a macro cell [1,2]. Compared with macrocells, the microcells have lower transmission power and greater density and allows the reuse of network resources. Using certain interference management methods, a heterogeneous structure can significantly increase the system capacity [3,4]. Load imbalance is a severe problem in heterogeneous networks, that is, most users in the network are more inclined to connect to a macro base stations with a higher power, resulting in small cells with low-load and insufficient use of resources [5].

The commonly used solution is to artificially expand the coverage area of the microcell and summarize the edge users into the microcell service so that resources can be reused between multiple cells, improve the performance of the entire network and the edge users of the microcell [6]. On this basis, if multiple users are served in the same resource dimension, the network capacity can be further improved [7]. With the rapid growth of user service requirements and the number of users, how to further increase the throughput of the microcell has become a key concern of the academic and industrial circles. Multiple access technology has always played an important role in the development of wireless communications [8]. To ensure good system throughput while maintaining a low cost of the reception, the industry proposes to adopt a new multiple access multiplexing method, namely, non-orthogonal multiple access (NOMA) [9]. In mobile communications from 1G to 4G, Orthogonal Multiple Access (OMA) technologies have been applied which are frequency division multiple access (FDMA), time division multiple access (TDMA), code division multiple access (CDMA), and orthogonal frequency division multiple access (OFDMA) technology [10].

Moreover, due to the emergence of new services, the number of terminal connections has also shown rapid growth [11]. To avoid interference, the number of users that can be carried simultaneously by traditional orthogonal multiple access (OMA) is limited by the number of resources and it has been unable to support such a huge number of connections. The 5G introduces NOMA to handle diverse connection application scenarios and increase the spectrum efficiency to safeguard users’ QoS [12]. NOMA actively introduces interference information at the transmitter which is the fundamental distinction between multiple users share frequency resources and distinguish users only by power [13]. Users with good channel conditions are allocated less power while users with poor channel conditions are allocated more power [14]. The base station sends the signal to the user using superposition coding. At the receiving end, only the successive interference cancellation (SIC) method can be used to separate the signals of multiple users. Therefore, in comparison, although the strength of the useful signal is reduced, the channel resources that can be accessed by each user increases and the NOMA system can obtain a higher system capacity. Reference [15] proposed a power allocation algorithm to improve the energy efficiency of the NOMA system. Literature [16,17] studied in detail the power allocation algorithm to maximize fairness among users. In [18], the authors presented a proportional fairness-based resource allocation strategy that maximizes the user fairness by deploying the least fairness in multiplexed users. However, the resultant objective function is non-convex and it must be changed to convex form using the best Karush-Kuhn-Tucker (KKT) constraints as it has higher computational complexity and poor practicability. Reference [19] proposed fixed power allocation (FPA) and fractional transmission power allocation (FTPA) algorithms with lower complexity. However, the FPA algorithm did not consider the actual channel quality, and the throughput performance was poor. The FTPA algorithm considers the issues such as channel quality and path loss, but due to the simple power allocation method, it’s performance still needs to be improved. Reference [20] also shows that in terms of spectrum efficiency, NOMA performance is 30% higher than traditional OMA.

The user clustering and power allocation issues of the NOMA system have received extensive attention, and many scholars have conducted in-depth studies. The proportional fair scheduling algorithm [21] has been proven to achieve a better balance between the system capacity and user fairness by maximizing the product of the average user throughput in the cell, that is, user fairness can be achieved at the expense of some system performance. Therefore, most of the literature has adopted this algorithm when studying the NOMA system. Reference [22] studied the NOMA system based on proportional fair scheduling and introduced three power allocation algorithms, namely iterative water-filling (WF), FTPA and FPA. Under the condition that the transmission power of the base station is limited at the same time as the QoS of each user, the authors in [23] studies the optimal power allocation scheme to maximize the total throughput of two matched users. Reference [24] aims to improve the spectrum efficiency and edge user throughput at the same time using an iterative WF algorithm for power allocation, which has better performance but higher complexity. Different from [24], the authors in [25] proposed a step-by-step power allocation scheme, that is, first allocate the base station transmit power to each spectrum resource block and then used the FTPA on each resource block. For simplicity, it does not consider the instantaneous characteristics of the channel. The total power allocated to each resource block is equal, which obviously cannot achieve the optimal performance.

In order to overcome the limitations of the above literature, this study presents a novel algorithm. The main contributions of this article are as follows:

•   According to different user channel conditions, an iterative WF scheme is implemented between all frequency bands for power allocation, and then user matching and power allocation are performed in each frequency band according to the proportional and fair scheduling.

•   Considering the factors such as deep fading, there may be errors in the process of signal demodulation and separation.

•   This paper simulates the error-free propagation model and error propagation model.

After simulation analysis, the proposed technique significantly reduces complexity while increasing system throughput and ensuring user fairness, and the two propagation models outperform the power allocation scheme in [25].

2  System Model

Suppose a cellular system has a base station (BS), and there are K users in the cell evenly distributed in the coverage of the base station. The total bandwidth of the system is Wtot, which is equally divided into S channels. The base station transmits power is Ptot. In this paper, both the base station and the user are equipped with an antenna. Let Us={k1,k2,…,kn(s)} represents the set of users superimposed on frequency band s, and n(s) represents the number of users on frequency band s. The base station allocates different powers to users and then superimposes the signals for transmission. The superimposed signal xs on frequency band x is expressed as follows:

xs=∑i=1n(s)⁡ps,kixs,ki(1)

where, xs,ki denotes the i-th user’s broadcast signal on the s frequency band, and ps,ki represents the transmit power of the i-th user on the frequency band s.

At the receiving end, the received signal of user km on frequency band s is:

ys,km=hs,kmxs+ws,km=hs,km(ps,kmxs,km+∑i=1,i≠mn(s)⁡ps,kixs,ki)+ws,km(2)

where them, hs,km denotes the integrated channel gain from the BS to km user on s frequency band, including Rayleigh fading and path loss, and ws,km represents additive white Gaussian noise, and the power is ns,km. ∅s,km=|hs,km|2/ns,km represents the noise normalized channel gain of the user km on the frequency band s.

2.1 Error-Free Propagation Model

Successive interference cancellation technology allows the signal to be detected and separated at the receiving end, and the process is shown in Fig. 1. To briefly introduce the SIC process, suppose there are two users k1 and k2 in a cell. The power allocated by the base station to users is p1 and p2 respectively. User k1 is close to the base station and the channel gain is h1, while user k2 is far away from the base station whose gain is h2, and h1>h2. Because the allocated power of user k1 is small, user k2 can treat the interference signal of user k1 as noise and directly demodulate its signal. The user k1 must first go through the SIC process to detect, reconstruct, and eliminate the signal of user k2, and finally demodulate its signal.

Figure 1: User detection process in SIC

If user k1 demodulates the signal of user k2 without errors and no residual interference, i.e., an ideal model of error-free propagation, then the data transmission rate of user k1 is:

R1=log2(1+p1|h1|2n12)(3)

The data transmission rate of user k2 is:

R2=log2(1+p2|h2|2p1|h2|2+n22)(4)

2.2 Error Propagation Model

The above model is based on the user k1 can correctly demodulate the signal of user k2, i.e., user k1 does not interfere with user k2 when demodulating its signal. This is a strong assumption. Many factors affect signal detection and demodulation, such as deep fading. Assuming that the signal detection and separation process of user k2 is not perfect, there will be interference when demodulating its signal, i.e., the error propagation model [26], then the data transmission rate of user k1 will become:

R1′=log2(1+p1|h1|2θp2|h1|2+n12)(5)

where, θ represents the error propagation factor, and 0≤θ≤1 and θ=0 means no error propagation. θ=1 means the worst case, i.e., user k1 fails to separate and delete the information of user k2, then it is considered as the interference for user k1, which is no different from not participating in the SIC process.

The above procedure is only the deployment of SIC process for two users. The multi-user SIC process is to demodulate the user signal level by level according to the noise normalized channel gain decreasing order of each user. The process is similar to Fig. 1, so it is not repeated here [27–30].

Assuming that each user in the cell can demodulate its signal correctly, i.e., there is no error propagation, the throughput of user km on frequency band s is:

Rs,km=WtotS(1+|hs,km|2ps,km∑i=1,|hs,km|2<|hs,ki|2n(s)⁡|hs,km|2ps,ki+ns,ki)(6)

Then, the throughput of the entire cell is:

R=∑j=1S⁡∑i=1n(j)⁡Rj,ki(7)

From the analysis of Eq. (7), it can be seen that user pairing and power allocation determine the throughput of the cell. Therefore, in order to improve the throughput of the cell, it is necessary to study the problem of user pairing and power allocation.

3  Analysis of Algorithms

3.1 Power Distribution Between Bands

The power allocation problem of the NOMA system is an optimization problem, which can be expressed by Eq. (8):

max∑j=1S⁡∑i=1n(j)⁡Rj,ki

Subject to:

Pj,ki≥0;j∈[1,s],i∈[1,n(i)]

∑j=1S⁡∑i=1n(j)⁡Pj,ki≤Ptot(8)

The optimal iterative water-filling method adopted in [24] can solve the above optimization problem, but this algorithm is an iterative power distribution algorithm between all subbands and users, and its complexity will increase with the increase of superimposed users in the subbands. A substantial increase is difficult to achieve in engineering, but its performance is undoubtedly better. Therefore, this paper draws on the idea of this algorithm, uses this algorithm to distribute power between the subbands, and then uses a power distribution algorithm based on proportional fair scheduling to distribute the power of users in the subband.

To complete the power allocation problem between subbands, Eq. (8) is rewritten as:

max∑j=1S⁡WtotSlog2(1+pjhj2Nj)

Subject to:

∑j=1S⁡pj≤Ptot(9)

where, hj represents the equivalent gain of the subband j, i.e., the channel gain of the subscriber with the optimal channel characteristics set on the subband j, and Nj represents the noise power.

Aiming at the solution of Eq. (9), the Lagrangian function Q is determined as follows:

Q=∑j=1S⁡log2(1+pjhj2Nj)−λ(∑j=1S⁡pj−Ptot)(10)

where, λ represents the Lagrangian multiplier.

Take the partial derivative of pj on both sides of Eq. (10) and make it equal to zero to obtain:

∂Q∂pj=1ln⁡2(hj2/Nj1+pjhj2/Nj)−λ=0(11)

From Eq. (11), we can get:

pj=1λln⁡2−Njhj2(12)

The expression of pj has been given, and the power of the subband can be obtained by iteration. In order to simplify Eq. (12), let β denote λln⁡2, and the specific iteration process is as follows in Algorithm 1.

At this point, the first step of sub-band power allocation is completed, and then only scheduling and power allocation are required for users within each sub-band.

3.2 Proportional Fair Scheduling Algorithm

In a NOMA system, a subband resource can serve multiple users at the same time. As a result, studying user scheduling tactics is critical for enhancing the spectrum efficiency. The proportional fair scheduling strategy has been proven to achieve a good balance between spectrum efficiency and user fairness. Therefore, this paper uses such a strategy for user matching. Its definition is as follows:

T(k;t+1)=(1−1tc)T(k;t)+1tc1S∑s=1S⁡Rs(k;t)(13)

where, tc represents the average time window length, t represents the frame time subscript, and Rs(k;t) represents the instantaneous data rate of user k on the subband s in the t-th frame time, which can be calculated by Eq. (6) if the user k is not scheduled, it is zero; T(k;t)represents the average throughput of user k for some time before time t.

The goal of the multi-user scheduling technique is to optimize the productivity of cell users’ average throughput. As a result, user scheduling and power allotment must adhere to the following guidelines:

fs(Us)=∏k∈Us⁡(1+Rs(k;t)(tc−1)T(k;t))(14)

Uc=arg⁡maxfs(Us)(15)

where, fs(Us) represents the user scheduling criterion, which can be maximized using the user matching and the allocation of base station transmit power; Uc represents the user set that makes the user scheduling criterion reach the maximum.

The remaining problem is to redistribute the allocated sub-band power to the users in Uc. In a non-orthogonal multiple access system, due to the existence of interference between users, power allocation not only affects the throughput of a certain user but also affects the throughput of other users. Therefore, power allocation is closely related to user matching. Therefore, the method in this paper is to allocate power for each user set first and then calculate the user scheduling criteria to obtain the largest user combination. The flow chart of the whole process is shown in Fig. 2.

Figure 2: Power distribution process using NOMA

3.3 In-Band Power Distribution

At present, many scholars have researched power allocation schemes, mainly including the following [10]: full-space search power allocation scheme, iterative water-filling power allocation scheme, fixed power allocation scheme, and fractional transmission power allocation scheme. The first two power distribution schemes are quite complex, so this paper has carried out a simulation analysis on the fixed power distribution scheme and the fractional transmission power distribution scheme. The idea of the fixed power allocation algorithm is to arrange the users in the user concentration in descending order of normalized channel gain, and then allocate power. Let δk denote user k after sorting, then the power allocated to user δk is:

ps(δk)=αFPAps(δk+1)(16)

where, αFPA(0≤αFPA≤1) represents a fixed power allocation factor, and the system throughput and user fairness change with the change of αFPA. With the increase of αFPA, users with poorer channel conditions can obtain more power. Because the power allocation is fixed, users at the receiving end know their power allocation factors, which can reduce the complexity of the receiver, which is also very helpful for the design of the SIC receiver.

The idea of the fractional transmit power allocation algorithm comes from the fractional transmit power control of the uplink of the LTE system [29]. Different from the fixed power allocation scheme, the fractional transmit power allocation scheme needs to display the control signaling to the user The power information is delivered to different users.

The power allocated to the k-th user is expressed as:

ps(k)=ps∑j∈Us⁡(hj2/Nj)−αFTPA(hk2Nk)−αFTPA(17)

where, αFTPA(0≤αFTPA≤1) represents the fractional transmit power allocation factor. When αFTPA = 0, the power distribution scheme evolves into an even distribution. With the increase of αFTPA, more power will be allocated to users with lower channel gain. Nj represents the noise power in the signal received by user j, and hj represents the channel gain.

3.4 Complexity Analysis

The iterative water-filling scheme in [24] requires iterative power allocation between all sub-band candidate users, taking into account the channel conditions of all candidate users. The proposed algorithm only needs to perform iterative power allocation between all sub-bands, and only considers the channel gains of users with the best channel conditions in a certain sub-band. In the process of power secondary allocation, a total of 2S times of multiplication operations and S times of addition operations, theoretically the complexity will be reduced by half. (See Fig. 10).

4  Simulation Results

4.1 Simulation Parameters

The proposed approach is simulated and examined using MATLAB software in this paper, and the algorithm from the literature [24,25] is compared. The simulation parameter settings are shown in Tab. 1.

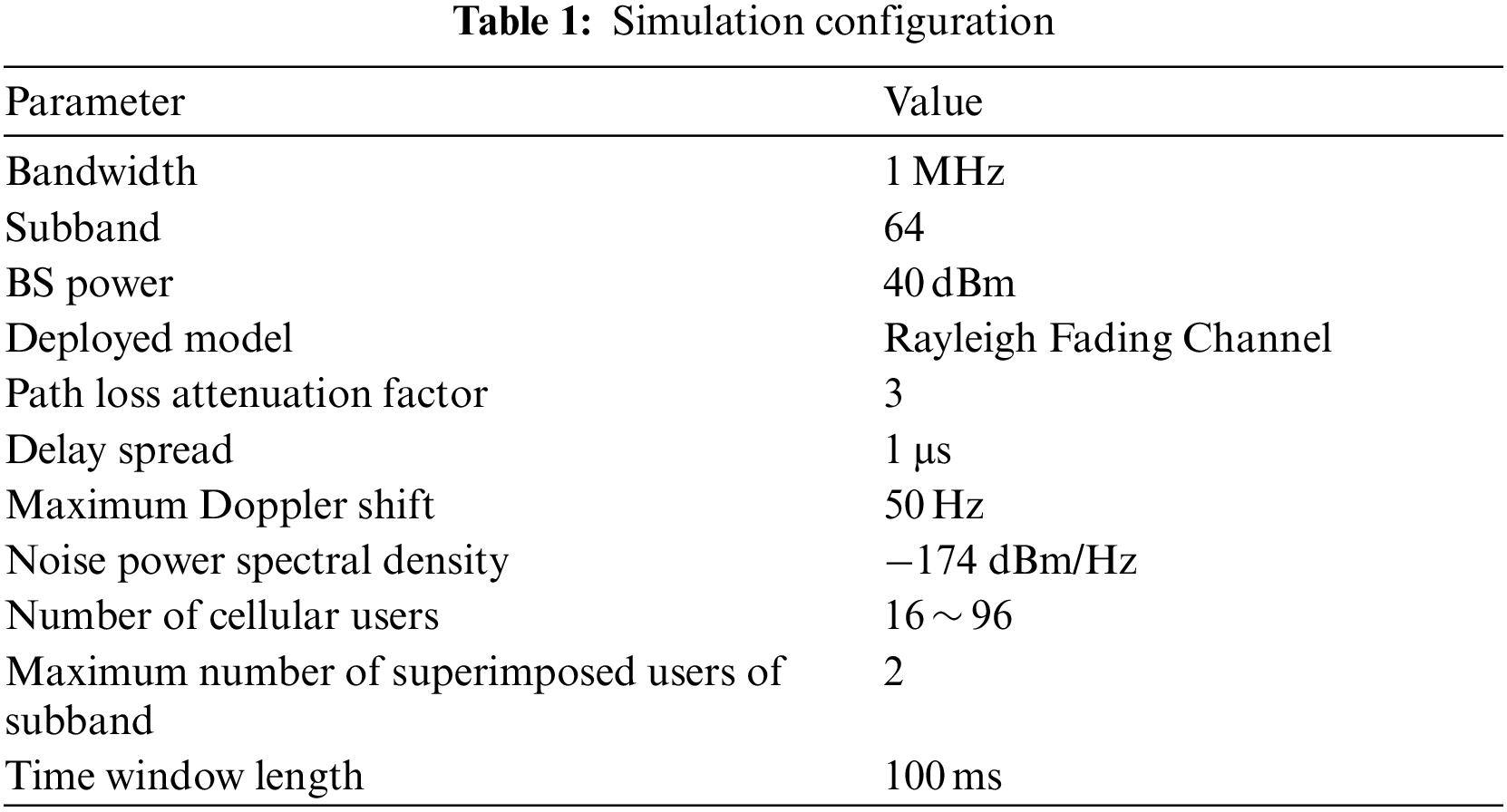
Assuming that the coverage of a cell’s base station is 500 m, the cell users are randomly and evenly distributed. To fully demonstrate the advantages of NOMA and make full use of spectrum resources, the number of cell users is set to 16, 32, 48, 64, 80, 96, and the maximum sub-band overlap number of users is 2. The total bandwidth of the system is 1 MHz, the number of subbands is 64, and the total transmission power of the base station is 40 dBm. The channel model adopts the Rayleigh fading channel, the time delay is extended to 1 μs, the maximum Doppler shift is 50 Hz, and the path loss attenuation factor is 3, which determines the loss of base station signal transmission to the user terminal, and the noise power spectral density is −174dBm/Hz. The length of the time window tc is 100 ms

4.2 Simulation Results

Under three distinct methods, Fig. 3 depicts the link between cell throughput and the number of cell users. The power allocation plan is a fractional transmission power allocation (FTPA) and its factor is αFTPA. The error propagation factor θ is fixed. It is 0.1. The results show that, the cell throughput increases as the number of cell user’s increases. Also, when the number of users is the same, the proposed algorithm is significantly better than references [10,18,24,25] algorithms. Compared with [25], the performance of the improved error-free propagation model is improved by about 10.8%. The performance of the error propagation model is improved by about 3.2%. Although the performance is not as good as the algorithm in [24], the complexity is greatly reduced.

Fig. 4 shows the relationship between the average throughput of cell users and the fractional power allocation factor αFTPA in the fractional transmit power allocation scheme. The number of users is fixed at 10, and the error propagation factor θ is fixed at 0.1. The algorithms of literature [10,18,24,25] are used for comparison with the proposed two propagation models. The results show that, with the increase of αFTPA, the average throughput of cellular users decreases. Because consumers with inferior channel conditions will receive more power, this is the case. Influenced by edge users, the system capacity decreases, but user fairness is guaranteed. Also, the performance of the two propagation models of the proposed algorithm is significantly better than the algorithms in [10,18,24,25], because the existing algorithms do not consider the time-varying characteristics of the channel during the initial power allocation, and evenly allocates the base station transmit power to each sub-resource blocks, and the improvement of system performance is limited.

Figure 3: Comparison of total cell throughput of algorithms against the number of users

Figure 4: The relationship between average cell throughput and fractional transmit power allocation factor αFTPA with K = 10

Fig. 5 shows the relationship between the average throughput of cell users and the fixed power allocation factor αFPA in the fixed power allocation scheme. The number of users is fixed at 10, and the error propagation factor θ is fixed at 0.1. The results show that, with the increase of αFPA, the throughput of the proposed algorithm has improved. This is because the proposed algorithm can well balance the user fairness and system performance, so the average throughput of cellular user’s increases. Also, the performance of the two propagation models of the proposed method is superior than references [10,18,24,25] algorithms. The reason has been explained in the analysis of Fig. 4, so it is not repeated here.

Figure 5: The relationship between average cell throughput and fixed power allocation factor αFPA with K = 10

Fig. 6 compares the throughput of the algorithms against the error propagation factor. Under the condition that the number of users is fixed at 10, two propagation models of the improved power allocation scheme are simulated. It can be seen from Fig. 6 that the cell throughput decreases as the error propagation factor increases. This is because the larger θ, the more serious the error propagation. As a result, users with poor channel conditions have a harder time detecting and distinguishing signals from those of other users, and interference is severe, resulting in lower throughput.

Figure 6: Comparison of two propagation models

Fig. 7 shows the effect of path loss on cell throughput under different algorithms. The power allocation plan is a fractional transmission power allocation plan, so the allocation factor αFTPA is 0.2, the error propagation factor θ is fixed as 0.1, and the number of users is fixed at 48. It can be seen from Fig. 7 that the cell throughput decreases as the path loss attenuation factor increases. When the user is in free space, for example, the path loss attenuation factor is 2, and the cell throughput is the highest, but signal propagation is more difficult in the real-time deployment. Without loss of generality, the simulation conditions in this article, fixed path loss attenuation factor is 3. Also, the difference between the user’s location and the environment will change the overall throughput of the cell, but the algorithm proposed in this paper is still better than the algorithms in [10,18,24,25].

Figure 7: The influence of path loss on cell throughput

Fig. 8 compared the spectral efficiency of the algorithms under increasing SNR. As can be seen from Fig. 8, the spectral efficiency of the proposed algorithm with error-free propagation shows better performance at each level of SNR. On the other hand, reference [10] shows better performance than the proposed algorithm with error propagation. The references [24,25] shows the worst spectral efficiency performance. Therefore, the proposed algorithm provides effective performance in NOMA systems.

The energy efficiency of the algorithms was evaluated in Fig. 9 as the number of users increased. The energy efficiency of the algorithms falls as the number of users rises, as seen in Fig. 9. However, the proposed algorithm shows provides better energy efficiency than references [10,18,24,25] algorithms.

Figure 8: SE evaluation of the proposed and existing schemes

Figure 9: Comparison of the energy efficiency of the algorithms

To further elaborate the effectiveness of the proposed algorithm, Fig. 10 evaluates the complexity in terms of the number of users. As can be seen from Fig. 10, when the number of users increases, the complexity of all algorithms increases. However, the complexity of the proposed algorithm is lower than references [10,18,24,25] algorithms which makes it useful and effective in NOMA systems.

Figure 10: Complexity comparison of the algorithms

In order to further validate the effectiveness of the proposed algorithm, we compared the spectral efficiency with reference [31] for different number of users (Fig. 11). As can be seen from Fig. 11, the spectral efficiency of the proposed algorithms is better than reference [31] algorithm for every user which indicates that the proposed algorithms have superior performance and provide better QoS to the users.

Figure 11: SE comparison of the proposed and reference [31] algorithm for increasing number of users

5  Conclusion

This research focuses on the power allocation problem in NOMA downlink systems and proposes a novel power allocation scheme with lower complexity, and conducts simulation analysis under two propagation models. To simplify the complexity of the process, an iterative water-filling technique is utilized to allocate the power amongst subband resource blocks. Then, an improved algorithm based on proportional fair scheduling is used to allocate the power between users. The numerical results show that the proposed algorithm fairness of user’s performance is sacrificed in exchange for lower complexity. As compared with the existing algorithms in [10,18,24,25], the performance of the error-free propagation model of the improved algorithm is improved by about 3.3%, 5.4%, 9.2%, and 10.8%. The performance of the error propagation model is improved by about 0.3%, 0.5%, 2.1%, and 3.2%. The next work will consider the integration of MIMO communications and evaluate the performance from various important factors.

Acknowledgement: The author would like to thanks the editors and reviewers for their review and recommendations.

Funding Statement: This project was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, under Grant No. G: 368-611-1442. The authors, therefore, acknowledge with thanks DSR for technical and financial support.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  O. Maraqa, A. S. Rajasekaran, S. A. Ahmadi, H. Yanikomeroglu and S. M. Sait, “A survey of rate-optimal power domain noma with enabling technologies of future wireless networks,” IEEE Communications Surveys & Tutorial, vol. 22, no. 4, pp. 2192–2235, 2020. [Google Scholar]

 2.  M. B. Shahab, R. Abbas, M. Shirvanimoghaddam and S. J. Johnson, “Grant-free non-orthogonal multiple access for iot: A survey,” IEEE Communications Surveys & Tutorial, vol. 22, no. 3, pp. 1805–1838, 2020. [Google Scholar]

 3.  L. Dai, B. Wang, Z. Ding, Z. Wang, S. Chen et al., “A survey of non-orthogonal multiple access for 5G,” IEEE Communications Surveys & Tutorial, vol. 20, no. 3, pp. 2294–2323, 2018. [Google Scholar]

 4.  S. M. Islam, N. Avazov, O. A. Dobre and K. Kwak, “Power-domain non-orthogonal multiple access (NOMA) in 5G systems,” IEEE Communications Surveys & Tutorial, vol. 19, no. 2, pp. 721–742, 2017. [Google Scholar]

 5.  O. Wang, R. Zhang, L. Yang and L. Hanzo, “Non-orthogonal multiple access: A unified perspective,” IEEE Wireless Communications, vol. 25, no. 2, pp. 10–16, 2018. [Google Scholar]

 6.  D. Wan, M. Wen, X. Cheng, S. Mumtaz and M. Guizani, “A promising non-orthogonal multiple access based networking architecture: Motivation, conception, and evolution,” IEEE Wireless Communications, vol. 26, no. 5, pp. 152–159, 2019. [Google Scholar]

 7.  M. Vaezi, R. Schober, Z. Ding and H. V. Poor, “Non-orthogonal multiple access: Common myths and critical questions,” IEEE Wireless Communications, vol. 26, no. 5, pp. 174–180, 2019. [Google Scholar]

 8.  W. K. New, C. Y. Leow, K. Navaie and Z. Ding, “Robust non-orthogonal multiple access for aerial and ground users,” IEEE Transactions on Wireless Communications, vol. 19, no. 7, pp. 4793–4805, 2020. [Google Scholar]

 9.  M. Baghana, S. Parsaeefard, M. Derakhshani and W. Saad, “Dynamic non-orthogonal multiple access and orthogonal multiple access in 5G wireless networks,” IEEE Transactions on Communications, vol. 67, no. 9, pp. 6360–6373, 2019. [Google Scholar]

10. R. A. Stoica, G. T. Abreu, T. Hara and K. Ishibashi, “Massively concurrent non-orthogonal multiple access for 5G networks and beyond,” IEEE Access, vol. 7, pp. 82080–82100, 2019. [Google Scholar]

11. J. A. Carvalho, D. Costa, F. M. Lima, R. Oliveira and U. Dias, “Non-orthogonal multiple access in two-hop wireless powered communication networks,” IEEE Wireless Communications Letters, vol. 9, no. 9, pp. 1398–1402, 2020. [Google Scholar]

12. B. Kim, Y. Park and D. Hong, “Partial non-orthogonal multiple access (P-NOMA),” IEEE Wireless Communications Letters, vol. 8, no. 5, pp. 1377–1380, 2019. [Google Scholar]

13. Y. Liu, Z. Qin, M. Elkashlan, Z. Ding, A. Nallanathan et al., “Nonorthogonal multiple access for 5G and beyond,” Proceedings of the IEEE, vol. 105, no. 12, pp. 2347–2381, 2017. [Google Scholar]

14. S. Alemaishat, O. A. Saraereh, I. Khan and B. J. Choi, “An efficient resource allocation algorithm for D2D communications based on noma,” IEEE Access, vol. 7, pp. 120238–120247, 2019. [Google Scholar]

15. H. Dong, Z. Yao, C. Haotong, M. Zhou and L. Yang, “Energy-efficient transmission design for downlink non-orthogonal multiple access network,” in IEEE Int. Conf. on Consumer Electronics, Taiwan, China, pp. 1–2, 2019. [Google Scholar]

16. C. Jinho, “Power allocation for max-sum rate and max-min rate proportional fairness in NOMA,” IEEE Communications Letters, vol. 20, no. 10, pp. 2055–2058, 2016. [Google Scholar]

17. Y. Lin, Z. Yang and H. Y. Guo, “Proportional fairness-based energy-efficient power allocation in downlink MIMO-NOMA system with statistical CSI,” China Communications, vol. 16, no. 12, pp. 47–55, 2019. [Google Scholar]

18. J. Li, D. Mei, D. Deng, I. Khan and P. Uthansakul, “Proportional fairness-based power allocation algorithm for downlink noma 5G wireless networks,” Computers, Materials & Continua, vol. 65, no. 2, pp. 1571–1590, 2020. [Google Scholar]

19. O. Nagisa, K. Yoshihisa and H. Kenichi, “Performance of non-orthogonal access with SIC in cellular downlink using proportional fair-based resource allocation,” in IEEE Int. Symp. on Wireless Communication Systems (ISWCS), Paris, France, pp. 476–480, 2012. [Google Scholar]

20. A. Benjebbour, Y. Saito, Y. Kishiyama, A. Li, A. Harada et al., “Concept and practical consideration of non-orthogonal multiple access (NOMA) for future radio access,” in Int. Symp. on Intelligent Signal Processing and Communication Systems, Naha, Japan, pp. 770–774, 2013. [Google Scholar]

21. Y. Saito, A. Benjebbour, Y. Kishiyama and T. Nakamura, “System-level performance evaluation of downlink non-orthogonal multiple access (NOMA),” in IEEE Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, pp. 611–615, 2013. [Google Scholar]

22. N. Otao, Y. Kishiyama and K. Higuchi, “Performance of non-orthogonal access with SIC in cellular downlink using proportional fair-based resource allocation,” in Int. Symp. on Wireless Communication Systems (ISWCS), Paris, France, pp. 476–480, 2012. [Google Scholar]

23. C. L. Wang, J. Y. Chen and Y. C. Ju, “Power allocation for a downlink non-orthogonal multiple access system,” IEEE Wireless Communication Letters, vol. 5, no. 5, pp. 532–535, 2016. [Google Scholar]

24. M. R. Hojeij, J. Farah, C. A. Nour and C. Douillard, “Resource allocation in downlink non-orthogonal multiple access (NOMA) for future radio access,” in IEEE 81st Vehicular Technology Conf. (VTC), Glasgow, UK, pp. 1–6, 2015. [Google Scholar]

25. A. Benjebbovu, A. Li, Y. Saito, Y. Kishiyama, A. Harada et al., “System-level performance of downlink noma for future LTE enhancements,” in IEEE Global Communication Conf. (GLOBECOM), Atlanta, USA, pp. 66–70, 2013. [Google Scholar]

26. H. Sun, B. Xie, R. Q. Hu and G. Wu, “Non-orthogonal multiple access with SIC error propagation in downlink wireless MIMO networks,” in IEEE 84th Vehicular Technology Conf. (VTC), Montreal, Canada, pp. 1–5, 2016. [Google Scholar]

27. J. H. Jang, K. B. Lee and Y. H. Lee, “Transmit power and bit allocations for OFDM systems in a fading channel,” in IEEE Global Communications Conf. (GLOBECOM), San Francisco, USA, pp. 858–862, 2003. [Google Scholar]

28. M. R. Hojeij, A. C. Nour, J. Farah and C. Douillard, “Waterfilling-based proportional fairness scheduler for downlink non-orthogonal multiple access,” IEEE Wireless Communications Letters, vol. 6, no. 2, pp. 230–233, 2017. [Google Scholar]

29. C. E. Garcia, P. V. Tuan, M. R. Camana and I. Koo, “Optimized power allocation for a cooperative noma system with swipt and an energy harvesting user,” International Journal of Electronics, vol. 107, no. 10, pp. 1704–1733, 2019. [Google Scholar]

30. C. Campola, R. Fontes, A. Molinaro, C. E. Rothenberg and A. Iera, “Slicing on the road: Enabling the automotive vertical through 5G network softwarization,” Sensors, vol. 18, no. 12, pp. 1–17, 2018. [Google Scholar]

31. J. Wang, Y. Wang and J. Yu, “Joint beam-forming, user clustering and power allocation for MIMO-NOMA systems,” Sensors Journal, vol. 22, no. 3, pp. 1–19, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.