Computers, Materials & Continua DOI:10.32604/cmc.2022.027629
Article

An Advanced Stochastic Numerical Approach for Host-Vector-Predator Nonlinear Model

Prem Junswang1, Zulqurnain Sabir2, Muhammad Asif Zahoor Raja3, Soheil Salahshour4, Thongchai Botmart5,* and Wajaree Weera5

1Department of Statistics, Faculty of Science, Khon Kaen University, Khon Kaen, 40002, Thailand
2Department of Mathematics and Statistics, Hazara University, Mansehra, Pakistan
3Future Technology Research Center, National Yunlin University of Science and Technology, Douliou, Yunlin, 64002, Taiwan
4Faculty of Engineering and Natural Sciences, Bahcesehir University, Istanbul, Turkey
5Department of Mathematics, Faculty of Science, Khon Kaen University, Khon Kaen, 40002, Thailand
*Corresponding Author: Thongchai Botmart. Email: thongbo@kku.ac.th
Received: 21 January 2022; Accepted: 16 March 2022

Abstract: A novel design of the computational intelligent framework is presented to solve a class of host-vector-predator nonlinear model governed with set of ordinary differential equations. The host-vector-predator nonlinear model depends upon five groups or classes, host plant susceptible and infected populations, vectors population of susceptible and infected individuals and the predator population. An unsupervised artificial neural network is designed using the computational framework of local and global search competencies of interior-point algorithm and genetic algorithms. For solving the host-vector-predator nonlinear model, a merit function is constructed using the differential model and its associated boundary conditions. The optimization of this merit function is performed using the computational strength of designed integrated heuristics based on interior point method and genetic algorithms. For the comparison, the obtained numerical solutions of networks models optimized with efficacy of global search of genetic algorithm and local search with interior point method have been compared with the Adams numerical solver based results or outcomes. Moreover, the statistical analysis will be performed to check the reliability, robustness, viability, correctness and competency of the designed integrated heuristics of unsupervised networks trained with genetic algorithm aid with interior point algorithm for solving the biological based host-vector-predator nonlinear model for sundry scenarios of paramount interest.

Keywords: Nonlinear; host-vector-predator system; adams results; global/local search methods; optimization; neural networks; statistical analysis

1  Introduction

There are various diseases in plants through microorganisms like protozoan fungi, nematode worms, bacteria, viruses and vector spreading viruses. A number of approaches have been applied to control the spread of diseases in plants named as predators, which work as a biological representative [1]. For the spreading diseases in the plants, the mathematical form of the modeling has a dynamic part in retrospectively to examine the vector-borne dynamics based on the plant viruses [2]. Jeger et al. studied the model based on the mathematical plant form to recognize the virus transmission and disease dynamics vectors [3]. After a year, Jeger et al. formed a classified system to reflect the dynamics of vector population to examine the viral spread impacts [4]. Rida et al. expressed the plant diseases, which are conveyed through the vectors [5]. Muryawi et al. discussed the dynamical form of a nonlinear system in the plant vector-borne dispersal diseases through insects [6]. He also worked on the nonlinear deterministic model and simulated to the hypothetical parameter values. A number of researchers formulated the epidemiological forms for a single type of vector/plant to investigate the host plant through two diseases. Khan et al. presented the EH − SH − SV− IH− IV− EVsystem that labels the dynamics of pine wilt disease [7]. Bokil et al. proposed a plant system based on the vector-virus using the policy of mud planting [8]. Donnelly et al. introduced a simple system to designate the dynamic population of vector mechanisms [9]. Anggriani et al. proposed a deterministic mathematical compartmental network using the vector-borne to control the impacts of insect vectors based on the virus of rice plant. The spread dynamics of diseases in the plants to deliver the protective, rouging, replanting and curative [10].

The mathematical form of a system designates the numerous complexities along with the various features. Few systems require high complexity cost particularly for simulation that are considered complex or stiff system. There are various formulation approaches that have been applied to the researcher's community for solving the nonlinear equation systems. Few of them are the Adams numerical scheme [11], Caputo fractional scheme [12], differential transformation method [13], variational iteration technique [14] and a few other methods that have been cited in these References [15–24].

The current study is related to design a computational framework to solve a class of host-vector-predator nonlinear model (HVPNM). The biological HVPNM depends upon five groups, host plant susceptible and infected populations, vectors population of susceptible and infected individuals and the predator population. An unsupervised artificial neural network (UANN) is designed using the computational framework of local and global search competencies of interior-point algorithm (IPA) and genetic algorithm (GA), i.e., UANN-GA-IPA. Suryaningrat et al. [25] proposed a host-vector system to adopt a predator that works as a biological agent using the disease vectors from plants. The biological HVPNM dependent upon five groups, host plant susceptible and infected populations, vectors population of susceptible and infected individuals and the predator population. The general form of the biological HVPNM together with the initial conditions (ICs) is presented as [26]:

{S′h(u)=μNh−β2Iv(u)Sh(u)(Nv)−1−μSh(u),Sh(0)=a1,I′h(u)=−μIh(u)+β2Iv(u)Sh(u)(Nv)−1,Ih(0)=a2,S′v(u)=−ηSv(u)+ηNv−εSv(u)P(u)−β1Sv(u)Ih(u)(Nh)−1,Sv(0)=a3,I′v(u)=−ηSv(u)−εP(u)Iv(u)+β1Sv(u)Ih(u)(Nh)−1,Iv(0)=a4,P′(u)=ε(Sv(u)+Iv(u))P(u)−δP(u)P(0)=a5.(1)

The state variables of the biological HVPNM with the suitable selections are accessible in Tab. 1, which is given as:

The stochastic numerical solvers have been implemented to solve in various applications, few of them are higher kind of singular models, dengue fever nonlinear model, singular form of fractional models, coronavirus system based on SITR, prey-predator system, doubly singular systems, and mosquito dispersal heterogeneous environmental model, see [27–30] and citations therein. Taking into account of these demonstrations, the authors are concerned to solve the biological HVPNM using the computational UANN-GA-IPA. Few novel inspirations of the UANN-GA-IPA are given as:

•   The numerical results of the biological HVPNM are accessible efficiently based on the computational UANN-GA-IPA measures.

•   The reliable, consistent and stable effects of the biological HVPNM validate the computational procedures of the UANN-GA-IPA.

•   The endorsement of the presentation is stated by using different statistical measures to solve the biological HVPNM on twenty trials using the computational form of the UANN-GA-IPA.

•   The values of the absolute error (AE) in good measures authenticate the consistency and reliability of the computational form of the UANN-GA-IPA.

•   The computational form of the UANN-GA-IPA are efficiently applied to solve the biological HVPNM used effortlessly for better considerations.

The other parts of the paper parts are derived as: Section 2 designates the computational performances of the UANN-GA-IPA together with the statistical operators. Section 3 demonstrates the result reproductions. Section 4 shows the concluding remarks and future research guidance.

2  Designed Approach: UANN-GA-IPAS

The current section presents a computational framework based on the UNN-GA-IPA to solve the biological HVPNM in two ways.

•   A merit function is constructed using the designed system and its ICs.

•   The necessary measures are derived based on the UANN-GA-IPA hybridization.

2.1 Designed Procedures

The mathematical proposals of the biological HVPNM together with its derivatives are given as:

[S^h(u),I^h(u),S^v(u),I^v(u),P^(u)]=[∑k=1rbSh,kT(wSh,ku+fSh,k),∑k=1rbIh,kT(wIh,ku+fIh,k),∑k=1rbSv,kT(wSv,ku+fSv,k),∑k=1rbIv,kT(wIv,ku+fIv,k),∑k=1rbP,kT(wP,ku+fP,k)],(2)

[S^h′(u),I^h′(u),S^v′(u),I^v′(u),P^′(u)]=[∑k=1rbSh,kT′(wSh,ku+fSh,k),∑k=1rbIh,kT′(wIh,ku+fIh,k),∑k=1rbSv,kT′(wSv,ku+fSv,k),∑k=1rbIv,kT′(wIv,ku+fIv,k),∑k=1rbP,kT′(wP,ku+fP,k)],

where, T authenticates the merit function, S^h, I^h, S^v, I^v and P^ indicate the proposed solutions, while W represents an unidentified weight vector, which is given as:

W=[WSh,WIh,WSv,WIv,WP],

for WSh=[bSh,ωSh,fSh], WIh=[bIh,ωIh,fIh], WSv=[bSv,ωSv,fSv], WIv=[bIv,ωIv,fIv] and WP=[bP,ωP,fP], where

@l@bSh=[bSh,1,bSh,2,bSh,3,…,bSh,r],bIh=[bIh,1,bIh,2,bIh,3,…,bIh,r],bSv=[bSv,1,bSv,2,bSv,3,…,bSv,r],bIv=[bIv,1,bIv,2,bIv,3,…,bIv,r]wP=[wP,1,wP,2,wP,3,…,wP,r],wSh=[wSh,1,wSh,2,wSh,3,…,wSh,r],wIh=[wIh,1,wIh,2,wIh,3,…,wIh,r],wSv=[wSv,1,wSv,2,wSv,3,…,wSv,r],wIv=[wIv,1,wIv,2,wIv,3,…,wIv,r],wP=[wP,1,wP,2,wP,3,…,wP,r],fSh=[fSh,1,fSh,2,fSh,3,…,fSh,r],fIh=[fIh,1,fIh,2,fIh,3,…,fIh,r],fSv=[fSv,1,fSv,2,fSv,3,…,fSv,r],fIv=[fIv,1,fIv,2,fIv,3,…,fIv,r],fP=[fP,1,fP,2,fP,3,…,fP,r].

The Log-Sigmoid function used as an activation function, mathematically T(u)=1(1+exp⁡(−u)) is applied in the above network is given as:

[S^h(u),I^h(u),S^v(u),I^v(u),P^(u)]=[∑k=1rbSh,k1+e−(wSh,ku+fSh,k),∑k=1rbIh,k1+e−(wIh,ku+fIh,k),∑k=1rbSv,k1+e−(wSv,ku+fSv,k),∑k=1rbIv,k1+e−(wIv,ku+fIv,k),∑k=1rbP,k1+e−(wP,ku+fP,k)],[S^′h(u),I^′h(u),S^′v(u),I^′v(u),P^′(u)]=[∑k=1rbSh,kwSh,ke−(wSh,ku+fSh,k)(1+e−(wSh,ku+fSh,k))2,∑k=1rbIh,kwIh,ke−(wIh,ku+fIh,k)(1+e−(wIh,ku+fIh,k))2,∑k=1rbSv,kwSv,ke−(wSv,ku+fSv,k)(1+e−(wSv,ku+fSv,k))2,∑k=1rbIv,kwIv,ke−(wIv,ku+fIv,k)(1+e−(wIv,ku+fIv,k))2,∑k=1rbP,kwP,ke−(wP,ku+fP,k)(1+e−(wP,ku+fP,k))2].(3)

The mathematical formulation of the merit function becomes as:

Ξ=Ξ1+Ξ2+Ξ3+Ξ4+Ξ5+Ξ6,(4)

Ξ1=1N∑K=1N[(S^′h)K−μNh+β2(I^v)K(S^h)K(Nv)−1+μ(S^h)K]2,(5)

Ξ2=1N∑K=1N[(I′h)K+μ(Ih)K−β2(Iv)K(Sh)K(Nv)−1]2,(6)

Ξ3=1N∑K=1N[(S′v)K+η(Sv)K−ηNv+ε(Sv)K(P)K+β1(Sv)K(Ih)K(Nh)−1]2,(7)

Ξ4=1N∑K=1N[(I′v)K+η(Sv)K+ε(P)K(Iv)K−β1(Sv)K(Ih)K(Nh)−1]2,(8)

Ξ5=1N∑K=1N[(P′)K−ε((Sv)K+(Iv)K)(P)K+δ(P)K]2,(9)

Ξ6=15[((S^h)0−a1)2+((I^h)0−a2)2+((S^v)0−a3)2+((I^v)0−a4)2+((P^)0−a5)2],(10)

where (S^h)K=Sh(uK),(I^h)K=Ih(uK),(S^v)K=Sv(uK),(I^v)K=Iv(uK),P^K=P(uK),χK=hK and Nh=1. Similarly, Eqs. (4) to (9) is the mathematical form of a merit function based on the biological HVPNM, whereas, Eq. (10) is a merit function using the ICs.

2.2 Optimization Performance: UANN-GA-IPA

This section shows the optimization performances of the biological HVPNM using the computational measures based on the UANN-GA-IPAS.

A global search process GA is a well-known famous optimization procedure, which is applied to solve the nonlinear and linear models. This process is performed to handle both unconstrained/constrained models using the selection process and normally implemented to regulate the precise population results for solving the numerous steep/complicated systems of ideal training. Recently, GA is performed/executed in many applications including the hospitalization outflow models, feature assortment in cancer microarray, images of brain tumor, vehicle routing models, prediction differential system, radiation protective in the borate-bismuth glasses, optimization procedures of cloud service, liver disease systems and many more.

IPA is an optimization local search procedure, which is normally applied to solve constrained/unconstrained systems. IPA is an efficient algorithm that is applied to calculate the competent results. Recently, IPA is used in constant nonlinear models’ identification, monotone linear complementarity systems with the symmetrical cones, viscus fluids, magnetic three-dimensional sparse inversion, sufficient LCPs scheme of algebraically equivalent revolution, second kind of cone programming, singular higher order systems and many others. The GA-IPA hybridization scheme is applied to control the slowness of GA, and the GAIPA is shown in Tab. 2.

2.3 Performance Measures

In this section, the performance measures in terms of variance account for (VAF), semi-interquartile range (S.I.R) and Theil's inequality coefficient (TIC) together with the global representations are executed to solve the biological HVPNM is mathematically formulated as:

{[VAFSh,VAFIh,VAFSv,VAFIv,VAFP]=[(1−var((Sh)k−(S^h)k)var(Sh)k)∗100,(1−var((Ih)k−(I^h)k)var(Ih)k)∗100,(1−var((Sv)k−(S^v)k)var(Sv)k)∗100,(1−var((Iv)k−(I^v)k)var(Iv)k)∗100,(1−var(Pk−P^k)var(Pk))∗100][EVAFSh,EVAFIh,EVAFSv,EVAFIv,EVAFP]=[|100−VAFSh,100−VAFIh,100−VAFSv,100−VAFIv,100−VAFP|].(11)

{S.I.R=−12(Q1−Q3),Q1&Q3representthequartile 1\& quartile3,(12)

[TICSh,TICIh,TICSv,TICIv,TICP]=[1n∑k=1n((Sh)k−(S^h)k)2(1n∑k=1n(Sh)k2+1n∑k=1n(S^h)k2),1n∑k=1n((Ih)k−(I^h)k)2(1n∑k=1n(Ih)k2+1n∑k=1n(I^h)k2),1n∑k=1n((Sv)k−(S^v)k)2(1n∑k=1n(Sv)k2+1n∑k=1n(S^v)k2),1n∑k=1n((Iv)k−(I^v)k)2(1n∑k=1n(Iv)k2+1n∑k=1n(I^v)k2),1n∑k=1n(Pk−P^k)2(1n∑k=1nPk2+1n∑k=1nP^k2),],(13)

where S^h, I^h, S^v, I^v and P^ are the approximate solution form.

3  Results and Discussions

This section provides the numerical outcomes of the biological HVPNM given in the model (1) using the UANN-GA-IPA. The obtained outcomes of the biological HVPNM are compared with the biological HVPNM with the Adams results, convergence investigations, AE and performance values are derived through different statistical operatives. The simplified mathematical form of the biological HVPNM using the suitable parameter values is provided as: The merit function using the biological HVPNM is provided as:

{S′h(u)=2.5−0.025Sh(u)−0.0015Iv(u)Sh(u),Sh(0)=50,I′h(u)=0.0015Sh(u)Iv(u)−0.025Ih(u),Ih(0)=50,S′v(u)=1.25−0.025Sv(u)−0.015P(u)Sv(u)−0.0005Ih(u)Sv(u),Sv(0)=10,I′v(u)=0.0005Sv(u)Ih(u)−0.015Iv(u)P(u)−0.025Sv(u),Iv(0)=40,P′(u)=0.015Iv(u)P(u)+0.015Sv(u)P(u)−0.125P(u)P(0)=3.(14)

Ξ=1N∑K=1N([ (S^′h)K−2.5+0.0015(S^h)K(Iv)K+0.025(S^h)K ]2+[ (I′h)K+0.025(Ih)K−0.0015(Iv)K(Sh)K ]2+[ (S′v)K+0.025(Sv)K−1.25+0.015(Sv)K(P)K+0.0005(Sv)K(Ih)K ]2+[ (I′v)K+0.025(Sv)K+0.015(P)K(Iv)K−0.0005(Sv)K(Ih)K ]2+[ (P′)K−0.015(P)K(Iv)K−0.015(Sv)K(P)K+0.125(P)K ]2)+15[ ((S^h)0−50)2+((I^h)0−50)2+((S^v)0−10)2+((I^v)0−40)2+(P^0−3)2 ].(15)

The biological HVPNM provided in the system (1) is executed to optimize the fitness function through the UANN-GA-IPA to form the parameters of the NNs on the basis of 30 variables. The ideal values of the weight vectors are derived to solve the biological HVPNM. The mathematical formulations obtained through UANN-GA-IPA are given as:

S^h(u)=3.47461+e(−1.6224u+19.4060)−12.54411+e(−0.5491u−0.3284)−1.5.54411+e(0.7347u−15.7735)−15.72141+e(−6.2276u+18.3474) −16.29461+e(1.1266u+18.5486)−4.12641+e(0.8914u−7.3676)+4.14351+e(−7.5660u−8.8420)−16.03351+e(−4.4111u+19.6276) +3.02881+e(−14.5175u−18.4874)−18.87351+e(2.1370u+6.2740),(16)

I^h(u)=6.97761+e(−0.5375u+8.0255)+4.67901+e(−0.5016u+7.6212)+3.70911+e(−3.0830u−9.6962)+15.39441+e(−9.2656u+19.1732) +2.30511+e(1.0775u+7.0150)+2.50321+e(0.8237u−4.7315)+13.68281+e(0.5350u+0.5298)−14.32691+e(2.5704u+7.2673) −0.24931+e(1.8264u−14.6750)+11.46211+e(6.5546u−15.9241),(17)

S^v(u)=8.90191+e(19.9710u+12.2750)−6.78271+e(−0.4060u+0.5991)−3.50071+e(0.3782u−3.9606)+8.80231+e(19.7391u+16.0021) −11.94081+e(−17.5383u−13.9080)+0.13531+e(−7.3213u−17.8130)−2.47271+e(5.7174u+19.9997)−4.68831+e(0.7867u−12.4458) −2.36881+e(2.3318u+12.4458)−1.09651+e(1.0664u−2.6329),(18)

I^v(u)=8.90191+e(−1.9644u+10.3397)−6.78271+e(−3.4215u−7.3254)+8.80231+e(−1.2424u−1.6570)−11.94081+e(1.5443u−1.1242) −11.94081+e(1.5443u−1.1242)+0.13531+e(−12.0117u−19.4255)−2.47271+e(10.9352u+8.0995)−4.68831+e(−0.8939u−7.8416) −2.36881+e(−0.8939u−7.8416)−1.09651+e(−13.1828u−12.2091),(19)

P^(u)=5.06501+e(1.2230u−2.2080)+0.75451+e(8.0951u+15.0765)+056141+e(−0.8688u−4.4348)−0.57581+e(0.7020u−2.7516) +1.68841+e(2.0241u−4.1483)+2.78311+e(1.7131u−4.3795)+0.54211+e(19.5540u+12.2355)−0.83151+e(−1.2643u−3.0184) +1.43361+e(−0.6437u−14.2708)+6.26531+e(0.8689u−0.8370).(20)

The illustrations related to the weight vectors, result comparison as well as AE are derived in Figs. 1–3 using the UANN-GA-IPA based on the biological HVPNM. The values of the best weight vectors are drawn in Figs. 1a–1e using 30 variables or 10 neurons. The performances of the results comparison for solving the biological HVPNM are provided in Figures (f to j). The mean and best outcomes using the UANN-GA-IPA have been compared with the reference Adams results for solving the biological HVPNM. The accurate and specific performances of the UANN-GA-IPA and the reference solutions have been noticed on the basis of the matching of the outcomes. The AE based on the mean and best solutions is demonstrated in Figs. 2a–2e for the biological HVPNM. It is observed that the AE best outcomes of the Sh(u), Ih(u), Sv(u), Iv(u) and P(u) are calculated around 10−05–10−08, 10−05–10−07, 10−05–10−06, 10−04–10−06 and 10−05–10−07, while the mean values of the AE for the classes Sh(u), Ih(u), Sv(u), Iv(u) and P(u) are calculated around 10−04–10−06, 10−03–10−06, 10−03–10−05, 10−02–10−04 and 10−04–10−06. The EVAF, MAD and TIC operator performances for the biological HVPNM are presented in the subfigure 2. For Sh(u), the best EVAF, MAD and TIC operators lie around 10−10–10−11, 10−04–10−06 and 10−09–10−10. For Ih(u), the best EVAF, MAD and TIC operators lie around 10−09–10−10, 10−05–10−06 and 10−08–10−10. For Sv(u), the best EVAF, MAD and TIC operators calculated around 10−08–10−09, 10−05–10−06 and 10−09–10−10. For Iv(u), the best EVAF, MAD and TIC operators found 10−09–10−10, 10−05–10−06 and 10−08–10−10. For P(u), the best EVAF, MAD and TIC operators calculated 10−11–10−12, 10−05–10−06 and 10−10–10−11.

Figure 1: The comparison of the outcomes and best values of the weights for solving the biological HVPNM

Figure 2: AE values and the performances of the TIC, EVAF and MAD performances for the biological HVPNM

Figure 3: TIC performances and the histogram plots using the UANN-GA-IPA for the biological HVPNM

The graphs based on the statistical operatives and the performances of histogram are provided in Figs. 3 and 4 to solve the biological HVPNM. The convergence illustrations using the EVAF and TIC values are provided based on the biological HVPNM. It is observed that the TIC performances for Sh(u), Ih(u), Sv(u), Iv(u) and P(u) found around in the ranges of 10−07–10−10. The EVAF performances for Sh(u), Ih(u), Sv(u), Iv(u) and P(u) found around 10−06–10−11. It is observed that the best values of these operators through UANN-GA-IPA are calculated suitable for the EVAF and TIC operators.

Figure 4: EVAF performances and the histogram plots using the UANN-GA-IPA for the biological HVPNM

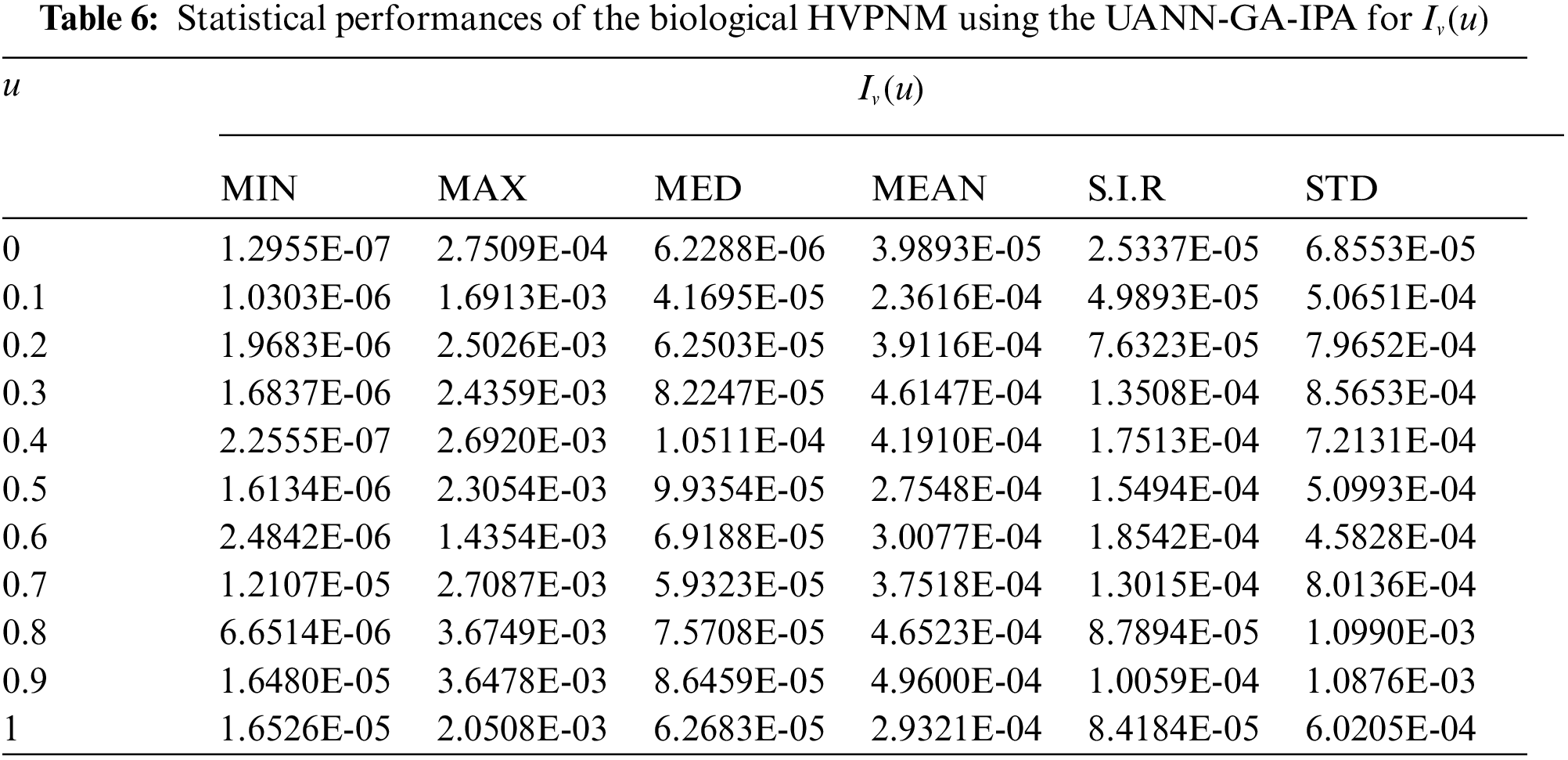
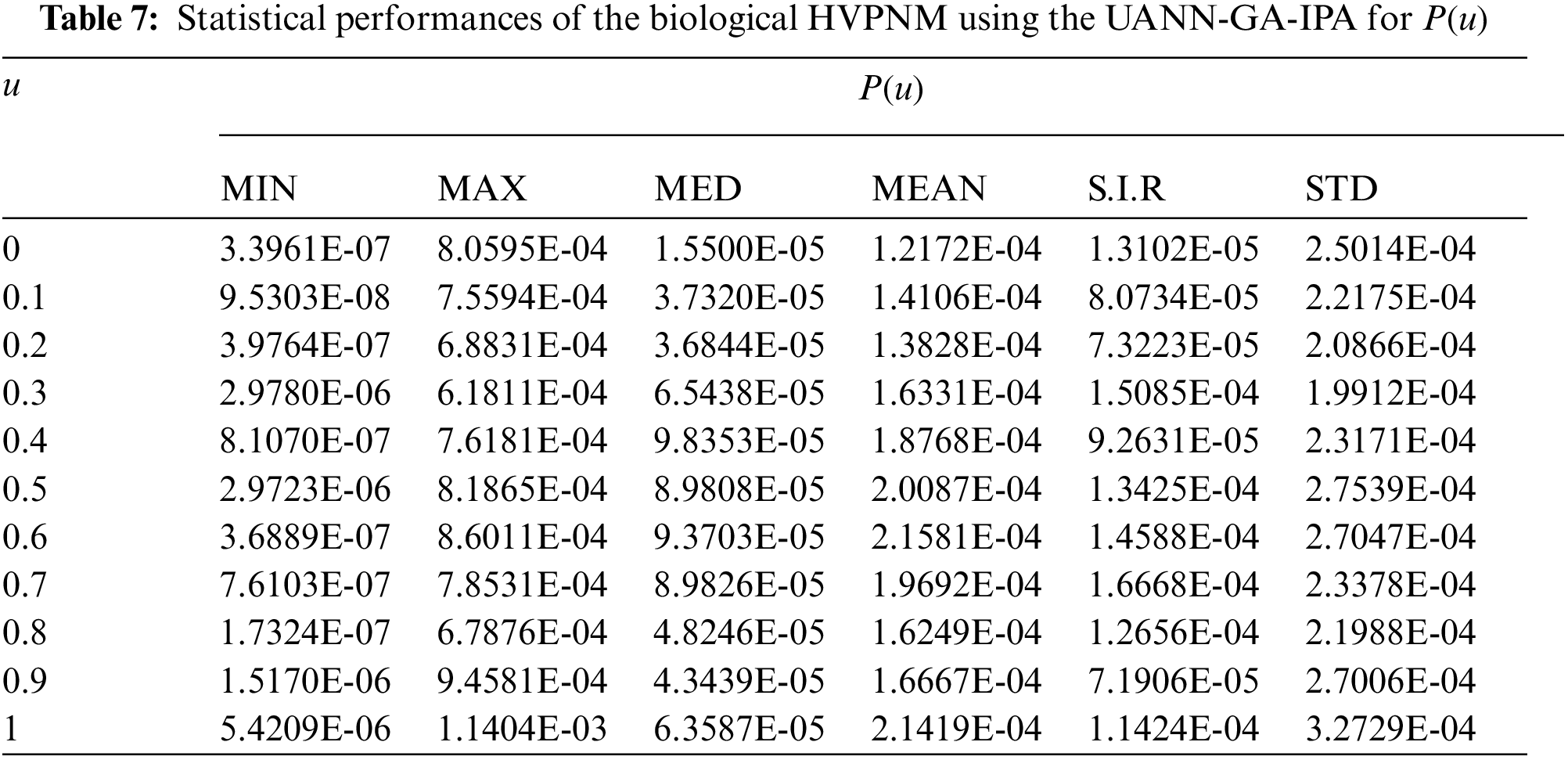
In order to authenticate the accuracy of the proposed UANN-GA-IPA for solving the biological HVPNM, Tabs. 3 to 7 are provided in the domain [0, 1] with the 0.1 step size. The values based on the Maximum (Max), S.I.R, Median (MED) standard deviation (STD), Mean and Minimum (Min) gages are provided in these Tables. The best values are defined in Min gages, while the Max gages shows the worst results. It is seen that the Min values lie around 10−07–10−10, 10−05–10−08, 10−06–10−07, 10−05–10−07 and 10−06–10−08 for Sh(u), Ih(u), Sv(u), Iv(u) and P(u), whereas, the Max gages even show the worst results are found around 10−03–10−05 for each class of the biological HVPNM. The Mean, STD, MED and S.I.R gages are also found in good measures that lie around 10−05–10−07, 10−06–10−07, 10−05–10−07 and 10−07–10−08, respectively. It is concluded from these evidences that the proposed approach UANN-GA-IPA is reliable and consistent for solving the biological HVPNM.

The best global operator performances of the TIC, MAD and EVAF are provided in Tab. 8 using the UANN-GA-IPA by taking 20 independent executions for solving the biological HVPNM. The global MED performances based on the EVAF, MAD and TIC found around 10−07–10−09, 10−09–10−10 and 10−05–10−06, while the S.I.R global measures for the EVAF, MAD and TIC are calculated around 10−07–10−09, 10−09–10−10 and 10−04–10−05 for solving the biological HVPNM. These optimal values obtained through the global measures authenticate the precision and exactness of the designed UANN-GA-IPA.

4  Conclusions

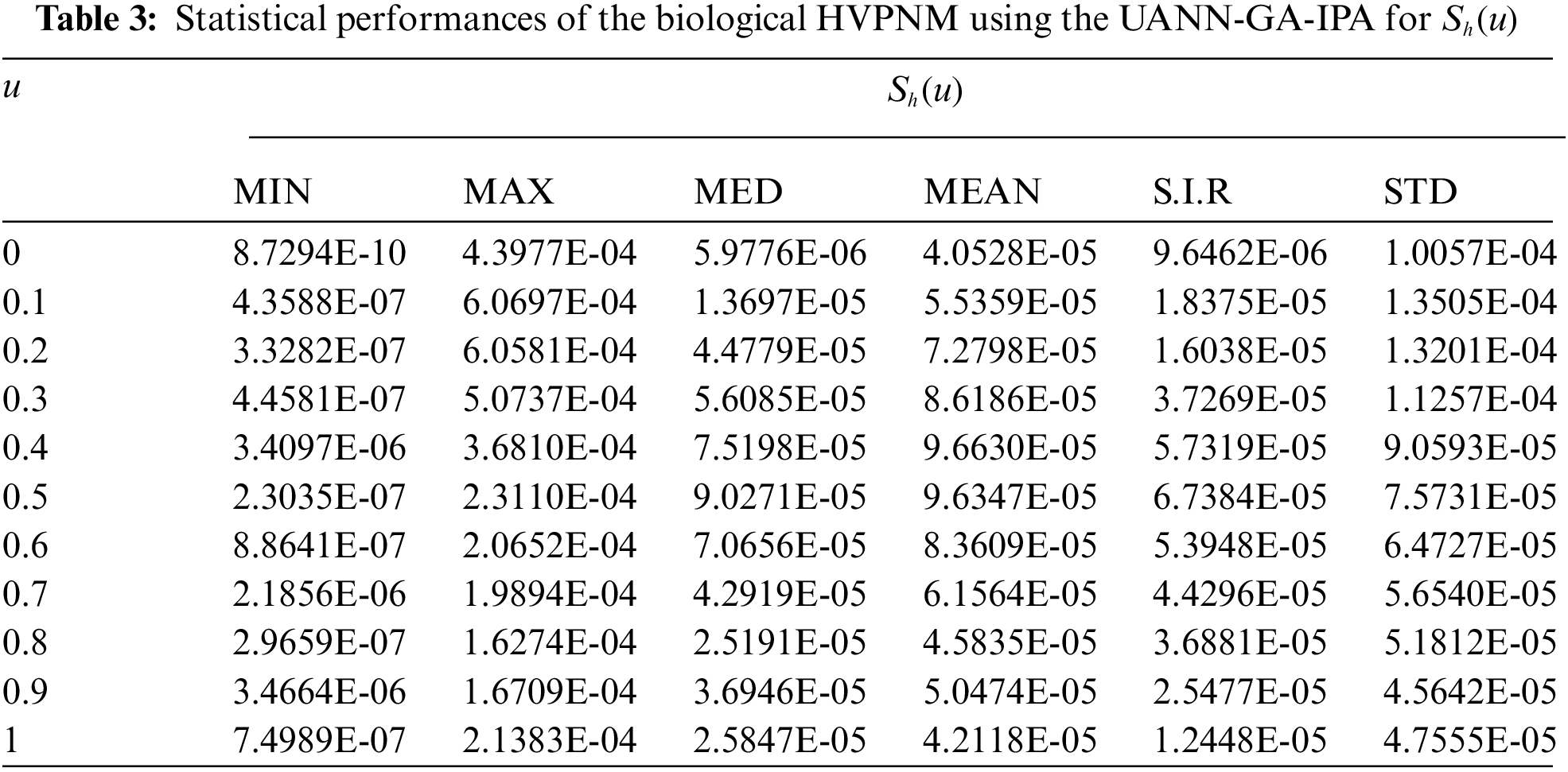
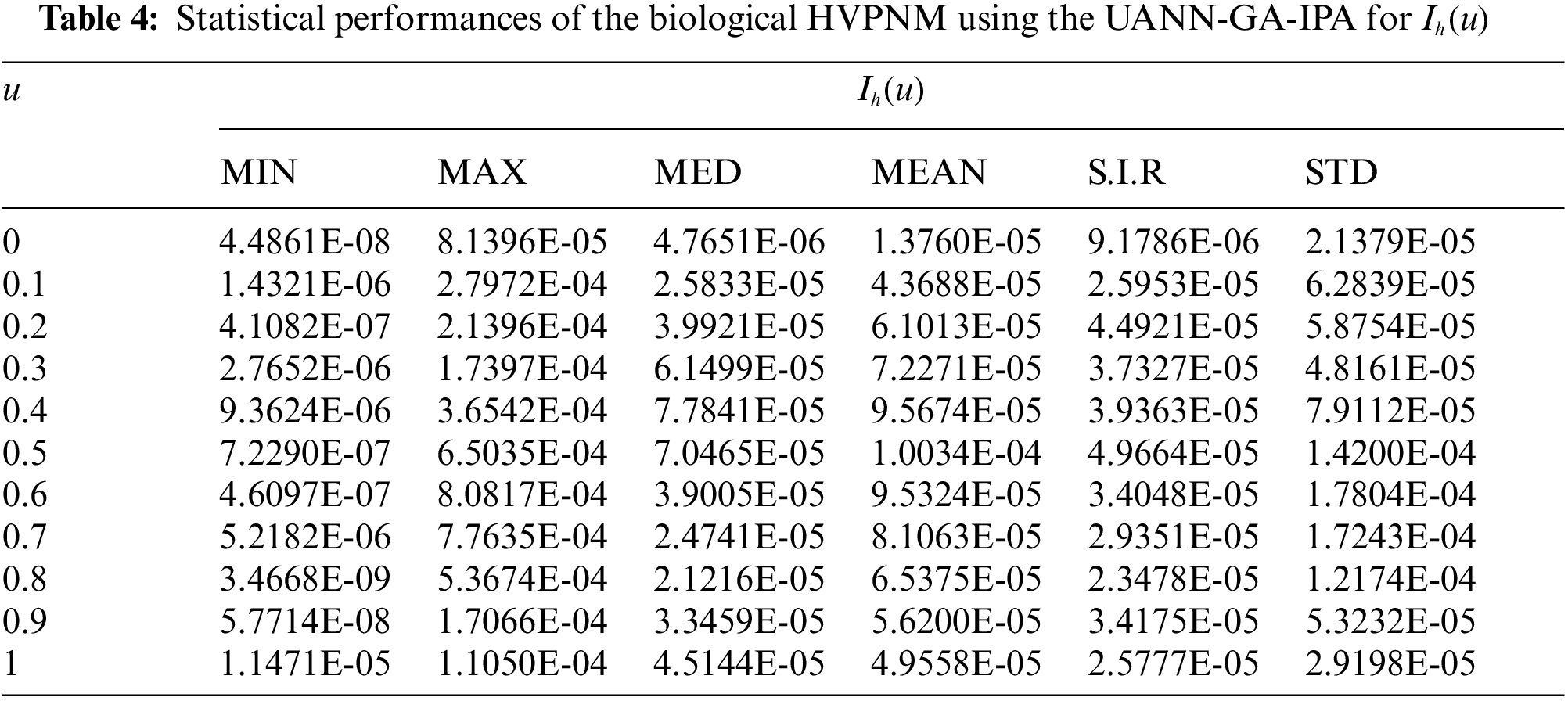
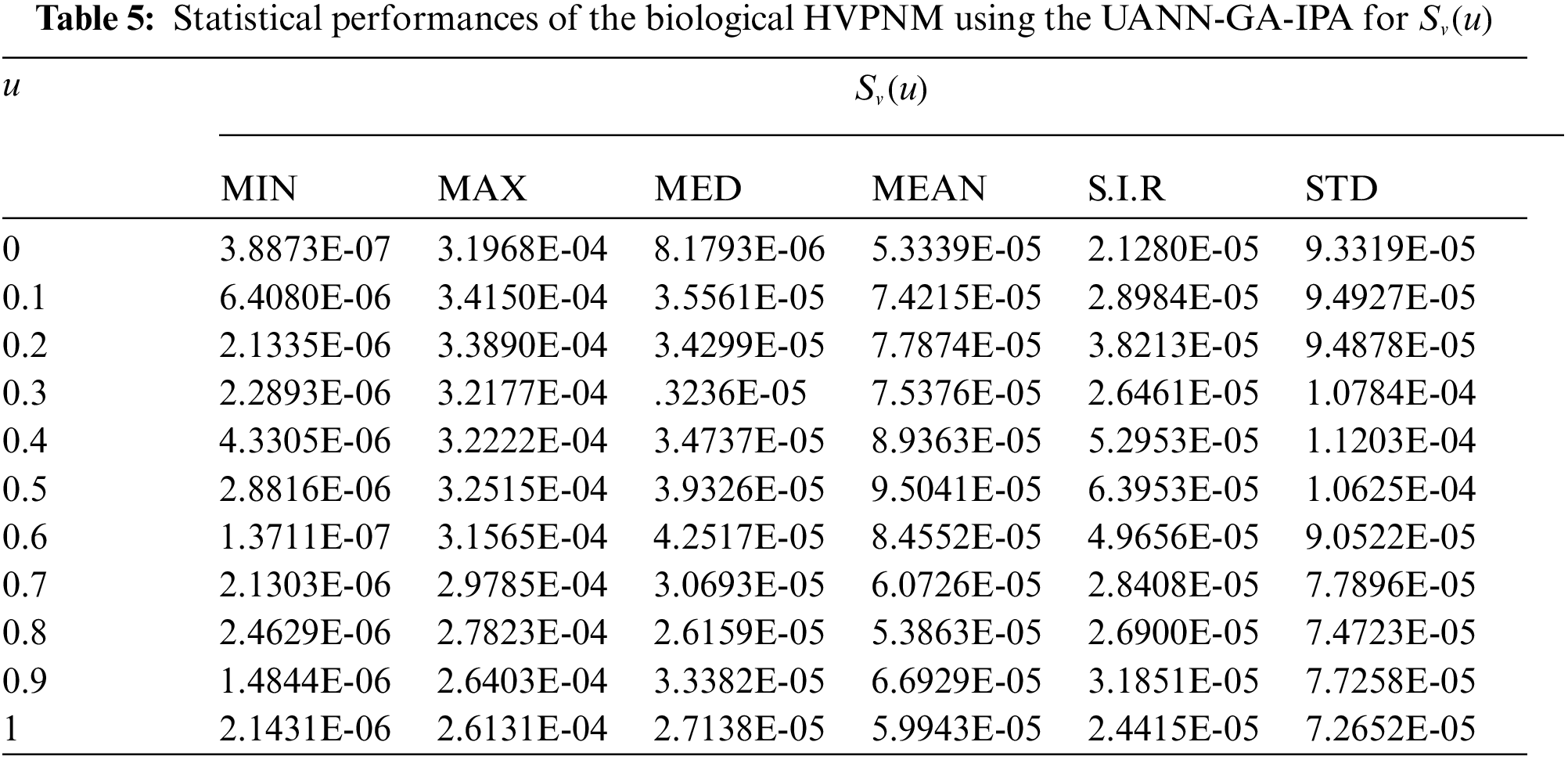
The present study is related to design a computational framework to solve a class of biological host-vector-predator nonlinear model. This biological model is dependent upon five groups, host plant susceptible and infected populations, vectors population of susceptible and infected individuals and the predator population. An unsupervised artificial neural network is introduced based on the computational framework of local and global search competencies of interior-point algorithm and genetic algorithm. An error function based on the differential model and its ICs is designed and the optimization is performed using the computational heuristic of UANN-GA-IPA for solving the biological nonlinear model. The satisfactory performances have been obtained through the comparison of the proposed numerical outcomes of the biological nonlinear model through UANN-GA-IPA and the reference solutions. The AE values obtained in good measures, i.e., 10−06 to 10−08 for solving each class of the nonlinear biological model. The EVAF and TIC gages have been considered in good illustrations to solve the biological nonlinear model. In addition, the MAD values are also calculated in good ranges for solving the nonlinear model. The STD, Mean, MED, Min, Max, S.I.R and Max gages have been assessed for twenty independent trials to validate the correctness of the designed UANN-GA-IPA. Furthermore, the global representations through the statistical performances in terms of MED and S.I.R have been proficiently applied to solve the nonlinear biological model.

In future, the proposed computational UANN-GA-IPA is implemented to solve the fractional order singular systems, fluid natured models and many others of paramount interest [31–35].

Funding Statement: This research received funding support from the NSRF via the Program Management Unit for Human Resources & Institutional Development, Research and Innovation (Grant Number B05F640088).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  G. N. Agrios, Plant Pathology, 5th ed., San Diego, CA: Academic Press, 2005. [Google Scholar]

 2.  W. Suryaningrat, N. Anggriani and A. K. Supriatna, “On application of differential transformation method to solve host-vector-predator system,” in Journal of Physics: Conference Series, vol. 1722, no. 1, pp. 1–9, 2021. [Google Scholar]

 3.  M. J. Jeger, Z. Chen, G. Powell, S. Hodge and F. Van den Bosch, “Interactions in a host plant-virus–vector–parasitoid system: Modelling the consequences for virus transmission and disease dynamics,” Virus Research, vol. 159, no. 2, pp. 183–193, 2011. [Google Scholar]

 4.  M. Jeger, Z. Chen, E. Cunningham, G. Martin and G. Powell, “Population biology and epidemiology of plant virus epidemics: From tripartite to tritrophic interactions,” European Journal of Plant Pathology, vol. 133, no. 1, pp. 3–23, 2012. [Google Scholar]

 5.  S. Z. Rida, M. Khalil, H. A. Hosham and S. Gadellah, “Mathematical model of vector-borne plant disease with memory on the host and the vector,” Progress in Fractional Differentiation and Applications, vol. 2, no. 4, pp. 277–285, 2016. [Google Scholar]

 6.  A. L. M. Murwayi, T. Onyango and B. Owour, “Mathematical analysis of plant disease dispersion model that incorporates wind strength and insect vector at equilibrium,” Journal of Advances in Mathematics and Computer Science, vol. 22, pp. 1–17, 2017. [Google Scholar]

 7.  M. A. Khan, K. Shah, Y. Khan and S. Islam, “Mathematical modeling approach to the transmission dynamics of pine wilt disease with saturated incidence rate,” International Journal of Biomathematics, vol. 11, no. 3, pp. 1–20, 2018. [Google Scholar]

 8.  V. A. Bokil, L. J. S. Allen, M. J. Jeger and S. Lenhart, “Optimal control of a vectored plant disease model for a crop with continuous replanting,” Journal of Biological Dynamics, vol. 13, no. sup1, pp. 325–353, 2019. [Google Scholar]

 9.  R. Donnelly, G. W. Sikazwe and C. A. Gilligan, “Estimating epidemiological parameters from experiments in vector access to host plants, the method of matching gradients,” PLoS Computational Biology, vol. 16, no. 3, pp. 1–15, 2020. [Google Scholar]

10. N. Anggriani, M. Mardiyah, N. Istifadah and A. K. Supriatna, “Optimal control issues in plant disease with host demographic factor and botanical fungicides,” IOP Conference Series: Materials Science and Engineering, vol. 332, no. 1, pp. 1–10, 2018. [Google Scholar]

11. Y. G. Sánchez, Z. Sabir and J. L. Guirao, “Design of a nonlinear SITR fractal model based on the dynamics of a novel coronavirus (COVID-19),” Fractals, vol. 28, no. 8, pp. 1–6, 2020. [Google Scholar]

12. A. Elsonbaty, Z. Sabir, R. Ramaswamy and W. Adel, “Dynamical analysis of a novel discrete fractional SITRS model for COVID-19,” Fractals, vol. 29, no. 8, pp. 1–15, 2021. [Google Scholar]

13. Y. Guerrero Sánchez, Z. Sabir, H. Günerhan and H. M. Baskonus, “Analytical and approximate solutions of a novel nervous stomach mathematical model,” Discrete Dynamics in Nature and Society, vol. 2020, pp. 1–9, 2020. [Google Scholar]

14. Z. Sabir, M. G. Sakar, M. Yeskindirova and O. Saldir, “Numerical investigations to design a novel model based on the fifth order system of Emden–Fowler equations,” Theoretical and Applied Mechanics Letters, vol. 10, no. 5, pp. 333–342, 2020. [Google Scholar]

15. H. Durur, O. Tasbozan and A. Kurt, “New analytical solutions of conformable time fractional bad and good modified Boussinesq equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 447–454, 2020. [Google Scholar]

16. M. T. Gencoglu and P. Agarwal, “Use of quantum differential equations in sonic processes,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 21–28, 2021. [Google Scholar]

17. T. A. Sulaiman, H. Bulut and H. M. Baskonus, “On the exact solutions to some system of complex nonlinear models,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 29–42, 2021. [Google Scholar]

18. F. Evirgen, S. Uçar and N. Özdemir, “System analysis of HIV infection model with 4 under non-singular kernel derivative,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 139–146, 2020. [Google Scholar]

19. A. Yokus, H. Durur and H. Ahmad, “Hyperbolic type solutions for the couple Boiti-Leon-Pempinelli system,” Series: Mathematics and Informatics, vol. 35, no. 2, pp. 523–531, 2020. [Google Scholar]

20. G. Kan, L. Wang, Y. Chen, A. A. Bahaddad and M. A. Khder, “Beam control method for multi-array antennas based on improved genetic algorithm,” Applied Mathematics and Nonlinear Sciences, vol. 7, pp. 1–8, 2021. [Google Scholar]

21. B. Kouider and A. Polat, “Optimal position of piezoelectric actuators for active vibration reduction of beams,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 385–392, 2020. [Google Scholar]

22. M. E. I. Martínez, J. A. Antonino-Daviu, P. F. de Córdoba and J. A. Conejero, “Higher-order spectral analysis of stray flux signals for faults detection in induction motors,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 2, pp. 1–14, 2020. [Google Scholar]

23. T. Li and W. Yang, “Supply chain planning problem considering customer inventory holding cost based on an improved tabu search algorithm,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 2, pp. 557–564, 2020. [Google Scholar]

24. G. Chen, C. Chen, Y. Yuan and L. Zhu, “Modelling and simulation analysis of high-pressure common rail and electronic controlled injection system for diesel engine,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 2, pp. 345–356, 2020. [Google Scholar]

25. W. Suryaningrat, N. Anggriani, A. K. Supriatna and N. Istifadah, “The optimal control of rice tungro disease with insecticide and biological agent,” AIP Conference Proceedings, vol. 2264, no. 1, pp. 1–12, 2020. [Google Scholar]

26. W. Suryaningrat, N. Anggriani and A. K. Supriatna, “On application of differential transformation method to solve host-vector-predator system,” Journal of Physics: Conference Series, vol. 1722, no. 1, pp. 1–9, 2020. [Google Scholar]

27. Z. Sabir, S. Saoud, M. A. Z. Raja, H. A. Wahab and A. Arbi, “Heuristic computing technique for numerical solutions of nonlinear fourth order Emden–Fowler equation,” Mathematics and Computers in Simulation, vol. 178, pp. 534–548, 2020. [Google Scholar]

28. M. Umar, Z. Sabir and M. A. Z. Raja, “Intelligent computing for numerical treatment of nonlinear prey–predator models,” Applied Soft Computing, vol. 80, pp. 506–524, 2019. [Google Scholar]

29. Z. Sabir, M. A. Z. Raja, J. L. Guirao and M. Shoaib, “A novel design of fractional meyer wavelet neural networks with application to the nonlinear singular fractional Lane-Emden systems,” Alexandria Engineering Journal, vol. 60, no. 2, pp. 2641–2659, 2021. [Google Scholar]

30. Z. Sabir, M. A. Z. Raja and D. Baleanu, “Fractional mayer neuro-swarm heuristic solver for multi-fractional order doubly singular model based on lane-emden equation,” Fractals, vol. 29, no. 5, pp. 1–15, 2021. [Google Scholar]

31. A. Raza, M. Rafiq, D. Alrowaili, N. Ahmed, I. Khan et al., “Design of computer methods for the solution of cervical cancer epidemic model,” Computers Materials & Continua, vol. 70, no. 1, pp. 1649–1666, 2022. [Google Scholar]

32. K. Abodayeh, A. Raza, M. Rafiq, M. S. Arif, M. Naveed et al., “Analysis of pneumonia model via efficient computing techniques,” Computers Materials & Continua, vol. 70, no. 3, pp. 6073–6088, 2022. [Google Scholar]

33. A. Raza, M. Rafiq, J. Awrejcewicz, N. Ahmed and M. Mohsin, “Dynamical analysis of coronavirus disease with crowding effect, and vaccination: A study of third strain,” Nonlinear Dynamics, vol. 107, pp. 3963–3982, 2022. [Google Scholar]

34. A. Raza, J. Awrejcewicz, M. Rafiq, N. Ahmed and M. Mohsin, “Stochastic analysis of nonlinear cancer disease model through virotherapy and computational methods,” Mathematics, vol. 10, no. 3, pp. 1–18, 2022. [Google Scholar]

35. A. Raza, J. Awrejcewicz, M. Rafiq and M. Mohsin, “Breakdown of a nonlinear stochastic nipah virus epidemic models through efficient numerical methods,” Entropy, vol. 23, no. 12, pp. 1–19, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.