DOI:10.32604/cmc.2022.027967

| Computers, Materials & Continua DOI:10.32604/cmc.2022.027967 |  |
| Article |
A Truck Scheduling Problem for Multi-Crossdocking System with Metaheuristics
1International University-Vietnam National University, Vietnam National University, HoChiMinh City, 70000, Vietnam
2Faculty of Commerce, Van Lang University, Ho Chi Minh City, 70000, Vietnam
*Corresponding Author: Nguyen Van Thanh. Email: thanh.nguyenvan@vlu.edu.vn
Received: 29 January 2022; Accepted: 23 March 2022
Abstract: The cross-docking is a very important subject in logistics and supply chain managements. According to the definition, cross-docking is a process dealing with transhipping inventory, in which goods and products are unloaded from an inbound truck and process through a flow-center to be directly loaded onto an outbound truck. Cross-docking is favored due to its advantages in reducing the material handing cost, the needs to store the product in warehouse, as well decreasing the labor cost by eliminating packaging, storing, pick-location and order picking. In cross-docking, products can be consolidated and transported as a full load, reducing overall distribution costs. In this paper, we focus on a truck scheduling at the multi-door, multi-crossdocking network with inventory constraints and process capability constraints. In this model, a truck can visit severals docks for loading or unloading many types products. This situation is very common in reality. This study also developed an exact mathematical model using mixed-integer linear programming (MILP) with the objective of minimizing the makespan to obtaint the benchmark in small scale problems. Large scale problems are solved through Simulated Annealing (SA) algorithm and Tabu Search (TS) algorithm. Performance of these algorithms will be compared to benchmarks obtained from solver as well as to each other.
Keywords: Truck scheduling; multi-door; multi-crossdocking network; simulated annealing; tabu search
As the global markets on supply chain has seen an influx of competitors during the past few years, it is pertinent that manufactures, retailers and distributors strive to optimize costs to increase their competitiveness. Driven by such demand, the idea of cross docking was hailed. It was defined by [1] that cross-docking is a process dealing with transshipping inventory, in which goods and products are unloaded from an inbound truck and process through a flow-center to be directly loaded onto an outbound truck. The impact of cross-docking was proved to be highly beneficial in reducing warehousing cost, which takes up around 30% of the product sales cost, when Walmart first pioneering its implementation. In 1992, by putting the cross-docking model into effects across 82% of its inventory, Walmart became the most profitable retailer globally, successfully reduced its cost 2%–3% [2]. One of the earliest works addressing short-term scheduling in cross-dock belongs to [3] whose work is renowned for considering 32 models. The general aim was to generate a sequence of receiving inbound and outbound truck at each door to minimize the makespan. Later on, [4] applied and concluded that the TS metaheuristics could effectively solve a cross-docking problem. The literatures regarding truck scheduling are quite well documented over the year. Williams in [5] was the first who contributed his work to this topic’s literature. The problem, with the objective of minimizing the makespan, was solved using genetic algorithm in combination with simulation model. Another study was of [6], which focused on generating sequences of trucks entering the door, and solutions are developed based on different assumptions to the problem. It was concluded that heuristic algorithm performed better or as well as dynamic programming with or without prior assumption of known truck sequencing. Reference [7] tackled a simplified cross-dock model to gain the underlying complexity of truck sequencing problem, which was split into sub problems of inbound and outbound sequencing separately.
Reference [8] investigated the truck scheduling problem with constraint of time window and deadline for truck departure. Though the paper successfully touched on real-world constraint, the model was simplified to only cross dock with single inbound/outbound door, which may not be applicable to a real situation [8]. The methodology was developed using a hybrid metaheuristic between SA and Keshtel algorithm. Reference [9] also tackled the truck scheduling problem with time window constraints but expanded the problem to multi-door cross docking system. The objective was minimizing tardiness of outbound truck and proposed TS and SA for generating the solution. For multi-door cross-dock, a few studies have taken the approach similar to that of flow shop with parallel machines. Reference [10] is one of the first research which followed such route. Similarly, [11] also applied the idea to their cases with the addition of time-indexed variables. The problem was approached by using constructive polynomial-time algorithm and more traditional scheduling algorithm like Johnson’s rule-based algorithm [12]. The topic also consists of works from works from [11–14]. The work of [14] was constructed predicated on the work of [10] on the two-stage hybrid cross-docking scheduling. The new work appends that of [10] as the authors used time-indexed model as opposed to the original completion time and precedence model. The study went on to develop the solution using compressed differential heuristic and compared the result coined from both models [14]. The problem continued to be expanded to multi cross-docking system, or cross-dock network. Reference [15] first contributed to this topic with a multi cross-dock model to minimize the operational cost. Aside from the trucking scheduling constraint, inventory balance was calculated to deduce the holding cost and inventory level against the capacity. The solution was generated by TS and SA metaheuristics, which were compared against the simple greedy algorithm [16]. Reference [16] presented their work on multi-cross dock which intimately adhered to the previously proposed notations by [3], therefore shared similarity to that of [13]. The work approached the problem of truck scheduling by using sequencing variable. The limitation, however, is the failure to regard the capacity and the increased complexity from the approach. The problem was solved using firefly and SA metaheuristics. The most recent work was that of [17], in which the problem of truck scheduling to find the minimum makespan was done for a multi-serviced/purposed crossdocking network. The problem was solely approached by devising a MILP model [17]. Other extension of cross-docking and its application can be shown in the works [18], where the authors applied particle swarm optimization (ωc-PSO) to minimize the makespan. A cosine decreasing strategy of inertia weight was applied in this study to balance between exploit and explore. Furthermore, crossover strategy is presented to prevent the algorithm from falling into local optimum. The integrated model of routing inbound vehicles between suppliers and cross-docks and outbound vehicles between cross-docks and retailers was considered in [19]. Different to our work, this study aimed to minimize the total cost by optimizing assignment of products to suppliers and retailers instead of scheduling trucks consideration. The problem was solved through endosymbiotic evolutionary algorithm. Multi-objectives for cross-docking problem was studied by [20]. In this study, the authors investigated truck scheduling in a rail–road physical internet cross-docking hub considering energy consumption. The two main objectives were to minimize the energy consumption and cost of outbound truck. The problem was different to this study since main variables were only whether a truck should be assigned to a dock. The multiple-dock visit was not allowed and dock capacity was also not considered in this study. Other extension and related works of cross-dock problems were presented in [21,22]. Though cross-docking problem has been rigorously explored since the 90s, scheduling problems do not take much proportion in the literary vault. For problem regarding multi-cross dock alone, there have only been two papers publicly released, to the best of our knowledge. The aim of this paper is to devise a mathematical model and well as suitable approaches for solution development of large-sized problems to obtain the aim and satisfy all requirement from the company. The model should reflect on the real condition to a certain extent to acquire a level of applicability, which can serve as a foundation for future development. The scope of the problem will fall within the spectrum of crossdocking operational planning through scheduling. However, it will only concern with the exterior operations involving coordinating the trucks, the unloading and loading. This study has some resemblance to the work of [17], however; it differentiates itself with other researches by expanding the problem to multi-door, multi-crossdocking network. Furthermore, the model also allows multi visiting of shipping and receiving trucks to other docks. At each dock, trucks will load or unload some kinds of products which are specified by the dock. Load or unload splitting are also permitted in this model. Dock capacity is also considered here so that the model is very similar to real-practice case. The rest of the paper is organized as follows. Section 2 elaborates on the problem description and crossdocking system, with the corresponding mathematical model, followed by the presenting of algorithms to solve large-sized problems in Section 3. Result analysis is presented in Section 4 and lastly, section 5 recapitulates the paper in discussion and conclusion.
In this paper, the study will focus on the cross-docking process which involve separate, multiple docks that have the capability to handle different types of products. All cross docks allow temporary storages, but at the end of the day, the inventory in all cross docks has to be zero. In addition, the layout is symmetrical, meaning there are an equal number of inbound and outbound doors for each dock. We also assume that the inbound doors and outbound doors are separate, meaning each set has single purpose. At all times, each door can only process one truck and preemption is not allowed. Furthermore, the number of loaded products has to be equal or larger than the demand.
In our model, the super scripts R and S represent for variables relating to process of receiving and shipping, respectively.
Indices 
r index of receiving trucks,
s index of shipping trucks,
d index of docks, 
p index of product types,
t index of time periods,
Parameters
α Time for handling an unit item
γ Transition time of the truck between the docks
BigM A very large number
Variables
Subject to
The Eq. (2) claims that the makespan must be greater or equal to the leaving dock time of all shipping trucks
The Eqs. (3)–(6) ensure that a receiving truck can only visit a dock if it is allowed and its unloaded quantity to this dock is zero in case of no visitation
This imposed the time window constraints on receiving trucks. The receiving truck cannot enter the dock before its allowed soonest enter time in Eq. (7).
The Eqs. (10)–(12) state that if a receiving truck visits dock d then dock h, the associating variable
The Eq. (13) says that the total unloaded quantity at all docks must be equal to the quantity the receiving truck carrying
The Eqs. (14) and (15) ensure that if t is greater than the entering time dock d of receiving truck r,
The Eqs. (16) and (17) guarantee that if t is smaller than the leaving time dock d of receiving truck r,
The Eqs. (18)–(21) forces the constraint that if t is in the range of entering time and leaving time dock d and the receiving truck r also visits the dock
The Eqs. (22) and (23) show that and at any time a receiving truck can only be served by one dock and total number of receiving trucks is served by a dock d cannot be greater than the number of its door.
We also apply the same physical constraints for the shipping trucks, which creates Eqs. (24)–(44).
The total unload at a dock is assumed to be affected right after the receiving truck r enter the dock. If
The same idea is applied for constructing the constraints of shipping trucks. However; the total load to a shipping truck up to time t is calculated immediately after the shipping trucks enter the docks,
By forcing the inventory level is always greater or equal to zero and smaller than capacity through Eqs. (51) and (52), we ensure that the receiving trucks only visits the dock when the dock has enough product for satisfying their load demands.
To solve the small-scale problems, CPLEX Optimizer engine which is developed by IBM company was used to create the benchmark. However, due to the NP-hard property of the original problems, when the size increases metaheuristic algorithms must be adopted. In this study, TS and SA are also implemented and results obtained from CPLEX are used as benchmarks. During TA and SA, this study applies two common following algorithms for creating initial solutions and assignment process. The Fig. 1 shows how the initial solutions are created while Fig. 2 explains about the assignment process.

Figure 1: Algorithm for creating initial solution

Figure 2: Algorithm for assignment
TS and SA are chosen is due to its simplicity in the process of creating new solution in the process of exploring and exploiting, and the foundation of such process is the neighborhood search method. In this paper, the neighborhood search is implemented through two swapping methods in Fig. 3. The object of swapping is the sequence of receiving trucks, the sequence of shipping trucks and the sequence of docks for the first truck. These are also the input into the evaluation function to calculate the corresponding makespan.
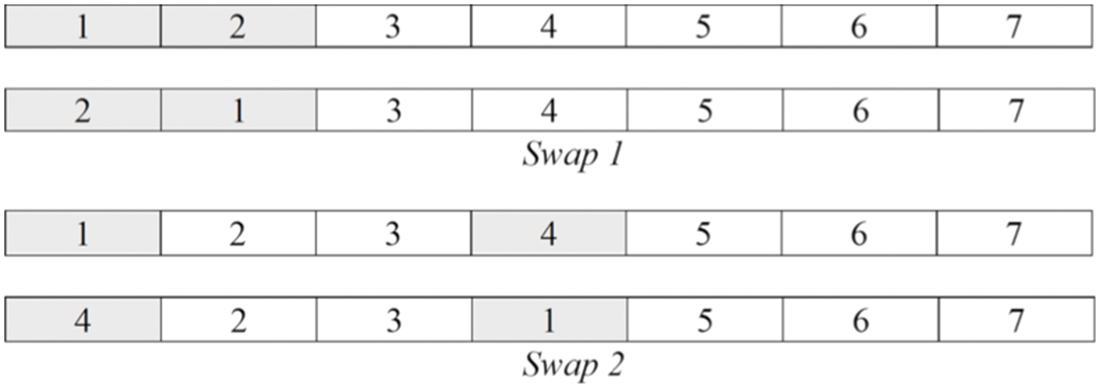
Figure 3: Swapping methods
The pseudo code of TS is described in Fig. 4.

Figure 4: Pseudo code of Tabu Search algorithm
For simulated annealing algorithm, we verify its performance with two versions. The first one employs the sigmoid function which is presented in Fig. 5. The second one applies the metropolis function which is described in Fig. 6.

Figure 5: SA Sigmoid function

Figure 6: SA Metropolis function
To conduct result analysis, ten data sets with different scales are considered. The data set information and the results obtained from CPLEX are given in Tab. 1.
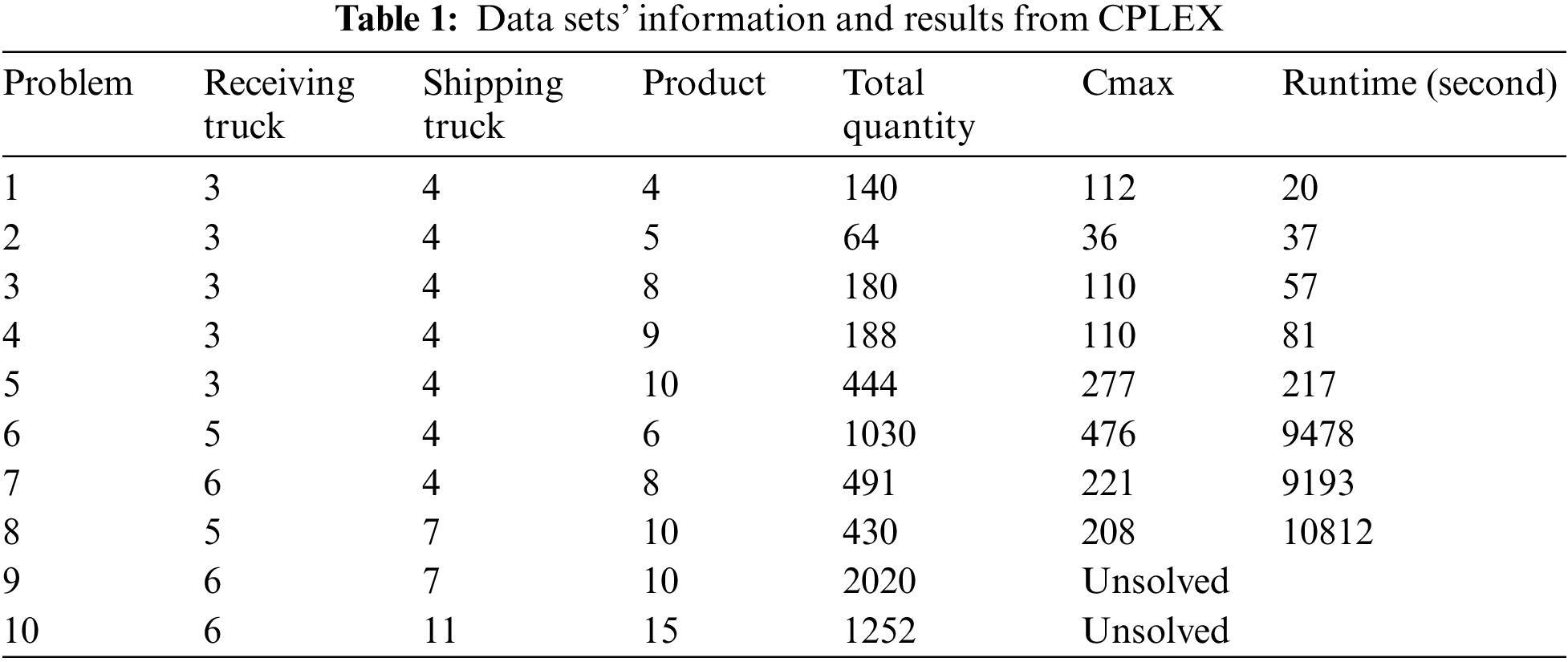
For small-scaled problems, CPLEX works quite well in terms of run time, which only takes less than 2 minutes to solve. When there is increase in the number of trucks and product quantity, the run time grows exponentially as can be seen from the data set 6 to 10.
The comparison between results for both TA and SA and CPLEX are shown in the Tab. 2.
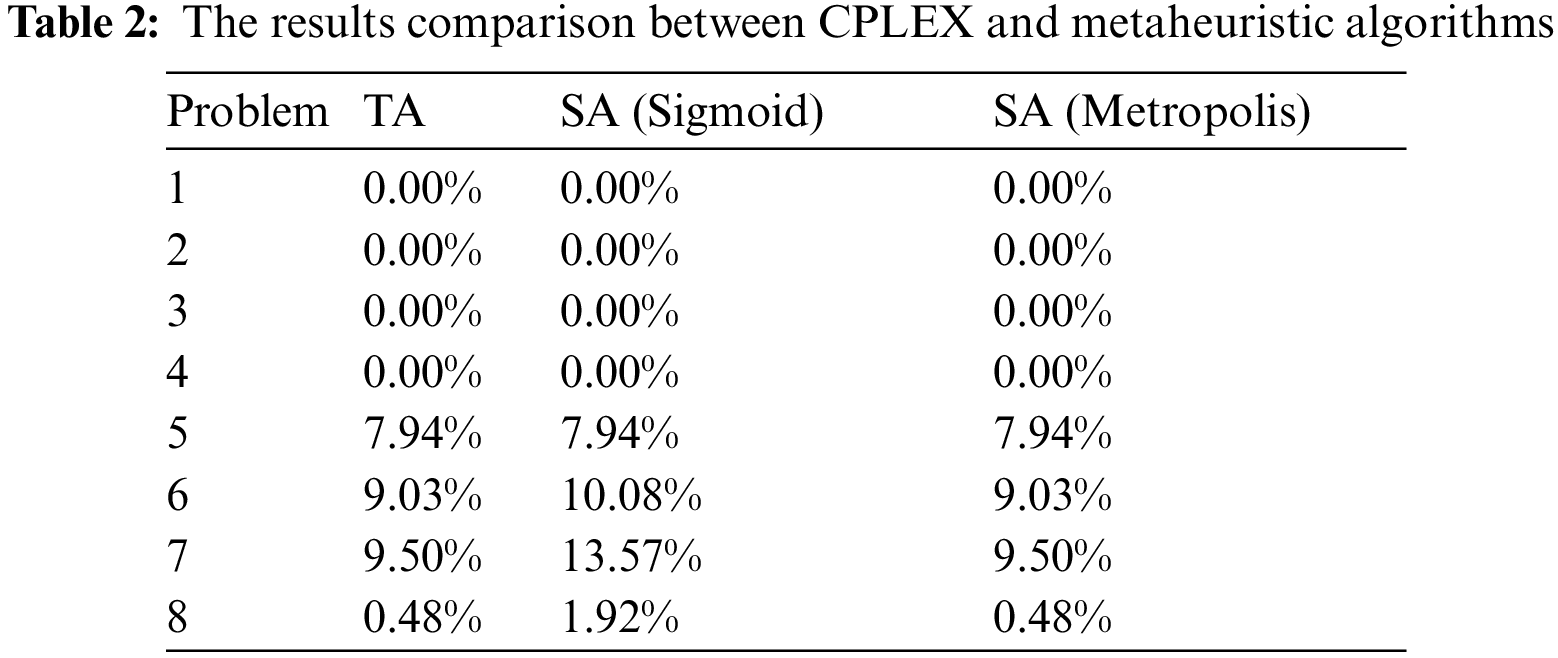
In the Tab. 2 the percentage is calculated as Eq. (53)
On an overall viewpoint, SA Metropolis algorithm yields most promising results when comparing with 2 other methods in gap.
In conclusion, to solve the problem of truck scheduling in crossdocking network, 3 approaches are taken. The first is using MILP in conjunction with CPLEX to solve for the exact solution. However, because of its restriction to small-sized problems, TS and SA are implemented to search for the makespan of large-sized problems. The two metaheuristics exhibit the tradeoff between producing a consistent and good result and having short run time. In general, the results from the approaches proved to be not only optimal and feasible to the constraints of the system, but also managed to adhere and comply to several practical conditions. The result also proves the credibility and feasibility of the model as well as the algorithm. Regarding the all-encompassing and real-life adherent nature of the proposed model, not only does it make a solid contribution to the topic’s literature but also serve as a foundation for further development of the program into software. Further study on this topic can be expanded to include the interior operations of the crossdocking network. Another direction is to expand the problem downstream by combining the truck scheduling problem with the vehicle routing problem to the customers. Although the algorithm obtained reliable results, this study still encountered some challenges in handling the most difficult constraint in the crossdocking problem, the concurrency of load and unload. This concurrency creates challenges in ensuring the feasibility of system state as well as the solutions deriving from the neighborhood. The feasibility is only assured through very carefully checked and revised mechanism. This process sometime takes long time for specific cases.
Funding Statement: The authors wish to express their gratitude to International University-Vietnam National University, Van Lang University, Vietnam for financial support for this research.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. L. Ladier and G. Alpan, “Cross-docking operations: Current research versus industry practice,” Omega, vol. 62, no. 1, pp. 145–162, 2016. [Google Scholar]
2. G. Stalk, P. Evans and L. Shulman, “Competing on capabilities: The new rules of corporate strategy,” Harvard Business Review, vol. 70, no. 2, pp. 57–69, 1992. [Google Scholar]
3. W. Yu, “Operational strategies for cross docking systems,” Ph.D. dissertation, Iowa State University, 2002. [Google Scholar]
4. W. Yu and P. J. Egbelu, “Scheduling of inbound and outbound trucks in cross docking systems with temporary storage,” European Journal of Operational Research, vol. 184, no. 1, pp. 377–396, 2008. [Google Scholar]
5. D. L. McWilliams, P. M. Stanfield and C. D. Geiger, “The parcel hub scheduling problem: A simulation-based solution approach,” Computers & Industrial Engineering, vol. 49, no. 3, pp. 393–412, 2005. [Google Scholar]
6. M. Y. Maknoon and P. Baptiste, “Cross-docking: Scheduling of incoming and outgoing semi trailers,” International Journal of Logistics Research and Applications, vol. 12, no. 1, pp. 249–261, 2009. [Google Scholar]
7. N. Boysen, M. Fliedner and A. Scholl, “Assembly line balancing: Which model to use when,” International Journal of Production Economics, vol. 111, no. 2, pp. 509–528, 2008. [Google Scholar]
8. A. Golshahi-Roudbaneh, M. Hajiaghaei-Keshteli and M. M. Paydar, “Cross-dock scheduling considering time windows and deadline for truck departures,” Scientia Iranica, vol. 28, no. 1, pp. 532–546, 2021. [Google Scholar]
9. G. Ozden and I. Saricicek, “Scheduling trucks in a multi-door cross-docking system with time windows,” Bulletin of the Polish Academy of Sciences-Technical Sciences, vol. 67, no. 1, pp. 349–362, 2019. [Google Scholar]
10. F. Chen and K. Song, “Minimizing makespan in two-stage hybrid cross docking scheduling problem,” Computers & Operations Research, vol. 36, no. 6, pp. 2066–2073, 2009. [Google Scholar]
11. G. B. Fonseca, T. H. Nogueira and M. G. Ravetti, “A hybrid Lagrangian metaheuristic for the cross-docking flow shop scheduling problem,” European Journal of Operational Research, vol. 275, no. 1, pp. 139–154, 2019. [Google Scholar]
12. T. H. Nogueira, F. B. Coutinho, R. P. Ribeiro and M. G. Ravetti, “Parallel-machine scheduling methodology for a multi-dock truck sequencing problem in a cross-docking center,” Computers & Industrial Engineering, vol. 143, no. 1, pp. 1–20, 2020. [Google Scholar]
13. W. Wisittipanich and P. Hengmeechai, “Truck scheduling in multi-door cross docking terminal by modified particle swarm optimization,” Computers & Industrial Engineering, vol. 113, no. 1, pp. 793–802, 2017. [Google Scholar]
14. P. M. Cota, B. M. R. Gimenez, D. P. M. Araujo, T. H. Nogueira, M. C. Souza et al., “Time-indexed formulation and polynomial time heuristic for a multi-dock truck scheduling problem in a cross-docking centre,” Computers & Industrial Engineering, vol. 95, no. 1, pp. 135–143, 2016. [Google Scholar]
15. P. Chen, Y. Guo, A. Lim and B. Rodrigues, “Multiple crossdocks with inventory and time windows,” Computer & Operations Research, vol. 33, no. 1, pp. 43–63, 2006. [Google Scholar]
16. M. M. Isfahani, R. T. Moghaddam and B. Naderi, “Multiple cross-docks scheduling using two meta-heuristic algorithms,” Computers & Industrial Engineering, vol. 74, no. 1, pp. 129–138, 2014. [Google Scholar]
17. G. C. Issi, R. Linfati and J. W. Escobar, “Mathematical optimization model for truck scheduling in a distribution center with a mixed service mode dock area,” Journal of Advanced Transportation, vol. 2020, no. 1, pp. 1–13, 2020. [Google Scholar]
18. Y. Ye, J. Li, K. Li and H. Fu, “Cross-Docking truck scheduling with product unloading/loading constraints based on an improved particle swarm optimisation algorithm,” International Journal of Production Research, vol. 56, no. 16, pp. 5365–5385, 2018. [Google Scholar]
19. K. Y. Lee, J. S. Lim and S. S. Ko, “Endosymbiotic evolutionary algorithm for an integrated model of the vehicle routing and truck scheduling problem with a cross-docking system,” Informatica, vol. 30, no. 3, pp. 481–502, 2019. [Google Scholar]
20. T. Chargui, A. Bekrar, M. Reghioui and D. Trentesaux, “Multi-Objective sustainable truck scheduling in a rail-road physical internet cross-docking hub considering energy consumption,” Sustainability, vol. 11, no. 11, pp. 1–23, 2019. [Google Scholar]
21. O. Theophilus, M. A. Dulebenets, J. Pasha, O. F. Abioye and M. Kavoosi, “Truck scheduling at cross-docking terminals: A follow-up state-of-the-art review,” Sustainability, vol. 11, no. 19, pp. 1–23, 2019. [Google Scholar]
22. R. K. Mavi, M. Goh, N. K. Mavi, F. Jie, K. Brown et al., “Cross-docking: A systematic literature review,” Sustainability, vol. 11, no. 11, pp. 1–19, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |