DOI:10.32604/cmc.2022.027970

| Computers, Materials & Continua DOI:10.32604/cmc.2022.027970 |  |
| Article |
Swarming Computational Approach for the Heartbeat Van Der Pol Nonlinear System
1Department of Mathematics and Statistics, Hazara University, Mansehra, Pakistan
2Faculty of Engineering and Natural Sciences, Bahcesehir University, Istanbul, Turkey
3Department of Mathematics, Faculty of Science, Khon Kaen University, Khon Kaen, 40002, Thailand
4Department of Statistics, Faculty of Science, Khon Kaen University, Khon Kaen, 40002, Thailand
*Corresponding Author: Prem Junsawang. Email: prem@kku.ac.th
Received: 30 January 2022; Accepted: 15 March 2022
Abstract: The present study is related to design a stochastic framework for the numerical treatment of the Van der Pol heartbeat model (VP-HBM) using the feedforward artificial neural networks (ANNs) under the optimization of particle swarm optimization (PSO) hybridized with the active-set algorithm (ASA), i.e., ANNs-PSO-ASA. The global search PSO scheme and local refinement of ASA are used as an optimization procedure in this study. An error-based merit function is defined using the differential VP-HBM form as well as the initial conditions. The optimization of the merit function is accomplished using the hybrid computing performances of PSO-ASA. The designed performance of ANNs-PSO-ASA is implemented for the numerical treatment of the VP-HBM dynamics by fluctuating the pulse shape adjustment terms, external forcing factor and damping coefficient with fixed ventricular contraction period. To perform the correctness of the present scheme, the obtained numerical results through the designed ANN-PSO-ASA will be compared with the Adams numerical method. The statistical investigations with larger dataset are provided using the “mean absolute deviation”, “Theil’s inequality coefficient” and “variance account for” operators to perform the applicability, reliability, and effectiveness of the designed ANNs-PSO-ASA scheme for solving the VP-HBM.
Keywords: Particle swarm optimization; van der Pol heartbeat system; statistical analysis; artificial neural networks; active-set algorithm; numerical computing
To signify the heart functions theoretically, the Van der Pol (VP) oscillatory systems have been introduced like as relaxation, chaotic behavior, periodicity, and bifurcations [1–3]. The solutions of the nonlinear VP heartbeat model (HBM), i.e., VP-HBM are provided using the strength of stochastic based procedures of artificial neural networks (ANNs) under the optimization of particle swarm optimization (PSO) and active set algorithm (ASA), i.e., ANNs-PSO-ASA. The mathematical representation of VP model of heart dynamics based on the nonlinear oscillator is provided as [4]:
where the length of heart fiber is represented by u, a is the heartbeat pulse shape, while the ventricular contraction period is represented by e. The parameters v1 and v2 are the asymmetric spans, factor d is used to replace a cubic term by the harmonic forcing in the standard form of VP and g(t) is the external forcing factor.
Many analytical and numerical schemes have been presented for the approximate solutions of the model given in Eq. (1). Some of them are Adomian decomposition technique [5], homotopy analysis technique [6], parameter-expanding technique [7], linearization technique [8] and Laplace decomposition technique [9], etc. These existing approaches have their specific limitations, and drawbacks. However, the stochastic ANNs-PSO-ASA techniques have never been applied to solve the bioinformatics systems based on the VP-HBM.
The stochastic numerical ANNs techniques are proficient to present the precise and consistent framework to solve the efficient form of the optimization models, which arise in numerous fields [10–14]. Some recent ANNs based schemes contain SIR nonlinear system [15], food chain supply models [16,17], nonlinear smoke models [18,19], higher order singular system [20], nonlinear prey-predator model [21], three-point multi-singular model [22], mosquito dispersal system [23] and many more [24–29]. The above work motivated the author to present an accurate, alternate, reliable, robust computing procedure for the dynamical VP-HBM. In the present work, stochastic solvers based on ANNs optimized with the combinations of PSO-ASA to examine the VP dynamics of heartbeat model using the hybrid of PSO-ASA. To check the accurateness of the present scheme, the Adams method (AM) is applied as a reference solution. Three scenarios of VP model (1) have been taken by fixing the ventricular contraction period value, pulse shape modification factor and the damping coefficients.
Few novel factors of this study are provided as:
• A novel design of the proposed stochastic ANNs-PSO-ASA is presented effectively for solving the biological nonlinear VP-HBM.
• The correctness of the proposed ANNs-PSO-ASA is observed using the comparison of proposed and numerical reference solutions.
• The small values of the absolute error performances indicate the precision of the proposed ANNs-PSO-ASA.
• The performance indices using different operators to check the reliability of the proposed ANNs-PSO-ASA scheme are provided for the biological nonlinear VP-HBM.
• Different statistical operators using the performance of the best results, median (Med) and semi-interquartile range (SIR) have also been provided using the performance of ANNs-PSO-ASA scheme for the biological nonlinear VP-HBM.
The rest of the work is planned as: Section 2 shows the heart modeling. Section 3 represents the design modeling along with the optimization process. Section 4 describes the performance indices. Section 5 is designed based on the numerical results and the concluding remarks with future research directions are given in the last section.
In this section, a brief explanation to solve the VP systems is provided. The VP systems were introduced initially for relaxation oscillator to describe the electronic circuit models [30] and later implementing frequently in the theoretical based cardiac rhythm models. The mathematical form of VP heart classical model based on a nonlinear oscillator [31] is written as:
where a and b are the constant coefficients associated with the duffing/damping parameters. The VP oscillation based on the heart models is presented by Effati et al. [32]. The VP traditional heart model given in Eq. (1) is changed later and its properties are modified using the joining fixed points, stable and saddle node at
The association into these couple fixed points does not change. The amended form of the model (3) using a current parameter e to modify the depolarization period, is given as:
The above model given in Eq. (4) is updated by changing the damping time
The condition
The above Eq. (6) shows the nonlinear VP oscillator with the characteristic of cardiac rhythm.
Neural network mathematical model (1) is designed by exploiting the approximation theory strength in the form of continuous mapping. The solution networks
where the vectors
For solving the biological system (1), a merit function is provided as:
Where
where
3.1 Optimization Process: PSO-ASA
For the solution of the VP-HBM, the hybridization of the PSO-ASA is provided to train the unknown modifiable ANNs parameters.
PSO is known as a swarming global search method introduced in the last decade of the nineteen centuries. PSO has wider range of applications in different fields of the applied sciences and engineering. PSO has a short memory process of the optimization [33,34]. PSO has a number of applications in communication networks [35], solar photovoltaic system [36], clustering high-dimensional data [37], multilevel thresholding [38], growth of energy reserve by considering vehicle-to-grid [39], gene selection in cancer classification [40], humanoid robots [41] and collective robotic search applications [42].
In PSO, every single candidate outcome using an optimization model indicates a particle. To observe the optimal performances of the scheme, the primary swarms spread in the large number of ranges. In the swarm, an objective function is defined by using the fitness value of the problem and the iterative process is used to get the optimal solutions. The optimal solutions iteratively obtained by adjusting the parameters runs in the PSO. The position and the velocity in the swarm is simplified by using the preceding local as well as global best positions are
Where Vi and Xi vectors represent the ith velocity vector and swarm particle, respectively,
ASA is a local optimization search algorithm and applied as a constrained/unconstrained optimization-based problems. ASA is such a significant algorithm that is used in the theory of optimization, as it regulates which constraints will affect the final optimization results. Few recent applications of the ASA are predictive control systems [43], real-time ideal control [44], large-scale of non-smooth optimization models together with box constraints [45], calcium imaging data [46] and non-negative least squares systems [47]. In this work, the optimization procedures through the combination of the PSO-ASA are applied for solving the VP-HBM. Fig. 1 shows the graphical abstract of the proposed scheme for solving the biological model.
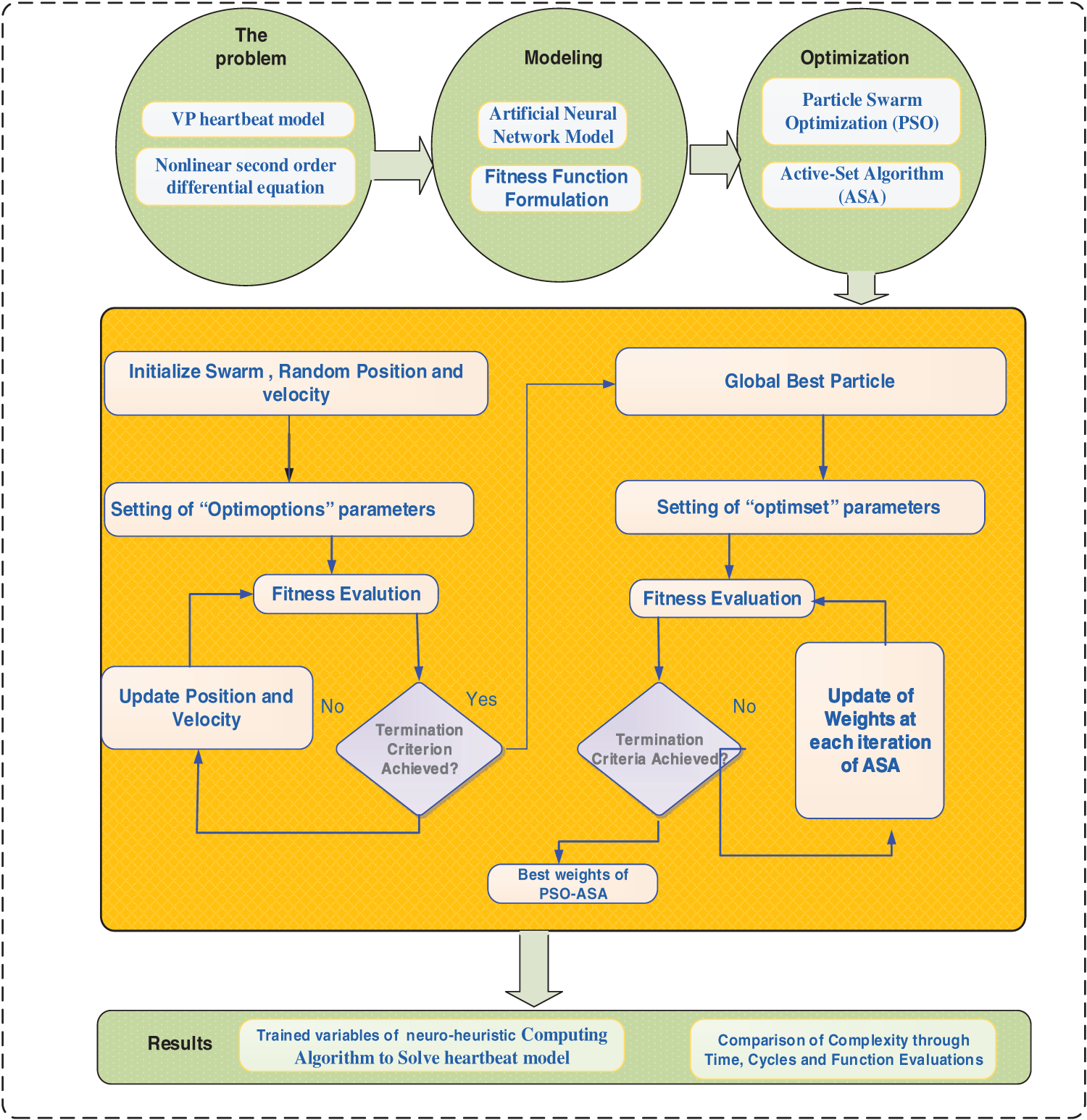
Figure 1: Graphical abstract of present scheme for VP system of heartbeat model
The performance analysis for VP-HBM is constructed for “variance account for (VAF)” “mean absolute deviation (MAD)” and “Theil’s inequality coefficient (TIC)”. These presentations are applied to examine the designed methodologies of the system. The mathematical form of these operators MAD, VAF and TIC is given as:
where j is the grid point, u and

5 Numerical Results and Discussion
The numerical results of the present scheme are accessible for two different problems of the nonlinear VP heart model. Different values for each problem are taken using the asymmetric damping parameters and pulse shape variation factor a. The comparison of the proposed solutions with reference Adams numerical values is performed. To demonstrate the worth of the present design scheme, numerical results are presented in the form of graphical illustrations as well as tabulated form.
Problem 1:
Consider the heartbeat dynamical VP model given in Eq. (1) have been used by varying a, and different performances of v1 and v2. While e is fixed term implemented to switch the atrial shrinkage period. The term d presents to exchange the harmonic forcing of standard VP model. Three different scenarios have been provided using the heartbeat dynamical VP model are given as:
The heartbeat VP model for the above scenario is written as:
The fitness function for model (18) is written as:
The heartbeat VP model for the Scenario 2 is written as:
A merit function is defined for the above Eq. (20) is
The optimization of the above model is executed using the combination of PSO-ASA.
For the above scenario the model becomes as:
The fitness function of the model (22) is written as:
The optimization of the above model is executed with the combination of PSO-ASA. The obtained solutions are provided based on the weights for Scenario 1–3. Figs. 2 to 4 shows the best weights for scenario 1, 2 and 3.

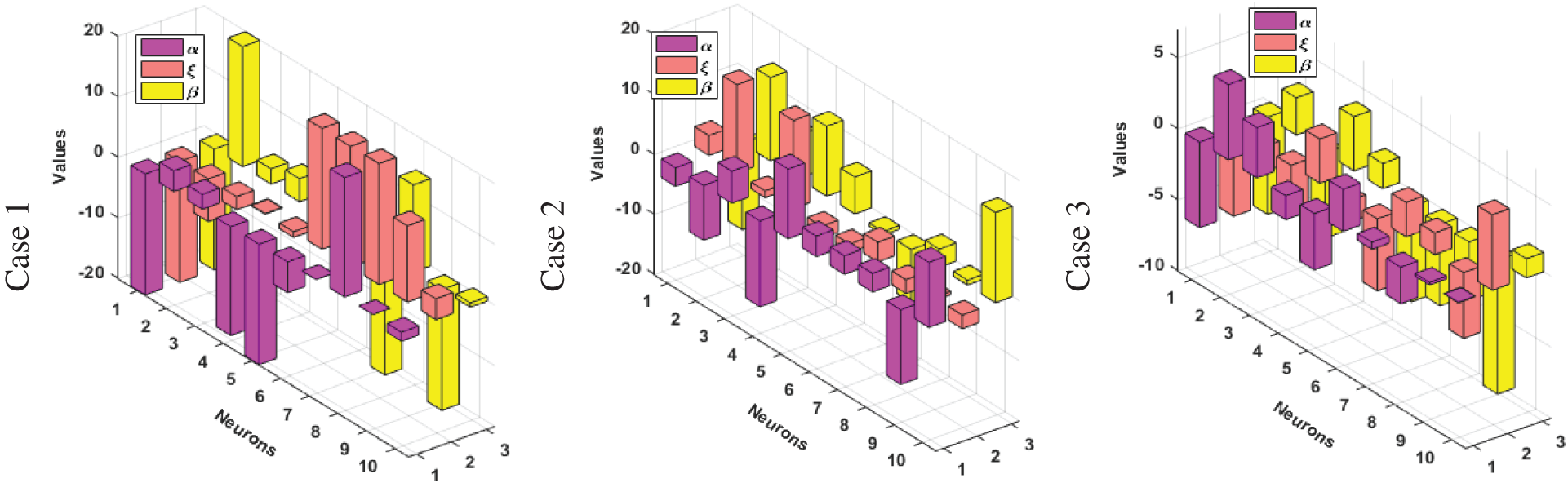
Figure 2: Set of weights for cases (1–3) of 1st scenario
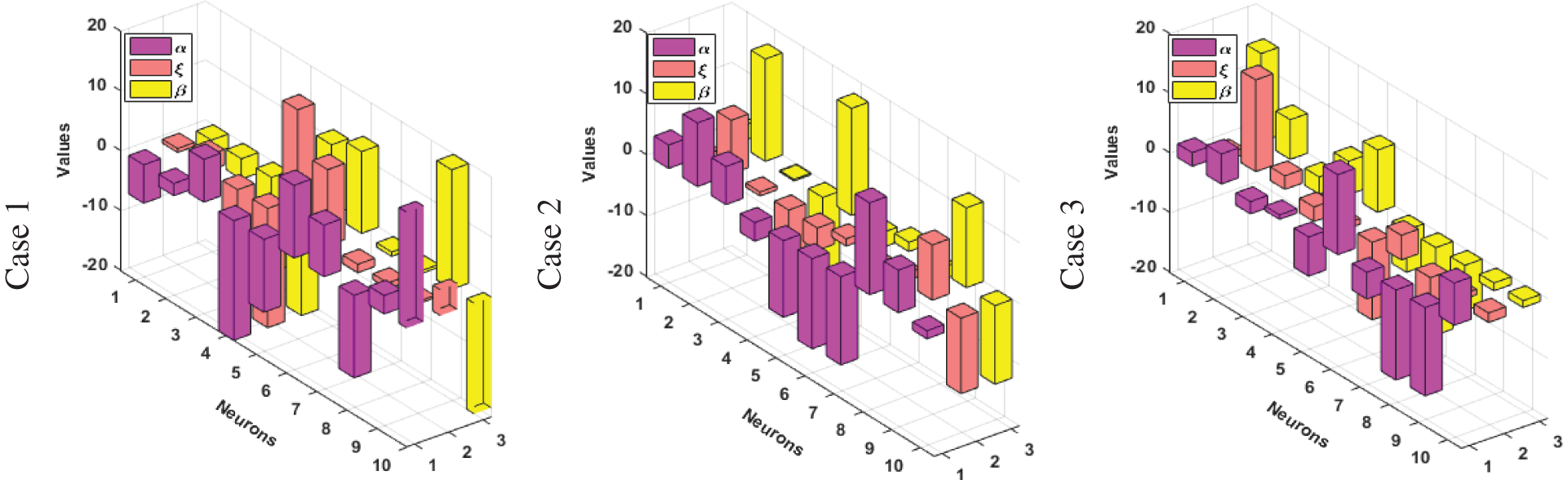
Figure 3: Set of weights for cases (1–3) of Scenario 2
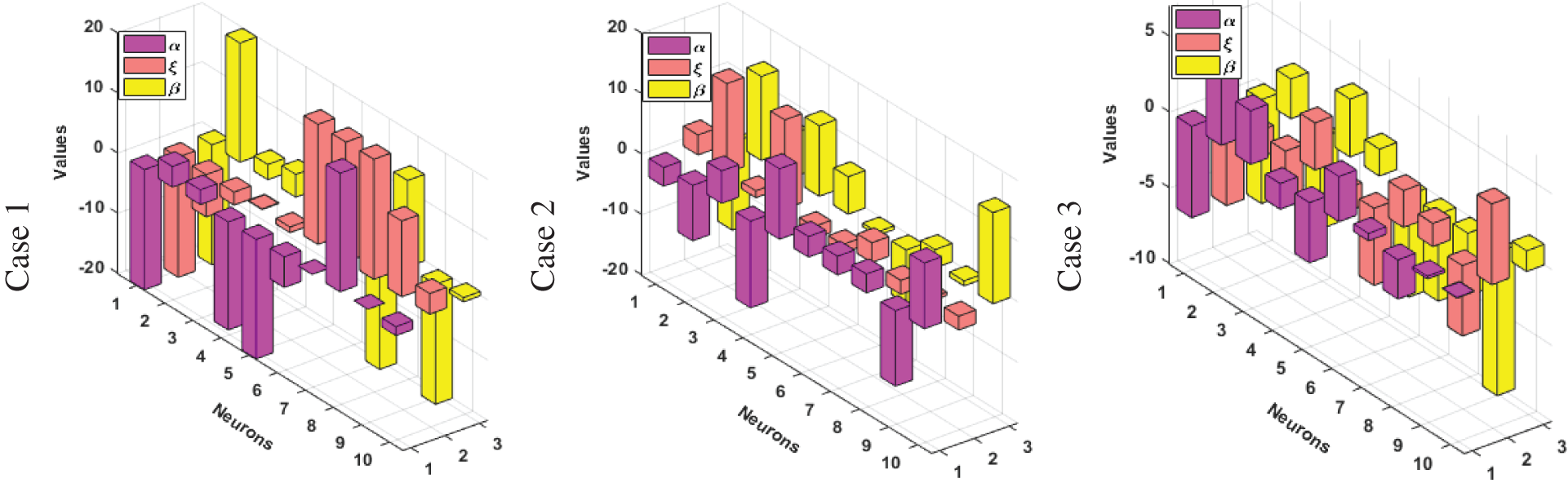
Figure 4: Set of weights for cases (1–3) of Scenario 3
Comparison of results and AE for the present solutions using the reference Adams results for Scenarios 1–3 are illustrated in Figs. 5–7. It is seen that the reference results and obtained results through ANN-PSO-ASA overlapped over one another for all cases of Scenarios 1–3. Moreover, the AE values lie between the ranges of 10−05 to 10−07, 10−04 to 10−05 for cases (1–3) of Scenario 1 and 2. The accuracy is achieved 10−04 to 10−06 for cases (2–3), while the values for case 1 lie around 10−02 to 10−04 of Scenario 3. To assess the convergence and accuracy of the present technique, hundred independent runs based on PSO-ASA are performed. The numerical statistical values based on minimum (Min), Med and SIR operators for hundred runs are tabulated in Tab. 2 for cases (1–3) of Scenario 1. The numerical statistical values based on the statistical operators for the other two Scenarios for hundred runs are tabulated in Tabs. 3 and 4. It is observed that Min values lie in the ranges of 10-05 to 10-11 for case 1, while for cases (2–3) the Min values lie around 10−06 to 10−11. The Med values lie around 10−04 to 10−08 for all cases of Scenario 1. However, the SIR values lie in good ranges for all cases of Scenario 1 and found to be around 10−04 to 10−06. Tab. 2 is based on the statistical values of Scenario 2 for all the cases. As a result, satisfactory level of values has been achieved for all the cases of Scenario 2 and 3. The Min values lie around 10−06 to 10−12, 10−04 to 10−08, 10−06 to 10−11 for cases (1–3). Whereas, the Med and SIR values for all cases lie in the ranges of 10−04 to 10−05.
For the performance, the fitness (FIT), MAD, ENSE and TIC are plotted in Figs. 8–10. The mathematical form of these operators is shown in Eqs. (9), (14), (16) and (17). Near optimum values observed for all the performances that establish the value, worth and significance of the present scheme.
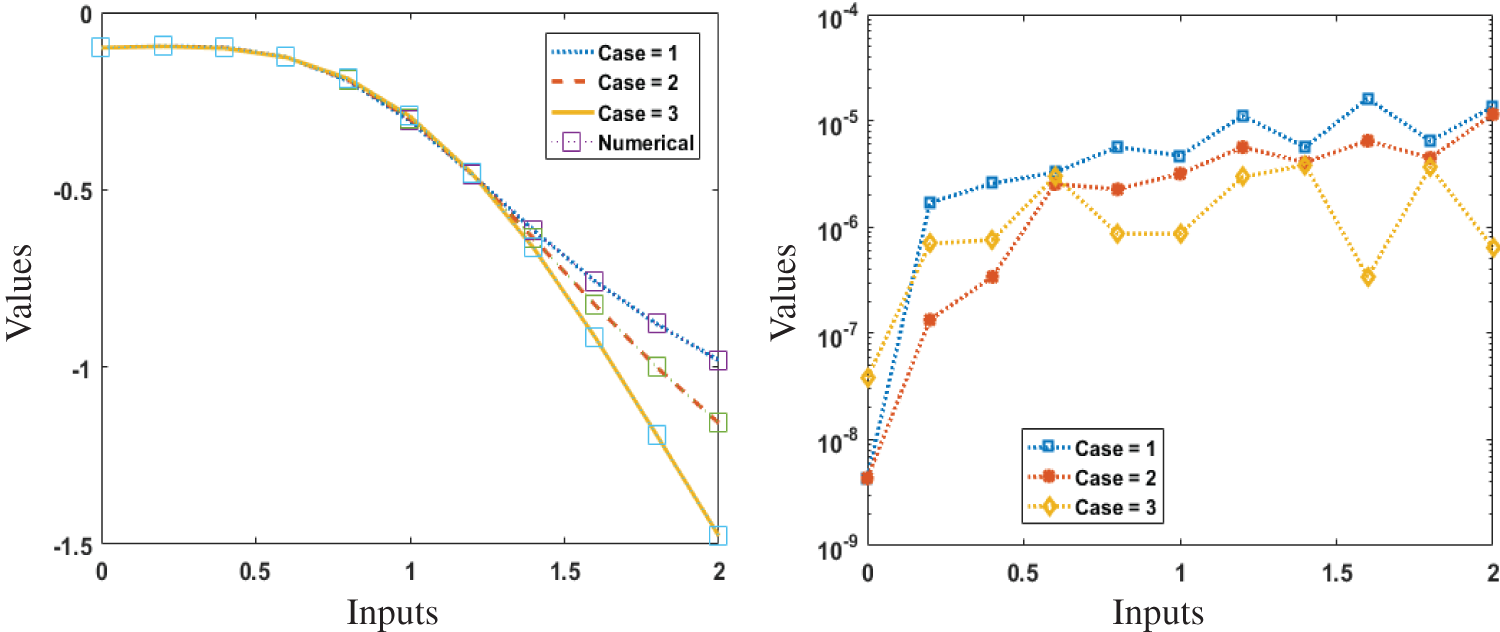
Figure 5: Comparison and AE of present results for cases (1–3) of Scenario 1
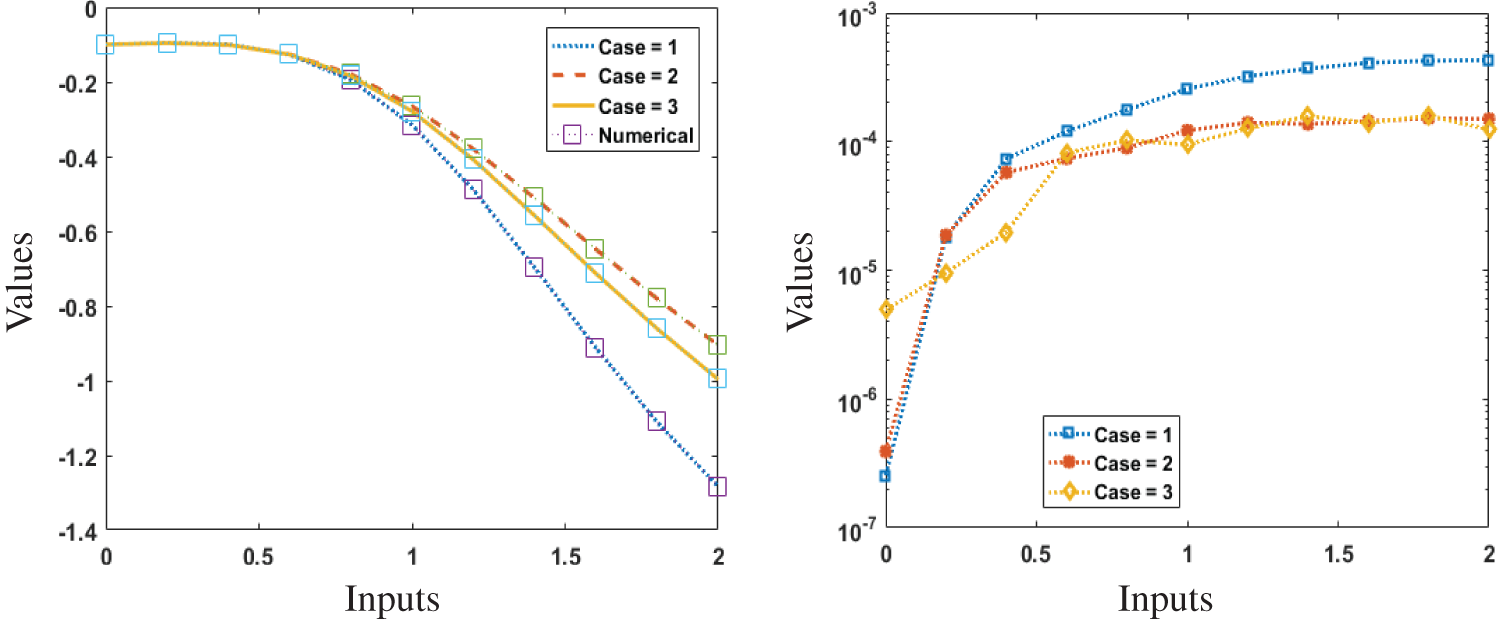
Figure 6: Comparison and AE of present results for cases (1–3) of Scenario 2
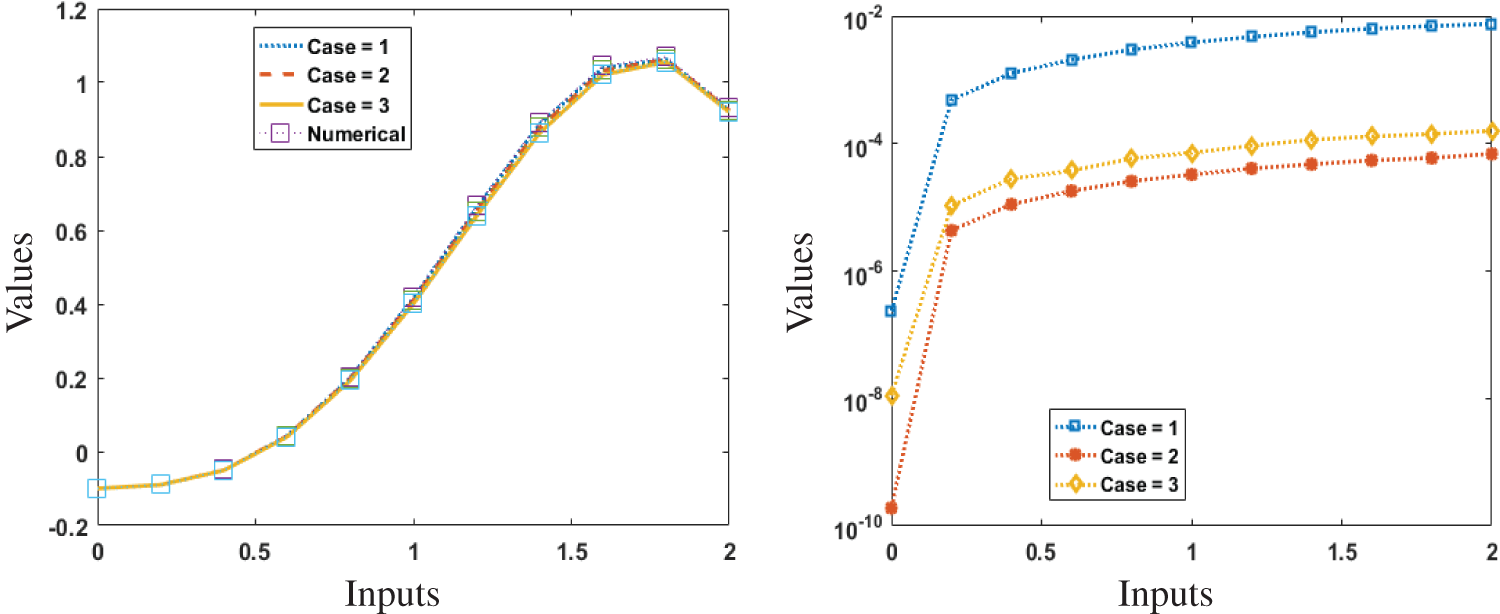
Figure 7: Comparison and AE of present results for cases (1–3) of Scenario 3
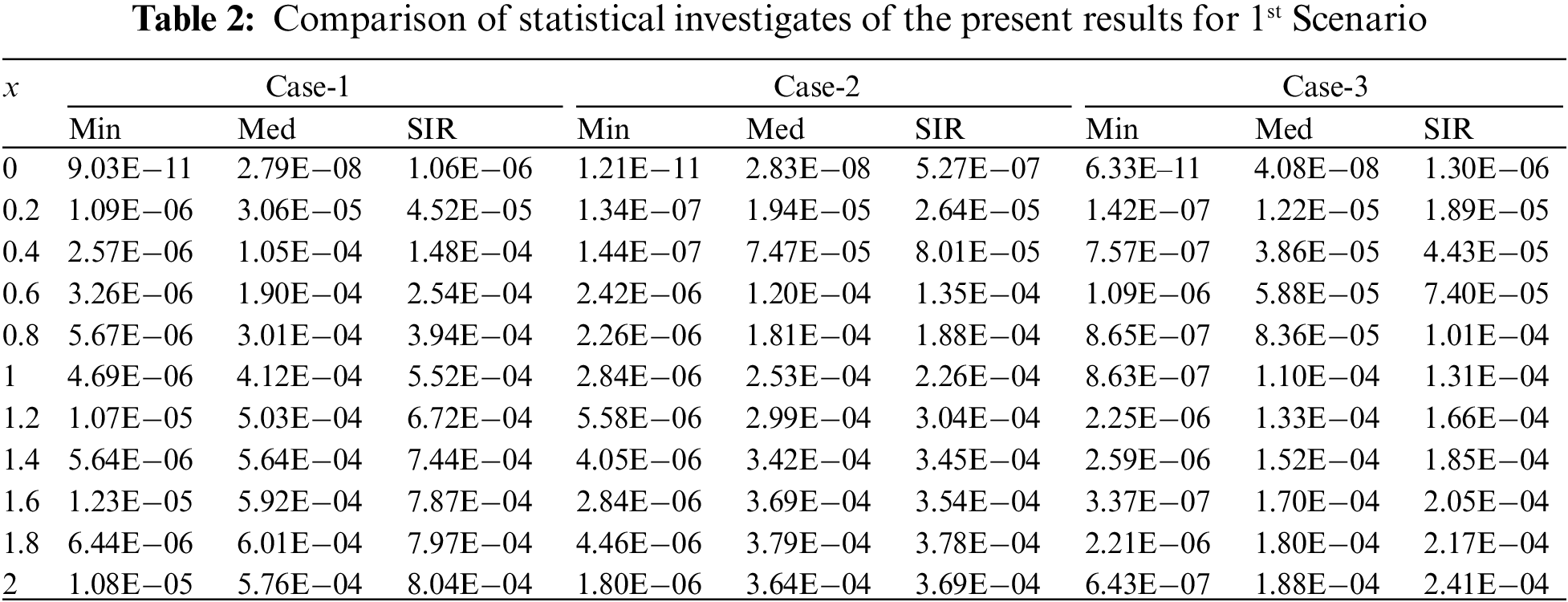
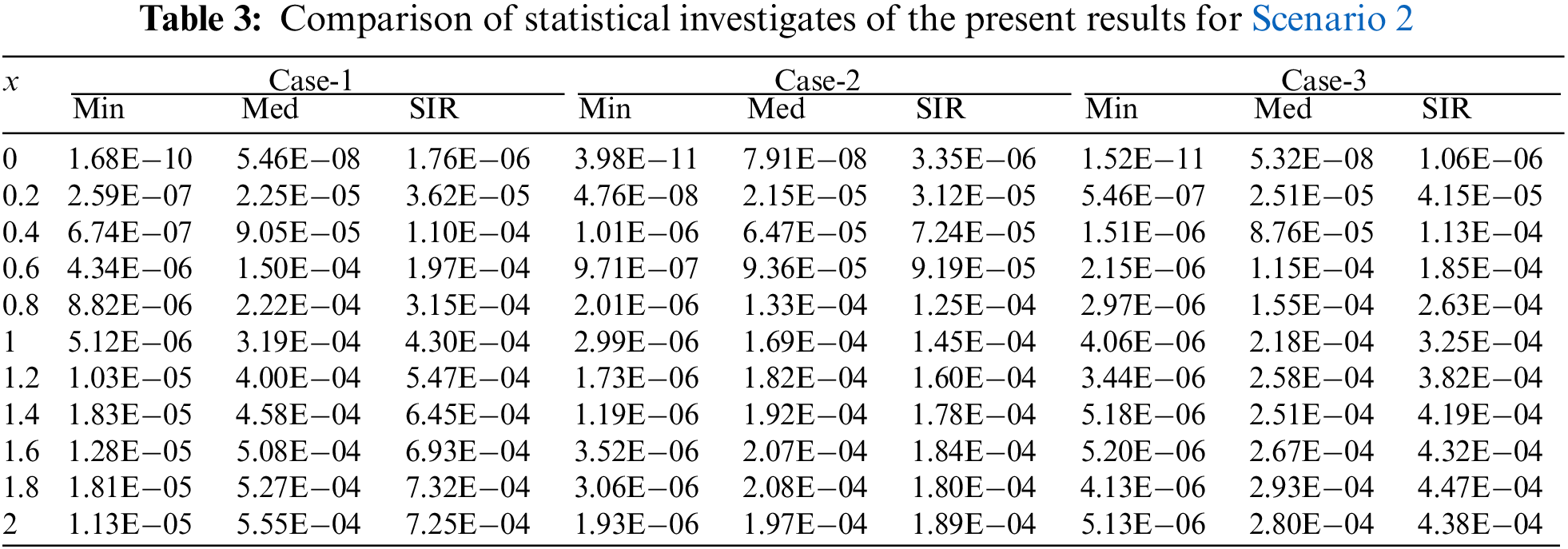
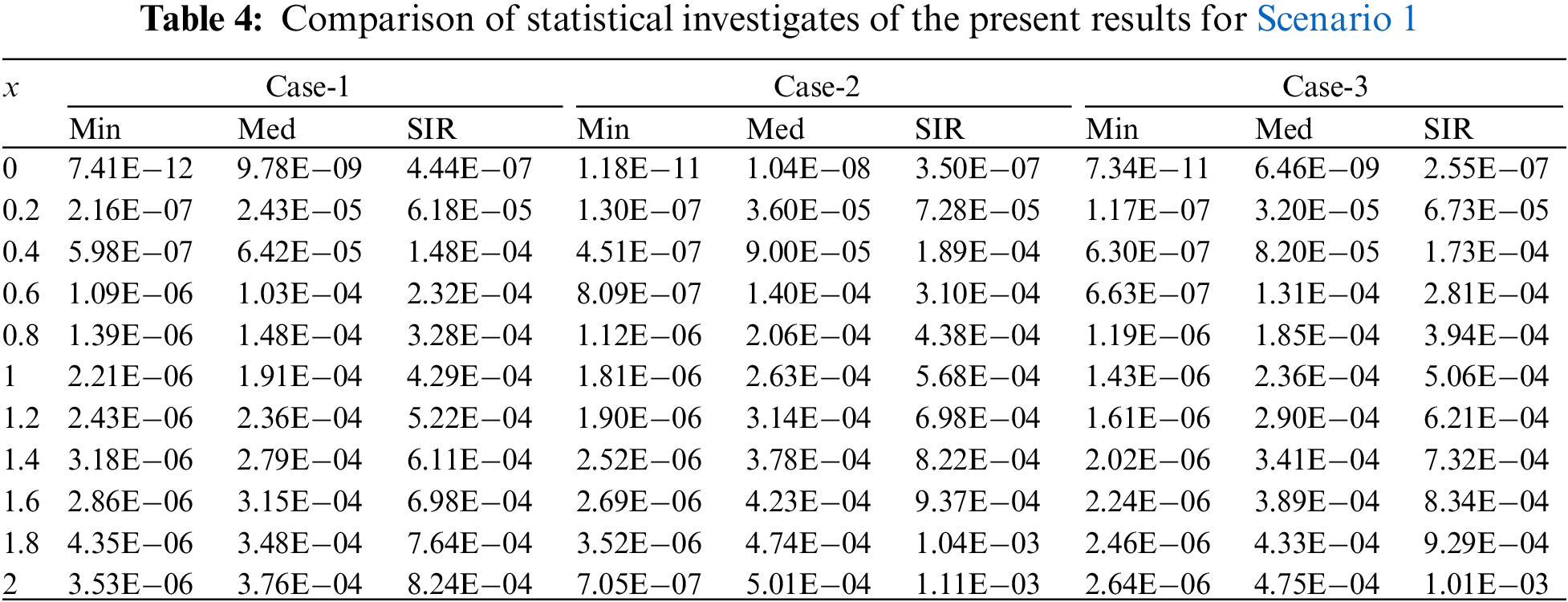
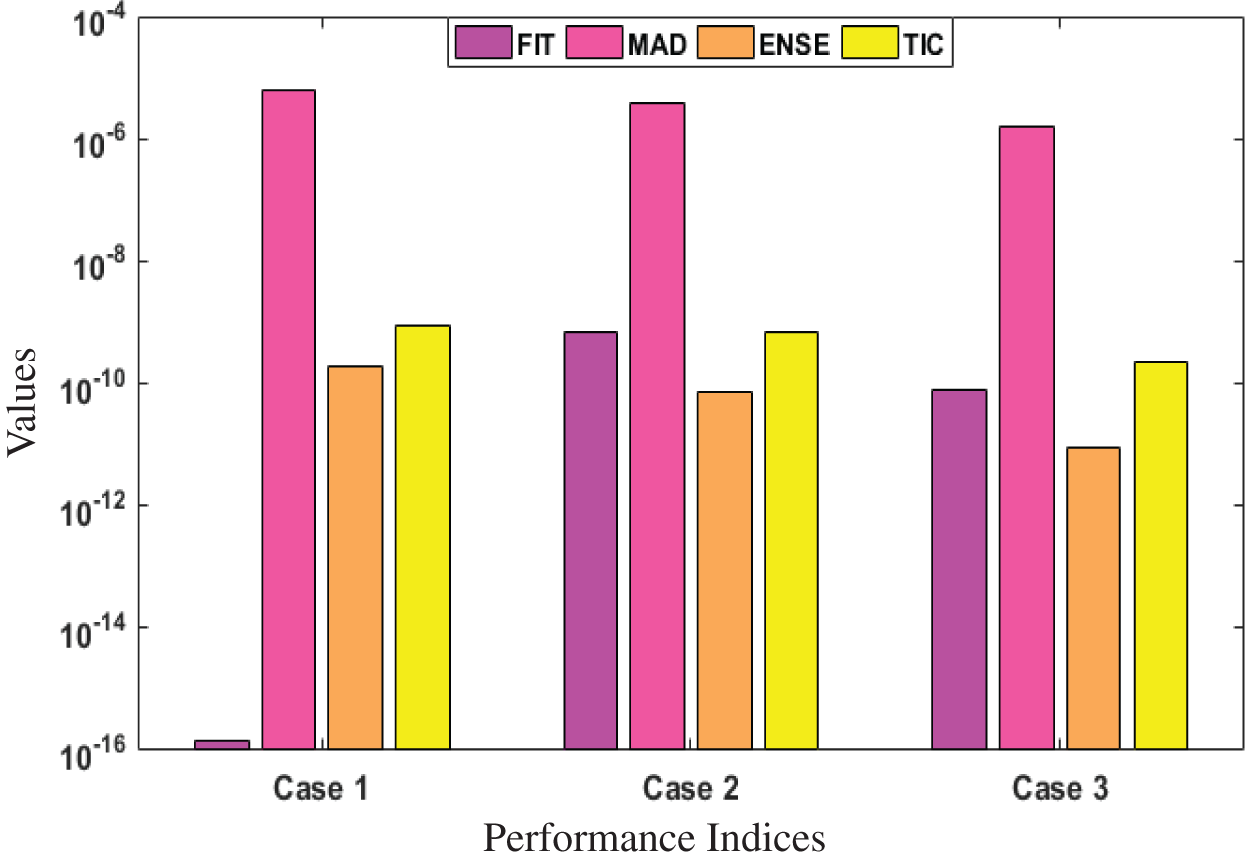
Figure 8: Performance indices for Cases (1–3) of Scenario 1
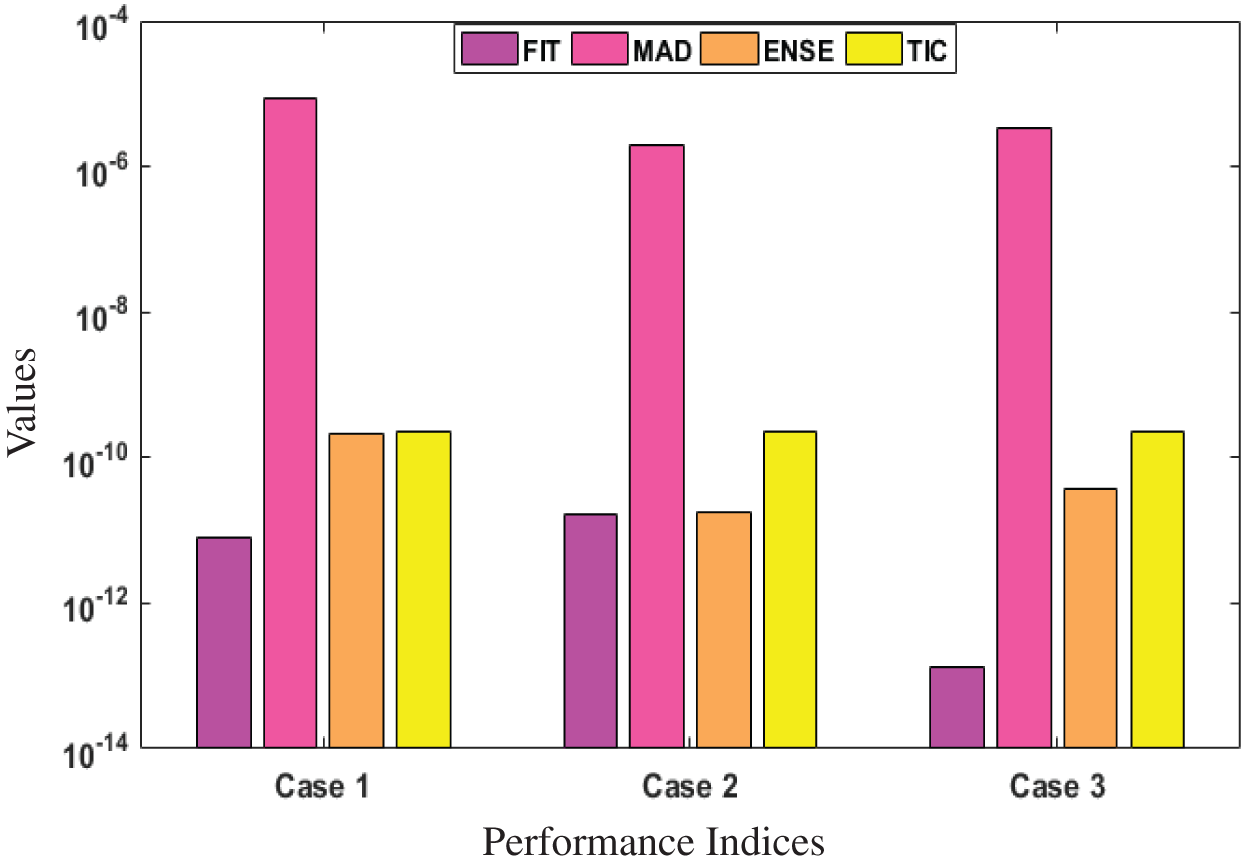
Figure 9: Performance indices for Cases (1–3) of Scenario 2
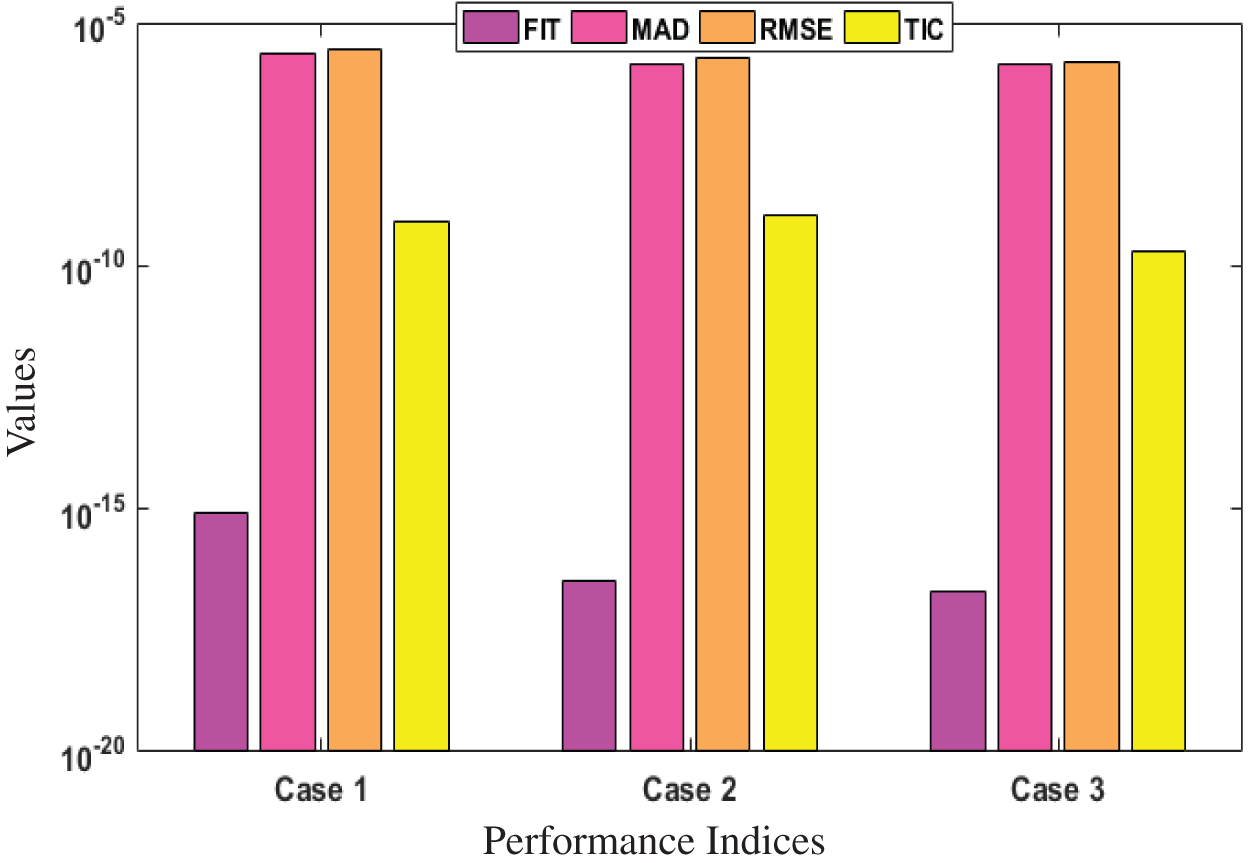
Figure 10: Performance indices for Cases (1–3) of Scenario 3
Following conclusions have been drawn based on the numerical experimentations for solving the VP-HBM using the designed ANNs-PSO-ASA as:
• Artificial neural network using the global and local search methodologies are successfully applied to solve the nonlinear Van der Pol system of heartbeat model numerically.
• The obtained numerical solutions for the Van der Pol system are overlapped with the reference solutions.
• The efficiency of the present algorithm is analysed using the statistical gages based on the median, semi-interquartile range and AE results for the designed model are performed close to zero, which shows the reliable accurateness of the present technique.
• Convergence and accuracy of proposed scheme are authenticated through steadily achieved the optimal performance operators based on MAD, ENSE and TIC in each case of the dynamical heartbeat model.
In future, the designed scheme can be used to solve the fluid dynamics systems [48–51], pantograph differential models [52], data protection systems [53,54]. prediction differential models [55] and nonlinear models based on biology [56,57].
Funding Statement: This research received funding support from the NSRF via the Program Management Unit for Human Resources & Institutional Development, Research and Innovation (Grant Number B05F640088).
Conflicts of Interest: The authors declare that there have no conflicts of interest to report regarding the present study.
1. K. Hall, D. J. Christini, M. Tremblay, J. J. Collins, L. Glass et al., “Dynamic control of cardiac alternans,” Physical Review Letters, vol. 78, no. 23, pp. 4518–4521, 1997. [Google Scholar]
2. K. Grudziński and J. J. Żebrowski, “Modeling cardiac pacemakers with relaxation oscillators,” Physica A: Statistical Mechanics and its Applications, vol. 336, no. 1–2, pp. 153–162, 2004. [Google Scholar]
3. A. M. dos Santos, S. R. Lopes and R. R. L. Viana, “Rhythm synchronization and chaotic modulation of coupled Van der Pol oscillators in a model for the heartbeat,” Physica A: Statistical Mechanics and its Applications, vol. 338, no. 3–4, pp. 335–355, 2004. [Google Scholar]
4. B. B. Ferreira, A. S. de Paula and M. A. Savi, “Chaos control applied to heart rhythm dynamics,” Chaos Solitons & Fractals, vol. 44, no. 8, pp. 587–599, 2011. [Google Scholar]
5. A. K. Shukla, T. R. Ramamohan and S. Srinivas, “A new analytical approach for limit cycles and quasi-periodic solutions of nonlinear oscillators: The example of the forced Van der Pol Duffing oscillator,” Physica Scripta, vol. 89, no. 7, pp. 1–10, 2014. [Google Scholar]
6. Y. M. Chen and J. K. Liu, “A study of homotopy analysis method for limit cycle of van der Pol equation,” Nonlinear Science and Numerical Simulation, vol. 14, no. 5, pp. 1816–1821, 2009. [Google Scholar]
7. A. Kimiaeifar, A. R. Saidi, A. R. Sohouli and D. D. Ganji, “Analysis of modified Van der Pol’s oscillator using He’s parameter-expanding methods,” Current Applied Physics, vol. 10, no. 1, pp. 279–283, 2010. [Google Scholar]
8. S. S. Motsa and P. Sibanda, “A note on the solutions of the Van der Pol and Duffing equations using a linearisation method,” Mathematical Problems in Engineering, vol. 2012, no. 1, pp. 1–10, 2012. [Google Scholar]
9. Y. Khan, M. Madani, A. H. M. E. T. Yildirim, M. A. Abdou and N. Faraz, “A new approach to Van der Pol’s oscillator problem,” Zeitschrift für Naturforschung, vol. 66, no. 10–11, pp. 620–624, 2011. [Google Scholar]
10. Z. Sabir, M. A. Z. Raja, M. Shoaib and J. G. Aguilar, “FMNEICS: Fractional Meyer neuro-evolution-based intelligent computing solver for doubly singular multi-fractional order Lane-Emden system,” Computational and Applied Mathematics, vol. 39, no. 4, pp. 1–18, 2020. [Google Scholar]
11. Z. Sabir, M. A. Z. Raja, J. L. Guirao and M. Shoaib, “Integrated intelligent computing with neuro-swarming solver for multi-singular fourth-order nonlinear Emden-Fowler equation,” Computational and Applied Mathematics, vol. 39, no. 4, pp. 1–18, 2020. [Google Scholar]
12. J. L. Guirao, Z. Sabir and T. Saeed, “Design and numerical solutions of a novel third-order nonlinear Emden-Fowler delay differential model,” Mathematical Problems in Engineering, vol. 2020, no. 3, pp. 1–9, 2020. [Google Scholar]
13. Z. Sabir, S. Saoud, M. A. Z. Raja, H. A. Wahab and A. Arbi, “Heuristic computing technique for numerical solutions of nonlinear fourth order Emden-Fowler equation,” Mathematics and Computers in Simulation, vol. 178, no. 7, pp. 534–548, 2020. [Google Scholar]
14. L. Pan, “Exploration and mining learning robot of autonomous marine resources based on adaptive neural network controller,” Polish Maritime Research, vol. 25, no. s3, pp. 78–83, 2018. [Google Scholar]
15. M. Umar, Z. Sabir, M. A. Z. Raja and Y. G. Sánchez, “A stochastic numerical computing heuristic of SIR nonlinear model based on dengue fever,” Results in Physics, vol. 19, no. 2, pp. 1–9, 2020. [Google Scholar]
16. N. Sk, P. K. Tiwari and S. Pal, “A delay nonautonomous model for the impacts of fear and refuge in a three species food chain model with hunting cooperation,” Mathematics and Computers in Simulation, vol. 192, no. 1, pp. 136–166, 2022. [Google Scholar]
17. Z. Sabir, M. R. Ali and R. Sadat, “Gudermannian neural networks using the optimization procedures of genetic algorithm and active set approach for the three-species food chain nonlinear model,” Journal of Ambient Intelligence and Humanized Computing, vol. 82, no. 9, pp. 1–10, 2022. [Google Scholar]
18. Z. Sabir, M. A. Z. Raja, A. S. Alnahdi, M. B. Jeelani and M. A. Abdelkawy, “Numerical investigations of the nonlinear smoke model using the Gudermannian neural networks,” AIMS Mathematical Biosciences and Engineering, vol. 19, no. 1, pp. 351–370, 2021. [Google Scholar]
19. Z. Sabir, T. Saed, M. S. Alhodaly, H. H. Alsulami and Y. G. Sánchez, “An advanced heuristic approach for a nonlinear mathematical based medical smoking model,” Results in Physics, vol. 32, pp. 1–13, 2021. [Google Scholar]
20. Z. Sabir, H. A. Wahab, S. Javeed and H. M. Baskonus, “An efficient stochastic numerical computing framework for the nonlinear higher order singular models,” Fractal and Fractional, vol. 5, no. 4, pp. 1–14, 2021. [Google Scholar]
21. M. Umar, Z. Sabir and M. A. Z. Raja, “Intelligent computing for numerical treatment of nonlinear prey-predator models,” Applied Soft Computing, vol. 80, no. S48, pp. 506–524, 2019. [Google Scholar]
22. Z. Sabir, D. Baleanu, M. Shoaib and M. A. Z. Raja, “Design of stochastic numerical solver for the solution of singular three-point second-order boundary value problems,” Neural Computing and Applications, vol. 33, no. 7, pp. 2427–2443, 2021. [Google Scholar]
23. M. Umar, M. A. Z. Raja, Z. Sabir, A. S. Alwabli and M. Shoaib, “A stochastic computational intelligent solver for numerical treatment of mosquito dispersal model in a heterogeneous environment,” The European Physical Journal Plus, vol. 135, no. 7, pp. 1–23, 2020. [Google Scholar]
24. Z. Sabir, M. A. Manzar, M. A. Z. Raja, M. Sheraz and A. M. Wazwaz, “Neuro-heuristics for nonlinear singular Thomas-Fermi systems,” Applied Soft Computing, vol. 65, no. 6, pp. 152–169, 2018. [Google Scholar]
25. M. A. Z. Raja, M. Umar, Z. Sabir, J. A. Khan and D. Baleanu, “A new stochastic computing paradigm for the dynamics of nonlinear singular heat conduction model of the human head,” The European Physical Journal Plus, vol. 133, no. 9, pp. 1–21, 2018. [Google Scholar]
26. Z. Sabir, M. A. Z. Raja, M. Umar and M. Shoaib, “Neuro-swarm intelligent computing to solve the second-order singular functional differential model,” The European Physical Journal Plus, vol. 135, no. 6, pp. 1–19, 2020. [Google Scholar]
27. Z. Sabir, H. A. Wahab, M. Umar and F. Erdoğan, “Stochastic numerical approach for solving second order nonlinear singular functional differential equation,” Applied Mathematics and Computation, vol. 363, no. 7–8, pp. 1–11, 2019. [Google Scholar]
28. M. Umar, Z. Sabir, F. Amin, J. L. Guirao and M. A. Z. Raja, “Stochastic numerical technique for solving HIV infection model of CD4 + T cells,” The European Physical Journal Plus, vol. 135, no. 6, pp. 1–19, 2020. [Google Scholar]
29. Z. Sabir, M. A. Z. Raja, J. L. Guirao and M. Shoaib, “A neuro-swarming intelligence based computing for second order singular periodic nonlinear boundary value problems,” Frontiers in Physics, vol. 8, pp. 1–12, 2020. [Google Scholar]
30. B. Van Der Pol and J. Van Der Mark, “The heartbeat considered as a relaxation oscillation, and an electrical model of the heart,” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, vol. 6, no. 38, pp. 763–775, 1928. [Google Scholar]
31. Z. M. Ge and M. Y. Hsu, “Chaos in a generalized van der Pol system and in its fractional order system,” Chaos Solitons & Fractals, vol. 33, no. 5, pp. 1711–1745, 2007. [Google Scholar]
32. S. Effati and M. H. N. Skandari, “Optimal control approach for solving linear Volterra integral equations,” International Journal of Intelligent Systems and Applications, vol. 4, no. 4, pp. 40–46, 2012. [Google Scholar]
33. Y. Shi and R. C. Eberhart, “Empirical study of particle swarm optimization,” in Proc. of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, pp. 1945–1950, 1999. [Google Scholar]
34. A. P. Engelbrecht, Computational intelligence: An introduction. Chichester, UK: Technology & Engineering: John Wiley & Sons Ltd, pp. 632, 2007. [Google Scholar]
35. M. Shen, Z. H. Zhan, W. N. Chen, Y. J. Gong, J. Zhang et al., “Bi-velocity discrete particle swarm optimization and its application to multicast routing problem in communication networks,” IEEE Transactions on Industrial Electronics, vol. 61, no. 12, pp. 7141–7151, 2014. [Google Scholar]
36. A. Khare and S. Rangnekar, “A review of particle swarm optimization and its applications in solar photovoltaic system,” Applied Soft Computing, vol. 13, no. 5, pp. 2997–3006, 2013. [Google Scholar]
37. A. A. Esmin, R. A. Coelho and S. Matwin, “A review on particle swarm optimization algorithm and its variants to clustering high-dimensional data,” Artificial Intelligence Review, vol. 44, no. 1, pp. 23–45, 2015. [Google Scholar]
38. B. Akay, “A study on particle swarm optimization and artificial bee colony algorithms for multilevel thresholding,” Applied Soft Computing, vol. 13, no. 6, pp. 3066–3091, 2013. [Google Scholar]
39. J. Soares, T. Sousa, H. Morais, Z. Vale, B. Canizes et al., “Application-specific modified particle swarm optimization for energy resource scheduling considering vehicle-to-grid,” Applied Soft Computing, vol. 13, no. 11, pp. 4264–4280, 2013. [Google Scholar]
40. E. Alba, J. Garcia-Nieto, L. Jourdan and E. G. Talbi, “Gene selection in cancer classification using PSO/SVM and GA/SVM hybrid algorithms,” in Proc. of the IEEE Congress on Evolutionary Computation, Singapore, pp. 284–290, 2007. [Google Scholar]
41. K. B. Lee and J. H. Kim, “Multiobjective particle swarm optimization with preference-based sort and its application to path following footstep optimization for humanoid robots,” IEEE Transactions on Evolutionary Computation, vol. 17, no. 6, pp. 755–766, 2013. [Google Scholar]
42. S. Doctor, G. K. Venayagamoorthy and V. G. Gudise, “Optimal PSO for collective robotic search applications,” in Proc. of the 2004 Congress on Evolutionary Computation (IEEE Cat. No.04TH8753), Portland, OR, USA, pp. 1390–1395, 2004. [Google Scholar]
43. S. Koehler, C. Danielson and F. Borrelli, “A primal-dual active-set method for distributed model predictive control,” Optimal Control Applications and Methods, vol. 38, no. 3, pp. 399–419, 2017. [Google Scholar]
44. R. Quirynen, A. Knyazev and S. Di Cairano, “Block structured preconditioning within an active-set method for real-time optimal control,” in 2018 European Control Conf. (ECC), Limassol, Cyprus, pp. 1154–1159, 2018. [Google Scholar]
45. Y. Li, G. Yuan and Z. Sheng, “An active-set algorithm for solving large-scale nonsmooth optimization models with box constraints,” PlOS One, vol. 13, no. 1, pp. 1–16, 2018. [Google Scholar]
46. J. Friedrich and L. Paninski, “Fast active set methods for online spike inference from calcium imaging,” Advances In Neural Information Processing Systems, vol. 29, pp. 1984–1992, 2016. [Google Scholar]
47. J. M. Myre, E. Frahm, D. J. Lilja and M. O. Saar, “TNT-NN: A fast active set method for solving large non-negative least squares problems,” Procedia Computer Science, vol. 108, no. 2, pp. 755–764, 2017. [Google Scholar]
48. T. Sajid, S. Tanveer, M. Munsab and Z. Sabir, “Impact of oxytactic microorganisms and variable species diffusivity on blood-gold Reiner-Philippoff nanofluid,” Applied Nanoscience, vol. 11, no. 1, pp. 321–333, 2020. [Google Scholar]
49. T. Sajid, S. Tanveer, Z. Sabir and J. L. G. Guirao, “Impact of activation energy and temperature-dependent heat source/sink on Maxwell-Sutterby fluid,” Mathematical Problems in Engineering, vol. 2020, pp. 1–15, 2020. [Google Scholar]
50. Z. Sabir, R. Akhtar, Z. Zhiyu, M. Umar and M. Imran etal, “A computational analysis of two-phase casson nanofluid passing a stretching sheet using chemical reactions and gyrotactic microorganisms,” Mathematical Problems in Engineering, vol. 2019, no. 4, pp. 1–12, 2019. [Google Scholar]
51. M. Umar, R. Akhtar, Z. Sabir, H. A. Wahab, Z. Zhiyu et al., “Numerical treatment for the three-dimensional eyring-powell fluid flow over a stretching sheet with velocity slip and activation energy,” Advances in Mathematical Physics, vol. 2019, no. 1, pp. 1–12, 2019. [Google Scholar]
52. W. Adel and Z. Sabir, “Solving a new design of nonlinear second-order Lane-Emden pantograph delay differential model via Bernoulli collocation method,” The European Physical Journal Plus, vol. 135, no. 5, pp. 1–12, 2020. [Google Scholar]
53. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]
54. X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]
55. Z. Sabir, J. L. Guirao, T. Saeed and F. Erdoğan, “Design of a novel second-order prediction differential model solved by using adams and explicit Runge-Kutta numerical methods,” Mathematical Problems in Engineering, vol. 2020, no. 3, pp. 1–7, 2020. [Google Scholar]
56. Y. Guerrero Sánchez, Z. Sabir, H. Günerhan and H. M. Baskonus, “Analytical and approximate solutions of a novel nervous stomach mathematical model,” Discrete Dynamics in Nature and Society, vol. 2020, pp. 1–9, 2020. [Google Scholar]
57. Y. G. Sánchez, Z. Sabir and J. L. Guirao, “Design of a nonlinear SITR fractal model based on the dynamics of a novel coronavirus (COVID-19),” Fractals, vol. 28, no. 8, pp. 1–6, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |