[BACK]
Computers, Materials & Continua
DOI:10.32604/cmc.2022.025245 |  |
| Article | |
Quaternion Integers Based Higher Length Cyclic Codes and Their Decoding Algorithm
Muhammad Sajjad1, Tariq Shah1,*, Mohammad Mazyad Hazzazi2, Adel R. Alharbi3 and Iqtadar Hussain4
1Department of Mathematics, Quaid-I-Azam University, Islamabad, 45320, Pakistan
2Department of Mathematics, College of Science, King Khalid University, Abha, 61413, Saudi Arabia
3College of Computing and Information Technology, University of Tabuk, Tabuk, 71491, Saudi Arabia
4Department of Mathematics, Statistics and Physics, Qatar University, Doha, 2713, Qatar
*Corresponding Author: Tariq Shah. Email: stariqshah@gmail.com
Received: 17 November 2021; Accepted: 15 February 2022
Abstract: The decoding algorithm for the correction of errors of arbitrary Mannheim weight has discussed for Lattice constellations and codes from quadratic number fields. Following these lines, the decoding algorithms for the correction of errors of n=p−12 length cyclic codes (C) over quaternion integers of Quaternion Mannheim (QM) weight one up to two coordinates have considered. In continuation, the case of cyclic codes of lengths n=p−12 and 2n−1=p−2 has studied to improve the error correction efficiency. In this study, we present the decoding of cyclic codes of length n=φ(p)=p−1 and length 2n−1=2φ(p)−1=2p−3 (where p is prime integer and φ is Euler phi function) over Hamilton Quaternion integers of Quaternion Mannheim weight for the correction of errors. Furthermore, the error correction capability and code rate tradeoff of these codes are also discussed. Thus, an increase in the length of the cyclic code is achieved along with its better code rate and an adequate error correction capability.
Keywords: Mannheim distance; monoid ring; cyclic codes; parity check matrix extension; syndromes decoding; code rate and error correction capability
1 Introduction
The study of the features of codes and their suitability for various applications is known as coding theory. Data compression, error detection and correction, security, data storage, and data transmission are all performed by codes. Code words are used in some digital communication systems for error correction or detection. Because of this, all code words in a message may have the same pattern of digits. As a result, the message becomes more redundant. As part of the message identification, each code word (without the first) in the message would have a code syndrome. The cyclic code does not utilize these syndromes for error correction. When a message's code words have been switched in specific sections of the system, simple decoding methods may reveal this. To decide which syndromes are appropriate, random and burst error correction codes are analyzed and compared to one another.
A perfect code is defined as one that achieves a bound (the sphere-packing bound) in a given metric. Perfect codes have long piqued the interest of coding theorists and mathematicians, since they play an essential theoretical and practical role in coding theory. Over finite fields, several perfect codes with regard to the Hamming metric are known, [1–5]. In the perspective of Hamming distance, the single error correction of cyclic codes (C) over the ring Zm of integers modulo m are defined by Han et al. [6]. Then, Tamm et al. [7] established that integer’s cyclic codes for general construction are perfect, and these codes are used for single error correction.
Though, in [8] Huber investigated that cyclic codes over Gaussian integers for two-dimensional signal space are perfect for one Mannheim error, and he further shaded light on the difference in Hamming and Mannheim distances. On the other hand, in [9] Huber substantiated the Mac William’s theorem for the codes having symbols from a finite field with a two-dimensional modulo metric. Neto et al. [10] spoke the cyclic codes over Gaussian integers Z[i] for Mannheim weight one and two, besides he has given a comparison of these cyclic codes with the cyclic codes having symbols from the ring Z[w] of algebraic integers. Nevertheless, Kostadinov [11] derived the bit error probability of the transmitted code word of an integer cyclic code using quadrature amplitude modulation (QAM). For two-dimensional signal patterns like QAM, Severe coding difficulties arise from the algebraic theory of block-cyclic codes over finite fields.
The cyclic, Bose Chaudhuri Hocquenghem (BCH), Srivastava, alternant, and Goppa codes having symbols from a unitary finite commutative ring R, are described by Andrade et al. in [12]. Accordingly, for this purpose, they used the factor ring of polynomial ring R[x] in one indeterminate x. Özen et al. [13] has introduced Quaternion Mannheim (QM) distance as a metric and give a decoding procedure of Cyclic codes of length n=p−12 over Quaternion integers. Andrade et al. [14,15] has given the modified Berlekamp-Massey decoding algorithm for cyclic, BCH, Goppa, alternan and Srivastava codes designed by the monoid ring R[x,12Z0] analogue to the codes obtained by polynomial ring R[x]. In continuation, Shah et al. [16,17] in the place of a polynomial ring, the construction of cyclic, BCH, Goppa, alternan and Srivastava codes over a finite ring are realized by the monoid ring.
Özen et al. in [18] further contributed some results on the construction of cyclic codes over some finite Quaternion integer rings with respect to the QM distance. However, Güzeltepe et al. [19] has discussed Gaussian, Lipschitz, and Hurwitz weight codes for error correction and revealed that these codes are perfect. A comparison of the code rate, bandwidth, and average energy is also part of the study of [19]. Following the cyclic code’s design through monoid ring as described in [14–19] have introduced the decoding of C over Quaternion integers of length n=p−12 for QM weight two. Moreover, they also discussed the corresponding 2n−1=p−2 length cyclic codes of the n=p−12 length cyclic codes for QM weight one and two.
The goal of this work is to demonstrate a decoding procedure for cyclic codes of length n=φ(p)=p−1 with QM weight one and two by following the lines drawn in [13,20]. In addition, followed monoid ring technique given in [20] for the designing of cyclic codes, the decoding procedure of the cyclic codes of length 2n−1=2φ(p)−1=2p−3 with QM weight one and two is obtained. Thus, a gain in the increase code rate of cyclic codes due to prime p, is achieved.
The rest of the paper is laid out as follows: Related work is discussed in Section 2. In Section 3, single and double error-correcting cyclic codes of length n=φ(p)=p−1 for QM weight one and two by following techniques in [10,20]. In Section 4, the parity check matrix (H) of the cyclic code of length n=φ(p)=p−1 is extended to parity check matrix (H) of the cyclic code of length 2n−1=2φ(p)−1=2p−3. Consequently, single and double error-correcting cyclic codes of length 2n−1=2φ(p)−1 for QM weight one and two through monoid rings by following techniques in [20] is obtained. In Section 5, code length and code rates comparison of the cyclic codes for different odd primes. Finally, Section 6, concluded the findings of the study and future directions respectively.
2 Preliminaries
This section provides the key concepts and basic findings that will be used in the study of upcoming sections. First of all, we recall definition of Quaternion integers, QM weight, QM distance and some related results.
2.1 Hamilton Quaternion Integers
By following [21], the Hamilton Quaternion algebra over the set of the real number R, indicate by H(R), is the associative unital algebra by the following conditions.
1. H(R)={b0+b1i+b2j+b3k:b0,b1,b2,b3∈R} is free R module.
2. Multiplicative identity is 1.
3. i2=j2=k2=−1 and jk=−kj=i,ki=−ik=j,ij=−ji=k.
The Quaternion integer ring H(Z)={b0+b1i+b2j+b3k:b0,b1,b2,b3∈Z} is contain in H(R), where Z is the ring of integers. If q=b0+b1i+b2j+b3k is a Quaternion integer, then q¯=b0−b1i−b2j−b3k is the Quaternion conjugate of q. N(q)=qq¯=b02+b12+b22+b32 is the norm of q. A Quaternion integer q having only two parts one is scalar part b0 and other is vector part b1i+b2j+b3k. In Quaternion integer’s commutative property of multiplication is not hold. It is possible only in case of two vector part of quaternion integers are parallel.
Define H(K) as: H(K)={c+dV:c,d∈Z}, Where V indicates (i+j+k). H(K) is a subring of the Quaternion integer ring H(Z), then the commutative property of multiplication holds over H(K).
Theorem: In [21], the set of natural numbers for each odd rational prime p, there is a prime π∈H(Z), such that N(π)=p=ππ¯. In particular, p is not prime in H(Z).
Corollary: In [18], π∈H(Z) is prime in H(Z) if and only if N(π) is prime in Z.
Definition: In [18], let residue class of H(K)π is H(K) modulo π, π=a+bV. Then, the modulo function
ω:H(K)={c+dV:c,d∈Z}→H(K)π define as ω(q)=z mod π=q−[qπ¯ππ¯]ππ.¯
where z∈H(K)π. In the above expression, the number of [.] is rounding to the nearest integer. Quaternion integer rounding should be possible by rounding the coefficients of vector part and scalar part independently to the nearest integer.
Definition: Let β,ρ∈H(K)π and α=β−ρ=(b0+b1i+b2j+b3k)(mod π). The QM weight of γ be characterized as WQM(α)=|b0|+|b1|+|b2|+|b3|
and Quaternion Mannheim distance dQM(α) between β and ρ is defined as WQM(α)=dQM(ρ,β)
Remark: Indeed, Quaternion Mannheim weight WQM is a metric.
2.2 Construction of Cyclic Codes
Construction of cyclic codes of length n=φ(p)=p−1 by following the techniques of [10]. Let ξ is the primitive element of H(K)π, p be a prime in Z, where π=b0+b1i+b2j+b3k, p=ππ¯ and ξp−1=1. Then cyclic code (C) defined by H as follows;
H=(ξ0ξ1⋯ξφ(p)−1⋮⋱⋮ξ0ξt+1⋯ξ(t+1)(φ(p)−1))(1)
where t is nonnegative integer less than n. A vector c=(c0,c1,…,cφ(p)−1)∈H(K)πn is a codeword of C if and only if Hctr=0. If c(z)=∑j=0n−1cjzj is a codeword polynomial, then c(ξi+1)=0,for i=0,1,2,⋯,t. The polynomial f(z)=(z−ξ)(z−ξ2)⋯(z−ξt+1) is the generator polynomial of cyclic code C, and C=⟨f(z)⟩ is a principle ideal of H(K)π[z]/⟨zn−1⟩. If we multiple c(z) by z(mod(zn−1)), then zc(z)=c0z+c1z2+⋯+cn−1zn. But we know that zn=1. Therefore, if c(z)∈C, then zc(z)∈C. Thus, multiply c(z) by z(mod(zn+1)) means the following:
1. For Cyclic Shift c(z) shift one place to the right.
2. Locating the initial symbol of the new codeword by rotating the coefficient cn−1 by π radians.
3 Error Correction of Cyclic Codes of Length n=φ(p) for QM Weights One and Two
This section consists of decoding method for C of length n=φ(p) that uses the techniques in [ [13], Section 3, and Section 4 ] and [ [17], Section 3, Theorem 2, Lemma 1 and Theorem 3] to rectify single and double errors of QM weight one and two.
3.1 Single Error Correcting Cyclic Codes of QM Weight One
Let ξ is the primitive element of H(K)π, π=b0+b1i+b2j+b3k, p=ππ¯ and ξp−1=1 Then,
H=(ξ0ξ1ξ2⋯ξφ(p)−1)(2)
G=(−ξ110⋯0⋮⋱⋮−ξφ(p)−100⋯1)(3)
The one QM error-correcting codes of length n=φ(p) can be constructed by H. Then C defined by H in Eq. (2) is able to correct any QM error of weight one. The possible error values are 1 or −1. For the decoding procedure first step is to find the syndrome S(r)=Hrtr with the help of H and the received vector r. Then the error value is computed by Sξ−l, where l(mod n=φ(p)) is a non-negative integer which is helpful for error location. Hence, c=r−e is the corrected codeword.
Illustration: Let π=4+i+j+k, p=19, n=φ(p)=18 and ξ=2. Then, H and G by using Eqs. (2) and (3) and ξ be the primitive element of H(K)π, see Tab. 1 respectively;

H=(ξ0ξ1ξ2⋯ξ17)G=(−ξ110⋯0⋮⋱⋮−ξ1700⋯1) r=(1−i−j−k,1,−1+i+j+k,0,0,0,0,0,0,0,0,0,0,0,0,0,0,−1)1×18 S(r)=Hrtr=i+j+k≡ξ11(modπ) 11≡11(mod 18), it means error occur in received vector at location 12. Hence error value is Sξ−11=1(mod π). c=(1−i−j−k,1,−1+i+j+k,0,0,0,0,0,0,0,0,−1,0,0,0,0,0,−1).
Hctr=O(mod π). Hence, c is a codeword of C.
Perfect codes of Lengthn=φ(p) for QM Weight One:
The cyclic codes defined by H of length n=φ(p)=p−1 in Eq. (2), can be generalized as
H=(ξ0ξ1ξ2⋯ξφ(pr)−1)(4)
The cyclic codes defined by the generalized H are perfect in Eq. (4), by the sphere packing bound, since we have pn−r(n+2)=pn−rpr=pn.
3.2 Double Error Correcting Cyclic Codes of QM Weight One
Theorem: Let cyclic code (C) defined by H in Eq. (1). Then cyclic code (C) can be correct error as the form e(x)=ejxj+eixi, where 0≤WQM(ej),WQM(ei)≤1.
Proof: Consider two errors occur at two different places l1,l2 in received r and two error vectors e1,e2 of QM weight 0≤wQM(e1),WQM(e2)≤1. First, find syndromes with the help of H and the transpose of received vector r as;
H=(ξ0ξ1ξ2⋯ξφ(p)−1ξ0ξ2ξ4⋯ξ2φ(p)−2)(5)
S(r)=Hrtr=(s1s2)(modπ)(6)
Now we find a polynomial h(x) for the location and correction of errors as follows:
h(x)=(x−ξl1)(x−ξl2)=x2−(ξl1+ξl2)x+ξl1.ξl2=x2−s1x+η(7)
Where we can get η by syndromes. From s1=ξl1+ξl2,s2=ξ2l1+ξ2l2 and η=ξl1ξl2. we get
s12−s2=(ξ2l1+ξl2)2−(ξ2l1+ξ2l2)=2ξl1ξl2=2η(8)
s12−s22=2η2=η(modπ)(9)
Thus, h(x) helps for the locations and error values. If ξ1l1 and ξ2l2 are roots of h(x), then l1(modn)=m1, l2(modn)=m2 are locations of error and error values are e1=ξl1m1, e2=ξl2m2 which having three possibilities. If both two syndrome s1 and s2 are zeros then no error occurs. If s12=s2≠0, then one error occurs. If s12≠s2 and s1≠0, then two error occurs.
Illustration: Let π=4+i+j+k, p=19, n=φ(p)=18 and ξ=2. Then, H by using Eq. (5) and elements see Tab. 1 respectively; H=(ξ0ξ1ξ2⋯ξ17ξ0ξ2ξ4⋯ξ34),
r=(1−i−j−k,1,−1+i+j+k,0,0,0,0,0,0,0,0,0,0,0,0,0,0,−1)1×18 S(r)=Hrtr=(i+j+k2−2i−2j−2k)=(ξ11ξ17)(mod π)=(s1s2), Both syndromes s1, s2 are non-zeros and s12≠s2≠0. Hence two error occurs. By Eq. (9), η=s12−s22=ξ13(mod π). Hence error polynomial by Eq. (7) is h(x)=x2−ξ11x+ξ13. Error locator polynomial roots h(x) are ξl1=ξ4 and ξl2=ξ9, so, error locations are 4 and 9 in received vector r. Hence, error values are el1=1 and el2=1. c=(1−i−j−k,1,−1+i+j+k,0,−1,0,0,0,0,−1,0,0,0,0,0,0,0,−1)1×18.
Hctr=O( mod π). Hence, c is a codeword of C.
Theorem: The cyclic code C defined by H in Eq. (1) has the minimum QM distance dQM≥4. If p be a prime in Z then π be a prime in H(Z), where p=ππ¯≥19 and t=1.
Proof: The decoder’s ability to distinguish between single and double errors is all that is required in this proof. Assume QM weight error is one. Then, s12=s2≠0(modπ). From Eq. (7),
x1,2=s1±s2s12=s1±s12(10)
Hence, the decoder can differentiate in single and double errors.
3.3 Single Error Correcting Cyclic Codes of QM Weight Two
Theorem: Let ξ is the primitive element of H(K)π, π=b0+b1i+b2j+b3k and p=ππ¯. Let a cyclic code C of length n=φ(p)=p−1 define by H.
H=(ξ0ξ1ξ2⋯ξφ(p)−1ξ0ξ2ξ4⋯ξ2φ(p)−2)(11)
then the error of code C can be correct as of the form e(x)=elxl, where 1≤wQM(el)≤2.
Proof: Let ξi is error which occurred in location j, where 0≤i≤n−1 and 0≤j≤n−1. Let e(x)=ξixj be the error structure. Then, s1=ξj+i and s2=ξ2j+i are syndromes. Let s1=ξl1 and s2=ξl2 are the basis of sjj=1,2.
{s1=ξj+i,⟹j+i≡l1(modp−1)s2=ξ2j+i,⟹2j+i≡l2(modp−1)(12)
Eq. (11) having unique solution at j=l2−l1 (mod p−1), i=l1−j (mod p−1). Hence we conclude that error is occurred in location (l2−l1)(mod n) with magnitude ξi.
Illustration: Let π=4+i+j+k, p=19, n=φ(p)=18 and ξ=2. Then, we have H by using Eq. (11) and elements of Tab. 1 respectively; H=(ξ0ξ1ξ2⋯ξ17ξ0ξ2ξ4⋯ξ34)(2×18),
r=(1,−1,−1+i+j+k,0,0,0,0,0,0,0,0,0,0,0,0,0,0,−1)1×18 S(r)=Hrtr=(3i+3j+3k3i+3j+3k)=(ξ6ξ6)(mod π)=(s1s2), Both syndromes s1, s2 are non-zeros. By using Eq. (12), {s1=ξ6,⟹j+i≡6(mod18)s2=ξ6,⟹2j+i≡6(mod18), Solve the above system, we get error location j=0 and error magnitude ξ6=3i+3j+3k.
e=(3i+3j+3k,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)1×18. c=(−2+i+j+k,−1,−1+i+j+k,0,0,0,0,0,0,0,0,0,0,0,0,0,0,−1)1×18 Hctr=O (mod π). Hence, c is a codeword of C.
3.4 Double Error Correcting Cyclic Codes of QM Weight Two
Theorem: Let a cyclic code C of length n=φ(p) define by H as:
H=(ξ0ξ1ξ2⋯ξφ(p)−1ξ0ξ2ξ4⋯ξ2φ(p)−2ξ0ξ3ξ6⋯ξ3φ(p)−3ξ0ξ4ξ8⋯ξ4φ(p)−4)(13)
Then,
1. ξl2−ξl1≠0, where l1, l2∈Z,0≤l1<l2≤n−1
2. S1S3−S22≠0, otherwise, in received vector only one coordinate is in error.
Proof: 1. Suppose ξl2−ξl1=0. Then, ξl2=ξl1 this implies that ξl1−l2=1. So, n|(l1−l2). But n>n−1≥l1−l2, a contradiction that the order of ξ is n.
2. S1.S3−S22=0. Then, S1.S3=S22. If and only if ξ2l1S1x+ξ2l2S12−ξ2l2S1x=(ξl2−ξl1)2x2+ξ2l2S12+2ξl2(ξl1−ξl2)S1x. If and only if (ξl1−ξl2)2x2+2ξl1+l2S1x−ξ2l1S1x−ξ2l2S1x=0.Therefore, either x=0 or (ξl1−ξl2)2x+2ξl1+l2S1−ξ2l1S1−ξ2l2S1=0. if x=0 then it is not possible because ρl+s≠0. If (ξl1−ξl2)2x+2ξl1+l2S1−ξ2l1S1−ξ2l2S1=0, then x=(ξl1−ξl2)2.S1(ξl1−ξl2)2=S1.If and only if y=0. That’s also correct, if and only if ξl2+s=0. This is a contradiction that until in a received vector only one coordinate is in error. Hence, S1.S3−S22≠0 whenever two errors occurs.
Theorem: Let a cyclic code C of length n=φ(p) define by H as:
H=(ξ0ξ1ξ2⋯ξφ(p)−1ξ0ξ2ξ4⋯ξ2φ(p)−2ξ0ξ3ξ6⋯ξ3φ(p)−3ξ0ξ4ξ8⋯ξ4φ(p)−4); then the error of C can be corrected as the form e(x)=el1xl1+el2xl2, where 0≤l1<l2≤n−1 with, 0≤WQM(el1),WQM(el2)≤2.
Proof: Consider el1≠0 and el2≠0. In previous Theorem either el1=0 or el2=0. So by the help of H there are four syndromes
{S1=el1ξl1+el2ξl2S2=el1ξ2l1+el2ξ2l2S3=el1ξ3l1+el2ξ3l2S4=el1ξ3l1+el2ξ3l2(14)
Let u=el1ξl1 and v=el2ξl2, we get the following linear system of equations
{S1=u+vS2=uξl1+vξl2S3=uξ2l1+vξ2l2S4=uξ3l1+uξ3l2(15)
Two errors can be correct in code C if and only if the Eq. (14) has only unique solution. Since el1≠0 and el2≠0, then the system has unique solution. By using u+v=S1 then Eq. (13) becomes,
{(ξl1−ξl2)u=S2−ξl2S1(ξ2l1−ξ2l2)u=S3−ξ2l2S1(ξ3l1−ξ3l2)u=S4−ξ3l2S1(16)
which implies that
(ξl1+ξl2)(S2−ξl2S1)=S3−ξ2l2S1(17)
(ξ2l1+ξl1ξl2+ξ2l2)(S2−ξl2S1)=S4−ξ3l2S1(18)
Consider S=ξl1+ξl2 and P=ξl1ξl2. Then
{S(S2−ξl2S1)=S3−ξ2l2S1(S2−P)(S2−ξl2S1)=S4−ξ3l2S1(19)
From Eq. (16), we get P=SS2−S3S1, Since S1≠0, from Eq. (17), we get
S=S1S4−S2S3S1S3−S22(20)
S1S3−S22≠0, otherwise in a received vector only one coordinate is in error. By Eqs. (17) and (18),
P=S2S4−S32S1S3−S22(21)
X2−SX+P=0(22)
is the equation of sum and product of roots and the roots of this equation are x1=ξl1 and x2=ξl2,where l1 and l2 are error locations and error values are
{el1=S2−ξl2S1ξl1(ξl1−ξl2)el2=S2−ξl1S1ξl2(ξl2−ξl1)(23)
Illustration: Let π=4+i+j+k, p=19, n=φ(p)=18 and ξ=2. Then, H is define by using Eq. (13) and elements of Tab. 1 respectively;
H=(ξ0ξ1ξ2⋯ξ17ξ0ξ2ξ4⋯ξ34ξ0ξ3ξ6⋯ξ51ξ0ξ4ξ8⋯ξ68)(4×18),r=(0,1,0,0⋯0,−1)1×35 S(r)=Hrtr=(−3i−3j−3k−2+2i+2j+2k13)=(ξ15ξ81ξ13)(modπ)=(S1S2S3S4), Here, S1,S2,S3 and S4 are four syndromes. By using Eqs. (20) and (21), we get, S=ξ15 and P=1. X2−ξ15X+1=0, and roots of this equation are ξ and ξ17. The error occurs at position 1 and 17 in the received vector r. By Eq. (23), the error values are 1 and −1. e=(0,1,0,0,⋯0,−1)1×18,c=(0,0,0,0⋯0,0)1×18
Hctr=O(modπ). Hence c is a codeword of C.
4 Parity Check Matrix Extensions of n=φ(p) Length to 2n−1=2φ(p)−1 Length Cyclic Codes and Error Correction of these Codes for QM Weight One and Two through Monoid Rings
Parity check matrix extension of C of length n = φ(p) to 2n−1=2φ(p)−1 length and this constructed parity check matrix is in blocks of parity check matrices by following techniques in [ [20], Section 4] will be discussed in this Section. Furthermore, single and double error correction of these cyclic codes for quaternion mannheim weight one and two through moniod ring using techniques in [ [20]; Section 5].
Let an associative ring and semigroup are (B,+,.) and (Q,∗). Let a set Y of all finite non zero functions from Q into B. Let a ring Y which defines by binary operation addition and multiplication as: For h,g∈Y,s′∈Q, (h+g)(s′)=h(s′)+g(s′),(h.g)(s′)(x+a)n=∑t′∗u′=s′h(t′).g(u′).
It is clear that the sum is obtained by the pairs (t′,u′) elements of Q so that s′=t′∗u′ and for any t′,u′∈S if s′ is not expressed as the form t′∗u′, then (h.g)s′=0. Hence Y is called a semigroup ring of Q over B. If Q is monoid, then Y is known as a monoid ring. Hence Y ring is characterized by B[Q], here Q indicates multiplicative semigroup and Y written as ∑s′∈Qh(s′)s′. Here Y shows B[X,Q], where Q shows additive semi group. Here isomorphism between additive semigroup Q and multiplicative semigroup {Xs′:s′∈Q}, Hence h′∈B[X,Q] shows unique canonical form of non zero elements ∑k=1nh(sk′)Xsk′=hXsk′, where hk is non-zero and sk′≠(s′)j. The idea of order and degree is not commonly used for the semigroup rings if we take ordered semigroup Q, i.e., if ∑k=1nh(sk′)Xsk′, s1′<s2′<s3′⋯<sn′ is the canonical form of the non-zero element h∈B[X,Q], then deg(h)=sn′ and ord(h)=s′. Now, if integral domain is R, then for g,h∈B[X,Q], then deg(g+h)=deg(g)+deg(h),ord(g.h)=ord(g)+ord(h). If Q is not Z0 and B would be an associative ring, semigroup B[X,Q] is called polynomial ring B[X]. Of course, B[X]=B[X,Z0]⊂B[X12Z0]. For semigroup ring concepts the Gilmer’s book [22] is better. Extension of parity check matrix H of C of length 2n−1=p−2 in [ [17]; Section 4]; By following these parity check matrices, we describe H of C of length 2n−1=2φ(p)−1=2p−3 as follows:
H=((ξ12)0(ξ12)1⋯(ξ12)2φ(p)−1−1⋮⋱⋮(ξ12)0(ξ12)(2t+1)⋯(ξ12)(2t+1)(2φ(p)−1−1))(24)
1. H can be written in block form H11,H12,H21 and H22 as: H=(H11H12H21H22); H11=((ξ12)0(ξ12)1⋯(ξ12)φ(p)−1⋮⋱⋮(ξ12)0(ξ12)(t+1)⋯(ξ12)(t+1)(φ(p)−1)); H21=((ξ12)0(ξ12)2(t2)+1⋯(ξ12)(φ(p)−1)(2(t2)+1)⋮⋱⋮(ξ12)0(ξ12)2t+1⋯(ξ12)(φ(p)−1)(2t+1)); H12=((ξ12)φ(p)⋯(ξ12)(2φ(p)−1)−1⋮⋱⋮(ξ12)(t+1)(φ(p))⋯(ξ12)(t+1)((2φ(p)−1)−1)); H22=((ξ12)(φ(p))(2(t2)+1)⋯(ξ12)((2φ(p)−1)−1)(2(t2)+1)⋮⋱⋮(ξ12)(φ(p))(2t+1)⋯(ξ12)((2φ(p)−1)−1)(2t+1)) Here, H11 is equal to H of length n=φ(p)=p−1 as like in Eq. (1).
2. Parity check matrix of n=φ(p)=p−1 length is extended to 2n−1=2(ξ12)(p)−1=2p−3 length parity check matrix by adding rows and columns.
4.1 Single Error Correcting Cyclic Codes of Length 2n−1=2φ(p)−1 for QM Weight One
Let ξ12 is the primitive element of H(K)π, p be a prime in Z, π=b0+b1i+b2j+b3k, p=ππ¯ and (ξ12)p−1=1. Then, H and G are define as;
H=((ξ12)0(ξ12)1⋯(ξ12)2φ(p)−2)(25)
G=((ξ12)010⋯0⋮⋱⋮(ξ12)000⋯1)(26)
The one QM error-correcting codes of length 2n−1=2φ(p)−1 can be constructed by H. Then C defined by H in Eq. (25) can correct any QM error of weight one. 1 or −1 are the values of one quaternion Mannheim errors. For the decoding procedure first step is to find the syndrome S(r)=Hrtr with the help of H and the received vector r. Then the error value is computed by S(ξ12)−l, where l(mod 2φ(p)−1) is a non-negative integer which helps for error locations. Hence, c=r−e is the corrected codeword.
Illustration: Let π=4+i+j+k, p=19, 2n−1=2φ(p)−1=35 and ξ12=2. Then, H, G by Eqs. (25) and (26) and the primitive element of H(K)π from Tab. 2 respectively;

H=(12−i−j−k⋯1−i−j−k); G=(−110⋯0⋮⋱⋮−1+i+j+k00⋯1)
r=(1,0,−1+i+j+k,0,0,⋯,−1)1×35, S(r)=Hrtr=−1+i+j+k≡(ξ12)7(modπ)
The error location is 7≡7( mod 35) then, we get error value as S(ξ12)−7=1( mod π).
c=(1,0,−1+i+j+k,0,0,0,0,−1,0,⋯,−1)1×35. Hctr=O(mod π). Hence c is a corrected codeword of C.
4.2 Double Error Correcting Cyclic Codes of Length 2n−1=2φ(p)−1 for QM Weight One
Theorem: Let a cyclic code C of length 2n−1=2φ(p)−1 define by H.
H=((ξ12)0(ξ12)1(ξ12)2⋯(ξ12)2φ(p)−2(ξ12)0(ξ12)2(ξ12)4⋯(ξ12)4φ(p)−4)(27)
Then C can correct any error in the form e(x)=ej(zj2)+ei(zi2), where 0≤WQM(ej),WQM(ei)≤1.
Proof: Consider double error is occur at two different places l1,l2 in received r and two error vectors e1,e2 of quaternion mannheim weight as, 0≤wQM(e1),WQM(e2)≤1. First find syndromes by help of parity check matrix H in Eq. (27) and transpose of received vector r as;
S(r)=Hrtr=(s1s2)(modπ)(28)
Now we find a polynomial h(x) for the location of errors as follows:
h(x12)=(x12−ξl12)(x12−ξl22)=x−(ξl12+ξl22)x12+(ξl12).(ξl22)=x−s1x12+η(29)
we get η by syndromes. From s1=ξl12+ξl22,s2=ξl1+ξl2 and η=ξl12.ξl22. we get
s12−s2=(ξl12+ξl22)2−(ξl1+ξl2)=2ξl12.ξl22=2s(30)
s12−s22=2η2=η(modπ)(31)
Thus, h(x) lead us to find the location and error values. If ξl12 and ξl22 are roots of h(x), then l1(mod 2n−1)=m1, l2(mod 2n−1)=m2 are locations of error and error values are e1=ξl12m1, e2=ξl22m2. Then there are possibilities. If both two syndrome s1 and s2 are zeros then no error occurs. If s12=s2≠0, then one error occurs. If s12≠s2 and s1≠0, then two error occurs.
Illustration: Let π=4+i+j+k, p=19, 2n−1=2φ(p)−1=35 and ξ12=2. Then, H by using Eq. (27) and Tab. 2 respectively; H=(12⋯1−i−j−k1−i−j−k⋯2−i−j−k)2×35,
r=(1−i−j−k,1,−1+i+j+k,0,⋯,0,−1)1×35 S(r)=Hrtr=(1−1)=((ξ12)0(ξ12)9)(modπ)=(s1s2), Both syndromes s1, s2 are non-zeros and s12≠s2≠0. Hence two error occurs. By Eq. (31), η=s12−s22=1(modπ). Hence error polynomial by Eq. (29) is h(x12)=x−x12+1. The error locator polynomial h(x12) has roots (ξ12)l1=(ξ12)3 and (ξ12)l2=(ξ12)15, so, error locations are 3 and 15 in received vector r. Hence, error values are el1=1 and el2=1. c=(1−i−j−k,1,−1+i+j+k,−1,0,0,0,0,0,0,0,0,0,0,0,−1,0,⋯,0,−1)1×35.
Hctr=O(modπ). Hence c is a corrected codeword of C.
4.3 Single Error Correcting Cyclic Codes of Length 2n−1=2φ(p)−1 for QM Weight Two
Theorem: Let ξ12 is the primitive element of H(K)π , π=b0+b1i+b2j+b3k and p=ππ¯. Let a cyclic code C of length 2n−1=2φ(p)−1=2p−3 define by H.
H=((ξ12)0(ξ12)1(ξ12)2⋯(ξ12)2φ(p)−2(ξ12)0(ξ12)2(ξ12)4⋯(ξ12)4φ(p)−4)(32)
then C can correct errors as the form of e(x)=el(xl2), where 1≤wQM(el)≤2.
Proof: Suppose that (ξ12)i is error magnitude, 0≤i≤2n−2 has occurred in location j, where 0≤j≤2n−2. Let e(x)=(ξ12)ixj be the error pattern. Then, s1=(ξ12)j+i and s2=(ξ12)2j+i are syndromes. Let s1=(ξ12)l1 and s2=(ξ12)l2 are the basis of sjj=1,2. We have
{s1=(ξ12)j+i,⟹j+i≡l1(modφ(p))s2=(ξ12)2j+i,⟹2j+i≡l2(modφ(p))(33)
Eq. (33) having unique solution at j=l2−l1( mod p−1), i=l1−j( mod p−1). Hence, error is occurred in location (l2−l1)( mod 2n−1) with magnitude (ξ12)i.
Illustration: Let π=4+i+j+k, p=19, n=φ(p)=18 and (ξ12)=2. Then, H is defined by using Eq. (32) and Tab. 2 respectively; H=(12⋯1−i−j−k1−i−j−k⋯2−i−j−k)2×35,
r=(1,−1,−1+i+j+k,0,0,0,0,0,0,0,0,0,0,0,0,0,0,−1,0⋯0,0)1×35 S(r)=Hrtr=(3i+3j+3k3i+3j+3k)=((ξ12)6(ξ12)6)(modπ)=(s1s2), {s1=(ξ12)6,⟹j+i≡6(mod18)s2=(ξ12)6,⟹2j+i≡6(mod18)
Solve the above system and get error location j=0 and error magnitude (ξ12)6=3i+3j+3k.
e=(3i+3j+3k,0,0,⋯0,0)1×35 r=(1,−1,−1+i+j+k,0,0,0,−3i−3j−3k,0,0,0,0,0,0,0,0,0,0,−1,0⋯0,0)1×35 Hctr=O(modπ). Hence c is a codeword of cyclic code C.
4.4 Double Error Correcting Cyclic Codes of Length 2n−1=2φ(p)−1 for QM Weight Two
Lemma: Let C be a cyclic code of length 2n−1=2φ(p)−1 define by H as:
H=((ξ12)0(ξ12)1(ξ12)2⋯(ξ12)2φ(p)−2(ξ12)0(ξ12)2(ξ12)4⋯(ξ12)4φ(p)−4(ξ12)0(ξ12)3(ξ12)6⋯(ξ12)6φ(p)−6(ξ12)0(ξ12)4(ξ12)8⋯(ξ12)8φ(p)−8)(34)
then,
1. (ξ12)l2−(ξ12)l1≠0, where l1, l2∈Z,0≤l1<l2≤2n−2.
2. S1S3−S22≠0, otherwise in received vector only one coordinate is in error.
Proof:
1. Suppose (ξ12)l2−(ξ12)l1=0. Then, (ξ12)l2=(ξ12)l1 this implies that (ξ12)l1−l2=1.So, (2n−1)|(l1−l2). But 2n−1>n−1≥l1−l2, a contradiction that the order of (ξ12) is 2n−1.
2. S1.S3−S22=0. Then, S1.S3=S22 if and only if (ξ12)2l1S1x+(ξ12)2l2S12−(ξ12)2l2S1x=((ξ12)l2−(ξ12)l1)2x2+(ξ12)2l2S12+2(ξ12)l2((ξ12)l1−(ξ12)l2)S1x if and only if ((ξ12)l1−(ξ12)l2)2x2+2(ξ12)l1+l2S1x−(ξ12)2l1S1x−(ξ12)2l2S1x=0. Therefore, either x=0 or ((ξ12)l1−(ξ12)l2)2x+2(ξ12)l1+l2S1−(ξ12)2l1S1−(ξ12)2l2S1=0. if x=0 then it is not possible because ρl+s≠0. If ((ξ12)l1−(ξ12)l2)2x+2(ξ12)l1+l2S1−(ξ12)2l1S1−(ξ12)2l2S1=0, then x=((ξ12)l1−(ξ12)l2)2.S1((ξ12)l1−(ξ12)l2)2=S1. If and only if y=0. That is, if and only if (ξ12)l2+s=0. This is a contradiction unless in a received vector only one coordinate is in error. Thus, S1.S3−S22≠0. So, two error occurs.
Theorem: Let C be a cyclic code of length 2n−1=2φ(p)−1 defined by H in previous Theorem.
Then error of C can be correct in the form of e(x)=el1xl1+el2xl2, where 0≤l1<l2≤2n−2 with, 0≤WQM(el1),WQM(el2)≤2.
Proof: Consider el1≠0 and el2≠0. In Lemma, either el1=0 or el2=0. So by the help of parity check matrix there are four syndromes
{S1=el1(ξ12)l1+el2(ξ12)l2S2=el1(ξ12)2l1+el2(ξ12)2l2S3=el1(ξ12)3l1+el2(ξ12)3l2S4=el1(ξ12)3l1+el2(ξ12)3l2(35)
Let u=el1(ξ12)l1 and v=el2(ξ12)l2, we get the following linear system of equations
{S1=u+vS2=u(ξ12)l1+v(ξ12)l2S3=u(ξ12)2l1+v(ξ12)2l2S4=u(ξ12)3l1+v(ξ12)3l2(36)
Two errors can be correct in cyclic code C if and only if the Eq. (35) has only unique solution. Since el1≠0 and el2≠0, then the system has unique solution. By using u+v=S1, then Eq. (34) becomes,
{((ξ12)l1−(ξ12)l2)u=S2−(ξ12)l2S1((ξ12)2l1−(ξ12)2l2)u=S3−(ξ12)2l2S1((ξ12)3l1−(ξ12)3l2)u=S4−(ξ12)3l2S1(37)
((ξ12)l1+(ξ12)l2)(S2−(ξ12)l2S1)=S3−(ξ12)2l2S1(38)
((ξ12)2l1+(ξ12)l1(ξ12)l2+(ξ12)2l2)(S2−(ξ12)l2S1)=S4−(ξ12)3l2S1(39)
Consider S=(ξ12)l1+(ξ12)l2 and P=(ξ12)l1(ξ12)l2. Then
{S(S2−(ξ12)l2S1)=S3−(ξ12)2l2S1(S2−P)(S2−(ξ12)l2S1)=S4−(ξ12)3l2S1(40)
From Eq. (37), we get P=SS2−S3S1, Since S1≠0, from Eq. (38) we get
S=S1S4−S2S3S1S3−S22(41)
Let S1S3−S22≠0, otherwise in a received vector only one coordinate is in error. Put Eq. (38) in Eq. (39) we get
P=S2S4−S32S1S3−S22(42)
(X12)2−S(X12)+P=0(43)
is the equation of sum and product of roots and the roots of this equation are x1=(ξ12)l1 and x2=(ξ12)l2,where l1 and l2 are error locations and error values are
{el1=S2−(ξ12)l2S1(ξ12)l1((ξ12)l1−(ξ12)l2)el2=S2−(ξ12)l1S1(ξ12)l2((ξ12)l2−(ξ12)l1)(44)
Illustration: Let π=4+i+j+k, p=19, 2n−1=2φ(19)−1=35 and (ξ12)=2. Then, Parity check matrix H by Eq. (34)and Tab. 2 respectively; H=((ξ12)0(ξ12)1(ξ12)2⋯(ξ12)34(ξ12)0(ξ12)2(ξ12)4⋯(ξ12)68(ξ12)0(ξ12)3(ξ12)6⋯(ξ12)102(ξ12)0(ξ12)4(ξ12)8⋯(ξ12)136),
r=(0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,−1,0,0,⋯0)1×35 S(r)=Hrtr=(−3i−3j−3k−2+2i+2j+2k13)=((ξ12)15(ξ12)81(ξ12)13)(modπ)=(S1S2S3S4), By Eqs. (41) and (42) we get, S=ξ15 and P=1. (X12)2−(ξ12)2(X12)+P=0, and roots of this equation are ξ and ξ17. Error occurs at position 1 and 17 in the received vector. By using Eq. (44), the error values are 1 and −1. e=(0,1,0,0,⋯0,−1)1×35, c=(0,0,0,0,⋯0,0)1×35. Hctr=O(modπ). Hence, c is a corrected codeword of C.
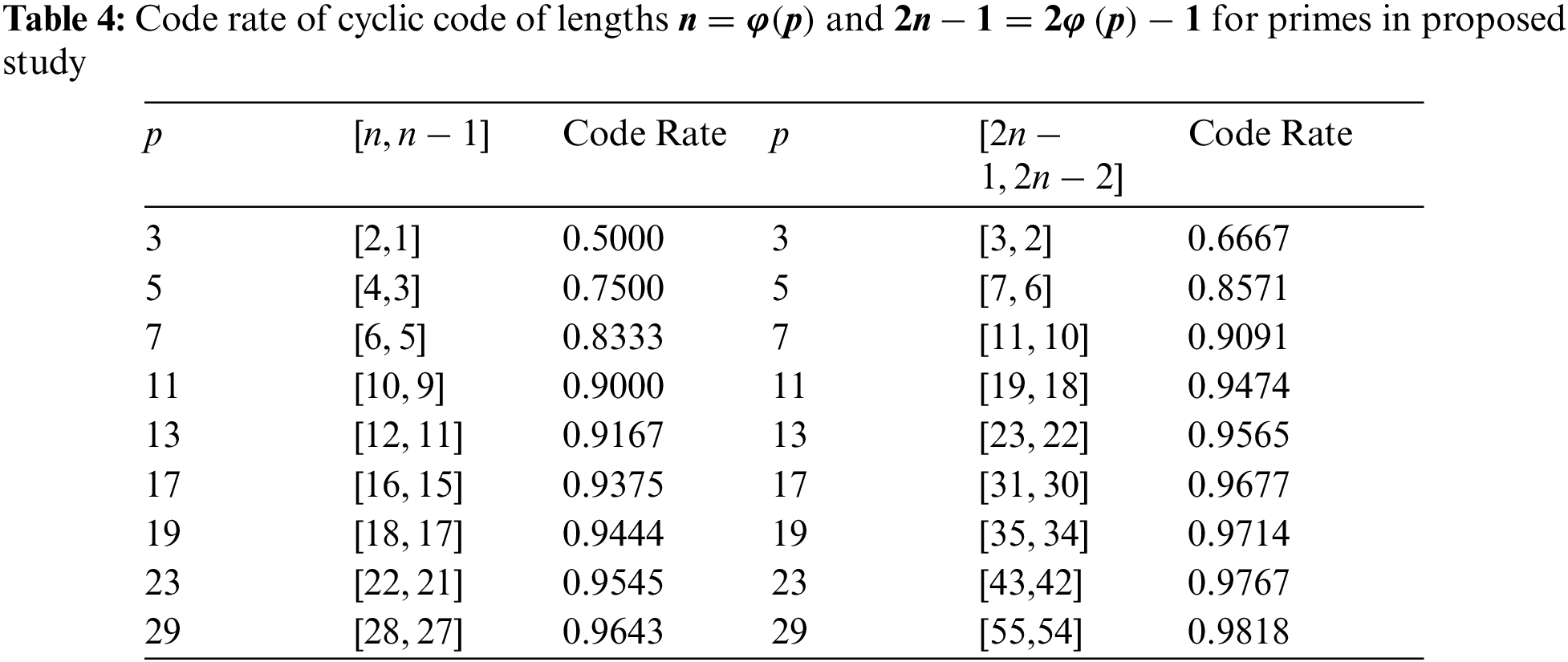
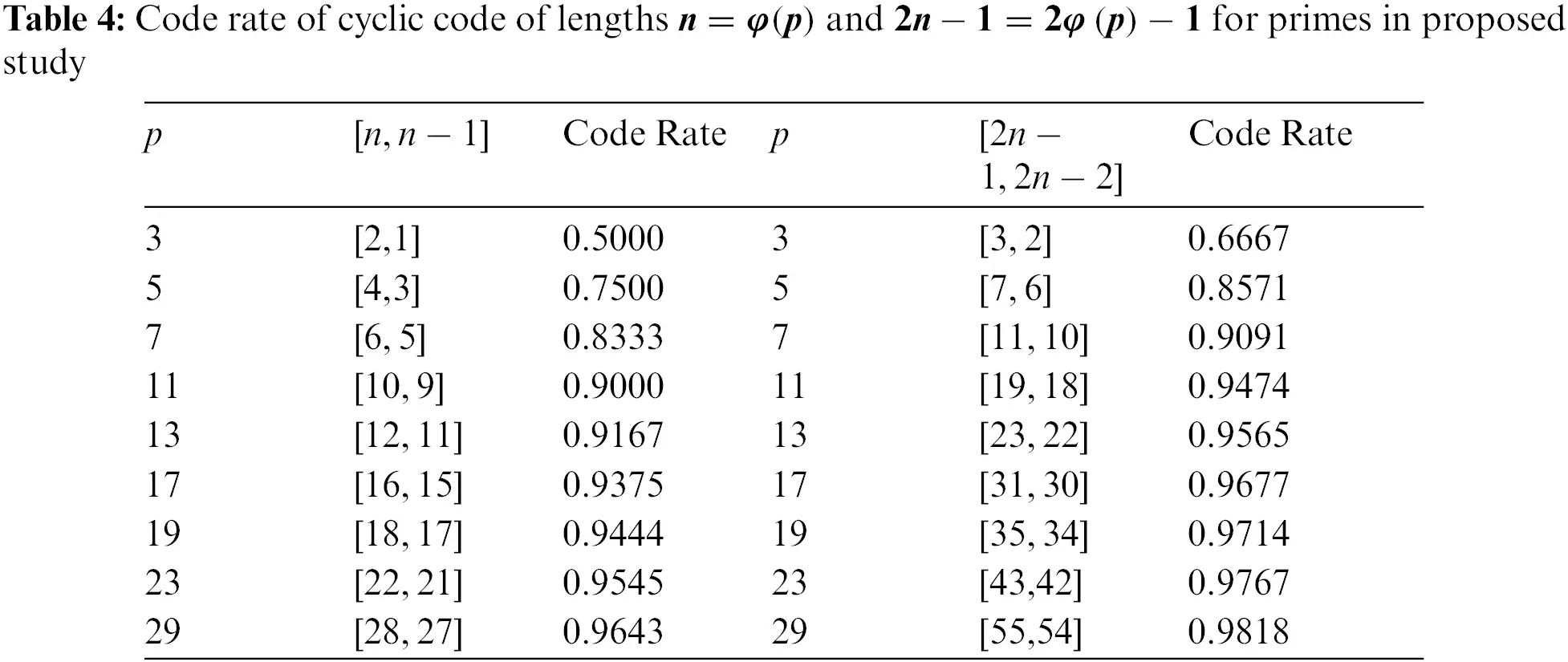
5 Lengths and Code Rates of Cyclic Codes Comparison
In this section, we will discuss the lengths and the code rates of cyclic codes for every prime p. In [13], Özen et al. have discussed the cyclic codes of length n=p−12 for every prime p. According to this length n=p−12, code rate of the cyclic code will be n−1n=p−3p−1. Similarly, In [17] Shah et al. have discussed the cyclic code of length 2n−1=p−2 for every prime p. According to this length 2n−1=p−2, the code rate of C will be 2n−22n−1=p−3p−2, which shown in the table and pictorial depictions given below:
Tab. 3 shows the previous results of lengths and code rates of paper cited [13] and [17]. Which are given in the last of these papers. And Tab. 4 shows our proposed word according to Tab. 3.
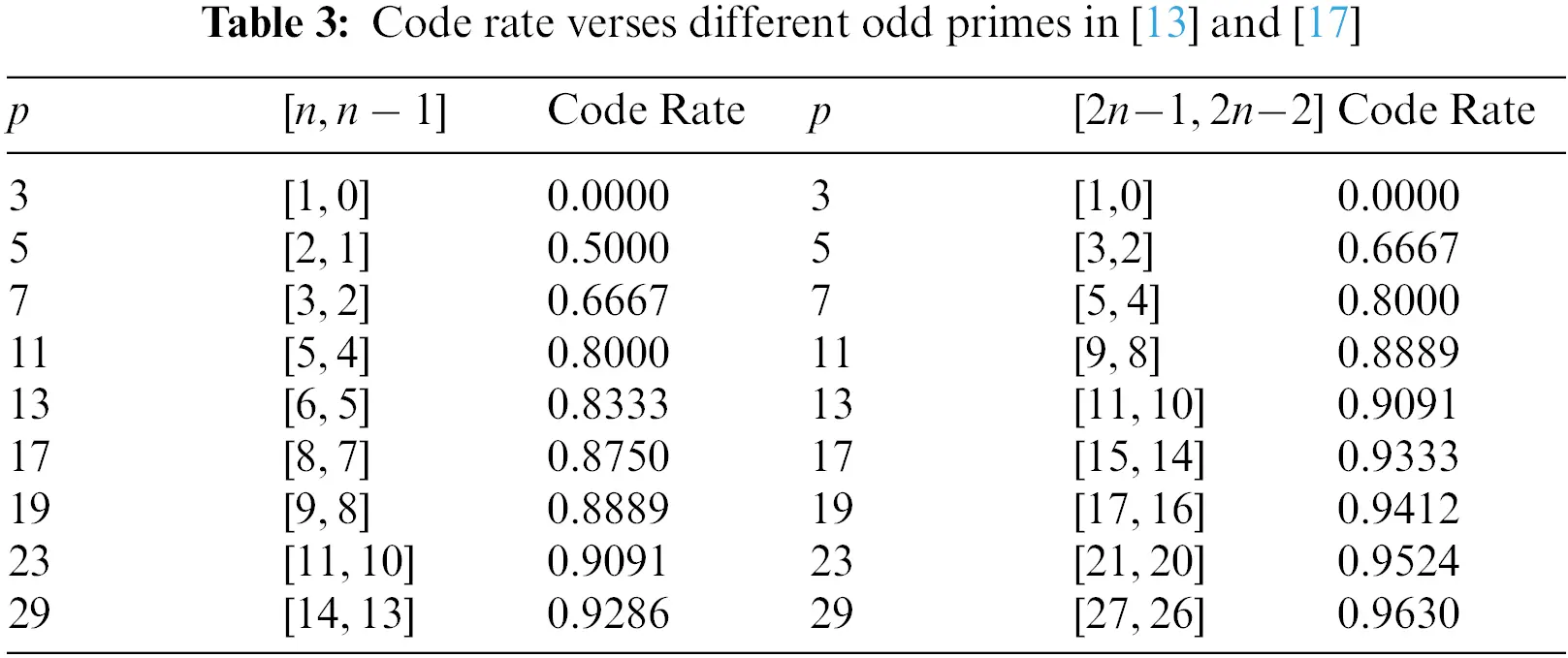

Figures 1, 2, 3 and 4: Code Rate of C of Length n=p−12 and 2n−1=p−2 for Primes in [13] and [17]
However, in proposed study by following [13] and [17], the cyclic codes of length n=φ(p)=p−1 for every prime p. According to this length n=φ(p)=p−1, code rate of C will be n−1n=φ(p)−1φ(p)=p−2p−1. Also, the cyclic codes of length 2n−1=2φ(p)−1=2p−3 for every prime p. According to this length 2n−1=2φ(p)−1=2p−3, code rate of C will be 2n−22n−1=2φ(p)−22φ(p)−1=2p−42p−3, shown in the table and pictorial depictions given below;

Figures 5, 6, 7 and 8: Code Rate of Cyclic Code of Lengths n=φ(p) and 2n−1=2φ(p)−1 for Primes in Proposed Study
Mutual comparison of Lengths and Code Rates of the Cyclic Codes of lengths n=p−12, 2n−1=p−2 with n=φ(p)=p−1 and 2n−1=2φ(p)−1 Lengths and Code Rates of Cyclic Codes as:
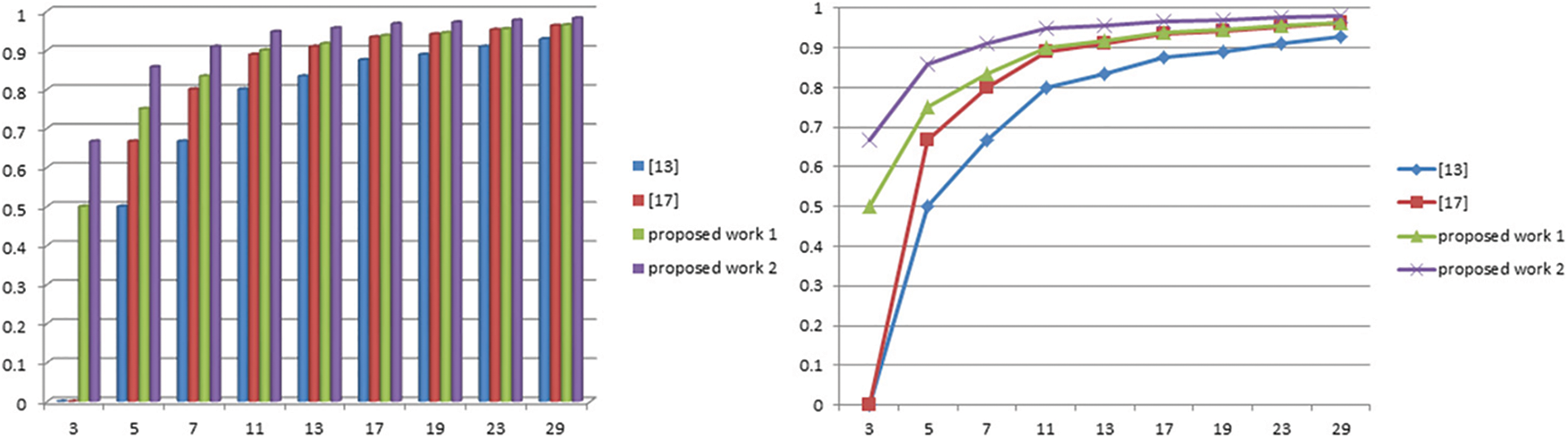
Figures 9 and 10: Mutual comparison of proposed work with previous existing works
We observed that if the length of the cyclic codes increases due to prime p, then the code rate and error correction capability of C will be better.
6 Conclusions
The following are the contributions of this study for the efficacy of the cyclic codes over Quaternion integers of QM weight. An effective and consistent modified decoding algorithm for the cyclic codes of lengths n=φ(p) and 2n−1=2φ(p)−1 to obtain the error correction capability has been furnished. The length of cyclic codes increased due to large prime p. For a given prime p, a higher code rates for cyclic codes of lengths n=φ(p)=p−1 and 2n−1=2p−3 is achieved as compared to the code rates of cyclic codes having lengths n=p−12 and 2n−1=p−2. The error correction capability of the cyclic codes of lengths n=φ(p)=p−1 and 2n−1=2φ(p)−1=2p−3 has been improved and it is better than the customary case of the cyclic codes of lengths n=p−12 and 2n−1=p--2.
Furthermore, the decoding procedure on the base of quaternion integers may be extended to the decoding procedure of octonion integers.
Funding Statement: The authors extend their gratitude to the Deanship of Scientific Research at King Khalid University for funding this work through research groups program under grant number R. G. P. 1/85/42.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. M. Best, “Perfect codes hardly exist,” IEEE Transactions on Information Theory, vol. 29, no. 3, pp. 349–351, 1983. [Google Scholar]
2. V. Lint and H. Jacobus, “Nonexistence theorems for perfect error correcting codes,” Computers in Algebra and Number Theory (Proceedings, New York NY, USA, March 25-26, 1970SIAM-AMS Proceedings, American Mathematical Society, vol. 4, pp. 89–95, 1971. [Google Scholar]
3. H. J. Conway and N. J. A. Sloane, “Self-dual codes over the integers modulo 4,” Journal of Combinatorial Theory, Series A, vol. 62, no. 1, pp. 30–45, 1993. [Google Scholar]
4. A. Tietavainen, “On the nonexistence of perfect codes over finite fields,” SIAM Journal on Applied Mathematics, vol. 24, no. 1, pp. 88–96, 1973. [Google Scholar]
5. V. A. Zinoviev and V. K. Leontiev, “The nonexistence of perfect codes over Galois fields,” Probl. Control and Inform. Theory, vol. 2, no. 2, pp. 123–132, 1973. [Google Scholar]
6. A. J. Han and H. Morita, “Codes over the ring of integers modulo m,” IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, vol. 81, no. 10, pp. 2013–2018, 1998. [Google Scholar]
7. Tamm and Ulrich, “On perfect integer codes,” in Proc. Int. Symp. on Information Theory IEEE, vol. 9, no. 1, pp. 117–120, 2005. [Google Scholar]
8. K. Huber, “Codes over Gaussian integers,” IEEE Transactions on Information Theory, vol. 40, no. 1, pp. 207–216, 1994. [Google Scholar]
9. K. Huber, “The MacWilliams theorem for two-dimensional modulo metrics,” Applicable Algebra in Engineering, Communication and Computing, vol. 8, no. 1, pp. 41–48, 1997. [Google Scholar]
10. T. P. D. N. Neto, T. Pires, J. C. Interlando, O. M. Favareto, M. Elia et al., “Lattice constellations and codes from quadratic number fields,” IEEE Transactions on Information Theory, vol. 47, no. 4, pp. 1514–1527, 2001. [Google Scholar]
11. H. Kostadinov, H. Morita and N. Manev, “Derivation on bit error probability of coded QAM using integer codes,” IEICE TRANSACTIONS on Fundamentals of Electronics Communications and Computer Sciences, vol. 87, no. 12, pp. 3397–3403, 2004. [Google Scholar]
12. D. Andrade, A. Aparecido and R. J. Palazzo, “Linear codes over finite rings,” Trends in Computational and Applied Mathematics, vol. 6, no. 2, pp. 207–217, 2005. [Google Scholar]
13. M. Özen and M. Güzeltepe, “Codes over quaternion integers,” European Journal of Pure and Applied Mathematics, vol. 3, no. 4, pp. 670–677, 2010. [Google Scholar]
14. D. Andrade, A. Aparecido, T. Shah and A. Khan, “Cloud Goppa codes through generalized polynomials and its decoding principle,” International Journal of Applied Mathematics, vol. 23, no. 3, pp. 517–526, 2010. [Google Scholar]
15. D. Andrade, A. Aparecido, T. Shah and A. Khan, “A note on linear codes over semigroup rings,” TEMA (São Carlos), vol. 12, no. 2, pp. 79–89, 2011. [Google Scholar]
16. T. Shah, A. Khan and A. A. Andrade, “Encoding through generalized polynomial codes,” Computational & Applied Mathematics, vol. 30, no. 2, pp. 349–366, 2011. [Google Scholar]
17. T. Shah, A. Khan and A. A. D. Andrade, “Constructions of codes through the semigroup ring B [X; 122Z0] and encoding,” Computers & Mathematics with Applications, vol. 62, no. 4, pp. 1645–1654, 2011. [Google Scholar]
18. M. Özen and M. Güzeltepe, “Cyclic codes over some finite quaternion integer rings,” Journal of the Franklin Institute, vol. 348, no. 7, pp. 1312–1317, 2011. [Google Scholar]
19. M. Güzeltepe and O. Heden, “Perfect Mannheim, Lipschitz and Hurwitz weight codes,” Mathematical Communications, vol. 19, no. 2, pp. 253–276, 2014. [Google Scholar]
20. T. Shah and S. S. Rasool, “On codes over quaternion integers,” Applicable Algebra in Engineering, Communication and Computing, vol. 24, no. 6, pp. 477–496, 2013. [Google Scholar]
21. G. F. Davidoff, P. Sarnak and A. Valette, “Elementary number theory, and Ramanujan graphs,” Cambridge University Press, vol. 55, pp. 45–80, 2003. [Google Scholar]
22. R. Gilmer, “Commutative semigroup rings,” University of Chicago Press, Chicago, London, vol. 22, no. 1, pp. 63–129, 1984. [Google Scholar]