Computers, Materials & Continua DOI:10.32604/cmc.2022.026751
Article

Chosen-Ciphertext Attack Secure Public-Key Encryption with Keyword Search

Hyun Sook Rhee*

Samsung Electronics Co. Ltd., Suwon-si, 16677, Korea
*Corresponding Author: Hyun Sook Rhee. Email: hyunsook.rhee@gmail.com
Received: 04 January 2022; Accepted: 02 March 2022

Abstract: As the use of cloud storage for various services increases, the amount of private personal information along with data stored in the cloud storage is also increasing. To remotely use the data stored on the cloud storage, the data to be stored needs to be encrypted for this reason. Since “searchable encryption” is enable to search on the encrypted data without any decryption, it is one of convenient solutions for secure data management. A public key encryption with keyword search (for short, PEKS) is one of searchable encryptions. Abdalla et al. firstly defined IND-CCA security for PEKS to enhance it’s security and proposed consistent IND-CCA secure PEKS based on the “robust” ANO-CCA secure identity-based encryption(IBE). In this paper, we propose two generic constructions of consistent IND-CCA secure PEKS combining (1) a hierarchical identity based encryption (for short, HIBE) and a signature scheme or (2) a HIBE, an encapsulation, and a message authentication code (for short, MAC) scheme. Our generic constructions identify that HIBE requires the security of a signature or a MAC as well as the weaker “ANO-CPA security (resp., IND-CPA security)” of HIBE than “ANO-CCA security (resp., IND-CCA security)” of IBE required in for achieving IND-CCA secure (resp., consistent) PEKS. Finally, we prove that our generic constructions satisfy IND-CCA security and consistency under the security models.

Keywords: Searchable encryption; public-key encryption with keyword search; chosen ciphertext security; data privacy

1  Introduction

As various services are transferred into the cloud environment, the safe management of information stored on the cloud storage is one of the important issues. Countries have enacted legislation to reduce the damage caused by exposure to privacy of their own citizens through personal information protection laws such as GDPR(General Data Protection Regulation) [1] and LGPD(Brazilian General Data Protection Law) [2] etc. The laws mandate that personal information be encrypted when stored or transmitted. Searchable encryption is a very useful primitive for providing the functionality of “searching on encrypted data”. Recently, there has been intensive interest in searchable encryption [3–14]. As a variant of searchable encryption on a store-and-forward system, the notion of public-key encryption with keyword search (PEKS) was suggested by Boneh et al. [15]. Informally, a PEKS scheme enables an email server to correctly test whether or not a given keyword is present in an encrypted email without revealing any information on the email. In PEKS, the sender generates a PEKS ciphertext CTw of a keyword w under the public key of the receiver and sends the PEKS ciphertext CTw along with an encrypted email message to a server. To retrieve the email messages containing a keyword w′ from the server, a receiver provides the server with a trapdoor Tw′ (which is generated under the receiver’s secret key). The server then runs a test function with CTw and Tw′ to identify whether or not w=w′, and forwards the corresponding email messages to the receiver.

As security of public key encryption, IND-CPA (indistinguishability under a chosen plaintext attack) requires that it should be infeasible for an adversary to compute any information on a plaintext when given its ciphertext and the corresponding public key [16]. In PEKS, a keyword is a plaintext. The security condition of a PEKS system [15] requires that an adversary (or the server) runs the test function with the inputs, CTw and Tw′, without learning any information on keywords except the fact that two keywords w and w’ are equal. This security condition has been considered as IND-CPA in PEKS. If a PEKS scheme does not provide the confidentiality of a keyword, the privacy of the email message is not guaranteed. Additionally, PEKS should provide consistency [3] that requires that the server’s test function with the inputs, CTw and Tw′, returns “true” if w=w′, and returns “false” otherwise. If a PEKS system does not meet the consistency condition, email messages may be incorrectly routed.

Abdalla et al. [3,15] showed that an IND-CPA PEKS scheme can be constructed from an ANO-CPA (anonymity under chosen plaintext attack) identity-based encryption (IBE) scheme and that a consistent PEKS scheme can be constructed from an IND-CPA IBE scheme. Here, “an IBE scheme is anonymous” means that the ciphertext does not reveal the identity of the intended recipient. In PKE, the notion of IND-CPA security only considers an adversary that may choose plaintexts of its choice and generate the corresponding ciphertexts. IND-CPA security does not guarantee indistinguishability under a chosen ciphertext attack (IND-CCA security), where an adversary can choose ciphertexts of its choice and obtain the corresponding plaintexts. It has been shown that chosen ciphertext attacks are practical [17–19] and IND-CCA security is considered as the minimum level of security for a encryption scheme to be deployed in practice.

The goal of this paper is to design a consistent IND-CCA secure PEKS scheme. An IND-CCA secure PEKS scheme in a random oracle can be easily derived from the decryptable searchable encryption proposed by Fuhr et al. [20]. However, this approach does not guarantee consistency of the result. In PKE(public key encryption) & PEKS schemes [4,8,12,14], INC-CCA security had been considered. Strictly speaking, ‘‘ciphertext of a message” instead of ‘‘PEKS chiphertext of a keyword” is the target of the IND-CCA security. However, when data is stored in real environments such as the cloud storage, it is encrypted using symmetric key encryption such as AES(Advanced Encryption Standard). Hence, applying an encryption of data with a PKE is bound to be limited.

Meanwhile, analogously to the result in [3,15], an IND-CCA PEKS scheme can be directly constructed from an ANO-CCA secure IBE scheme. In taking this approach, Abdalla et al. [4] identified that “robustness” is the property necessary for a consistency in the resulting PEKS scheme. Here, “robustness” means the difficulty of producing a ciphertext valid under two different encryption keys. They mentioned “Boneh-Flanklin IBE scheme [21]” as satisfying both “robustness” and “ANO-CCA security” among the IBE schemes [4]. Compared to the result of Abdalla et al. in Tab. 1, our main contribution is enable to construct consistent IND-CCA secure PEKS scheme by using the underlying schemes which satisfy the weaker security (ANO-CPA security) than ANO-CCA security. Also, since general constructions can be developed using proven safety primitives codes, the generic constructions to solve new security issues can be applied immediately in the development environment to speed up application time. So, proposing various general constructions using different primitives (such as a public-key encryption (for short, PKE), a signature, a MAC, and a hash etc) will maximize utilization in real life.

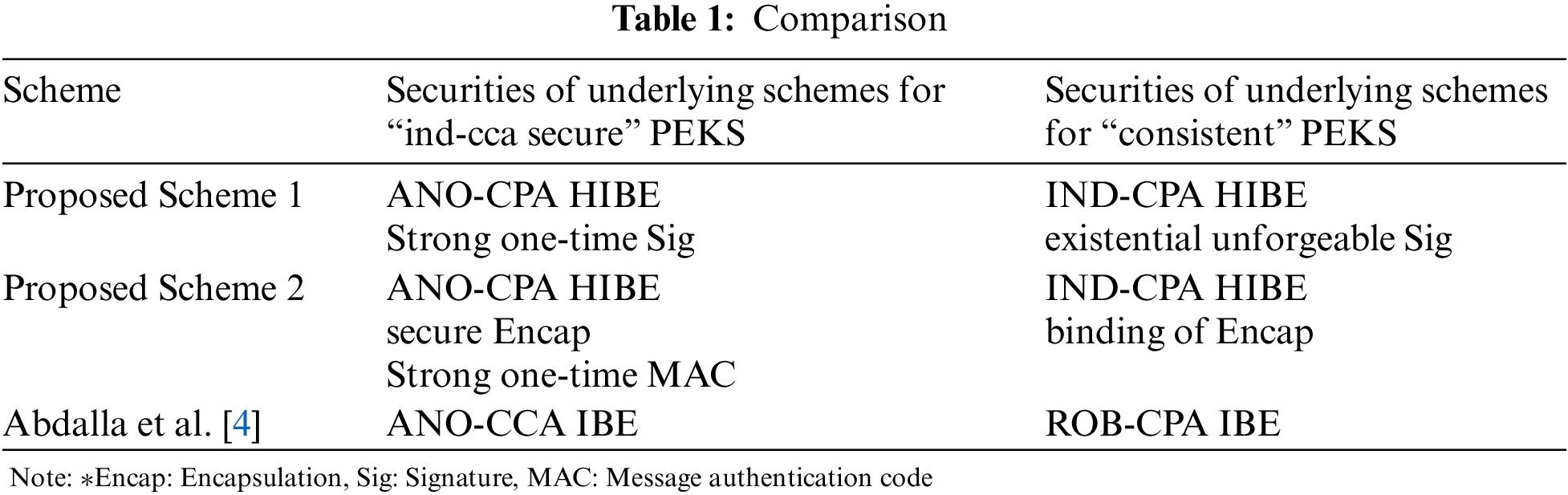
In this paper, for alternatives for providing the consistent IND-CCA secure PEKS, we propose two generic constructions: For IND-CCA security of PEKS, one is based on any ANO-CPA secure two-level hierarchical IBE (HIBE) and a strong one-time signature, and the other is based on ANO-CPA secure two-level HIBE, a secure encapsulation, and a strong one-time MAC. For consistency of PEKS, one is based on any IND-CPA secure two-level HIBE and an existential unforgeable signature and the other is based on any IND-CPA secure two-level HIBE and a computational binding encapsulation.

IND-CCA security of PEKS. In chosen plaintext attack of PEKS, an adversary is given access to a trapdoor oracle. An adversary can chose a keyword w of its own and obtain the trapdoor Tw of w quering the trapdoor oracle. The adversary then can test whether or not w is present in a given PEKS ciphertext CT by running a test function with inputs CT and Tw. In chosen ciphertext attack of PEKS, an adversarial model is strengthened so that it can freely chose a PEKS ciphetext CT and is given access to a test oracle. The test oracle takes as inputs a PEKS ciphertext CT and a keyword w and outputs the test result whether or not CT is an encryption of w. The IND-CCA of PEKS requires that for given two keywords w0 and w1 and a challenge PEKS ciphertext CT∗, it is infeasible for an adversary to distinguish which keywords has been encrypted, provided the test query of the form (CT∗, wb) (b=0,1) has never been submitted to the test oracle.

We note that (CT∗, w) or (CT, wb ) (b=0,1) still can be queried to the test oracle, for w≠wb and CT≠CT∗. In particular, to provide IND-CCA security, a PEKS scheme should have a mechanism to validate a PEKS ciphertext CT in a query of the form (CT, wb). That is, honestly-generated PEKS ciphertexts should be distinguishable from PEKS ciphertexts that are forged with CT∗. In our generic constructions, a PEKS ciphertext CT of a keyword w is generated in such a way that the party who encrypted w can be authenticated by the addition of a signature or MAC of the party. This enforces that an attacker should counterfeit a signature or MAC to forge a valid PEKS ciphertext.

Consistency of PEKS. In [3], it was shown that the confidentiality (IND-CPA security) of the IBE scheme is sufficient for the computational consistency of a CPA secure PEKS scheme. (Computational consistency means that it is hard for any polynomial-time adversary to find distinct keywords w and w′ such that the result of the test function with CTw and Tw′ is true.) To provide computational consistency in our two constructions for IND-CCA secure PEKS, we identify that the confidentiality (IND-CPA security) of the HIBE scheme as well as existentially unforgeability of a signature scheme or binding property of an encapsulation scheme are required.

Paper Organization. The remainder of this paper is organized as follows. We review several primitives that are necessary for our constructions, such as the HIBE, Signature and MAC schemes in Section 2. In Section 3, we review the notions “IDN-CPA security” and “consistency” in a PEKS scheme and propose two generic constructions of a PEKS scheme and add the flowchat of PEKS encryption process to help understand. In Section 4, we establish the security and computational consistency of our two generic constructions for a PEKS scheme. Finally, Section 5 concludes the paper.

2  Preliminaries

We review the notation and recall the definitions of a hierarchical identity-based encryption (HIBE) scheme, a strong one-time signature scheme and a secure message authentication code. We also review the concepts of security and anonymity for HIBE schemes.

Notation : For any string x, |x| denotes its length. For any set S, |S| denotes its size. The symbol k denotes a security parameter. We let a←b denote the assignment to a the result of evaluating b. We say a function µ is negligible if for any constant k, there exists N such that µ(n)<1/nk for n>N.

2.1 Hierarchical Identity-Based Encryption

A hierarchical identity-based encryption (HIBE) scheme is an extension of an IBE scheme [9,22] in which an identity is a vector of strings ID=(ID1,…,IDt) (1≤t≤ℓ) and the components of the identity are arranged in a hierarchy. The number of components in this vector is called the level of the identity and is denoted as |ID|. The setup algorithm SetupHIBE generates public parameters PP and a master secret key mk as the private key at depth 0. (Note that an IBE system is a HIBE where all identities are at depth 1.) In HIBE, a user has delegatory capabilities. That is, a user possessing his private key dID for an (t−1)-level identity ID=(ID1,…,IDt−1) can generate private keys dID′ for the child identities ID′=(ID1,…,IDt−1,IDt), where IDt−1∈ID is a random identity without the master secret key mk. For any ID=(ID1,…,ID|ID|) with |ID|≥1 we let par[ID]=ID′=(ID1,…,ID|ID|−1).

Definition 2.1. A ℓ-level hierarchical identity-based encryption (HIBE) scheme HIBE = (SetupHIBE, KeyGenHIBE, KeyDerHIBE, EncHIBE, DecHIBE ) for identities of length n (where ℓ, n are polynomially-bounded functions) consists of five PPT algorithms as follows.

• SetupHIBE(k) takes as input a security parameter k, and outputs public parameters PP and a master secret key mk.

• KeyGenHIBE(mk,ID) takes as input mk, and an arbitrary identity vector ID=(ID1,…,IDt) (t≤ℓ), where IDi∈{0,1}n. It outputs the corresponding private key dID. We write this as dID←KeyGenHIBE(mk,ID).

• KeyDerHIBE (PP,dpar[ID], ID) takes as input a private key corresponding to the parent’s identity vector dpar[ID]=d(ID1,…,IDt−1), and an arbitrary identity vector ID=(ID1,…,IDt) (t≤ℓ), where IDi∈{0,1}n. It outputs the corresponding private key dID. We write this as dID ← KeyDerHIBE (PP, dpar[ID], ID).

• EncHIBE (PP, ID, M) takes as input PP, an arbitrary identity vector, ID ∈ ({0,1}n)≤ℓ, and M∈M, where M is a finite message space. It outputs a ciphertext C.

• DecHIBE (ID, C, dID.) takes as input an arbitrary identity vector ID ∈ ({0,1}n)≤ℓ, C∈C, and its associated private key dID. It outputs either M∈M or a symbol ⊥ which indicates failure. We write this as M←DecHIBE (ID, C, dID). As usual, this algorithm must satisfy the correctness constraint, that is, for every M∈M, if C is the output of EncHIBE with input PP, ID, M) and dID. is a valid private key of ID, then M is the result of applying DecHIBE with the inputs (ID, C, dID). That is, for the given PP, we have

where the probability is taken over the coins of EncHIBE.

Confidentiality and Anonymity of HIBE : Suppose that HIBE = (SetupHIBE, KeyGenHIBE, KeyDerHIBE, EncHIBE, DecHIBE ) is a ℓ-level HIBE scheme and A is a PPT adversary. Let ℓ=ℓ(k) and n=n(k). Let IDi∈{0,1}n be a string and ID ∈ ({0,1}n)≤ℓ be an arbitrary identity vector. Let anc(⋅) be the function that returns the set of ancestors of the input identity vector. We suppose that the adversary A may adaptively ask for the private key that corresponds to any identity vector ID, as long as ID is not a prefix of the target identity vector ID* , where in the first experiment of confidentiality (resp., second experiment of anonymity), ID* is the identity vector ID (resp., the identity vectors ID0 or ID1). The adversary is given the private key dID for ID using mk and KeyDerHIBE(·).

The confidentiality (HIBE-IND-CPA) and anonymity (HIBE-ANO-CPA) of the HIBE scheme against adaptive chosen-plaintext attacks, which is defined using the following experiments as shown in Tabs. 2 and 3, follows [3,23]. We say that A succeeds if b=b′ in ExpHIBE,Ahibe-ind-cpa-b(k), and denote the probability of this event by PrHIBEAhibe-ind-cpa-b[Succ]. The adversary’s advantage is defined as:

We also say that A succeeds if b=b′ in ExpHIBE,Ahibe-ano-cpa-b(k), and denote the probability of this event by PrHIBEAhibe-ano-cpa-b[Succ]. The adversary’s advantage is defined as:

Definition 2.2. We say that a HIBE scheme HIBE is HIBE-IND-CPA secure (resp., HIBE-ANO-CPA secure) if the advantage AdvHIBE,Ahibe-ind-cpa-b(k) (resp., AdvHIBE,Ahibe-ano-cpa-b(k) of any probabilistic polynomial-time (PPT) adversary A is negligible in the security parameter k.

2.2 Signature Scheme

We recall the standard functional definition for signature schemes and the definition for strong one-time security that is appropriate for signature schemes.

Definition 2.3. A signature scheme Sig=(G, Sign,Vrfy)consists of three PPT algorithms as follows.

• G(k) takes a security parameter k as input, and outputs a pair of verification key and signing key (vk,sk). We assume for simplicity that the length of vk is fixed for any given value of k.

• Sign(sk,M) takes as input a signing key sk and a message M∈M, and outputs a signature σ.

• Vrfy(vk,M,σ) takes as input a verification key vk, a message M, and a signature σ, and outputs a bit b∈{0,1} (where b=1 signifies “valid” and b=0 signifies “invalid”).

We require that Vrfy(vk,M,σ)=1 under (vk,sk)←G(1k), M∈M, and σ←Sign(sk,M).

Security of Signature Schemes: The securities (strong unforgeability or existential unforgeability) for signature schemes [24] are defined using the above experiments in Tab. 4. We define the advantages of A in the corresponding experiments as:

Definition 2.4. We say that a signature scheme Sig is a strong one-time signature (resp., existential unforgeable one-time signature) if for any PPT adversary A, we have that AdvSig,Asuf-oma(k) (resp., AdvSig,Aeuf-oma(k)) is negligible.

2.3 Encapsulation Scheme

We review encapsulation schemes which may be viewed as weak variants of commitment, and the security notions of encapsulation schemes [24].

Definition 2.5. An encapsulation scheme Encap=(Init,S,R) consists of three PPT algorithms as follows.

• Init(k) takes a security parameter k as input, and outputs a string pub.

• S(k,pub) takes a security parameter k and pub, and outputs (r,com,dec) with r∈{0,1}k.

We refer to com as the commitment string and dec as the decommitment string.

• R(pub,com,dec) takes as input (pub,com,dec), and outputs r∈{0,1}k∪{⊥}.

We require that for all pub output by Init and for all (r,com,dec) output by S(k,pub), we have R(pub,com,dec)=r.

Security of Encapsulation Schemes : The security notions of binding and hiding in an encapsulation scheme [24] are defined using the above experiment in Tab. 5. We define the advantages of A in the corresponding experiments as:

Definition 2.6. We say that an encapsulation scheme Encap is secure if for any PPT adversary A, AdvEncap,Ahiding(k) and AdvEncap,Abinding(k) are negligible.

2.4 Message Authentication Code Scheme

We review a definition for message authentication codes and a definition for strong unforgeability that is appropriate for message authentication codes.

Definition 2.7. A message authentication code (MAC) scheme MAC=(SigMac,VrfyMac) consists of two PPT algorithms as follows.

• SigMac(sk,M) takes as input a key sk∈{0,1}k and a message M∈M, and outputs a tag tag, and we denote this by tag←SigMac(sk,M).

• VrfyMac(sk,M,tag) takes as input a key sk, a message M, and a tag tag, and outputs a bit b∈{0,1} (where b=1 signifies “valid” and b=0 signifies “invalid”).

We require that for all sk ∈ {0, 1}k, all M ∈ M, and all tag tag output by SigMac(sk, M), we have VrfyMac(sk,M,tag)=1.

Security of Message Authentication Codes : The security (strong unforgeability) for MAC [24] is defined using the above experiment in Tab. 6. We define the advantage of A in the corresponding experiment as:

Definition 2.8. We say that a message authentication code scheme MAC=(SigMac,VrfyMac) is a strong one-time MAC (i.e., strong unforgeable against chosen one-message attack) if for any PPT adversary A, AdvMAC,Asuf−oma(k) is negligible.

2.5 PEKS Scheme

We review a definition of public key encryption with keyword search (PEKS) suggested by Boneh et al. [15], the definitions of the security against chosen-ciphertext attacks (PEKS-IND-CCA) and the consistency in PEKS.

Definition 2.9. A PEKS scheme PEKS=(Gen, Trapdoor, PEKS, Test) consists of four PPT algorithms as follows.

• Gen(k) takes a security parameter k as input, and generates a pair of public and secret keys (PK, SK) of the receiver R.

• Trapdoor(SK,w) takes as inputs a receiver’s secret key SK and a keyword, w. It then generates a trapdoor Tw.

• PEKS(PK,w) takes as inputs a receiver’s public key PK and a keyword, w. It returns a ciphertext CT on the keyword w.

• Test(CT,Tw) takes as inputs a ciphertext CT and a trapdoor Tw.. It outputs ‘yes’ if w=w′ and ‘no’ otherwise, where CT = PEKS(PK,w′).

Confidentiality(IND-CCA security) of PEKS: The IND-CCA security for PEKS is defined using the experiment in Tab. 7. We define the advantage of A in the corresponding experiment as:

where the probability is taken over all possible coin flips of all the algorithms involved.

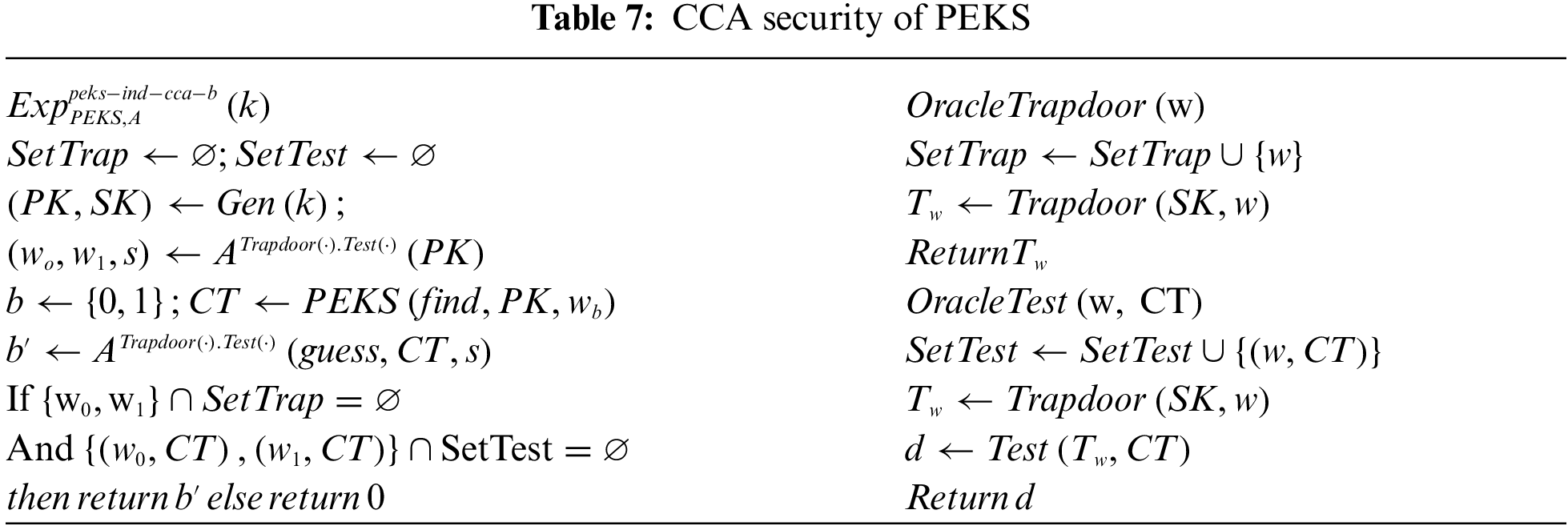
Definition 2.10. We say that a PEKS scheme is semantically secure against an adaptive chosen- ciphertext attack (PEKS-IND-CCA secure) if for any PPT adversary , APEKS,Apeks-ind-cca(k) is negligible.

Consistency of PEKS: In [3], Abdalla et al. identified the concept of the consistency of PEKS schemes and defined computational and statistical relaxations of the notion of perfect consistency. They showed that Boneh et al.’s PEKS scheme is computationally consistent. Suppose there is an adversary A that wants to make consistency fail. Let PEKS=(Gen, Trapdoor, PEKS, Test) be a PEKS scheme. The adversary A is associated with the experiment in Tab. 8. We define the advantage of A in the corresponding experiment as:

where the probability is taken over all possible coin flips of all the algorithms involved.

Definition 2.11. We say that a PEKS scheme is “perfectly consistent” if the advantage is 0 for all (computationally unrestricted) adversaries A, “statistically consistent” if the advantage is negligible for all (computationally unrestricted) adversaries) A, and “computationally consistent” if the advantage is negligible for all probabilistic polynomial-time (PPT) adversaries A.

3  Generic Construction of PEKS Scheme

In this Section, we provide two generic constructions of a consistent IND-CCA secure PEKS scheme. The first generic construction combines an anonymous (ANO-CPA secure) and confidential (IND-CPA secure) 2-level HIBE scheme HIBE = (SetupHIBE, KeyGenHIBE, KeyDerHIBE, EncHIBE, DecHIBE), which handles identities of length 2 and a strong one-time signature scheme Sig=(G, Sign,Vrfy) in which the verification key out-put by G(1k) has length n(k). The second generic construction combines an anony- mous (ANO-CPA secure) and confidential (IND-CPA secure) 2-level HIBE scheme HIBE = (SetupHIBE, KeyGenHIBE, KeyDerHIBE, EncHIBE, DecHIBE), which handles identities of length 2, a secure encapsulation scheme scheme Encap=(Init,S,R) in which commitments com output by S have length n(k) and a strong one-time message authentication code scheme MAC=(SigMac,VrfyMac).

We use a delegation property of the HIBE scheme and a security of the signature scheme (or the message authentication code (MAC)) to construct an IND-CCA secure PEKS scheme. In our first construction, to generate a PEKS ciphertext CT of a keyword w, the sender first generates a key-pair (vk,sk) for a strong one-time signature scheme, chooses a random message R, generates a HIBE ciphertext C of R with the vector of identities (w∥vk) and finally signs on C using sk to obtain a signature σ. Then CT consists of the verification key vk, the HIBE ciphertext C, the message R and the signature σ. To search the corresponding ciphertext CT with a keyword w′, the receiver derives the private key SKw′ corresponding to w′ and gives it to the server. Suppose that CT =(vk,C,R,σ) is a PEKS ciphertext. Then the server first verifies the signature σ on C with respect to vk and stops if the verification fails. (That is, the test algorithm checks if C is generated by an identical signer.) Otherwise, the server can generate the private key SK(w′∥vk) by using SKw′ and a key-derivation algorithm to decrypt the HIBE ciphertext C using the underlying HIBE scheme. If the result of decryption R ′ of C is identical to R, then the server obtains the test result 1. (This result 1 means that the w′ that is used to generate the private key SKw′ is identical to w which is used to generate the ciphertext CT.)

In our second construction, the idea of constructing for an IND-CCA security by using a strong MAC is similar to that employed in the first construction.

We examine the required security conditions of primitives, such as the HIBE, sig-nature, and MAC schemes, which are used to produce generic constructions for a computationally consistent IND-CCA secure PEKS scheme.

3.1 Our Constructions

The first construction of a PEKS scheme, using an anonymous (HIBE-ANO-CPA) 2-level HIBE scheme HIBE = (SetupHIBE, KeyGenHIBE, KeyDerHIBE, EncHIBE, DecHIBE), and a strong one-time signature scheme scheme Sig=(G, Sign,Vrfy), proceeds as follows.

• Gen(k): This algorithm runs SetupHIBE(k) to obtain (PP, mk). The public key is PK = PP and the secret key is SK = mk. It outputs (PK, SK)=(PP, mk).

• Trapdoor(SK,w): Let w∈{0,1}n be a keyword. To generate a trapdoor Tw of w, the trapdoor algorithm runs d0w←KeyGenHIBE(SK,0w). The trapdoor is Tw=d0w.

• PEKS(PK,w): To encrypt a keyword w∈{0,1}n under the public key PK, this algorithm picks a random message R∈M and runs G(k) to obtain the pair of signing and verification key (sk,vk). It computes A←EncHIBE(PK,0w∥1vk,R) and σ←Sign(sk,A∥R) to generate a PEKS ciphertext CT =[C1,C2,C3,C4]=[vk,A,R,σ].

• Test(CT, Tw): Let CT =[C1,C2,C3,C4] be a ciphertext and Tw=d0w be a trapdoor. To obtain the test result, this algorithm first checks if Vrfy (C1,C2,C3,C4) = 1. If not, it simply outputs ⊥. Otherwise, it computes d(0w∥1vk)←KeyDerHIBE(Tw,1C1) and A′←DecHIBE(d(0w∥1vk),C3). If A′=C2, it outputs 1; else, it outputs 0.

The second construction of PEKS scheme, using anonymous (HIBE-ANO-CPA) 2-level HIBE scheme HIBE = (SetupHIBE, KeyGenHIBE, KeyDerHIBE, EncHIBE, DecHIBE), a secure encapsulation scheme Encap = (Init, S, R), and a strong one-time MAC scheme MAC=(SigMac,VrfyMac), proceeds as follows.

• Gen(k): This algorithm runs SetupHIBE(k) to obtain (PP, mk). The public key is PK = PP and the secret key is SK = mk. It outputs (PK, SK)=(PP, mk).

• Trapdoor(SK,w): Let w∈{0,1}n be a keyword. To generate a trapdoor Tw of w, the trapdoor algorithm runs d0w←KeyGenHIBE(SK,0w). The trapdoor is Tw=d0w.

• PEKS(PK,w): To encrypt a keyword w∈{0,1}n under PK, this algorithm computes (r,com,dec)←S(k, pub), A←EncHIBE(PK,0w∥1com,dec), and tag←SigMac(r,A). It generates a PEKS ciphertext CT =[C1,C2,C3]=[com,A,tag].

• Test(CT, Tw): Let CT =[C1,C2,C3] and Tw=d0w. This algorithm computes d(0w∥1com)←KeyDerHIBE(Tw,1C1), dec′←DecHIBE(d(0w∥1com),C2), and r′←R(pub,C1,dec′) to obtain a string r′ . If r′≠⊥ and VrfyMac(r′,C2,C3)=1, it outputs 1; else, it outputs 0.

3.2 Flowchat of PEKS Encryption Process

The Fig. 1 shows the flowchart of the encryption module for our construction of PEKS scheme. It provides detail work-flow of the module to compute the encrypted keyword “PEKS ciphertext”.

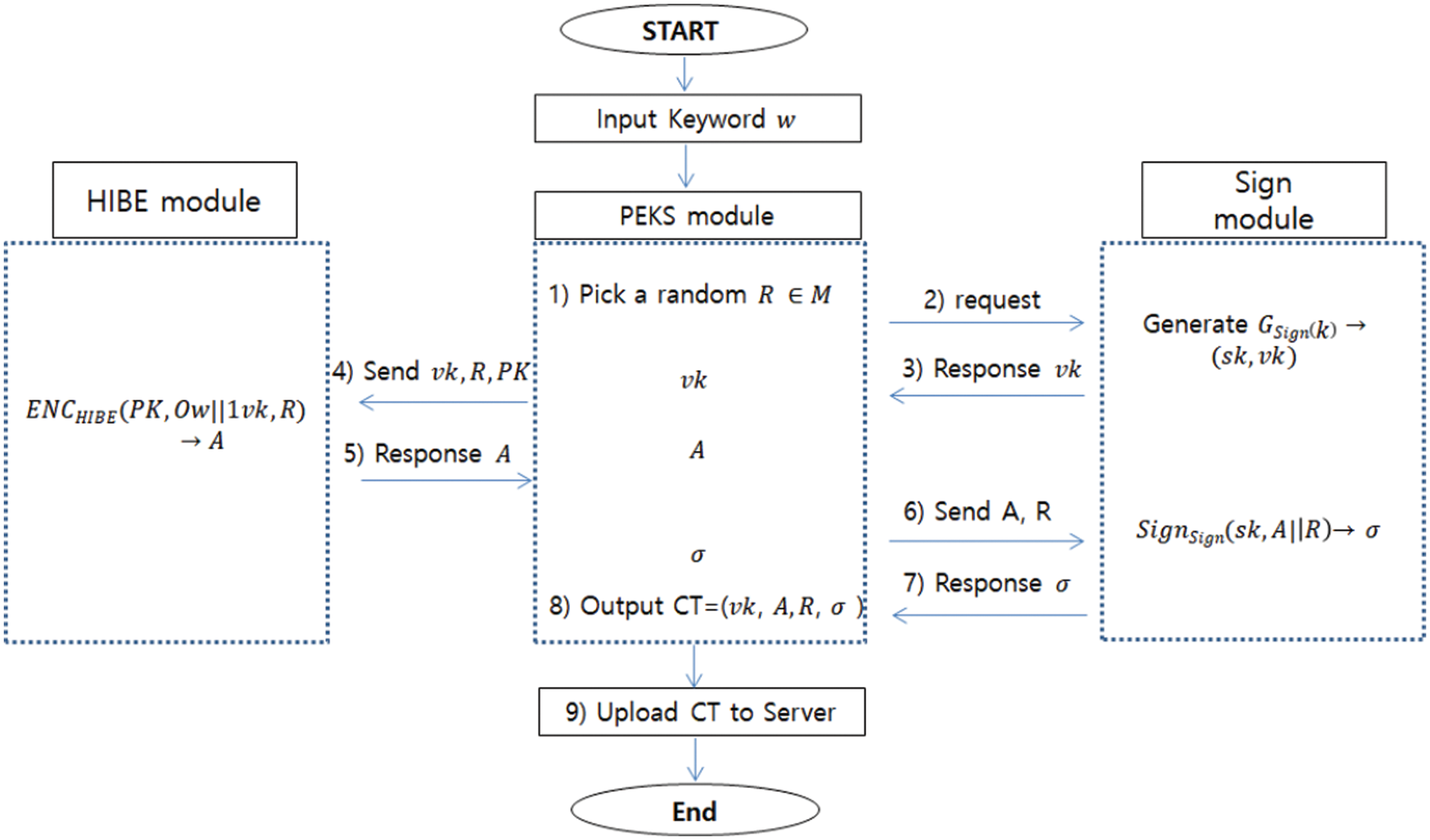
Figure 1: Flowchat for PEKS encryption process

4  Security Proofs

We now show that the confidentiality and consistency of proposed generic constructions are satisfied. In Theorem 4.1. and Theorem 4.2., we identify that (1) the confidentiality (specif.,IND-CCA security) of the first PEKS scheme comes from combining the anonymity (ANO-CPA security) of the 2-level HIBE and the strong one-time security of Sig and (2) the confidentiality (specif., IND-CCA security) of the second PEKS scheme comes from combining the anonymity (ANO-CPA security) of 2-level HIBE, the security of Encap and the strong one-time security of Mac. In Theorem 4.3. and Theorem 4.4., we identify that (3) the computational consistency of the first PEKS scheme comes from combining the confidentiality (HIBE-IND-CPA) of the 2-level HIBE and the existential unforgeability of Sig and (4) the computational consistency of the second PEKS scheme comes from combining the confidentiality (HIBE-IND-CPA) of 2-level HIBE and the binding property of Encap. The idea underlying the proof about the security of the PEKS scheme draws from Boneh et al. [24].

Theorem 4.1. If HIBE is HIBE-ANO-CPA secure and Sig is a strong one-time signature scheme, then the first construction for PEKS scheme is PEKS-IND-CCA secure.

Proof. Let Π′ denote the HIBE scheme and Π denote the PEKS scheme. Suppose that there is a PPT adversary A which has an advantage ϵ′ in attacking the PEKS-IND-CCA security of the PEKS scheme Π. We can construct a PPT adversary B attacking the HIBE-ANO-CPA security of HIBE scheme Π′ and a PPT forger F forging a signature with respect to a strong one-time signature scheme Sig with a probability exactly PrΠ,APEKS[Forge]. Here, we let [vk∗,A∗,R∗,σ∗] denote the challenge ciphertext received by A and Forge denote the event that A submits a valid ciphertext <[vk∗,A,R,σ],w> to the test oracle Test(·) with (A∗,R∗,σ∗)≠(A,R,σ) but for Vrfy(vk*,A,R,σ)=1. Let Succ denote the event that A’s output bit b′ is identical to the bit b about the keyword wb used to construct the challenge ciphertext CT∗=[vk∗,A∗,R∗,σ∗], where (sk∗,vk∗)←G(k), A∗←EncHIBE(PK,0wb∥1vk∗,R∗), and σ∗←Sign(sk∗,A∗||R∗). Let C denote a challenger against B and F. We prove the following claims.

Claim 1. PrΠ,APEKS[Forge] is negligible.

Claim 2. |PrΠ,APEKS[Succ ∧Forge¯]+12PrΠ,APEKS[Forge]−12| is negligible.

To show that these imply the theorem, note that

which is negligible given the stated claims.

Proof of Claim 1. F is defined as follows. C begins by supplying B with the verification key vk* outputted by G. F runs SetupHIBE(k) to obtain (PP, mk) and gives PP to A. Note that F can answer any test queries of A using the decryption oracle DecHIBE(⋅) of HIBE scheme. If A happens to submit a valid ciphertext [vk*, A, R, σ] to its test oracle before requesting the challenge ciphertext, then F simply outputs the forgery (A, R, σ) and stops. Otherwise, if A sends the messages,w0,w1, the forger F proceeds as follows.

- F chooses a random b ∈ {0, 1} and a random message R∈M and computes A∗←EncHIBE(PP,0wb∥1vk∗,R∗),. It obtains a signature σ∗ from F’s signing oracle Sign(·) on A∗. Finally, F gives the challenge ciphertext [vk∗, A, R, σ ] to A.

- If A sends a valid ciphertext [vk∗, A, R, σ ] to its test oracle, note that (A∗,R∗,σ∗)≠(A,R,σ). Then F simply outputs (A, R, σ) as forgery. It is easy to see that F’s success probability is exactly PrΠ,APEKS[Forge].

Proof of Claim 2. B is defined as follows. C begins by supplying B with the public parameters PP(= PKR) of HIBE as the public key PKR of the receiver R. Let SetTrap=∅, SetTest=∅, and SetVer=∅,. To construct B’s attack on the HIBE scheme in the sense of the security (anonymity) of the HIBE scheme, we use A as follows.

- On trapdoor queries w, B sets SetTrap = SetTrap ∪ {w} and makes a extraction query with an identity 0w to C and C runs the KeyGenHIBE algorithm to obtain the private key Tw=d0w about the identity 0w. C returns the private key d0w to B and B forwards d0w (as the resulting trapdoor Tw) to A. Note that since w≠w0,w1 of A, (w∥vk) is not a prefix of the target identity vector (w∥vk∗) of B, where vk is any verification key.

- On ciphertext queries [CT, w], B parses CT as[C1,C2,C3,C4] = [vk, A, R, σ] and proceeds as follows.

1. B sets SetVer=SetVer∪{vk}.

2. Before the challenge ciphertext CT∗=[vk∗,Ab,R∗,σ∗] is created, B proceeds as follows.

(2.a) If Vrfy(C1,C2,C3,C4) = 1, then B requests an extraction query for an identity (0w∥1vk) to obtain d(0w∥1C1) from C. B checks if  DecHIBE(PKR,d(0w∥1vk),C2)=C3. If so, then B responds with 1; otherwise, B responds with 0.

(2.b) If Vrfy(C1,C2,C3,C4)≠1 , then B gives ⊥ back to A.

3. After CT∗=[vk∗,Ab,R∗,σ∗] is created, B proceeds as follows.

(3.a) If vk=vk∗ and Vrfy(C1,C2,C3,C4) = 1(i.e., in the event that Forge occurs), then B aborts and outputs a random bit.

(3.b) If vk=vk∗ and (C1,C2,C3,C4)≠1, then B gives ⊥ back to A.

(3.c) If vk≠vk∗ and Vrfy(C1,C2,C3,C4) = 1, then B submits the extraction query for (0w∥1vk) to C and C gives d0w∥1vk=d0w∥1C1 back to B. B checks if  DecHIBE(PKR,d(0w∥1vk),C2)=C3. If so, then B responds with 1; otherwise, B responds with 0.

- On the challenge query (PKR,w0,w1), B proceeds as follows.

1. B runs G(k) to generate (sk∗,vk∗) such that SetVer∩{vk∗}=∅. B chooses a random message R∗∈M and gives a suitable challenge query (0w0∥1vk∗,0w1∥1vk∗,R∗) to C.

2. B obtains Ab←EncHIBE(PP,0wb∥1vk∗,R∗) from C, computes σ∗←Sign(sk∗,Ab||R∗), and gives the challenge ciphertext [vk∗,Ab,R∗,σ∗] back to A.

Eventually, A should make a guess b′ for b. Then B outputs b′ as its guess for b.

Note that B represents a legal adversarial strategy for attacking the anonymity (HIBE-ANO-CPA security) of Π′. Moreover, B provides a perfect simulation for A until the event Forge occurs. It is easy to see that and the left-hand-side of the above equation is negligible by the definition of the security of Π′. This completes the proof of the Theorem 4.1.

Theorem 4.2. If HIBE is HIBE-ANO-CPA secure and Encap is secure (in the sense of Definition 2.6), and Mac is a strong one-time message authentication code (MAC), then the second construction for PEKS scheme is PEKS-IND-CCA secure.

Proof. Since the proof of Theorem 4.2 is similar to that of Theorem 4.1, the detail of proof will be omitted. Theorem 4.3. If HIBE is HIBE-IND-CPA secure and Sig is an existential unforgeable signature scheme, then the first construction for PEKS scheme is computationally consistent.

Proof. Suppose there is a PPT adversary A which has an advantage ϵ′ in attacking the computational consistency of the PEKS scheme. We can construct a PPT adversary v attacking the HIBE-IND-CPA security of HIBE and a PPT forger F forging a signature with respect to an existential unforgeable signature scheme Sig with a probability of exactly PrΠ,APEKS[wForge].. Let C denote a challenger against B and F. Suppose that A outputs a pair of distinct keywords (w, w′) such that DecHIBE(PK,C∗,Tw′)=R′ (R∗≠R′) and Vrfy(vk∗,C∗,R′,σ∗) = 1, where (vk∗,R∗,C∗,σ∗) is a PEKS ciphertext of a random message R∗∈M and C∗←EncHIBE(PK,0w∥1vk∗,R∗). Here, wForge denotes the event that F finds a valid ciphertext (vk∗,C∗,R′,σ∗) (R∗≠R′) with the computationally consistency pair (w, w′) (w≠ w′). We prove the following claims.

Claim 3. PrΠ,APEKS[wForge] is negligible.

Claim 4. |PrΠ,APEKS[Succ ∧wForge¯]+12PrΠ,APEKS[wForge]−12| is negligible.

As in Theorem 4.1, we can prove Theorem 4.3 by establishing the above two clams.

Proof of Claim 3. F is defined as follows. C begins by supplying B with the verification key vk∗ output by G. runs SetupHIBE(k) to obtain (PP, mk) and gives PP to A. Suppose that A outputs a computationally consistency pair of keywords (w, w′) such that Test(CTw,Tw′) = 1, where CTw=PEKS(PP,w) and Tw′=Trapdoor(mk,w′). For every random message R∗∈M, A computes C∗←EncHIBE(PK,0w∥1vk∗,R∗) and sends (vk∗,R∗,C∗) to B and gets back a signature Sign(sk,A∥R)=σ∗ from C. Then CTw=(vk∗,R∗,C∗,σ∗) is a valid PEKS ciphertext. If  DecHIBE(PK,C∗,Tw′)=R∗ then F fails. If  DecHIBE(PK,C∗,Tw′)=R′ (R∗≠R′) then F simply outputs the forgery (vk∗,R′,C∗,σ∗)(R∗≠R′) and stops. Since Test(CTw,Tw′) = 1 should be satisfied, Vrfy(vk∗,R′,C∗,σ∗)=1. It is easy to see that F’s success probability is exactly PrΠ,APEKS[wForge].

Proof of Claim 2. B is defined as follows. C begins by supplying B with the public parameters PP(= PKR) of HIBE as the public key PKR of the receiver R. B runs G(k) to generate (sk,vk).

In its find stage, the given master public key PKR=PP, A runs A(PK) to obtain the keywords w, w’ such that Test(CTw,Tw′) = 1, where CTw=PEKS(PP,w) and Tw′=Trapdoor(mk,w′).

B chooses random message R0 and R1 (|R0 | = |R1|) and gives the challenge value (0w∥1vk, R0, R1) to C. B obtains a ciphertext C∗←EncHIBE(PK,0w∥1vk,Rb) from C. Here, the candidates of the valid PEKS ciphertext CT are [vk, R0, C∗, σ0] and [vk, R1, C∗, σ1], where σb = Sign(sk, C∗∥Rb)(b = 0, 1). B uses its  KeyDerHIBE oracle to obtain a secret key d(0w′∥1vk) corresponding to (0w′∥1vk) with a trapdoor Tw′=d0w′ . Since Test(PK, CT, Tw′) = 1, we obtain the result as the following equation.

Here, for every b′∈{0,1}, if R′≠Rb′ then B aborts and outputs a random bit. Otherwise, if  DecHIBE(PK,d(0w′∥1vk′),C)=R1 then it outputs 1; else, it outputs 0. It is easy to see that

This completes the proof of the Theorem 4.3.

Theorem 4.4. If HIBE is HIBE-IND-CPA secure, Encap satisfies a binding property, then the second construction for PEKS scheme is computationally consistent.

Proof. Since the proof of Theorem 4.4 is similar to that of Theorem 4.3, the detail of proof will be omitted.

5  Conclusion

General constructions have the advantage of being able to present protocols that provide new functions and safety using primitives that their securities previously been proven. [4,25] However, libraries such as Java, C, and the like may not support all kinds of functions that are cryptographic primitives. Hence, when considering the fact that you can select appropriate primitives depending on the development environment, it is meaningful to propose various general constructions using different primitives (as PKE, signature, massage authentication code, hash etc). Therefore, it is meaningful to propose a new type of generic construction using different types of primitives and to prove its security.

In this paper, we have examined the properties of the HIBE, signature and MAC, encapsulation schemes used to construct two confidential(IND-CCA secure) and computationally consistent generic constructions for PEKS schemes. We obtained the first generic construction by combining anonymous (ANO-CPA secure) 2-level HIBE and a secure signature scheme and the second by combining anonymous (ANO-CPA secure) 2-level HIBE, a secure encapsulation, and a secure MAC schemes [26]. A confidential PEKS scheme has resulted from the anonymity of the HIBE scheme and the security of the signature scheme (or of the MAC scheme). The computational consistency of the PEKS scheme has resulted from the confidential HIBE scheme and the security of the signature scheme (or the security of the encapsulation and MAC schemes). Hence, the proposed scheme will be one of the generic constructions for providing the consistent IND-CCA secure PEKS.

Funding Statement: The author received no specific funding for this study.

Conflicts of Interest: The author declare that they have no conflicts of interest to report regarding the present study.

References

 1.  General Data Protection Regulation (GDPR) – Official Legal Text, 2016. https://gdpr-info.eu. [Google Scholar]

 2.  Brazil’s General Data Protection Law (Lei Geral de Proteção de Dados - LGPD) Compliance, 2020. https://cpl.thalesgroup.com/engb/compliance/americas/brazil-general-data-protection-law. [Google Scholar]

 3.  M. Abdalla, M. Bellare, D. Catalano, E. Kiltz, T. Kohno et al., “Searchable encryption revisited: Consistency properties, relation to anonymous IBE, and extensions,” Journal of Cryptology, vol. 21, no. 3, pp. 350–391, 2008. [Google Scholar]

 4.  M. Abdalla, M. Bellare and G. Neven, “Robust encryption,” in Proc. TCC2010, LNCS 5978, Berlin, Germany, Springer, pp. 480–497, 2010. [Google Scholar]

 5.  J. Baek, R. Safavi-Naini and W. Susilo, “Public key encryption with keyword search revisited,” in Proc. ACIS2006, LNCS 5072, Springer: Perugia, Italy, pp. 1249–1259, 2008. [Google Scholar]

 6.  D. Boneh and B. Waters, “Conjunctive, subset, and range queries on encrypted data,” in Proc. Fourth IACR Theory of Cryptography Conf., TCC 2007, LNCS 4392, Springer: Berlin, Heidelberg, pp. 535–554, 2007. [Google Scholar]

 7.  B. Chor, E. Kushilevitz, O. Goldreich and M. Sudan, “Private information retrieval,” Journal of the ACM, vol. 45, no. 6, pp. 965–981, 1998. [Google Scholar]

 8.  Y. Chen, J. Zhang, D. Lin and Z. Zhang, “Generic constructions of integrated PKE and PEKS,” Journal of Designs, Codes and Cryptography, vol. 78, no. 2, pp. 493–526, 2016. [Google Scholar]

 9.  C. Gentry and A. Silverberg, “Hierarchical ID-based cryptography,” in Proc. ASIACRYPT2002, LNCS 2501, Springer: Queenstown, New Zealand, pp. 548–566, 2002. [Google Scholar]

10. Y. H. Hwang and P. J. Lee, “Public key encryption with conjunctive keyword search and its extension to a multi-user system,” in Proc. Pairing2007, LNCS 4575, Springer: Tokyo, Japan, pp. 2–22, 2007. [Google Scholar]

11. J. Katz, A. Sahai and B. Waters, “Predicate encryption supporting disjunctions, polynomial equations, and inner products,” in Proc. EUROCRYPT2008, LNCS 4965, Springer: Istanbul, Turkey, pp. 146–162, 2008. [Google Scholar]

12. S. Ma and Q. Huang, “A new framework of IND-CCA secure public key encryption with keyword search,” Computer Journal, vol. 63, no. 12, pp. 1849–1858, 2020. [Google Scholar]

13. H. S. Rhee, J. H. Park, W. Susilo and D. H. Lee, “Improved searchable public key encryption with designated tester,” in Proc. ASIACCS2009, New York, United States, pp. 376–379, 2009. [Google Scholar]

14. T. Suzuki, K. Emura and T. Ohigashi, “A generic construction of integrated secure-channel free PEKS and PKE and its application to EMRs in cloud storage,” Journal of Medical Systems, vol. 43, no. 5, pp. 1–15, 2019. [Google Scholar]

15. D. Boneh, G. D. Crescenzo, R. Ostrovsky and G. Persiano, “Public-key encryption with keyword search,” in Proc. EUROCRYPT2004, LNCS 3027, Springer: Interlaken, Switzerlan, pp. 506–522, 2004. [Google Scholar]

16. S. Goldwasser and S. Micali, “Probabilistic encryption,” Journal of Computer and System Sciences, vol. 28, no. 2, pp. 270–299, 1984. [Google Scholar]

17. J. Manger, “A Chosen ciphertext attack on RSA optimal asymmetric encryption padding (OAEP) as standardized in PKCS #1v2.0,” in Proc. CRYPTO’01, LNCS 2139, Springer: Santa Barbara, California, USA, pp. 230–238, 2001. [Google Scholar]

18. V. Shoup, “Why chosen ciphertext security matters,” IBM Research Report, RZ 3076, 1998. [Online]. Available: http://www.shoup.net/papers. [Google Scholar]

19. D. Bleichenbacher, “Chosen-ciphertext attacks against protocols based on the RSA encryption standard PKCS #1,” in Proc. CRYPTO’98, LNCS 1462, Springer: Santa Barbara, California, USA, pp. 1–12, 1998. [Google Scholar]

20. T. Fuhr and P. Paillier, “Decryptable searchable encryption,” in Proc. Provably Security’07, LNCS 4784, Springer: Wollongong, Australia, pp. 228–236, 2007. [Google Scholar]

21. D. Boneh and M. Franklin, “Identity-based encryption from the weil pairing,” SIAM Journal on Computing, vol. 32, no. 3, pp. 586–615, 2003. [Google Scholar]

22. J. Horwitz and B. Lynn, “Toward hierarchical identity-based encryption,” in Proc. EUROCRYPT 2002, LNCS 2332, Springer: Amsterdam, The Netherlands, pp. 466–481, 2002. [Google Scholar]

23. D. Boneh, A. Boldyreva, A. Desai and D. Pointcheval, “Key-privacy in public-key encryption,” in Proc. Asiacrypt2001, LNCS 2248, Springer: Gold Coast, Australia, pp. 566–582, 2001. [Google Scholar]

24. D. Boneh, R. Canetti, S. Halevi and J. Katz, “Chosen-ciphertext security from identity-based encryption,” SIAM Journal on Computing, vol. 36, no. 5, pp. 915–942, 2006. [Google Scholar]

25. Y. Wang, W. Susilo, J. Baek, J. Kim and I. Kim, “Generic construction of fair exchange scheme with semi-trusted adjudicator,” Journal of Wireless Mobile Networks, Ubiquitous Computing, and Dependable Applications, vol. 10, no. 4, pp. 68–87, 2019. [Google Scholar]

26. D. H. Duong, W. Susilo and V. C. Trinh, “Wildcarded identity-based encryption with constant-size ciphertext and secret key,” Journal of Wireless Mobile Networks, Ubiquitous Computing, and Dependable Applications, vol. 11, no. 2, pp. 74–86, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.