DOI:10.32604/cmc.2022.027885

| Computers, Materials & Continua DOI:10.32604/cmc.2022.027885 |  |
| Article |
Hyper-Parameter Optimization of Semi-Supervised GANs Based-Sine Cosine Algorithm for Multimedia Datasets
1Computer and Information Sciences Department, Universiti Teknologi PETRONAS, Seri Iskandar, 32610, Perak, Malaysia
2Centre for Research in Data Science (CERDAS), Universiti Teknologi PETRONAS, Seri Iskandar, 32610, Malaysia
3Mechanical Engineering Department, Universiti Teknologi PETRONAS, Seri Iskandar, 32610, Perak, Malaysia
4Department of Imaging Physics, The University of Texas MD Anderson Cancer Center, Houston, TX, USA
5University of Albaydha, Albaydha, Yemen
*Corresponding Author: Said Jadid Abdulkadir. Email: saidjadid.a@utp.edu.my
Received: 27 January 2022; Accepted: 30 March 2022
Abstract: Generative Adversarial Networks (GANs) are neural networks that allow models to learn deep representations without requiring a large amount of training data. Semi-Supervised GAN Classifiers are a recent innovation in GANs, where GANs are used to classify generated images into real and fake and multiple classes, similar to a general multi-class classifier. However, GANs have a sophisticated design that can be challenging to train. This is because obtaining the proper set of parameters for all models-generator, discriminator, and classifier is complex. As a result, training a single GAN model for different datasets may not produce satisfactory results. Therefore, this study proposes an SGAN model (Semi-Supervised GAN Classifier). First, a baseline model was constructed. The model was then enhanced by leveraging the Sine-Cosine Algorithm and Synthetic Minority Oversampling Technique (SMOTE). SMOTE was used to address class imbalances in the dataset, while Sine Cosine Algorithm (SCA) was used to optimize the weights of the classifier models. The optimal set of hyperparameters (learning rate and batch size) were obtained using grid manual search. Four well-known benchmark datasets and a set of evaluation measures were used to validate the proposed model. The proposed method was then compared against existing models, and the results on each dataset were recorded and demonstrated the effectiveness of the proposed model. The proposed model successfully showed improved test accuracy scores of 1%, 2%, 15%, and 5% on benchmarking multimedia datasets; Modified National Institute of Standards and Technology (MNIST) digits, Fashion MNIST, Pneumonia Chest X-ray, and Facial Emotion Detection Dataset, respectively.
Keywords: Generative adversarial networks; semi-supervised generative adversarial network; sine-cosine algorithm; SMOTE; principal component analysis; grid search
Since the invention of Generative Adversarial Networks (GANs), they have been extensively and almost exclusively applied for image generation. GANs are trained using two adversarial networks—a Discriminator and a Generator—working against each other under a min-max objective. Since 2014, many different variants of the GAN [1] model have been developed to improve the image generation task, e.g., Style Generative Adversarial Network (StyleGAN) [2]. StyleGAN is the architecture behind the famous website [3] that can generate realistic human faces that do not exist. Another famous variant of GAN is Wasserstein GAN (WGAN) [4]. In the original GANs or Deep Convolutional Generative Adversarial Networks (DCGANs), the Jensen-Shannon divergence is minimized to perplex the discriminator so that it cannot distinguish between real or fake images. However, in the case of Wasserstein Generative Adversarial Networks (WGANs), the Earth-Mover Distance (EMD) is minimized instead. This small change results in much better and more stable image generation results. Some other potential improvement on GANs is Big Generative Adversarial Network (BigGAN) [5], which is the most recent cutting-edge model applied on the ImageNet [6] model. The other one is Progressive GAN, where the authors add new blocks of convolutional layers to both the generator and the discriminator models, which then take help from the real image samples and try to generate high-resolution images from them. Also, Pix2Pix GAN [7] has several exciting applications, such as edge-maps to photo-realistic images [8]. Moreover, advanced technological tools such as Web 3.0 manipulate images to increase their quality or extract useful information from them. However, to optimize efficiency and avoid time wastage, images must be processed post-capture at a post-processing step [9]. The authors in [10,11] indicated that “Due to the small size and dense distribution of objects in UAV vision, most of the existing algorithms are difficult to detect effectively, while GAN can be used to generate more synthetic samples, including samples from different perspectives and those from the identical perspective yet having subtle distinctions, thus enabling deep neural network training.”
Semi-supervised learning is a machine learning technique where a small portion of data fed to the model is labeled during training, and the rest of the data is unlabelled. There are two types of learning. In semi-supervised learning, a small amount of labeled data is combined with a large amount of unlabeled data during training. On the other hand, supervised learning deals with only labeled training data. It is a unique case of insufficient supervision. Semi-supervised learning is considered the way to go in many recent problems as it curbs many problems related to overfitting training data due to huge amounts of unlabeled noisy data. Another reason why semi-supervised learning is gaining popularity these days is because there is a lack of labeled data many times since this requires human annotators, specialized equipment, and time-consuming tests [12]. All Generative models are applications of semi-supervised learning. Here, the labeled samples are the actual samples, while the generated samples are unsupervised. There are two main avenues for improvement in a GAN-based class— improve the GAN as a whole and/or target the specific class labels and generate samples accordingly. Conditional GANs (cGANS) [13] have been proposed for the same. Additional information, such as class labels connected with the input images, can improve the GAN. This enhancement could be in the form of more steady training, faster training, or higher quality generated images.
From this concept of cGANs, researchers have been able to develop methods for semi-supervised generative classification of generated images-SGAN [14], Auxiliary Classifier GAN (ACGAN) [15], and External Classifier GANs (ECGAN) [16]. The discriminator of a typical GAN discriminates between real and fake samples. The same architecture can be used to build a classifier with just the output layer different via transfer learning, by which we can classify the generated images as required during the semi-supervised training of the SGAN. The discriminator model is updated in the Semi-Supervised GAN to predict the labels for the classes needed as the output alongside the prediction for the Real/Fake labels. Hence, we can train the same discriminator and classifier models to predict the classes. That is how the semi-supervised GAN classifiers work. Similarly, there is a constant urge for improvement in the field of image classification, which led to the development of two improved types of GAN classifiers—Auxiliary Classifier GAN, which has two separated dense output layers, one for identifying the fake/real samples and the other one for the multi-class classification task [16]. In July 2021, High School Student Ayaan Haque developed the External Classifier GAN, containing three models—a generator, a discriminator, and an external multi-class classifier [17].
Hyperparameters lie at the heart of any machine learning or deep learning architecture. Without the tuned hyperparameters, it is impossible to obtain the best results for a task using that particular model. Searching for the correct set of hyperparameters manually is a very hectic task [18,19]. There are various mathematical computation methods and algorithms for performing Hyperparameter Tuning. Some computational methods include Random Search [20–22] and Grid Search [23,24]. Then there are some algorithms like Population-Based Training (PBT) [25], Grey Wolf Optimizer (GWO) [26,27] or Bayesian Optimization [28], and the Hyperband Method (BOHB) [29], which can be used for optimization. In this study, the proposed SGAN model was trained on four benchmark datasets: (i) MNIST Digits Dataset, (ii) MNIST Fashion Dataset, and (iii) Pneumonia Detection Chest X-Ray Dataset and (iv) Facial Emotion Recognition Dataset.
Once a working baseline was set up, the authors in this study progressed towards finding an optimal set of hyperparameters, like the learning rate for both the Generator and the Discriminator models. The authors further applied a hybrid metaheuristic optimization algorithm called Sine Cosine Algorithm (SCA) for hyperparameter tuning to obtain better results on the same datasets as above more efficiently than using Grid Search and Manual optimization. Finally, the results of each method were compared. Section 2, which follows this section, highlights the background and the related works of the study. Section 3 discusses the proposed research methodology, while Section 4 describes the experimental results of the proposed model. Lastly, Section 5 concludes the research and provides future work.
In the generative adversarial networks, there are two models the Generator (G) and the Discriminator (D) that are put up against one another in an adversarial fashion. The task of the G model is to take the input of random noise as input and output a fake image that is then fed to the D model. On its part, the D model tries to classify whether the image it got from the generator is real or fake. The task of the G model is to fool the D model and generate realistic fake images after epochs of training and backpropagation. The GAN architecture and the entire classification process are shown in Fig. 1.

Figure 1: GAN architecture
GANs were generally used for image synthesis from random noise. Hence, they were applied to different fields like fake image synthesis, data augmentation, and conditional image synthesis. However, recent advancements in the field of GANs have resulted in the diversified application of GANs. One such application is a classification of fake images generated by the Generator model. This field exploded with the advent of Conditional GANs. Conditional GANs are an extension of the minimax Generative Modelling (GANs) whereby the required class is passed as a part of the input to the Generator and the Discriminator, respectively, along with the random noise and the fake sample generated, respectively. This results in the generation of images belonging to a particular class as desired. This paper, though preliminary, opens up a whole new domain of interesting application of GANs. Fig. 2 present the conditional-GAN Architecture.

Figure 2: Conditional-GAN architecture
After this, many new GAN architectures were designed to solve the problem of image classification (both supervised and semi-supervised). Some of them are discussed below:
2.1 Semi-Supervised Classification with GANs (SGAN)
In this method, the authors classify a data point x into K classes using a standard classifier as an extension of the discriminator model. Thus, the discriminator model is designed to contain multiple output channels, i.e., (1) Binary Classifier for identifying fake vs. actual samples (2) K channels consisting of probabilities derived from applying soft-max activation function to the elements of K dimensional output vector. The K output logits are then passed through the softmax activation layer to predict the probability of the generated sample belonging to one of the K classes in the output column. This technique is widely known as SGAN [30,31].
2.2 Auxiliary Classifier GANs (AC-GAN)
The AC-GAN is another type of GAN classifier that changes the discriminator such that instead of taking the class labels as input (which was the case in Conditional GANs), it predicts the class labels of the generated image that was passed into the discriminator with Auxiliary Classifier. It makes the training process stable. Hence, the generator can generate high-quality images when its weights and biases get trained through forward and backward propagation. In this method, the authors pass the class labels along with the random noise at the Generator end. However, unlike the cGANs, the authors do not pass the labels at the Discriminator end. As before, the discriminator model must estimate whether the input image is real or fake and the image’s class label. There are two dense layers: one for the sample classification into fake or real and the other for categorical multi-class classification into K classes, to which the image belongs.
2.3 External Classifier GANs (ECGAN)
This is a semi-supervised GAN architecture where the fake image generated by the generator is used to improve image classification. Generally, the present models for classification with GANs (ACGAN, SGAN) have the same discriminator and classifier models, with the only difference being the output layer. EC-GAN attaches a GAN’s generator to a classifier, hence the name, as opposed to sharing a single architecture for discrimination and classification. The promising results of the algorithm could prompt new related research on how to use artificial data for many different machine learning tasks and applications. Thus, there are three separate models-generator, a discriminator, and a multi-class classifier. The Discriminator is trained in the classical fashion for GANs. The same goes for the classifier. In ECGANs, all the real samples must have labels assigned to them. The generated images are used as inputs for classification supplementation during training. In this case, the architecture follows a semi-supervised approach because the generated images do not have any labels. The generated images and labels are only kept if the model correctly predicts the sample class with a high probability (The labeling is done through a process of pseudo-labeling initially) [32].
The Google Brain paper mentions that GAN is sensitive to hyperparameter optimization because its benefit can override the cost function if it is not optimized correctly. Therefore, the performance of the cost functions can fluctuate within the different hyperparameter settings, and this fluctuation can occur when the developers do not know whether the GAN model is not working or they need to engage in a lengthy process. During training the GAN, hyperparameter tuning requires patience. Cost functions cannot work without spending time on the hyperparameter tuning since the new cost functions may introduce hyperparameter(s) with sensitive performance. Vanishing gradient exists during the GANs training process due to the multiplication of the gradient with small values through the backpropagation process. This causes the Neural Network to stop learning, distorting the accuracy. Therefore, enhancing GANs networks’ architectures leads to better performance in terms of prediction accuracy. Many factors affect GANs’ performance, which can be explored for a particular task to improve the prediction accuracy. For instance, generating the GANs weights based on meta-heuristic algorithms (like the Sine-Cosine Algorithm used in this study) instead of traditional manners will lead to better performance and overcome the limitations of existing work. This is the overview of what the proposed research is trying to achieve through the Weight Initialization of the discriminator and the classifier networks of the GAN in the proposed research.
This study aims to build a single Fine-Tuned Generative Adversarial Network Classifier Architecture that can efficiently perform binary and multi-class classification tasks and apply population-based meta-heuristic sine cosine algorithm [22,33,34] to initialize the parameters of the first layer, namely the weights and the biases. After this, the authors compared the results of the applied SCA model and the baseline model to look for improvement in train and test accuracies. Fig. 3 shows the proposed research methodology of this study.

Figure 3: Overall proposed research methodology
Hence, for the discriminator training, the data label coming from
For data coming from generator, the label is
Ultimately, the discriminator’s purpose is to classify the fake and real datasets appropriately. To do this, Eqs. (1) and (2) should be maximized, and the discriminator’s final loss function can be written as in Eq. (3).
In this case, the generator faces off against the discriminator. As a result, it will attempt to minimize Eq. (3), and the loss function is specified as,
Therefore, by combining Eqs. (3) and (4) considering the whole dataset, the final loss function will be as
3.1 Benchmark Datasets Description
For the task, the authors benchmarked the proposed model with four datasets that are all image-based classification datasets. These datasets are:
• MNIST Digits Dataset [35]-Contains handwritten examples of digits from 0-9 with the labels corresponding to each drawing showing the digit it represents.
• Fashion Dataset [36]-Contains examples of various garments (10 types) like - shirts, pants, boots, headwear, etc., and their corresponding labels.
• Pneumonia Detection from Chest X-Rays [37]-This dataset contains two classes, chest X-Ray images of healthy vs. pneumonic lungs.
• Facial Emotion Detection Dataset [38]-This is a tricky dataset with large-size images of seven different classes of facial emotions.
After that, the authors developed a Semi-Supervised GAN classifier. This is the proposed baseline model. Then, the authors fine-tuned the hyperparameters like the learning rates and the batch sizes for the SGAN model by Manual Searching. First, the authors preprocessed the data to get the images in the form of a pixel value table, with each of the scaled pixel values as the features and the target as the labels of the images. Next, the authors combined the generator, discriminator, and classifier models. In a broad sense, the classifier model is similar to the discriminator model; the only difference is the output layer. The discriminator has a sigmoid layer for classifying real/fake images, and the classifier has a softmax layer used to perform the multi-class classification. The authors also trained the proposed baseline model for classification tasks on all the benchmarking datasets. Squares 3 and 4 had class imbalances, leading to poorer results than expected. Hence, the authors decided to try two techniques to deal with the problem: (i) Synthetic Minority Oversampling Technique (SMOTE) [39] (ii) Principal Component Analysis (PCA) [40,41]. Furthermore, the authors built a script for applying Sine Cosine Algorithm for weights and biases initialization in the discriminator and the classifier models. The authors could not do the same thing for the generator model because its first layer was a Dense/Fully Connected Layer. As a result, there were too many parameters, such that it was practically impossible to train them all. After training all the combinations of the models, the authors trained them on all the four benchmarking datasets to get expected improvements upon using the Sine Cosine Algorithm to initialize the Parameters instead of doing it randomly.
3.2 Synthetic Minority Oversampling Technique
SMOTE is applied to those tabular datasets with a high degree of imbalance between the output classes. There are very few labels for some classes and a high number of labels for some classes. SMOTE is an oversampling technique that oversamples the examples from the minority classes so that the number of examples in the minority becomes equal to those in the majority classes [42]. Therefore, SMOTE can be considered a Data Augmentation Technique. SMOTE works by selecting examples in the feature spaces close together, distinguishing between the examples, and trying to draw a new instance at a point along that line [42]. To be more specific, a random illustration from the minority class is chosen first. Then, k of its nearest neighbors is found (typically, k = 5). A randomly chosen neighbor is chosen, and a synthetic example is created in feature space at a randomly chosen point between the two examples. Here, authors select some examples from the feature map and then try to make a class division between the selected data by the k-nearest neighbors (KNN), where authors generally take K to be 5. After this, they identify the minority classes and generate new samples on an imaginary line between two samples from the minority class. In this way, authors can generate as many new samples as required. Thus, SMOTE generates only new samples for the minority classes. However, some researchers suggest using random undersampling of the majority classes and oversampling the minority classes to obtain the best results. From the above discussion, the authors can figure out that one of the drawbacks of using SMOTE is that it does not consider the majority of classes at all. As a result, many times when there is not any clear distinction between the samples of the majority and minority classes, SMOTE often fails to generate perfect augmented samples.
3.3 Principal Component Analysis
PCA was also applied to the datasets for dimensionality reduction. Nonetheless, the idea did not lead to any improvement in the accuracy scores. Furthermore, reduction dimensions’ hyperparameter tuning did not significantly change scores, so the authors discarded the idea. PCA was implemented with an “auto” SVD solver. A default policy based on X.shape and n components select the solver: if the input data is greater than 500 × 500 and the number of features to extract is less than 80% of the lowest dimension of the data, the more efficient ‘randomized’ method is enabled. Otherwise, the exact full SVD is calculated and then optionally truncated.
Sine-Cosine Algorithm is a recent advancement in Metaheuristic Population-Based Optimization algorithms [43–48]. Seyedali Mirjalili proposed it in 2016. As is common to algorithms belonging to the same family, the optimization process consists of the movement of the individuals of the population within the search space, which represent approximations to the problem. For this purpose, SCA uses trigonometric sine and cosine functions. At each step of the calculation, it updates the solutions according to the following equations:
Where Xti denotes the position of the current agent at the iteration in the ith dimension; Pi is the position of the best agent at the iteration in the ith dimension. The random agents are r1, r2, r3, and r4.
r1 defines the afterward search space between the exterior and the solution space. r2 defines the amount of space left between the exterior and the solution space.
where T indicates the maximum iterations number and t is the iteration running. The a is a constant variable.

Presently, SCA is considered the best population-based method to find the optimal solution at the fastest speed. SCA is considered a meta-heuristic algorithm because it is a generalized algorithm that can be used to find solutions to various problems; it is not problem-dependent.
This section describes and discusses the proposed GAN model’s findings in this study. The first section focuses on the evaluation matrices used to evaluate the performance of the proposed model on four different datasets.
In this paper, four standard metrics are utilized to thoroughly evaluate the effectiveness and prediction of the proposed models: Accuracy, Precision, Recall, and F1-score. The following are the definitions of these four metrics:
As the name suggests, Confusion Matrix gives us a matrix as output and describes the complete performance of the model. Fig. 4 shows an Example Confusion Matrix of SGAN performance on Pneumonia Chest X-ray Dataset.

Figure 4: An example confusion matrix of SGAN performance on pneumonia Chest X-ray dataset
There are four essential terms:
• True Positives: The cases in which the authors predicted YES (1), and the actual output was also YES (1). (i.e., 379 in the figure above).
• True Negatives: The cases in which the proposed model predicted NO (0) and the actual output was NO (0). (i.e., 169 in the figure above).
• False Positives: The cases in which the proposed model predicted YES (1), and the actual output was NO (0). (i.e., 221 in the figure above).
• False Negatives: The cases in which the proposed model predicted NO (0) and the actual output was YES (1). (i.e., 11 in the figure above).
Accuracy: is the ratio of the number of correct predictions to the total number of input samples, i.e.,
Precision: is the ratio of the true positives predicted by the proposed model to the sum total of the labels predicted as true positives and false positives.
Recall: It is the number of correct positive results divided by the number of all relevant samples (all samples that should have been identified as positive).
F1-Score: is the Harmonic Mean between precision and recall. Hence, the value of the F1 score is always a real number between 0 and 1. This value captures how precise and accurate the model is in classifying the output classes for the labels.
The hyperparameters for the SGAN implementation on various datasets included the batch size of the data for training and the learning rates of the discriminator/classifier and the GAN in general. The Hyperparameters were selected using Grid Search and Manual Search over a discrete search space chosen after careful considerations by the authors. The information regarding the various hyperparameters is given in Tabs. 1 and 2.


4.3 Results of the Proposed Model
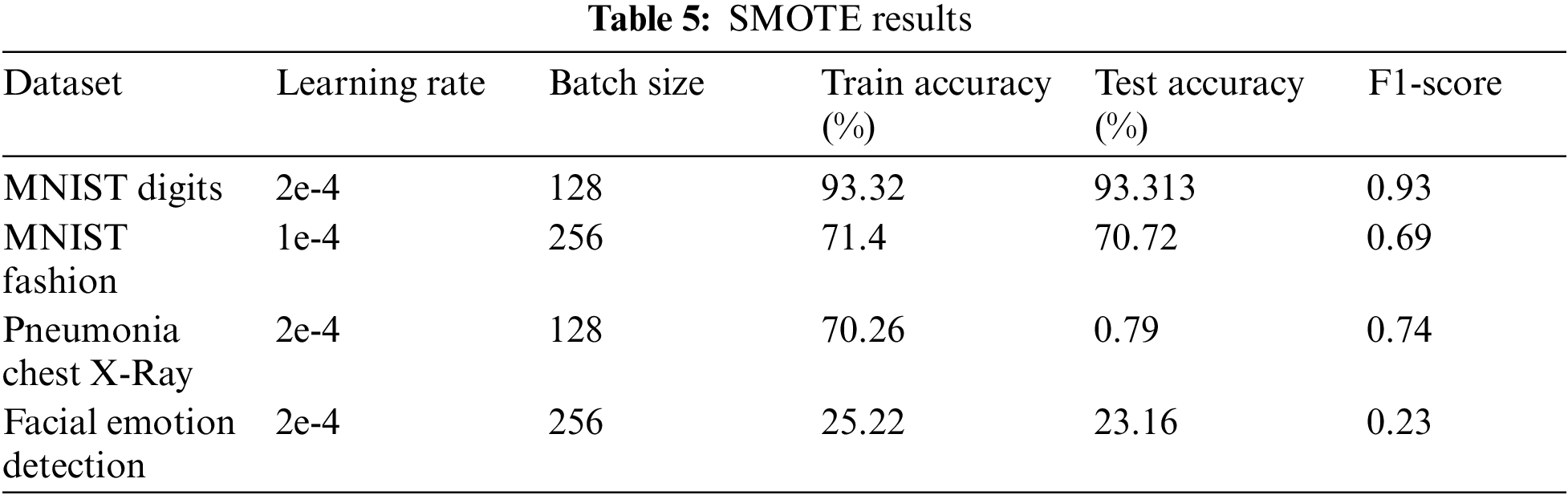
The Sine-Cosine Algorithm was implemented on the oversampled data using SMOTE. The authors named this result the SMOTE+SCA result. The authors expected to get the best results than all the previously experimented models because they had the dataset imbalance fixed, and the parameters were to be initialized using the SCA. For the Fashion MNIST dataset, the authors got around one improvement only for both the train and the test data. For the Pneumonia Detection dataset, they got an overwhelming increase of around 21% in the training accuracy and around 15% increase in accuracy over the baseline results for the test accuracy. The most satisfying results were obtained for the Facial Emotion Detection Dataset—the authors obtained over 30% accuracy for both train and test data for the first time since trying out all the different combinations of methods. Tab. 3 showed the results when the authors combined the proposed GAN model along with SMOTE and SCA methods.

4.4 Baseline and Balanced Dataset Results
The Baseline results consist of the classification results on the four datasets whereby the model is a simple Semi-Supervised GAN Classifier that is directly trained and tested on the pixel value tables of the images of the dataset. The results show that benchmark datasets like the MNIST Digits Dataset show superior results under baseline conditions, majorly due to how easy it is to classify handwritten digits given how complex and fine-tuned the SGAN classifier is. However, when a difficult dataset like the facial emotion detection dataset is considered, the model predicts a person’s facial emotion from the image of the face provided, the same complex SGAN classifier becomes counterproductive to inaccurate results in most cases. Evidently, GANs are difficult to train, and it is difficult to achieve good results at times. Tab. 4 shows the baseline model results.
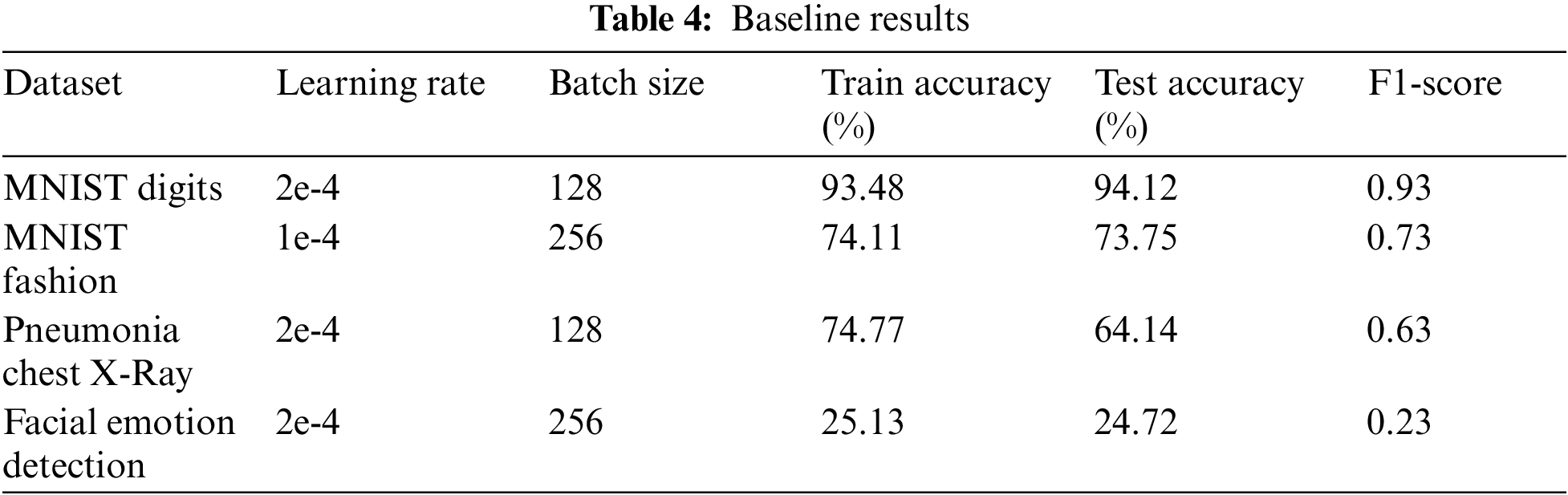
Next, the authors applied SMOTE, a minority oversampling technique, because of the four different datasets (MNIST digits and MNIST fashion). In contrast, the datasets like the pneumonia detection from chest X-Ray images and facial emotion detection had class imbalances. The authors expected to get similar results as the baseline results for the balanced datasets and significant improvements for the imbalanced datasets. However, the results were poorer for both MNIST digit and MNIST fashion datasets than the baseline results. This was somewhat expected since it is a balanced dataset. For the pneumonia chest X-Ray dataset, which was heavily imbalanced, the authors got very significant improvements of almost 20% for the train data and around 7% for the test data. For the facial emotion detection dataset, which was also imbalanced, the model did not show much improvement, which could have been due to the complexity and the size of the examples in the dataset. Another reason why SGAN could not perform better on the facial emotion dataset was that the GAN architecture might not have converged to a minimum error state, even after exhaustive grid search hyperparameter tuning. Tab. 5 shows the proposed model results after applying SMOTE technique.
Therefore, all the results are summarized in Fig. 5. The proposed SCA method showed outstanding improvement in performance over the sGAN method baseline. MNIST Digits & Fashion datasets have less or negative results due to their already balanced nature on applying SMOTE. Furthermore, when SCA was implemented for weight initialization, there was a considerable improvement over the SGAN and SGAN-SMOTE baselines. Similar observations were seen in the Pneumonia Chest X-Ray and Facial Emotion Detection datasets. However, in the Fashion-MNIST dataset, the performance of the sGAN baseline model slightly decreased after SMOTE was applied to the dataset. This might be because the dataset was already balanced, so SMOTE could not make a difference in the dataset label distribution.

Figure 5: F1-Score comparison across experiments
4.5 Comparison with Literature
This section compares the proposed GAN baseline model with the state-of-the-art models. Different deep learning methods have been used to perform classification in the literature. Some of these methods have been used as a comparison benchmark against our best-performing model. In the MNIST Dataset, our proposed model yields a test accuracy of 95.28%. Projection Net paper, on the other hand, gives the same performance of 95%. Recent developments such as Perceptron with a tensor train layer performed at 98.2%, which is way higher than our baseline model performance. Tab. 6 shows the comparison of the proposed method with related literature contributions.
In the MNIST Dataset, our proposed model yields a test accuracy of 94.86%. Similar work in neural networks such as CapsNet and Graph Convolutional Network achieves an accuracy score of 77% and 46%, respectively. In the Fashion MNIST, our proposed model surpasses machine learning methods such as Naive Bayes, Decision Trees, and Bayesian Forest by a considerable margin, which could be further seen in Tab. 6. Furthermore, in the Pneumonia Chest X-ray detection dataset, our proposed model’s performance is slightly lower than the pre-trained models such as DenseNet121. This might be because these architectures are trained on large scale datasets such as ImageNet, which gives these architectures a massive advantage over the non-pre-trained models

In this study, the authors proposed an SGAN classifier model that performs binary and multi-class classification accurately with the help of the Population-Based MetaHeuristic Sine Cosine Algorithm (SCA). While previous works majorly focused on a single dataset, we have implemented the proposed architecture on four different benchmark datasets to show the efficiency of the proposed model. The datasets used were the MNIST digits dataset, the MNIST Fashion dataset, Pneumonia Detection from Chest X-Rays dataset, and Facial Emotion Detection dataset. The class imbalance was addressed using the SMOTE method, which further led to a substantial improvement in the model’s performance. However, PCA did not yield better results. The application of SMOTE yielded better results on the imbalanced datasets, whereas we remained the same on datasets having balanced class distribution. One of the reasons why PCA might have failed is that the differentiating characteristics of the classes are not reflected in the variance of the variables. This is because PCA does not consider class information when calculating the principal components. Furthermore, the application of the Sine Cosine algorithm (SCA) used for initialization of weights and biases of Discriminator led to substantial improvement in the accuracy scores of the model. Lastly, this work could be further expanded by implementing the SCA algorithm to initialize weights and biases of the Generator efficiently without making it so computationally expensive. It is also suggestible to experiment with more benchmark datasets such as CIFAR-10 and CIFAR-100. To further improve the results, it is possible to use Auto-Encoders where the sheer number of parameters would benefit from their effective initialization through SCA.
Author Contributions: Conceptualization, A.A.; methodology, A.A.; S.J.A and A.M; software, A.A; validation, A.A. and A.M. formal analysis, A.A; S.J.A and A.M; data curation, A.A. and A.M. writing—original draft preparation, A.A.; A.M. and S.S; writing—review and editing, S.J.A. and Q.A visualization, A.A.; A.M. and S.S; supervision, S.J.A. project administration, S.J.A. funding acquisition, S.J.A. All authors have read and agreed to the published version of the manuscript.
Funding Statement: This research was supported by Universiti Teknologi PETRONAS, under the Yayasan Universiti Teknologi PETRONAS (YUTP) Fundamental Research Grant Scheme (YUTPFRG/015LC0-308).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu and D. Warde-Farley, “Generative adversarial nets,” Advances in Neural Information Processing Systems, vol. 2, no. 12, pp. 2672–2680, 2014. [Google Scholar]
2. T. Karras, S. Laine and T. en Aila, “A style-based generator architecture for generative adversarial networks, CoRR, abs/1812.04948,” 2018. [Online]. Available: http://arxiv.org/abs/1812.04948. [Google Scholar]
3. T. Karras, T. Aila, S. Laine and J. Lehtinen, “Progressive growing of GANs for improved quality, stability, and variation,” in 6th Int. Conf. Learn. Represent. ICLR 2018-Conf. Track Proc., New York City, USA, pp. 1–26, 2018. [Google Scholar]
4. Arjovsky, S. Chintala and L. Bottou, “Wasserstein GAN,” arXiv [stat.ML], 2017. [Online]. Available: http://arxiv.org/abs/1701.07875. [Google Scholar]
5. A. Brock, J. Donahue and K. en Simonyan, “Large scale GAN training for high fidelity natural image synthesis, CoRR, abs/1809.11096,” 2018. [Online]. Available: http://arxiv.org/abs/1809.11096. [Google Scholar]
6. J. Deng, W. Dong, R. Socher, L. Li et al., “ImageNet: A large-scale hierarchical image database,” in IEEE Conf. 639 on Computer Vision and Pattern Recognition, USA, pp. 248–255, 2009. [Google Scholar]
7. I. Phillip, J. Y. Zhu, T. Zhou and A. A. Efros, “Image-to-image translation with conditional adversarial networks, arXiv [cs.CV],” 2018. [Online]. Available: http://arxiv.org/abs/1611.07004. [Google Scholar]
8. D. Zhao, B. Guo and Y. Yan, “Parallel image completion with edge and color map,” Applied Sciences, vol. 9, no. 18, pp. 3856, 2019. [Google Scholar]
9. M. A. Albaom, F. Sidi, M. A. Jabar, R. Abdullah, I. Ishak et al., “The impact of tourist’s intention to use web 3.0: A conceptual integrated model based on TAM & DMISM,” Journal of Theoretical and Applied Information Technology, vol. 99, no. 24, pp. 6222--6238, 2021. [Google Scholar]
10. W. Sun, L. Dai, X. R. Zhang, P. S. Chang and X. Z. He, “RSOD: Real-time small object detection algorithm in uav-based traffic monitoring,” Applied Intelligence, vol. 92, no. 6, pp. 1–16, 2021. https://doi.org/10.1007/s10489-021-02893-3. [Google Scholar]
11. W. Sun, G. Z. Dai, X. R. Zhang, X. Z. He and X. Chen, “TBE-Net: A three-branch embedding network with part-aware ability and feature complementary learning for vehicle re-identification,” IEEE Transactions on Intelligent Transportation Systems, vol. 3, no. 12, pp. 1–13, 2021. https://doi.org/10.1109/TITS.2021.3130403. [Google Scholar]
12. X. Zhu and A. B. Goldberg, “Introduction to semi-supervised learning,” Synthesis Lectures on Artificial Intelligence and Machine Learning, vol. 3, no. 1, pp. 1–130, 2009. [Google Scholar]
13. M. Mirza and S. Osindero, “Conditional generative adversarial nets, USA,” pp. 1--7, 2014. [Online]. Available: http://arxiv.org/abs/1411.1784. [Google Scholar]
14. T. Chavdarova and F. Fleuret, “SGAN: An alternative training of generative adversarial networks,” in 2018 IEEE/CVF Conf. on Computer Vision and Pattern Recognition, New York City, USA, vol. 1, pp. 9407–9415, 2018. [Google Scholar]
15. A. Odena, C. Olah and J. Shlens, “Conditional image synthesis with auxiliary classifier GANs,” 34th Int. Conf. Mach. Learn. ICML, New York City, USA, vol. 6, pp. 4043–4055, 2017. [Google Scholar]
16. B. Sui, T. Jiang, Z. Zhang and X. Pan, “ECGAN: An improved conditional generative adversarial network with edge detection to augment limited training data for the classification of remote sensing images with high spatial resolution,” IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 14, pp. 1311–1325, 2021. [Google Scholar]
17. A. Haque, “EC-GAN: Low-sample classification using semi-supervised algorithms and GANs,” in The Thirty-Fifth AAAI Conf. on Artificial Intelligence (AAAI-21), New York City, USA, vol. 3, pp. 15797–15798, 2020. [Google Scholar]
18. A. Muneer, S. M. Fati, N. A. Akbar, D. Agustriawan and S. Tri Wahyudi, “iVaccine-Deep: Prediction of COVID-19 mRNA vaccine degradation using deep learning,” Journal of King Saud University - Computer and Information Sciences, vol. 9, no. 10, pp. 12522, 2021. [Google Scholar]
19. Q. Al-Tashi, E. A. P. Akhir, S. J. Abdulkadir, S. Mirjalili and T. M. Shami, “Classification of reservoir recovery factor for oil and gas reservoirs: A multi-objective feature selection approach,” Journal of Marine Science and Engineering, vol. 59, no. 8, pp. 888, 2021. [Google Scholar]
20. M. G. Ragab, S. J. Abdulkadir and N. Aziz, “Random search one dimensional CNN for human activity recognition,” in 2020 Int. Conf. Comput. Intell. ICCI 2020, Ipoh City, Malaysia, vol. 2020, pp. 86–91, 2020. [Google Scholar]
21. A. Muneer, S. M. Taib, S. Naseer, R. F. Ali and I. A. Aziz, “Data-driven deep learning-based attention mechanism for remaining useful life prediction: Case study application to turbofan engine analysis,” Electronics, vol. 10, no. 20, pp. 2453, 2021. [Google Scholar]
22. A. Alqushaibi, S. J. Abdulkadir, H. M. Rais, Q. Al-Tashi, M. G. Ragab et al., “Enhanced weight-optimized recurrent neural networks based on sine cosine algorithm for wave height prediction,” Journal of Marine Science and Engineering, vol. 9, no. 5, pp. 524, 2021. [Google Scholar]
23. S. Naseer, R. F. Ali, A. Muneer and S. M. Fati, “IAmideV-deep: Valine amidation site prediction in proteins using deep learning and pseudo amino acid compositions,” Symmetry, vol. 13, no. 4, pp. 560, 2021. [Google Scholar]
24. M. G. Ragab, S. J. Abdulkadir, N. Aziz, Q. Al-Tashi, Y. Alyousifi et al., “A novel one-dimensional CNN with exponential adaptive gradients for air pollution index prediction,” Sustainability, vol. 12, no. 23, pp. 10090, 2020. [Google Scholar]
25. M. Jaderberg, V. Dalibard, S. Osindero, W. M. Czarnecki, J. Donahue et al., “Population based training of neural networks,” 2017, Available: http://arxiv.org/abs/1711.09846-2017. [Google Scholar]
26. R. Al-Wajih, S. J. Abdulkadir, N. Aziz, Q. Al-Tashi and N. Talpur, “Hybrid binary grey wolf with harris hawk’s optimizer for feature selection,” IEEE Access, vol. 9, no. 2, pp. 31662–31677, 2021. [Google Scholar]
27. Q. Al-Tashi, H. M. Rais, S. J. Abdulkadir and S. Mirjalili, “Feature selection based on grey wolf optimizer for oil gas reservoir classification,” in 2020 Int. Conf. Comput. Intell. ICCI 2020, Ipoh City, Malaysia, pp. 211–216, 2020. [Google Scholar]
28. M. G. Ragab, S. J. Abdulkadir, N. Aziz, H. Alhussian, A. Bala et al., “An ensemble one dimensional convolutional neural network with bayesian optimization for environmental sound classification,” Applied Sciences, vol. 11, no. 10, pp. 4660, 2021. [Google Scholar]
29. S. Falkner, A. Klein and F. Hutter, “BOHB: Robust and efficient hyperparameter optimization at scale,” in 35th Int. Conf. Mach. Learn. ICML 2018, New York City, USA, vol. 4, pp. 2323–2341, 2018. [Google Scholar]
30. T. Salimans, I. Goodfellow, W. Zaremba, V. Cheung, A. Radford et al., “Improved techniques for training GANs,” Advances in Neural Information Processing Systems, vol. 5, no. 12, pp. 2234–2242, 2016. [Google Scholar]
31. A. Odena, “Semi-supervised learning with generative adversarial networks,” in the data efficient machine learning workshop at ICML, New York City, USA, pp. 1–3, 2016. [Google Scholar]
32. A. Haque, A.-A.-Z. Imran, A. Wang and D. Terzopoulos, “Generalized multi-task learning from substantially unlabeled multi-source medical image data,” J. Mach. Learn. Biomed. Imaging, vol. 25, no. 10, pp. 11–12, 2021. [Google Scholar]
33. L. Abualigah and A. Diabat, “Advances in sine cosine algorithm: A comprehensive survey,” Artificial Intelligence Review, vol. 54, no. 4, pp. 1–42, 2021. [Google Scholar]
34. H. Shutari, N. Saad, N. B. M. Nor, M. F. N. Tajuddin, A. Alqushaibi et al., “Towards enhancing the performance of grid-tied VSWT via adopting sine cosine algorithm-based optimal control scheme,” IEEE Access, vol. 9, pp. 139074–139088, 2021. [Google Scholar]
35. L. Deng, “The mnist database of handwritten digit images for machine learning research,” IEEE Signal Processing Magazine, vol. 29, no. 6, pp. 141–142, 2012. [Google Scholar]
36. H. Xiao, K. Rasul and R. Vollgraf, “Fashion-MNIST: A novel image dataset for benchmarking machine learning algorithms,” August 2017. Available: http://arxiv.org/abs/1708.07747. [Google Scholar]
37. Kaggle, “Chest x-ray images (pneumonia),” 2018. [Online]. Available: https://www.kaggle.com/paultimothymooney/chest-xray-pneumonia-2018. [Google Scholar]
38. Kaggle, “FER-2013https://www.kaggle.com/msambare/fer2013-2021. [Google Scholar]
39. N. V. Chawla, K. W. Bowyer, L. O. Hall and W. P. Kegelmeyer, “Snopes.com: Two-striped telamonia spider,” J. Artif. Intell. Res, vol. 16, no. 28, pp. 321–357, 2002. [Google Scholar]
40. S. Wold, K. Esbensen and P. Geladi, Principal component analysis, Chemometrics and Intelligent Laboratory Systems, Amsterdam, Netherlands, vol. 2, pp. 37–52, 1987. [Google Scholar]
41. S. M. Fati, A. Muneer, N. A. Akbar and S. M. Taib, “A continuous cuffless blood pressure estimation using tree-based pipeline optimization tool,” Symmetry, vol. 13, no. 4, pp. 686, 2021. [Google Scholar]
42. A. Muneer, S. M. Taib, S. M. Fati, A. O. Balogun and I. A. Aziz, “A hybrid deep learning-based unsupervised anomaly detection in high dimensional data,” Computers, Materials & Continua, vol. 70, no. 3, pp. 5363–5381, 2022. [Google Scholar]
43. M. Dorigo, M. Birattari and T. Stutzle, “Ant colony optimization,” IEEE Computational Intelligence Magazine, vol. 1, no. 4, pp. 28– 39, 2006. [Google Scholar]
44. A. H. Gandomi, X. S. Yang and A. H. Alavi, “Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems,” Engineering with Computers, vol. 29, no. 1, pp. 17–35, 2013. [Google Scholar]
45. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in In Proc. of ICNN’95-Int. Conf. on Neural Networks, Perth, WA, Australia, vol. 4, pp. 1942–1948, 1995. [Google Scholar]
46. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Advances in Engineering Software, vol. 95, no. 5, pp. 51–67, 2016. [Google Scholar]
47. S. Mirjalili, “SCA: A sine cosine algorithm for solving optimization problems,” Knowledge-Based Systems, vol. 96, no. 3, pp. 120–133, 2016. [Google Scholar]
48. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, no. 3, pp. 46–61, 2014. [Google Scholar]
49. E. Larsen, D. Noever, K. MacVittie and J. Lilly, “Overhead-MNIST: Machine learning baselines for image classification,” 6th Int. Conf. Learn. Represent. ICLR 2018-Conf. Track Proc., New York City, USA, vol. 19, no. 11, pp. 1–6, 2021. [Google Scholar]
50. C. Zhang, X. Pan, H. Li, A. Gardiner, I. Sargent et al., “A hybrid MLP-CNN classifier for very fine resolution remotely sensed image classification,” ISPRS Journal of Photogrammetry and Remote Sensing, vol. 140, no. 6, pp. 133–144, 2018. [Google Scholar]
51. S. Jain and V. Kumar, “Garment categorization using data mining techniques,” Symmetry, vol. 12, no. 6, pp. 984, 2020. [Google Scholar]
52. S. Misra, S. Jeon, S. Lee, R. Managuli, I. S. Jang et al., “Multi-channel transfer learning of chest X-ray images for screening of COVID-19,” Electronics, vol. 9, no. 9, pp. 1388, 2020. [Google Scholar]
53. A. Ambati and S. R. Dubey, “AC-CovidNet: Attention guided contrastive CNN for recognition of covid-19 in chest x-ray images,” 2021. [Online]. Available: http://arxiv.org/abs/2105.10239-2021. [Google Scholar]
54. D. Zhang, F. Ren, Y. Li, L. Na and Y. Ma, “Pneumonia detection from chest x-ray images based on convolutional neural network,” Electronics, vol. 10, no. 13, pp. 1512, 2021. [Google Scholar]
55. J. H. Kim, A. Poulose and D. S. Han, “The extensive usage of the facial image threshing machine for facial emotion recognition performance,” Sensors, vol. 21, no. 6, pp. 2026, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |