Computers, Materials & Continua DOI:10.32604/cmc.2022.028921
Article

Dynamics of Fractional Differential Model for Schistosomiasis Disease

Thongchai Botmart1, Wajaree Weera1,*, Muhammad Asif Zahoor Raja2, Zulqurnain Sabir3, Qusain Hiader4, Gilder Cieza Altamirano5, Plinio Junior Muro Solano6 and Alfonso Tesen Arroyo6

1Department of Mathematics, Faculty of Science, Khon Kaen University, Khon Kaen, 40002, Thailand
2Future Technology Research Center, National Yunlin University of Science and Technology, Douliou, Yunlin, 64002, Taiwan
3Department of Mathematics and Statistics, Hazara University, Mansehra, 21120, Pakistan
4Department of Mathematics, University of Gujrat, Gujrat, 50700, Pakistan
5Universidad Nacional Autónoma de Chota, Chota, 06121, Peru
6Universidad Nacional Pedro Ruiz Gallo, Lambayeque, 14013, Peru
*Corresponding Author: Wajaree Weera. Email: wajawe@kku.ac.th
Received: 21 February 2022; Accepted: 30 March 2022

Abstract: In the present study, a design of a fractional order mathematical model is presented based on the schistosomiasis disease. To observe more accurate performances of the results, the use of fractional order derivatives in the mathematical model is introduce based on the schistosomiasis disease is executed. The preliminary design of the fractional order mathematical model focused on schistosomiasis disease is classified as follows: uninfected with schistosomiasis, infected with schistosomiasis, recovered from infection, susceptible snail unafflicted with schistosomiasis disease and susceptible snail afflicted with this disease. The solutions to the proposed system of the fractional order mathematical model will be presented using stochastic artificial neural network (ANN) techniques in conjunction with the Levenberg-Marquardt backpropagation (LMBP), referred to as ANN-LMBP. To illustrate the preciseness of the ANN-LMBP method, mathematical presentations of three different values focused on fractional order will be performed. These statics performances are taken in these investigations are 78% and 11% for both learning and certification. The accuracy of the ANN-LMBP method is determined by comparing the values obtained by the database Adams-Bash forth-Moulton scheme. The simulation-based error histograms (EHs), MSE, recurrence, and state transitions (STs) will be offered to achieve the capability, accuracy, steadiness, abilities, and finesse of the ANN-LMBP method.

Keywords: Biological model; fractional order; schistosomiasis disease; artificial neural networks; reference results; Levenberg-Marquardt backpropagation

1  Introduction

Schistosomiasis disease (SD) is a parasitic disease produced by worms of the species Schistosoma. Schistosomiasis was treated for approximately 206 million people in 2016. However, the observed number of people expected to treat in 2016 was 89.2 million [1]. This disease instigated by tapeworms, which are members of the monophyletic Platyhelminthes and the species Schistosoma [2–4]. In 1905, a doctor in Changde discovered Schistosoma camellia eggs on an 18-year-old farm worker. The life cycle of schistosomiasis is complicated. It consists primarily of two rapacious host stages, human and larva, as well as two free pelagic stages, cercariae and miracidia. Roundworms in host organism eggs, which may pass through the large intestine and into the eco system with the faces. After entering fresh water, the eggs initiate to hatch and grow into miracidia. The unrestricted miracidia then infect the snail intermediate hosts, which is known as the larval development. The snails produce a large number of cercariae and release them into the water via asexual reproduction. Free-moving cercariae can damage the skin and enter the bloodstream, where they sophisticated into adults when humans come into contact with water.

Schistosomiasis mathematical analysis is not new, but it is typically expressed in the form of boundary value problems. Several researchers have used a deterministic approach to develop new schistosomiasis approaches or modify existing ones [5–7]. Fractional calculus has been widely used in real-world problems in recent years to describe genetic properties, energy dissipation effects, cognition, and harm structures. The Riemann–Liouville (RL) and Caputo fractional operators are excellent definitions of fractional differential equations, which are defined as the complexity of a given polynomial function/its derivative and the heat dissipation feature as a kernel [8]. These operators are non-local, according to this definition. The singularity caused by the energy decay kernel function on the other hand, includes multiple considerable computational difficulties necessitating the introduction of numerical solutions.

Fractional calculus (FC) was invented in the time of Newton, but it has recently piqued the interest of many academics. Over the last thirty years, the most fascinating leaps in industry sectors have been discovered within the structure of FC. The idea of the fractional derivative has been modernized due to the complexities affiliated with the characteristic of inhomogeneity. The behavior of multifaceted media with a diffusion process can be captured using fractional differential operators. It has been a very valuable tool, but many problems can now be demonstrated more helpfully and precisely using ordinary differential equations of any order. Many scholars began to work on simplistic calculus to reveal their points of view while analyzing a wide range of complex phenomena as a result of the rapid development of computational techniques with computer software systems. Many senior researchers proposed various concepts for fractional-order and integral operators, which arranged the foundation [9–14]. Many researchers have recently considered fractional calculus to be a more efficient approach than integer-order calculus when examining real-world problems suggested using mathematical models. For instance in [15], authors take into account the different derivative identified with the assistance of the non-singular operative in order to examine the fibroid surveillance model in [16], a new fractional concept along with a control scheme for the infection of dengue infection has been efficiently and successfully highlighted in [17], researchers consider the computational method in order to typify the efficiency while an For instance in [15], authors take into account the different derivative identified with the assistance of the non-singular operative in order to examine the fibroid surveillance model in [16], a new fractional concept along with a control scheme for the infection of dengue infection has been efficiently and successfully highlighted in [17], researchers consider the computational method in order to typify the efficiency while analyzing blood sugar levels and infectious diseases. The mathematical and analytical results for the equations highlighting these models play an important role in depicting the nature of nonlinear problems in associated fields of science [18–30].

Recent advances in fractional calculus (FC) theory have resulted in the creation of two notable operators, Caputo–Fabrizio and Atangana–Baleanu. The new derivatives mentioned above have non-singular kernels and do not use energy-distribution. The Atangana–Baleanu operator is mainly focused on the simple Mittag-Leffler method, which has powerful forces because its diffusional effects are collaborations with good assumptions. The Caputo–Fabrizio estimation is also based on exponential law, which can be found in a variety of natural phenomena and has a fusion effect with numerical depiction. These operators have demonstrated that they are the future for demonstrating a variety of scientific progressions such as turbulent theory, life processes, heat flux problems, operations research, and financial problems, among others [31–38].

This research is related to the development of a fractional order mathematical model focused on the evolution of the schistosomiasis disease. The use of fractional order derivatives is implemented to observe more precise performances of the mathematical equation. The novel fractional order mathematical model solutions will be described using stochastic artificial neural network (SANN) processes in conjunction with Levenberg-Marquardt backpropagation (LMBP), i.e., ANN-LMBP.

1.    To solve the dynamic behavior of the schistosomiasis disease, the ANN system is proposed effectively using LMBP optimization processes.

2.    The consistent overlapped results obtained by LMBP and the Adams achievements verify the proposed approach.

3.    The performance is certified by using various statistics values to accomplish the numerical performances of the schistosomiasis disease model.

The paper is systematized as: Section 2 demonstrates the configuration of the fractional order mathematical equation, Section 3 contains the stochastic contributions, Section 4 is created on ANN-LMBP method, Section 5 is intended using simulation procedures, and the final part contains concluding remarks.

2  Mathematical Form of The Delay Differential Two-Prey and One-Predator System Model

The model defines the total humanity at time ε, symbolized by N(ε), into susceptible persons who are uninfected with schistosomiasis W(ε), those who have been infected with schistosomiasis A(ε), and those who have healed from the kind of disease infection Q(ε). As a result, the whole social population is N=W+A+Q. Furthermore, N1 divides the total snail populations into vulnerable snails that uninfected with schistosomiasis U and those that have been infested with schistosomiasis infectious V. This indicates that N1=U+V represents the total vector population. The following non-linear ordinary differential equations are derived from the interlinkages with the compartments.

{dW(ε)dε=λ1−α1SW(ε)+γQ(ε)−β1W(ε),W0=k1,dA(ε)dε=α1SW(ε)−(β1+δ)A(ε),A0=k2,dQ(ε)dε=δ−(γ+β1)Q(ε),Q0=k3,dE(ε)dε=λ2−α2A(ε)E(ε)−β2E(ε),E0=k4,dS(ε)dε=α2A(ε)E(ε)−β2S(ε).S0=k5.(1)

Tab. 1 contains characterizations of the mathematical model built on the schistosomiasis disease of each parameter.

The current research aims to provide numerical simulations of a fractional order mathematical formula based on the schistosomiasis disease using artificial intelligence (AI) and ANN-LMBP. The following is the structure of the fractional order mathematical model focused on the schistosomiasis disease:

{d(τ)W(ε)dε(τ)=λ1−α1SW(ε)+γQ(ε)−β1W(ε),W0=k1,d(τ)A(ε)dε(τ)=α1SW(ε)−(β1+δ)A(ε),A0=k2,d(τ)Q(ε)dε(τ)=δ−(γ+β1)Q(ε),Q0=k3,d(τ)E(ε)dε(τ)=λ2−α2A(ε)E(ε)−β2E(ε),E0=k4,d(τ)S(ε)dε(τ)=α2A(ε)E(ε)−β2S(ε).S0=k5.(2)

In this system, τ is the fractional order derivative of the numerical schistosomiasis disease model.

3  Novel Stochastic Solvers Features

The current section demonstrates the stochastic operator performances when solving the fractional order computational schistosomiasis disease model with ANN-LMBP. Stochastic software solvers have been examined in the literature to solve complicated, singular, and rigid systems [39–41]. Stochastic optimization algorithms have been recently used to perform simulation studies of nonlinear computer virus propagation model [42], infection control model [43], Lane-Emden systems [44], functional order approaches [45], and nonlinear dynamic HIV systems [46–49]. The purpose of this work is to review and develop a fractional order mathematical schistosomiasis disease model using mathematical procedures based on the ANN-LMBP. These references [50–54] present a number of applications-based time-fractional derivatives. The following are some novel characteristics of ANN-LMBP for solving the fractional order mathematical model:

•   A design fractional order and numerical solutions are introduced to tackle the mathematical schistosomiasis disease model.

•   Using the stochastic ANN-LMBP methods, the numerical performance evaluation of the built mathematical schistosomiasis model is provided.

•   The proposed ANN-LMBP method is validated by computing the mathematical results of three multiple varieties depending on fractional order derivatives.

•   The accuracy and precision of the computing ANN-LMBP method are validated by comparing obtained and citation (Adams-Bashforth-Moulton) discussions.

•   The correctness of the ANN-LMBP method is obtained through absolute error (AE), which is skillful in good procedures for performing mathematical schistosomiasis disease model.

•   The stagnation, STs, correlation, MSE, and EHs measures validate the reliability and serviceability of the constructed ANN-LMBP method for mathematical schistosomiasis model solution.

4  Proposed Procedures: ANN-LMBP Method

This part of the study describes the proposed ANN-LMBP method for presenting the numerical schistosomiasis disease model solutions. The proposed ANN-LMBP scheme is introduced in two stages: the substantial performances of the ANN-LMBP method and the operational plans for solving the mathematical schistosomiasis model using the ANN-LMBP method. The significant operator performances-based L-MBNNs technique is provided.

The designed approach for solving the nonlinear fractional differential model is displayed in Fig. 1 and is based on the number of layer optimization procedures of the ANN-LMBP method. This study statics performances are 78 percent, 11 percent, and 11 percent for training, certification, and checking for tackling the fractional order computer simulation based on the schistosomiasis disease.

Figure 1: Workflow based fractional order derivative of the mathematical disaster of human anxiety model using the ANN-LMBP method

5  Results and Discussions

In this portion, three different variability of fractional order differential equations of the mathematical schistosomiasis disease model using ANN-LMBP are presented. Each type mathematical representation is as follows:

Case 1: Consider a fractional order mathematical model based on the schistosomiasis disease by using

τ=0.5, λ1=0.1, α1=0.12, β1=0.15, β2=0.18, δ=0.2, γ=0.23, λ2=0.23, α2=0.3, k1=0.1, k2=0.1, k3=0.3 and k4=0.4, k5=0.5.

{d(0.5)W(ε)dε(0.5)=0.1−0.12S(ε)W(ε)+0.23Q(ε)−0.15W(ε),W0=0.1,d(0.5)A(ε)dε(0.5)=0.12W(ε)S(ε)−(0.15+0.2)A(ε),A0=0.2,d(0.5)Q(ε)dε(0.5)=0.2−(0.23+0.15)Q(ε),Q0=0.3,d(0.5)E(ε)dε(0.5)=0.23−0.3A(ε)E(ε)−0.15E(ε),E0=0.4,d(0.5)S(ε)dε(0.5)=0.15A(ε)E(ε)−0.15S(ε).S0=0.5.(3)

Case 2: Consider the use of a fractional order mathematical model based on the schistosomiasis disease τ=0.7, λ1=0.1, α1=0.12, β1=0.15, β2=0.18, δ=0.2, γ=0.23, λ2=0.23, α2=0.3, k1=0.1, k2=0.1, k3=0.3 and k4=0.4, k5=0.5.

{d(0.7)W(ε)dε(0.7)=0.1−0.12S(ε)W(ε)+0.23Q(ε)−0.15W(ε),W0=0.1,d(0.7)A(ε)dε(0.7)=0.12W(ε)S(ε)−(0.15+0.2)A(ε),A0=0.2,d(0.7)Q(ε)dε(0.7)=0.2−(0.23+0.15)Q(ε),Q0=0.3,d(0.7)E(ε)dε(0.7)=0.23−0.3A(ε)E(ε)−0.15E(ε),E0=0.4,d(0.7)S(ε)dε(0.7)=0.15A(ε)E(ε)−0.15S(ε).S0=0.5.(4)

Case 3: Consider a fractional order mathematical model based on the schistosomiasis disease by using τ=0.9, λ1=0.1, α1=0.12, β1=0.15, β2=0.18, δ=0.2, γ=0.23, λ2=0.23, α2=0.3, k1=0.1, k2=0.1, k3=0.3 and k4=0.4, k5=0.5.

{d(0.9)W(ε)dε(0.9)=0.1−0.12S(ε)W(ε)+0.23Q(ε)−0.15W(ε),W0=0.1,d(0.9)A(ε)dε(0.9)=0.12W(ε)S(ε)−(0.15+0.2)A(ε),A0=0.2,d(0.9)Q(ε)dε(0.9)=0.2−(0.23+0.15)Q(ε),Q0=0.3,d(0.9)E(ε)dε(0.9)=0.23−0.3A(ε)E(ε)−0.15E(ε),E0=0.4,d(0.9)S(ε)dε(0.9)=0.15A(ε)E(ε)−0.15S(ε).S0=0.5.(5)

The numerical representations using the outcomes of the fractional order mathematical schistosomiasis disease model are discussed utilizing ANN-LMBP method with 13 numbers of neurons and data selection as 78%, 11%, and 11% for training, certification, and testing, respectively. Fig. 2 depicts the structure of the input, hidden, and output neurons.

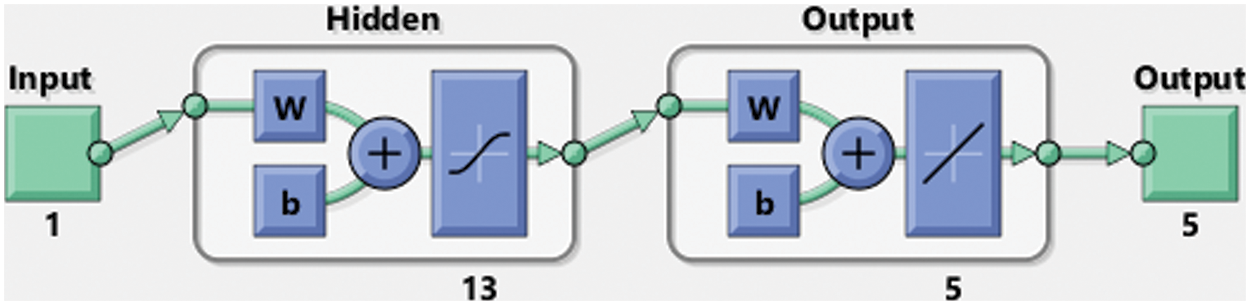
Figure 2: Designed ANN-LMBP method for schistosomiasis disease

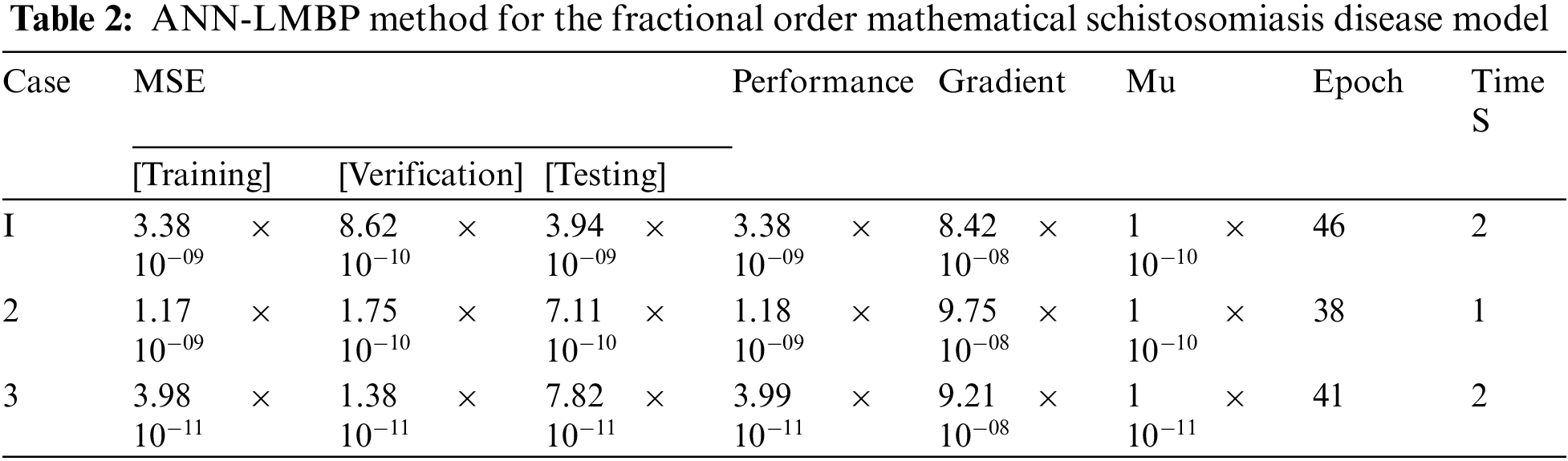
Figs. 3–5 show the fractional order mathematical schistosomiasis disease model developed using the ANN-LMBP method. The perfect EHs, curves, validations, and STs for the fractional order derivative mathematical schistosomiasis model are shown in Figs. 3 and 4. The best results of the fractional order mathematical schistosomiasis disease model (SDM) were obtained at epochs 38, 41, and 46, which were measured as 1.7573 × 10−10, 4.9824 × 10−10 and 8.6225 ×10−10. For the cases 1, 2 and 3, the gradient performances are 9.75 × 10−08, 9.2105 × 10−08, and 8.4198 × 10−08. The graphical methodologies demonstrate the convergence of the ANN-LMBP method for solving the fractional order mathematical (SD) model. The profitability of the results and EHs for the fractional order mathematical schistosomiasis disease (SD) model using the ANN-LMBP technique is shown in Fig. 4. These result valuations compare the performances of the review literature and reference solutions. The training, testing, and substantiation results for the fractional order mathematical (SD) model are plotted. The second section of Fig. 4 discusses the EHs values, which are 1.97 ×10−05, −3.6 × 10−06, and 3.16 × 10−07 for cases 1, 2, and 3. The correlation schemes for the fractional order mathematical (SDM) using the ANN-LMBP method are shown in Fig. 5. Using the ANN-LMBP method, the correlation for the fractional order mathematical (SD) model is found to be one. The precision of the ANN-LMBP method for the fractional order mathematical (SD) model is labelled by its training, testing, and substantiation accomplishments. Tab. 2 shows the MSE for the fractional order mathematical (SD) model by using ANN-LMBP method after verification, complexity, checking, training, generations, and backpropagation.

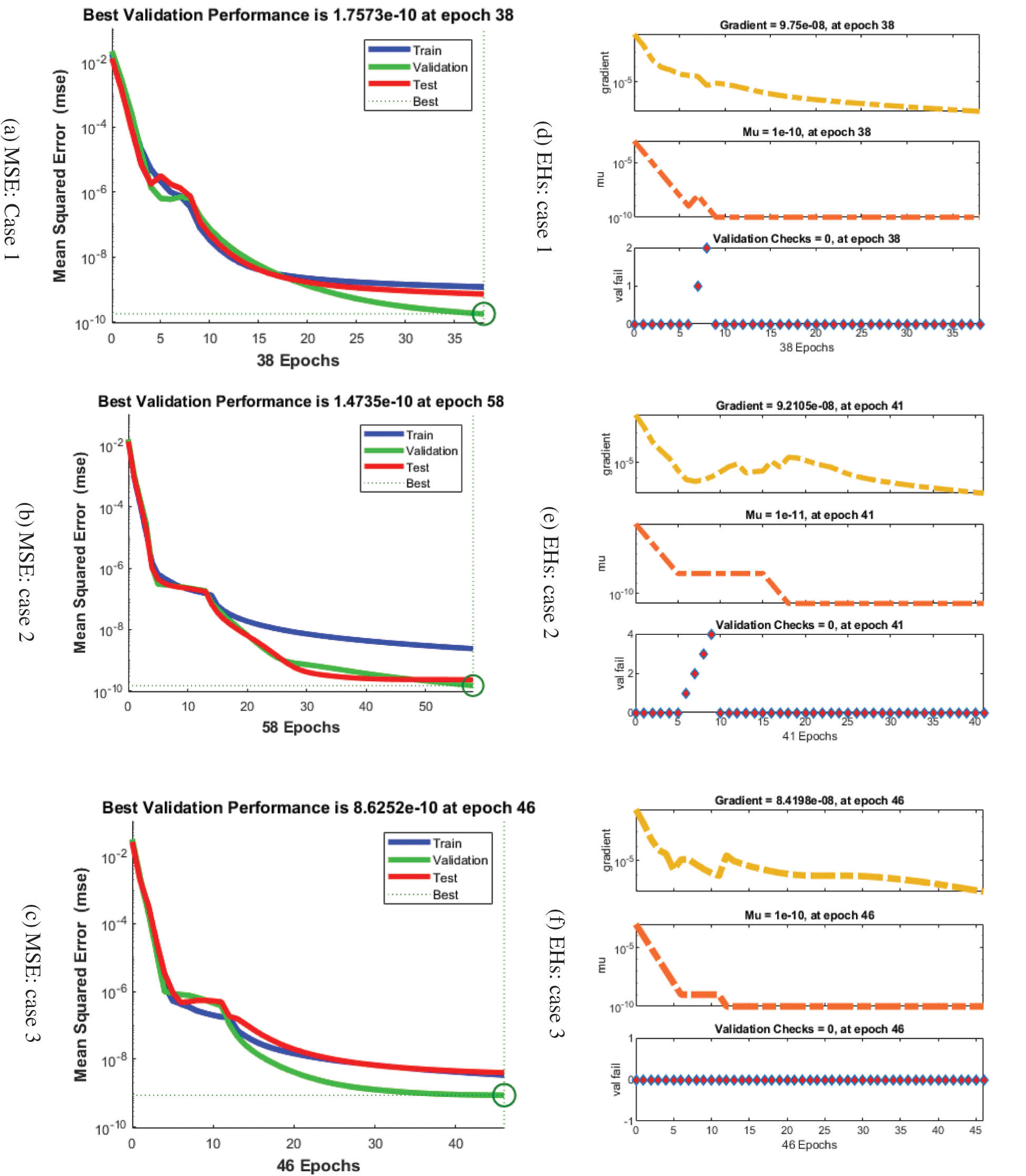
Figure 3: MSE and STs performances for the fractional order system

Figure 4: Results and EHs performances for the fractional order system

Figure 5: Regression performances for the fractional order system

The correctness of the proposed ANN-LMBP method for the fractional order mathematical (SD) model is observed in Figs. 6 to 7 based on the result comparison and AE performances. The calculated form of the numerical solutions has been drawn to solve the nonlinear model using the ANN-LMBP method. The matching of the calculated and reference results has been illustrated in Fig. 6. These plots present the precision of the ANN-LMBP method for the fractional order mathematical schistosomiasis disease model. The performances of AE to solve the fractional order mathematical (SD) model using the stochastic paradigms are plotted in Fig. 7.

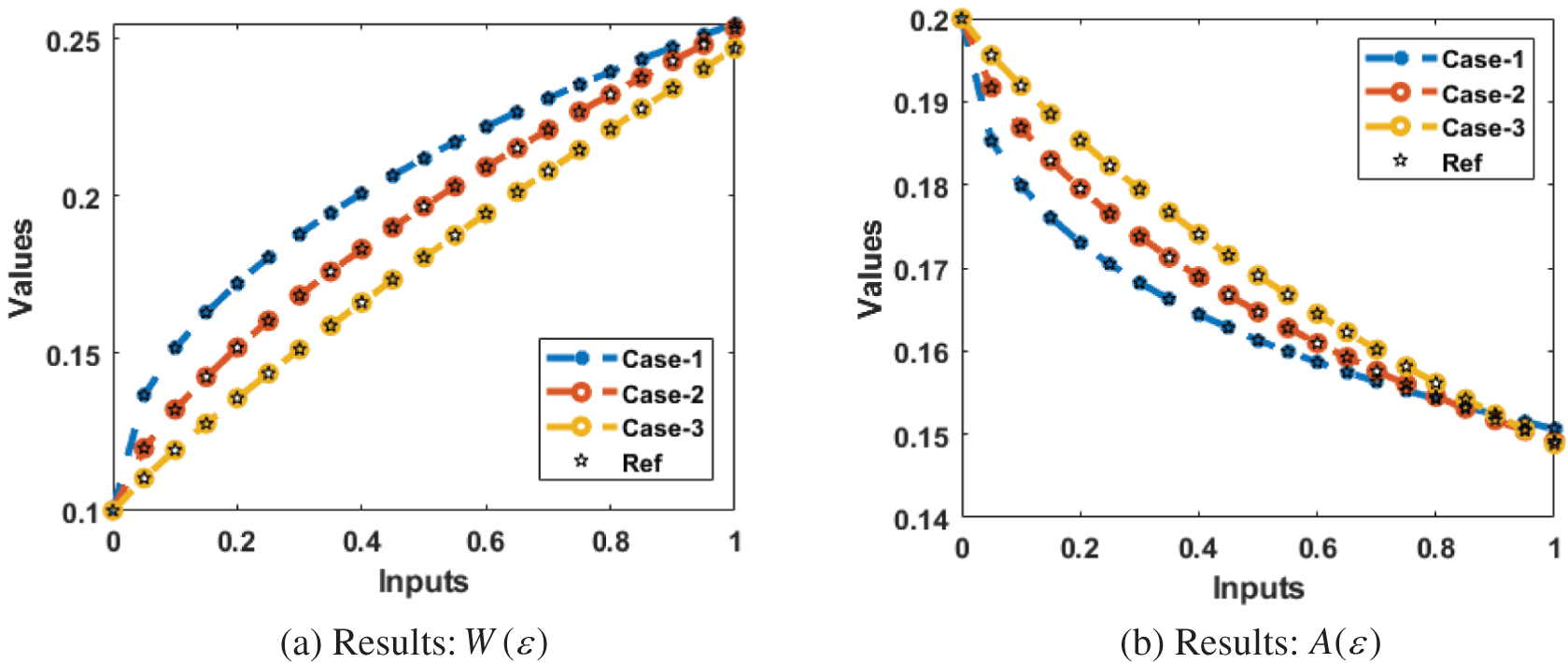
Figure 6: Comparison of the performances for the fractional order system

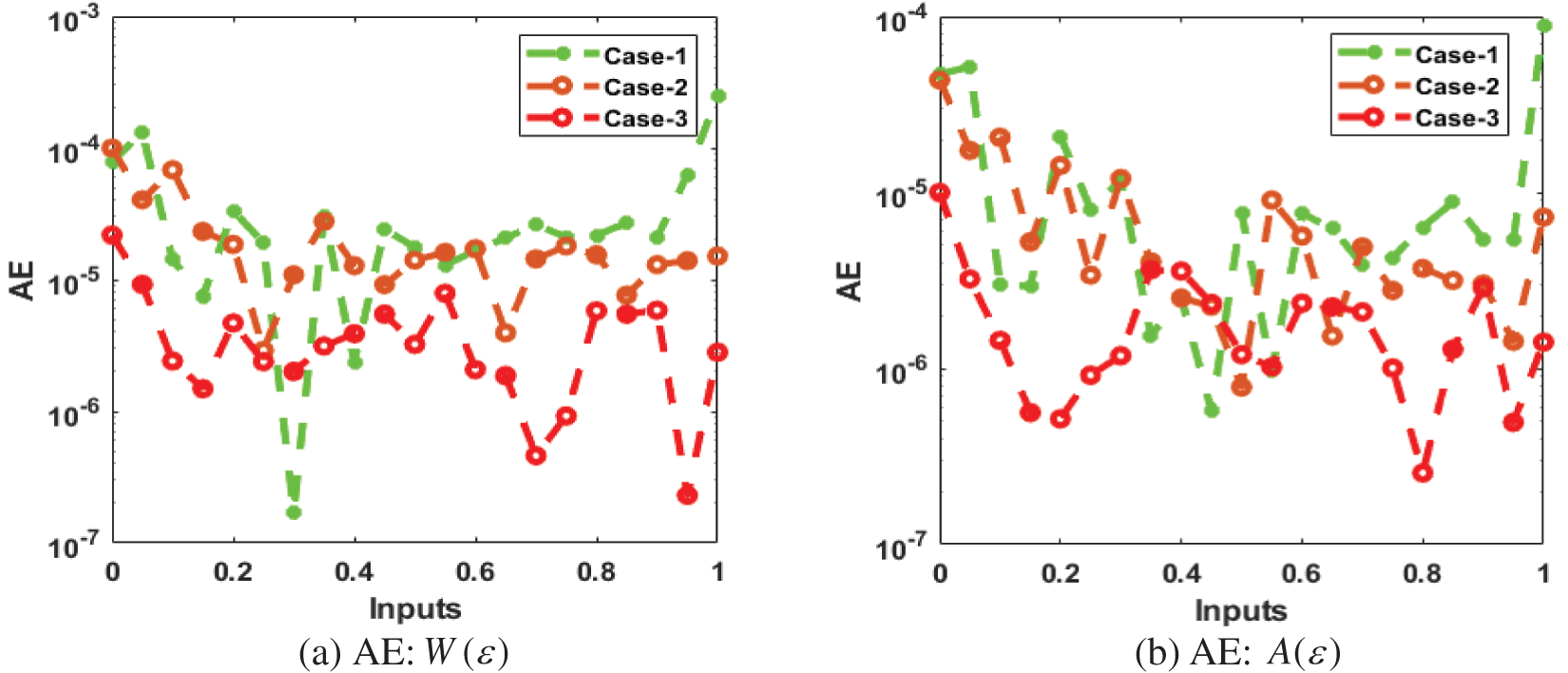
Figure 7: AE for the performances for the fractional order system

The AE is provided based on the not infected with schistosomiasis W(ε), infected with schistosomiasis A(ε), recovered from infection Q(ε), susceptible snail not afflicted with schistosomiasis disease E(ε) and susceptible snail afflicted with this disease S(ε). It is observed that the not infected with schistosomiasis W(ε) lie around 10−04 to 10−06, 10−05 to 10−07 and 10−05 to 10−07 for the case 1, 2 and 3. The AE for the people infected with schistosomiasis A(ε) lie around 10−04 to 10−04, 10−05 to 10−04 and 10−05 to 10−06 for the case 1, 2 and 3. The AE for the people recovered from infection Q(ε) found 10−04 to 10−04, 10−05 to 10−04 and 10−05 to 10−06 for the case 1, 2 and 3. Similarly, the AE for the behaviors E(ε)& S(ε) found 10−04 to 10−05, 10−05 to 10−05 and 10−06 to 10−07 for the case 1, 2 and 3. These best AE values represent the exactness of proposed ANN-LMBP method for the fractional order mathematical (SD) model.

6  Conclusion

In this presents study the numerical solutions of the fractional order mathematical model are presented based on the schistosomiasis disease. The goal of finding fractional order numerical solutions is to improve the accuracy of the mathematical model performance. The nonlinear mathematical system is divided into five dynamics, susceptible snail not infected with (SD) E(ε), susceptible snail afflicted with (SD) S(ε), not infected with schistosomiasis W(ε), recovered from infection Q(ε), and infected with schistosomiasis A(ε) order systems have never been used before by using the intended stochastic ANN-LMBP. It has been discovered that those who are not infected with schistosomiasis W(ε). To demonstrate the correctness of the ANN-LMBP method, numerical presentations of three different value parameters based on fractional order will be conducted. To solve the nonlinear fractional order system, thirteen neurons have been presented. This study statics performances are 78%, 11%, and 11% for training, certification, and testing for tackling the fractional order mathematical model based on schistosomiasis diseases. To determine the correctness of the ANN-LMBP method, the calculated values were compared to the Adams-Bashforth-Moulton. The MSE efficiency is reduced to locating numerical solutions of the ANN-LMBP technique for solving the fractional order derivative mathematical model based on the schistosomiasis disease. The ANN-LMBP method capability and dependability are demonstrated using numerical representations based on STs, EHs, MSE, correlation, and regression. The ANN-LMBP method achieves precision by using a fractional order mathematical model and comparing the obtained and reference results.

In future given methodology can be implemented to many fractional and integer order systems of utmost significance [55–65].

Funding Statement: This research is supported by Department of Mathematics, Faculty of Science, Khon Kaen University, Fiscal Year 2022.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  World Health Organization, “Schistosomiasis (Bilharzia),” 2022. [Online]. Available: https://www.who.int/schistosomiasis/en/. [Google Scholar]

 2.  B. Oyinloye, F. Adenowo, N. Gxaba and A. Kappo, “The promise of antimicrobial peptides for treatment of human schistosomiasis,” Current Drug Targets, vol. 15, no. 9, pp. 852–859, 2014. [Google Scholar]

 3.  A. F. Adenowo, B. E. Oyinloye, B. I. Ogunyinka and A. P. Kappo, “Impact of human schistosomiasis in sub-saharan africa,” The Brazilian Journal of Infectious Diseases, vol. 19, no. 2, pp. 196–205, 2015. [Google Scholar]

 4.  E. T. Chiyaka, G. Magombedze and L. Mutimbu, “Modelling within host parasite dynamics of schistosomiasis,” Computational and Mathematical Methods in Medicine, vol. 11, no. 3, pp. 255–280, 2010. [Google Scholar]

 5.  T. D. Mangal, S. Paterson and A. Fenton, “Predicting the impact of long-term temperature changes on the epidemiology and control of Schistosomiasis: A mechanistic model,” PLoS One, vol. 3, no. 1, pp. 1–9, 2008. [Google Scholar]

 6.  K. O. Okosun and R. Smith, “Optimal control analysis of malaria-schistosomiasis co-infection dynamics,” Mathematical Biosciences and Engineering, vol. 14, no. 2, pp. 377–405, 2017. [Google Scholar]

 7.  Z. Chen, L. Zou, D. Shen, W. Zhang and S. Ruan, “Mathematical modelling and control of schistosomiasis in hubei province,” China Acta Tropica, vol. 115, no. 1–2, pp. 119–125, 2010. [Google Scholar]

 8.  D. Baleanu, K. Diethelm, E. Scalas and J. J. Trujillo, Fractional calculus: Models and numerical methods. Singapore: World Scientific Publishing, 2012. [Google Scholar]

 9.  P. Agarwal and R. Singh, “Modelling of transmission dynamics of Nipah virus (NivA fractional order approach,” Physica A: Statistical Mechanics and its Applications, vol. 547, no. 1, pp. 1–15, 2020. [Google Scholar]

10. P. Agarwal, J. J. Nieto, M. Ruzhansky and D. F. Torres, Analysis of infectious disease problems (Covid-19) and their global impact. Singapore: Springer, 2021. [Google Scholar]

11. S. Salahshour, A. Ahmadian, N. Senu, D. Baleanu and P. Agarwal, “On analytical solutions of the fractional differential equation with uncertainty: Application to the Basset problem,” Entropy, vol. 17, no. 2, pp. 885–902, 2015. [Google Scholar]

12. A. ul Rehman, R. Singh and P. Agarwal, “Modeling, analysis and prediction of new variants of covid-19 and dengue co-infection on complex network,” Chaos Solitons & Fractals, vol. 150, no. 1, pp. 1–19, 2021. [Google Scholar]

13. P. Agarwal, M. A. Ramadan, A. A. Rageh and A. R. Hadhoud, “A fractional-order mathematical model for analyzing the pandemic trend of COVID-19,” Mathematical Methods in the Applied Sciences, vol. 44, no. 1, pp. 1–18, 2021. [Google Scholar]

14. R. Singh, A. U. Rehman, M. Masud, H. A. Alhumyani, S. Mahajan et al., “Fractional order modeling and analysis of dynamics of stem cell differentiation in complex network,” AIMS Mathematics, vol. 7, no. 4, pp. 5175–5198, 2022. [Google Scholar]

15. D. Baleanu, A. Jajarmi, S. S. Sajjadi and D. Mozyrska, “A new fractional model and optimal control of a tumor-immune surveillance with non-singular derivative operator,” Chaos: An Interdisciplinary Journal of Nonlinear Science, vol. 29, no. 8, pp. 1–15, 2019. [Google Scholar]

16. A. Jajarmi, S. Arshad and D. Baleanu, “A new fractional modelling and control strategy for the outbreak of dengue fever,” Physica A: Statistical Mechanics and its Applications, vol. 535, no. 7, pp. 1–14, 2019. [Google Scholar]

17. A. Jajarmi, B. Ghanbari and D. Baleanu, “A new and efficient numerical method for the fractional modeling and optimal control of diabetes and tuberculosis co-existence,” Chaos: An Interdisciplinary Journal of Nonlinear Science, vol. 29, no. 9, pp. 1–15, 2019. [Google Scholar]

18. A. M. S. Mahdy, “Numerical solutions for solving model time-fractional Fokker–Planck equation,” Numerical Methods for Partial Differential Equations 37(2):1120–1135, 2021. [Google Scholar]

19. A. M. S. Mahdy and E. S. M. Youssef, “Numerical solution technique for solving isoperimetric variational problems,” International Journal of Modern Physics C, vol. 32, no. 1, pp. 1–14, 2021. [Google Scholar]

20. Y. A. Amer, A. M. S. Mahdy, T. T. Shwayaa and E. S. M. Youssef, “Laplace transform method for solving nonlinear biochemical reaction model and nonlinear Emden-Fowler system,” Journal of Engineering and Applied Sciences, vol. 13, no. 17, pp. 7388–7394, 2018. [Google Scholar]

21. Y. A. Amer, A. M. S. Mahdy and H. A. R. Namoos, “Reduced differential transform method for solving fractional-order biological systems,” Journal of Engineering and Applied Sciences, vol. 13, no. 20, pp. 8489–8493, 2018. [Google Scholar]

22. M. M. Khader, N. H. Swetlam and A. M. S. Mahdy, “The Chebyshev collection method for solving fractional order Klein-Gordon equation,” WSEAS Transactions on Mathematics, vol. 13, pp. 2224–2880, 2014. [Google Scholar]

23. M. I. Othman, A. M. S. Mahdy and R. M. Farouk, “Numerical solution of 12th order boundary value problems by using homotopy perturbation method,” Journal of Mathematics and Computer Science, vol. 1, no. 1, pp. 14–27, 2010. [Google Scholar]

24. A. M. S. Mahdy, Y. A. E. Amer, M. S. Mohamed and E. Sobhy, “General fractional financial models of awareness with Caputo-Fabrizio derivative,” Advances in Mechanical Engineering, vol. 12, no. 11, pp. 1–9, 2020. [Google Scholar]

25. A. M. S. Mahdy, K. A. Gepreel, K. Lotfy and A. A. El-Bary, “A numerical method for solving the Rubella ailment disease model,” International Journal of Modern Physics C, vol. 32, no. 7, pp. 1–15, 2021. [Google Scholar]

26. A. M. S. Mahdy, M. S. Mohamed, K. Lotfy, M. Alhazmi, A. A. El-Bary et al., “Numerical solution and dynamical behaviors for solving fractional nonlinear rubella ailment disease model,” Results in Physics, vol. 24, pp. 1–10, 2021. [Google Scholar]

27. A. M. S. Mahdy, M. Higazy and M. S. Mohamed, “Optimal and memristor-based control of a nonlinear fractional tumor-immune model,” Materials & Continua, vol. 67, no. 3, pp. 3463–3486, 2021. [Google Scholar]

28. A. M. S. Mahdy, K. Lotfy, W. Hassan and A. A. El-Bary, “Analytical solution of magneto-photothermal theory during variable thermal conductivity of a semiconductor material due to pulse heat flux and volumetric heat source,” Waves in Random and Complex Media, vol. 31, no. 6, pp. 2040–2057, 2021. [Google Scholar]

29. A. K. Khamis, K. Lotfy, A. A. El-Bary, A. M. Mahdy and M. H. Ahmed, “Thermal-piezoelectric problem of a semiconductor medium during photo-thermal excitation,” Waves in Random and Complex Media, vol. 31, no. 6, pp. 2499–2513, 2021. [Google Scholar]

30. A. H. Bukhari, M. A. Z. Raja, N. Rafiq, M. Shoaib, A. K. Kiani et al., “Design of intelligent computing networks for nonlinear chaotic fractional Rossler system,” Chaos Solitons & Fractals, vol. 157, no. 8, pp. 111985, 2022. [Google Scholar]

31. M. S. Abdo, S. K. Panchal, K. Shah and T. Abdeljawad, “Existence theory and numerical analysis of three species prey-predator model under Mittag-Leffler power law,” Advances in Difference Equations, vol. 2020, no. 1, pp. 1–16, 2020. [Google Scholar]

32. S. T. Thabet, M. S. Abdo and K. Shah, “Theoretical and numerical analysis for transmission dynamics of COVID-19 mathematical model involving Caputo-Fabrizio derivative,” Advances in Difference Equations, vol. 2021, no. 1, pp. 1–17, 2021. [Google Scholar]

33. M. B. Jeelani, A. S. Alnahdi, M. S. Abdo, M. A. Abdulwasaa, K. Shah et al., “Mathematical modeling and forecasting of COVID-19 in Saudi Arabia under fractal-fractional derivative in Caputo sense with power-law,” Axioms, vol. 10, no. 3, pp. 1–23, 2021. [Google Scholar]

34. W. Shatanawi, M. S. Abdo, M. A. Abdulwasaa, K. Shah, S. K. Panchal et al., “A fractional dynamics of tuberculosis (TB) model in the frame of generalized Atangana-Baleanu derivative,” Results in Physics, vol. 29, no. 104739, pp. 1–12, 2021. [Google Scholar]

35. F. Jarad, T. Abdeljawad and Z. Hammouch, “On a class of ordinary differential equations in the frame of Atangana-Baleanu fractional derivative,” Chaos Solitons & Fractals, vol. 117, no. 1, pp. 16–20, 2018. [Google Scholar]

36. K. Ait Touchent, Z. Hammouch, T. Mekkaoui and F. Belgacem, “Implementation and convergence analysis of homotopy perturbation coupled with sumudu transform to construct solutions of local-fractional PDEs,” Fractal and Fractional, vol. 2, no. 3, pp. 1–12, 2018. [Google Scholar]

37. S. Uçar, E. Uçar, N. Özdemir and Z. Hammouch, “Mathematical analysis and numerical simulation for a smoking model with Atangana-Baleanu derivative,” Chaos, Solitons & Fractals, vol. 118, pp. 300–306, 2019. [Google Scholar]

38. M. Yavuz and N. Ozdemir, “Comparing the new fractional derivative operators involving exponential and Mittag-Leffler kernel,” Discrete & Continuous Dynamical Systems-S, vol. 13, no. 3, pp. 995–1006, 2020. [Google Scholar]

39. Z. Sabir, T. Botmart, M. A. Z. Raja, R. Sadat, M. R. Ali et al., “Artificial neural network scheme to solve the nonlinear influenza disease model,” Biomedical Signal Processing and Control, vol. 75, no. 103594, pp. 1–13, 2022. [Google Scholar]

40. Z. Sabir, M. A. Z. Raja, S. R. Mahmoud, M. Balubaid, A. Algarni et al., “A novel design of Morlet Wavelet to solve the dynamics of nervous stomach nonlinear model,” International Journal of Computational Intelligence Systems, vol. 15, no. 1, pp. 1–15, 2022. [Google Scholar]

41. Z. Sabir, M. A. Z. Raja, T. Botmart and W. Weera, “A neuro-evolution heuristic using active-set techniques to solve a novel nonlinear singular prediction differential model,” Fractal and Fractional, vol. 6, no. 1, pp. 1–14, 2022. [Google Scholar]

42. M. A. Z. Raja, A. Mehmood, S. Ashraf, K. M. Awan and P. Shi, “Design of evolutionary finite difference solver for numerical treatment of computer virus propagation with countermeasures model,” Mathematics and Computers in Simulation, vol. 193, no. 5, pp. 409–430, 2022. [Google Scholar]

43. Z. Sabir, M. A. Z. Raja and Y. Guerrero-Sánchez, “Solving an infectious disease model considering its anatomical variables with stochastic numerical procedures,” Journal of Healthcare Engineering, vol. 2022, no. 8, pp. 1–12, 2022. [Google Scholar]

44. Z. Sabir, M. A. Z. Raja, M. Umar, M. Shoaib and D. Baleanu, “FMNSICS: Fractional Meyer neuro-swarm intelligent computing solver for nonlinear fractional Lane-Emden systems,” Neural Computing and Applications, vol. 34, pp. 4193–4206, 2022. [Google Scholar]

45. M. A. Abdelkawy, Z. Sabir, J. L. Guirao and T. Saeed, “Numerical investigations of a new singular second-order nonlinear coupled functional Lane-Emden model,” Open Physics, vol. 18, no. 1, pp. 770–778, 2020. [Google Scholar]

46. M. Umar, Z. Sabir, M. A. Z. Raja, H. M. Baskonus, S. W. Yao et al., “A novel study of Morlet neural networks to solve the nonlinear HIV infection system of latently infected cells,” Results in Physics, vol. 25, no. 6803, pp. 1–13, 2021. [Google Scholar]

47. Y. Guerrero-Sánchez, M. Umar, Z. Sabir, J. L. Guirao and M. A. Z. Raja, “Solving a class of biological HIV infection model of latently infected cells using heuristic approach,” Discrete & Continuous Dynamical Systems-S, vol. 14, no. 10, pp. 3611–3628, 2021. [Google Scholar]

48. M. Umar, Z. Sabir, M. A. Z. Raja, J. G. Aguilar, F. Amin et al., “Neuro-swarm intelligent computing paradigm for nonlinear HIV infection model with CD4+ T-cells,” Mathematics and Computers in Simulation, vol. 188, no. 1, pp. 241–253, 2021. [Google Scholar]

49. Z. Sabir, M. Umar, M. A. Z. Raja, H. M. Baskonus and W. Gao, “Designing of Morlet wavelet as a neural network for a novel prevention category in the HIV system,” International Journal of Biomathematics, vol. 14, no. 2250012, pp. 1–12, 2021. [Google Scholar]

50. N. I. Chaudhary, M. A. Z. Raja, Z. A. Khan, A. Mehmood and S. M. Shah, “Design of fractional hierarchical gradient descent algorithm for parameter estimation of nonlinear control autoregressive systems,” Chaos, Solitons & Fractals, vol. 157, no. 3, pp. 111913, 2022. [Google Scholar]

51. A. A. Khan, S. M. Shah, M. A. Z. Raja, N. I. Chaudhary, Y. He et al., “Fractional LMS and NLMS algorithms for line echo cancellation,” Arabian Journal for Science and Engineering, vol. 46, no. 10, pp. 9385–9398, 2021. [Google Scholar]

52. N. I. Chaudhary, M. A. Z. Raja, Z. A. Khan, K. M. Cheema and A. H. Milyani, “Hierarchical quasi-fractional Gradient descent method for parameter estimation of nonlinear ARX systems using key term separation principle,” Mathematics, vol. 9, no. 24, pp. 1–14, 2021. [Google Scholar]

53. Z. Masood, M. A. Z. Raja, N. I. Chaudhary, K. M. Cheema and A. H. Milyani, “Fractional dynamics of stuxnet virus propagation in industrial control systems,” Mathematics, vol. 9, no. 17, pp. 1–27, 2021. [Google Scholar]

54. H. Durur, O. Tasbozan and A. Kurt, “New analytical solutions of conformable time fractional bad and good modified Boussinesq equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 447–454, 2020. [Google Scholar]

55. M. S. Abdo, S. K. Panchal, K. Shah and T. Abdeljawad, “Existence theory and numerical analysis of three species prey-predator model under Mittag-Leffler power law,” Advances in Difference Equations, vol. 2020, no. 1, pp. 1–16, 2020. [Google Scholar]

56. S. T. Thabet, M. S. Abdo and K. Shah, “Theoretical and numerical analysis for transmission dynamics of COVID-19 mathematical model involving Caputo-Fabrizio derivative,” Advances in Difference Equations, vol. 2021, no. 1, pp. 1–17, 2021. [Google Scholar]

57. V. M. Pérez-García, S. Fitzpatrick, L. A. Pérez-Romasanta, M. Pesic, P. Schucht et al., “Applied mathematics and nonlinear sciences in the war on cancer,” Applied Mathematics and Nonlinear Sciences, vol. 1, no. 2, pp. 423–436, 2016. [Google Scholar]

58. H. M. Baskonus, H. Bulut and T. A. Sulaiman, “New complex hyperbolic structures to the lonngren-wave equation by using sine-gordon expansion method,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 129–138, 2019. [Google Scholar]

59. Z. Sabir, M. Umar, M. A. Z. Raja, I. Fathurrochman and H. Hasan, “Design of Morlet wavelet neural network to solve the non-linear influenza disease system,” Applied Mathematics and Nonlinear Sciences, vol. 7, no. 1, pp. 1–16, 2022. [Google Scholar]

60. A. Yokuş and S. Gülbahar, “Numerical solutions with linearization techniques of the fractional Harry Dym equation,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 35–42, 2019. [Google Scholar]

61. A. Imran, A. Waheed, S. Javeed, D. Baleanu, M. Zeb et al., “Investigation of electroosmosis flow of copper nanoparticles with heat transfer due to metachronal rhythm,” Thermal Science, vol. 25, no. 2, pp. 193–198, 2021. [Google Scholar]

62. M. Dewasurendra and K. Vajravelu, “On the method of inverse mapping for solutions of coupled systems of nonlinear differential equations arising in nanofluid flow, heat and mass transfer,” Applied Mathematics and Nonlinear Sciences, vol. 3, no. 1, pp. 1–14, 2018. [Google Scholar]

63. F. Dusunceli, “New exact solutions for generalized (3+1) shallow water-like (SWL) equation,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 2, pp. 365–370, 2019. [Google Scholar]

64. E. İlhan and İ.O. Kıymaz, “A generalization of truncated M-fractional derivative and applications to fractional differential equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 171–188, 2020. [Google Scholar]

65. A. Waheed, A. Imran, S. Javeed, D. Baleanu, M. Zeb et al., “Study of electro-osmotic nanofluid transport for scraped surface heat exchanger with heat transfer phenomenon,” Thermal Science, vol. 25, no. 2, pp. 213–218, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.