DOI:10.32604/cmc.2022.025767

| Computers, Materials & Continua DOI:10.32604/cmc.2022.025767 |  |
| Article |
Secure Cancelable Template Based on Double Random Phase Encoding and Entropy Segmentation
1Faculty of Engineering, Electrical Engineering Department, Minia University, Minia, 61111, Egypt
2Department of Electronics and Electrical Communications Engineering, Faculty of Electronic Engineering, Menoufia University, Menoufia, 32952, Egypt
3Department of Computer Engineering, College of Computers and Information Technology, Taif University, Taif 21944, Saudi Arabia
*Corresponding Author: Ahmed M. Ayoup. Email: ayoup.2012@hotmail.com
Received: 04 December 2021; Accepted: 09 February 2022
Abstract: In this paper, a proposed cancellable biometric scheme is based on multiple biometric image identifiers, Arnold’s cat map and double random phase encoding (DRPE) to obtain cancellable biometric templates. The proposed segmentation scheme that is used to select the region of interest for generating cancelable templates is based on chaos entropy low correlation statistical metrics. The objective of segmentation is to reduce the computational cost and reliability of template creation. The left and right biometric (iris, fingerprint, palm print and face) are divided into non-overlapping blocks of the same dimensions. To define the region of interest (ROI), we select the block with the highest entropy. To shorten the registration process time and achieve a high level of security, we select 25% of the image volume of the biometric data. In addition, the low-cost security requirement lies in the use of selective encryption (SE) technology. The step of selecting the maximum entropy is executed on all biometric blocks. The maximum right and left multi-biometric blocks are arranged in descending order from the entropy perspective and select 50% of each biometric couple and store the single matrix. The obtained matrix is scrambled with a certain number of iterations using Arnold’s Cat Map (ACM).The obtained scrambled matrix is encrypted with the DRPE to generate the cancellable biometric templates, which are further concatenated. The simulation results display better performance of the suggested cancellable biometric system in noise scenarios using the area under the receiver operating characteristic (AROC). The strength of the suggested technique is examined with correlation, irregular deviation, maximum difference and maximum deviation. The recommended proposed approach shows that the ability to distinguish the authentic and imposter biometrics of user seven in different levels of the noise environment.
Keywords: Image identifier computation segmentation; ACM; (DRPE)
biometrics have gained attention in all countries as a surefire way to stabilize entry and exit for men and women with features such as voice, hand-writing and walking. In concept, each person has a physiological or behavioral parameter that is used to determine male or female identity, as long as they meet criteria such as permanence, universality, uniqueness and achievement.
The main concept of biometric authentication is to collect the biometric data of a legal person, collect various characteristics from the biometric authentication method to data reduction and store the characteristics of the persons in repositories. This is known as the training method. The biometrics acquisition phase, testing phase and individual characteristics are derived from the biometric inputs of human subjects compared to the characteristics within the repositories [1–3].
A biometric system in real can work with single or multiple models [4]. These models as one-sided structures are based on evidence of data hand-over for authentication of the individuals. A single-mode biometric machine contains a sensor template for collecting biometric features. A trait-derived unit implements a male or female feature to extract a characteristic object that is a feature-dense illustration. A labeled unit for identifying similarity or noting the difference between characteristics, a reference memory extractor array to generate matching results, as well to a decision unit to identify the authorized person or presumed person, is shown in Fig. 1.

Figure 1: Unimodal biometric system [4]
Although the unimodal biometric systems have several advantages, they must deal with various problems, such as noise in the captured information due to incomplete acquisition. Moreover, the biometric data may be contaminated by noise, which may lead to false rejections and failure to obtain a group of people and result in no wrong records. Forged behavior stamps are usually vulnerable to spyware attacks, in which the attacker imitates the same stamp as the registered item.
Within-class variation, the biological characteristics obtained through verification should not be similar to those established through manual registration, which is called intra-class variation, which represents the symmetry between the classes. The large symmetry between the classes increases the biometric error rate or False Accept Rate (FAR). In order to eliminate the problem of one-biometric data being stolen, multi-biometric is the suitable solution. The multi-biometric data can be collected and merged for more than one biometric. The fusion of biometric comes has several standards. The different fusion degrees of multi-model biological characteristics are shown in Fig. 2. The researchers adopt the most advanced model security technology, as shown in Fig. 2.

Figure 2: Various levels of fusion in multi-model biometric systems [4]
This article is divided into five parts. The first part introduces the cancellable biometrics, privacy aspects of the biometric systems, the key aspects of the proposed revocable biometric algorithm and the contribution and novelty of the proposed cancellable multi-biometric system. In the second part, we describe the differences in the related work of researchers. In the third part, we introduce the proposed algorithm and test it. In the fourth part, we show the simulation results and finally, in the last part, we explain the conclusions and future work.
1.1 Generation of Biometric Templates
All biometric identity verification systems have two main stages: registration stage and verification or authentication stage. In the registration stage, the biometric data obtained is registered to the user. In the identity verification stage, the user is identified through real-time comparison between biometrics with stored biometric data. The biometric system includes four main levels [5]. Biometric data collection, pre-processing, feature extraction and template creation and comparison are shown in Fig. 3.

Figure 3: Block diagram of the biometric verification system [5]
1.2 Security and Privacy Issues of the Biometric System
Biometric identification is a more secure method of identity verification and fraudsters have found new ways to bypass the security of biometric systems. The serious problem with biometric systems is the lack of biometric privacy. Attackers can easily obtain personal fingerprints and biometric data. There are eight points to attack the biometric systems [6]. Fig. 4 shows several attacks on biometric systems at different checkpoints. Tab. 1 shows possible solutions to possible attacks against biometric systems.

Figure 4: Different attacks points in biometric systems for verification [6]

1.3 Effectiveness of the Proposed Selective Multi-biometric System Compared to Traditional Ones
• The proposed efficiency of the multi-pattern reversible technology reduces the over-recording process and biometric recognition process. Moreover, we use multiple biometric features in the registration process to strengthen the cancellable template generation.
• The presented method for registration and authentication is very simple in 1.52 s, which makes it suitable for real-time applications.
• The proposed cancellable security metrics such as entropy, correlation, etc., are more appropriate for security tests.
• The proposed cancelable biometrics system has very good results in terms of AROC under noise conditions. This makes the proposed technology more suitable for different environments.
Several attempts have been made by various researchers in the area of cancellable biometrics. Jagadeesan et al. [7] presented a powerful technique that relies not only on fingerprints but also on multi-model biometrics such as iris to generate a reliable cryptographic key. Security has been greatly improved with the problem of serving a large number of users. Initially, the stamp details are stripped in addition to the texture features of the fingerprint and biometric iris. The extract features are then incorporated into the feature grades to generate the multi-biometric model. Simply, a multi-biometric model is generated with a 256-bit crypto key.
Wong et al. [8] proposed a fingerprint security approach to verify fingerprint details. The proposed scheme is used to derive binary models that are protected by detail descriptor applications such as Minutiae Vicinity Decomposition ‘(MVD)’. The MVD is used to capture a series of constant chaotic geometric elements in addition to random fingerprint projections. Messy MVD is developed using minutiae vicinities set's custom technology. The binary model has a constant area of detail noise protecting the location and direction of detail efficiency. Complementary bitwise operations were too fast.
Kaur et al. [9] Empirical statistics are based on AR face materials in addition to BERC visual face materials. They show that the technology offers model security, the ability to generate cancellable templates and identification precision. The security assessment shows that the proposed technology is very robust against replay attacks.
Another technique adopted user-specific tokens to generate phase-revocable binary features in addition to the amount style of the log-Gabor filter. (Sree et al., 2016) [10]. For a reliable multi-biometric database (face and fingerprints), a combined approach was used that relies on the essence of the fuzzy vault and biometrics. This preliminary approach converts biometric images prior to feature extraction. Extracted face plus fingerprint are used. The information of the functions is a combination of previous standard-setting functions to protect the merged biometric data in addition to the fuzzy vault. Empirical statistics show that the technique has high identification accuracy with GAR and FAR of 98.1% and 2%, respectively.
Tarif et al. [11] this method offer a massive standard model of security. It can resist much stronger geometric attacks Authentic biometric information can be obtained from a transformation model when an intruder gets the private key.
Li et al. [12] proposed a structure of protection based on statistics in which the theoretical method of data and computational security is adopted. It builds fingerprint-based multiple biometric cryptosystems. The work essentially consists of two sections, a new bio-cryptosystem-oriented security assessment framework and a functional structure of multi-biometric cryptosystems based on decision level fusion (MBCD) based on fingerprints. Hash functions are used in the structure of the MBCD to protect each of the biometric seals. It uses additional storage space. Mixing cryptosystems combine more than just model security techniques to create a biometric encryption technique. The mixing processes depend on the robustness of the element techniques in order to offer a combination process with great security and user-friendliness that they have higher execution costs plus process complications.
A mixed technique has been developed that adds a non-invertible conversion and a safe design (Bringer et al.) [13]. The technique has the error-correcting ability of the secure scheme to detect a lower irreversible transformation identification accuracy with FRR at 35% and FAR at 5.53%. It also forces the definition to be implemented without compromising the integrity of the stored models.
In an identical manner, the Bloom filter was applied to transform the face models before the transformed models were protected with the auxiliary data (Butt et al.) [14]. Bloom filters create a non-invertible model that improves the protection technology. No authenticated biometric models are found from the auxiliary data. Even so, the use of bloom filters reduces the schema identification performance. A blending technique can also be offered by “combining” a diffuse compromise technique with a fuzzy vault Nagar et al. [15]. This technology provides a better identification result (GAR = 95% plus FAR = 0.01%) as well as two-stage protection for stored fingerprint templates. The security check makes it clear that the crossover technique increases the lower entropy (an indication of security) of the fuzzy vault from 31 bits to 47 bits. The protected face model uses a technique that combines three approaches, a random projection, a transformation approach that preserves discrimination and a fuzzy engagement approach (Feng et al., 2010) [16]. 16.68%. It also increases identification accuracy by 4% to 15%.
3 Proposed Cancellable Biometric Encryption Technique
The suggested cancellable multi-model hybrid template scheme based on DRPE is presented and the calculation of the chaos entropy identifier is presented. The proposed technique follows nine phases. Figs. 5 and 6 show the block diagram of the left and the right cancellable biometric proposal and inscription of the correct technique selection, single matrix generation, Arnold’s map permutation of matrix block selectionand the permuted matrix encoding using DRPE.

Figure 5: Proposed block diagram of cancellable left biometric technique enrollment

Figure 6: Proposed block diagram of cancellable right biometric enrollment
In the first and second phases, the left and right multi-biometric images (iris, palm, fingerprints and face) are divided into an identical number of volume and non-overlapping blocks. The calculation of the maximum entropy is used for each separate block and the left multi-biometric blocks. The 25% of the highest values of the blocks of lowest correlation and maximum entropy are selected in descending order
In the third phase; the highest entropy value selected in the left and right fingerprints is ordered in descending order and is taken at 50%. The higher entropy locks the couple fingerprint values. In addition, the highest entropy value selected in the left and right irises are placed in descending order and 50% of the highest entropy block values are taken from the iris of the pair. The highest selected entropy value in the left and right palms are placed in descending order and 50% of the highest entropy block values are taken from the palms. The selected area block with the highest entropy is selected.
In the seventh phase, the maximum entropy blocks that are biometrically selected from each pair or face are grouped in a single matrix. In the eighth phase, the clustered matrix is permuted with Arnold's cat-map to reduce the correlation between the pixels and to make the change diffuse. In the ninth phase, Arnold’s cat map output is applied to DRPE to encrypt the pooled matrix to create the encrypted biometric template. Fig. 7 shows the phases of generating the encrypted template.

Figure 7: The phases of the generation encrypted templates
Phase 1: Input Multi-Biometric
Multi-biometric systems depend on several information sources of biometric data. To capture the individual data, a multi-biometric system is described in one of the following six sets [17]: multi-sensor, multi-algorithm, multi-instance, multi-sample and multi-model, (see Fig. 8).

Figure 8: Sources of information for biometric fusion [17]
Phase 2: Image Segmentation
We propose an image identifier that is easy for everyone to calculate. The image is divided into non-overlapping blocks and each block is equal to row and column. The total number of blocks depends on the bit size of the image. Fig. 9 shows the technique for calculating an identifier with 16 blocks, with phase 2 called the calculation of the image identifier.

Figure 9: Image identifier computation
Phase 3: Entropy Calculation
Entropy computation is applied on the separate image bulks to calculate the
Phase 4: Selection of Maximum Entropy
In order to identify the region of interest '(ROI)' in each sensitive area, the blocks that have the maximum entropy numbers are selected. For the lowest encryption time and highest security, the selected bundles should make up 25% of the volume of the incoming biometric image.
Phase 5: Repeat the Steps from Phase 1 to Phase 4
The calculation of the image identifier is applied to each input biometric, which is divided into non-overlapping bundles, as well as the entropy calculation for each block and the selection of the maximum entropy in each image does not exceed 25% of the bulk input image volume.
Phase 6: Rearrange and Select the Four Max Entropy Selections in Descending Order of Each Input Image
After the maximum entropy selection in each biometric image not exceed 25% of the input image blocks. The selected blocks are rearranged in descending order in each image separately. Then, we can result seven images (left and right palm, left and right fingerprint, left and right iris and face), where each image is composed of four blocks in descending order.
Phase 7: Rearrangement of the Max Entropy Selected in One Matrix
The selected biometric image blocks of iris couple biometric and the selected biometric image blocks of a finger couple biometric and the selected biometric image blocks of palm couple biometric and the selected biometric image blocks of face respectively are grouped in one matrix.
Phase 8: Arnold’s Cat Map Permutation
The grouped matrix is applied to Arnold’s cat map permutation; Arnold’s cat map is a widespread approach applied in the random number generator [18,19]. It is occurrence is rapid and simple to apply in the operation flow object in expression of storage plus process objects. Only a small functions (chaotic maps) and several parameters (initial state) were completely perfect applied if the process occupy fully a long time.
Arnold's cat map is a chaotic two-dimensional map that is used to change the pixel positions of an image without removing data from the image. It also offers more safety and better effects. Image (you don't need a cat) is multiplied by a messy looking conversion to authenticate the image in its pixels. Moreover, the transformation over time is constant.
Phase 9: Double Random Phase Encoding (DERP)
Arnold's permutation output is an entry to DRPE. It is one of the most popular optical coding techniques. The publicity for this program stems from the ability to implement it even if the optical setup uses lenses any of the software. Fig. 10 shows the optical setup required for the DRPE algorithm.

Figure 10: Proposed setup of the DRPE encryption [22]
The technique presented in Fig. 10 is recognized as 4f optical coding system. Expands to four focal lengths and only needs two lenses plus two random phase masks. In general DRPE encoding, the input image is applied at the input level, which is a focal length away from the input lens and a Fourier transform at one focal length from the lens on the other side.
A random phase mask is used at the input level, plus another random phase mask is used in the Fourier plane to enhance the safety level. The inverse Fourier transform (FT) is used in the second section 2f of the second lens setup. Therefore, it is justified that the acquired encoded image is in the spatial domain. DRPE has a high level of immunity to attack [20,21]. The complete encryption process using the DRPE algorithm can be illustrated with the following form [22]:
where FT relates to the Fourier transform, ψ(x, y) is related to the encrypted image in the spatial domain, φn(x, y) relates to the first spatial-domain random phase mask (RPM1), plus φm (u, v) relates to the second frequency-domain random phase mask (RPM2).Two of the random phase masks are two two-dimensional matrices of equal size as f (x, y) with a symmetrically arranged quantity of 0 and 2π. The obtained phase masks are randomly required for effective image coding. Various possible random distributions such as the regular as well as Gaussian distributions that are able to be used in phase masks. In addition, Fourier analysis developed in two dimensions, a concept such as FrFT that extended to application in the field of image coding [23,24]. The FrFT is only a time/frequency level turnover of 2D- FT with a specified fractional order. They are described as follows [24]:
where R (α, β)(x, y, u, v) is the base function of the FrFT, plus α and β are the fractional orders in two dimensions. The FrFT can occur of the FT in the DRPE encoding for image encryption [1]. The inverse FrFT is described as follows:
where x and y are the dimensions of the image [25–31]. The recent research in this study is to utilize the DRPE in the encryption of selected matrices or features deprived from biometric pictures to create cancellable models that can be hired to protect biometric techniques of face, iris, fingers and palms.
The proposed authentication system treats most threat models for a biometric authentication system. In registration technique, the multi-biometric image of the user is registered in the database through the input multi-biometric divided into non-overlapping blocks and chaos entropy selected is applied and the generated matrix is applied to Arnold’s cat map, then the output of Arnold permutation is applied to double random phase encoding encryption to generated template encryption.
In the first step of authentication, the collected array of the input user is identical to the array stored in the database. If it matches once stored, the user is authenticated, as shown at Fig. 11. If the user is not authenticated, the last operation will not be completed. For more security, the last step of the proposed algorithm is completed and the generated template is matched with the stored template to ensure a more authenticated user.

Figure 11: Block diagram of the proposed authentication technique
We use correlation values to remove the correlation among a test pattern and the biometric templates. The proposed cancellable technique can be applied to any image format. The performance assessment of a cancellable biometric system depends on the evaluation of metric parameters such as genuine and impostor distributions, genuine and impostor ROC curves and encryption parameters tests. The simulation results were implemented in MATLAB 2014a on an Intel (R), Core (TM) i7-4600U, CPU @ 2.10 GHz and 8 GB laptop running windows 7. The Girl picture is utilized for unauthorized data and samples of cancellable face templates are used with the suggested technique as authorized data. The girl display in Fig. 12.

Figure 12: The
The specimen of the cancellable face template is illustrated in Fig. 13 and Tabs. 2 and 3. The specimen of the cancellable face template is shown in Fig. 13. Tab. 6 shows the output stages of hybrid multi-model cancellable template biometric scheme based on irreversible data hiding and chaos entropy identifier computation.

Figure 13: The


The proposed cancellable encryption performance evaluation is applied to the individual face template. Statistical metrics are used to assess the proposed scheme as shown in Tabs. 4 and 5.


5.2 Cancellable Biometric Results
For a better analysis of the proposed cancellable encryption tests such as the genuine and imposter distributions, the ROC curves in the existence of noise at various degrees and the correlation score. The ROC curve refers to the relation among true positive rate (TPR) plus false-positive rate (FPR) at multiple lower limits. The FRR calculates the probability of falsely rejecting a face likes an intruder (intra-class) face style, as well as the FPR, calculate the probability of falsely accepting an intruder or imposter face style like a genuine (inter-class) face style.
Fig. 14 shows regularity over a specific bandwidth, which is a demanded feature for a large level of security for integer valuation of the suggested cancel-able techniques. The genuine plus imposter distributions for two techniques have been evaluated, as displayed in Fig. 15, as well as the ROC curves have also been evaluated, as displayed in Fig. 16. Tab. 6. Evaluation metrics for the suggested cancelable biometric technique in the existence of noise.
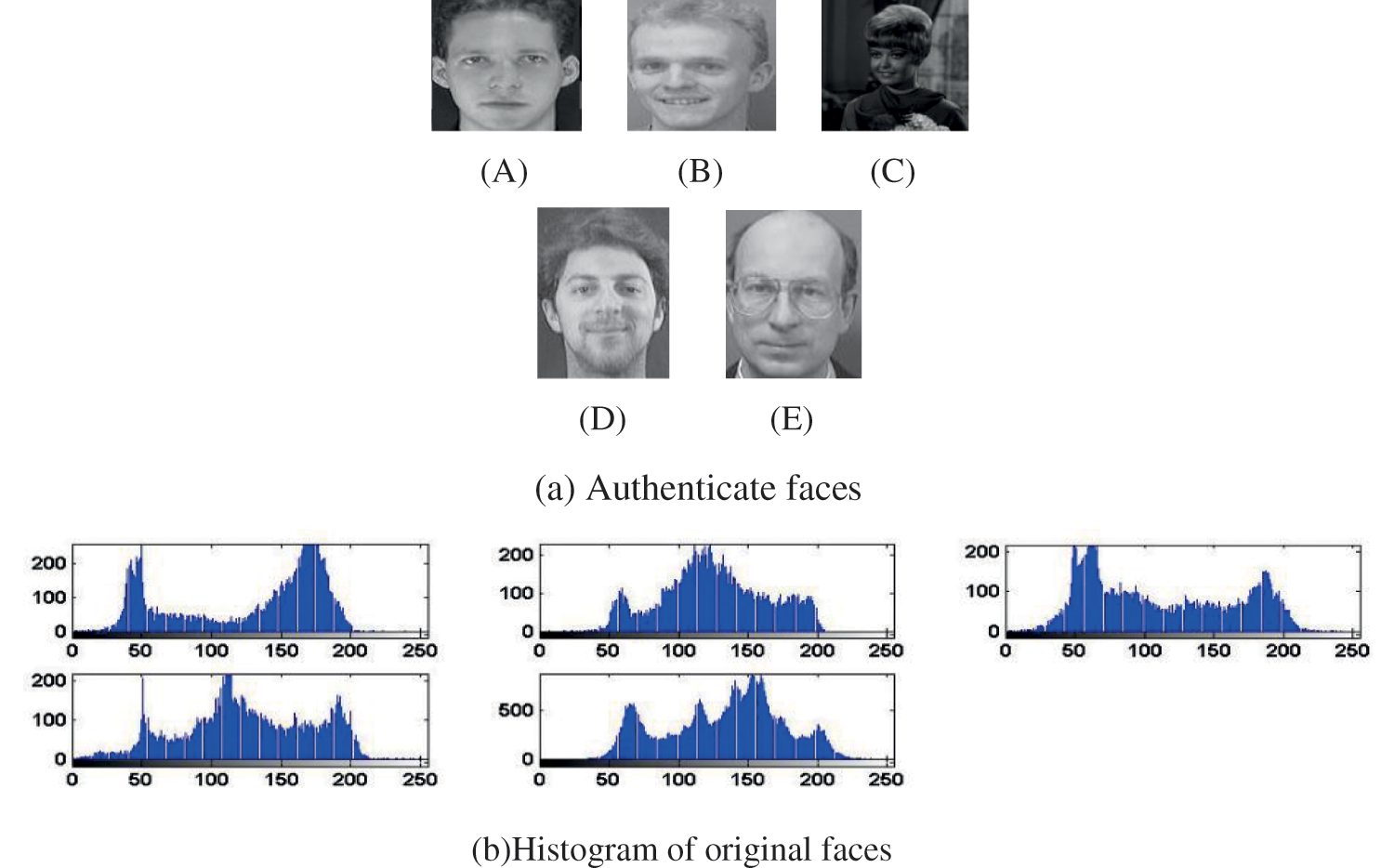
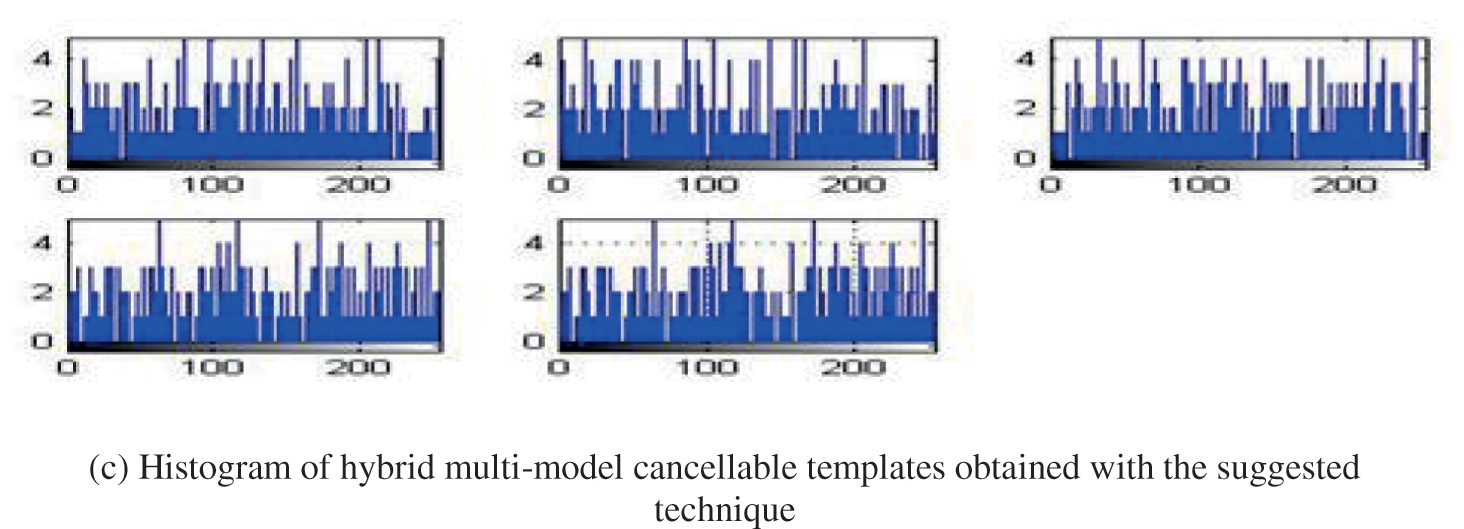
Figure 14: Histograms of (a) Authenticate faces plus (b) Multi-Model cancellable templates obtained with the suggested technique

Figure 15: Genuine and imposter ROC curves for the suggested cancellable biometric technique

Figure 16: Genuine and imposter distributions for the suggested cancellable biometric technique

This paper presents an effective model of a hybrid multiple biometric model based on a cryptosystem for cancellable biometric and an uncommon chaotic image identifier computation. Building a biometric model for the invented template and suggested collecting the speed and chaos of the cat map, segmenting the image ID, which selects a part of the biometrics and not all biometrics using selective coding theory and the selected multi-metric image speed and safety DRPE. Benefits and challenges of using multi-metric biometrics suggested overcoming single-mode hurdles and eight potential attacks on biometric registration and addressing authentication and recognition issues.
Finally, the simulation results obtained for biometric techniques capable of canceling include low EER values, high identification values, large AROC values in the presence of noise and the low time generation model makes the reversible motion suitable for time application and increases the robustness of the coding model with minimal error rate. Future work may include work to develop new algorithms for medical image communication using machine learning technology. We are considering investigating the effect of other complex channel degradations on the proposed framework.
Acknowledgement: The authors would like to thank the Head of Research, Taif University Research Support Project # (TURSP2020/214), Taif University, Taif, Saudi Arabia, for supporting the research work.
Funding Statement: This study was funded by the Dean of the Faculty of Scientific Research, Taif University Research Support Project (TURSP2020/214), Taif University, Taif, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. K. Jain, A. Ross and K. Nandakumar, “Introduction to biometrics1st ed., ,New York, USA: Springer Science & Business Media, pp. 97–149, 2011. [Google Scholar]
2. A. Abaza, A. Ross, C. Hebert, M. Harrison and M. Nixon, “A survey on ear biometrics,” ACM Computing Surveys (CSUR), vol. 45, no. 2, pp. 1–35, 2013. [Google Scholar]
3. S. Sapkal and R. Deshmukh, “Biometric template protection with fuzzy vault and fuzzy commitment,” in proceedings of the second International Conference on Information and Communication Technology for Competitive Strategies, pp. 1–6, 2016. [Google Scholar]
4. E. Maiorana, P. Campisi, J. Fierrez, J. Ortega-Garcia and A. Neri, “Cancelable templates for sequence-based biometrics with application to on-line signature recognition,” IEEE Transactions on Systems, Manand Cybernetics-Part A: Systems and Humans, vol. 40, no. 3, pp. 525–538, 2010. [Google Scholar]
5. K. Delac and M. Grgic, “A survey of biometric recognition methods,” Proceedings. Elmar-2004.46th International Symposium on Electronics in Marine, pp. 184–193, 2004. [Google Scholar]
6. W. Schindler and W. Killmann, “Evaluation Criteria for True (Physical) Random Number Generators Used in cryptographic Applications,” in revised papers from the 4th international workshop on cryptographic hardware and embedded systems (CHES ’02) Springer-verlag, Berlin, Heidelberg, pp. 431–449, 2002. [Google Scholar]
7. A. Jagadeesan, T. Thillaikkarasi and K. Duraiswamy, “Cryptographic key generation from multiple biometric modalities: Fusing minutiae with iris feature,” International Journal of Computer Applications, vol. 6, no. 2, pp. 16–26, 2010. [Google Scholar]
8. W. Wong, M. Wong and Y. Kho, “Multi-line code: A low complexity revocable fingerprint template for cancelable biometrics,” Journal of Central South University, vol. 20, no. 5, pp. 1292–1297, 2013. [Google Scholar]
9. H. Kaur and P. Khanna, “Cancel-able features using log-Gabor filters for biometric authentication,” Multimedia Tools and Applications, vol. 76, no. 4, pp. 4673–4694, 2017. [Google Scholar]
10. K. Sree and A. Rathore, “Impulse commutated high-frequency soft-switching modular current-fed three-phase DC/DC converter for fuel cell applications,” IEEE Transactions on Industrial Electronics, vol. 64, no. 8, pp. 6618–6627, 2016. [Google Scholar]
11. E. Tarif, S. Wibowo, S. Wasimi and A. Tareef, “A hybrid encryption/hiding method for secure transmission of biometric data in multimodal authentication system,” Multimedia Tools and Applications, vol. 77, no. 2, pp. 2485–2503, 2018. [Google Scholar]
12. C. Li, J. Hu, J. Pieprzyk and W. Susilo, “A new bio cryptosystem-oriented security analysis framework and implementation of multi-biometric cryptosystems based on decision level fusion,” IEEE Transactions on Information Forensics and Security, vol. 10, no. 6, pp. 1193–1206, 2015. [Google Scholar]
13. J. Bringer, H. Chabanne and B. Kindarji, “The best of both worlds: Applying secure sketches to cancelable biometrics,” Science of Computer Programming, vol. 74, no. 1–2, pp. 43–51, 2008. [Google Scholar]
14. M. Butt and N. Damer, “Helper data scheme for 2D cancelable face recognition using bloom filters,” IWSSIP 2014 Proceedings, pp. 271–274, 2014. [Google Scholar]
15. A. Nagar, K. Nandakumar and A. Jain, “A hybrid biometric cryptosystem for securing fingerprint minutiae templates,” Pattern Recognition Letters, vol. 31, no. 8, pp. 733–741, 2010. [Google Scholar]
16. Y. Feng, P. Yuen and A. Jain, “A hybrid approach for generating secure and discriminating face template,” IEEE Transactions on Information Forensics and Security, vol. 5, no. 1, pp. 103–117, 2009. [Google Scholar]
17. A. Ross, A. Jain and K. Nandakumar, Handbook of Multi-biometrics., New York, NY, USA: Springer, vol. 6, pp. 37–58, 2006. [Google Scholar]
18. E. Avaroğlu, “Pseudorandom number generator based on Arnold cat map and statistical analysis,” Turkish Journal of Electrical Engineering & Computer Sciences, vol. 25, no. 1, pp. 633–643, 2017. [Google Scholar]
19. P. Gupta, S. Singh and I. Mangal, “Image encryption based on arnold cat map and S-Box,” International Journal of Advanced Research in Computer Science and Software Engineering, vol. 8, no. 4, pp. 807–812, 2014. [Google Scholar]
20. P. Refregier and B. Javidi, “Optical image encryption based on input plane and Fourier plane random encoding,” Optics Letters, vol. 20, no. 7, pp. 767–769, 1995. [Google Scholar]
21. Y. Frauel, A. Castro, T. Naughton and B. Javidi, “Resistance of the double random phase encryption against various attacks,” Optics Express, vol. 15, no. 16, pp. 10253–10265, 2007. [Google Scholar]
22. W. Qin, X. Meng and W. He, “Improved known plaintext attack on optical encryption based on double random phase encoding,” in Symp. on Photonics and Optoelectronics, 2010, pp. 1–4, 2010. [Google Scholar]
23. S. C. Pei and M. H. Yeh, “Two dimensional discrete fractional Fourier transform,” Signal Processing, vol. 67, no. 1, pp. 99–108, 1998. [Google Scholar]
24. H. Ozaktas and O. Aytür, “Optimal filtering in fractional Fourier domains,” IEEE Transactions on Signal Processing, vol. 45, no. 5, pp. 1129–1143, 1997. [Google Scholar]
25. S. Rajput and N. Nishchal, “Optical double image security using random phase fractional Fourier domain encoding and phase-retrieval algorithm,” Optics Communications, vol. 388, pp. 38–46, 2017. [Google Scholar]
26. G. Unnikrishnan, J. Joseph and K. Singh, “Optical encryption by double-random phase encoding in the fractional Fourier domain,” Optics Letters, vol. 25, no. 12, pp. 887–889, 2000. [Google Scholar]
27. Goodman Joseph W., Introduction to Fourier Optics, 3rd ed., Englewood, Colo: Roberts & Co, 2005. [Google Scholar]
28. M. Joshi and K. Singh, “Color image encryption and decryption for twin image in fractional Fourier domain,” Optics Communications, vol. 281, no. 23, pp. 5713–5720, 2008. [Google Scholar]
29. X. Zhu, Y. Wang, W. Hu and J. D. Reiss, “Practical considerations on optimizing multistage decimation and interpolation process,” IEEE International Conference on Digital Signal Processing (DSP), pp. 370–374, 2016. [Google Scholar]
30. O. Ouda, N. Tsumura and T. Nakaguchi, “on the security of bio encoding based cancelable biometrics,” IEICE TRANSACTIONS on Information and Systems, vol. 94, no. 9, pp. 1768–1777, 2011. [Google Scholar]
31. A. Ross and A. Othman, “Visual cryptography for biometric privacy,” IEEE Transactions on Information Forensics and Security, vol. 6, no. 1, pp. 70–81, 2010. [Google Scholar]
32. ORL Database, Available online: https://www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html(accessedon1June2020). [Google Scholar]
33. A. Riad, A. Hussein, H. Kasem and A. El-Azm, “A new efficient image encryption technique based on Arnold and idea algorithms,” International Conference on Image and Information Processing (ICIIP 2012) IPCSIT, vol. 46, IACSIT Press, Singapore, 2012. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |