Computers, Materials & Continua DOI:10.32604/cmc.2022.026672
Article

Metaheuristic Optimization for Mobile Robot Navigation Based on Path Planning

El-Sayed M. El-kenawy1,2, Zeeshan Shafi Khan3,*, Abdelhameed Ibrahim4, Bandar Abdullah Aloyaydi5, Hesham Arafat Ali2,4 and Ali E. Takieldeen2

1Department of Communications and Electronics, Delta Higher Institute of Engineering and Technology, Mansoura, 35111, Egypt
2Faculty of Artificial Intelligence, Delta University for Science and Technology, Mansoura, 35712, Egypt
3Computer Science Department, College of Engineering and Computer Science, Mustaqbal University, Buraidah, Saudi Arabia
4Computer Engineering and Control Systems Department, Faculty of Engineering, Mansoura University, Mansoura, 35516, Egypt
5Department of Mechanical Engineering, Qassim University, Buraidah, 51452, Saudi Arabia
*Corresponding Author: Zeeshan Shafi Khan. Email: zskhan@uom.edu.sa
Received: 31 December 2021; Accepted: 09 February 2022

Abstract: Recently, the path planning problem may be considered one of the most interesting researched topics in autonomous robotics. That is why finding a safe path in a cluttered environment for a mobile robot is a significant requisite. A promising route planning for mobile robots on one side saves time and, on the other side, reduces the wear and tear on the robot, saving the capital investment. Numerous route planning methods for the mobile robot have been developed and applied. According to our best knowledge, no method offers an optimum solution among the existing methods. Particle Swarm Optimization (PSO), a numerical optimization method based on the mobility of virtual particles in a multidimensional space, is considered one of the best algorithms for route planning under constantly changing environmental circumstances. Among the researchers, reactive methods are increasingly common and extensively used for the training of neural networks in order to have efficient route planning for mobile robots. This paper proposes a PSO Weighted Grey Wolf Optimization (PSOWGWO) algorithm. PSOWGWO is a hybrid algorithm based on enhanced Grey Wolf Optimization (GWO) with weights. In order to measure the statistical efficiency of the proposed algorithm, Wilcoxon rank-sum and ANOVA statistical tests are applied. The experimental results demonstrate a 25% to 45% enhancement in terms of Area Under Curve (AUC). Moreover, superior performance in terms of data size, path planning time, and accuracy is demonstrated over other state-of-the-art techniques.

Keywords: Mobile robot; swarm optimization; robot route planning; neural networks

1  Introduction

Mobile robots are used in different fields to carry out critical unmanned tasks, including military operations, industrial automation and rescue operations [1]. In order to achieve efficiency in the use of mobile robots, route planning is one of the essential parameters. Route planning can be defined as: in any working environment; a mobile robot selects an optimum or suboptimal route that will take the robot from a starting state to the goal state based on predefined performance criteria [2]. An efficient route planning algorithm on one side will save the time to reach the goal state, and on the other side, it will also keep the robot safe from wear and tear. Due to above mentioned significant role of route planning algorithm, the topic is now becoming popular among the research community [3,4].

Mobile robots are necessary to respond under real-time constraints, which cannot be realized by hardware with restricted computational power. Moreover, mobile robots are essential to be controlled simultaneously by single or multiple users. Nonexistence of scalability, absent real-time performance, and allowing one mobile robot to be controlled at a time reflect challenging concerns in the literature of finding the best route of mobile robots. While designing a mobile robot route, three requirements are generally considered. Firstly, environment modeling is performed. In environment modeling, a natural map in which a mobile robot must operate is translated to a map features format that can easily be stored. The second requirement is the need for optimization criteria, while the third requirement is the path discovery algorithm [5]. A path search method is used to establish a collision-free route between the home and destination points in the state space that meets the optimization criteria i.e., path length, smoothness, safety degree, etc.

Efficiency and accuracy in route planning can be achieved firstly by designing an environment model that will better understand the environmental factors. Environmental modeling will significantly reduce the complexity involved in route planning. Different approaches can be used as techniques for environment modeling, including the framework space approach, the free space approach, the cell decomposition approach, the topological approach, and the probabilistic roadmap approach [5].

An optimization criterion must be set in the route planning process. Several variables can play an important role and can be included in the criteria for optimization inside the rote planning for mobile robots. Three often used optimization criteria are path length, smoothness, and degree of safety. Heuristic approaches and artificial intelligence algorithms are the two broad types of methods used to design route planning or optimization algorithms. Metaheuristic algorithms solve unexpected issues because of having intelligence and prior knowledge of random search the two elements of population-based heuristic algorithms [6]. Metaheuristic algorithms select exploration to thoroughly examine the search space, while metaheuristics select the exploitation stage for the area’s local search.

This paper proposes the PSOWGWO algorithm to combine the hunting behavior of Grey Wolf Optimization (GWO) and the social behavior of Particle Swarm Optimization (PSO) to have efficient route planning for mobile robots. The optimization procedure begins with a random set of agents in the proposed optimizer. To measure the statistical efficiency of the proposed algorithm, Wilcoxon rank-sum and ANOVA statistical tests are applied. Moreover, the algorithm’s superior performance in data size, path planning time, and accuracy is tested over other state-of-the-art techniques.

To organize this paper, related work is presented in Section 2. The proposed model is explained in Section 3, while results are shown and discussed in Section 4. Finally, the conclusion and future directions are discussed in Section 5.

2  Literature Review

Map facilities have interested extensive studies on the fast computation of driving directions in road networks. Finding the best route amongst two points can be modeled as the shortest path problem on weighted graphs. The field of mobile robots is continuously gaining popularity among the research community. To solve the issues of identification, and categorization Dynamic Neural Networks (DNNs) have previously shown a significant degree of proficiency [2,4]. Advanced application examples of DNNs include recognizing deformable objects, estimating their state and pose for grasping, semantic task, path specification, and recognizing object and surface properties such as sharp objects that could harm human collaborators or wet/slippery floors. This section of the paper discusses current mobile robots and route planning work.

The development of low-cost sensing technology has benefited robots by delivering an abundance of potentially rich and multimodal data. However, the concerned issue still is the techniques for deriving meaningful and usable state representations from such data. To solve this issue, numerous machine learning techniques and algorithms exist, including Artificial Neural Network (ANN), Support Vector Machine (SVM), K-Nearest Neighbor (KNN) and Decision Tree (DT) [2,4]. The main objective of all these algorithms is to generalize and forecast data. ANN is an intelligent mathematical model inspired by the biological nervous system. The Multilayer Perceptron (MLP) architecture is one of the most often used feedforward ANN designs. MLP comprises a single input layer, one or more hidden layers, and a single output layer. The structure of MLP is shown in Fig. 1.

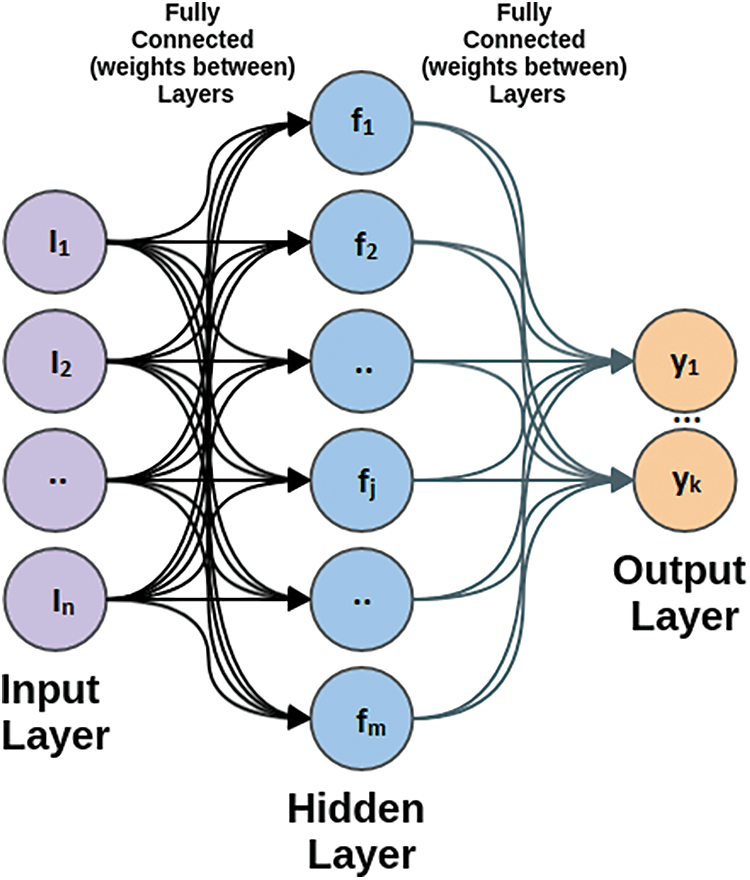
Figure 1: Structure of multilayer perceptron

Metaheuristic algorithms solve unexpected issues because of having intelligence and prior knowledge of random search [7,8]. Exploration and exploitation are two elements of population-based heuristic algorithms. Metaphors employ algorithms to represent natural phenomena or human behavior in contemporary life. PSO is another optimizer that mimics individual movements and interactions in a bird flock or fish school. Every individual is moved by their own best-known location and by the best position of the swarm. It is a stable, easy to execute, and appropriate cooperation model, but the difficulty is finding initial parameters. Some applications of PSO include gene clustering, antenna design, vehicle routing, control design, and dimensional reduction [9].

The Differential Evaluation (DE) optimizer is based on the concept of survival of the fittest. DE starts with a random population, and a new candidate is created by mixing old candidates with mutant solutions. This optimizer’s strong convergence promotes population variety and adaptation in the context of changing conditions. It takes a long time to converge, and it is also hard to determine the parameters [7]. The GWO algorithm simulates the leadership, social structure, and hunting behavior of grey wolves [9–13]. The first two stages are encircling and attacking the victim. This optimizer must have a balance between exploration and exploitation [14]. Due to high search accuracy, it is easy to execute, but it causes premature convergence as the variables to increase the performance of the algorithm decreases. It’s used in feature selection, clustering, robotics, and route finding.

Sundran proposed genetic optimization technique with B Spline deals with the static environment for global route planning [15]. An Enhanced Artificial Potential Field (E-APF) generates navigation trajectories, and Sudhakara et al. used this E-APF technique for the route planning of the mobile robots [16]. Based on the inertia moment parameter, an optimization technique for route planning of mobile robots is proposed by Lu et al. [3]. Applications of Genetic Algorithm (GA), Differential Evolution (DE), PSO, and Cuckoo Search Algorithm (CSA) in a dynamic environment are studied by Wahab et al. [7]. By keeping the balance between intensification and diversification, Das et al. worked to select the deadlock-free shortest path. Alam et al. proposed a collision-free PSO-based algorithm for shortest path selection for mobile robots with static obstacles [17]. Sanyal studied different available solutions for route planning of mobile robots under static and dynamic environments [18]. After conducting the above extensive review of the literature, it is concluded that Area Under Curve (AUC) is one of the essential parameters that still needs improvement in the context of route planning in mobile robots [19–21].

2.1 Problem Formulation

The mobile robot path planning challenge is typically conveyed as follows: for an assumed mobile robot and a depiction of an environment, it is required to find a path among two stated locations, a start point and an endpoint. The path should be free of collision and satisfies certain optimization criteria. According to this definition, a path planning problem is considered an optimization problem. Most of the recent methods stated above and in the recent literature used to solve the path planning problem are according to two factors, (i) the path planning algorithms (local or global) (ii) the environment type (dynamic or static).

2.2 Plan of Solution

Overcoming the problem depicted above requires considering the following three objectives to obtain accurate and efficient solutions, (i) path safety, path length, and path smoothness (related to the energy consumption). (ii) test the proposed PSOWGWO; realistic scenarios for the path’s calculation have been used. (iii) comparison of the proposal with other state-of-the-art approaches, showing the advantages of PSOWGWO. In particular, to evaluate the obtained results, we applied specific quality metrics. Moreover, a statistical analysis is also performed to demonstrate the statistical evidence of the obtained results.

3  The Proposed PSOWGWO Model

Due to efficient computing and capacity to cope with an unpredictable environment, it is noticed that smart strategies for robot navigation problems are gaining much attraction from the research community. In this paper, an algorithm PSOWGWO, based on PSO and an enhanced weighted GWO based algorithm, is designed and applied in order to provide an efficient solution for route planning of mobile robots. The proposed model mainly consists of 4 main steps, as shown in Fig. 2.

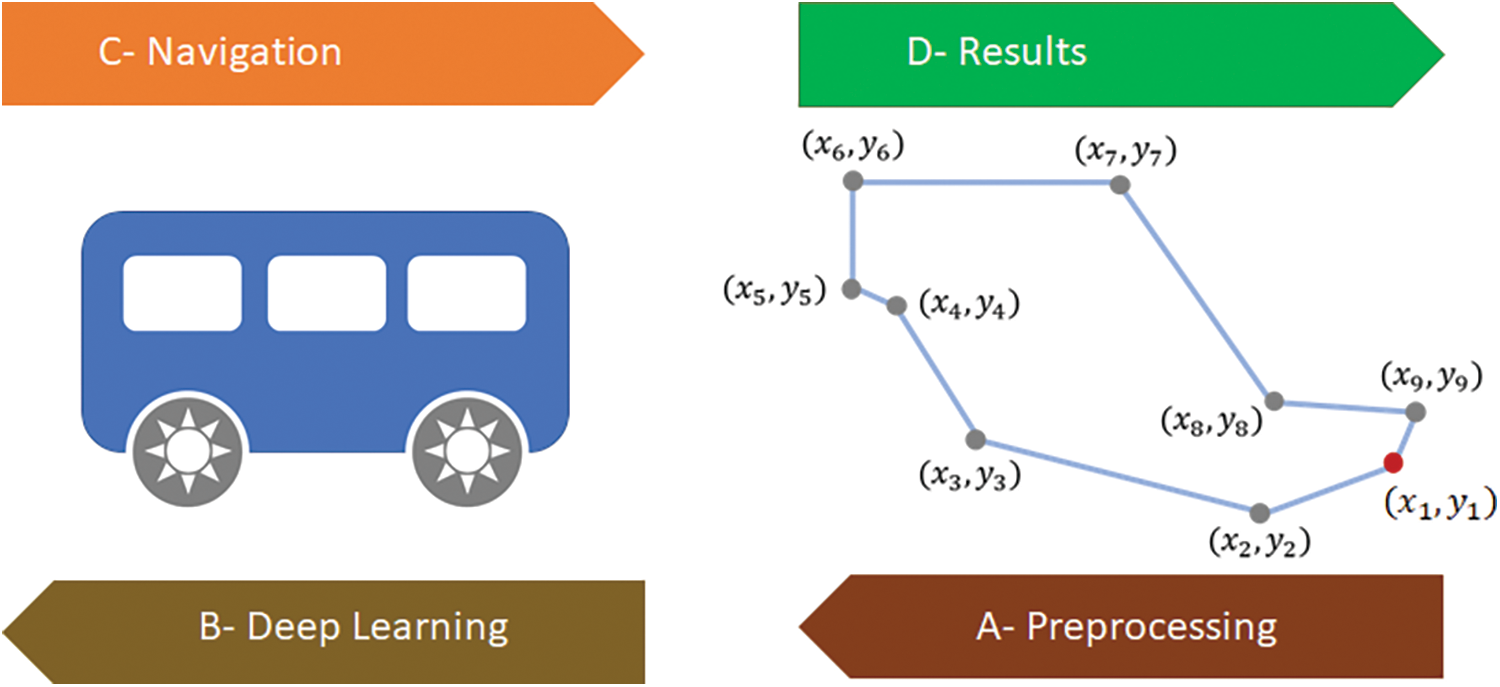
Figure 2: Structure of the proposed model

The first step is the preprocessing step that includes configuration parameters for the proposed optimization and population for search space. The second step is about training deep neural network parameters in order to choose the best path, while the third step selects the best navigation path planning. The fourth and final step statistically evaluates the quality of proposed algorithms.

PSOWGWO combines the social behavior of PSO with the hunting behavior of GWO. In the proposed hybrid optimizer, the optimization procedure begins with a random set of agents. The set actively suppressed potential solutions, and following that, the fitness function for each person’s iteration is computed, and the top three leaders are designated as alpha, beta, and delta. The population is then split into two equal groups. The proposed hybrid method divides the population into two groups where the first group adheres to PSO procedures and the second group adheres to GWO processes. The first group follows the PSO procedure strictly, while the second group adheres to GWO processes.

Fitness functions are used to determine each PSOWGWO solution’s quality. Classification error rate and the number of chosen features are the two main variables that affects the fitness function. A satisfactory solution is to select a subset of features with a minimum classification error rate and a smaller number of selected features. The following equation is used to determine the quality of each solution for E(D) represents error rate.

Fitness=h1E(D)+h2|s||f| , h1 ϵ [0, 1] , h2=1− h1(1)

The presented PSOWGWO algorithm is shown in Algorithm 1 step by step. In this way, the search area is thoroughly searched for potential locations, those are then exploited with the help of PSO and weighted GWO. As shown in Fig. 3, the flowchart explains the presented PSOWGWO algorithm. The flowchart shows that the PSO and the WGWO are executed 50/50% in statice manner during iterations.

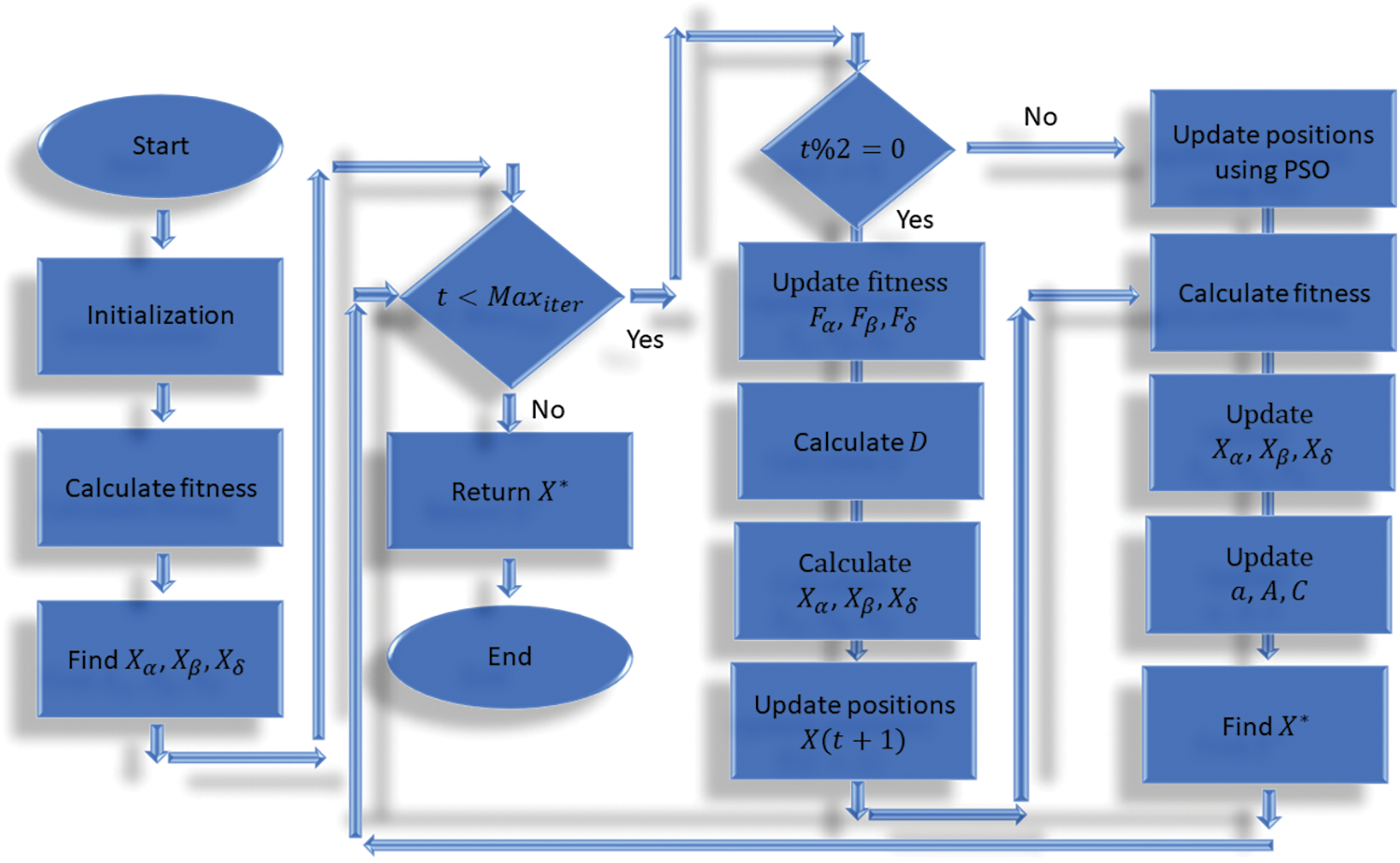
Figure 3: PSOWGWO optimization algorithm

The PSOWGWO algorithm complexity analysis can be explained as follows.

•   Step 1: initialize PSOWGWO population: O (1).

•   Step 2: initialize PSOWGWO parameters: O (1).

•   Step 3: initialize iteration counter: O (1).

•   Step 4: evaluate fitness function evaluation: O (n).

•   Step 5: find the three best solutions: O (n).

•   Step 9: update first fitness: O (Maxiter × n).

•   Step 10: update second fitness: O (Maxiter × n).

•   Step 11: update third fitness: O (Maxiter × n).

•   Step 16: update positions by WGWO: O (Maxiter × n).

•   Step 19: update positions by PSO: O (Maxiter × n).

•   Step 21: evaluate fitness function evaluation: O (Maxiter × n).

•   Step 22: find the three best solutions: O (Maxiter × n).

•   Step 23: update PSOWGWO parameters: O (Maxiter).

•   Step 24: find the best solution: O (Maxiter).

•   Step 25: increase iteration counter: O (Maxiter).

Thus, from the above analysis, the complexity of the PSOWGWO algorithm is O (Maxiter × n) and the total complexity of the algorithm can be O (Maxiter × n × d) for d variables.

Algorithm 1: Proposed PSOWGWO Algorithm

4  Results and Discussion

Path planning for mobile robots’ results in quick and fast responses, as well as it also minimizes the wear and tears on the robot that then results in saving the cost. For the route planning of mobile robots, several approaches have been suggested and documented in the scientific literature. In the heuristic technique, sub-targets are determined at each phase of the rolling calculation. These sub-targets are then implemented using real-time planning in the current PSOWGWO algorithm. When the suggested algorithm (PSOWGWO) is started, the sub-targets are updated with the new information gleaned from the move, which continues until the planning job is done.

4.1 Parameter Optimization

Experimental configurations of the PSOWGWO algorithm those are used to determine the fitness function for a specific solution are shown in Tab. 1. The number of agents is determined to 30 and the algorithms number of runs are counted to be 20.

Dynamic Neural Networks (DNNs) may be considered as an extension of unidirectional recurrent neural networks, with an addition of a second hidden layer and the reversal of the direction of the connections between the hidden layers. As a consequence, this model is capable of incorporating information from both the past and the future. The output ut can be calculated depending on the values of {vi}i≠t={v1,…,vt}

Q(ut|{vi}i≠t)=σ(Wuyhty+Wuzhtz+zu)(2)

where Wu is the weight matrix connecting the hidden layer to the output layer, hty is calculated based on the weight matrix that connects the input layer to the hidden layer and the weight matrix that connects hidden to hidden layer. zu is the output layer bias vectors, and σ represents the activation function.

A DNN employs weights to perform two essential functions: the first is to determine the rate of output impacted by the input, and the second is to govern the learning rate of the hidden layer. The result is created by multiplying the weights assigned to the inputs and then adding them together like linear regression. Weights are the numerical values which describe the number of neurons involved in a specific interaction. If the inputs are vj(j=1,…,n), the weights are wj(j=1,…,n), and each neuron satisfies the following equation then each neuron is said to be a spiking unit. As a consequence of this

u=f(v)=∑j=1n⁡vjwj(3)

where n is the input number. The array multiplication may be used to calculate the weighted sum, for the most part. The bias of a neuron is an extra variable that may affect the neuron’s output in addition to the weighted sum of the neuron’s inputs. The final products that neural cells provide is:

u=f(v)=∑j=1n⁡vjwj+H(4)

where H is the bias.

4.2 Path Planning

There are many potential paths to pick from but finding the ideal one (the one that would need the least amount of travel or cost) is something that mathematicians and computer scientists have been attempting to solve for years and years. The proposed model divides the issue into smaller sub-problems that may be tackled individually. There are multiple potential answers to each sub-problem, and the solution chosen for one point may impact the possible solutions of future sub-problems. It is a system for addressing a sequence of subproblems, each with several alternative solutions. In the scenario of selecting the best path, the main two issues include the selection of start point and the next step. In order to determine the overall performance of the proposed model; it is evaluated using a series of simulated situations, such as the one shown in Fig. 4.

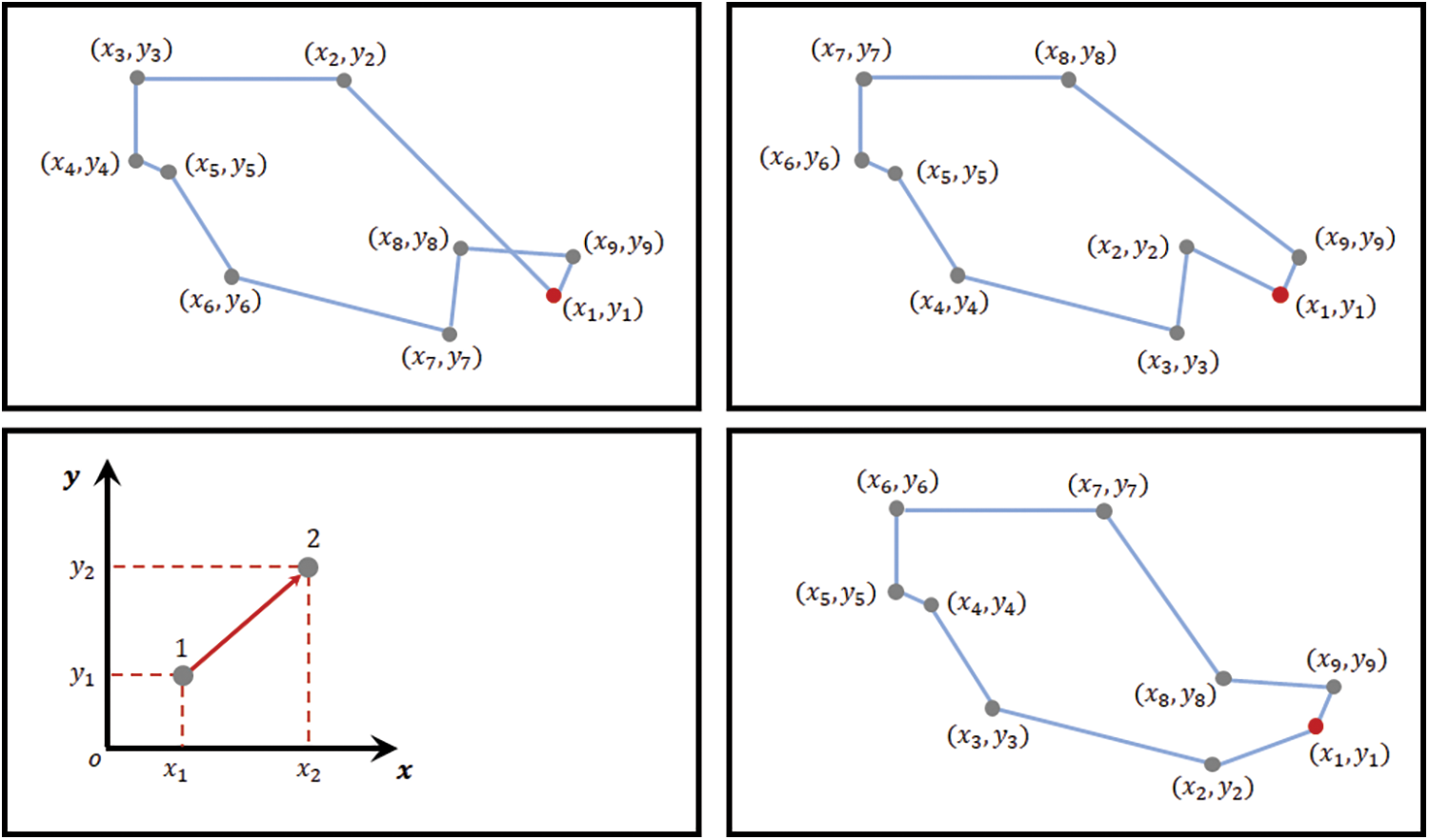
Figure 4: Automatic navigation results of PSOWGWO

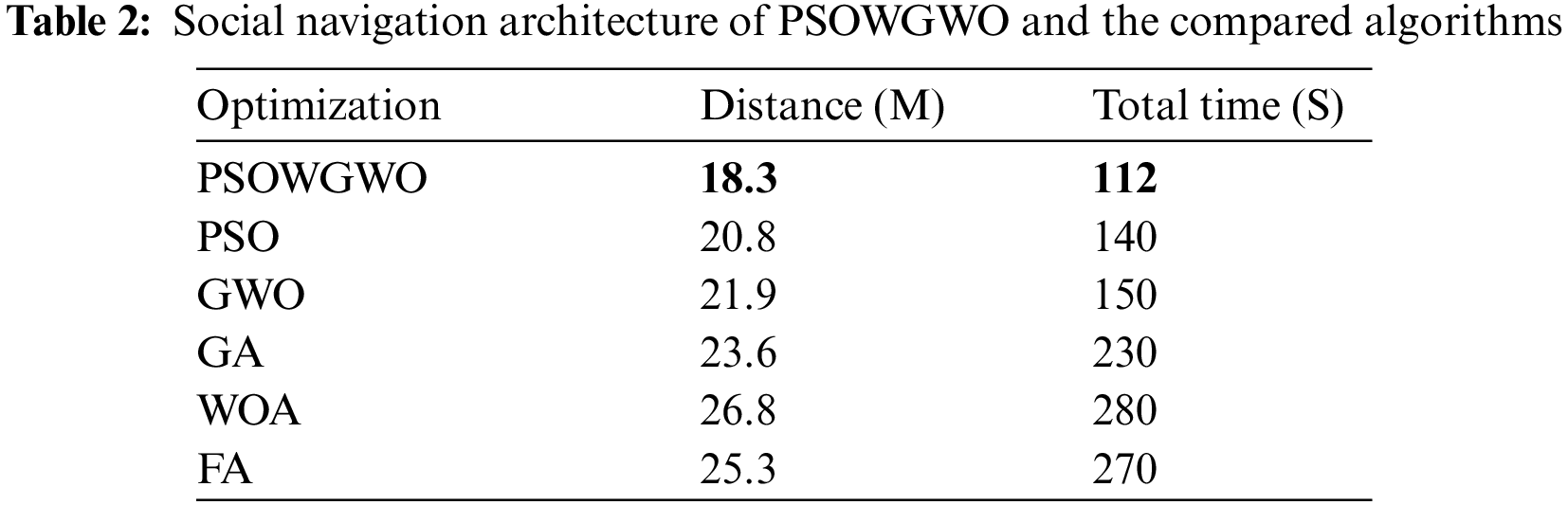
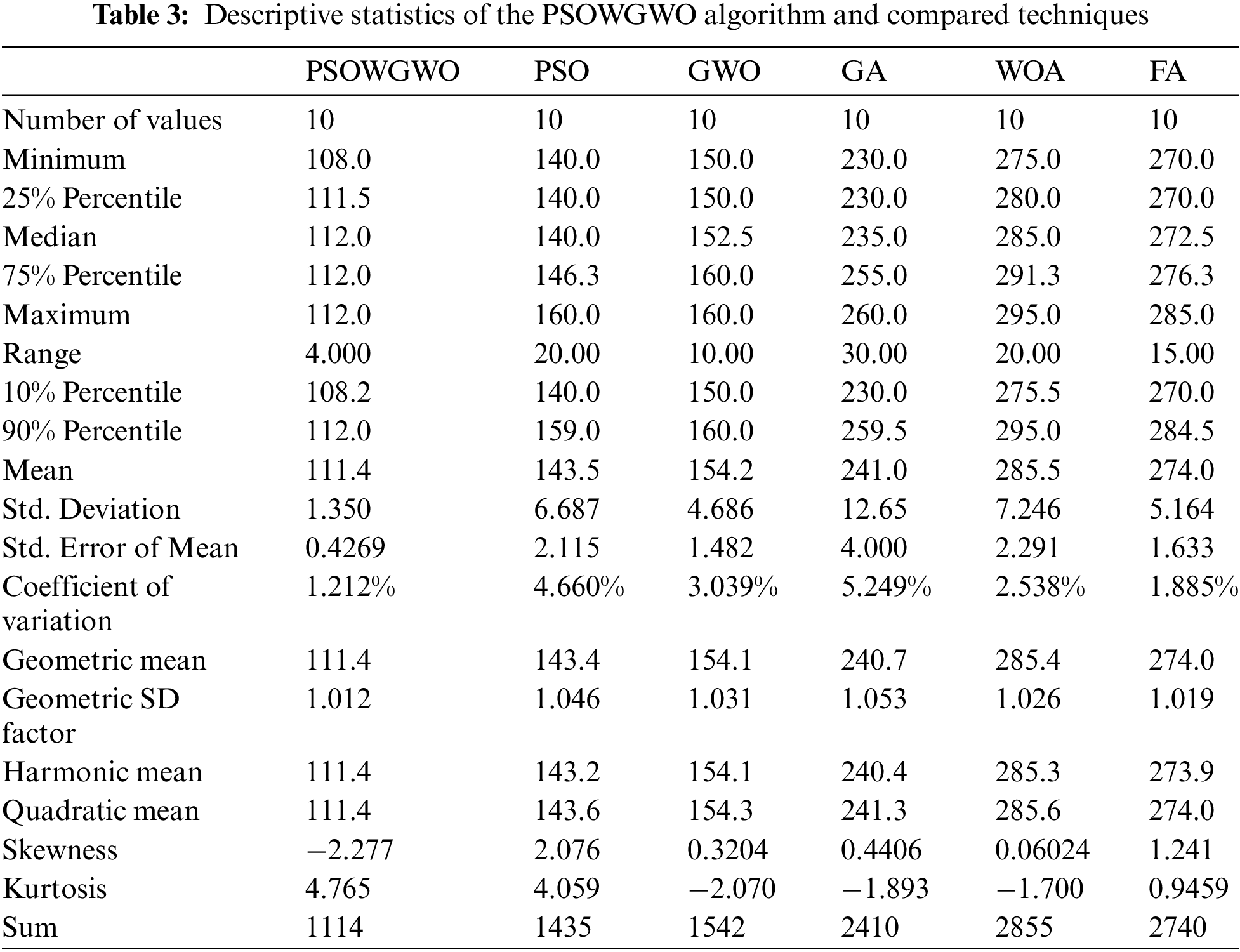
Automatic navigation is a fundamental problem in robotics, and numerous alternative algorithms are developed to provide courses those are either length or time optimum. The social navigation architecture output results using the proposed and state of the art algorithms are shown in Tab. 2 based on distance and total time parameters. The PSOWGWO algorithm is compared with PSO [22], GWO [23,24], GA [25], WOA [26], and FA [27] algorithms. Tab. 3 shows the descriptive statistics of the proposed PSOWGWO algorithm and compared techniques.

The ANOVA and Wilcoxon Signed Rank Test statistical methodologies are used to compare the populations in order to establish the efficiency of the proposed solution over the other available solutions. The results of the ANOVA and two-way tests are shown in Tabs. 4 and 5. Following is an example of how to create a statistical hypothesis for this test:

•   The null hypothesis (H0) states that there is no statistically significant difference between the groups.

•   The alternative hypothesis (H1) states a statistically significant difference between the means of two populations, which is the distinction.

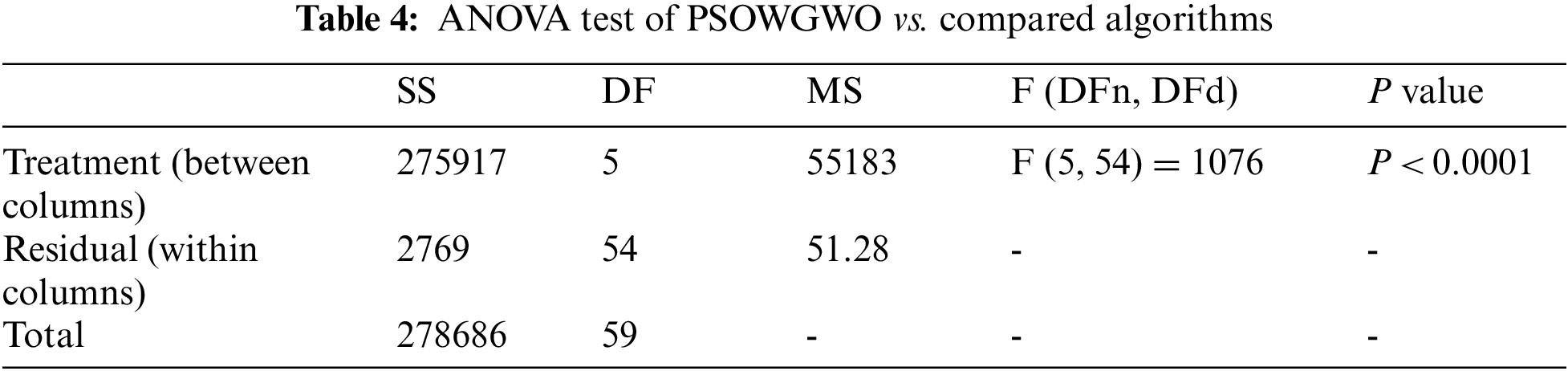
Fig. 5 shows different plots of residual and actual values to confirm the quality of the proposed algorithm. The histogram of the performance of the analyzed strategies in comparison to the proposed algorithm is shown in Fig. 6. The performance of several algorithms about the objective function is observed. It should also be noted that the lowest, maximum, and average values obtained using the proposed model are almost identical. Fig. 7 illustrates the stability of the proposed (PSOWGWO) algorithm.

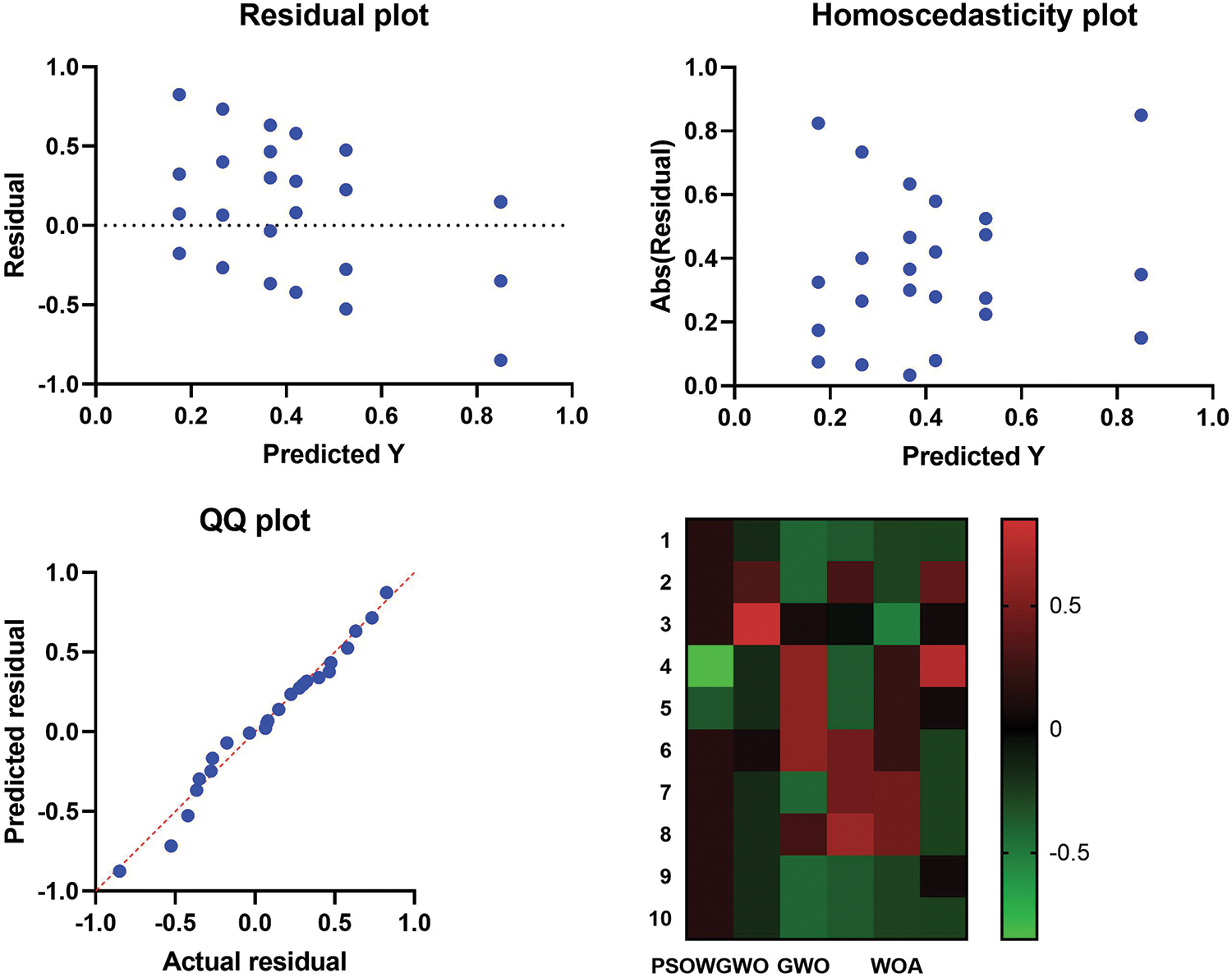
Figure 5: Plots of residual and actual values

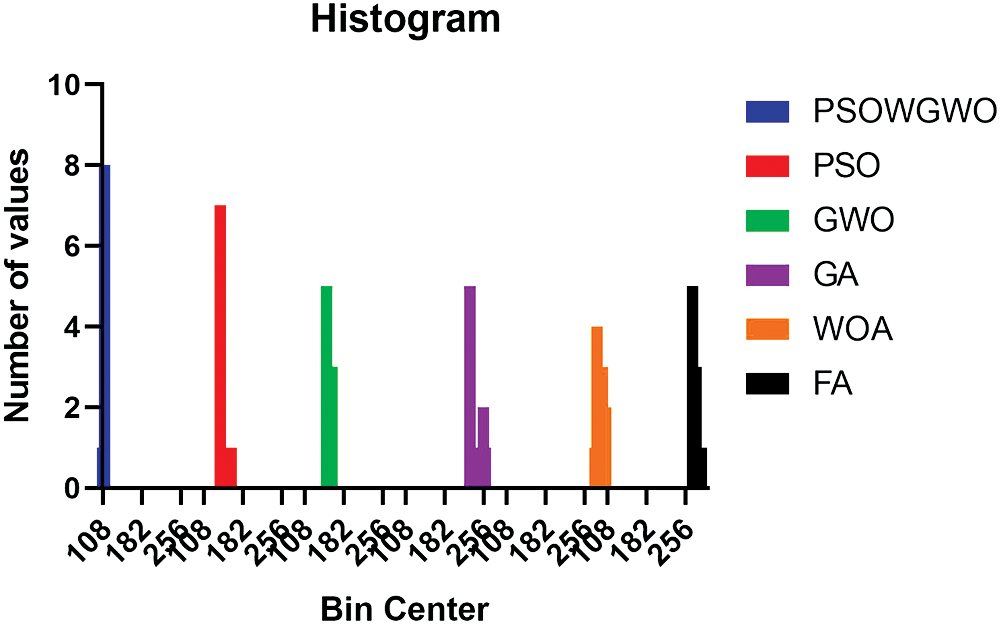
Figure 6: Histogram of the proposed and compared algorithms

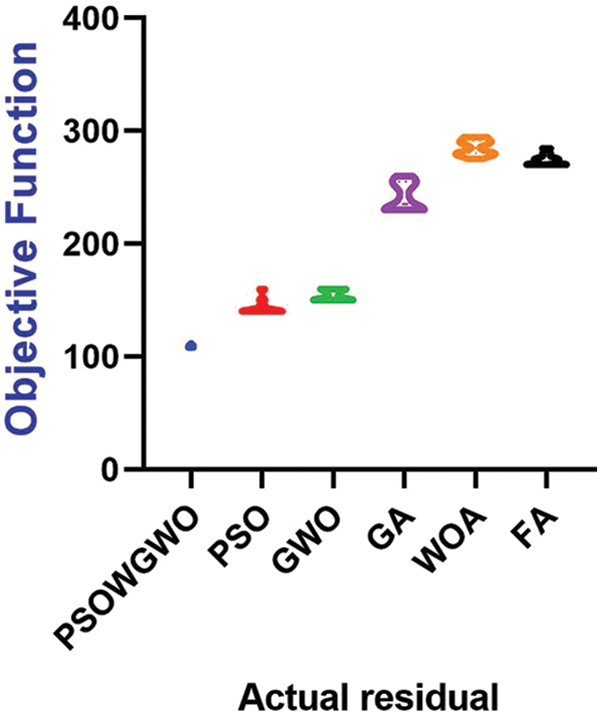
Figure 7: The performance of several algorithms against the fitness/objective function

Additionally, the ROC analysis is performed on a standard of ranking and findings from continuous diagnostic tests. The accuracy indices derived from classification, notably the area under the curve (AUC) that provide a meaningful comprehension of the variety. Fig. 8 demonstrates that the AUC value of the proposed model is much higher than that of previous strategies.

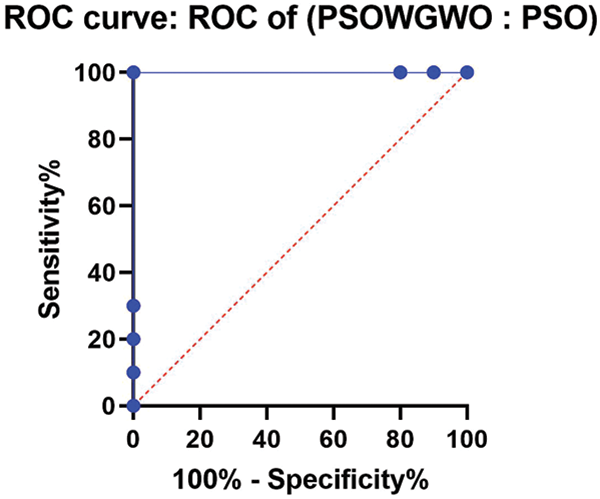
Figure 8: ROC analysis of the PSOWGWO algorithm against PSO algorithm

5  Conclusion

In an environment with obstacles, finding a plausible route for a mobile robot is one among the popular research areas. The goal of a route planning algorithm is to move from a given start state to goal state within minimum time and cost. Our proposed PSOWGWO algorithms utilized the benefit of both, PSO procedure and enhanced GWO process. The algorithm has a preprocessing phase and the deep learning phase along with selection of best route planning. The results demonstrate the efficiency and superiority of the PSOWGWO algorithm in terms of AUC and other performance measures. Furthermore, The ANOVA and Wilcoxon Signed Rank Test statistical methodologies are also used to compare the populations in order to establish the efficiency of the proposed solution over the other available solutions.

Acknowledgement: The researcher(s) would like to thank the Deanship of Scientific Research, Qassim University for funding the publication of this project.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  G. Fragapane, R. Koster, F. Sgarbossaa and J. O. Strandhagena, “Planning and control of autonomous mobile robots for intralogistics: Literature review and research agenda,” European Journal of Operational Research, vol. 294, no. 2, pp. 405–426, 2021. [Google Scholar]

 2.  K. Karur, N. Sharma, C. Dharmatti and J. Siegel, “A survey of path planning algorithms for mobile robots,” Vehicles, vol. 3, pp. 448–468, 2021. [Google Scholar]

 3.  X. Lu, H. Bao, Y. He, J. Huang, Q. Wang et al., “Intelligent route planning model of industrial robot based on inertia moment parameter optimization,” in 2021 IEEE Int. Conf. on Computer Science, Electronic Information Engineering and Intelligent Control Technology (CEI), Fuzhou, China, pp. 630–634, 2021. [Google Scholar]

 4.  K. Cai, C. Wang, J. Cheng, S. Song, C. W. de Silva et al., “Mobile robot path planning in dynamic environments: A survey,” Instrumentation, vol. 6, no. 2, pp. 90–100, 2019. [Google Scholar]

 5.  X. Zhong, J. Tian and H. Hu, “Hybrid path planning based on safe A* algorithm and adaptive window approach for mobile robot in large-scale dynamic environment,” Journal of Intelligent & Robotic Systems, vol. 99, pp. 65–77, 2020. [Google Scholar]

 6.  Y. Ding, W. Luo and K. Sycara, “Heuristic-based multiple mobile depots route planning for recharging persistent surveillance robots,” in 2019 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), Macau, China, pp. 3308–3313, 2019. [Google Scholar]

 7.  M. N. A.-Wahab, S. N.-Meziani and A. Atyabi, “A comparative review on mobile robot path planning: Classical or meta-heuristic methods?,” Annual Reviews in Control, vol. 50, pp. 233–252, 2020. [Google Scholar]

 8.  P. K. Das and P. K. Jena, “Multi-robot path planning using improved particle swarm optimization algorithm through novel evolutionary operators,” Applied Soft Computing, vol. 92, Article ID 106312, pp. 1–24, 2020. [Google Scholar]

 9.  C. Qu, W. Gai, M. Zhong and J. Zhang, “A novel reinforcement learning based grey wolf optimizer algorithm for unmanned aerial vehicles (UAVs) path planning,” Applied Soft Computing, vol. 89, Article ID 106099, pp. 1–12, 2020. [Google Scholar]

10. W. Zhang, S. Zhang, F. Wu and Y. Wang, “Path planning of UAV based on improved adaptive grey wolf optimization algorithm,” in IEEE Access, vol. 9, pp. 89400–89411, 2021. [Google Scholar]

11. N. Toufan and A. Niknafs, “Robot path planning based on laser range finder and novel objective functions in grey wolf optimizer,” SN Applied Sciences, vol. 2, pp. 1324, 2020. [Google Scholar]

12. R. Kumar, L. Singh and R. Tiwari, “Path planning for the autonomous robots using modified grey wolf optimization approach,” Journal of Intelligent & Fuzzy Systems, vol. 40, no. 5, pp. 9453–9470, 2021. [Google Scholar]

13. R. Kumar, L. Singh and R. Tiwari, “Comparison of two meta–heuristic algorithms for path planning in robotics,” in 2020 Int. Conf. on Contemporary Computing and Applications (IC3A), Lucknow, India, pp. 159–162, 2020. [Google Scholar]

14. E. -S. M. El-Kenawy, S. Mirjalili, S. S. M. Ghoneim, M. M. Eid, M. El-Said et al., “Advanced ensemble model for solar radiation forecasting using sine cosine algorithm and newton’s laws,” in IEEE Access, vol. 9, pp. 115750–115765, 2021. [Google Scholar]

15. K. Sundaran, “Genetic algorithm based optimization technique for route planning of wheeled mobile robot,” in 2018 Fourth Int. Conf. on Advances in Electrical, Electronics, Information, Communication and Bio-Informatics (AEEICB), Chennai, India, pp. 1–5, 2018. [Google Scholar]

16. P. Sudhakara, V. Ganapathy and K. Sundaran, “Route planning of a wheeled mobile robot (WMR) using enhanced artificial potential field (E-APF) method,” in 2018 Int. Conf. on Communication, Computing and Internet of Things (IC3IoT), Chennai, India, pp. 12–15, 2018. [Google Scholar]

17. M. S. Alam, M. U. Rafique and M. U. khan, “Mobile robot path planning in static environments using particle swarm optimization,” in International Journal of Computer Science and Electronics Engineering (IJCSEE), vol. 3, no. 3, pp. 253–257, 2015. [Google Scholar]

18. A. Sanyal, M. N. Zafar, J. C. Mohanta and A. M. Faiyaz, “Path planning approaches for mobile robot navigation in various environments: A review,” in Advances in Interdisciplinary Engineering, Lecture Notes in Mechanical Engineering, Singapore: Springer, pp. 555–572, 2021. [Google Scholar]

19. M. M. Eid, F. Alassery, A. Ibrahim and M. Saber, “Metaheuristic optimization algorithm for signals classification of electroencephalography channels,” Computers, Materials & Continua, vol. 71, no. 3, pp. 4627–4641, 2022. [Google Scholar]

20. E. -S. M. El-kenawy, A. Ibrahim, N. Bailek, K. Bouchouicha, M. A. Hassan et al., “Hybrid ensemble-learning approach for renewable energy resources evaluation in Algeria,” Computers, Materials & Continua, vol. 71, no. 3, pp. 5837–5854, 2022. [Google Scholar]

21. E. -S. M. El-kenawy, A. Ibrahim, N. Bailek, K. Bouchouicha, M. A. Hassan et al., “Sunshine duration measurements and predictions in saharan Algeria region: An improved ensemble learning approach,” Theoretical and Applied Climatology, vol. 2021, pp. 1–17, 2021. [Google Scholar]

22. A. Ibrahim, M. Noshy, H. A. Ali and M. Badawy, “PAPSO: A power-aware VM placement technique based on particle swarm optimization,” in IEEE Access, vol. 8, pp. 81747–81764, 2020. [Google Scholar]

23. A. Ibrahim, A. Tharwat, T. Gaber and A. E. Hassanien, “Optimized superpixel and adaboost classifier for human thermal face recognition,” Signal, Image and Video Processing, vol. 12, pp. 711–719, 2018. [Google Scholar]

24. E. -S. El-Kenawy and M. Eid, “Hybrid gray wolf and particle swarm optimization for feature selection,” International Journal of Innovative Computing, Information and Control, vol. 16, no. 3, pp. 831–844, 2020. [Google Scholar]

25. E. -S. M. El-Kenawy, M. M. Eid, M. Saber and A. Ibrahim, “MbGWO-SFS: Modified binary grey wolf optimizer based on stochastic fractal search for feature selection,” in IEEE Access, vol. 8, pp. 107 635–107 649, 2020. [Google Scholar]

26. E. S. M. El-Kenawy, A. Ibrahim, S. Mirjalili, M. M. Eid and S. E. Hussein, “Novel feature selection and voting classifier algorithms for COVID-19 classification in CT images,” in IEEE Access, vol. 8, pp. 179317–179335, 2020. [Google Scholar]

27. E. M. Hassib, A. I. El-Desouky, L. M. Labib and E. -S. M. T. El-Kenawy, “Woa + brnn: An imbalanced big data classification framework using whale optimization and deep neural network,” Soft Computing, vol. 24, pp. 5573–5592, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.