Computers, Materials & Continua DOI:10.32604/cmc.2022.027939
Article

Blockchain-Based Light-Weighted Provable Data Possession for Low Performance Devices

Yining Qi1,2,*, Zhen Yang3, Yubo Luo4, Yongfeng Huang1,2 and Xing Li1,2

1Tsinghua University, Beijing, 100084, China
2Beijing National Research Center for Information Science and Technology, Beijing, 100084, China
3Beijing University of Posts and Telecommunications, Beijing, 100084, China
4University of North Carolina at Chapel Hill, North Carolina, 27599, USA
*Corresponding Author: Yining Qi. Email: qyn18@mails.tsinghua.edu.cn
Received: 29 January 2022; Accepted: 19 April 2022

Abstract: Provable Data Possession (PDP) schemes have long been proposed to solve problem of how to check the integrity of data stored in cloud service without downloading. However, with the emerging of network consisting of low performance devices such as Internet of Things, we find that there are still two obstacles for applying PDP schemes. The first one is the heavy computation overhead in generating tags for data blocks, which is essential for setting up any PDP scheme. The other one is how to resist collusion attacks from third party auditors with any possible entities participating the auditing. In this paper, we propose a novel blockchain-based light-weighted PDP scheme for low performance devices, with an instance deployed on a cloud server. We design a secure outsourced tag generating method for low performance devices, which enables a kind of “hash-sign-switch” two-phase tag computing. With this method, users with low performance devices can employ third party auditors to compute modular exponential operations that accounts for the largest portion of computation overhead in tag generation, without leaking their data content. Chaincodes in blockchain network ensure the correctness of such outsourcing and prevent collusion attacks. The security analysis and performance evaluation prove that our scheme is both secure and efficient.

Keywords: Provable data possession; outsourced computation; blockchain; smart contract; chameleon hash

1  Introduction

Cloud computing has become one of the most successful information techniques in recent years. Benefiting from the features of pooling resources, easy maintenance, broad network access, rapid elasticity and pay-as-you-go business model, cloud computing has been serving a wide range of clients, especially enterprises. The rise of cloud computing certainly advanced the transformation of viewing how to setup and deploy a database for large scale application, from private local storage to public remote service [1]. With this shift comes the problem that physical control of outsourced data has been transferred to cloud service providers (CSP), while its sovereignty remains with users. This isolation leads to an emerging issue between users and cloud service providers: since the integrity of outsourced data is hard to be always guaranteed, in some certain situations cloud service providers may incline to conceal the fact [2], in pursuit of commercial interests, that part or even whole of data has been corrupted or deleted (often occurs on data rarely accessed). The gap of trust between users and CSP asks for an effective solution to check the integrity of outsourced data, without having to download the original content, since its scale can be extremely large.

Aiming at this target, cloud data auditing schemes have been proposed to settle possible dispute between users and cloud service providers. There have been two kinds of data integrity auditing schemes already: Proof of Retrievability (POR) and Provable Data Possession (PDP). Both of two schemes offer remote data integrity verification with common properties, such as replay attack resistance and verification without downloading. Quite a few following works devote to improving various aspects of cloud data integrity auditing scheme, especially in order to adapt to novel application scenarios. However, with progress and promotion of low-power network, typically the Internet of Things (IoT) [3], there still remain several unmet needs that impede cloud data integrity auditing applying to the emerging scenarios.

Numerous IoT end nodes are connected to the network via gateways. IoT end nodes, compared with typical computer terminals, often consist of devices with lower power and performance, due to economic and environmental considerations. Through connection management layer with possible edge nodes (if necessary) [4], data generated by low-performance end devices is transferred to large-scale computing platform for further processing, often cloud computing platform. Similarly, this cloud-boosting IoT network also suffers from the problem of lacking trust in data integrity. Even more seriously, lower performance of IoT end devices make necessary computation quite difficult for either PDP or POR scheme.

When we discuss how to relieve computation overhead for low-performance devices, it is easy to consider outsourcing computation task in the first place [5]. Most existing PDP works do support public auditing via Third Party Auditor (TPA). Nevertheless, revisiting these schemes, the so-called “public” auditing only refers to outsourcing the computation of generating auditing request and verifying integrity proof, which are originally supposed to be done by users. Another large part of computation overhead, generating tags for data blocks, still requires to be done by the user itself. According to common practice of PDP scheme, each data block should obtain a corresponding tag, which requires modular power operation on large prime multiplication commutative group. Generating block tags and integrity share similar computational complexity (both requiring modular power operation), while computational capacities of IoT end devices and cloud servers are rather different. What is more serious, since block tags must be calculated based on the data freshly generated, heavy overhead will slow down process of uploading, which is no doubt detrimental to some time-sensitive scenarios. A possible reason for setting this crucial issue aside quite a long time may be the risk of key and privacy leakage, considering that both are necessary in tag generation. Generally speaking, a novel PDP scheme which can reduce computational overhead for low-performance IoT devices, is in active demanded.

On the other hand, even though we find some efficient methods of outsourcing tag generation to TPA, the whole system still suffers from the trust issue of TPA reliability. Previous PDP schemes ignore this problem more or less, assuming that TPA is semi-trusted, meaning honest but curious. It is easy to point out that semi-trusted assumption is unpractical in real world and TPA can possibly collude with user or cloud to repudiate the other one. Taking this into account, we design a credible efficient PDP scheme to solve the aforementioned obstacles.

Contribution. (1) We introduce a construction of blockchain-based PDP scheme, which enables collusion-resistant distributed integrity verification via smart contract. (2) We propose a novel outsourced tag generation method relieving the computation overhead for low performance devices. (3) We analyze the security of our proposed scheme and evaluate its performance. Specifically, we deploy an instance of our scheme on VPS, performing some benchmark tests.

2  Related Work

On the basis of some preliminary works [6,7], Juels et al. [8] propose the concept of “proof of retrievability” (POR), while Ateniese et al. [9] publish their first provable data possession (PDP) scheme. These two solutions start with different approaches and both verify the data integrity of files on untrusted storages. POR scheme uses spot-checking and error-correcting codes to find and fix the possible data damages. Particularly, some “sentinels” are precomputed for error detection based on designated blocks randomly embedded in files, which, however, hampers the implementation of data dynamics. The following works [10–16] pay attention to the issues of security and encoding performance of POR schemes, ignoring the problem of data dynamics. Wang et al. [17] firstly fill in the blank, holding the advantage of data recovery based on erasure coding. Totally speaking, recent years POR works such as [18–20] focuses on exploring some emerging fields and applying new techniques. But no one solve the aforementioned problem for low performance devices successfully.

Different from POR, the first PDP scheme makes use of RSA-based homomorphic tags, which contain the block indices to prevent replacement. Similarly, the original PDP also suffers from the problem of how to provide effective support for data dynamics. Then Ateniese et al. [21] try to propose an improvement of their prior work for allowing some limited operations of data dynamics. However, the improved version fails to support block insertion, because the security of the original PDP scheme seriously relies on indices contained in hash values of tags, which are hard to maintain in data dynamics.

To solve this problem, Erway et al. [22] propose the first complete dynamic data possession auditing scheme, taking advantage of random balance tree authentication skip list. Wang et al. [23] constructs their own dynamic public auditing scheme based on a steadier structure of Merkle Hash Tree (MHT). Both employ the hash tree to manage the indices alteration in data dynamics. On this basis, Liu et al. [24] and Tang et al. [25] respectively propose improved schemes aiming at multiple replica and multiple clouds. Meanwhile, the MHT deficiencies of [23] begins to rise. First of all, it lacks efficient method for querying blocks and has the risk of tree degeneration. Mo et al. make twice attempts that they propose the new Coordinate Merkle Hash Tree (CMHT) in [26] and a self-balancing B+ tree [27], each with some additional purposes.

On the other hand, Zhu et al. [28] propose a new structure called index-hash table to maintain the block indices in PDP scheme with a later extension for multi-cloud scenario proposed in [29]. The index-hash table is a linear linked list, which can be used to query and maintain indices of blocks. Focusing on the deficiencies of first index-hash table, Yang et al. [30] add time stamps to enhance the security table records. Jin et al. [31] propose simplified “index switcher” and apply it to arbitrating result of dynamic cloud data auditing. Tian et al. [32] offer a two-dimension table to raise its efficiency. However, no matter MHT-based scheme or index-hash table ones, aforementioned works avoid the problem of overhead in tag generation, until the proposal of [33] and [34]. The work of [34] try to outsource the tag generation computation to TPA, but is obsessed with the possible data leaking. They choose the method of blinded signature, which, however, ask for frequent modular exponentiation and bilinear map computing. These two kinds of operations are quite unpractical for low performance devices. By contrast, work [33] notice the issue and firstly propose the application of “hash-sign-switch” idea, taking an important step further. But the authors lack a secure outsourced computing method, thus they limit their scheme to devices with power fluctuations. That is to say, the devices adapted to this scheme must have moments holding strong computing resources and do the tag generation themselves.

3  Problem Statement

In this section, we firstly describe the framework of cloud-chain integrated auditing system and its security model. Then aiming at the requirements for low performance devices network and security threats, we propose design goals to instruct the following scheme construction. Finally, we give the description of some preliminaries.

3.1 System Model

As illustrated in Fig. 1, the system architecture of blockchain-based PDP scheme consists of the following entities:

User: users in IoT network are terminal devices which generate and upload data. For some economic and environmental considerations, these devices often only have low capacity of both computation and storage.

Cloud Service Provider (CSP): Cloud service providers offer storage for users in IoT network. CSPs are responsible for the maintenance of data in vehicular network, and should respond to any authenticated cloud audit requests.

Third Party Auditor (TPA): Third Party Auditors perform public auditing tasks authorized by users, including partially outsourced tag computation and integrity proof verification. In blockchain network, there are usually several servers assuming the role, because a blockchain transaction requires more than one endorsement. Different from previous works, TPAs in our new framework do not have to be trusted or semi-trusted. Instead, they can be a set of auditors from multiple sources, with security guaranteed by blockchain mechanism.

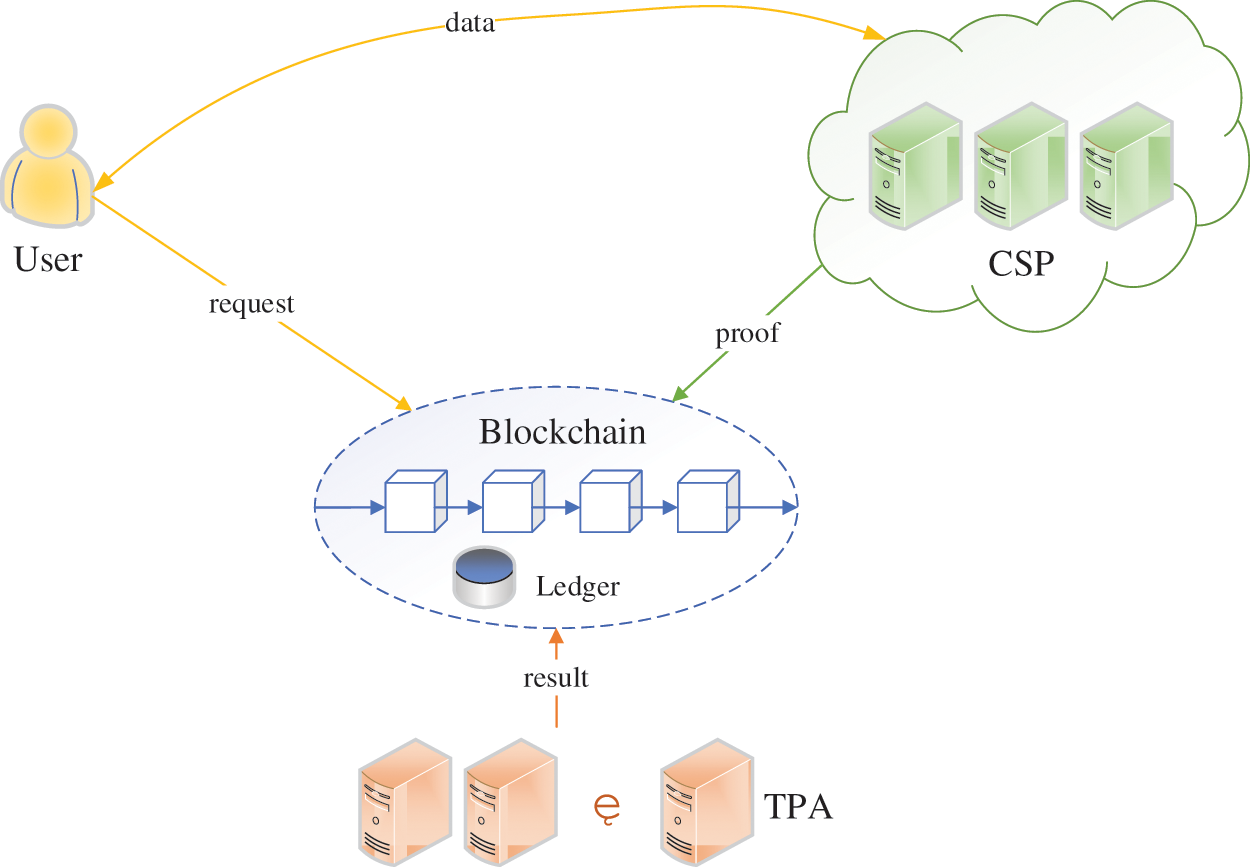
Figure 1: System model

3.2 Security Model

Here we define security against possible adversaries (TPA, CSP) for our blockchain-based PDP scheme. First, all the algorithms for blockchain-based light-weighted PDP scheme are defined as follows:

Setup(1k)→(sk,pk). This algorithm generates necessary private and public keys (sk,pk) according to given security parameter 1k.

TagPreC(sk,pk)→σ∗. This algorithm is run by user to obtain pre-computed tags by outsourcing task to TPA. Pre-computed tags are generated on the basis of random bytes and will be converted into “real” tags later uploaded with data.

TagConv(σ∗,m,sk)→σ. Once having data blocks to be uploaded to cloud, user invokes this algorithm to convert pre-computed tags into formal ones actually used in PDP scheme, then sends tags to distributed blockchain ledger L, and data blocks to cloud respectively.

Challenge(pk,L)→chal. Similar to previous works, this algorithm is run to generate challenge request chal based on public key of user and meta data from blockchain ledger. Challenge request will include block indices required to be checked and other parameters necessary for integrity verification.

Prove(chal,L,m)→P. After receiving challenge request chal, cloud server generate integrity proof P according to original data m and its tag kept in blockchain ledger L. Then the proof will be sent back to TPAs in blockchain network.

Verify(P,pk)→(true,false). This algorithm is invoked by TPA to verify received integrity proof P from cloud service. It will output either true or false referring to whether the proof is accepted or not.

In blockchain-based light-weighted PDP scheme framework, an adversary can be user, cloud service or TPA. Different from previous works, here we relax the security assumption for user and TPA, considering that user may undermine credibility of CSP, or TPA may collude with either user or CSP. Furthermore, there should be more than one auditor in the network playing the role of TPA, and these auditors are also likely to collude partly. A foremost assumption is, most–at least more than half–auditors should be semi-trusted, otherwise PDP verification will receive an inauthentic result with very high probability. Now we give the definition of blockchain-based PDP security model based on a series of Cloud Audit games.

Definition 1. (Correctness of Blockchain-based Cloud Audit) A blockchain-based cloud audit scheme is secure if for any probabilistic polynomial time (PPT) adversary, the probability of winning the first kind of cloud audit game in the following way is negligible, unless either there exists an extractor that can extract data with high probability by resetting and challenging the adversary polynomial many times, or the adversary colludes with majority of auditors in blockchain network.

Cloud Audit Game 1: Played by the challenger who plays the role of user as well as TPA which check integrity proof, vs. the adversary who acts as cloud storage. If cloud storage successfully submits integrity proof that passes the verification by TPA, it wins the game.

Definition 2. (Non-repudiation of Blockchain-based Cloud Audit) A blockchain-based cloud scheme is free from repudiation if for any probabilistic polynomial time (PPT) adversary who plays the role of either user or server, the possibility to win the second kind of cloud audit game in the following way relies on behaving consistently with the majority of auditors in blockchain network. In other words, it should be honest.

Cloud Audit Game 2: Played by the challenger who plays the role of TPA which checks integrity proof, vs. the adversary who acts as either cloud storage or user. If adversary successfully repudiates verification result from TPA, it wins the game.

Definition 3. (Privacy-Preserving of Blockchain-based Cloud Audit) A blockchain-based cloud scheme is privacy-preserving if for any probabilistic polynomial time (PPT) adversary who plays the role of TPA, the probability to win the third kind of cloud audit game in the following way lies in whether there exists an extractor that can extract data with high probability by resetting and challenging the adversary polynomial many times.

Cloud Audit Game 3: Played by the challenger who plays the role of users who outsource data tags computing and integrity auditing tasks to blockchain network, vs. the adversary who acts as TPA. If adversary successfully extracts a data block according to its tag, it wins the game.

3.3 Preliminary

Two-Phase Signature Generation. Previous work [33] build a two-phase signature protocol which enables dividing the process of signature generation with different computation overhead: offline phase and online phase. Offline phase possesses relatively large computation overhead and can be performed without being given the message to be signed. By contrast, online phase only requires for low computation overhead but can be executed only if message is given. Separation of computation overhead makes the protocol a good practice for signature generation for low-performance devices. Actually, literature [33] has already built a PDP tag generation protocol for devices with computing source varied cyclically. That is to say, users can execute offline phase when connected to high-performance power, and quickly deal with online phase as soon as data is generated, even if computing source is low. Nevertheless, not all low-performance devices have opportunity to access to high-performance device. In next section we will try to explore another way–outsource the offline phase to TPA.

Chameleon hash functions have several excellent features that make it quite suitable for constructing a two-phase signature protocol. First of all, every chameleon hash function is controlled by a pair of public and private keys. With both two keys, the hash value can be computed efficiently, specifically, even faster than SHA-1 based one-way chain. However, it is hard to obtain a collision of certain hash value without holding the private key, but can be computed with even less overhead than generated for the first time, only if both keys are told. This makes chameleon hash functions quite fit for two-phase computing. Here we give a two-phase signature construction based on chameleon hash function defined in [33].

Let G1 be a multiplicative cyclic group and big prime p be its order. Denote a generator of G1 as g. Choose a random element x←Zp∗ as private key, then compute y=gx as public key. For each message m0∈Zp, choosing a random element r0←Zp, chameleon hash value is defined as HCH(m0,r0)=ym0gr0=gxm0+r0. For any entity holding private key x, given a new message m(m≠m0), a collision can be computed efficiently as r=(m−m0)x+r0, where HCH(m,r)=HCH(m0,r0). However, such a collision will be hard to find when private key x is not given.

This one-way function with back door makes itself easy to construct a two-phase signature protocol. It is called a “hash-sign-switch” method proposed by Shamir and Tauman. In the first phase, a pair of (m0,r0) is randomly chosen to compute hash value HCH(m0,r0). In the second phase, once received the real message m, HCH(m0,r0) can be quickly switched to HCH(m,r) and the cost is simply computing r. The disparity of computing overhead between two phases enables an outsourced tag generation method, which means we can employ TPA to compute PDP tags without sending real data blocks.

Bilinear Map. Our scheme is based on bilinear maps. Let G1 be a Gap Diffie-Hellman (GDH) group and G2 be another multiplicative cyclic groups with prime order p. A bilinear map e is a map e:G1×G1→G2 where the following properties hold:

Computability: for all u,v∈G1, the efficient algorithm for e(u,v) exists.

Non-degeneracy: e(g,h)≠1, where g,h both are generators of G1.

Bilinearity: for all u∈G1,v∈G2, and a,b∈Zp, e(ua,vb)=e(u,v)ab.

Blockchain Network and Smart Contract. Blockchain network is infrastructure based on distributed servers and devices, providing ledger and smart contract service to its users. Blockchain network is famous for its practice on the p2p digital cash Bitcoin and being promoted to more application scenarios. The essence of blockchain is using distributed consensus to validate a transaction occurring between two users. The distributed consensus techniques can resist collusion attack and history alteration. Smart contract, as its name, is a protocol enabling digital facilitation, execution and validation of contract. Combining blockchain network and smart contract, automatic performance of credible transactions without extra trust building becomes reality.

One of the most famous blockchain-based smart contract framework is Hyperledger Fabric. A detailed manual can be referred at the homepage. Here we only introduce some major characteristics:

A Fabric network consists of client node, peer node, ordering node, membership service, certificate authority and distributed ledger.

All the three kinds of nodes join in channel to conduct transactions. Transactions are done through smart contracts written in chaincode. A network can have multiple channels. Different channels can install different chaincodes.

A normal transaction process is as follows: client proposes a transaction via smart contract; after execution, the transaction result is sent to peer node; peer node, as endorser, checks the validity of transaction result and decides whether to send its endorsement to clients; finally, when the client collects enough endorsement, it sends the necessary data to ordering node, which will order transactions from different clients and write to the blocks in blockchain. Some specified data can be pushed to the distributed ledger according to smart contract defined in chaincode. That is to say, developers can write chaincode to customize their own smart contracts and database in ledgers.

4  Proposed Scheme

In this section, we present a blockchain-based construction of light-weighted PDP scheme with outsourced tag generation. First of all, we give a basic public auditing scheme including process of data uploading, auditing challenging and integrity verifying. Then we extend the basic scheme to an improved version with data dynamics.

4.1 Basic Scheme

We have already given all the algorithms for the proposed scheme in Section 2. The basic scheme consists of six algorithms: Setup, TagPreC, TagConv, Challenge, Prove and Verify. The details of constructions are described as follows, dividing into two phases.

Phase 1: Preprocessing

In this phase, user does necessary preparatory work for the whole scheme. Algorithm Setup generates private and public keys of user and only needs to be invoked for once, while TagPreC and TagConv, generating tags and uploading data blocks, should be called every time when required.

Setup(1k)→(sk,pk,param). Based on the global security input 1k, generate multiplicative cyclic groups G1,G2,GT of prime order p, where bilinear map e:G1×G2→GT holds. Select generators g∈G1,h∈G2 and choose random element x←G1,s←G2. Then compute y=gx,t=hs. The secret key for user is sk=(x,s), public key is pk=(y,t). Security parameter shared with every entity in blockchain network is param=(e,G1,G2,g,h), which will be used for computing in following phases.

TagPreC(sk,pk,param)→σ∗. User chooses random element pairs {wi,ri}i∈[1,K], where K is the number of required tags estimated by user according to its own needs within a certain time. Then compute zi=(wix+ri)s and send {zi}i∈[1,K] to blockchain network along with a request asking for outsourcing computation. TPA computes σi∗=gzi and returns result to blockchain network. After validating the result via endorsement mechanism, user accepts the outsourced pre-computed tags and stores them in local storage with original element pairs together.

TagConv(σ∗,w,r,m,sk)→σ. Once having a data block m to be uploaded to cloud, user randomly chooses an unused pre-computed tag σ∗ as well as its generating pair {w,r} to convert into a formal one. The conversion process consists of steps as follows: compute r′=(w−m)x+r, denote σ={σ∗,r′}. After that, upload data block to CSP, meanwhile send σ to blockchain network to record the uploading. The formal data tag σ will be stored in distributed ledger with index referring to data block, instead of MHT kept by CSP.

Phase 2: Auditing

This phase includes three steps: first, user invokes Challenge to generate auditing request; secondly, CSP calls Prove to send integrity proof as a response; finally, TPA checks the proof using Verify.

Challenge(c)→chal. As previous works, the proposed scheme offers probabilistic security, that means by checking only a part of data blocks, the corruption can be found with no less than a certain probability. When user decide to audit its own data, it first randomly chooses c blocks, denoting their indices as I={ij}j∈[1,c]. Secondly, choose random elements V={vj|vj∈Zp}j∈[1,c] for each index. Finally, a challenge request chal=(I,V) is sent to blockchain network.

Prove(chal,σ,m,param)→P. After receiving challenge request chal, CSP computes integrity proof P as follows:

μ=u+∑j=1cvijmij(1)

λ=yu(2)

where u∈Zp is randomly chosen by CSP to blind the linear combination of data blocks, otherwise TPA may be able to learn {mij}. Let P=(μ,λ) and return it back to the blockchain network.

Verify(P,σ,pk,param)→(TRUE,FALSE). Once receiving the integrity proof P, each TPA in blockchain network checks whether equation e(λ⋅∏j=1c(σij∗)vij,h)=e(g∑j=1cvijrij′⋅yμ,t) holds, where σ={σij∗,rij′} are data tags stored in distributed ledger. That is to say, each TPA can obtain data tags via ledger from the nearest node in blockchain network, no longer relying solely on cloud storage. If the equation holds, accept and endorse the proof with output TRUE; otherwise reject it with output FALSE. When the blockchain network service collects enough endorsement, it will finally validate the integrity proof and write the result into block as a transaction. The other case is that fewer endorsement received within standard time than required, leading to the failure of CSP.

4.2 Data Dynamics

Generally speaking, data dynamics includes three kinds of operation: insertion, deletion and modification, which have already been supported by previous PDP schemes. Those solutions mostly rely on Merkle Hash Tree (MHT). Here we will show that updating data blocks is still fully enabled without MHT in our proposed scheme.

Update(utype,i,mnew,σnew∗,wnew,rnew,sk,V)→(σ,P). Since there are three kinds of operation in data dynamics, user should denote the specific operation type as utype to tell CSP which kind is selected, as well as the index i of data block to be updated. If the operation type is insertion or modification, new data block mnew and precomputed tag {σnew∗,wnew,rnew} are also required to generate new tag σ with private key sk following the method in TagConv. Random element set V is also required for verifying updating, which is selected following the method in Challenge. Deletion does not need new tag and these parameters should remain blank. After dealing with data tag, an updating request is sent to blockchain network, while the uploading of new block is executed in private between user and CSP. The blockchain network modifies the record of updated block in ledger and waits for the updating proof P from CSP. Once receiving the content of updating operation, CSP executes request and then generates integrity proof. The method of proving updating multiple blocks is the same as Prove. Particularly, the case of single block is the special situation that c=1.

The verification of updating can be implemented using Verify. Thus, we omit the duplicate statement.

5  Security Analysis

In this section, we evaluate the security our proposed scheme under the definition of security model in Section 2.

Theorem 1. (Correctness) The proposed scheme has the property of correctness. That is to say, when most auditors in blockchain network are honest, an integrity proof from CSP cannot pass verification unless CSP holds complete data.

Proof: First of all, we prove the correctness of bilinear mapping verification e(λ⋅∏j=1c(σij∗)vij,h)=e(g∑j=1cvijrij⋅yμ,t), since it is the foundation of the whole scheme.

e(λ⋅∏j=1c(σij∗)vij,h)

=e(gux⋅∏j=1cg(wijx+rij)s⋅vij,h)

=e(gux⋅∏j=1cg(mijx+rij′)s⋅vij,h)

=e(gux⋅gs∑j=1cvij(mijx+rij′),h)

=e(gux⋅gsx∑j=1cvijmij⋅gs∑j=1cvijrij′,h)

=e(gx(u+∑j=1cvijmij)⋅g∑j=1cvijrij′,hs)

=e(g∑j=1cvijrij⋅yμ,t)(3)

There are several key points involved in the proving process above:

•   Since the data tags σ={σij∗,rij} are stored in distributed ledger of blockchain network, for a certain TPA, the correctness of data tags is ensured by the ledger it refers to, which can be seen as authentic for an honest auditor.

•   On the premise that data tags are all correct, whether an integrity proof can pass verification only depends on the correctness of λ=yu and μ=u+∑j=1cvijmij. Excluding that u is chosen by CSP, the sole decisive factor is ∑j=1cvijmij, depending on whether CSP has data blocks {mij} intact.

•   If CSP tries to construct a valid μ without holding correct data blocks {mij}, it can be proved impossible. Known σij∗=gs(mijx+rij′) and rij′, colliding a value ε meeting condition gε=gmijx has the same difficulty as Discrete Logarithm Problem (DLP), which is considered to be impossible within polynomial time.

Theorem 2. (Non-repudiation) The proposed scheme has the property of non-repudiation. That is to say, when most auditors in blockchain network are honest, a minority of dishonest auditors cannot slander CSP if the outsourced data is intact.

Proof: The correctness of proposed scheme has been proved above. The implication here is that an honest auditor can always give right result of integrity verification. Thus, the correctness of final decision only relies on how the blockchain mechanism works. The validation of blockchain transaction is based on endorsements from auditors in network, and therefore a blockchain network with mostly honest members can resist malicious repudiation of auditing result. In fact, blockchain network is believed to be tamper-free within less than 51% collusion. Thus, we can say that the proposed scheme can stand up to attacks from a minority of dishonest auditors.

Theorem 3. (Privacy-Preserving) The proposed scheme is privacy-preserving, which means that any curious TPA cannot extract data from merely the content of either outsourced tag generation or integrity verification.

Proof: Proving the property of privacy-preserving for our proposed scheme consists of two parts: first of all, we prove that there is no data leakage in the process of outsourced tag generation; secondly, we prove the privacy-preserving of integrity verification.

To analyze the possible leakage risks in tag generation, we should consider not only the computing object σ∗=gz,z=(wx+r)s, but also the formal tags σ={σ∗=g(wx+r)s,r′=(w−m)x+r}. TPA is aware of each of (σ∗,z,r′,g,h,y=gx,t=hs), while (x,s,w,r,m) are kept secret. Since m is protected by x and blinded by w,r in r′, TPA cannot extract m or any other item solely relying on r′. The same situation also happens to z. Value of (wx+r) is able to resist leakage due to the protection of s. Thus, we can say that the process of outsourced tag generation is free of data leakage.

Our scheme shares similar integrity verification method to work [], with slight differences in details. So we can prove the property of privacy-preserving for integrity verification in the same way. First, μ=u+∑j=1cvijmij does not reveal any of {mij} to TPA, because the data blocks are protected by random elements {vij} and blinded by random u. And u cannot be inferred from λ=gu according to the difficulty of Discrete Logarithm Problem. Secondly, as aforementioned, data tags involved in verification is also free of privacy leakage. Therefore, the process of integrity verification is privacy-preserving.

6  Performance Evaluation

In this section, we evaluate the performance of our proposed scheme. Since the scheme in [33] is the state of art in the field of PDP for low-performance devices, we compare our proposal with it. Furthermore, considering that there are not many instances of blockchain-based PDP schemes, we perform a simulation instance of the proposed scheme based on Hyperledger Fabric. The instance is deployed on a Virtual Private Server (VPS) with CentOS 8_x64 system, using 1 CPU core@3.8GHz, 2048MB RAM and 55GB SSD. The smart contracts are implemented by JAVA, with Pairing-Based Cryptography library (jPBC@2.0.0) and Hyperledger Fabric SDK for JAVA (v1.4.1). We do some benchmark tests for the instance deployed on VPS, using Hyperledger Caliper-Benchmarks (caliper-cli@0.3.0).

6.1 Computational Cost on User Side

We compare the computational overhead on user side among our proposal and the work in [33], the state-of-the-art scheme for low performance devices. Considering that both are public auditable scheme, the comparison mainly focuses on the cost from tag generation.

The theoretical comparison is shown in Tab. 1, with various categories of computing operations. Specifically, it must be pointed out that the similar comparison between [33] and [35] shown in [33] only discuss the cost in “online” phase, ignoring the “offline” computation when connected to strong power.

From the table above we can see, for generating one tag, our proposed scheme only needs three times of Mulz and three times of Add, while [33] need H+2Exp+MulG and 2Exp+3Mulz+MulG+2Add respectively. It must be pointed out that different kinds of operations consume various amounts of computing resource. Generally speaking, H and Exp are much more expensive than other ones. According to the simulation shown in Tab. 2, the time cost of one H, Exp, Mulz, MulG and Add operations are 0.0616, 3.9453, 0.006, 0.0449 and 0.0031 ms respectively. The cost of an Exp operation is about 658 times more expensive than a Mulz operation and 1273 times more expensive than an Add operation. While the cost of an H operation is about 10 times more expensive than a Mulz operation and 20 times more expensive than an Add operation.

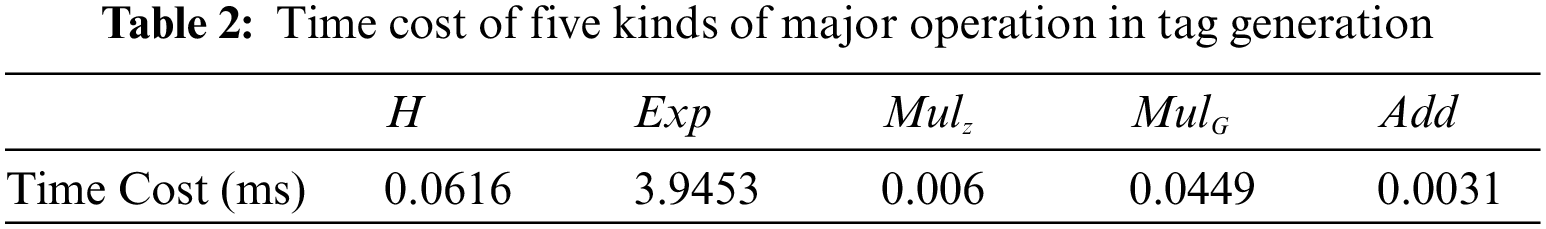
The simulation result of generating tags is shown in Fig. 2. We vary the number of blocks between 104 to 106. For better reflection of time cost in different phases of PDP scheme and keeping consistent to reference [33], we divide the time costs of into two kinds: the first one is called “Precomputing” corresponding to “Offline” phase, which are both executed in preparation; the second one is called “Uploading” compared with “Online” phase, which are both invoked when there are data blocks to be sent to cloud. It is obvious that both our proposal and the scheme in [33] have linear growth pattern in time cost, no matter precomputing or uploading, offline or online phase. Totally speaking, benefiting from the secure outsourced tag generation, time cost of our scheme has been reduced to 107.20 ms for 104 blocks and 2396.07 ms for 106 blocks respectively, while those for scheme [33] are 28.24 s and 2869.18 s, showing an order of magnitude difference. We also consider when uploading data tags as well as corresponding blocks to cloud, how long it will cost for necessary computing. Our scheme gives the answer that 39.76 ms for 104 blocks and 903.57 ms for 106 blocks respectively, while scheme [30] offers 24.56 and 1923.69 ms. Taking the randomness into account, we can say that two schemes show no order of magnitude difference on dealing with real-time data. On the user side cost, we can say that our proposed scheme shows high efficiency.

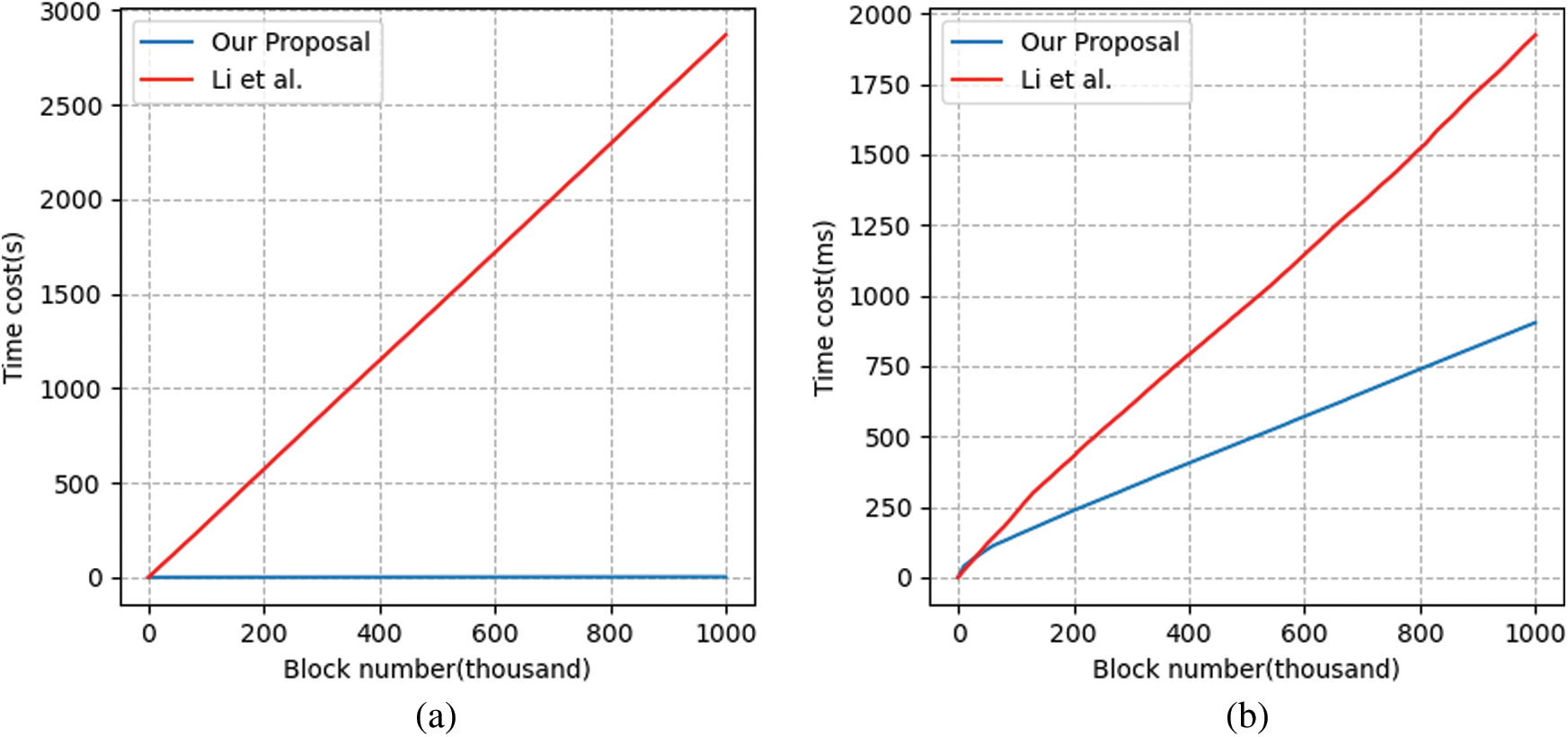
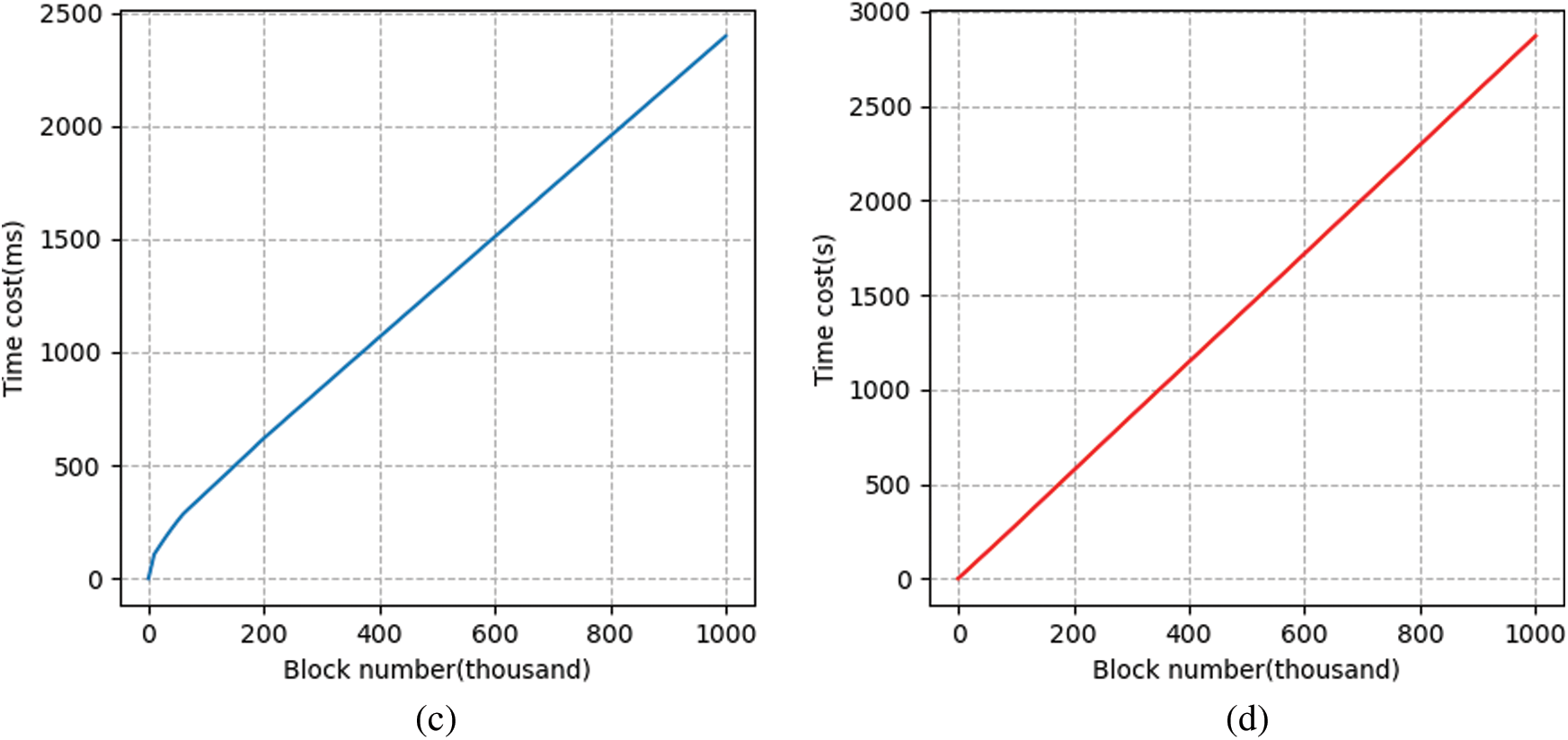
Figure 2: Time costs of generating tags. (a) Total costs comparison (b) Precomputing and online phase comparison (c) Total cost of our scheme (d) Total cost of [33]

6.2 Efficiency of Blockchain-based Auditing

As aforementioned, we deploy an instance of our proposed scheme on VPS. Based on platform provided by the open source blockchain project Hyperledger Fabric, we implement the chaincode via its SDK for JAVA. Fabric offers pluggable consensus services and editable endorsement policies, as well as necessary membership services and certificate authority management. We configure the benchmark test tool Hyperledger Caliper to evaluate the performance of our blockchain-based PDP scheme. Caliper enables users to write the test and network configuration, then launch an instance and execute required smart contracts defined in given chaincode automatically.

We implement every on-chain algorithm in our scheme, wrapped as functions. All the functions are contained in different scripts written in Node.js, in order to complete various tasks in PDP auditing. When some one wants to execute a certain smart contract, it just needs to run the scripts. Also, Caliper benchmark tests are based on executing these scripts.

Considering that some operations in our scheme are off-chain, the performance test only includes the generation of challenge and the verification for integrity proof, denoted as challengeGen and verify. We set a 7-round test, 100 times for each round, with the proportion of challenged blocks varying from 1%, 10%, 20%, 40% to 100%. Fig. 3 shows a general result of our benchmark test. We can see that the average latencies in steady status are 3.37–3.89 s for challengeGen and 32.94–37.39 s for verify. And the send rates, which is called transactions per second (TPS), vary from 59.2 to 63.9 for challengeGen and 24.3–25 for verify. We say “steady status” and omit the first-round results because throughout multiple times of such tests, the first-round results always obtain higher latencies and lower send rates. One possible reason is that the first round is executed just after the instantiation of chaincode and much resource of VPS has not been released yet. The benchmark test demonstrates the handling capacity of blockchain-based PDP scheme. In addition, we also count the resource utilization of the VPS during the whole test. Statistics of two typical rounds is shown in Fig. 4.

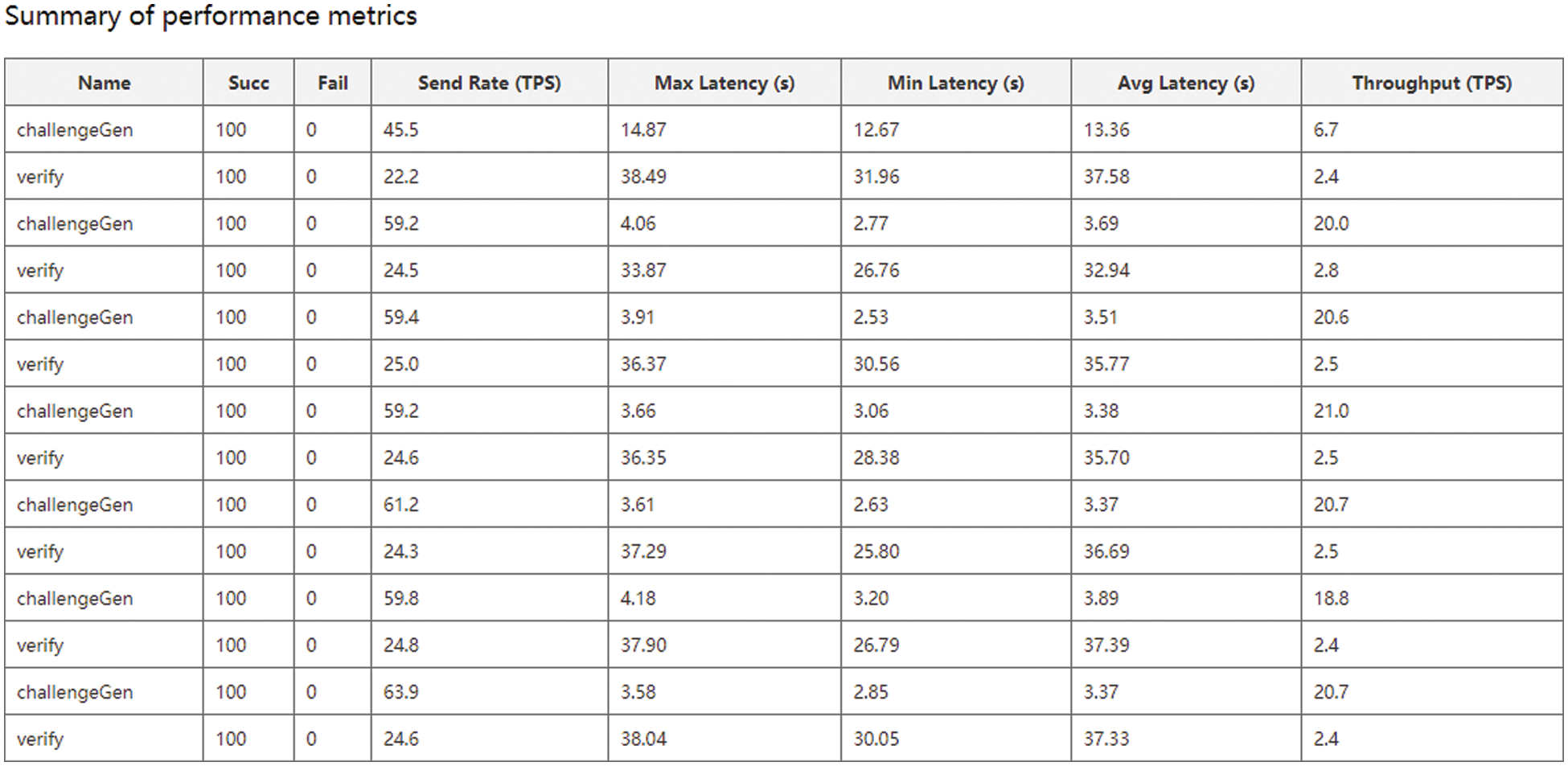
Figure 3: Summary of all test rounds

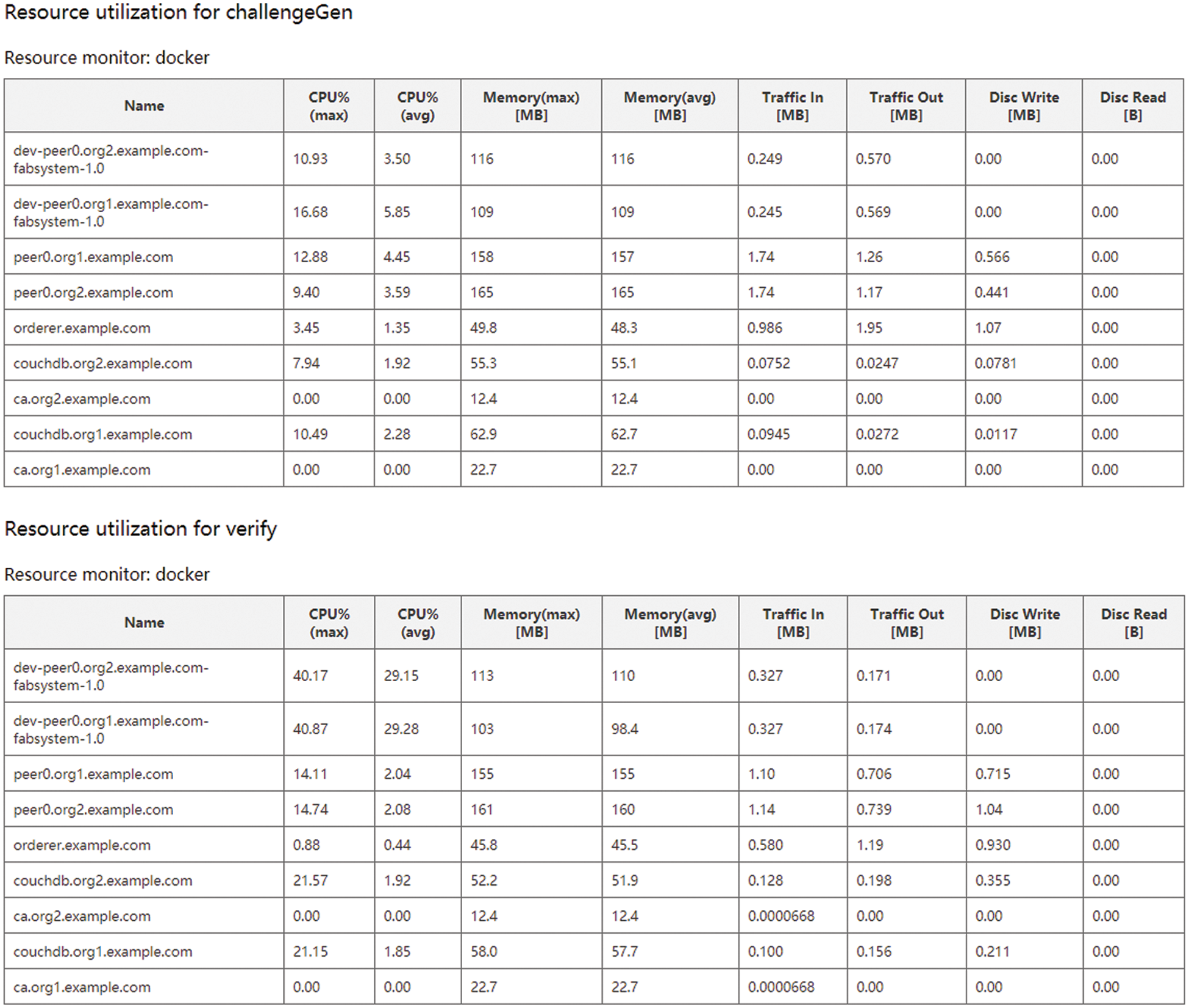
Figure 4: Typical resource utilization of each operation

7  Conclusion

This paper focuses on exploring a light-weighted PDP scheme for network consisting of low performance devices, such as IoT. We find out that heavy computation overhead for tag generation is the major burden preventing low performance device network from applying PDP to its service. Meanwhile, we also pay attention to solve the trust issue on possible collusion attack from TPA. Blockchain network and smart contracts offer a potential solution of reliable outsourced computation, which makes tag generation and integrity verification free from collusion attack. We design a novel method of outsourced tag generation as well as a blockchain-based PDP scheme. Security analysis and performance evaluation prove that our scheme is both secure and efficient.

Funding Statement: The work is supported by the National Key Research and Development Program of China (No. 2018YFC1604002) and the National Natural Science Foundation of China (Nos. U1836204, U1936208, U1936216 and 62002197).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Rudniy, “Data warehouse design for big data in academia,” Computers, Materials & Continua, vol. 71, no. 1, pp. 979–992, 2022. [Google Scholar]

 2.  R. Jia, Y. Xin, B. Liu and Q. Qin, “Dynamic encryption and secure transmission of terminal data files,” Computers, Materials & Continua, vol. 71, no. 1, pp. 1221–1232, 2022. [Google Scholar]

 3.  A. Berguiga and A. Harchay, “An IoT-based intrusion detection system approach for TCP SYN attacks,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3839–3851, 2022. [Google Scholar]

 4.  J. Almutairi and M. Aldossary, “Exploring and modelling IoT offloading policies in edge cloud environments,” Computer Systems Science and Engineering, vol. 41, no. 2, pp. 611–624, 2022. [Google Scholar]

 5.  L. Jiang and Z. Fu, “Privacy-preserving genetic algorithm outsourcing in cloud computing,” Journal of Cyber Security, vol. 2, no. 1, pp. 49–61, 2020. [Google Scholar]

 6.  M. Naor and G. N. Rothblum, “The complexity of online memory checking,” Journal of the ACM, vol. 56, no. 1, pp. 1–46, 2009. [Google Scholar]

 7.  A. Oprea, M. K. Reiter and K. Yang, “Space-efficient block storage integrity,” in Proc. of 12th Annual Network and Distributed System Security Symp. (NDSS), San Diego, California, USA, 2005. [Google Scholar]

 8.  A. Juels and B. S. Kaliski Jr, “Pors: proofs of retrievability for large files,” in Proc. of 14th ACM Conf. Computer and Communication Security (CCS '07), Alexandria, Virginia, USA, pp. 584–597, 2007. [Google Scholar]

 9.  G. Ateniese, R. D. Pietro, L. V. Mancini and G. Tsudik, “Scalable and efficient provable data possession,” in Proc. of 4th Int. Conf. on Security and Privacy in Communication Networks (SecureComm '08), Istanbul, Turkey, pp. 1–10. [Google Scholar]

10. H. Shacham and B. Waters, “Compact proofs of retrievability,” in Proc. of 14th Int. Conf. on Theory and Application of Cryptology and Information Security (ASIACRYPT '08), Melbourne, Australia, pp. 90–107, 2008. [Google Scholar]

11. K. D. Bowers, A. Juels and A. Oprea, “Proofs of retrievability: Theory and implementation,” in Proc. of the 2009 ACM Workshop on Cloud Computing Security, Chicago, Illinois, USA, pp. 43–54, 2009. [Google Scholar]

12. E. C. Chang and J. Xu, “Remote integrity check with dishonest storage server,” in Proc. of 13th European Symp. Research in Computer Security (ESORICS '08), Málaga, Spain, pp. 223–237, 2008. [Google Scholar]

13. M. Naor and G. N. Rothblum, “The complexity of online memory checking,” in Proc. of 46th Annual IEEE Symp. on Foundations of Computer Science (FOCS'05), Pittsburgh, Pennsylvania, USA, pp. 573–582, 2005. [Google Scholar]

14. N. Cao, S. Yu, Z. Yang, W. Lou and Y. T. Hou, “LT codes-based secure and reliable cloud storage service,” in Proc. of the 31st Annual IEEE Int. Conf. on Computer Communications (INFOCOM 2012), Orlando, Florida, USA, pp. 693–701, 2012. [Google Scholar]

15. J. Li and B. Li, “Cooperative repair with minimum-storage regenerating codes for distributed storage,” in Proc. of the 33rd Annual IEEE Int. Conf. on Computer Communications (INFOCOM 2014), Toronto, Canada, pp. 316–324, 2014. [Google Scholar]

16. X. Tang, Y. Qi and Y. Huang, “Fragile watermarking based proofs of retrievability for archival cloud data,” in Proc. of the 15th Int. Workshop on Digital-forensics and Watermarking (IWDW), Beijing, China, pp. 296–311, 2016. [Google Scholar]

17. C. Wang, Q. Wang and K. Ren, “Ensuring data storage security in cloud computing,” in Proc. of Int. Workshop on Quality of Service, Charleston, South Carolina, USA, pp. 1–9, 2009. [Google Scholar]

18. E. Stefanov, M. V. Dijk, A. Juels and A. Oprea, “Iris: A scalable cloud file system with efficient integrity checks,” in Proc. of the 28th Annual Computer Security Applications Conf., Orlando, Florida, USA, pp. 229–238, 2012. [Google Scholar]

19. D. Cash, A. Küpçü and D. Wichs, “Dynamic proofs of retrievability via oblivious RAM,” Journal of Cryptology, vol. 30, no. 1, pp. 22–57, 2017. [Google Scholar]

20. J. Li, L. Zhang, J. K. Liu, H. Qian and Z. Dong, “Privacy-preserving public auditing protocol for low-performance end devices in cloud,” IEEE Transactions on Information Forensics and Security, vol. 11, no. 11, pp. 2572–2583, 2016. [Google Scholar]

21. G. Ateniese, R. Burns, R. Curtmola, J. Herring, L. Kissner et al., “Provable data possession at untrusted stores,” in Proc. of 14th ACM Conf. Computer and Communication Security (CCS '07), Alexandria, Virginia, USA, pp. 598–609, 2007. [Google Scholar]

22. C. Erway, A. Küpçü, C. Papamanthou and R. Tamassia, “Dynamic provable data possession,” in Proc. of 16th ACM Conf. Computer and Communication Security (CCS '09), Chicago, Illinois, USA, pp. 213–222, 2009. [Google Scholar]

23. Q. Wang, C. Wang, K. Ren, W. Lou and J. Li, “Enabling public auditability and data dynamics for storage security in cloud computing,” IEEE Transactions on Parallel and Distributed Systems, vol. 22, no. 5, pp. 847–859, 2011. [Google Scholar]

24. C. Liu, R. Ranjan, C. Yang, X. Zhang, L. Wang et al., “MuR-DPA: Top-down levelled multi-replica Merkle hash tree based secure public auditing for dynamic big data storage on cloud,” IEEE Transactions on Computers, vol. 64, no. 9, pp. 2609–2622, 2015. [Google Scholar]

25. X. Tang, Y. Qi and Y. Huang, “Reputation audit in multi-cloud storage through integrity verification and data dynamics,” in Proc. of 2016 IEEE 9th Int. Conference on Cloud Computing (CLOUD), San Francisco, California, USA, pp. 624–631, 2016. [Google Scholar]

26. Z. Mo, Y. A. Zhou, S. G. Chen and C. Z. Xu, “Enabling non-repudiable data possession verification in cloud storage systems,” in Proc. of 2014 IEEE 7th Int. Conf. on Cloud Computing (CLOUD), Anchorage, Alaska, USA, pp. 232–239, 2014. [Google Scholar]

27. Z. Mo, Y. A. Zhou and S. Chen, “A dynamic proof of retrievability (POR) scheme with O(log n) complexity,” in Proc. of 2012 IEEE Int. Conf. on Communications (ICC), Ottawa, Canada, pp. 912–916, 2012. [Google Scholar]

28. Y. Zhu, H. Wang, Z. Hu, G. J. Ahn, H. Hu et al., “Dynamic audit services for integrity verification of outsourced storages in clouds,” in Proc. of ACM Symp. on Applied Computing (SAC’11), TaiChung, Taiwan, pp. 1550–1557, 2011. [Google Scholar]

29. Y. Zhu, H. Hu, G. J. Ahn and M. Yu, “Cooperative provable data possession for integrity verification in multi-cloud storage,” IEEE Transactions on Parallel and Distributed Systems, vol. 23, no. 12, pp. 2231–2244, 2012. [Google Scholar]

30. K. Yang and X. Jia, “An efficient and secure dynamic auditing protocol for data storage in cloud computing,” IEEE Transactions on Parallel and Distributed Systems, vol. 24, no. 9, pp. 1717–1726, 2013. [Google Scholar]

31. H. Jin, H. Jiang and K. Zhou, “Dynamic and public auditing with fair arbitration for cloud data,” IEEE Transactions on Cloud Computing, vol. 6, no. 3, pp. 680–693, 2018. [Google Scholar]

32. H. Tian, Y. Chen, C. C. Chang, H. Jiang, Y. Huang et al., “Dynamic-hash-table based public auditing for secure cloud storage,” IEEE Transactions on Services Computing, vol. 10, no. 5, pp. 701–714, 2017. [Google Scholar]

33. J. Li, L. Zhang, J. K. Liu, H. Qian and Z. Dong, “Privacy-preserving public auditing protocol for low-performance end devices in cloud,” IEEE Transactions on Information Forensics and Security, vol. 11, no. 11, pp. 2572–2583, 2016. [Google Scholar]

34. D. Liu, J. Shen, Y. Chen, C. Wang, T. Zhou et al., “Privacy-preserving data outsourcing with integrity auditing for lightweight devices in cloud computing,” in Int. Conf. on Information Security and Cryptology Inscrypt 2018, Proc.: Lecture Notes in Computer Science Book Series (LNCS, volume 11449), Cham, Springer, pp. 223–239, 2018. [Google Scholar]

35. C. Wang, S. S. M. Chow, Q. Wang, K. Ren and W. Lou, “Privacy-preserving public auditing for secure cloud storage,” IEEE Transactions on Computers, vol. 62, no. 2, pp. 362–375, 2013. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.