Computers, Materials & Continua DOI:10.32604/cmc.2022.030209
Article

Fuzzy MCDM for Improving the Performance of Agricultural Supply Chain

Le Thi Diem My1, Chia-Nan Wang1 and Nguyen Van Thanh2,*

1Department of Industrial Engineering and Management, National Kaohsiung University of Science and Technology, Kaohsiung City, Taiwan
2Faculty of Commerce, Van Lang University, Ho Chi Minh City, Vietnam
*Corresponding Author: Nguyen Van Thanh. Email: thanh.nguyenvan@vlu.edu.vn
Received: 21 March 2022; Accepted: 07 May 2022

Abstract: Fertilizer industry in Vietnam and globally have entered the saturation phase. With the growth rate slowing down, this poses challenges for the development impetus of the fertilizer industry in the next period. In fact, over the past few decades, Vietnam’s crop industry has abused excessive investment in chemical fertilizers, with organic fertilizers are rarely used or not at all, limiting crop productivity, increasing pests and diseases. To develop sustainable agriculture, Vietnam’s crop industry must limit the use of chemical fertilizers, increase the use of environmentally friendly organic and natural mineral fertilizers to produce clean agricultural products which is safe. Therefore, it is necessary to consider and choose the right supplier to ensure the goal of sustainable development. Spherical Fuzzy Analytic Hierarchy Process (SF-AHP), and the combinative distance-based assessment (CODAS) are new Multicriteria Decision Making (MCDM) method which can be used to solve supplier selection problem. This paper uses an effective solution based on a combined the concept of triple bottom line (TBL), SF-AHP and CODAS approach to help agriculture companies that need to select the best fertilizer supplier. This research can support supply chain managers to achieve supply chain systems that reduce not only sourcing costs, but also develop sustainable agriculture.

Keywords: Fuzzy theory; MCDM model; fertilizer; agricultural supply chain; optimization

1  Introduction

The agricultural industry is currently undergoing a restructuring process due to the trend of globalization, the constant fluctuations in the price of raw materials, labor and stricter regulations when exporting agricultural products.

As businesses expand over time and supply chain becomes more complex, ensuring a steady flow of goods is crucial for the survival of any company. In order to continuously produce sufficient and high-quality products for customers, manufacturers always look for the best supplier of materials that satisfies a number of criteria suitable for the customer needs. This creates a supplier selection problem that is very common in modern world logistics and supply chain management. As more and more suppliers enter the market and competition continuously arise to determine the best suitable supplier, customers must continuously look for the best options suitable for their needs and as each actor of the supply chain is complimented as a customer-supplier relationship, each stage of the supply chain proves crucial hence the supplier selection process is very important.

These big challenges require businesses to constantly innovate, increase their agility, and seize development opportunities. To do this task, it is imperative for companies in the agricultural sector to build a complete supply chain that can both meet production requirements at the smallest cost, while ensuring the highest safety, regulatory requirements, and environmental rules.

The concept of the triple bottom line resolves around profit, people, and planet where each category is considered in all business operations [1]. As supplier selection is a fundamental problem in today’s supply chain, applying this concept assists in the determination of the criteria suitable for the selection process to be smoother. Three elements of triple bottom line (TBL) are shown in Fig. 1.

Figure 1: Three elements of triple bottom line (TBL)

Multicriteria decision making (MCDM) or multicriteria decision analysis (MCDA) is a sub-discipline of operations research that explicitly evaluates multiple conflicting criteria in decision making. However, not all the models are able to solve the issue with the ambiguity of opinions from consultation of experts and literature therefore the application of fuzzy set is generally applied to solve this problem.

In this study, the author proposed a fuzzy MCDM for fertilizer supplier in agricultural supply chain. The aspects of the triple bottom line idea will be applied to determine a set of suitable criteria before applying the suitable decision-making model that would assist decision makers in deciding the best alternative in their supplier selection problem. After the application of triple bot-tom line is initiated in the set, two MCDM models including SF-AHP and CODAS are applied to determine a optimal supplier for the selection process.

2  Literature Review

There have been various studies about the application of MCDM models to solve complicate decision-making problems which involve multiple criteria. These models are applied in various fields and sectors. In the field of supply chain management, MCDM models are regularly applied to support solving problems such as facility location selection [2–6], supplier performance evaluation [7–11], distribution channel development [12,13], etc. Among these, supplier evaluation and selection processes, which involve multiple qualitative and quantitative criteria, are frequently supported by MCDM models.

Karsak and Dursun [14] developed an integrated fuzzy MCDM model to support the supplier evaluation and selection process of hospitals. The model employed Quality Function Development (QFD) methodology in combination with fuzzy information fusion and 2-tuple linguistic representation. The evaluation criteria are established based on the QFD method, and the criteria weights and performance scores of potential suppliers are calculated using House of Quality (HOQ) matrices. The proposed model was applied to a real-world case study of a hospital in Istanbul. Mao et al. [15] introduced a heterogeneous MCDM framework to support the sustainable supplier selection process. The proposed model was based on interval-valued intuitionistic fuzzy (IVIFNs) numbers and interactive multi-criteria decision making (TODIM) method. The proposed approach was applied to a real-world case study of a polymer manufacturer and the result of the model was compared with Simple weighted average method and fuzzy TOPSIS. Wang et al. [16] introduced a fuzzy MCDM model to support the supplier selection process of the edible oil manufacturers. In this research, the selection criteria were taken from the Supply Chain Operation Reference (SCOR) model, while the analytic hierarchy process (AHP) was used to calculate the criteria weights and the Data Envelopment Analysis (DEA) method was used to determine the performance score and ranking of the potential suppliers. The proposed model was applied to a real world case study of an edible oil manufacturer in Vietnam. Mohammed et al. [17] introduced a hybrid MCDM-FMOO model to support the supplier selection and order allocation process. In this study, the authors utilized a fuzzy AHP and fuzzy Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) methods to assess and rank potential suppliers. Then, a Fuzzy Multiobjective Optimization (FMOO) model was formulated to calculate the optimal order allocation plan. Nallusamy et al. [18] discussed the use of AHP in combination with fuzzy logic and Artificial Neural Network (ANN) in solving supplier selection model. Badi and Pamucar [19] developed a hybrid Grey theory Measurement of alternatives and ranking according to COmpromise solution (MARCOS) model to support the supplier selection process of the iron and steel manufacturing industry. The proposed model was applied to a real world case study of a Libyan iron and steel manufacturer. A comparative studied was performed where the result of the proposed model was compared to that of three other MCDM methods: Combinative Distance-Based Assessment (CODAS), TOPSIS, and VlseKriterijuska Optimizacija I Komoromisno Resenje (VIKOR).

In recent years, sustainability has been a major concern to supply chains around the world. There have been many literatures about the application of MCDM models in the sustainable supplier selection processes of supply chains. Chen et al. [20] developed a fuzzy MCDM approach to green supplier selection problems. The model utilized fuzzy AHP and fuzzy TOPSIS techniques to determine the ranking of potential suppliers while considering economic and environmental criteria. The proposed model was then applied to a real-world case study of a luminance enhancement film manufacturer. Quan et al. [21] introduced an MCDM based approach to the green supplier selection process within a large group of decision makers setting. In this research, the authors utilized interval valued intuitionistic uncertain linguistic sets to asset the performance of the potential suppliers regrading each evaluation criterion and a. Ant colony algorithm was utilized to divide the large group of decision makers into subgroups, then a linear programming model was developed to calculate the weights of the criteria, and an extended Multiplicative Multi-Objective Optimisation Based On Ratio Analysis (MULTIMOORA) model was used to rank the potential suppliers. Liou et al. [22] developed a combined approach to green supplier selection problems based on MCDM and data mining techniques. The authors utilized support vector machine (SVM) to identify important selection criteria from historical data, then fuzzy best worst method (BWM) was used to calculate the criteria weights, and finally fuzzy TOPSIS was applied to rank the potential suppliers. Memari et al. [23] develop a MCDM-based decision support tool for the sustainable supplier selection process. The authors employ an intuitionistic fuzzy TOPSIS to evaluate potential suppliers across nine criteria. The proposed model was then validated through a real-world case study of an automotive spare parts manufacturer. Zhao and Guo [24] introduced a fuzzy entropy TOPSIS model to evaluate the performance of potential green suppliers in the electric power industry. An empirical case study of a thermal power equipment supplier selection in China was performed to demonstrate the effectiveness and feasibility of the proposed model. Mohammed et al. [25] introduced a hybrid MCDM model to support supplier selection process with a focus on resilient sourcing. Also, Spearman rank correlation coefficient (SRCC) was also applied to examine the correlation between the suppliers’ ranking. The proposed approach was applied to the scrap metal supplier selection process of a steel manufacturer. The result suggested that the most important criterion was “trust”, followed by “cost”, while the least important one is “geographical location”. Wang et al. [26] propose a blockchain based decentralized reputation management system (BC-DRMS) for Internet of Everything (IoE) in 6G enabled Cybertwin architecture. Zhang et al. [27] proposes a real-time cutting model based on finite element and order reduction method, which improves the computational speed and ensure the real-time performance.

In this study, a MCDM-based approach is developed for the supplier selection of sustainable supply chains under uncertain decision-making environment. The selection criteria are ensured to satisfy the triple bottom line framework where economic, environmental, and social criteria are considered. The proposed method employs SF-AHP to calculate the criteria weights and CODAS method to determine the performance score and ranking of potential suppliers.

3  Methodology

3.1 Spherical Fuzzy Sets Theory

The spherical fuzzy sets theory has been applied in multiple MCDM models [28–33]. The membership function of a spherical fuzzy set is defined by three parameters: the degree of membership, the degree of non-membership, and the degree of hesitancy. Each of these parameters can have a value between 0 and 1 independently and the sum of the squared values of these parameters is at most 1.

A spherical fuzzy set B~S of the universe of Q1 is defined as.

B~S={x, (μB~S(x), vB~S(x) , πB~S(x))|xϵQ1}(1)

with:

μB~S(x) : U1→[0,1], vB~S(x) :Q1→[0,1], and πB~S(x) :Q1→[0,1](2)

And

0≤ μB~S2(x)+vB~S2(x)+πB~S2(x)≤1

with ∀x∈U1, μB~S(x) as the degree of membership, vB~S(x) as the degree of non-membership, and πB~S(x) as the hesitancy of x to B~S.

Basic arithmetic operations such as union, intersection, addition, multiplication, and power of spherical fuzzy sets are defined and demonstrated in the work of Gundogdu and Kahraman [34]. For these spherical fuzzy sets B~S=(μB~S, vB~S, πB~S) and H~S=(μB~S, vB~S, πB~S), basic arithmetic operations are performed as follows:

B~S∪H~S={max{μB~S,μH~S}, min{vB~S,vH~S},min{[1−((max{μB~S,μH~S})2+(min{vB~S,vH~S})2)]0.5, max{πB~S,πH~S}}}(3)

•   Intersection of B~S and H~S:

B~S∩H~S={min{μB~S,μH~S},max{vB~S,vH~S}, max{[1−((min{μB~S,μH~S})2+(max{vB~S,vH~S})2)]0.5,min{πB~S,πH~S}}}(4)

•   Addition of B~S and H~S:

B~S+H~S={(μB~S2+μH~S2−μB~S2μH~S2)0.5,vB~SvH~S,((1−μH~S2)πB~S2+(1−μB~S2)πH~S2−πB~S2πH~S2)0.5}(5)

•   Multiplication of B~S and  a  scalar (λ>0):

B~S×H~S={μB~SμH~S, (vB~S2+vH~S2−vB~S2vH~S2)0.5, ((1− vH~S2)πB~S2+(1− vB~S2)πH~S2−πB~S2πH~S2)0.5}(6)

•   Multiplication of B~S and  a  scalar (λ>0):

λ×B~S={(1−(1−μB~S2)λ)0.5,vB~Sλ, ((1−μB~S2)λ−(1−μB~S2−πB~S2)λ)0.5}(7)

•   Power of B~S, with λ>0:

B~Sλ={μB~Sλ, (1−(1−vB~S2)λ)0.5, ((1−vB~S2)λ−(1−vB~S2−πB~S2)λ)0.5}(8)

3.2 Spherical Fuzzy Analytic Hierarchy Process (SF-AHP) Model

The SF-AHP method has seven steps [34]:

Step 1: Build the model hierarchical structure.

A hierarchical structure with three levels is constructed. Level 1 is the goal of the model based on a score index. The score index is determined with n criteria, which is represented in Level 2 of the structure. A set of m alternative A (m≥2) is defined in Level 3 of the structure.

Step 2: Build pairwise comparison matrices of the criteria using spherical fuzzy judgement based on linguistic terms:

Eqs. (9) and (10) are applied to calculate the score indices (SI) of each alternative.

SI=|100∗[(μB~s−πB~s)2−(vB~s−πB~s)2]|(9)

1SI=1|100∗[(μB~s−πB~s)2−(vB~s−πB~s)2]|(10)

Step 3: Check the consistency of each pairwise comparison matrix.

CR=CIRI(11)

With CI as Consistency Index calculated as:

CI=λmax− nn−1(12)

where λmax is the maximum eigenvalue of the matrix, and n is the number of criteria.

Step 4: Obtain the fuzzy weights of criteria and alternatives.

Each alternative’s weight with respect to each criterion is obtained using the following equation:

 SWMk(B~Si1, …, B~Sin)=k1B~Si1+…+knB~Sin

=⟨[1−∏j=1n⁡(1−μB~sij2)kj]0.5, ∏j=1n⁡VB~sijkj, [∏j=1n⁡(1−μB~sij2)kj−∏j=1n⁡(1−μB~sij2−πB~sij2)kj]0.5⟩(13)

where w=1/n.

Step 5: Obtain the global weights using hierarchical layer sequencing.

The first way is using the score function in Eq. (14) to fuzzified the criteria weights:

S(k~jS)=|100∗[(3μB~s−πA~s2)2−(vB~s2−πB~s)2]|(14)

Then, the criteria weights are normalized using Eq. (15) and spherical fuzzy multiplication in Eq. (16) is applied:

k¯js=S(k~js)∑j=1n⁡S(k~js)(15)

B~Sij=k¯js∗B~Si=⟨(1−(1−μB~Si2)k¯js)1/2, vB~Sik¯js, ((1−μB~Si2)k¯js−(1−μB~Si2−πB~Si2)k¯js)1/2⟩(16)

The final ranking score (P~) for each alternative Bi is calculated using Eq. (17):

P~=∑j=1n⁡B~Sij=B~Si1+B~Si2+…+B~Sin(17)

Another option is to continue the calculation without the defuzzification of the criteria weights. The spherical fuzzy global weights are calculated as:

∏j=1n⁡B~Sij=B~Si1∗B~Si2∗…∗B~Sin(18)

3.3 CODAS Model

In this part, a novel approach (CODAS) for dealing with MCDM model situations is described. The attractiveness of alternatives is judged using two metrics in this technique. The fundamental and major metric is the Euclidean distance between alternatives and the negative-ideal. This sort of distance necessitates the use of a norm indifference space for criterion. The Taxicab distance, which is connected to the norm indifference space, is the secondary measure. Clearly, the option that is further away from the negative ideal solution is preferable. If two options are incomparable according to the Euclidean distance, the Taxicab distance is utilized as a secondary metric in this procedure. Although the norm indifference space is favored in the CODAS, two other types of indifference spaces might be explored. Based on the assumption that alternatives and criteria are accessible, the suggested method’s phases are as follows [35]:

Step 1: Create the decision-making matrix as shown below:

X=[xij]n×m=[x11x12…x1mx21x22…x2m⋅⋅⋅⋅xn1xn2…xnm](19)

where xij (xij ≥ 0) represents the performance score of the ith option on the jth criteria i∈ {1,2,…,n} and j∈ {1,2,…,m}).

Step 2: Produce a normalized decision matrix. The Eq. (20) for linear normalization of performance values is utilized.

nij={xijmaxixij     if  j∈ Nbmaxixijxij     if  j∈ Nc(20)

where Nb and Nc are the sets of benefit and cost criteria, respectively.

Step 3: Create a weighted normalized decision matrix. Eq. (21) is used to get the weighted normalized performance values.

Xnij=wjnij(21)

where wj(o<wj<1) signifies the weight of the jth criteria, and ∑j=1m⁡wj=1

Step 4: Find the negative-ideal solution (point) specified in the Eq. (22)

ns=[nsj]1×m(22)

nsj=minirij

Step 5: Using Eqs. (23) and (24), calculate the Euclidean and Taxicab distances of alternatives from the negative-ideal solution.

Ei=∑j=1m⁡(rij−nsj)2(23)

Ti=∑j=1m⁡|rij−nsj|(24)

Step 6: Create the relative assessment matrix shown in Eq. (25).

Ra=[hik]n×n(25)

hik=(Ei−Ek)+(ψ(Ei−Ek)×(Ti−Tk))

where k∈ {1, 2,…, n} and ψ signifies a threshold function to recognize the Euclidean equivalence.

ψ (x)=[{1 if|x|≥ τ 0 if |x|<τ]

In this function, τ is the threshold parameter that the decisionmaker can set. It is recommended that you set this option to a value between 0.01 and 0.05. If the difference between the Euclidean distances of two options is smaller than, the Taxicab distance is used to compare them.

Step 7: Using the equation, compute the assessment score for each possibility.

Hi=∑k=1n⁡hik(26)

Step 8: Sort the possibilities by decreasing assessment score value (H). The option with the highest is the best option.

4  Case Study

In agricultural production, fertilizer is one of the important materials, significantly contributing to increasing crop productivity, improving the quality of agricultural products, improving soil and protecting the environment. This paper uses an effective solution based on a combined the concept of triple bottom line, SF-AHP and CODAS approach to help agriculture companies that need to select the best fertilizer supplier. To examine the practicality and the effectiveness of the proposed approach for supplier selection and evaluation, a case is illustrated for evaluating sustainability performance of suppliers.

In the first stage of this study, the aspects of the triple bottom line idea will be applied to determine a set of suitable criteria based on TBL model (social factors, environmental factors, and economic factors) before applying the suitable decision-making model that would assist decision makers in deciding the best alternative in their supplier selection problem. SF-AHP hierarchy structure is shown in Fig. 2.

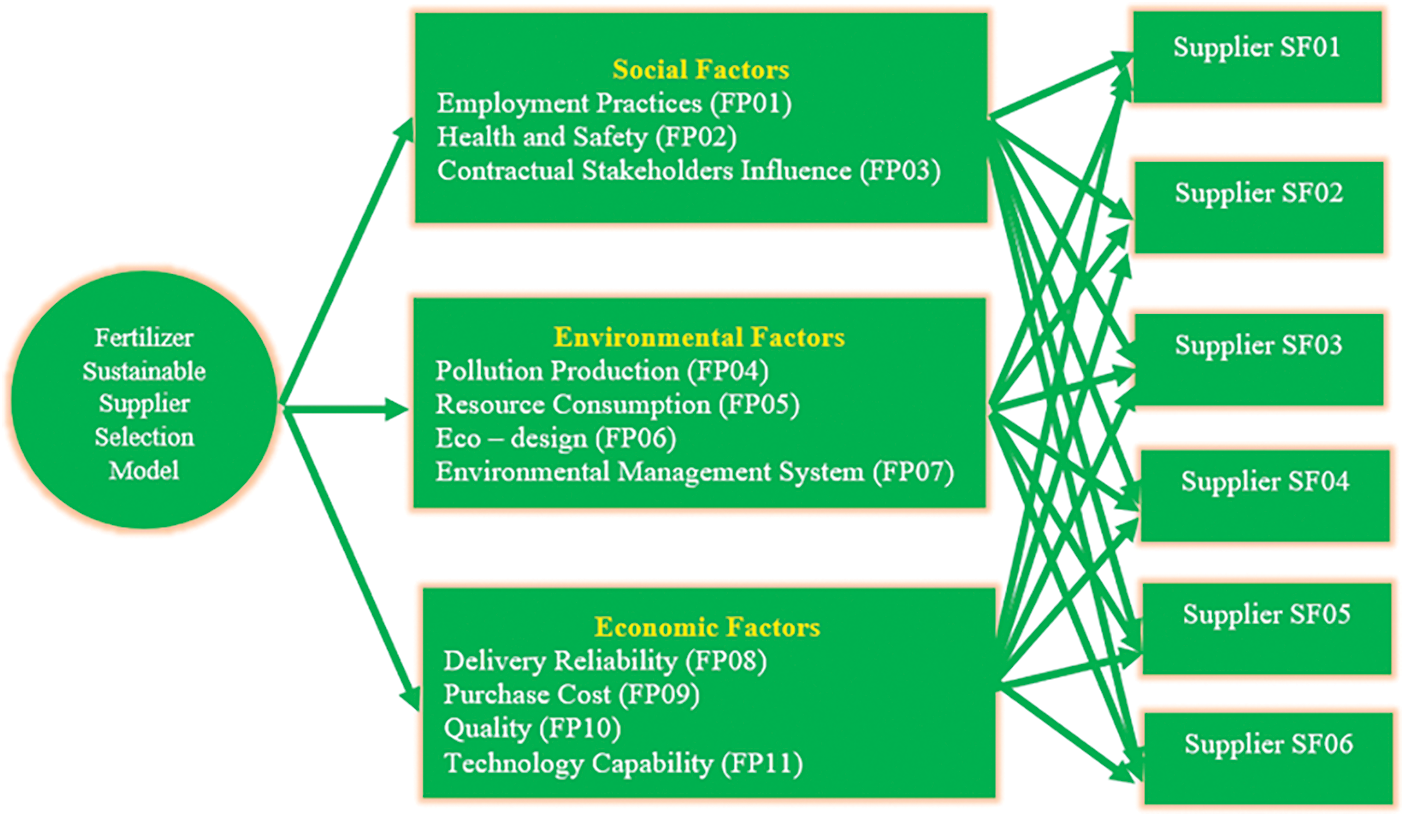
Figure 2: SF-AHP hierarchy structure

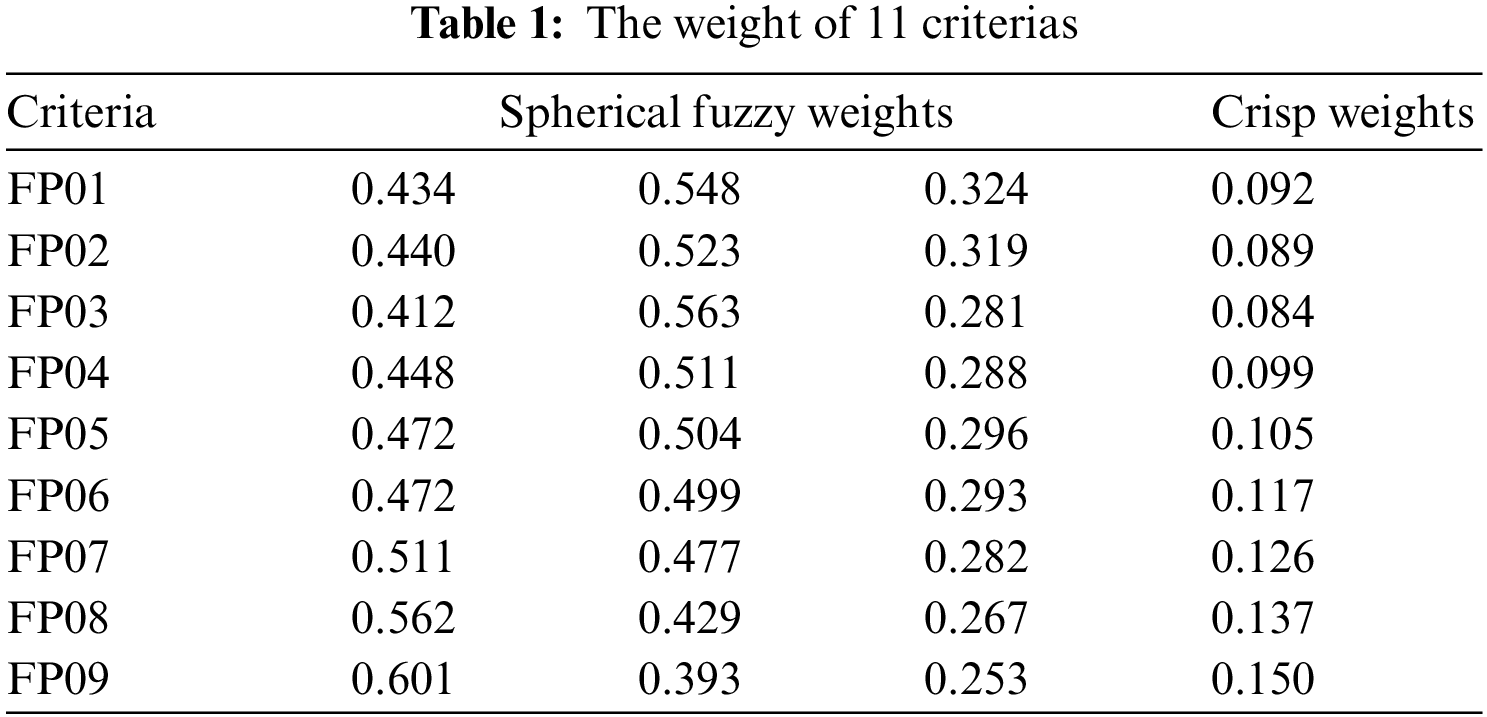
AHP is a Multi-Criteria Decision-Making (MCDM) method which can be used to solve supplier selection problem. The authors combined spherical fuzzy and analytical hierarchy process for determining the weight of all criteria in this stage. All input data are evaluated by Experts. A result of SF-AHP is shown in Tab. 1.

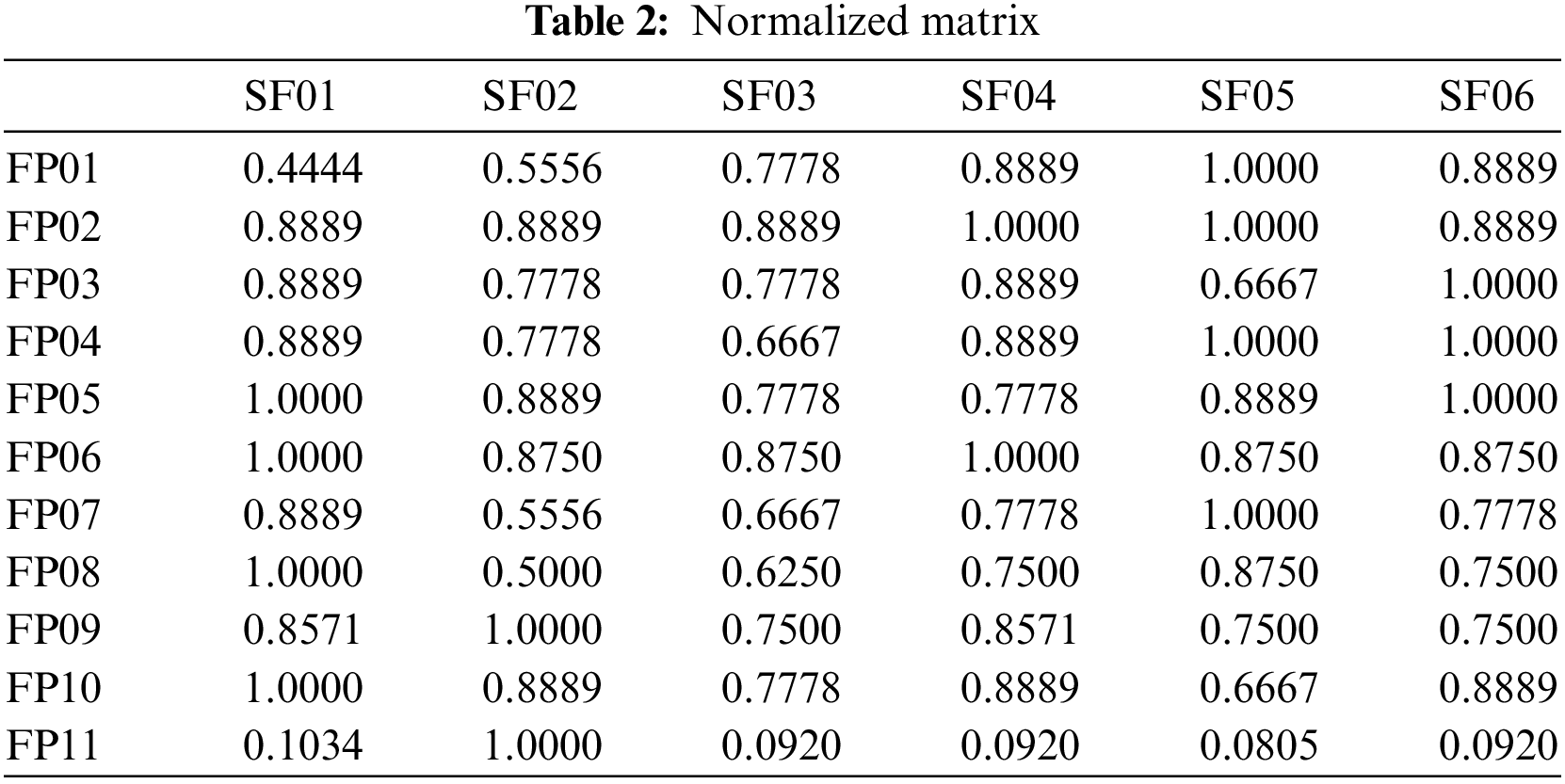
In final stage, a Combinative Distance-based Assessment (CODAS) method is used to handle MCDM problems. To determine the desirability of an alternative, this method uses the Euclidean distance as the primary and the Taxicab distance as the secondary measure, and these distances are calculated according to the negative-ideal point. The alternative which has greater distances is more desirable in the CODAS method. Normalized matrix of CODAS is shown in Tab. 2. The results of CODAS model are shown in Tabs. 3 to 4.

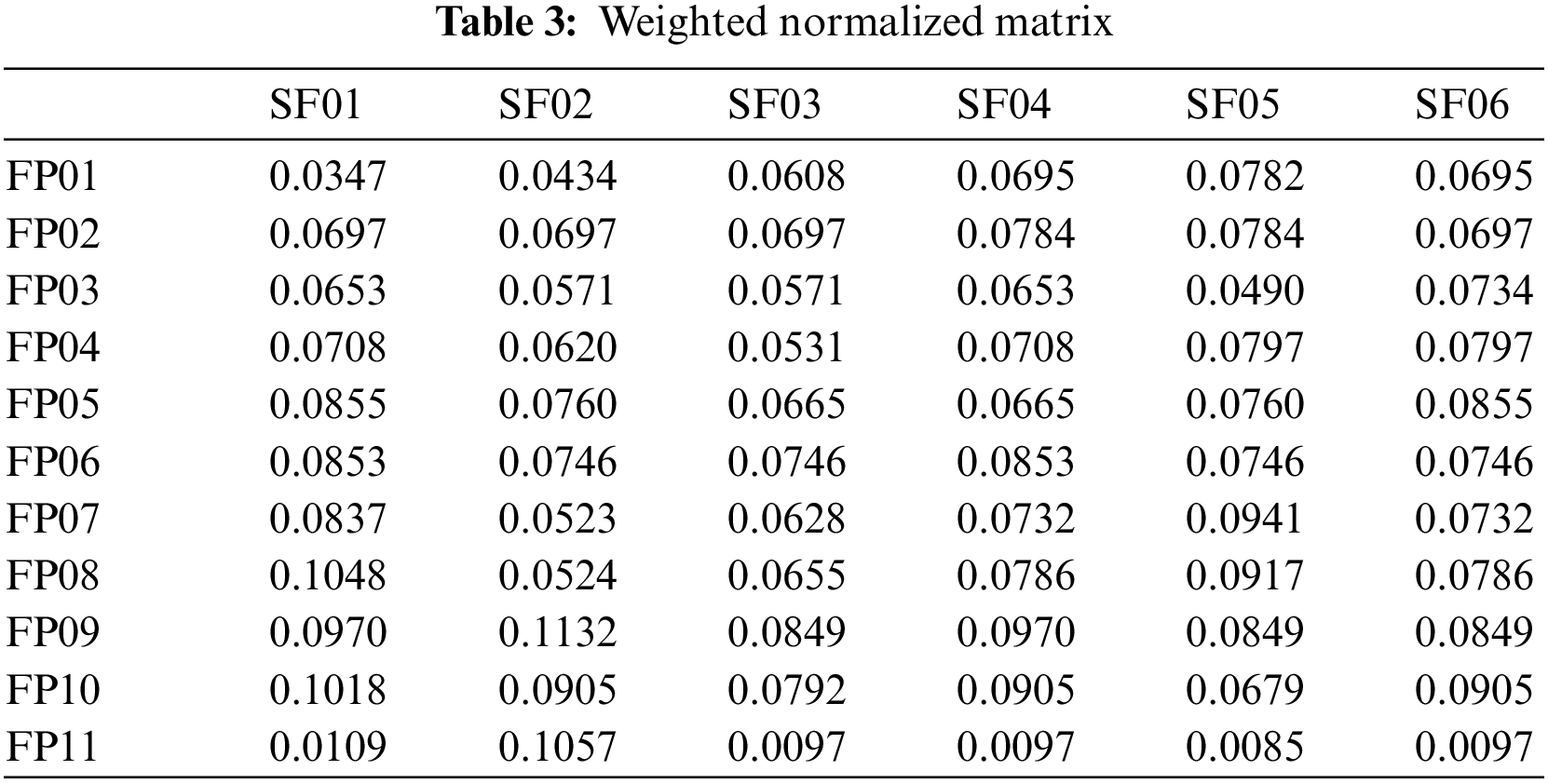
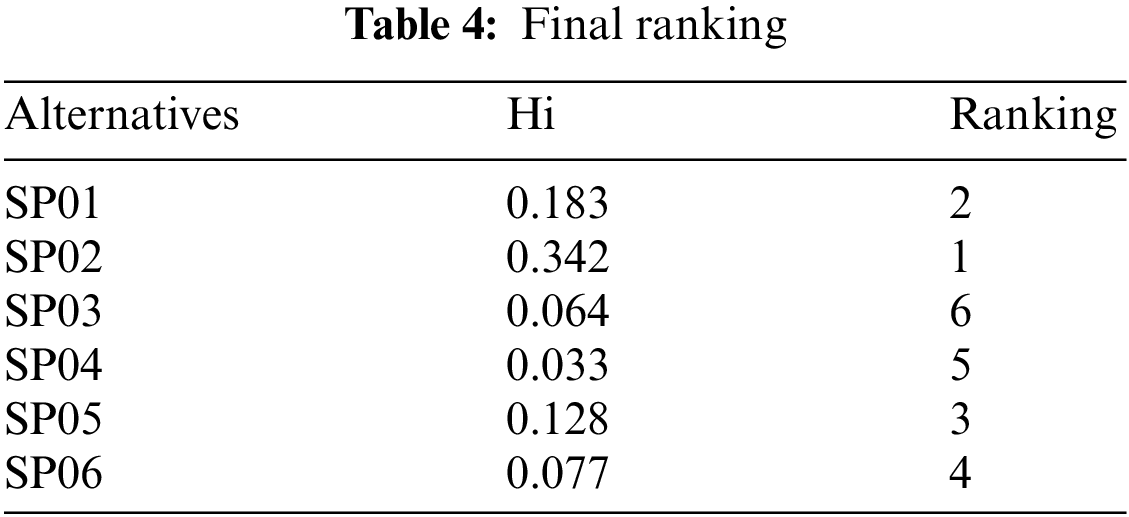
The calculated assessment values shows that the alternatives are prioritized as SP02 ≺ SP01 ≺ SP05 ≺ SP06 ≺ SP04 ≺ SP03. Therefore, we can select SP02 as the best alternative with respect to the assessment performed by the CODAS method.

5  Conclusion

The term sustainable supply chain has appeared a lot recently, when the global economy has been facing many problems with natural disasters, epidemics, and un-predictable risks. This makes supply chains broken, especially for global supply chains that will be more affected.

Supplier selection is a very important process for businesses, it will affect the efficiency of production and business activities of that business, thereby affecting the efficiency of the entire supply chain. At the same time, the process of making a decision to choose a supplier also costs businesses a decent amount of investment. Therefore, a right supplier selection decision will contribute to the sustainability of the supply chain and help businesses save their operating costs.

Supplier selection is not a new research direction, there have been many scientific reports on this research area. However, with different methodological approaches, there will be different results and levels of confidence. This study proposed an integrated TBL, SF-AHP and CODAS approach to supplier selection for a sustainable supply chain.

The main contribution of the study is to provide an effective and quality method for businesses in order to making the right supplier selection decision for sustainable supply chain. This hybrid approach can provide valuable insights, as well as provide a common, cross-sectoral approach to determining which suppliers to choose for a sustainable supply chain.

Acknowledgement: The authors wish to express their gratitude to Van Lang University, Vietnam for support for this research.

Funding Statement: The authors wish to express their gratitude to Van Lang University, Vietnam for financial support for this research.

Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.

References

 1.  J. Sarkis and D. Dhavale, “Supplier selection for sustainable operations: A triple-bottom-line approach using a Bayesian framework,” International Journal of Production Economics, vol. 166, pp. 177–191, 2015. [Google Scholar]

 2.  P. Kieu, V. Nguyen, V. Nguyen and T. Ho, “A spherical fuzzy analytic hierarchy process (SF-AHP) and combined compromise solution (COCOSO) algorithm in distribution center location selection: A case study in agricultural supply chain,” Axioms, vol. 10, no. 2, pp. 53, 2021. [Google Scholar]

 3.  S. Tadić, M. Krstić, V. Roso and N. Brnjac, “Dry port terminal location selection by applying the hybrid grey MCDM model,” Sustainability, vol. 12, no. 17, pp. 6983, 2020. [Google Scholar]

 4.  A. Budak, İ Kaya, A. Karaşan and M. Erdoğan, “Real-time location systems selection by using a fuzzy MCDM approach: An application in humanitarian relief logistics,” Applied Soft Computing, vol. 92, pp. 106322, 2020. [Google Scholar]

 5.  C. Wang, V. Nguyen, H. Thai and D. Duong, “Multi-criteria decision making (MCDM) approaches for solar power plant location selection in viet Nam,” Energies, vol. 11, no. 6, pp. 1504, 2018. [Google Scholar]

 6.  A. Ulutaş, F. Balo, L. Sua, E. Demir, A. Topal et al., “A new integrated grey MCDM model: Case of warehouse location selection,” Facta Universitatis, Series: Mechanical Engineering, vol. 19, no. 3, pp. 515, 2021. [Google Scholar]

 7.  F. Dweiri, S. Kumar, S. Khan and V. Jain, “Designing an integrated AHP based decision support system for supplier selection in automotive industry,” Expert Systems with Applications, vol. 62, pp. 273–283, 2016. [Google Scholar]

 8.  C. Wang, V. Nguyen, J. Kao, C. Chen and V. Nguyen, “Multi-criteria decision-making methods in fuzzy decision problems: A case study in the frozen shrimp industry,” Symmetry, vol. 13, no. 3, pp. 370, 2021. [Google Scholar]

 9.  M. Rezaeisaray, S. Ebrahimnejad and K. Damghani, “A novel hybrid MCDM approach for outsourcing supplier selection,” Journal of Modelling in Management, vol. 11, no. 2, pp. 536–559, 2016. [Google Scholar]

10. M. Yazdani, P. Chatterjee, E. Zavadskas and S. H. Zolfani, “Integrated QFD-MCDM framework for green supplier selection,” Journal of Cleaner Production, vol. 142, pp. 3728–3740, 2017. [Google Scholar]

11. H. Liu, M. Quan, Z. Li and Z. Wang, “A new integrated MCDM model for sustainable supplier selection under interval-valued intuitionistic uncertain linguistic environment,” Information Sciences, vol. 486, pp. 254–270, 2019. [Google Scholar]

12. T. Prabhuram, M. Rajmohan, Y. Tan and R. Johnson, “Performance evaluation of omni channel distribution network configurations using multi criteria decision making techniques,” Annals of Operations Research, vol. 288, no. 1, pp. 435–456, 2020. [Google Scholar]

13. R. Titiyal, S. Bhattacharya and J. Thakkar, “The distribution strategy selection for an e-tailer using a hybrid DANP VIKOR MCDM model,” Benchmarking: An International Journal, vol. 26, no. 2, pp. 395–433, 2019. [Google Scholar]

14. E. Karsak and M. Dursun, “An integrated fuzzy MCDM approach for supplier evaluation and selection,” Computers & Industrial Engineering, vol. 82, pp. 82–93, 2015. [Google Scholar]

15. R. Mao, J. You, C. Duan and L. Shao, “A heterogeneous MCDM framework for sustainable supplier evaluation and selection based on the IVIF-TODIM method,” Sustainability, vol. 11, no. 18, pp. 5057, 2019. [Google Scholar]

16. C. Wang, H. Tsai, T. Ho, V. Nguyen and Y. Huang, “Multi-criteria decision making (MCDM) model for supplier evaluation and selection for oil production projects in Vietnam,” Processes, vol. 8, no. 2, pp. 134, 2020. [Google Scholar]

17. A. Mohammed, I. Harris and K. Govindan, “A hybrid MCDM-FMOO approach for sustainable supplier selection and order allocation,” International Journal of Production Economics, vol. 217, pp. 171–184, 2019. [Google Scholar]

18. S. Nallusamy, D. Kumar, K. Balakannan and P. Chakraborty, “MCDM tools application for selection of suppliers in manufacturing industries using AHP, fuzzy logic and ANN,” International Journal of Engineering Research in Africa, vol. 19, pp. 130–137, 2015. [Google Scholar]

19. I. Badi and D. Pamucar, “Supplier selection for steel making company by using combined grey-marcos methods,” Decision Making: Applications in Management and Engineering, vol. 3, no. 2, pp. 37–48, 2020. [Google Scholar]

20. H. Chen, S. Chou, Q. Luu and T. Yu, “A fuzzy MCDM approach for green supplier selection from the economic and environmental aspects,” Mathematical Problems in Engineering, vol. 2016, pp. 1–10, 2016. [Google Scholar]

21. M. Quan, Z. Wang, H. Liu and H. Shi, “A hybrid MCDM approach for large group green supplier selection with uncertain linguistic information,” IEEE Access, vol. 6, pp. 50372–50383, 2018. [Google Scholar]

22. J. Liou, M. Chang, H. Lo and M. Hsu, “Application of an MCDM model with data mining techniques for green supplier evaluation and selection,” Applied Soft Computing, vol. 109, pp. 107534, 2021. [Google Scholar]

23. A. Memari, A. Dargi, M. Jokar, R. Ahmad and A. Rahim, “Sustainable supplier selection: A multi-criteria intuitionistic fuzzy TOPSIS method,” Journal of Manufacturing Systems, vol. 50, pp. 9–24, 2019. [Google Scholar]

24. H. Zhao and S. Guo, “Selecting green supplier of thermal power equipment by using a hybrid MCDM method for sustainability,” Sustainability, vol. 6, no. 1, pp. 217–235, 2014. [Google Scholar]

25. A. Mohammed, M. Yazdani, A. Oukil and E. Gonzalez, “A hybrid mcdm approach towards resilient sourcing,” Sustainability, vol. 13, no. 5, pp. 2695, 2021. [Google Scholar]

26. M. Wang, Z. Zhou and C. Ding, “ “Blockchain-based decentralized reputation management system for internet of everything in 6G-enabled cybertwin architecture,” Journal of New Media, vol. 3, no. 4, pp. 137–150, 2021. [Google Scholar]

27. X. Zhang, W. Zhang, W. Sun, H. Wu, A. Song et al., “A real-time cutting model based on finite element and order reduction,” Computer Systems Science and Engineering, vol. 43, no. 1, pp. 1–15, 2022. [Google Scholar]

28. I. Sharaf, “Spherical fuzzy VIKOR with SWAM and SWGM operators for MCDM,” Decision Making with Spherical Fuzzy Sets, vol. 392, pp. 217–240, 2020. [Google Scholar]

29. I. Otay and S. Atik, “Multi-criteria oil station location evaluation using spherical AHP&WASPAS: A real-life case study,” Advances in Intelligent Systems and Computing, vol. 1197, pp. 591–598, 2020. [Google Scholar]

30. S. Gül, “Spherical fuzzy extension of DEMATEL (SF-DEMATEL),” International Journal of Intelligent Systems, vol. 35, no. 9, pp. 1329–1353, 2020. [Google Scholar]

31. F. Gündoğdu and C. Kahraman, “Spherical fuzzy sets and spherical fuzzy TOPSIS method,” Journal of Intelligent & Fuzzy Systems, vol. 36, no. 1, pp. 337–352, 2019. [Google Scholar]

32. R. Yager, “Pythagorean fuzzy subsets,” 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), pp. 57–61, 2013. [Google Scholar]

33. F. Smarandache, A Unifying Field in Logics Neutrosophy: Neutrosophic Probability, set and Logic, American Research Press: Rehoboth, DE, USA, pp. 1–141, 1999. [Google Scholar]

34. F. Gündoğdu and C. Kahraman, “A novel spherical fuzzy analytic hierarchy process and its renewable energy application,” Soft Computing, vol. 24, no. 6, pp. 4607–4621, 2019. [Google Scholar]

35. I. Badi, A. Abdulshahed and A. Shetwan, “A case study of supplier selection for a steelmaking company in Libya by using the combinative distance-based assessment (CODAS) model,” Decision Making: Applications in Management and Engineering, vol. 1, no. 1, pp. 1–12, 2018. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.