| Computers, Materials & Continua DOI:10.32604/cmc.2022.029122 |  |
| Article |
New Decision-Making Technique Based on Hurwicz Criteria for Fuzzy Ranking
1Department of Computer Science and Engineering, VNR Vignana Jyothi Institute of Engineering and Technology, Hyderabad, India
2Department of Mathematics, Dr. APJ Abdul Kalam University Indore (M.P), India
3Department of Information Technology, VNR Vignana Jyothi Institute of Engineering and Technology, Hyderabad, India
4LBEF Campus, Kathmandu, 44600, Nepal
5Department of Management Information Systems, College of Applied Studies and Community Service, Imam Abdulrahman Bin Faisal University, Dammam, Saudi Arabia
6Laboratory of Nano-Smart Materials for Science and Technology (LNSMST), Department of Physics, Faculty of Science, King Khalid University, P.O. Box 9004, Abha 61413, Saudi Arabia
7Research Center for Advanced Materials Science (RCAMS), King Khalid University, P.O. Box 9004, Abha 61413, Saudi Arabia
8Nanoscience Laboratory for Environmental and Biomedical Applications (NLEBA), Semiconductor Lab., Department of Physics, Faculty of Education, Ain Shams University, Roxy, Cairo 11757, Egypt
9Department of Communications and Electronics, Delta Higher Institute of Engineering and Technology, Mansoura, 35111, Egypt
10Faculty of Artificial Intelligence, Delta University for Science and Technology, Mansoura, 35712, Egypt
11Operations Research Department, Faculty of Graduate Studies for Statistical Research, Cairo University, Giza, 12613, Egypt
12Department of Mathematics and Actuarial Science School of Sciences Engineering, The American University in Cairo, Egypt
*Corresponding Author: Ali Wagdy Mohamed. Email: aliwagdy@gmail.com
Received: 25 February 2022; Accepted: 21 April 2022
Abstract: Efficient decision-making remains an open challenge in the research community, and many researchers are working to improve accuracy through the use of various computational techniques. In this case, the fuzzification and defuzzification processes can be very useful. Defuzzification is an effective process to get a single number from the output of a fuzzy set. Considering defuzzification as a center point of this research paper, to analyze and understand the effect of different types of vehicles according to their performance. In this paper, the multi-criteria decision-making (MCDM) process under uncertainty and defuzzification is discussed by using the center of the area (COA) or centroid method. Further, to find the best solution, Hurwicz criteria are used on the defuzzified data. A new decision-making technique is proposed using Hurwicz criteria for triangular and trapezoidal fuzzy numbers. The proposed technique considers all types of decision makers’ perspectives such as optimistic, neutral, and pessimistic which is crucial in solving decision-making problems. A simple case study is used to demonstrate and discuss the Centroid Method and Hurwicz Criteria for measuring risk attitudes among decision-makers. The significance of the proposed defuzzification method is demonstrated by comparing it to previous defuzzification procedures with its application.
Keywords: Defuzzification; decision-making; fuzzy numbers; Hurwicz; multi-criteria decision-making; ranking order
Achieving fruitful decision-making is an important concern when choosing to apply machine learning techniques (or) aiming to impart artificial intelligence into machines that work upon the traditional logic theory. The idea behind this is to enable a machine to think like a human and in turn make humans ease the complexity in the decision-making process. The task of decision-making in everyday life is usually vague or uncertain. The ability to make decisions among humans differs significantly and depends on the knowledge and perception levels of an individual. Moreover, the decision-making process is more complex for blurred, vague, and qualitative data. It is thus a very big challenge under such uncertainty or vagueness to choose the best action from various available actions [1,2]. Recent research contributions insist that uncertainty, risk, and confidence should be taken into account with respect to multi-criteria decision-making (MCDM). The research addressed the uses of linguistic variables, triangular variables, and trapezoidal fuzzy numbers to represent the decision maker’s confidence and risk attitudes so as to achieve a more complete MCDM Solution. With this regard, specifically, this work addresses a travel problem to illustrate the computation process and demonstrate the suitability of the results that are used previously to assess MCDM. Defuzzification is a procedure of conversion to a fuzzy set into a crisp set or values and the useful method was proposed by Norman Fenton and Wei Wang to deal with this kind of decision-making problem under uncertainty [3]. For triangular fuzzy numbers in multi-criteria decision making, Salamai et al. both have analyzed the confidence and risk-taking capacity of a decision-maker [4–6]. So far, various defuzzification methods [7–9] are proposed by different mathematicians. El-kenawy et al. [10] applied three methods which include i) discretization, ii) modified transformation function, and iii) for trapezoidal fuzzy numbers, performing the center of gravity (COG) defuzzification using the slope-based method. One of the most common and useful de-fuzzification techniques is the method of the center of gravity (COG). It is also called the centroid method [11]. If the data is precise and quantitative, the Hurwicz criterion is used for decision-making. It must be noted that the Hurwicz criterion is not suitable for imprecise data. El-kenawy et al. [12] introduced the concept of fuzzy sets to process imprecise linguistic information. Hurwicz Criterion has a defining feature, i.e., it allows the decision-makers to simultaneously consider both the best and the worst possible outcomes. For this, the decision-makers choose a “coefficient of pessimism”, which is usually a decimal number between 0 and 1 and is denoted by alpha (α). The worst possible outcomes are emphasized by this number and the number (1 − α) determines the emphasis to be placed on the best outcomes. So, if the coefficient of pessimism is equal to 0.8 then, 0.2 is the emphasis on the best outcomes [13]. Given the aforementioned challenges, we present the following novel aspects of our study:
• To introduce a new ranking method using the centroid method or COA.
• To use Hurwicz criteria to defuzzify the triangular fuzzy numbers.
• To the extent the research to the trapezoidal fuzzy numbers which considers the risk attitude of the decision-maker.
The centroid method is used for defuzzifying the fuzzy numbers and a Hurwicz criterion is used to the defuzzified data. The Hurwicz criteria are used for triangular numbers and are extended for the trapezoidal fuzzy numbers as well which considers the risk attitude of the decision-maker.
In linguistic multi-criteria decision-making problems, the ranking of fuzzy numbers plays a very significant role. Numerous researchers have used several fuzzy ranking methods to solve decision-making problems using triangular and trapezoidal fuzzy numbers. Ye et al. [14] proposed a direct and simplified approach for computing triangular fuzzy Banzhaf values of cooperative games for a special class of cooperative games with coalitions’ values represented by triangular fuzzy numbers. They have suggested that interval-valued cooperative games are associated with the triangular fuzzy cooperative games and have proved that the Banzhaf values of the associated cooperative games together with the interval-valued cooperative games are non-decreasing functions and monotonic under same size monotonicity-like conditions. Furthermore, they have proved some properties of the triangular fuzzy Banzhaf values and illustrate the validity and applicability of the developed approach. Jing-Jing An et al. develop a new method for solving bi-matrix games with payoffs of intuitionistic fuzzy numbers (IFNs). In this method, a weighted mean-area ranking method based on a non-linear programming approach of intuitionistic fuzzy numbers was proposed [15]. Deng-Feng et al. [16,17] proposed some ranking methods which are based on the concept of value and ambiguity, a ratio of the value index to the ambiguity index, and applied it to solve multi-attribute decision-making problems where the ratings of alternatives are expressed using triangular intuitionistic fuzzy numbers. Savitha et al. [18] proposed some new methods for ranking Trapezoidal Fuzzy numbers based on the extent fuzzy analytic hierarchy processes which are used in developing fuzzy multi-criteria decision-making models. For compiling experts’ judgment arithmetic mean operations of fuzzy numbers have been used. Yadong et al. in [19] developed a long-term forecasting model based on static and dynamic fuzzy information granules for interval-valued time series (ITS). Hassib et al. [20] addresses the green supplier selection problem in and suggest the solution through the MCDM technique based on the novel Hamming distance function. Traditional ranking algorithms, on the other hand, are unsuitable for many real-time problems involving data with inherent ambiguity or impreciseness. Nguyen [21] proposed a method for ranking fuzzy numbers based on the Unified Index that combines the weighted mean known as the centroid value and the weighted area known as the attitude-incorporated left and right area. According to the authors, the unified index has the consistency property for ranking fuzzy numbers and their images, as well as for symmetric fuzzy numbers with an identical altitude, which is a critical property for accurate matching and/or retrieval of information in the field of computer vision and image pattern recognition. Many such popular examples are used for a wide range of fuzzy number comparative studies, and ranking performance is compared between the unified index and some recent representative indices. Wang [22] proposed a method for ranking triangular and trapezoidal fuzzy numbers based on the relative preference relation, in which a fuzzy preference relation with a membership function representing preference degree is used to compare two fuzzy numbers, and a relative preference relation is built on top of the fuzzy preference relation to rank a set of fuzzy numbers. According to Eid et al. [23], the difference function is used from the fuzzy preference relation between alternatives and extreme solutions to obtain weakness and strength matrices, which are then multiplied by the weight matrix to produce weighted weakness and strength indices, which are then converted into positive and negative indices. These two indices are combined to produce a total performance index, and then alternatives are sorted based on their related performance indices.
A fuzzy number is a fuzzy set à defined on the set of real numbers R if its membership functions Ã: R → [0, 1] has the following properties.
(i) If it is a convex fuzzy set.
i.e., μà (λx1 + (1 − λ) x2) ≥ min (μà (x1), μÃ(x2)), ∀x ∈ [0, 1], λ ∈ [0, 1]
(ii) If it is normal i.e., there exists an x ∈R such that if max μÃ(x) = 1.
(iii) If it is continuous piecewise.
A fuzzy number
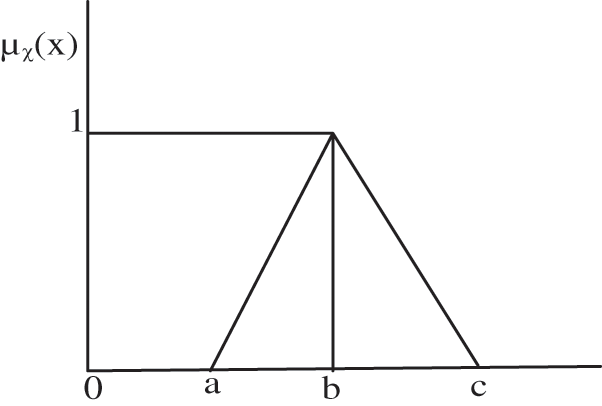
Figure 1: Illustration of triangular fuzzy number
A fuzzy number

Figure 2: Illustration of trapezoidal fuzzy number
Hurwicz’s rule (Criteria) [26] is a procedure that is applied within the decision-making process under uncertainty. This Hurwicz criterion strikes a balance between an optimistic and a pessimistic decision. First, take a value between 0 and 1, for the coefficient of realism “α”. A decision-maker is optimistic about the future when “α” is close to 1, and the decision-maker is pessimistic about the future when “α” is close to 0. The weighted outcome is given in Eq. (3).
3.5 General Fuzzy MCDM Approach
A general fuzzy multi-criteria decision making problem can be expressed as a decision matrix “
This normalization process deals with the criteria having different scales. To particularly obtain a performance matrix
Here M = max (xij3), for benefit criteria, N = max (xij3), for cost criteria.
It should be noted that this normalization process conserves the ranges of normalized triangular fuzzy numbers between 0 and 1 inclusive.
To obtain a weighted performance matrix, a weighted vector is multiplied with the fuzzy numbers in the decision matrix as
This section describes a novel decision-making technique for ranking fuzzy numbers that combine the centroid method and the Hurwicz criteria. In order to aid in the decision-making process, the area of region method is used for ranking fuzzy numbers. The proposed decision-making technique is unique in that it combines the centroid method and the Hurwicz criteria for ranking fuzzy numbers which are shown in Fig. 3.
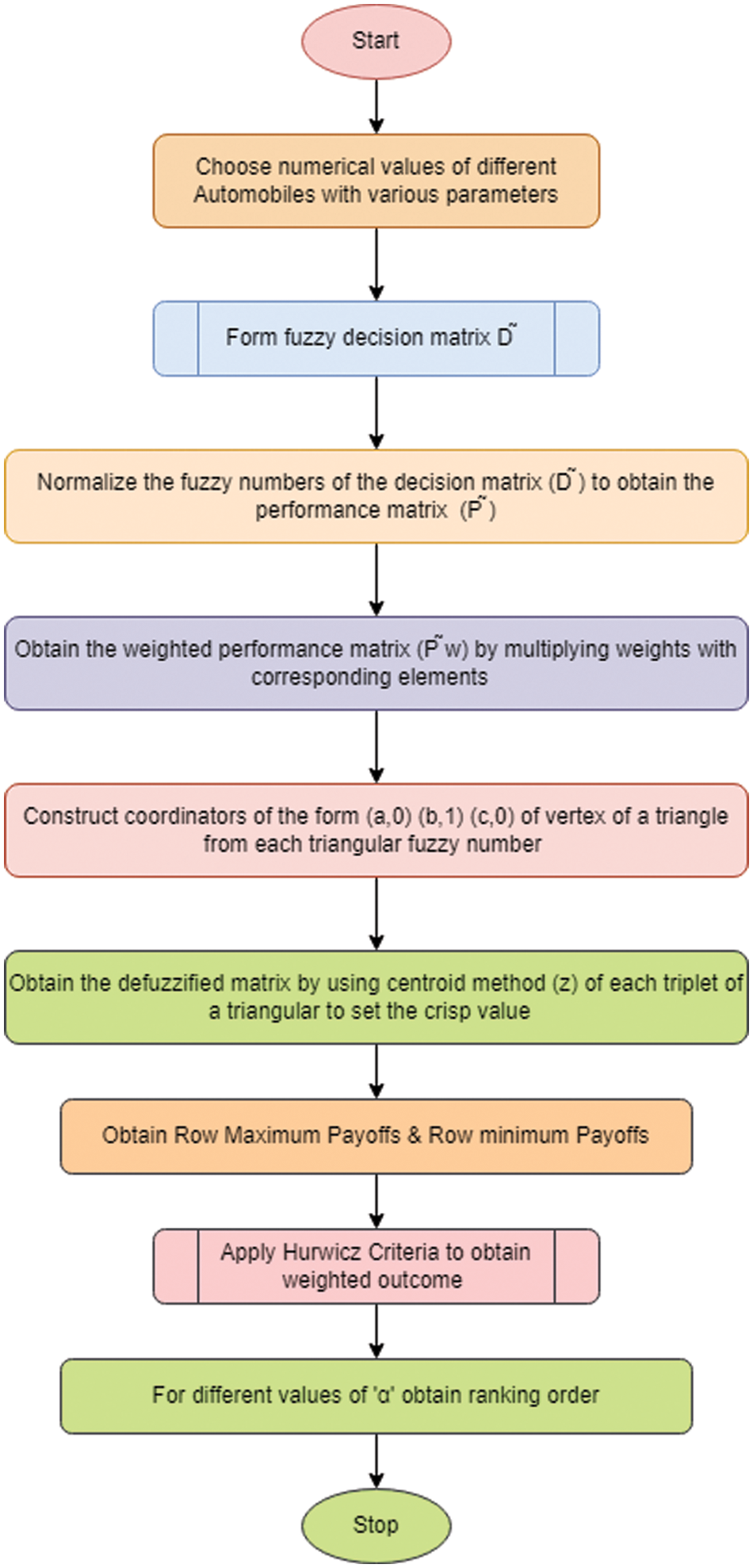
Figure 3: The architecture of the proposed flow diagram
Unlike conventional ranking methods, in this paper, we have extended our research with trapezoidal fuzzy numbers. The process flow diagram is shown in Fig. 3 and step by step process of the proposed technique is mentioned below:
1. Arrange fuzzy numbers of the problem in the form of a fuzzy decision matrix.
2. Obtain the performance matrix by normalizing the element of the decision matrix.
3. Find the weighted performance matrix by multiplying the weight with the corresponding elements of the performance matrix.
4. The centroid method is used after considering each triangular fuzzy number as the vertex of a triangle in the form (a, 0), (b, 1), (c, 0). (Same procedure can be done for the trapezoidal fuzzy numbers as well).
5. To find the weighted outcome for each row applies Hurwicz criteria.
6. The maximum value of the entire weighted outcome will be the best action.
4.1 Case Studies and Analysis of Results
In this section, the proposed method presented in the previous section is applied to a travel problem specification by considering different types of automobiles which include two, three, and four-wheeler vehicles. The decision matrix and its corresponding weight for different types of automobiles are shown in Tab. 1. In this example, the price criterion is measured in dollars and the journey time is measured in minutes. The comfort and satisfaction criterion is the value criterion measured on a scale of one to ten. Suppose that, the ratings are expressed in the decision matrix as triangular fuzzy numbers (for example, a two-wheeler vehicle journey such as a bike journey to the college costs 20 dollars, however, it can be as high as 25 dollars and as low as 15 dollars) [6]. This problem is illustrated with two different assumptions one is triangular fuzzy numbers and the second one is the trapezoidal fuzzy numbers. The numerical values in the fuzzy decision matrix are chosen arbitrary depending upon the type of the automobile as well as the distance e.g., in the case of two-wheeler the expenditure for instance the fuel cost is less (varies from 6 to 12 dollars) as compared to four-wheeler (varies from 15 to 25 dollars), but the four-wheeler is more comfort (its value varies from 7 to 10) as compared to the two-wheeler (its value varies from 2 to 4). The journey time for a two-wheeler (varies from 40 to 110 min) is more as compared to the four-wheeler (varies from 35 to 100 min) so on and so forth [26].

Step 1. Arrange fuzzy numbers of the problem in the form of a fuzzy decision matrix
Tab. 1 shows ratings in the decision matrix as triangular fuzzy numbers.
Step 2. Obtain the performance matrix by normalizing the element of the decision matrix
Tab. 2 shows a normalized fuzzy decision matrix which is obtained by the normalization process.

Step 3. Find the weighted performance matrix by multiplying the weight with the corresponding elements of the performance matrix.
Given below is the weighted performance matrix “
Here it should be noted that each triangular fuzzy number can be considered as the vertex of a triangle in the form (a, 0), (b, 1), (c, 0). Given below is the triangular fuzzy decision matrix “A”.
Step 4. The centroid method is used after considering each triangular fuzzy number as the vertex of a triangle in the form (a, 0), (b, 1), (c, 0). (Same procedure can be done for the trapezoidal fuzzy numbers as well).
The defuzzified matrix in Tab. 3 can be obtained by using the centroid method where each triplet represents a triangle, where the Centroid method is given as

For the first element of matrix A, the crisp is: z
Similarly, all the triplets can be obtained which are mentioned in Tab. 3.
The matrix in Tab. 4 represents the maximum and minimum payoffs.

Step 5. To find the weighted outcome for each row apply Hurwicz criteria
We now use Hurwicz criteria to obtain the weighted outcome which is represented in Tab. 5.

Where, Weighted outcome = (1 − α) (minimum payoff) + α (maximum payoff).
Tab. 6 below shows the ranking order obtained for different values of α.

The ranking order from Tab. 6 shows that with a fair (or) extreme optimistic approach the decision-maker will choose the four-wheeler vehicle as to the first alternative and the two-wheeler vehicle as to the second alternative.
4.2 For Trapezoidal Fuzzy Numbers
Tab. 7 represents the ratings in the decision matrix as trapezoidal fuzzy numbers. Three types of vehicles are considered. They are i) Two-wheeler, ii) Three-wheeler and iii) Four-wheeler. The parameters or attributes considered are expenditure, journey time, satisfaction, and comfort.

Tab. 8 represents the normalized fuzzy decision matrix.

Given below is the weighted performance matrix “B” which is obtained by multiplying the weight with its corresponding performance matrix.
Here, it should be noted that each triangular fuzzy number can be considered as the vertex of a triangle in the form (a, 0), (b, 1), (c, 1), (d, 0). Given below is the trapezoidal fuzzy decision matrix “B”.
The defuzzified matrix in Tab. 9 can be obtained by using the centroid method where each of the four tuples represents vertices of a quadrilateral.

The matrix in Tab. 10 represents the maximum and minimum payoffs.

We now use Hurwicz criteria to obtain the weighted outcome which is represented in Tab. 11. The expression for the weighted outcome is considered as Weighted outcome = (1 − α) (minimum payoff) + α (maximum payoff).

Step 6 Maximum value of the entire weighted outcome will be the best action. Finally, Tab. 12 below shows the ranking order obtained for different values of α.

The ranking order from Tab. 12 shows that with a fair (or) extreme optimistic approach the decision-maker may choose the four-wheeler vehicle as to the first alternative and the two-wheeler vehicle as to the second alternative. It should be noted that the ranking order for triangular fuzzy numbers as well as for trapezoidal fuzzy numbers is the same for this example.
4.3 Comparison with State-of-the-art Methods
This section compares our ranking method to those proposed by Lee-Kwang et al. [26], Baldwin et al. [27], Ibrahim et al. [28], Ghoneim et al. [29], Eid et al. [30], and Peneva et al. [31]. It’s worth noting that the pessimistic, neutral, and optimistic targets correspond to Lee-Kwang et al. method [26]. The fuzzy sets considered for comparison are shown in Fig. 4, and the comparative results are shown in Tab. 13.
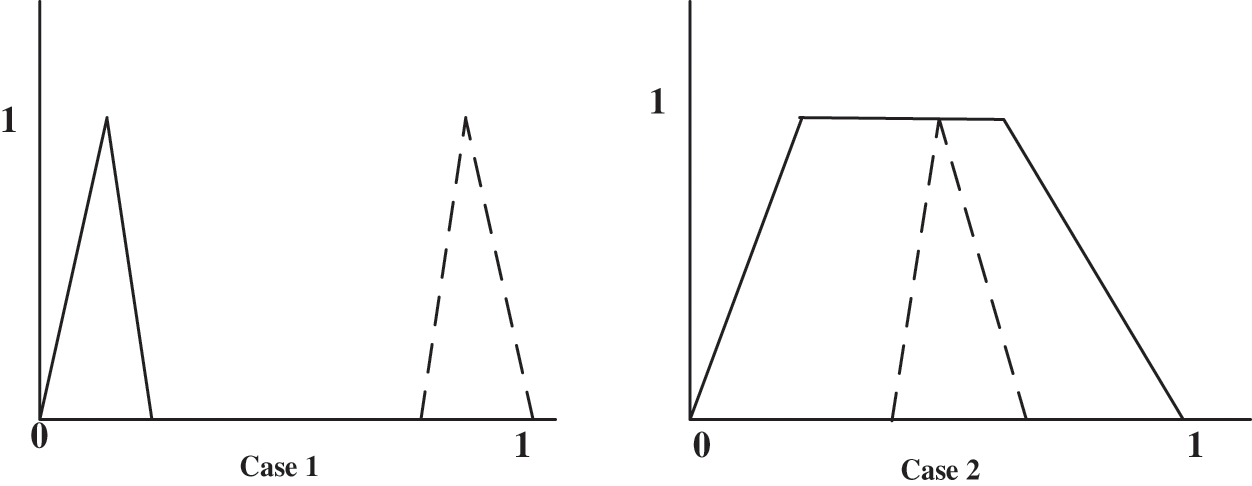
Figure 4: Fuzzy sets considered for comparison

From the outcomes, it should be underscored here that though all considered ranking methods permit an adjustment of the assessment methodology, it is challenging to see plainly how the difference in parameters in the last five strategies reflects the decision-makers’ attitude of evaluation. In Lee-Kwang et al. [26] and our techniques, fuzzy targets have an unmistakable semantics related to a well-deciphered assessment system, and henceforth, the adjustment of target reflects obviously and straightforwardly the comparing change in the demeanor of the decision-maker.
In this paper, to support the decision-making process, a new hybrid approach is used for ranking and defuzzify the fuzzy numbers into crisp numbers. The proposed method takes into consideration all types of decision makers’ perspectives which is crucial in solving decision-making problems. Hurwicz criteria are used under different risk attitudes of the decision-maker to find the best action. The defuzzification process is done by using the center of gravity (COG) or centroid method which is one of the best methods among several defuzzification methods that converts the triangular fuzzy quantity as well as the trapezoidal fuzzy quantity into a crisp quantity. Through a case study, it is shown that the proposed method provides strong discrimination ability which supports the decision-making process.
Acknowledgement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the research group project under grant number (KKU/RCAMS/G015-21). Also, the authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education, in Saudi Arabia, for funding this research work through project no.IFP-KKU-2020/10.
Funding Statement: The Research Center for Advanced Materials Science (RCAMS) at King Khalid University, Saudi Arabia, for funding this work under the Grant Number RCAMS/KKU/019-20.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. R. Bellman and L. Zadeh, “Decision making in a fuzzy environment,” Management Science, vol. 17, pp. 141–164, 1970. [Google Scholar]
2. J. Puerto, A. Marmol, L. Monroy and F. Fernandez, “Decision criteria with partial information,” International Transactions in Operational Research, vol. 7, pp. 51–65, 2000. [Google Scholar]
3. W. Wang and N. Fenton, “Risk and confidence analysis for fuzzy multi criteria decision making,” Knowledge Based Systems, vol. 19, pp. 430–437, 2006. [Google Scholar]
4. A. Salamai, E. -S. M. El-kenawy, and A. Ibrahim, “Dynamic voting classifier for risk identification in supply chain 4.0,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3749–3766, 2021. [Google Scholar]
5. A. Abdelhamid and S. Alotaibi, “Robust prediction of the bandwidth of metamaterial antenna using deep learning,” Computers, Materials & Continua, vol. 72, no. 2, pp. 2305–2321, 2022. [Google Scholar]
6. E. -S. M. El-Kenawy, S. Mirjalili, S. S. M. Ghoneim, M. M. Eid, M. El-Said et al., “Advanced ensemble model for solar radiation forecasting using sine cosine algorithm and newton’s laws,” IEEE Access, vol. 9, pp. 115750–115765, 2021. [Google Scholar]
7. A. Kandel and M. Friedman, “Defuzzification using most typical values,” IEEE Transactions on Systems, Managment, and Cybernetics, vol. 28, no. 6, pp. 901–906, 1998. [Google Scholar]
8. A. Reham, E. -S. M. El-kenawy and M. Saber, “A proposed routing protocol for mobile ad hoc networks,” International Journal of Computer Applications, vol. 178, no. 1, pp. 26–30, 2019. [Google Scholar]
9. E. Broekhoven and B. Baets, “Fast and accurate center of gravity defuzzification of fuzzy system outputs defined on trapezoidal fuzzy partitions,” Fuzzy Sets and Systems, vol. 157, pp. 904–918, 2006. [Google Scholar]
10. E. -S. M. El-kenawy, H. F. Abutarboush, A. W. Mohamed and A. Ibrahim, “Advance artificial intelligence technique for designing double T-shaped monopole antenna,” Computers, Materials & Continua, vol. 69, no. 3, pp. 2983–2995, 2021. [Google Scholar]
11. A. Ibrahim, S. Mirjalili, M. El-Said, S. S. M. Ghoneim, M. Al-Harthi et al., “Wind speed ensemble forecasting based on deep learning using adaptive dynamic optimization algorithm,” IEEE Access, vol. 9, pp. 125787–125804, 2021. [Google Scholar]
12. E. -S. M. El-kenawy, A. Ibrahim, N. Bailek, K. Bouchouicha, M. A. Hassan et al., “Sunshine duration measurements and predictions in saharan Algeria region: An improved ensemble learning approach,” Theoretical and Applied Climatology, vol. 2021, pp. 1–17, 2021. [Google Scholar]
13. H. Hassan, A. I. El-Desouky, A. Ibrahim, E. -S. M. El-Kenawy and R. Arnous, “Enhanced QoS-based model for trust assessment in cloud computing environment,” IEEE Access, vol. 8, no. 1, pp. 43752–43763, 2020. [Google Scholar]
14. Y. -F. Ye and D. -F. Li, “A direct approach to compute triangular fuzzy banzhaf values of cooperative games with coalitions’ values represented by triangular fuzzy numbers,” IEEE Transactions on Fuzzy Systems, vol. 29, no. 6, pp. 1567–1575, 2021. [Google Scholar]
15. A. Jing-Jing, L. Deng-Feng and N. Jiang-Xia, “A mean-area ranking based non-linear programming approach to solve intuitionistic fuzzy bi-matrix games,” Journal of Intelligent & Fuzzy Systems, vol. 33, no. 1, pp. 563–573, 2017. [Google Scholar]
16. L. Deng-Feng, N. Jiang-Xia and M. Zhang, “A ranking method of triangular intuitionistic fuzzy numbers and application to decision making,” International Journal of Computational Intelligence Systems, vol. 3, no. 5, pp. 522–530, 2010. [Google Scholar]
17. L. Deng-Feng, “A ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problems,” Computers and Mathematics with Applications, vol. 60, no. 6, pp. 1557–1570, 2010. [Google Scholar]
18. M. Savitha and M. George, “New methods for ranking of trapezoidal fuzzy numbers,” Advances in Fuzzy Mathematics, vol. 12, no. 5, pp. 1159–1170, 2017. [Google Scholar]
19. H. Yadong, J. Shurong, Y. Fusheng, Z. Wenyi, W. Xiao et al., “Linear dynamic fuzzy granule based long-term forecasting model of interval-valued time series,” Information Sciences, vol. 586, pp. 563–595, 2022. [Google Scholar]
20. M. Hassib, I. El-Desouky, M. Labib and E. -S. M. El-kenawy, “WOA + BRNN: An imbalanced big data classification framework using whale optimization and deep neural network,” Soft Computing, vol. 24, no. 1, pp. 5573–5592, 2020. [Google Scholar]
21. T. Nguyen, “Methods in ranking fuzzy numbers: A unified index and comparative reviews,” Complexity, vol. 2017, pp. 1–13, 2017. [Google Scholar]
22. Y. Wang, “Ranking triangle and trapezoidal fuzzy numbers based on the relative preference relation,” Applied Mathematical Modelling, vol. 39, no. 2, pp. 586–599, 2015. [Google Scholar]
23. M. Eid, E. -S. M. El-kenawy and A. Ibrahim, “A new hybrid video encryption technique based on chaos cryptography,” Journal of Computer Science and Information Systems, vol. 2, no. 2, pp. 1–8, 2021. [Google Scholar]
24. D. Dubois and H. Prade, “Operations on fuzzy numbers,” International Journal of Systems Science, vol. 9, no. 1, pp. 613–626, 1978. [Google Scholar]
25. E. -S. M. El-kenawy, M. Eid and A. Hamdy, “A new model for measuring customer utility trust in online auctions,” International Journal of Computer Applications, vol. 176, no. 1, pp. 36–39, 2020. [Google Scholar]
26. H. Lee-Kwang and J. -H. Lee, “A method for ranking fuzzy numbers and its application to decision-making,” IEEE Transactions on Fuzzy Systems, vol. 7, no. 6, pp. 677–685, 1999. [Google Scholar]
27. J. Baldwin and N. Guild, “Comparison of fuzzy sets on the same decision space,” Fuzzy Sets and Systems, vol. 2, no. 1, pp. 213–231, 1979. [Google Scholar]
28. A. Ibrahim, H. A. Ali, M. M. Eid and E. -S. M. El-Kenawy, “Chaotic harris hawks optimization for unconstrained function optimization,” in Int. Computer Engineering Conf. (ICENCO), Cairo, Egypt, pp. 153–158, 2020. [Google Scholar]
29. S. S. M. Ghoneim, T. A. Farrag, A. A. Rashed, E. -S. M. El-Kenawy and A. Ibrahim, “Adaptive dynamic meta-heuristics for feature selection and classification in diagnostic accuracy of transformer faults,” IEEE Access, vol. 9, pp. 78324–78340, 2021. [Google Scholar]
30. M. M. Eid, E. -S. M. El-Kenawy and A. Ibrahim, “A binary sine cosine-modified whale optimization algorithm for feature selection,” in 4th National Computing Colleges Conf. (NCCC 2021), Taif, Saudi Arabia, pp. 1–6, 2021. [Google Scholar]
31. V. Peneva and I. Popchev, “Comparison of clusters from fuzzy numbers,” Fuzzy Sets and Systems, vol. 97, pp. 75–81, 1998. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |