| Computers, Materials & Continua DOI:10.32604/cmc.2022.029437 |  |
| Article |
Swarming Computational Techniques for the Influenza Disease System
1Department of Mathematics Statistics and Computer, Faculty of Science, Ubon Ratchathani University, Ubon Ratchathani, 34190, Thailand
2Department of Mathematics and Statistics, Hazara University, Mansehra, 21120, Pakistan
3Universidad Nacional Autónoma de Chota, Cajamarca, 06121, Perú
4Future Technology Research Center, National Yunlin University of Science and Technology, 123 University Road, Section 3, Douliou, Yunlin, 64002, Taiwan
5Universidad Nacional de Frontera, Sullana, Perú
6Department of Mathematics, Faculty of Science, Khon Kaen University, Khon Kaen, 40002, Thailand
*Corresponding Author: Wajaree Weera. Email: wajawe@kku.ac.th
Received: 04 March 2022; Accepted: 25 May 2022
Abstract: The current study relates to designing a swarming computational paradigm to solve the influenza disease system (IDS). The nonlinear system’s mathematical form depends upon four classes: susceptible individuals, infected people, recovered individuals and cross-immune people. The solutions of the IDS are provided by using the artificial neural networks (ANNs) together with the swarming computational paradigm-based particle swarm optimization (PSO) and interior-point scheme (IPA) that are the global and local search approaches. The ANNs-PSO-IPA has never been applied to solve the IDS. Instead a merit function in the sense of mean square error is constructed using the differential form of each class of the IDS and then optimized by the PSOIPA. The correctness and accuracy of the scheme are observed to perform the comparative analysis of the obtained IDS results with the Adams solutions (reference solutions). An absolute error in suitable measures shows the precision of the proposed ANNs procedures and the optimization efficiency of the PSOIPA. Furthermore, the reliability and competence of the proposed computing method are enhanced through the statistical performances.
Keywords: Disease; influenza model; reference results; particle swarm optimization; artificial neural networks; interior-point scheme; statistical investigations
The world faces many severe viruses; one of the dangerous diseases is influenza, which preys on the bronchi, upper parts of the respiratory systems, throat, and nose. Influenza sometimes affects the lungs of humans badly. However, this disease is not as dangerous as that can lead the death. The recovery process from this disease is high, and most individuals get healthier in a few days. This disease is dangerous for older individuals or those who have serious infections, like cancer, heart, diabetes, kidney problems, and lung issues. The epidemic influenza rate always lies around 5% to 15% per annum of that population that is affected by the breathing system. The epidemic rate is reported between 3 to 5 million yearly, and the number of casualties has been reported to be 250,000 to 500,000 [1]. Many mathematical epidemiological differential systems contain ordinary differential equations that indicate the assumptions of the parameters. These systems refer to the transmitting, infected, susceptible, and recovered variables.
Various schemes have been used to solve the mathematical form of the influenza disease system (IDS). Astuti et al. [2] used a step-by-step transformation method for the resistance of the IDS. Alzahrani et al. [3] provided a scheme to find a fractional-order solution to the pandemic IDS. Erdem et al. [4] provided the mathematical soundings of the SIQR influenza system based on the quarantine effects. Sabir et al. [5] presented Morlet wavelet neural network for the nonlinear IDS. Sun et al. [6] indicated the optimization for assigning the infected individuals during the outbreak of the IDS. González-Parra et al. [7] proposed a fractional kind of epidemiological system for simulating the outbreaks of this disease. Ghanbari et al. [8] presented an analysis of the two systems of the avian influenza outbreak to relate the derivatives of the fractal-fractional using the effects of memorabilia and power through Mittag-Leffler. In another study, Sabir et al. [9] provided the soft computing procedures for the solutions of the IDS. Tchuenche et al. [10] signified the coverage of media effects based on the influenza disease. Schulze-Horsel et al. [11] studied the infection and apoptosis of the virus-induced based on the influenza vaccine production. Patel et al. [12] applied the procedures of the genetic algorithms to propose the optimal vaccination strategies for the IDS. Hovav et al. [13] provided a system flow to accomplish influenza’s distribution and inventory of vaccines. Kanyiri et al. [14] signified the optimal control based on influenza and pulmonic congestion.
The influenza disease system (IDS) is dependent upon four classes, susceptible individuals (S(y)), infected people (I(y)), recovered individuals (R(y)), and cross-immune people (C(y)). The IDS is mathematically given as [15]:
where β is the spread rate from susceptible to infected,
The purpose of this work is to calculate the numerical performances of the IDS by using the artificial neural networks (ANNs) together with the computational paradigm-based particle swarm optimization (PSO) and interior-point scheme (IPA) that are the global and local search approaches. The stochastic computational approaches have been provided to solve a variety of submissions, like coronavirus models [17,18], the fractional form of the singular systems [19,20], singular functional systems [21,22], higher kinds of nonlinear systems [23,24], Lotka Volterra system [25], dengue fever formulation of the model [26] and differential form of the multi-singular system [27,28]. Based on these applications, the authors are interested in finding the solutions to the IDS based on the computational paradigm of ANNs using the hybridization of PSOIPA. Few novel paradigms of the novel scheme are presented as:
• The proposed form of the ANNs using the hybrid computing-based PSOIPA is provided to solve the IDS.
• Consistent, reliable, and stable outcomes from the IDS authenticate the performance of the ANNs using the hybrid computing-based PSO-IPA.
• The absolute error (AE) values are performed in suitable measures that indicate the consistency of the ANNs using the hybrid-computing based PSO-IPA.
• The numerical performance of the ANNs using the hybrid computing based PSO-IPA is recognized through the statistical observations for the IDS.
• The designed ANNs procedure with the hybrid computing-based PSO-IPA scheme is effortlessly executed to solve the IDS with inclusive and easy to understanding.
The other parts of the paper are organized as follows: Section 2 shows the method used to solve the IDS. Section 3 presents the statistical procedures. Section 4 shows the results and discussions. Finally, the last Section provides the concluding remarks.
In this section, the proposed methodology based on the artificial neural network procedures is provided using the optimization of the PSO-IPA to solve the influenza disease system (IDS). Furthermore, a merit function using the differential IDS is also provided, along with the necessary setting for PSO-IPA hybridization.
This section shows the IDS that has susceptible individuals (S(y)), infected people (I(y)), recovered individuals (R(y)), and cross-immune people (C(y)). The proposed outcomes of these categories are shown as follows:
W is an unidentified weight vector, provided as:
The efficient form of the log-sigmoid function [29] is mathematically presented as
The merit function is written as:
where
The present section shows the ANNs procedures using the hybrid computing-based PSO-IPA to solve the IDS. The complete detail of these procedures is given.
The Neuro swarming computational paradigm PSO is an optimization algorithm, applied as a global search scheme. PSO is functional to regulate the specific population to solve the numerous stiff systems based on optimal training. PSO is used to alter the of global genetic algorithm process introduced by Eberhart et al. in the previous century [30]. Executing the process of PSO is easy and straightforward due to the short requirements of the memory [31]. Few recent submissions of PSO are the parameter estimation [32], wind turbine through pitch control model [33], benchmark optimization [34], reactive power dispatch models [35], electric circuits based nonlinear systems [36], the adaptive tune of PID controller [37] and approximation of undrained based shear soil strength [38].
In the process of search space investigations, a single candidate solution of the optimization procedure is known as a particle. During the optimization process of PSO, an initial swarm spread in the greater ranges. To enhance the PSO, the scheme provides optimal outcomes based on the process of iteration
where Vi is the velocity, Xi is the position, and the inertia vector is
The convergence of the PSO is performed rapidly using the hybridization of the local search method. Therefore, an efficient and quick local search IPA is applied to solve the IDS. The global best PSO performances are applied as an initial input using the optimization of IPA. The local search IPA has been implemented to solve diverse applications. Few recent submissions of the IPA are control of active-noise model [39], aircraft parts riveting simulation [40], assorted complementary monotone systems [41], nonlinear identification models [42] and economic load dispatch framework [43], singular third kind of systems [44], nervous stomach nonlinear system [45] and singular natured of pantograph differential models [46]. The hybridization of PSO-IPA is applied in this study to solve the IDS. The detail of the procedure is provided in Tab. 1, and the Proposed ANNs procedure using the optimization performances of PSOIPA for the IDS is drawn in Fig. 1.

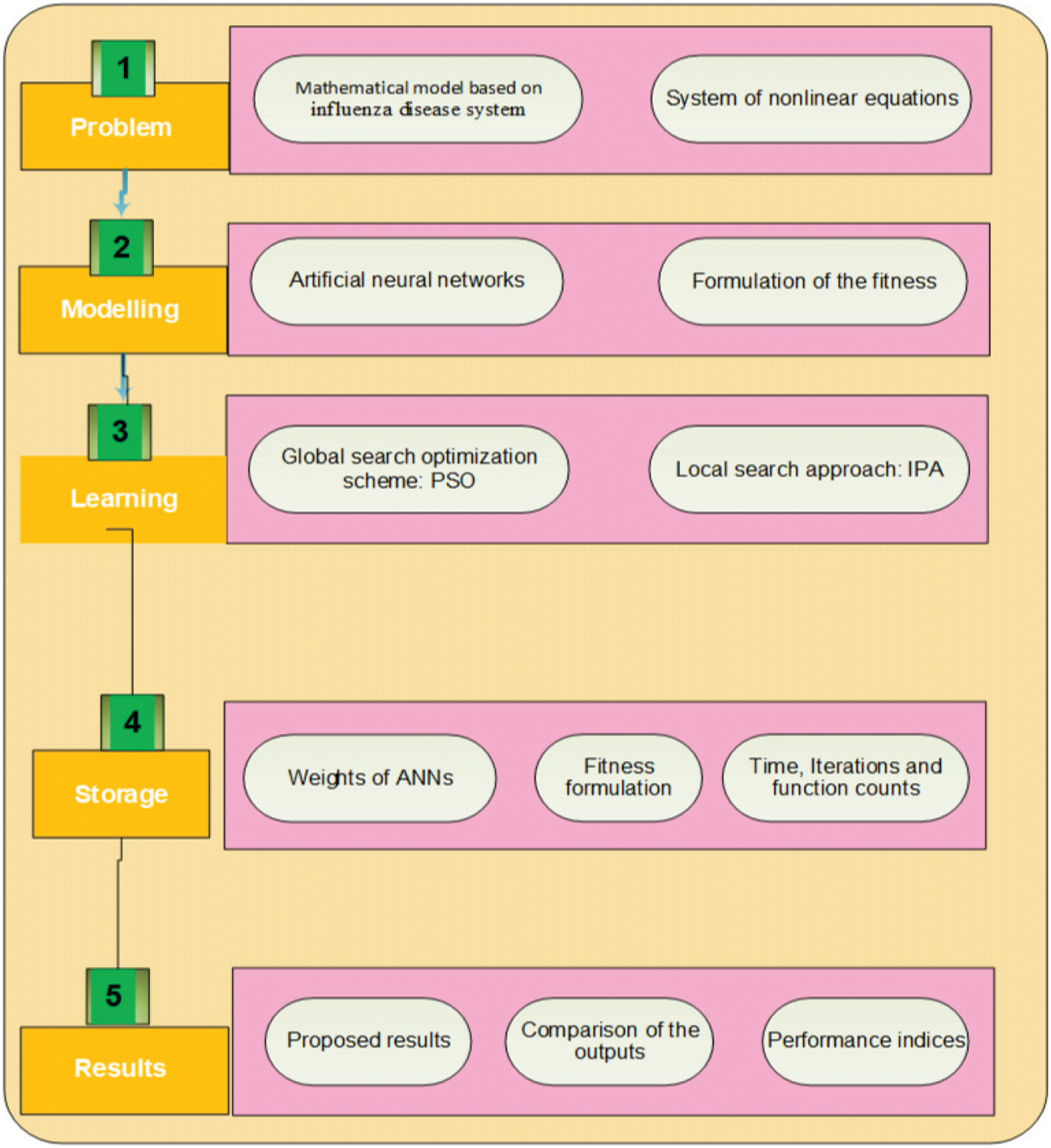
Figure 1: Proposed ANNs procedures using the optimization performances of PSOIPA for the IDS
The statistical indices based on the semi-interquartile (SIR), variance account for (VAF), mean square error (MSE), Theil’s inequality coefficient (TIC), and their Global measures are described to solve the influenza disease system (IDS). The mathematical form of these operators is provided as:
In this section, the simulations are provided to solve the influenza disease system (IDS) using the ANN procedures and the optimize of the PSO-IPA. Finally, the mathematical form of the IDS by using the appropriate values is given as:
A merit function for the above IDS is provided as:
The optimization procedures based on the PSO-IPA to solve the IDS are verified for 20 runs. The proposed outcomes of the IDS are stated to find the best weights using the Eqs. (18)–(21), and the graphical depictions of these weights are illustrated in Fig. 1.
The proposed numerical outputs are achieved in the Eqs. (18)–(21) using 0.05 step size in the interval [0, 1] to present the numerical outcomes of IDS. These numerical values are graphically presented based on the best weights in Figs. 2a–2d. The illustrations of the obtained output with the reference performances are given in Figs. 2e–2h. The solutions of the IDS using the ANN procedures and the optimization of the PSO-IPA and comparison are performed with the reference results. Fig. 3 illustrates the performances of the AE to check the correctness of the procedures to solve the IDS. One can find that the best AE for the respective classes of the IDS was found on 10−07–10−08, 10−07–10−10, 10−07–10−08, and 10−07–10−09. These classes’ mean performances were10−05–10−06, 10−06–10−08, 10−06–10−07 and 10−06–10−08. Fig. 4 indicates the EVAF, MSE, and TIC measures for the IDS, which were found around 10−11–10−12, 10−09–10−10, 10−10–10−11 and 10−11–10−12 for the respective categories of the IDS, 10−14–10−15 for each category of the IDS and 10−11–10−12 for each category of the IDS. These best, most precise, and accurate performances enhance the competence of the ANN procedures and optimize the PSO-IPA for solving the IDS.
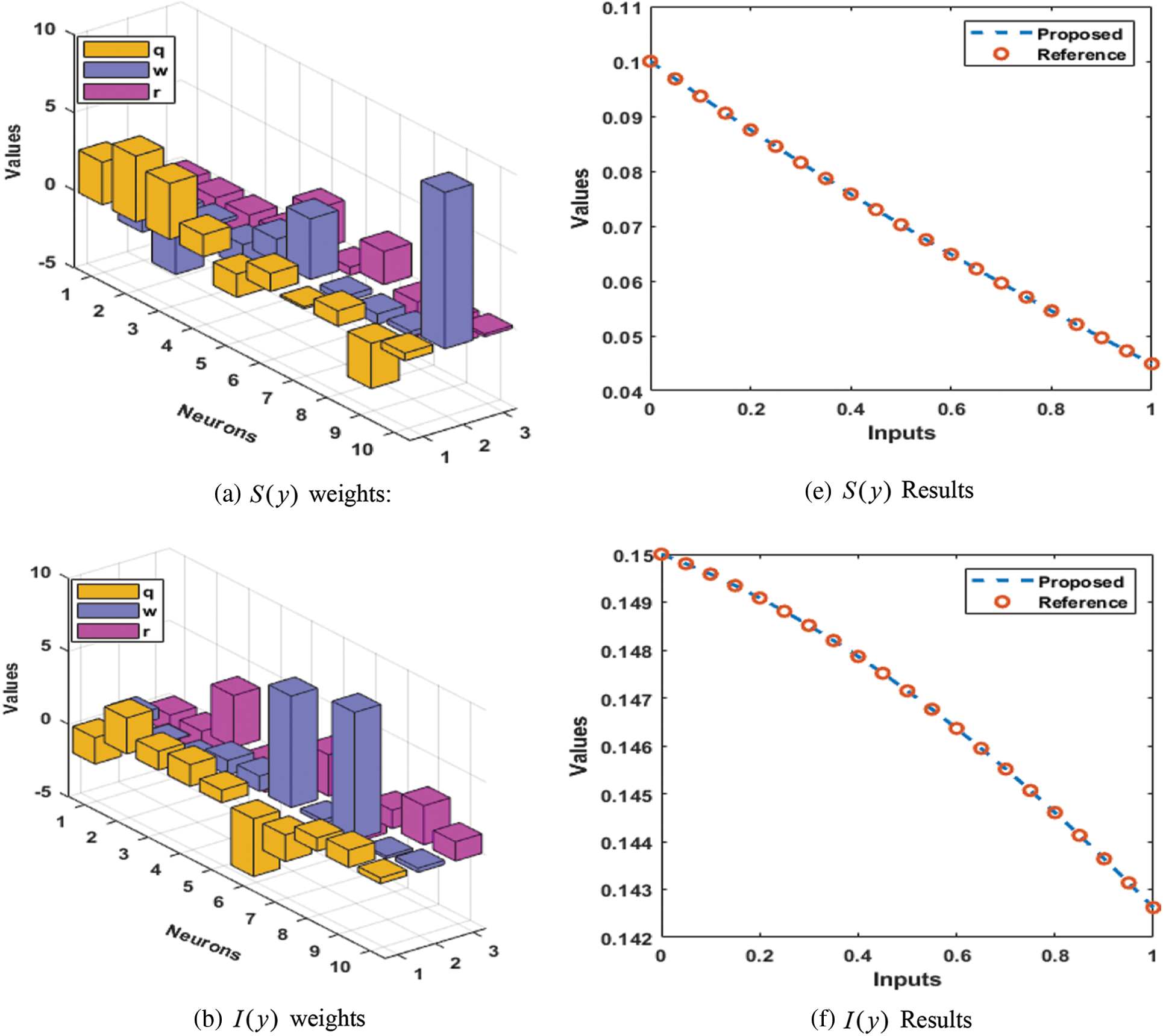
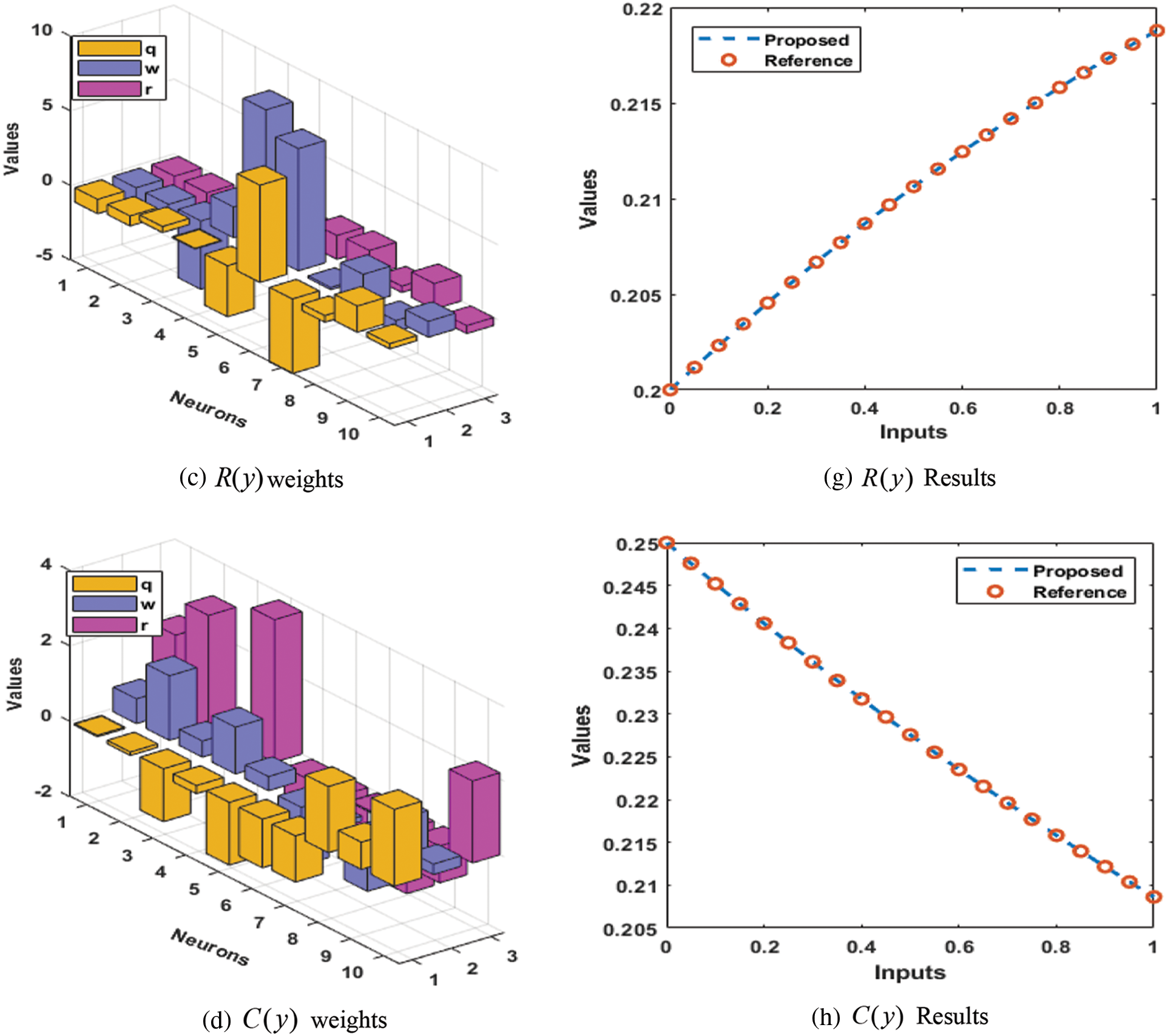
Figure 2: Best weights and comparison for the mathematical model based on IDS
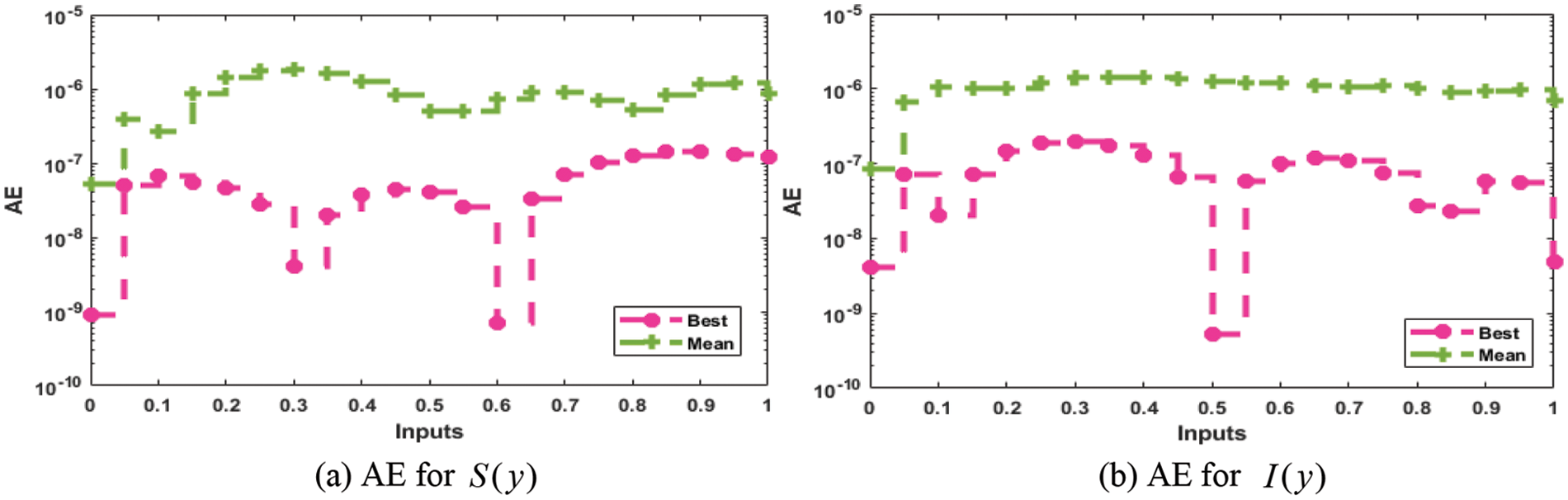
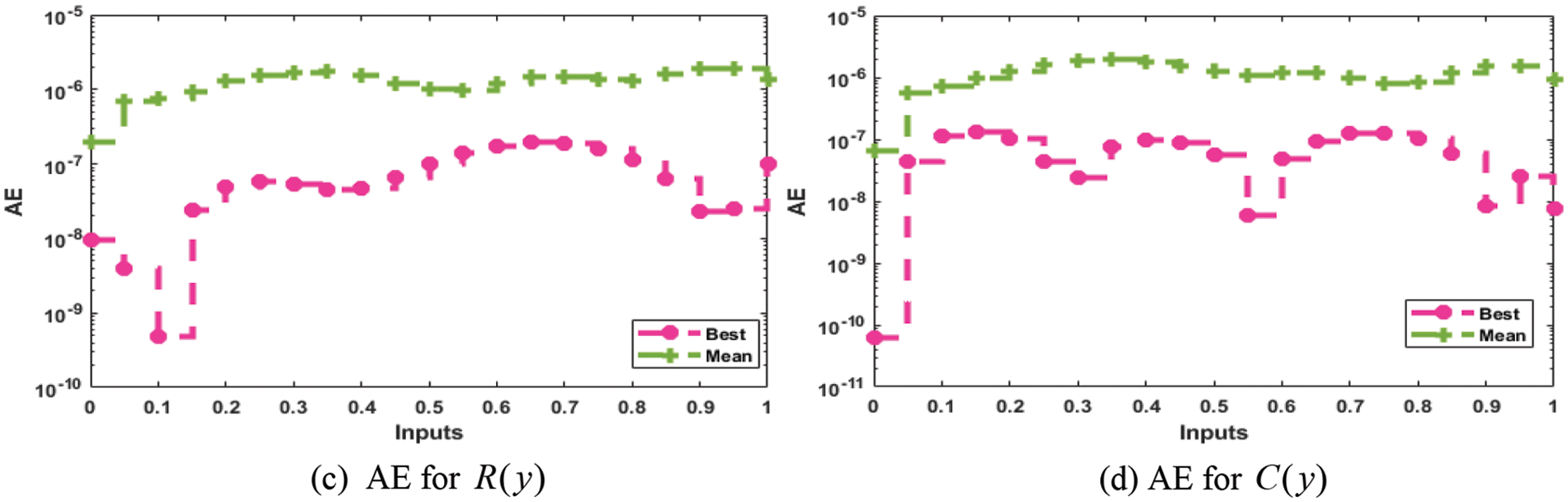
Figure 3: AE for the mathematical model based on IDS
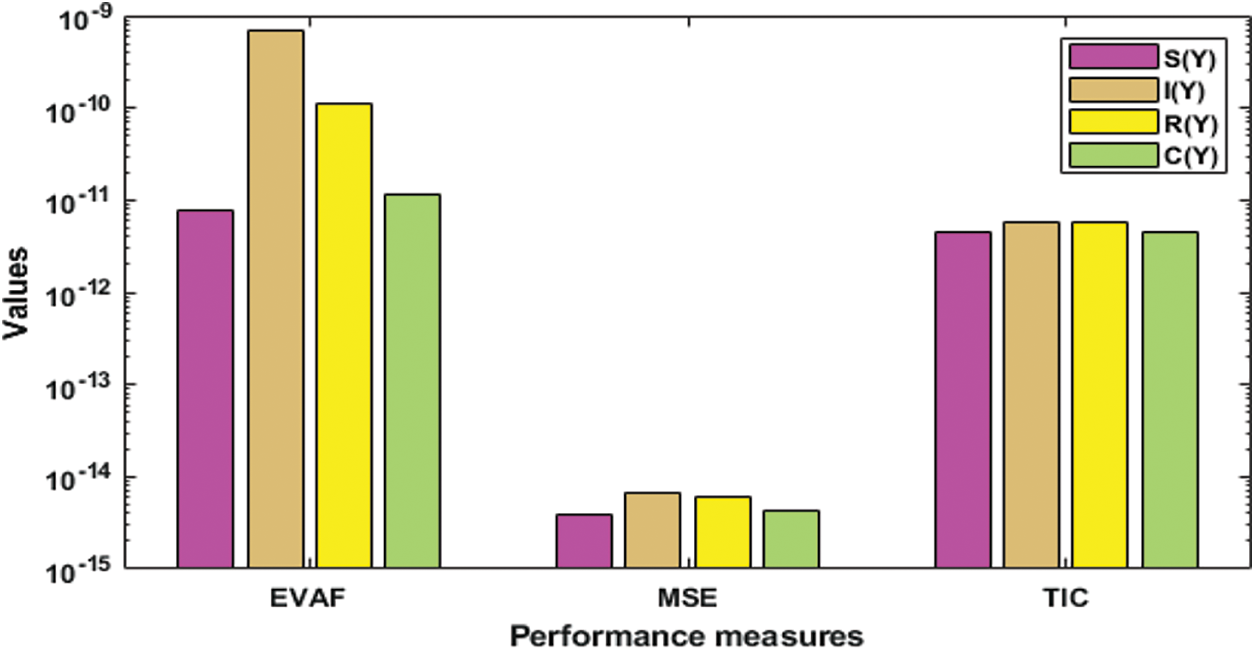
Figure 4: EVAF, MSE, and TIC measure performances for the mathematical IDS model
The MSE performances for these classes found around 10−11–10−15, 10−12–10−13, 10−11–10−14, and 10−11–10−13. Moreover, TIC performances for these classes calculate as 10−10–10−12, 10−10–10−11, 10−09–10−11 and 10−09–10−12. These ideal performances indicate the correctness of the ANNs procedures and the optimization of the PSO-IPA to solve the IDS.
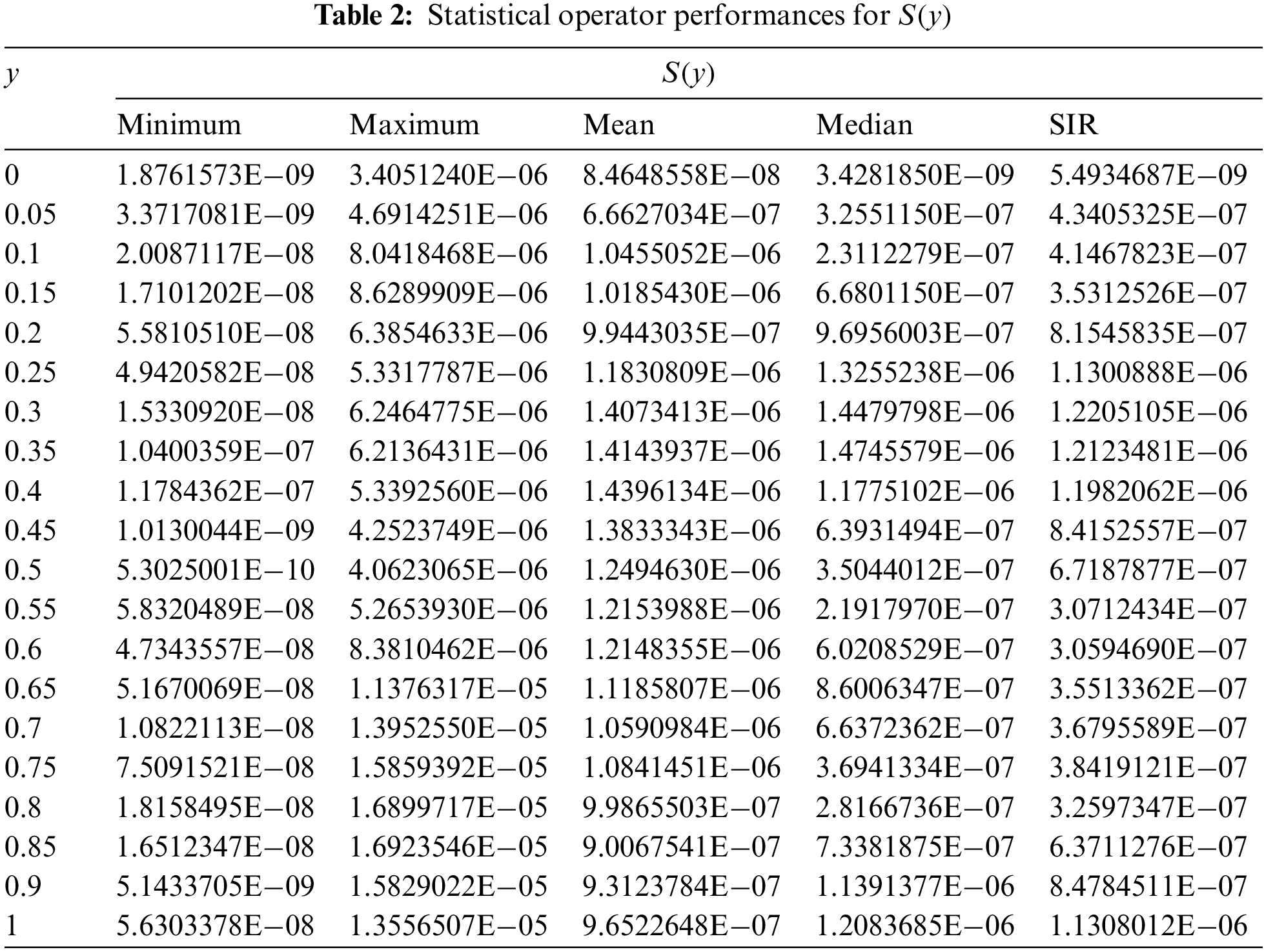
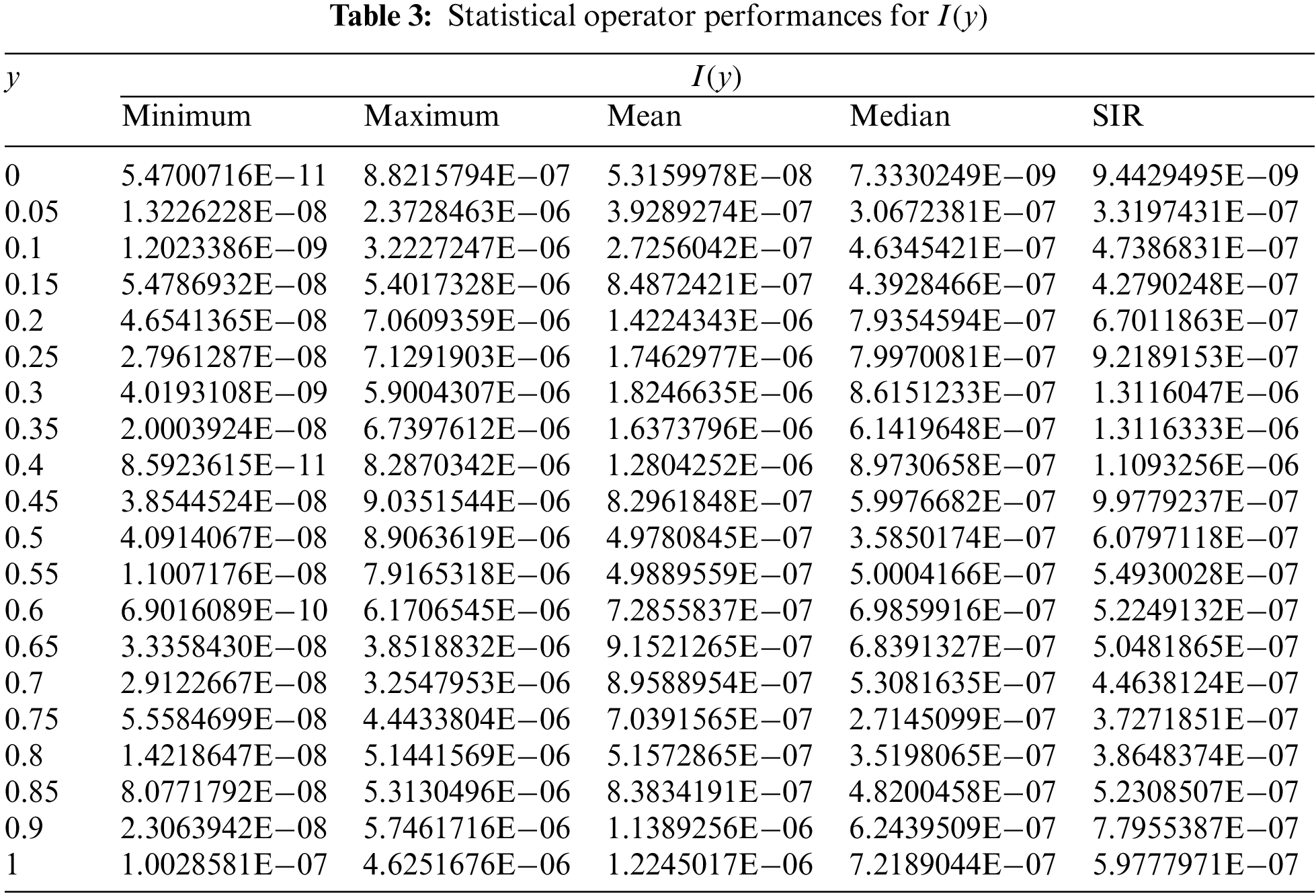
To check more accurateness, validation, and precision of the scheme, the statistical performances are tabulated in Tabs. 2–5 for the Minimum, Maximum, Mean, MSE, Median and SIR operators to solve the IDS. The Minimum gages represent the best outcomes, calculated for each class of the IDS 10−08–10−09, 10−08–10−11, 10−07–10−11, and 10−08–10−11. The worst results are indicated through the Maximum performances for the respective classes of the IDS, which lie as 10−05–10−06, 10−06–10−07, 10−05–10−07, and 10−06–10−07. Moreover, the Mean, Median and SIR operator performances are calculated as 10−06–10−07 for each class of the IDS. These calculated performances signify the importance of the ANNs procedures for the mathematical form of IDS. Through these measures the proposed scheme is stable, accurate, and precise for solving the IDS.
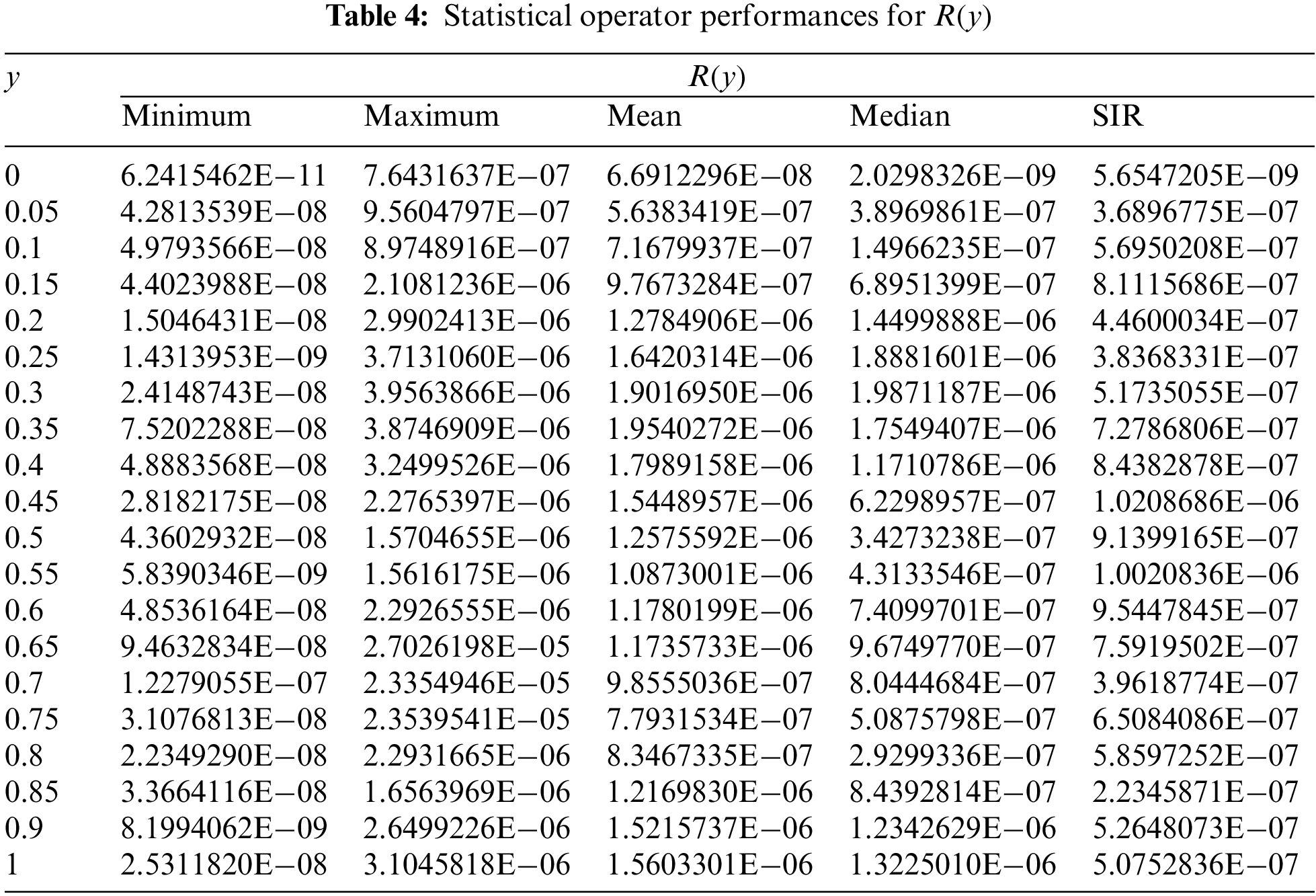
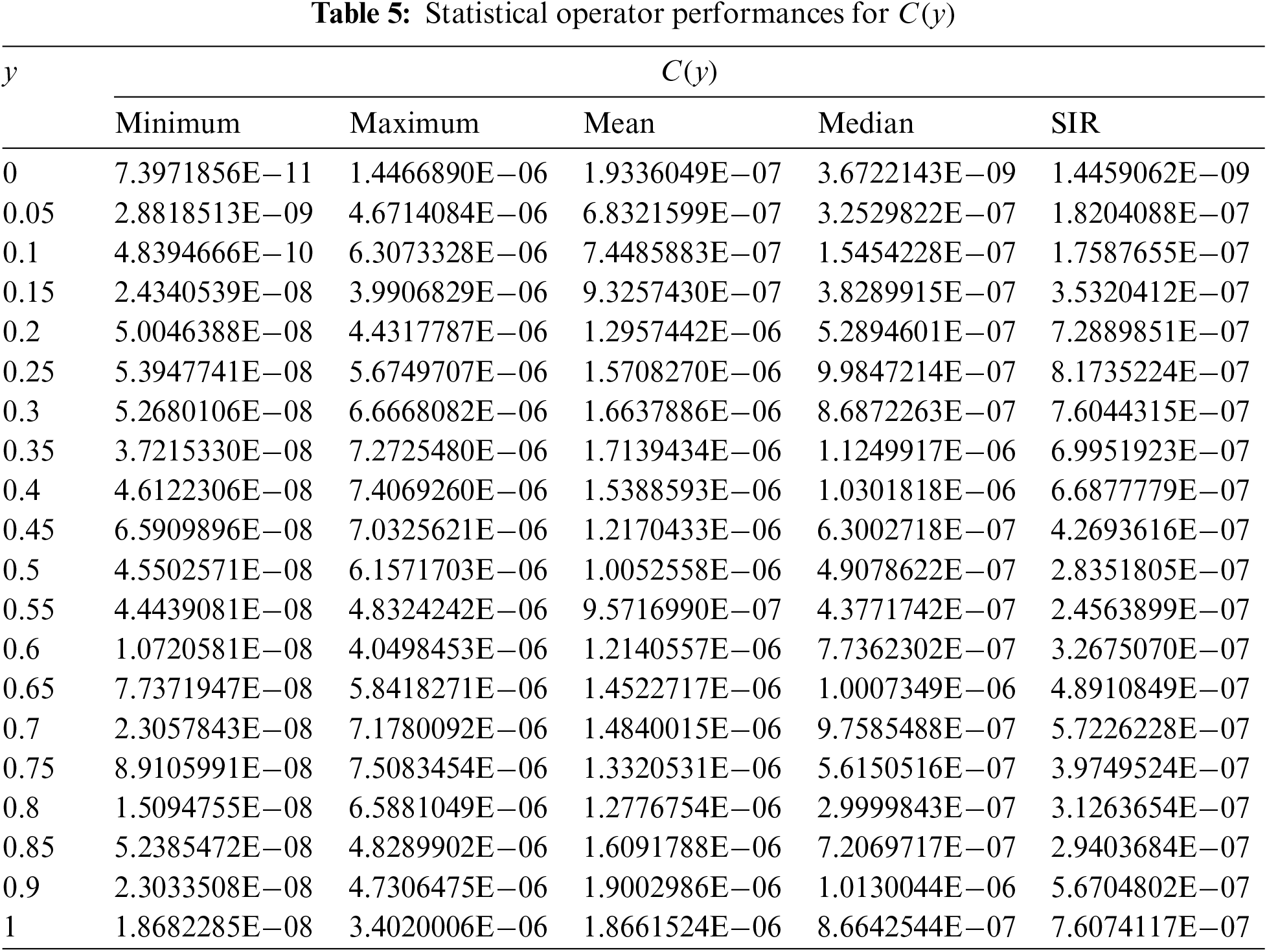
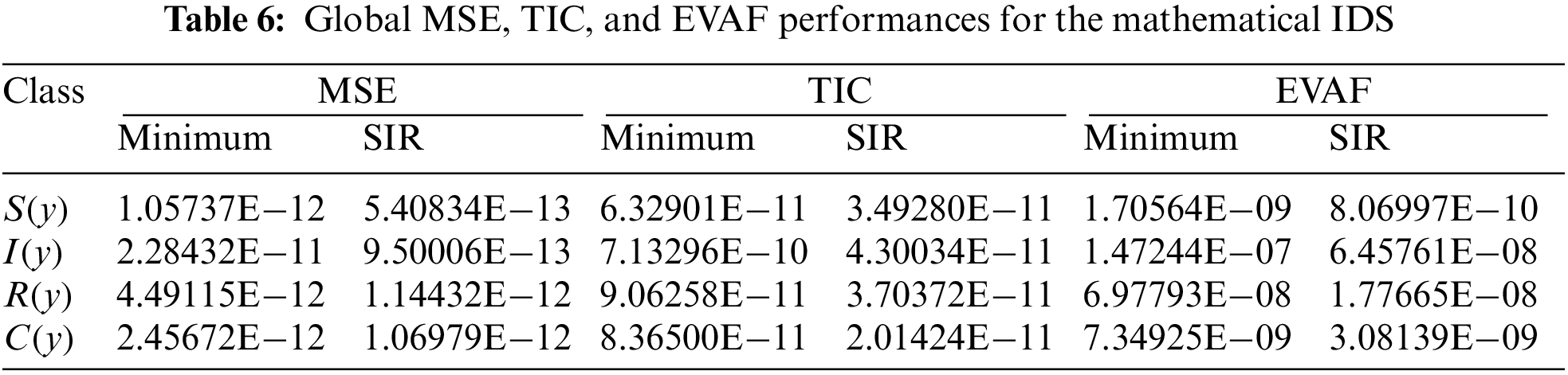
The global MSE, TIC, and EVAF operator performances using the 40 executions to solve the IDS through the ANNs procedures, along with the optimization of the PSOIPA for solving the IDS, are provided in Tab. 6. These global presentations for the Minimum values were 10−11–10−12, 10−10–10−11, and 10−07–10−09. At the same time, these performances for the SIR are calculated as 10−12 to 10−13, 10−11–10−12, and 10−08–10−10. These obtained ideal performances through these global operators indicate the correctness, precision, and accuracy of the ANNs procedures and the optimization of the PSOIPA for solving the IDS.
This work aims to design a swarming computational paradigm for the influenza disease system. The mathematical form of the influenza disease system is dependent upon four classes, susceptible individuals, infected people, recovered individuals, and cross-immune people. The numerical performances of the influenza disease system are presented by using the artificial neural networks together with the swarming computational paradigms and interior-point scheme, which are the global and local search approaches. To find the numerical performances, a merit function is constructed based on the differential form of the influenza system and then optimization is performed by using the hybrid competency of the PSOIPA. The curve fitting log-sigmoid is used as a merit function along with ten numbers of neurons or 30 variables as well as the whole process is used for 20 trials to solve the nonlinear system. The achieved performances are based on the ANNs and the hybrid computing framework of PSOIPA. Furthermore, the AE is performed in suitable measures for each class of the model, which is found as 10−04 to 10−06 as well as the performance measures are also calculated in suitable measures. Finally, the exactness of the stochastic scheme is performed by using the comparison of the obtained and reference solutions. The precise statistical EVAF, MSE, TIC, and MAD operator performances, along with the global operators, signify the solver reliability in solving the influenza model. Moreover, the statistical Minimum, Maximum, Mean, MSE, Median, and SIR operators further endorse the correctness of the ANNs-PSOIPA procedure.
Future Research Directions: In the future, the designed stochastic procedure can be executed to solve the higher order systems [47–53] and biological population systems [54,55].
Funding Statement: This research received funding support from the NSRF via the Program Management Unit for Human Resources & Institutional Development, Research and Innovation (Grant Number B05F640092).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. C. Sarda, P. Palma and J. Rello, “Severe influenza: Overview in critically ill patients,” Current opinion in critical care, vol. 25, no. 5, pp. 449–457, 2019. [Google Scholar]
2. F. Astuti, A. Suryanto and I. Darti, “Multi-step differential transform method for solving the influenza virus model with disease resistance,” IOP Conference Series: Materials Science and Engineering, vol. 546, no. 5, pp. 1–10, 2019. [Google Scholar]
3. E. O. Alzahrani and M. A. Khan, “Comparison of numerical techniques for the solution of a fractional epidemic model,” The European Physical Journal Plus, vol. 135, no. 1, pp. 1–28, 2020. [Google Scholar]
4. M. Erdem, M. Safan and C. Castillo-Chavez, “Mathematical analysis of an SIQR influenza model with imperfect quarantine,” Bulletin of Mathematical Biology, vol. 79, no. 7, pp. 1612–1636, 2017. [Google Scholar]
5. Z. Sabir, M. Umar, M. A. Z. Raja, I. Fathurrochman and H. Hasan, “Design of Morlet wavelet neural network to solve the non-linear influenza disease system,” Applied Mathematics and Nonlinear Sciences, vol. 7, pp. 1–16, 2022. [Google Scholar]
6. L. Sun, G. W. DePuy and G. W. Evans, “Multi-objective optimization models for patient allocation during a pandemic influenza outbreak,” Computers & Operations Research, vol. 51, pp. 350–359, 2014. [Google Scholar]
7. G. González-Parra, A. J. Arenas and B. M. Chen-Charpentier, “A fractional order epidemic model for the simulation of outbreaks of influenza A (H1N1),” Mathematical Methods in the Applied Sciences, vol. 37, no. 15, pp. 2218–2226, 2014. [Google Scholar]
8. B. Ghanbari and J. F. Gómez-Aguilar, “Analysis of two avian influenza epidemic models involving fractal-fractional derivatives with power and Mittag-Leffler memories,” Chaos: An Interdisciplinary Journal of Nonlinear Science, vol. 29, no. 12, pp. 123113, 2019. [Google Scholar]
9. Z. Sabir, A. A. A. Ibrahim, M. A. Z. Raja, K. Nisar, M. Umar et al., “Soft computing paradigms to find the numerical solutions of a nonlinear influenza disease model,” Applied Sciences, vol. 11, no. 18, pp. 1–16, 2021. [Google Scholar]
10. J. M. Tchuenche, N. Dube, C. P. Bhunu, R. J. Smith and C. T. Bauch, “The impact of media coverage on the transmission dynamics of human influenza,” BMC Public Health, vol. 11, pp. 1–16, 2011. [Google Scholar]
11. J. Schulze-Horsel, M. Schulze, G. Agalaridis, Y. Genzel and U. Reichl, “Infection dynamics and virus-induced apoptosis in cell culture-based influenza vaccine production-flow cytometry and mathematical modeling,” Vaccine, vol. 27, no. 20, pp. 2712–2722, 2009. [Google Scholar]
12. R. Patel, I. M. Longini Jr and M. E. Halloran, “Finding optimal vaccination strategies for pandemic influenza using genetic algorithms,” Journal of Theoretical Biology, vol. 234, no. 2, pp. 201–212, 2005. [Google Scholar]
13. S. Hovav and D. Tsadikovich, “A network flow model for inventory management and distribution of influenza vaccines through a healthcare supply chain,” Operations Research for Health Care, vol. 5, pp. 49–62, 2015. [Google Scholar]
14. C. W. Kanyiri, L. Luboobi and M. Kimathi, “Application of optimal control to influenza pneumonia coinfection with antiviral resistance,” Computational and Mathematical Methods in Medicine, vol. 2020, pp. 1–15, 2020. [Google Scholar]
15. L. Jódar, R. J. Villanueva, A. J. Arenas and G. C. González, “Nonstandard numerical methods for a mathematical model for influenza disease,” Mathematics and Computers in Simulation, vol. 79, no. 3, pp. 622–633, 2008. [Google Scholar]
16. R. Casagrandi, L. Bolzoni, S. A. Levin and V. Andreasen, “The SIRC model and influenza A,” Mathematical Biosciences, vol. 200, no. 2, pp. 152–169, 2006. [Google Scholar]
17. M. Umar, Z. Sabir, M. A. Z. Raja, F. Amin, T. Saeed et al., “Integrated neuro-swarm heuristic with interior-point for nonlinear SITR model for dynamics of novel COVID-19,” Alexandria Engineering Journal, vol. 60, no. 3, pp. 2811–2824, 2021. [Google Scholar]
18. M. Umar, Z. Sabir, M. A. Z. Raja, M. Shoaib, M. Gupta et al., “A stochastic intelligent computing with neuro-evolution heuristics for nonlinear SITR system of novel COVID-19 dynamics,” Symmetry, vol. 12, no. 10, pp. 1–17, 2020. [Google Scholar]
19. Z. Sabir, M. A. Z. Raja and D. Baleanu, “Fractional mayer neuro-swarm heuristic solver for multi-fractional order doubly singular model based on Lane-Emden equation,” Fractals, vol. 29, no. 5, pp. 1–15, 2021. [Google Scholar]
20. Z. Sabir, M. A. Z. Raja, J. L. Guirao and M. Shoaib, “A novel design of fractional meyer wavelet neural networks with application to the nonlinear singular fractional Lane-Emden systems,” Alexandria Engineering Journal, vol. 60, no. 2, pp. 2641–2659, 2021. [Google Scholar]
21. Z. Sabir, J. L. Guirao and T. Saeed, “Solving a novel designed second order nonlinear lane–Emden delay differential model using the heuristic techniques,” Applied Soft Computing, vol. 102, pp. 1–12, 2021. [Google Scholar]
22. J. L. Guirao, Z. Sabir and T. Saeed, “Design and numerical solutions of a novel third-order nonlinear Emden–Fowler delay differential model,” Mathematical Problems in Engineering, vol. 2020, pp. 1–9, 2020. [Google Scholar]
23. Z. Sabir, S. Saoud, M. A. Z. Raja, H. A. Wahab and A. Arbi, “Heuristic computing technique for numerical solutions of nonlinear fourth order Emden–Fowler equation,” Mathematics and Computers in Simulation, vol. 178, pp. 534–548, 2020. [Google Scholar]
24. Z. Sabir, M. A. Z. Raja, J. L. Guirao and M. Shoaib, “Integrated intelligent computing with neuro-swarming solver for multi-singular fourth-order nonlinear Emden–Fowler equation,” Computational and Applied Mathematics, vol. 39, no. 4, pp. 1–18, 2020. [Google Scholar]
25. M. Umar, Z. Sabir and M. A. Z. Raja, “Intelligent computing for numerical treatment of nonlinear prey–predator models,” Applied Soft Computing, vol. 80, pp. 506–524, 2019. [Google Scholar]
26. M. Umar, Z. Sabir, M. A. Z. Raja and Y. G. Sánchezand, “A stochastic numerical computing heuristic of SIR nonlinear model based on dengue fever,” Results in Physics, vol. 19, pp. 1–9, 2020. [Google Scholar]
27. M. A. Z. Raja, J. Mehmood, Z. Sabir, A. K. Nasab and M. A. Manzar, “Numerical solution of doubly singular nonlinear systems using neural networks-based integrated intelligent computing,” Neural Computing and Applications, vol. 31, no. 3, pp. 793–812, 2019. [Google Scholar]
28. Z. Sabir, M. A. Z. Raja, M. Shoaib and J. F. Aguilar, “FMNEICS: Fractional meyer neuro-evolution-based intelligent computing solver for doubly singular multi-fractional order Lane–Emden system,” Computational and Applied Mathematics, vol. 39, no. 4, pp. 1–18, 2020. [Google Scholar]
29. M. Umar, M. A. Z. Raja, Z. Sabir, A. S. Alwabli and M. Shoaib, “A stochastic computational intelligent solver for numerical treatment of mosquito dispersal model in a heterogeneous environment,” The European Physical Journal Plus, vol. 135, no. 7, pp. 1–23, 2020. [Google Scholar]
30. Y. Shi and R. C. Eberhart, “Empirical study of particle swarm optimization,” in Proc. of the 1999 Congress on Evolutionary Computation-CEC99, Washington, DC, USA, pp. 1945–1950, 1999. [Google Scholar]
31. A. P. Engelbrecht, Computational Intelligence: An Introduction, 2nd ed., Chichester, U.K.: John Wiley & Sons Ltd., 2007. [Google Scholar]
32. V. S. Özsoy, M. G. Ünsal and H. H. Örkcü, “Use of the heuristic optimization in the parameter estimation of generalized gamma distribution: Comparison of GA, DE, PSO and SA methods,” Computational Statistics, vol. 35, no. 4, pp. 1895–1925, 2020. [Google Scholar]
33. M. Kamarzarrin and M. H. Refan, “Intelligent sliding mode adaptive controller design for wind turbine pitch control system using PSO-SVM in presence of disturbance,” Journal of Control Automation and Electrical Systems, vol. 31, no. 4, pp. 912–925, 2020. [Google Scholar]
34. A. Duary, M. S. Rahman, A. A. Shaikh, S. T. A. Niaki and A. K. Bhunia, “A new hybrid algorithm to solve bound-constrained nonlinear optimization problems,” Neural Computing and Applications, vol. 32, no. 16, pp. 12427–12452, 2020. [Google Scholar]
35. Z. Sabir, M. A. Z. Raja, T. Botmart and W. Weera, “A neuro-evolution heuristic using active-set techniques to solve a novel nonlinear singular prediction differential model,” Fractal and Fractional, vol. 6, no. 29, pp. 1–14, 2022. [Google Scholar]
36. A. Mehmood, A. Zameer, M. S. Aslam and M. A. Z. Raja, “Design of nature-inspired heuristic paradigm for systems in nonlinear electrical circuits,” Neural Computing and Applications, vol. 32, no. 11, pp. 7121–7137, 2019. [Google Scholar]
37. E. M. El-Gendy, M. M. Saafan, M. S. Elksas, S. F. Saraya and F. F. Areed, “Applying hybrid genetic–PSO technique for tuning an adaptive PID controller used in a chemical process,” Soft Computing, vol. 24, no. 5, pp. 3455–3474, 2020. [Google Scholar]
38. B. T. Pham, C. Qi, L. S. Ho, T. Nguyen-Thoi, N. Al-Ansari et al., “A novel hybrid soft computing model using random forest and particle swarm optimization for estimation of undrained shear strength of soil,” Sustainability, vol. 12, no. 6, pp. 1–16, 2020. [Google Scholar]
39. M. A. Z. Raja, M. S. Aslam, N. I. Chaudhary and W. U. Khan, “Bio-inspired heuristics hybrid with interior-point method for active noise control systems without identification of secondary path,” Frontiers of Information Technology & Electronic Engineering, vol. 19, no. 2, pp. 246–259, 2018. [Google Scholar]
40. M. Stefanova, S. Yakunin, M. Petukhova, S. Lupuleac and M. Kokkolaras, “An interior-point method-based solver for simulation of aircraft parts riveting,” Engineering Optimization, vol. 50, no. 5, pp. 781–796, 2018. [Google Scholar]
41. M. R. Sicre and B. F. Svaiter, “A O(1/k3/2) hybrid proximal extragradient primal–dual interior point method for nonlinear monotone mixed complementarity problems,” Computational and Applied Mathematics, vol. 37, no. 2, pp. 1847–1876, 2018. [Google Scholar]
42. J. Umenberger and I. R. Manchester, “Specialized interior-point algorithm for stable nonlinear system identification,” IEEE Transactions on Automatic Control, vol. 64, no. 6, pp. 2442–2456, 2018. [Google Scholar]
43. M. A. Z. Raja, U. Ahmed, A. Zameer, A. K. Kiani and N. I. Chaudhary, “Bio-inspired heuristics hybrid with sequential quadratic programming and interior-point methods for reliable treatment of economic load dispatch problem,” Neural Computing and Applications, vol. 31, no. 1, pp. 447–475, 2019. [Google Scholar]
44. Z. Sabir, M. A. Z. Raja, A. Kamal, J. L. Guirao, D. N. Le et al., “Neuro-swarm heuristic using interior-point algorithm to solve a third kind of multi-singular nonlinear system,” Mathematical Biosciences and Engineering, vol. 18, no. 5, pp. 5285–5308, 2021. [Google Scholar]
45. Y. G. Sánchez, Z. Sabir, H. Günerhan and H. M. Baskonus, “Analytical and approximate solutions of a novel nervous stomach mathematical model,” Discrete Dynamics in Nature and Society, vol. 2020, pp. 1–9, 2020. [Google Scholar]
46. K. Nisar, Z. Sabir, M. A. Z. Raja, A. A. A. Ibrahim, F. Erdogan et al., “Design of morlet wavelet neural network for solving a class of singular pantograph nonlinear differential models,” IEEE Access, vol. 9, pp. 77845–77862, 2021. [Google Scholar]
47. M. S. M. Selvi and L. Rajendran, “Application of modified wavelet and homotopy perturbation methods to nonlinear oscillation problems,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 2, pp. 351–364, 2019. [Google Scholar]
48. L. Akin, “New principles of non-linear integral inequalities on time scales,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 2, pp. 387–394, 2021. [Google Scholar]
49. H. Durur, O. Tasbozan and A. Kurt, “New analytical solutions of conformable time fractional bad and good modified Boussinesq equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 447–454, 2020. [Google Scholar]
50. A. O. Akdemir, E. Deniz and E. Yüksel, “On some integral inequalities via conformable fractional integrals,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 489–498, 2021. [Google Scholar]
51. M. Gürbüz and Ç. Yıldız, “Some new inequalities for convex functions via Riemann-Liouville fractional integrals,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 537–544, 2021. [Google Scholar]
52. H. M. Baskonus, H. Bulut and T. A. Sulaiman, “New complex hyperbolic structures to the lonngren-wave equation by using sine-gordon expansion method,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 129–138, 2019. [Google Scholar]
53. E. İlhan and İ. O. Kıymaz, “A generalization of truncated M-fractional derivative and applications to fractional differential equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 171–188, 2020. [Google Scholar]
54. J. Ul. Rahman, D. Lu, M. Suleman, J. H. He and M. Ramzan, “He–Elzaki method for spatial diffusion of biological population,” Fractals, vol. 27, no. 5, pp. 1–11, 2019. [Google Scholar]
55. Z. Sabir, T. Botmart, M. A. Z. Raja, R. Sadat, M. R. Ali et al., “Artificial neural network scheme to solve the nonlinear influenza disease model,” Biomedical Signal Processing and Control, vol. 75, no. 103594, pp. 1–14, 2022. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |