| Computers, Materials & Continua DOI:10.32604/cmc.2022.030490 |  |
| Article |
State-of-Charge Estimation of Lithium-Ion Battery for Electric Vehicles Using Deep Neural Network
1Department of Electrical and Electronics Engineering, Dayananda Sagar College of Engineering, Bengaluru, 560078, Karnataka, India
2Department of Electrical and Electronics Engineering, National Institute of Technology, Tiruchirapalli, 620015, Tamil Nadu, India
3Department of Electrical and Electronics Engineering, M S Ramaiah Institute of Technology, Bengaluru, 560054, Karnataka, India
4Department of Electrical and Electronics Engineering, M. Kumarasamy College of Engineering, Karur, 639113, Tamil Nadu, India
5Electrical Engineering Department, College of Engineering, King Khalid University, Abha, 61421, Saudi Arabia
6Computers and Communications Department, College of Engineering, Delta University for Science and Technology, Gamasa, 35712, Egypt
7Faculty of Technology, The Gateway, De Montfort University, Leicester, LE1 9BH, United Kingdom
8Department of Mathematics, College of Arts and Sciences, Prince Sattam bin Abdulaziz University, Wadi Aldawaser, 11991, Saudi Arabia
*Corresponding Author: Kottakkaran Sooppy Nisar. Email: n.sooppy@psau.edu.sa
Received: 27 March 2022; Accepted: 28 April 2022
Abstract: It is critical to have precise data about Lithium-ion batteries, such as the State-of-Charge (SoC), to maintain a safe and consistent functioning of battery packs in energy storage systems of electric vehicles. Numerous strategies for estimating battery SoC, such as by including the coulomb counting and Kalman filter, have been established. As a result of the differences in parameter values between each cell, when these methods are applied to high-capacity battery packs, it has difficulties sustaining the prediction accuracy of overall cells. As a result of aging, the variation in the parameters of each cell is higher as more time is spent in operation. It is suggested in this study to establish an SoC estimate model for a Lithium-ion battery by employing an enhanced Deep Neural Network (DNN) approach. This is because the proposed DNN has a substantial hidden layer, which can accurately predict the SoC of an unknown driving cycle during training, making it ideal for SoC estimation. To evaluate the nonlinearities between voltage and current at various SoCs and temperatures, the proposed DNN is applied. Using current and voltage data measured at various temperatures throughout discharge/charge cycles is necessary for training and testing purposes. When the method has been thoroughly trained with the data collected, it is used for additional cells cycle tests to predict their SoC. The simulation has been conducted for two different Li-ion battery datasets. According to the experimental data, the suggested DNN-based SoC estimate approach produces a low mean absolute error and root-mean-square-error values, say less than 5% errors.
Keywords: Artificial intelligence; deep neural network; Li-ion battery; parameter variation; SoC estimation
As a result of the widespread fossil fuel consumption, environmental degradation and energy constraints are becoming progressively major problems worldwide. Authorities are devoting an extensive interest to the growth and commercialization of renewable energy sources. Electric vehicles (EVs) have gained a considerable amount of attention in recent decades, both from the government and from industries. Many types of EVs have appeared in recent years on the market, including pure EVs, hybrid EVs, fuel-cell EVs, and others [1]. Rechargeable batteries in EVs are becoming increasingly popular, with lead-acid, lithium-ion, nickel-cadmium, and nickel-hydrogen batteries, among the most popular. Because of its high energy density and high power per unit cell weight, Li-ion batteries have become the most widely utilized technology in EVs, enabling the development of various types of batteries with decreased weight and size at reasonable rates. Lithium-ion batteries are the most common battery used in EVs today. Several firms prefer lithium-ion batteries over other types of batteries because of their advantages, such as fast charging, high power, low pollution, and extended life, and the share of lithium-ion batteries in the market is growing all the time [2]. So, it is no surprise that Battery Management System (BMS) has garnered much interest in recent years. The BMS is in-charge of transferring data between the EV’s battery pack and energy management scheme. The BMS comprises control strategies and all algorithms required to ensure the battery pack’s effectiveness and safety, including methods for identifying battery conditions such as State-of-Charge (SoC) and State-of-Health (SoH). SoC extraction indicates how much charge remains in the battery pack and is required to determine the EV’s lasting distance [3] accurately. As a result, a precise estimate of the battery’s SoC is required. Nevertheless, because of the nonlinear characteristics of batteries, particularly at high currents and low temperatures, the automobile industry still faces a problem in improving SoC estimate methodologies. The authors of [4] suggested an enabled state-of-health estimate approach for EVs that was based on the incremental capacity analysis method. Cell imbalance is considered when a battery pack’s equivalent incremental capacity value computation is combined with cell-level battery evaluations to achieve the desired result. A multistage alternate current approach for lithium-ion batteries was proposed in [5], and the authors discussed their findings. The authors of [6] discussed a data-driven technique for determining battery charging capacity based on EV operating data.
Coulomb Counting (CC), Kalman Filter (KF), look-up table, Extended Kalman Filter (EKF), State Observer (SO), and Particle Filter (PF) are some of the SoC estimate methods available today. When it comes to determining SoC, one of the most prevalent approaches is the CC method, which estimates SoC by adding up all of the currents over a while. However, because of the flaws in the data, it is difficult to make an accurate SoC estimation, especially because the inaccuracy is compounding with time [7,8]. Other approaches, including KF, SO, EKF, and PF, can sufficiently estimate the SoC because they do not rely solely on the current accumulation for their calculations. These methods, however, necessitate the use of an exact battery model with parameters to provide an accurate estimate of SoC [9]. As discussed earlier, when estimating the SoC, the look-up table and CC methods are frequently utilized. They do have inherent limits, and over time, more complex techniques such as the model-based estimate method have progressively supplanted them in popularity. It has also been proposed that the lookup table, CC, and model-based approaches can be combined with the non-linear state prediction method to increase the estimated capability of the methods [10,11]. The Sliding mode observer, H-
On the other hand, an effort has been made to predict the SoC using the data-driven estimation technique, proven to be successful. In most cases, classic Machine Learning (ML) techniques such as support vector machines, fuzzy logic controllers, Artificial Neural Networks (ANN), and other permutations of the methods were used. Generally, traditional ML algorithms employ no more than two layers of computing layers in their implementation. This is particularly important in the case of the ANN. Although significant advancements have been made in recent years, the traditional ANN has now been elevated to the status of being advanced [12,14,15]. The potential of the standard ANN is considerably increased by raising the number of processing layers, which was formerly not achievable because of software or hardware constraints [12] but is now feasible due to technological advances. When it comes to SoC estimate, the approaches are generally divided into two groups: non-recurrent and recurrent algorithms, with recurrent methods knowing the past and non-recurrent methodologies just relying on the information entered at the current step, respectively. There have been numerous successful applications of the non-recurrent Feedforward Neural Network (FNN) and the recurrent Long Short-Term Memory (LSTM) algorithms for SoC estimation, and both were shown to be convincing strategies among the many other ML models [16,17]. The authors of [18] presented a load classification Neural Network (NN) that has been used to assess the SoC of the batteries using information taken from twelve US06 driving cycle examinations; nevertheless, various types of NNs should be utilized for idle, discharging, and charging operations, respectively. Using this strategy, the average estimation error is 3%, lower than the error achieved without further filtering. Furthermore, because the validation is limited to a pulse discharge test, it is impossible to predict how well the approach will function in a real-world setting. An SVM with a sliding window is employed to enhance computational speed when modeling the battery in [19], and a Mean Absolute Error (MAE) of less than 3% is attained. Nevertheless, as demonstrated in the preceding works, it is possible to accomplish this result in combination with an EKF. The authors of [20] coupled adaptive wavelet NNs with a wavelet transformation to predict the SoC, leading to a new composite wavelet NN model based on the Levenberg–Marquardt algorithm. It was suggested in [21] that a more accurate back-propagation NN-based SoC prediction model for lithium-ion batteries be developed. To enhance the precision and resilience of the model, principal component analysis and particle group optimization algorithms are employed. Numerous research explicitly studied different approaches using Convolutional Neural Networks (CNNs) for battery SoH estimation, including different types of CNNs. Using a CNN in combination with a gated Recurrent NN (RNN) and two CNNs in combination with a random forest, it is demonstrated that both combinations increase SoH estimation [22]. The authors of [23] have utilized a CNN and a support vector machine, both used to estimate SoH, and the results were compared. The authors of [24] have trained a CNN model to predict battery capacity based on the observed impedance and SoC variables collected during the experiment. After all that, it has been demonstrated that using a different sampling strategy, such as defined SoC phases rather than defined time steps, is useful for battery SoH estimation when using FNN, CNN, or LSTM [25]. SoC estimate using a Nonlinear Autoregressive Exogenous neural network (NARX) is of specific interest to Zhang [26], who plans to contrast the anticipated outcome with that obtained using EKF. NARX outperforms its competitors in terms of accuracy and fast convergence of SoC estimates, as demonstrated by comparing the two systems. A new sort of NN is introduced, which brings together two different types of architecture. One is utilized for training purposes, while the other is used for testing purposes. This research discusses how to predict time series processes by including sequential data as input to a NN model. The expressive ability and generalization performance of a NN are both excellent, but the network lacks “memory ability.” “Memory ability” can be characterized as the capacity of a system to independently learn and utilize the “co-occurrence frequency” of elements or characteristics in past data without the need for external training.
Deep Neural Network (DNNs) is an upgraded form of the ANN, which is simply an ANN with ‘deeper’ functional layers. Combine DNN’s performance with intelligent training schemes and modifications, and it becomes the best in fields such as natural language processing, speech recognition, and computer vision. The concept of utilizing DNN to estimate SoC, on the other hand, is quite new. Scientists have effectively utilized two dissimilar forms of DNN to forecast the SoC of the Li-ion battery pack. The authors of [9] also recommended utilizing multilayer perceptron DNN to forecast the state-of-charge to improve accuracy. Nonetheless, other DNN variations have not yet been investigated for SoC estimation. The authors of [16] utilized an LSTM network that was trained and tested on specific drive cycles to achieve their results. The results reveal that even without filtering techniques, the outputs are quite encouraging. This research was prompted by recent technological breakthroughs. DNN is undoubtedly one of the most powerful approaches that can be utilized to deal with the problem of SoC estimation. According to numerous research, DNNs with strong computing layers may tackle any sort of nonlinearity and can be used as a highly accurate function. In this work, we examine and evaluate a variety of DNN architectures and training methods using a publicly available dataset. Despite the fact that the instances deliberated in this work are very introductory, it is anticipated that the adaptability of the proposed DNN would give significant usefulness and adaptability when more data and processing power are added to the system for potential developments.
The remaining sections of the paper are organized as follows. The DNN concept is discussed briefly in Section 2. The proposed DNN structure for SoC estimation is discussed in detail in Section 3. Section 4 describes the experimental setup and the dataset preparation used in this investigation. Section 4 also summarizes the findings. Lastly, Section 5 concludes the paper.
2 Architecture of the Proposed Deep Neural Network
This section presents the architecture of the proposed enhanced Deep Neural Network (DNN). In addition, the hyper-parameters of the DNN model are also discussed.
2.1 Architecture of the Proposed DNN
The FNN and the RNN structures are the two most frequently utilized architectures in ML [12,27]. The interactions between neurons are the key trait that distinguishes the two types of neurons. The linking of neurons in the FNN design does not result in the formation of a cycle. The flow of information exclusively in one direction, from the source to the destination layer, results from this constraint. Neurons in the RNN, on the other hand, can generate cyclic connections. With the help of cyclic connections, information can be transmitted not only in a unidirectional fashion from one layer to another but also in the other manner. An illustration of the variation in neuron connectivity is depicted in Fig. 1.
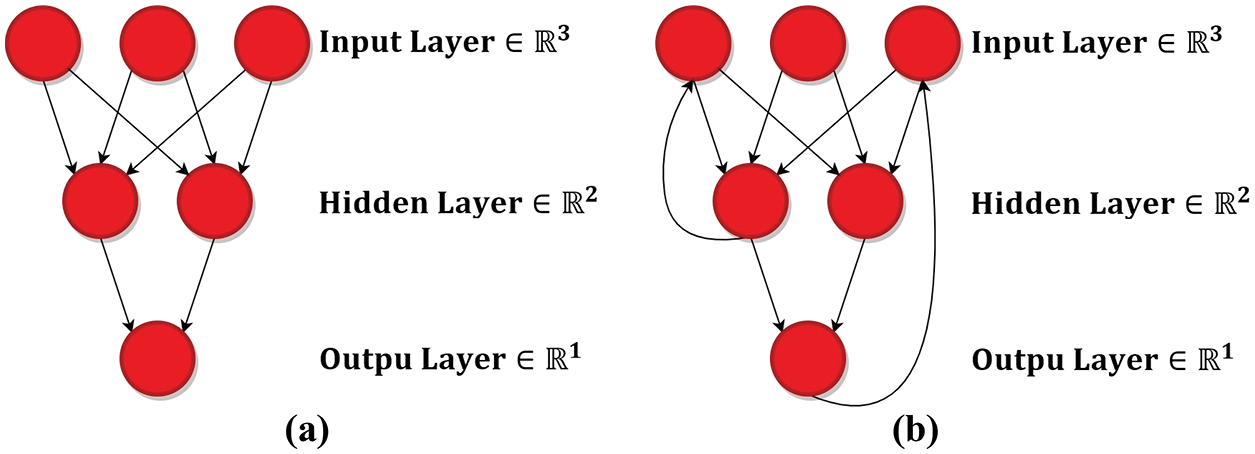
Figure 1: Interconnections of neurons; (a) FNN (acyclic), (b) RNN (cyclic)
DNN is a type of FNN architecture that belongs to the class of DNN. DNN is composed of at least three computational layers, which are as follows: the input layer, hidden layers, and output layer. Because the deep neural network has been widely employed in the literature on a wide range of time series prediction and classification models, this study evaluates the modeling capabilities of the deep neural network on the problem of estimating the SoC of the lithium-ion battery. It is utilized in this configuration to plot the battery variables, such as instantaneous current and voltage, temperature, and average current and voltage to the battery SoC. According to mathematics, the vector of outputs and inputs is specified as
where
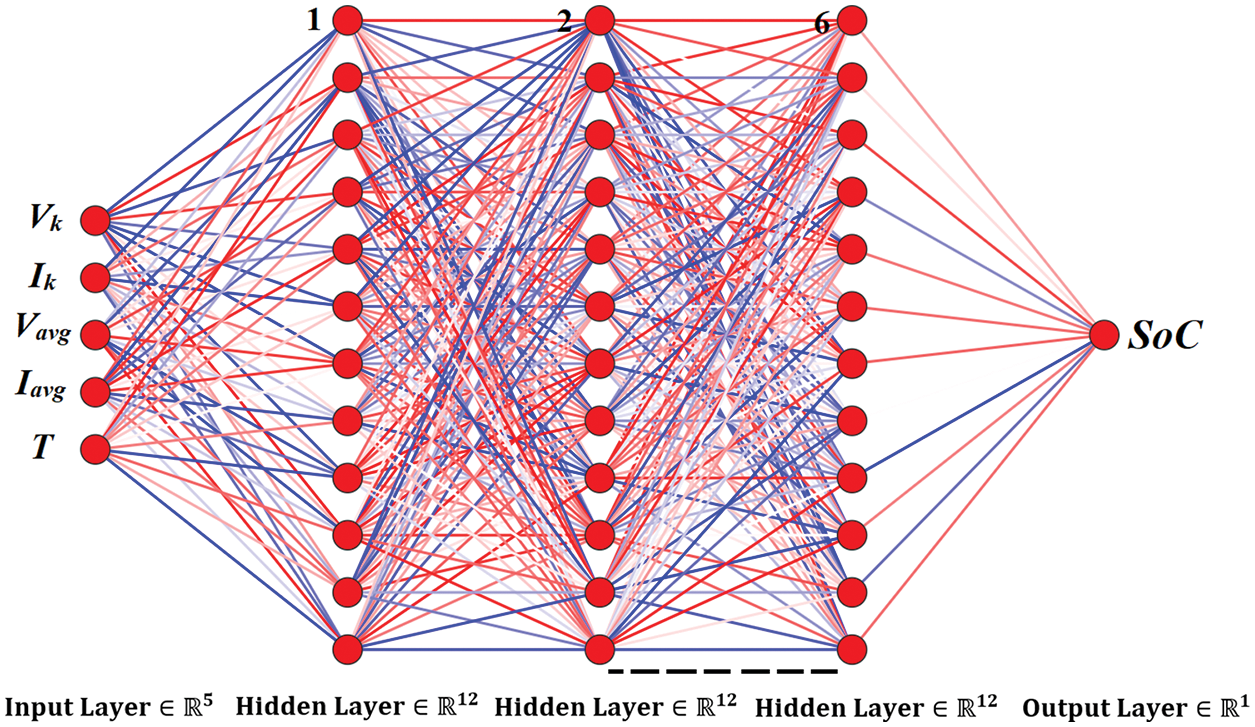
Figure 2: Architecture of the proposed DNN
The activation function of the perceptron
where
where
In this case, the learning variables are the bias and weights settings, which are calculated during the training phase. The structure can also be designed with different outputs and with varied numbers of neurons in each layer by making minor adjustments.
The majority of ML algorithms provide a variety of hyperparameters that can be used to influence the algorithm’s performance and behavior. When working with the DNN, there seems to be a set of hyperparameters that must be selected in advance of use. Among the most significant hyperparameters to consider are those listed in Tab. 1. As illustrated in Tab. 1, the number of potential permutations resulting from the choice possibilities is exponentially large, as is the number of possible combinations. In addition, as the number of hidden neurons and layers rises, the search space for the hyperparameters expands exponentially. Because of this, determining the optimal configuration of hyperparameters can be a time-consuming effort. At the moment, a variety of hyperparameter tuning techniques are available to search for the optimal combination of parameters. The next step in this investigation is to look into one of the most critical hyperparameters that can significantly impact the performance of the DNN is the number of hidden layers. The choice of the other hyperparameters is based on a variety of analytically recognized heuristics that have been selected from the literature. DNNs with lower than 2 hidden layers with 30 neurons per layer can model battery SoC estimation with acceptable precision in recent studies [16] and [28]. Theoretically, expanding the number of hidden layers and neurons in a deep neural network model, given that overfitting does not happen. Overfitting is a serious problem in raising the number of hidden layers and neurons. In recent developments in nonlinearity, a compelling replacement to the generally recognized SELU and RELU functions has been proposed. When compared to the usage of ELU nonlinearity, the use of SELU nonlinearity is recognized to save the training period while also improving accuracy. In the proposed DNN, the Sigmoid and SELU functions are used for all hidden neurons.

3 Proposed Deep Neural Network Training Approach
This segment delves into the numerous training approaches used in the experiment to train the suggested deep neural network framework, including the training and optimization methodology and the loss functions and error indicators. The optimization algorithm performs a significant part of the quest for a convergence point throughout the training of a proposed deep neural network. It is possible to achieve greater DNN effectiveness by employing the appropriate optimization technique. Typically, Stochastic Gradient Descent (SGD) optimization has been employed to train deep neural networks. Nevertheless, numerous new advancements recommend that a faster optimization technique, such as the stochastic gradient descent with momentum, root mean square propagation, Adam optimizer, Nesterov Adam optimizer, are discussed in various literature to improve the solution accuracy. This paper employs the SGD with a momentum optimization algorithm to optimize the DNN framework. In order to train the proposed DNN model, the SGD with momentum optimization technique is employed with a batch size of 256. The batch size is defined by the level of hardware memory that is presently accessible. Iterative adjustment of the learnable parameters, such as weight and bias values, is performed for supervised learning algorithms to reduce the error between the experimental and estimated values. The estimated value is signified by the vector
It is possible to backpropagate errors by computing the partial derivative of the losses with respect to each learnable variable, which is then employed to modify the values of the hyperparameters. Because the procedure is iterative, the procedure is often performed numerous times until the training termination criteria have been met. Iterations are referred to as epochs in this paper, and the termination criteria that are applied are dependent on the validation tolerance. The learning rate, which has an initial value of 0.01, is multiplied by the learning rate drop factor, which is 0.1, every 500 epochs until about the completion of the training phase. The validation patience parameter, which has a value of 2100 epochs, specifies how several epochs of training would be conducted before a decrease in error is achieved. The training process for most network architectures is repeated several times (five times in this paper) with various initial model parameters to guarantee that a solution near the global optimum is obtained rather than a solution near the optimal local solution, which would be undesirable. The whole process of the proposed model to estimate the SoC of Li-ion battery is illustrated in Fig. 3.
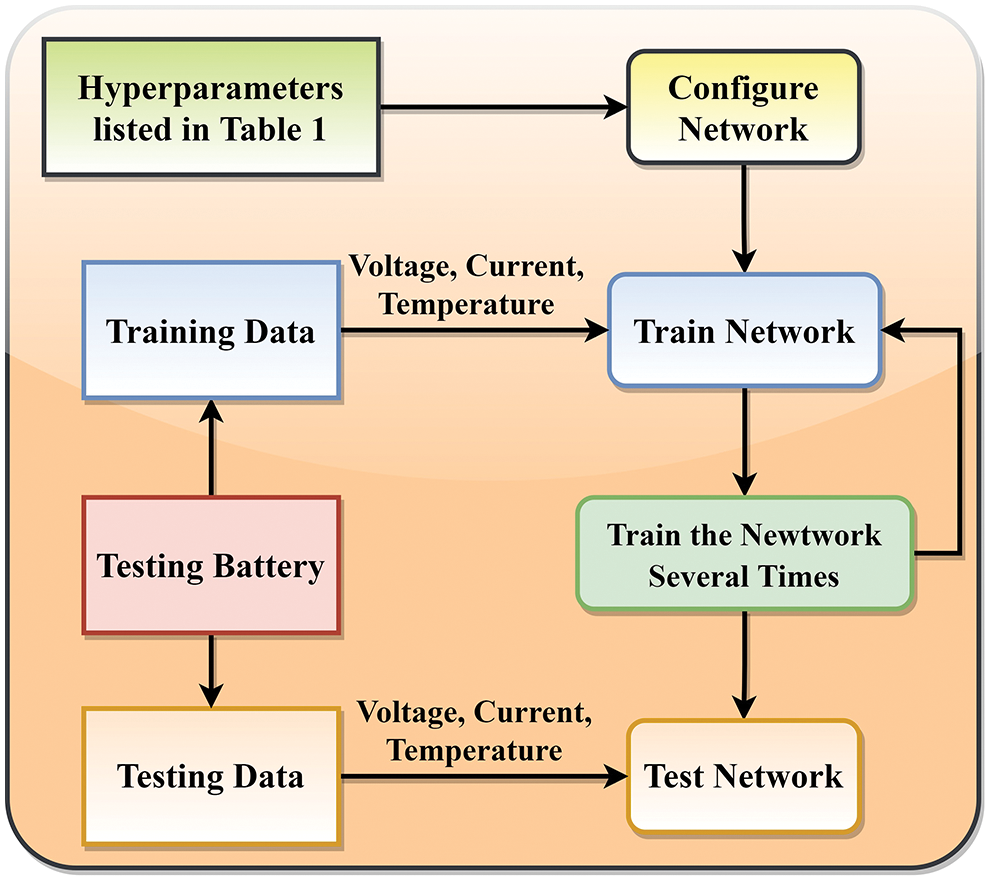
Figure 3: Application of the proposed DNN for SoC estimation
Apart from RMSE, to assess the effectiveness of the DNN models, a variety of other error metrics are also employed. Mean Percent Absolute Error (MPAE), Mean Absolute Error (MAE), and Mean Squared Error (MSE) are a few other error metrics. In this paper, RMSE and MAE are evaluated. The formulas to find all other metrics are given below.
4.1 Battery Dataset and Preparation
The study was performed in an 8 cubic feet thermal laboratory with a 75 A, 5 V Digatron firing circuits universal battery tester channel. The voltage and current precision were within 0.1% of the full scale for the 3 Ah LG HG2 cell under test. A variety of experiments were carried out at four different temperatures, with the battery being charged after each test at a rate of one cycle per second to 4.2 V with a 50 mA cut-off when the battery temperature reached 22°C or above. In this paper, the dataset at ambient temperatures of 25°C, 10°C, 0°C, and −10°C is considered. The driving cycle output profiles are performed until the cell has been discharged to 95% of its 1C discharge capacity at the appropriate temperature. From [29], the entire dataset was obtained for the study. Drive cycles are frequently employed in assessing EVs to analyze vehicle characteristics such as pollutants and energy consumption [30]. The application of multiple drive cycles to Li-ion batteries while simultaneously recording the battery variables gives valuable information for simulating the influence of real-world driving cycles on cell behavior and characteristics in a laboratory setting. The Unified Driving Schedule (LA92), Supplemental Federal Test Procedure (US06), Beijing Dynamic Stress Test (BJDST), Urban Dynamometer Driving Schedule (UDDS), Federal Urban Driving Schedule (FUDS), Dynamic Stress Test (DST), and Highway Fuel Economy Driving Schedule (HWFET), are among the most frequently used. The voltage, current, and temperature of LG HG2 cells under various drive cycles for different temperature conditions, such as 25°C, 10°C, and 0°C are shown in Figs. 4–6. Figs. 4a–4c illustrates various drive cycles, such as LA92, UDDS, and US06 of LG HG2 cells under 0°C temperature. Similarly, Figs. 5a–5c illustrates various drive cycles, such as LA92, UDDS, and US06 of LG HG2 cells under 10°C temperature, and Figs. 6a–6c illustrates various drive cycles, such as LA92, UDDS, and US06 of LG HG2 cells under 25°C temperature. The cell is first charged using a constant current (CC) charging method and then drained using the UDDS, LA92, and US06 driving cycles at four distinct temperatures (−10°C, 0°C, 10°C, and 25°C) one after another.
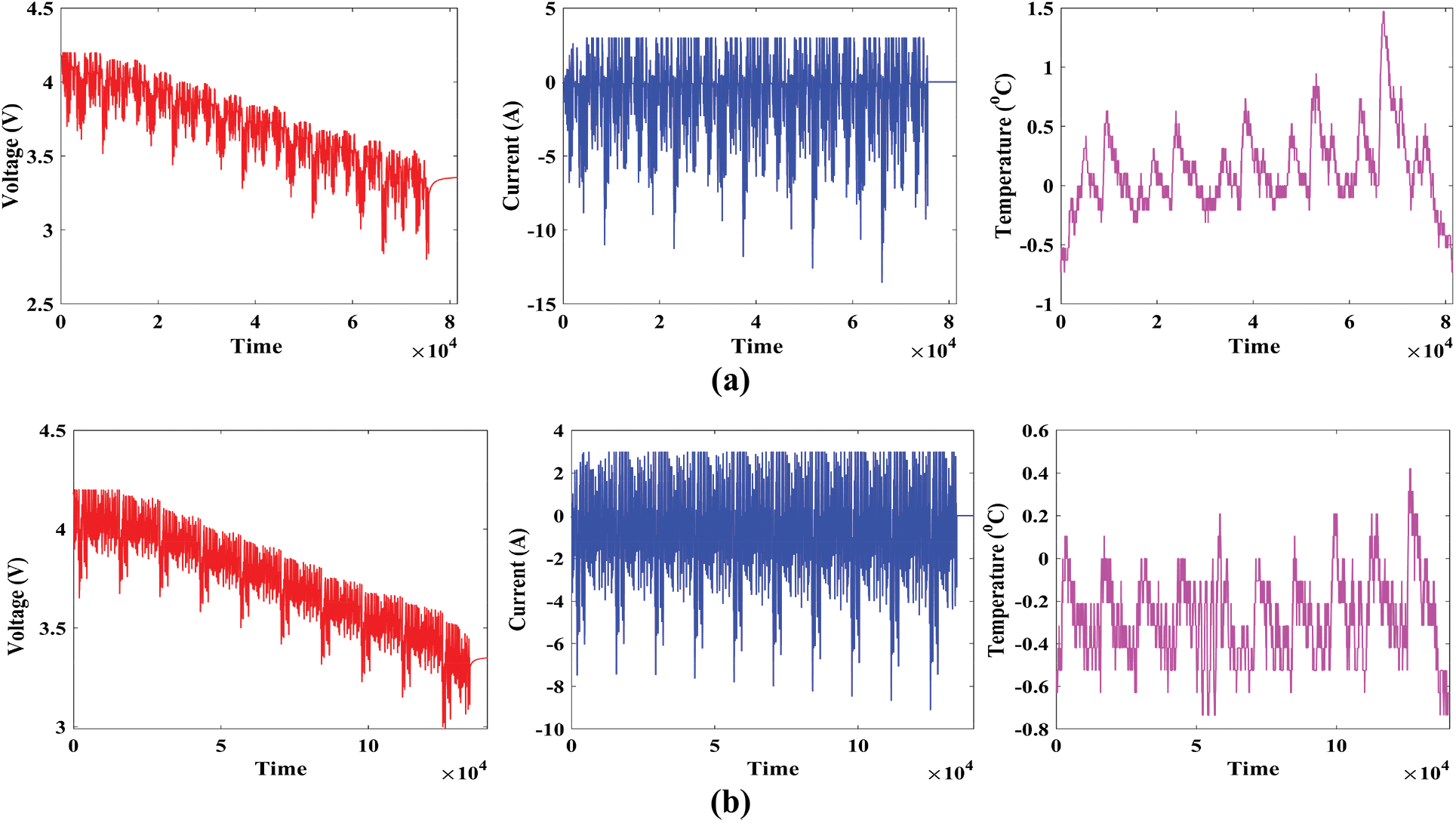
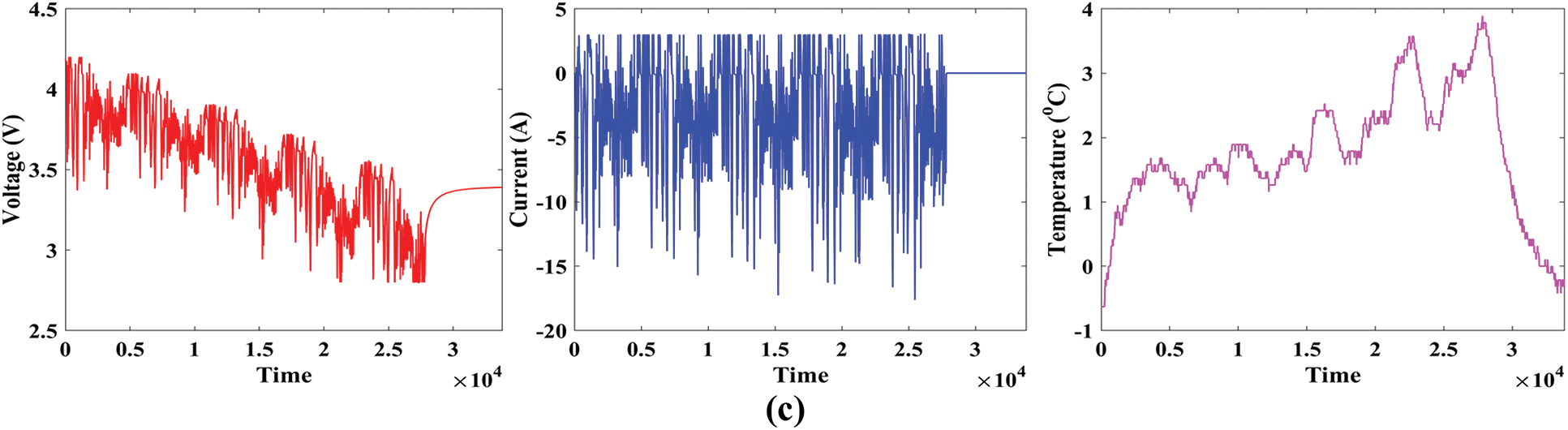
Figure 4: Drive cycles of LG HG2 under 0°C; (a) LA92, (b) UDDS, (c) USO6
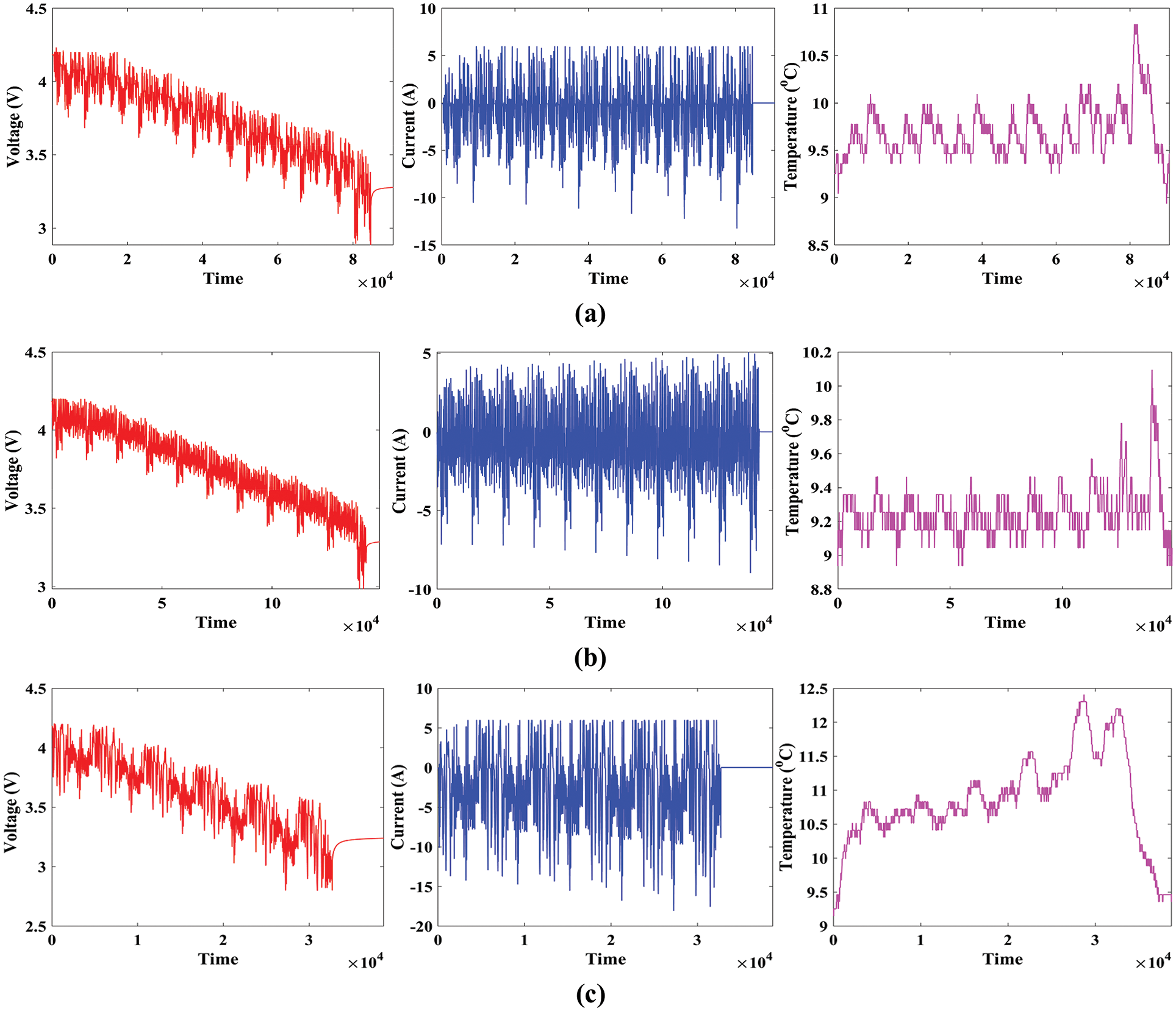
Figure 5: Drive cycles of LG HG2 under 10°C; (a) LA92, (b) UDDS, (c) USO6
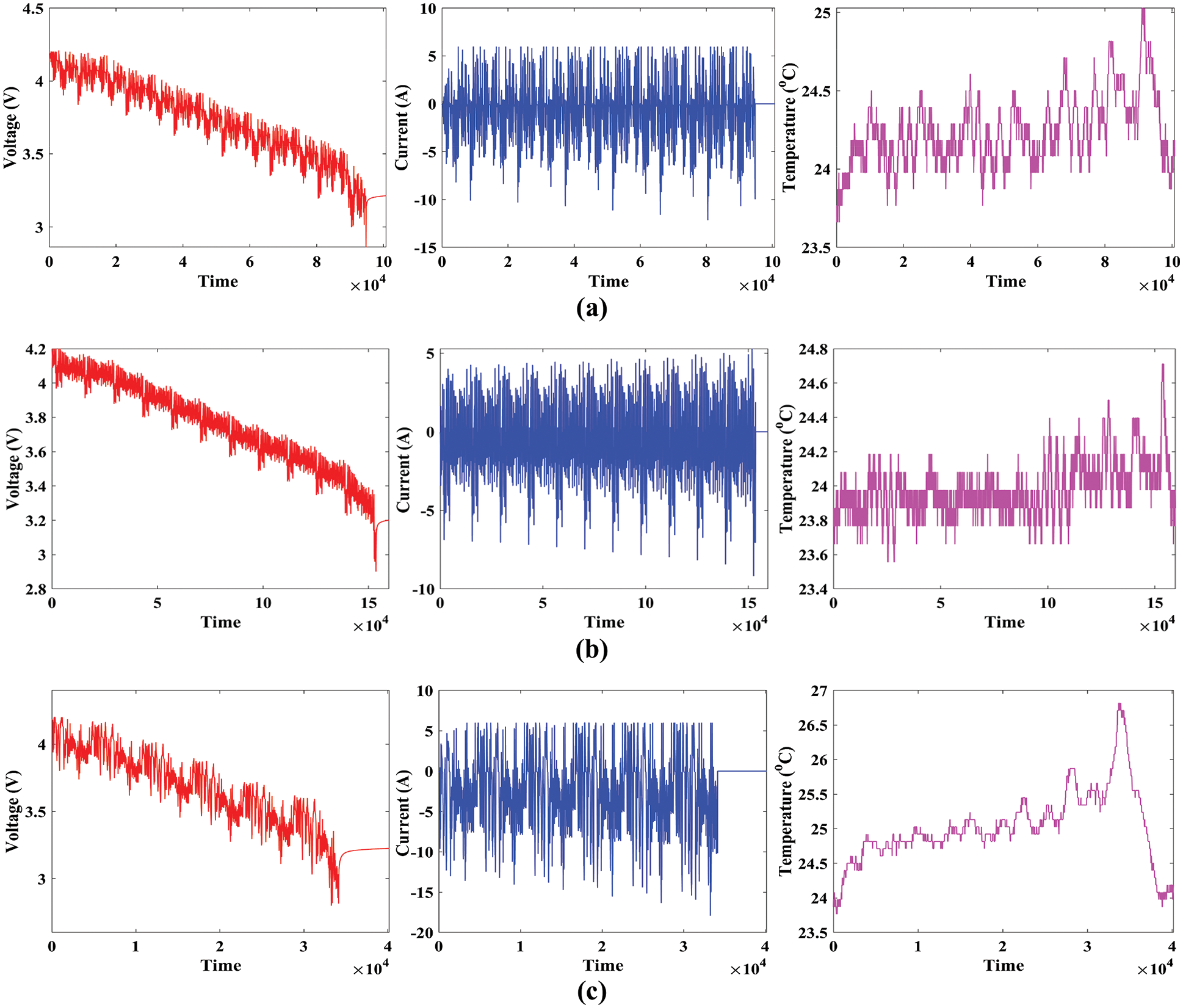
Figure 6: Drive cycles of LG HG2 under 25°C; (a) LA92, (b) UDDS, (c) USO6
Tab. 1 shows the hyperparameter values for the proposed DNN model. The proposed DNN model is developed using the MATLAB tool, which runs on Intel (R) Core (TM) i5-10300H CPU @4.4GHz with 16 GB memory. The proposed DNN runs 5 times to obtain accurate solutions. The RMSE and MAE error measures, as well as the R2 regression coefficient, are used to assess the overall effectiveness of the proposed DNN. The presence of low error metrics and high R2 values implies outstanding results.
4.2.1 Assessment of Training Dataset
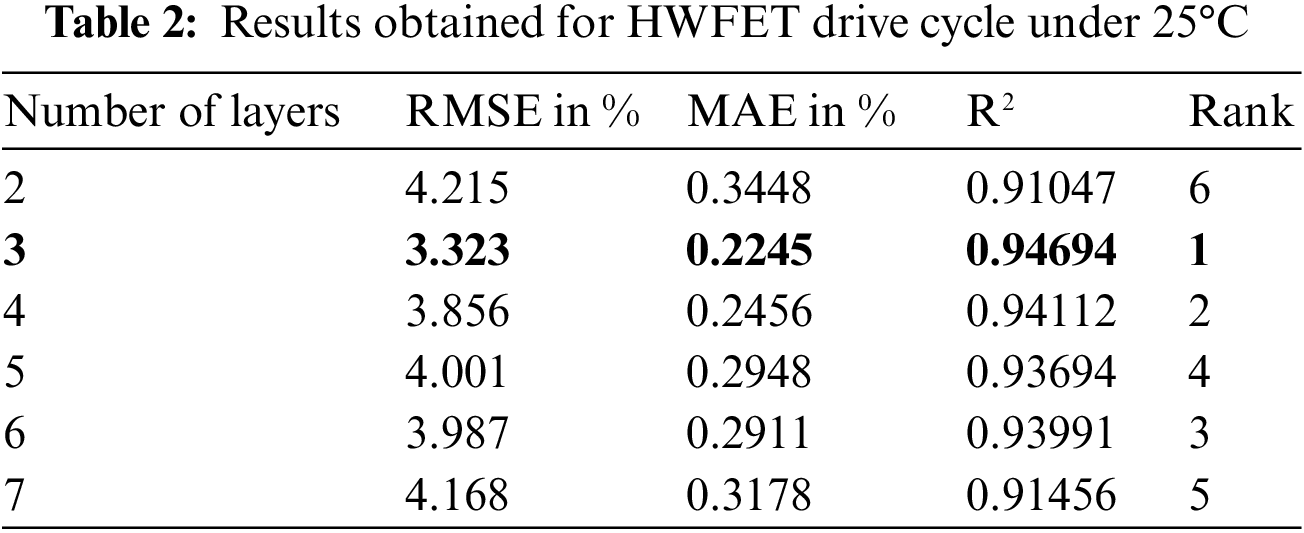
In order to find the optimal number of hidden layers or to observe the impact of the depth of DNN, the training was conducted using different layers, such as 2, 3, 4, 5, 6, and 7, with 40 neurons per layer. For this investigation, only the HWFET drive cycle with 25°C was considered. The error metrics and R2 obtained by the DNN with all different layers are listed in Tab. 2. The strongest DNN model, as determined by the error metrics, is indicated by the ranking column, which is ranked using the quicksort method. The findings show that the 3-layer DNN is the highest performing structure, with the smallest error values on MAE and RMSE and the greatest R2 regression coefficient of the model evaluated. The 2-layer DNN is, predictably, the model with the worst performance. The authors concluded that 3 layers with 40 neurons per layer gave the best results based on the results obtained. Therefore, in this paper, 3 layers with 40 neurons per layer are considered for all the drive cycles of EVs. Extending the level of the DNN usually results in improved accuracy up to a maximum of 6-layers. The MAE increases as the number of layers increases after the 6-layer.
4.2.2 Assessment on Testing Dataset
It is investigated in this subsection how well DNN performs on the test data, which comprises the UDDS, LA92, and US06 driving cycle data sets. DNN demonstrated excellent performance on the test set, as shown in Tab. 3. From the findings, it can be shown that the 3-layer DNN with 40 neurons per layer reasonably outperformed all other models, together with the 7-layer model, throughout the whole driving cycle. On the testing dataset, the 7-layer model was surprisingly ranked 5th, which was a surprising result. As discussed earlier, the strongest DNN model, as determined by the error metrics, is indicated by the ranking column, which is ranked using the quicksort method. The findings show that the 3-layer DNN is the highest performing structure, with the smallest error values on MAE and RMSE and the greatest R2 regression coefficient of the model evaluated. The 2-layer DNN is, predictably, the model with the worst performance. Based on the results obtained, the authors concluded that 3 layers with 40 neurons per layer gave the best results of all.
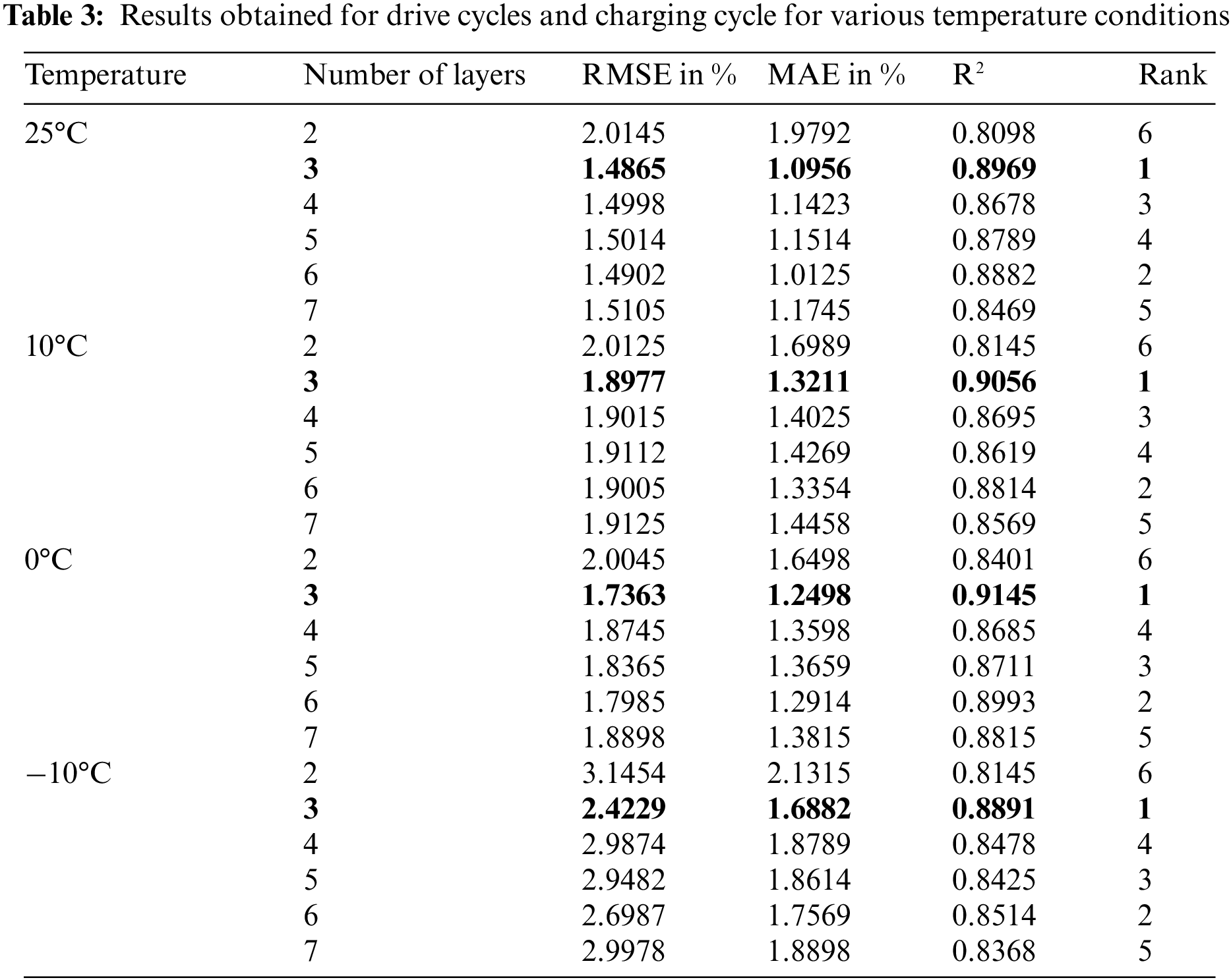
As discussed earlier, the proposed DNN model is executed 5 times individually to observe the best solutions. In order to visualize all the statistical measures, such as Maximum (MAX), RMSE, and MAE during all five different runs, the bar charts for all temperature conditions are presented in Figs. 7–9, respectively. Because of its reasonable accuracy, all the values are obtained and recorded only for 3-layer DNN with 40 neurons per layer. Fig. 7 shows the maximum values obtained by the proposed DNN model during five runs for different temperature conditions. Similarly, Fig. 8 shows the RMSE values obtained by the proposed DNN model during five runs for different temperature conditions. In addition, Fig. 9 shows the MAE values obtained by the proposed DNN model during five runs for all different temperature conditions.
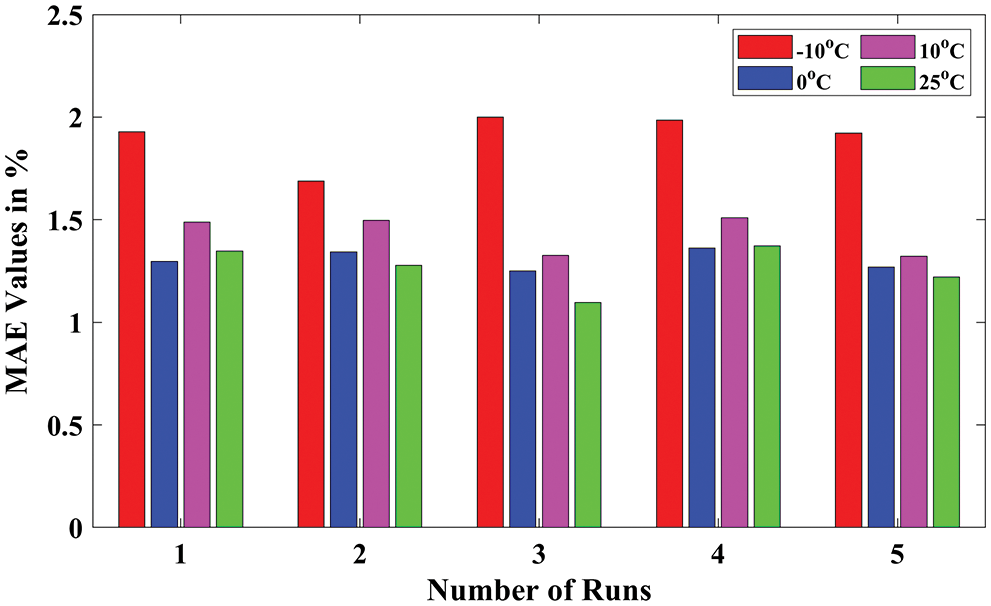
Figure 7: MAE values obtained by proposed DNN for all temperature conditions
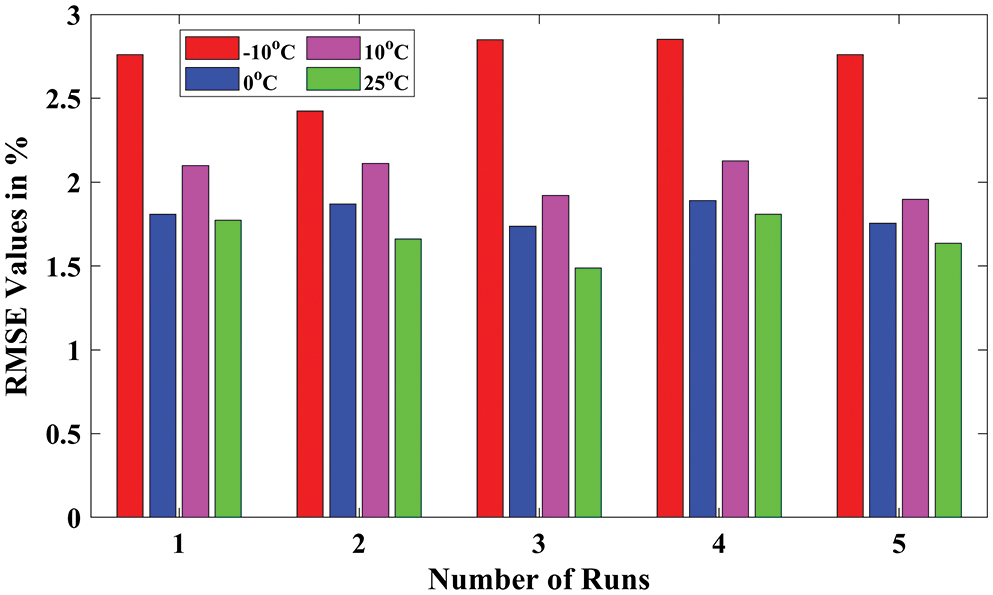
Figure 8: RMSE values obtained by proposed DNN for all temperature conditions
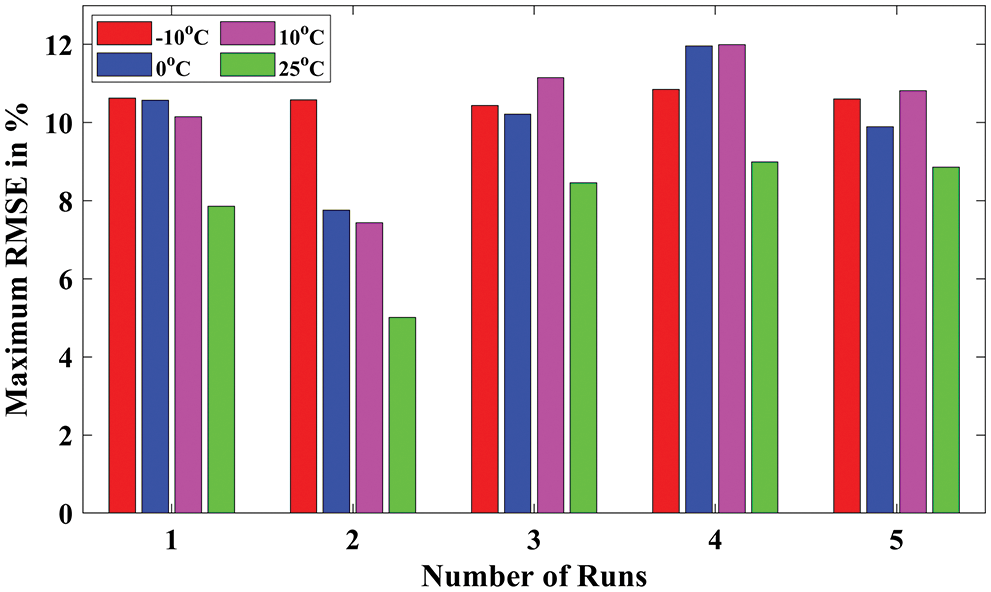
Figure 9: Maximum (MAX) RMSE values obtained by proposed DNN for all temperature conditions
This paper, related to prior efforts in [28], in which a shallow NN is trained and assessed on the same drive cycle, aims to validate that a DNN has a stronger generalization ability across multiple drive cycles and temperature fluctuations. The findings demonstrate that deeper models can fairly accurately forecast the state-of-charge of an unknown number of driving cycles, given that there is no overfitting. Figs. 10 to 12 demonstrate that the 3-layer DNN with 40 neurons per layer can predict SoC values with high accuracy when assessed on the UDDS, LA92, and US06 drive cycles.
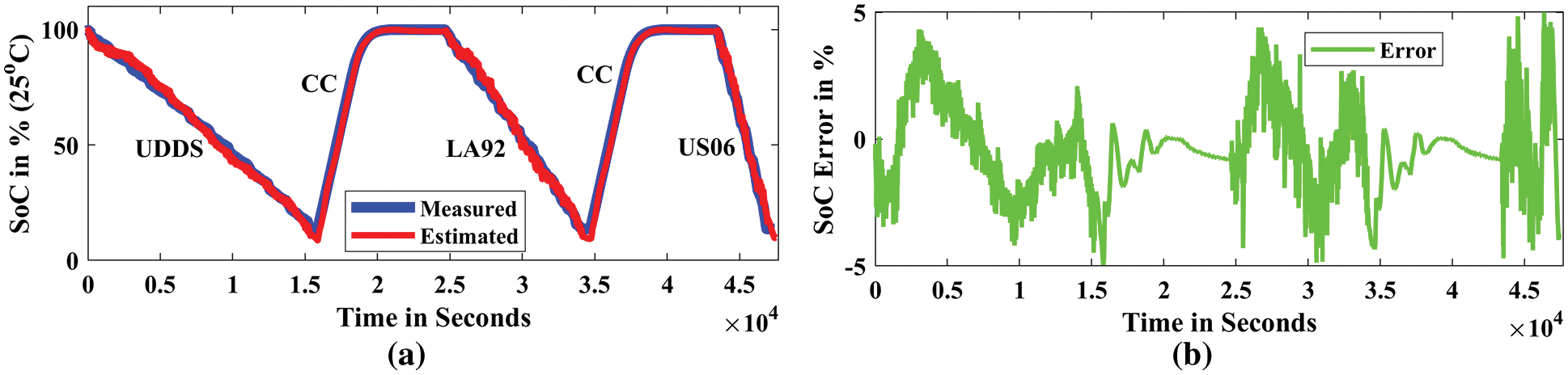
Figure 10: Estimated SoC for all drive cycles (25°C); (a) SoC estimation in %, (b) SoC prediction error in %
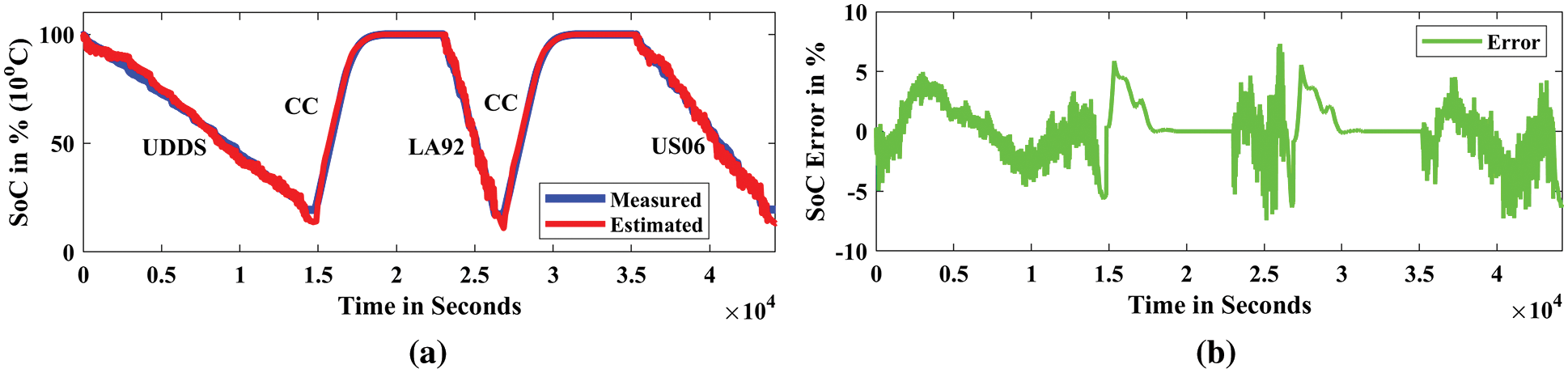
Figure 11: Estimated SoC for all drive cycles (10°C); (a) SoC estimation in %, (b) SoC prediction error in %
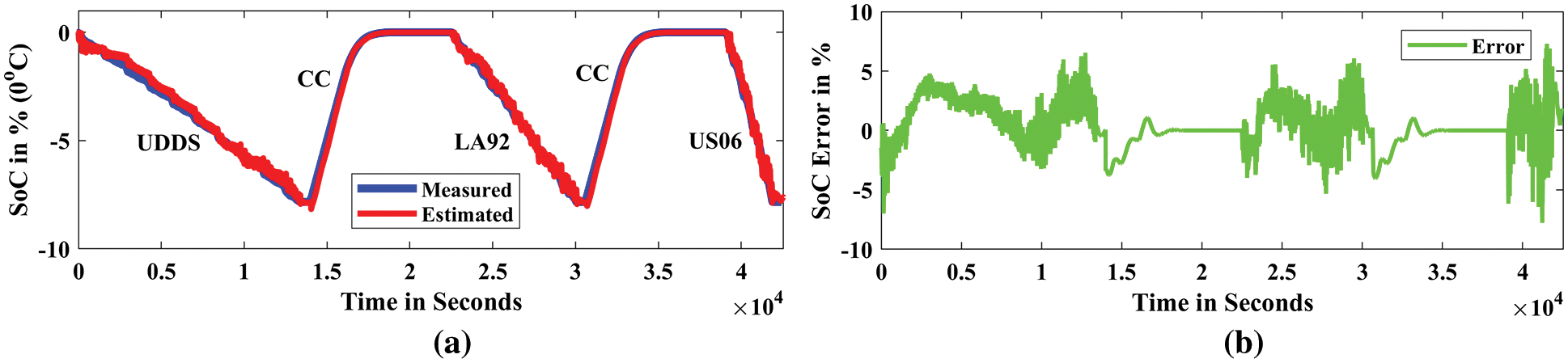
Figure 12: Estimated SoC for all drive cycles (0°C); (a) SoC estimation in %, (b) SoC prediction error in %
The estimated and measured SoC, as well as the SoC estimation error for the LG HG2 battery under 25°C, are displayed in the time domain graph in Fig. 10. Fig. 10a shows the curve fitting of the experimental SoC and predicted SoC. Fig. 10b shows the error between the experimental and estimated SoC under the 25°C temperature condition. Similarly, the measured and estimated SoC, as well as the SoC estimation error for the LG HG2 battery under 10°C, are also displayed in the time domain graph in Fig. 11. Fig. 11a shows the curve fitting of the experimental SoC and predicted SoC. Fig. 11b shows the experimental and estimated SoC error. In addition, The measured and estimated SoC, as well as the SoC estimation error for the LG HG2 battery under 0°C, are also displayed in the time domain graph in Fig. 12. Finally, the measured and estimated SoC, as well as the SoC estimation error for the LG HG2 battery under -10oC, are also displayed in the time domain graph in Fig. 13. Fig. 13a shows the curve fitting of the experimental SoC and predicted SoC. Fig. 13b shows the experimental and estimated SoC error. Fig. 12a shows the curve fitting of the experimental SoC and predicted SoC. Fig. 12b shows the experimental and estimated SoC error. The low percentage error (less than 5%) for both the drive and charging cycles. Therefore, it is concluded from the simulation results that the proposed DNN model with 3-hidden layers with 40 neurons per layer outperformed the SoC estimation of EV Li-ion batteries.
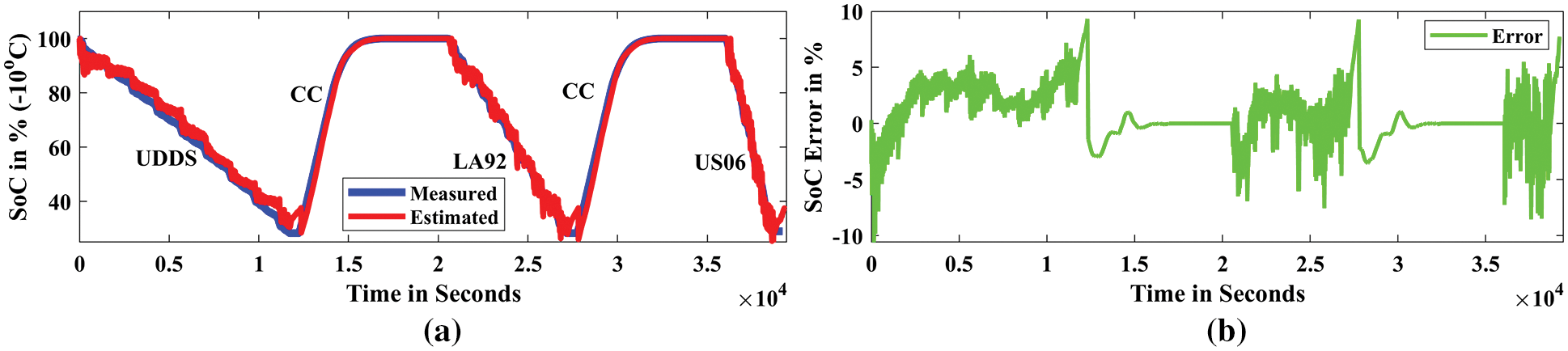
Figure 13: Estimated SoC for all drive cycles (−10°C); (a) SoC estimation in %, (b) SoC prediction error in %
In this research, a new DNN-based SoC prediction methodology for Li-ion batteries is developed, and the effectiveness of the methodology is demonstrated through simulation results. The SoC estimation of the LG HG2 battery under different temperature conditions has been effectively attained with less than 5% error. This work demonstrated that the 3-layer DNN model used in the HWFET drive cycle could predict the SoC of UDDS, LA92, and US06 drive cycles with a good degree of accuracy, as demonstrated in the experimental section. This paper supports the assumption that a deep neural network with appropriate hidden layers can generalize the forecast tendency of SoC from one driving cycle to another, as demonstrated. Similarly, it was proved that extending the depth of the DNN (from 2 to 7 layers) results in a reduction in error metrics. Therefore, the proposed DNN model appears to be quite promising, and its use in EV SoC estimate scenarios should be thoroughly examined when applying machine learning techniques. This study makes an important contribution by advancing the development of Li-ion batteries SoC estimation through the DNN algorithm, which results in enhanced SoC estimate performance and reduced error rates under various EV drive cycle trials.
The investigators anticipate that the contextual information provided in the input data would play a significant role in improving the accuracy of the SoC estimate in future studies. It is possible to train advanced deep learning models such as the deep convolutional NNs and long short-term memory to take advantage of time-related data to improve accuracy. Also essential is the consideration of the robustness of SoC prediction models to inaccuracies in current, voltage, and temperature sensor data, as well as the development of new methods for more accurate SoC estimation as the battery ages. It can also be applied to real-time applications, such as time series prediction, load forecasting, etc.
Acknowledgement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University (KKU) for funding this research project Number (R.G.P.2/133/43).
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. C. Vidal, O. Gross, R. Gu, P. Kollmeyer and A. Emadi, “xEV li-ion battery low-temperature effects-review,” IEEE Transactions on Vehicular Technology, vol. 68, no. 5, pp. 4560–4572, 2019. [Google Scholar]
2. C. Zhu, F. Lu, H. Zhang and C. C. Mi, “Robust predictive battery thermal management strategy for connected and automated hybrid electric vehicles based on thermoelectric parameter uncertainty,” IEEE Journal of Emerging and Selected Topics in Power Electronics, vol. 6, no. 4, pp. 1796–1805, 2018. [Google Scholar]
3. C. Vidal, P. Kollmeyer, E. Chemali and A. Emadi, “Li-ion battery state of charge estimation using long short-term memory recurrent neural network with transfer learning,” in Proc. of IEEE Transportation Electrification Conf. and Expo (ITEC), Detroit, MI, USA, pp. 1–6, 2019. [Google Scholar]
4. C. She, L. Zhang, Z. Wang, F. Sun, P. Liu et al., “Battery state of health estimation based on incremental capacity analysis method: Synthesizing from cell-level test to real-world application,” IEEE Journal of Emerging and Selected Topics in Power Electronics, vol. 10, no. 1, pp. 28–41, 2022. [Google Scholar]
5. S. Guo, R. Yang, W. Shen, Y. Liu and S. Guo, “DC-AC hybrid rapid heating method for lithium-ion batteries at high state of charge operated from low temperatures,” Energy, vol. 238, no. B, pp. 121809, 2022. [Google Scholar]
6. A. Samanta, S. Chowdhuri and S. S. Williamson, “Machine learning-based data-driven fault detection/diagnosis of lithium-ion battery: A critical review,” Electronics, vol. 10, no. 11, pp. 1309, 2021. [Google Scholar]
7. R. Xiong, J. Cao, Q. Yu, H. He and F. Sun, “Critical review on the battery state of charge estimation methods for electric vehicles,” IEEE Access, vol. 6, pp. 1832–1843, 2018. [Google Scholar]
8. M. Premkumar, M. K. Ramasamy, K. Kanagarathinam and R. Sowmya, “SoC estimation and monitoring of li-ion cell using kalman-filter algorithm,” International Journal on Electrical Engineering and Informatics, vol. 6, no. 4, pp. 418–427, 2018. [Google Scholar]
9. E. Chemali, P. J. Kollmeyer, M. Preindl and A. Emadi, “State-of-charge estimation of li-ion batteries using deep neural networks: A machine learning approach,” Journal of Power Sources, vol. 400, no. 5, pp. 242–255, 2018. [Google Scholar]
10. M. Zhang and X. Fan, “Review on the state of charge estimation methods for electric vehicle battery,” World Electric Vehicle Journal, vol. 11, no. 1, pp. 23, 2020. [Google Scholar]
11. Z. Nan, L. Hong, C. Jing, C. Zeyu and F. Zhiyuan, “A fusion-based method of state-of-charge online estimation for lithium-ion batteries under low-capacity conditions,” Frontiers in Energy Research, vol. 9, pp. 790295, 2021. [Google Scholar]
12. D. N. T. How, M. A. Hannan, M. S. H. Lipu, K. S. M. Sahari, P. J. Ker et al., “State-of-charge estimation of li-ion battery in electric vehicles: A deep neural network approach,” in Proc. of IEEE Industry Applications Society Annual Meeting, MD, USA, pp. 1–8, 2019. [Google Scholar]
13. V. Chandran, C. K. Patil, A. Karthick, D. Ganeshaperumal, R. Rahim et al., “State of charge estimation of lithium-ion battery for electric vehicles using machine learning algorithms,” World Electric Vehicle Journal, vol. 12, no. 1, pp. 38, 2021. [Google Scholar]
14. M. A. Hannan, M. S. H. Lipu and A. Hussain, “Toward enhanced state of charge estimation of lithium-ion batteries using optimized machine learning techniques,” Scientific Reports, vol. 10, no. 1, pp. 4687, 2020. [Google Scholar]
15. J. Chen, Q. Ouyang, C. Xu and H. Su, “Neural network-based state of charge observer design for lithium-ion batteries,” IEEE Transactions on Control Systems Technology, vol. 26, no. 1, pp. 313–320, 2018. [Google Scholar]
16. E. Chemali, P. J. Kollmeyer, M. Preindl, R. Ahmed and A. Emadi, “Long short-term memory networks for accurate state-of-charge estimation of li-ion batteries,” IEEE Transactions on Industrial Electronics, vol. 65, no. 8, pp. 6730–6739, 2018. [Google Scholar]
17. C. Vidal, P. Malysz, M. Naguib, A. Emadi and P. J. Kollmeyer, “Estimating battery state of charge using recurrent and non-recurrent neural networks,” Journal of Energy Storage, vol. 47, pp. 103660, 2022. [Google Scholar]
18. S. Tong, J. H. Lacap and J. Wan Park, “Battery state of charge estimation using a load-classifying neural network,” Journal of Energy Storage, vol. 7, pp. 236–243, 2016. [Google Scholar]
19. J. Meng, G. Luo and F. Gao, “Lithium polymer battery state-of-charge estimation based on adaptive unscented kalman filter and support vector machine,” IEEE Transactions on Power Electronics, vol. 31, no. 3, pp. 2226–2238, 2016. [Google Scholar]
20. D. Cui, B. Xia, R. Zhang, Z. Sun, Z. Lao et al., “A novel intelligent method for the state of charge estimation of lithium-ion batteries using a discrete wavelet transform-based neural network,” Energies, vol. 11, no. 4, pp. 995, 2018. [Google Scholar]
21. M. S. H. Lipu, M. A. Hannan, A. Hussain and M. H. M. Saad, “Optimal BP neural network algorithm for state of charge estimation of lithium-ion battery using PSO with PCA feature selection,” Journal of Renewable and Sustainable Energy, vol. 9, no. 6, pp. 064102, 2017. [Google Scholar]
22. N. Yang, Z. Song, H. Hofmann and J. Sun, “Robust state of health estimation of lithium-ion batteries using convolutional neural network and random forest,” Journal of Energy Storage, vol. 48, no. 4, pp. 103857, 2022. [Google Scholar]
23. S. Shen, M. Sadoughi, X. Chen, M. Hong and C. Hu, “A deep learning method for online capacity estimation of lithium-ion batteries,” Journal of Energy Storage, vol. 25, no. 2, pp. 100817, 2019. [Google Scholar]
24. A. Rastegarpanah, J. Hathaway and R. Stolkin, “Rapid model-free state of health estimation for end-of-first-life electric vehicle batteries using impedance spectroscopy,” Energies, vol. 14, no. 9, pp. 2597, 2021. [Google Scholar]
25. S. Jo, S. Jung and T. Roh, “Battery state-of-health estimation using machine learning and preprocessing with relative state-of-charge,” Energies, vol. 14, no. 21, pp. 7206, 2021. [Google Scholar]
26. Y. Zhang, C. Zhao and S. Zhu, “State of charge estimation of li-ion batteries based on a hybrid model using nonlinear autoregressive exogenous neural network,” in Proc. of IEEE PES Asia-Pacific Power and Energy Engineering Conf., Kota Kinabalu, Malaysia, pp. 772–777, 2018. [Google Scholar]
27. J. Schmidhuber, “Deep learning in neural networks: An overview,” Neural Networks, vol. 61, no. 3, pp. 85–117, 2015. [Google Scholar]
28. M. A. Hannan, M. S. H. Lipu, A. Hussain, M. H. Saad and A. Ayob, “Neural network approach for estimating state of charge of lithium-ion battery using backtracking search algorithm,” IEEE Access, vol. 6, pp. 10069–10079, 2018. [Google Scholar]
29. P. Kollmeyer, C. Vidal, M. Naguib and M. Skells, “LG 18650HG2 Li-ion battery data and example deep neural network xev soc estimator script,” Mendeley Data, vol. V2, pp. 1–20, 2020. [Google Scholar]
30. C. Vidal, P. Kollmeyer, M. Naguib, P. Malysz, O. Gross et al., “Robust xEV battery state-of-charge estimator design using deep neural networks,” SAE International Journal of Advances and Current Practices in Mobility, vol. 2, no. 5, pp. 2872–2880, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |