| Computers, Materials & Continua DOI:10.32604/cmc.2022.030547 |  |
| Article |
Bipolar Interval-Valued Neutrosophic Optimization Model of Integrated Healthcare System
1Department of Mathematics and Statistics, International Islamic University, Islamabad, Pakistan
2Department of Mathematics, Faculty of Arts and Sciences, Yildiz Technical University, Esenler, 34210, Istanbul, Turkey
3NUST Business School Islamabad, Pakistan
4Department of Mathematics and Computer Science, University of Oradea, Oradea, 410087, Romania
*Corresponding Author: Georgia Irina Oros. Email: georgis_oros_ro@yahoo.co.uk
Received: 29 March 2022; Accepted: 27 May 2022
Abstract: Bipolar Interval-valued neutrosophic set is another generalization of fuzzy set, neutrosophic set, bipolar fuzzy set and bipolar neutrosophic set and thus when applied to the optimization problem handles uncertain data more efficiently and flexibly. Current work is an effort to design a flexible optimization model in the backdrop of interval-valued bipolar neutrosophic sets. Bipolar interval-valued neutrosophic membership grades are picked so that they indicate the restriction of the plausible infringement of the inequalities given in the problem. To prove the adequacy and effectiveness of the method a unified system of sustainable medical healthcare supply chain model with an uncertain figure of product complaints is used. Time, quality and cost are considered as satisfaction level to choose best supplier for medicine procurement. The proposed model ensures 99% satisfaction for cost reduction, 63% satisfaction for the quality of product and 64% satisfaction for total time taken in medicine supply chain.
Keywords: Bipolar fuzzy set; neutrosophic set; interval-valued neutrosophic set; bipolar interval-valued neutrosophic set; supply chain fuzzy optimization
Fuzzy set theory offers not only an influential, significant and powerful role in depiction of imprecision and uncertainties, but also caters the subjectivity and vagueness of natural languages. To handle with uncertainty and imprecision, notion of fuzzy sets is formerly proposed by Zadeh [1]. In fuzzy sets each entity of a set is given a grade of membership whose values are given between zero and one. But it is a fact that not all logical and actual models depends only on evident evaluations of participation and true value of membership. There may emerge state of affairs where the level of non-enrollment and grades of non-membership is additionally needed with that of membership degree. Atanassov [2] combined this strength of rejection together with acceptance strength in new sets and named them as intuitionistic fuzzy set. His idea opened a new era towards generalizations of fuzzy sets as well as the mathematical modeling employing these generalizations. To model indeterminacy and inconsistency Samaranche [3] presented the idea of neutrosophic sets. These sets are independently characterized by three grades of memberships named acceptance grade, indeterminacy grade and grade of rejection. Neutrosophic model and its applications have been studied by many analysts with enormous and endless applications [4–16].
In real life scenario, wherever fuzzy sets and generalizations are taken into account, one merely has to rely on experts’ opinion to determine membership, non-membership and indeterminacy grades. For this purpose, real numbers between 0 and 1 are used to accommodate and quantify more elements while assigning them membership grades based on quantitative and deterministic attributes. This approach may fulfill the purpose theoretically but in real life it would be an unreliable judgment. There is also a common observation that a rigid numerical value cannot be considered realistic and error free if assigned to mere an experts opinion. Therefore Wang et al. [10] presented the ideology of interval-valued neutrosophic sets for a more realistic problem solving approach. The central idea is to restrict the magnitude of ambiguity by allotting intervals to the membership grades.
Bosc et al. [17] stated that bipolarity refers to the affinity of the human brain to motive and reconcile on possible alternatives based on negative and positive effects. Positive statistics refers to what is plausible, acceptable, permitted, wanted or measured as being satisfactory. Conversely negative articulations define what is unattainable, impermissible, dismissed, impossible or rejected. Negative deliberations relate to the constraints, since they impact which qualities or items must be dislodged and rejected (i.e., those that don’t achieve the constrains), while positive deliberations compare to needs, as they affirms which articles are greatly desirable than others (i.e., accomplish consumer expectations) without denying those that don’t fulfill the requirements. A vast assortment of human policy making, particularly multi-agent policy examination and choice assessment relies upon twofold or bipolar critical thinking on a positive end and a negative end. A couple of them may incorporate effect and manifestation, joint effort and contest, input and feedforward, friendship and ill will, shared advantages and clashing advantages and many more. It is debated that positive and negative causal connections should not be covered in a summation if they are not neutralizing in the meantime, or not from same sources, or not through same ways. Boolean set and its augmentations are unipolar that cannot be straightforwardly used to characterize bipolar truth for conception. Wei et al. [18] uses interval-valued bipolar fuzzy information for multiple attribute decision making problems. To evade the representational limitations of unipolar frameworks, a bipolar framework was proposed by Lee [19,20]. Deli et al. [21] presented the idea of Bipolar neutrosophic sets and their application based on multi-criteria decision making. Deli et al. [22] coined the idea of interval-neutrosophic sets with that of bipolarity and proposed interval valued bipolar neutrosophic sets. Further Broumi et al. [23] have developed an algorithm for finding minimum spanning tree where the edge weights is marked by interval-valued bipolar neutrosophic number.
Optimization strategies and theory plays a significant part in the assortment of domains to manage various real-world or genuine issues. Various methods have been acquainted to deal with problems in wide fields including engineering and supply issues. Over the most recent couple of years optimization approaches readily be given more attention. Progression in computing skills and increased dependency on real-like problems based on optimization are behind this change and many amazing proposition have been presented by numerous analysts and researchers. These issues give rise to the current expansions in the field of optimization methods, theory and applications. Some more recent applications of optimization problems in engineering, medical diagnosis, synthetic biology and transport infrastructure are given in [24–33].
Usually in optimization problems, it has been seen that a little change in the given conditions or constraints may provide better solutions to the given problem. A few times it isn’t helpful to consider exact requisites as a large number of these are acquired by assessment, or by researchers’ observations. Due to uncertainty involved in subjectivity of human languages and also in natural matters we cannot exactly predict or define the results of these matters. Such types of real-life problems always demand special attentions for solution [34–36]. Fuzzy optimization methods simplify the frameworks comprising vagueness more than any probability based stochastic optimization [37–42]. If ever we come across such a system where there is vagueness present in it along with the bipolar interval valued numeric, connecting the expression “ambiguity” with bipolar interval-valued fuzziness we consider bipolar interval-valued optimization to be a last alternative for our problem.
The resources required to provide products or services to a target customer are referred to as the supply chain. Strategic sourcing in healthcare is often a highly complicated and fragmented operation. This process and the allocation of resources become more complex if the data available contains fuzziness. Recent enriched technological and innovative, organizational and financial progressions in health-care organizations have given expanded admittance of dealing with patients [43–47]. Rendering to a delineation by the World Bank, world fatality rate have decreased to 7.75 per thousand persons in 2014 from 17.8 in 1960 [48]. Many dynamic elements have been involved in this decrease in the expiry rate like better-quality disease management, improved health-care facilities, and accessibility of drugs. Regardless of these improvements, advances in medical services foundation, supply chain management and infrastructure are unavoidable. Thus, for patients’ safety and recovery the accessibility to the suitable medicine with the perfect and balanced formula for the exact patient at the exact time in the accurate scale is needed.
Current work aims to construct and crack a medicine supply-chain model in interval-valued bipolar neutrosophic environment. This supply chain model is designed for a healthcare system that is integrated as-well as uncertain in-terms of product complaints. In its modest form a supply chain is the activities needed by the association to provide services or goods to the buyers. The conventional medical health-care facilities are restricted to drug organizations, patients and hospitals. Prescribed study comprises of a unified medi-care framework which likewise incorporates the role of public authority and healthcare department. The current work is divided into six sections. The first section provides a quick overview of fuzzy sets and extensions, focusing on bipolar interval-valued neutrosophic sets. Section two describes the whole medical supply chain model in detail. In addition, objective functions and model constraints are briefly examined. Section three discusses the proposed approach. Section four contains a numerical example based on the model developed in section two. A solution based on the prescribed approach is given in section five. For comparison in this section, satisfaction levels are considered. Lastly, section six comprises the conclusion. Development of proposed technique to determine the solution of this multi-objective and multi-period optimization problem in interval-valued bipolar neutrosophic backdrop is the motivation and objective of current study.
For the proposed study a group of contractors: a health division and a network of clinics and hospitals have been decided. The chain of clinics and hospitals need to choose the most appropriate dealer for the medicines based on the business trio that are cost, time and quality.
Indicators
Parameters
CL: cost of labor
CEH
CT: cost of transportation
Decision variable
1. The production limit of each dealer and price of specific medicine remains the same for the whole year.
2. In each period quality assurance cost remains the same.
3. The number of complaints regarding quality of product received by the manufacturer is uncertain.
4. The quality of units of medicine delivered over in the last year is known.
5. Labor cost remains the same throughout the year.
6. Carbon emission cost for handling and energy cost and carbon emission tax for transportation of medicines are known and fixed.
7. It is an integrated medi-care design in which chain of health centers pays the transportation expenditures.
The brief account of every objective function and constraints used to model the problem mathematically are as follow:
There are numerous factors effecting cost of medicine supply chain. At various level of this network different kinds of charges and dues are involved. Despite that, this particular problem is bound to the following costs.
The first term in the above equation depicts the cost of production, labour, energy and carbon emission handling. Labour cost, carbon emission handling cost and energy cost will remain the same throughout the specific period. The second term comprises of transportation cost and carbon emission tax for transportation and the cost of quality inspection done by health care department
Three types of times are involved in medicine supply network. First is the manufacturing time, second is the quality inspection time by the health care authorities and lastly the transportation time.
Here, the first term of the objective function describe the time taken by the suppliers or dealers in the manufacturing and second term is the sum of transportation time and time taken by health care department for quality inspection.
2.3.3 Quality Involved in Medicine Supply Chain
There are also many parameters to measure the quality level in the medicine supply chain; however the prescribed model rely on the complaints launched by the customers to maintain the quality level of suppliers. Mathematical modeling of quality function is described below:
Since number of complaints by the consumers is taken as quality assurance parameter; therefore, quality function is also minimized in the model. These complaints are highly uncertain because the suppliers do not know exactly about the number of complaints received regarding quality of certain products. Thus, fuzzy theory is used to handle the uncertainty associated with the model.
The process to determine the deviation in the fuzzy variable associated with quality function and comprises of three steps. In the first step, any of the fuzzy membership grades like trapezoidal or triangular can be taken. Afterwards, in the second step, fuzzification technique of conversion of a crisp function into a fuzzy function will be applied and at the last step defuzzification process will be followed. Again for defuzzification any of the already developed techniques like centroid method, first or last maxims, weighted average method, signed-distance method, center of largest area, and many more. Therefore, the equivalent defuzzified quality complaint function using signed-distance method is given below as
All the above stated objectives are subjected to the constraints given below:
This constraints limit the purchase by putting sum of quantity of medicine provided by dealers equals to the demand generated by health care units.
Quality constraints guarantees the standard acceptance quality limit.
Capacity constraint shows that the manufacturing capacity of dealers for any specific medicine should be greater than or equal to the quantity of medicine provided by dealer.
2.4.4 Non-negativity Constraints
this constraint ensures that the quantity must always be positive.
The value of binary variable is 1 when the quantity is released by the dealer and otherwise 0.
Multi-objective optimization problems occurred while dealing with optimization of non-commensurable, conflicting and multiple objective functions subject to certain conditions and circumstances. A general representation of a multi objective optimization problem with q constraints,
such that,
where
Problem (10) is reconsidered in a fuzzy environment as:
Find x such that,
and
where
To build up bipolar interval-valued membership functions of different target capacities we could initially acquire the table of positive solutions. Lower and upper bound of each membership grade is acquired by using this positive solution table.
The confluence
where,
where
Solution Methodology: In this model, bipolar interval-valued neutrosophic optimization technique is employed to solve multi-objective and multi-period problem. Following steps are followed to solve prescribed model.
Step 1: Table of positive solutions is attained by solving each objective function from set of
Step 2: Lower and upper bound of every objective function is attained by using below given relations
where
Step 3: Possible membership grades for bipolar interval valued neutrosophic linear programming problem is constructed as below.
where
Step 4: Transformed bipolar interval-valued neutrosophic optimization problem is given by
such that
with
such that
also,
where,
This part portray the use and efficacy of the prescribed model and approach. A real-life integrated medical supply chain application is used for further illustration and validation of the model as well as of solution approach.
Numerical Example: To tackle the prescribed model, we assume an example which is just hypothetical. Three medical healthcare units are situated in the central city, which are responsible for providing medi-care facilities to the nearby regions and surrounding areas (see Fig. 1). A large number of patients visit these healthcare units daily but randomly. As these patients come with diverse complaints and different diseases, therefore, hospitals need to buy various types of medicines on a regular basis. This particular example requires the medicine procurement for a time period of three months and also hospitals are keen to buy four medicines. Four different dealers are found in a 100 km range. The procurement division in the healthcare department is allocated with the duty of medicine purchase. Swift delivery, high quality and low cost are the parameters set by healthcare systems in the evaluation of the best supplier. It is decided to seek help from the healthcare department which has a system of conducting external audits for the evaluation of medicines based on quality, expenditure and delivery time.
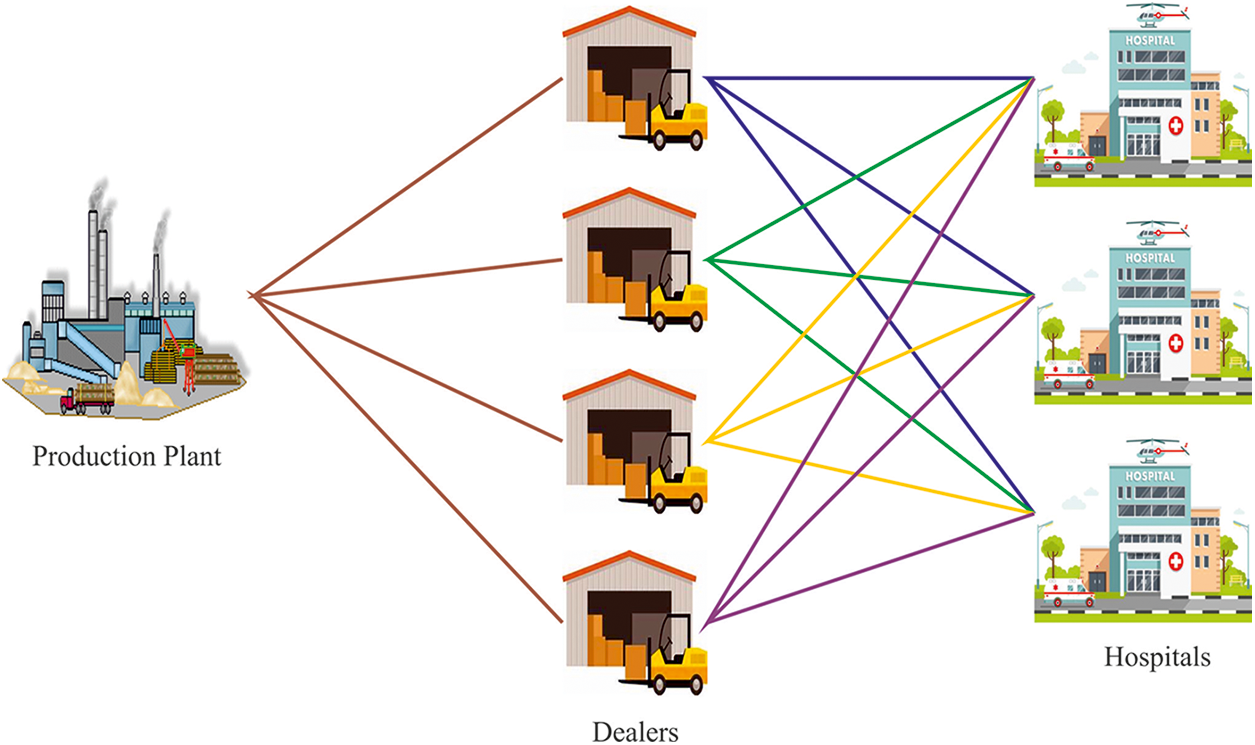
Figure 1: Medical healthcare supply chain network
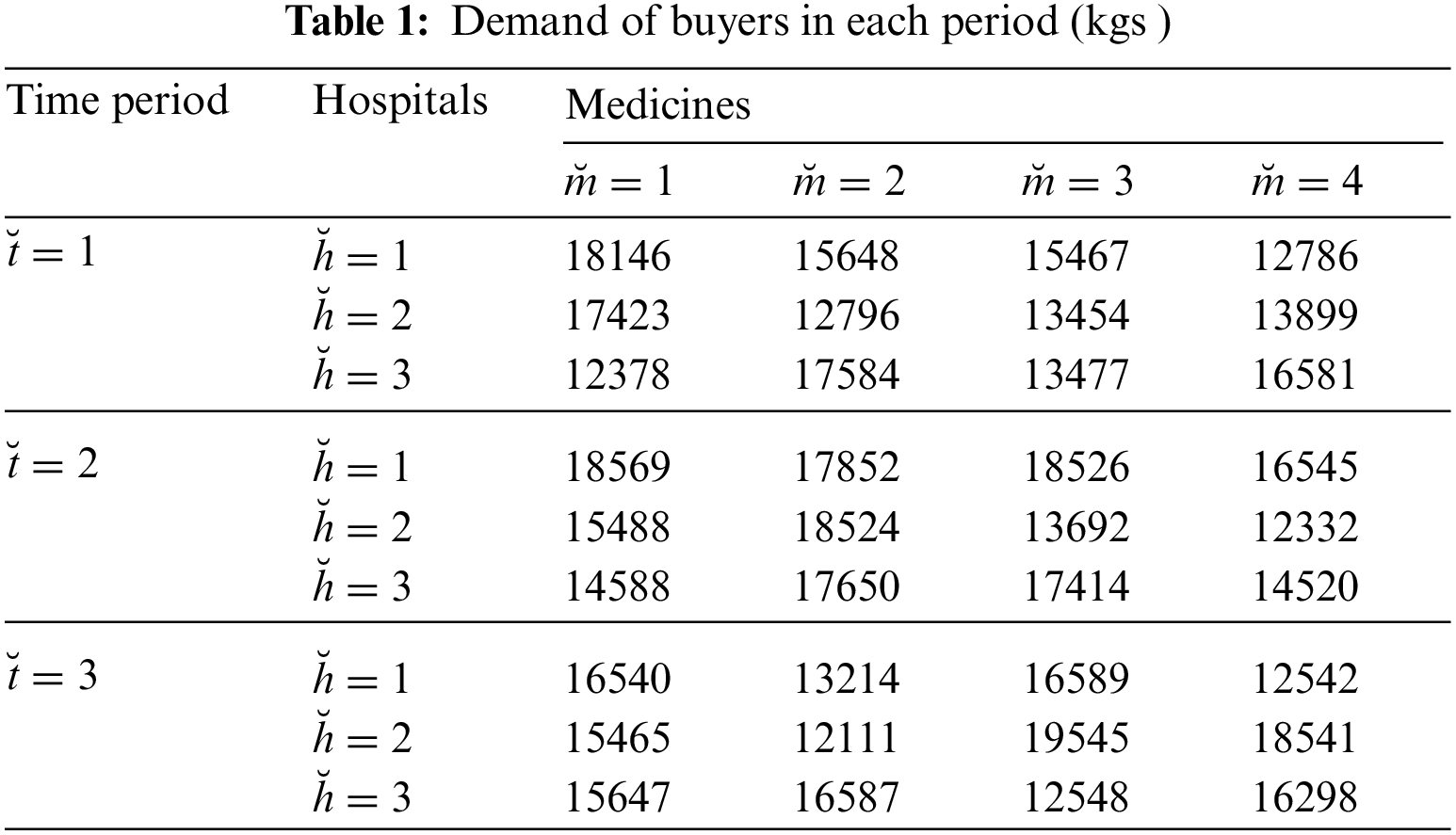
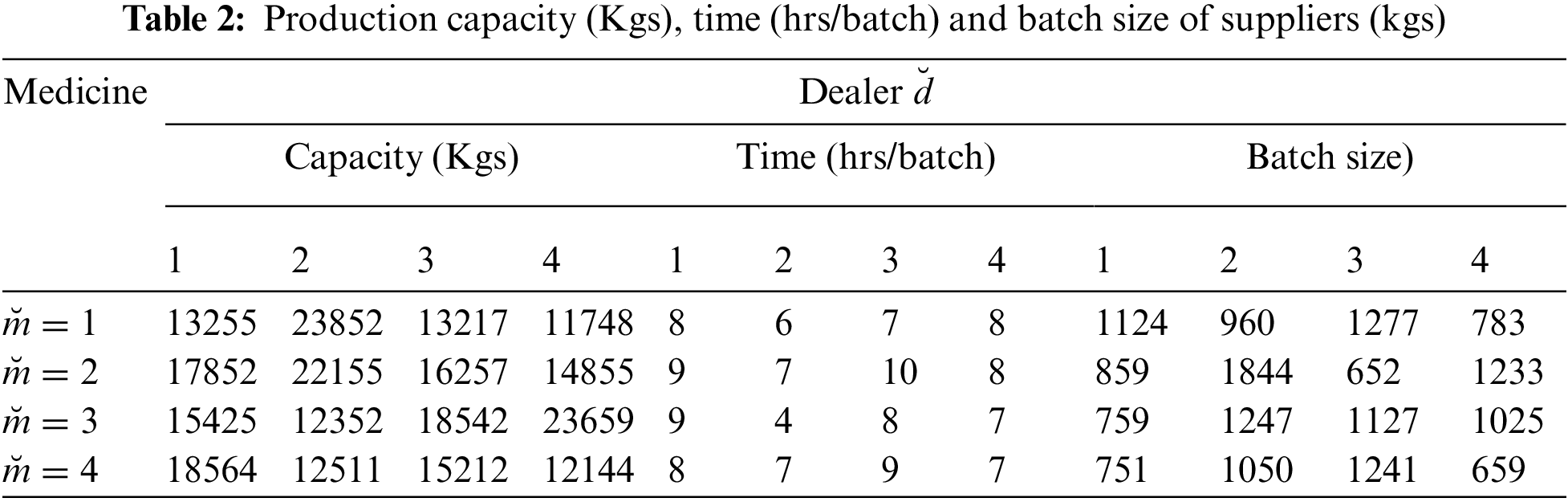
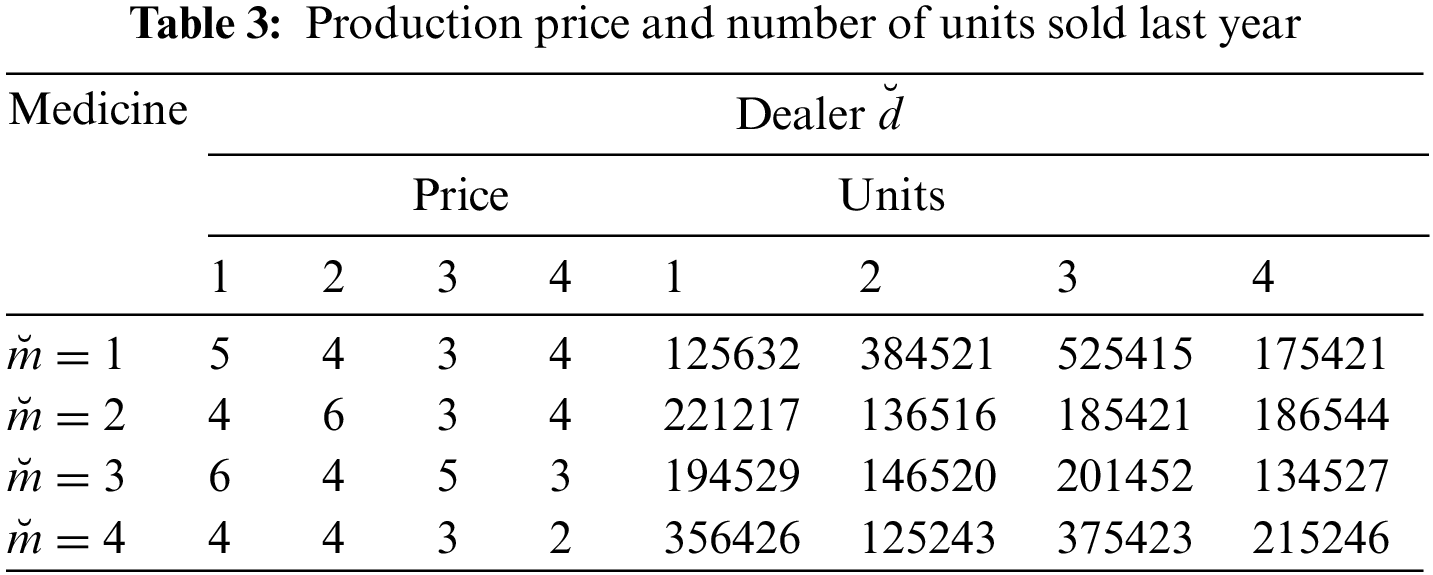
Hospital administration buys those medicines approved by the healthcare department, which means that the hospitals require verification and approval of the department to purchase medicines. Expected demand by the hospitals for each medicine for the coming three months is provided in Tab. 1 whereas capacity, production time and batch size of each month of each dealer for every medicine is given in Tab. 2. Whereas the production price and number of units sold in the last year are enlisted in Tab. 3. Tab. 4 exhibits the distance among the dealers and health care units. Quota of each medicine sold by each dealer in the past one year and customers complaints are evaluated by using the data for past year for each dealer is presented in Tab. 5.

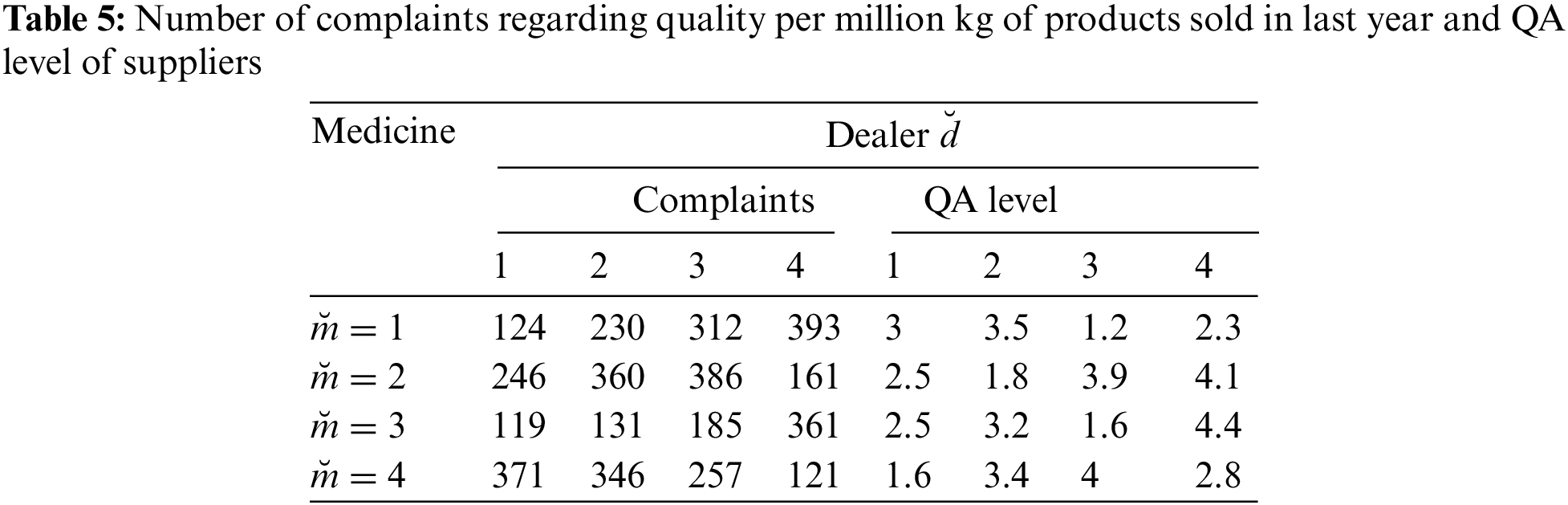
Standard acceptance level for this particular model is
5 Solution and Analysis Based on Numerical Results
Bipolar interval-valued neutrosophic optimization technique is applied to solve given numerical example. Step by step solution procedures are discussed in Section 3. Payoff table is constructed as per the procedure discussed in step 1.
The proposed technique includes the conversion of multi-objective problems to single objectives. Step 2 is applied to calculate the lower and upper bounds of each objective from the payoff matrix. Step 3 is followed to construct whole sets of membership grades. And lastly, the optimal value of each objective function is attained by following the procedure explained in step 4. The numerical findings were made on a personal computer with 4 GB RAM and a 2.50 GHz processor using MATLAB (R2017a).
5.1 Satisfaction Level and Percentage Achievement of Goals
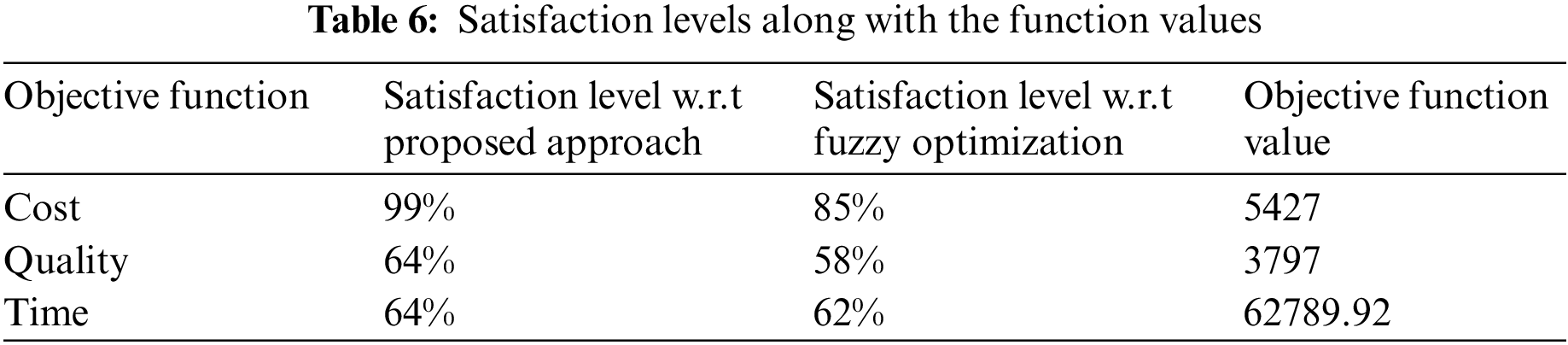
Tab. 6 shows the optimal function and the level of satisfaction attained for each objective. The level of satisfaction scales the relative rate of divergence of attained function values from the function values at higher and lower bounds. Closer the optimum value to the lower bound higher will be the satisfaction level. It is merely possible to achieve 100% satisfaction due to the dependency of lower and upper bounds on other objectives and constraints. Tab. 6 shows a 99% satisfaction is achieved for cost, 63% for quality and 64% for time. Percentage and priority of these goals and objectives differs from corporation to corporation. In setting the goals top level administration plays a significant role. For the given model, with conflicting objectives, bipolar interval-valued neutrosophic optimization still provides good results and better level of satisfactions are achieved.
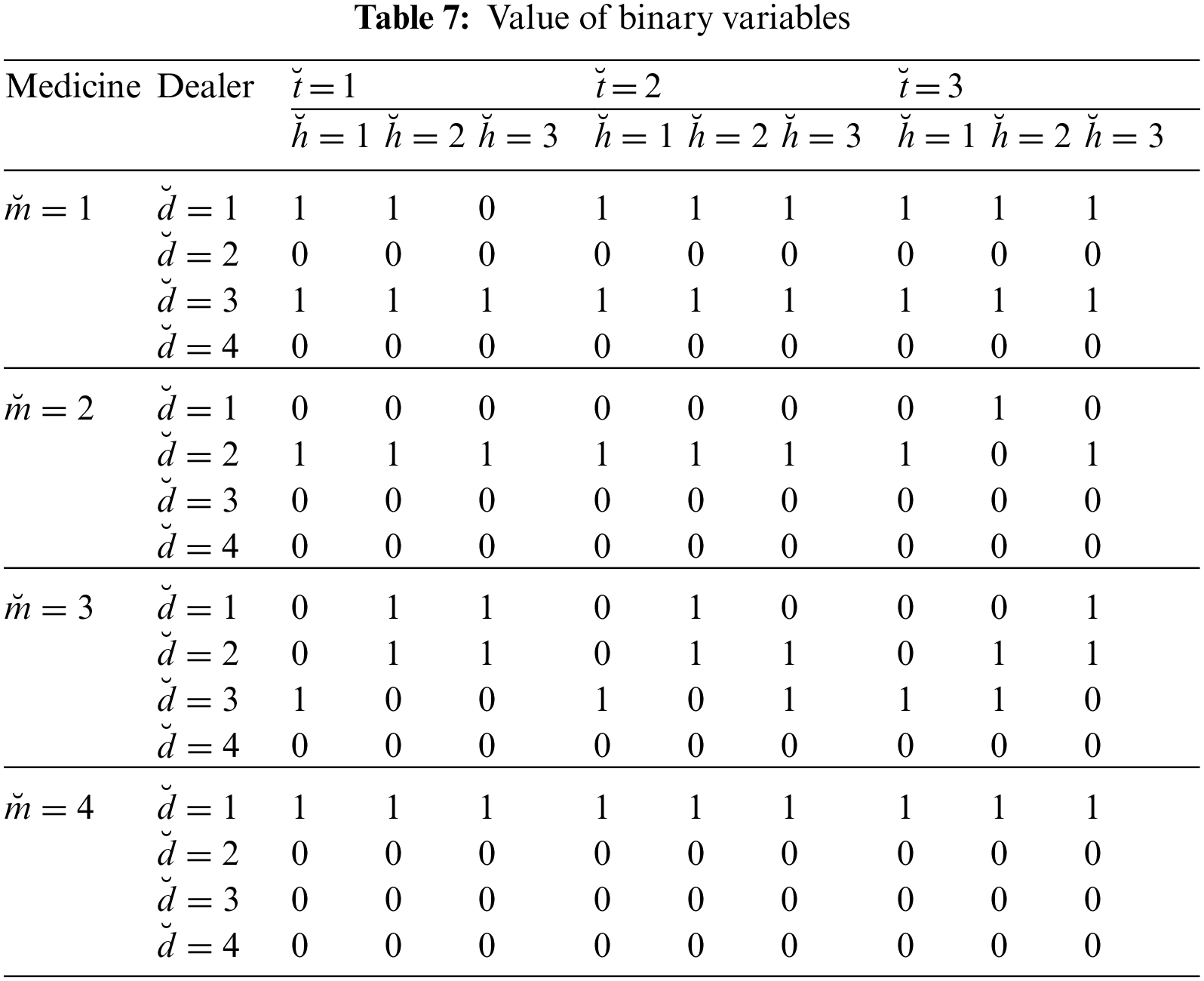
Tabs. 7 and 8 shows the values of decision variables in each period with respect to each medicine and supplier. Values of binary variable provided in Tab. 7 clearly show the most suitable supplier for specific medicine in some particular time period to each hospital. Acquiring the specified objectives while satisfying the conflicting constraint actually proves the success of any optimization method. Demand constraint is the primary constraint in the given model. From Tab. 1 the demand of medicine
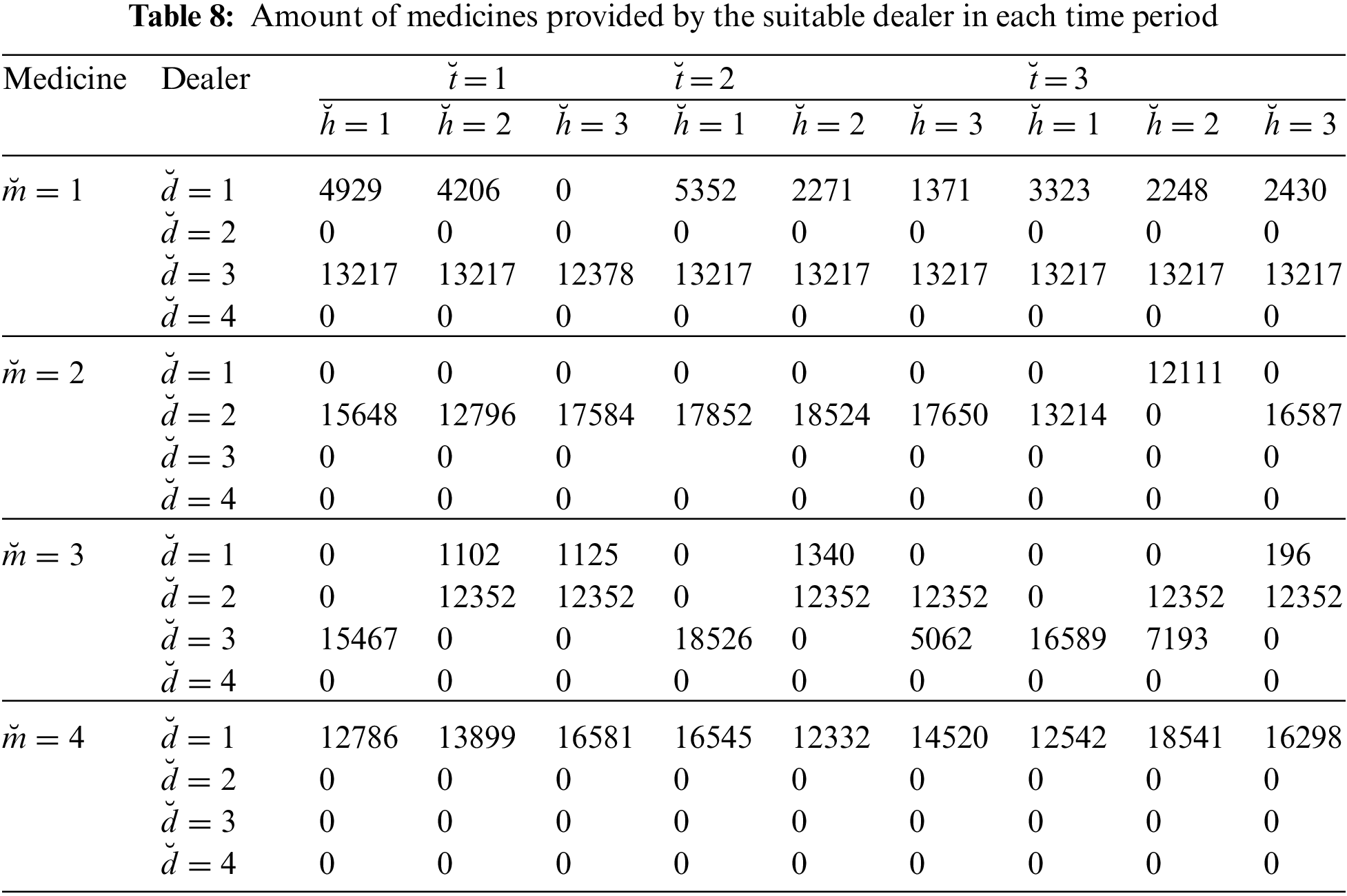
Selection of the most appropriate supplier in the procurement process of a healthcare system is always very challenging. Current work is an effort to model an integrated multi-objective and multi-period medicine supply chain problem to evaluate suppliers on the account of less number of quality complaints against per million units’ release of medicine, production, transportation and external audit cost and time taken for manufacturing and logistics. Current model is also taking care of the environmental aspect and effect of structured network. To minimize the effects of greenhouse gases a carbon emission cost and carbon emission tax for transportation of medicines are also infused in the prescribed model. To ensure the maintenance of quality this model also incorporates QAL constraint and significant input of health care department. On time delivery is also assured in the given model by minimizing manufacturing time, delivery time and quality inspection time. For illustration purpose a numerical model of three health care units, four dealers, and four medicines for three months of planning time period is considered. Bipolar interval-valued neutrosophic optimization is employed to attain optimality of the proposed model and the results achieved are quite satisfactory. Proposed approach not only convert this complicated multi-objective model into single objective but also provided 99% satisfaction for cost reduction, 63% satisfaction for the quality of product and 64% satisfaction for total time taken. To purchase different medicines procurement department can use the data of decision variables to select best dealer for each hospital. Future line of business may involve the purchase of life saving medical equipment from national and international markets, making it a global supply chain model. Since the environmental impact is also taken into account in the proposed model so in future it can be modified and upgarded for the managemet of any complex sustainable supply chain network.
Funding Statement: The research has been partially funded by the University of Oradea, within the Grants Competition “Scientific Research of Excellence Related to Priority Areas with Capitalization through Technology Transfer: INO-TRANSFER-UO”, Project No. 323/2021.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. L. A. Zadeh, “Fuzzy sets,” Information and Control, vol. 8, no. 3, pp. 338–353, 1965. [Google Scholar]
2. K. Atanassov, “Intuitionistic fuzzy sets,” Fuzzy Sets and Systems, vol. 20, pp. 87–96, 1986. [Google Scholar]
3. F. Smarandache, A Unifying Field in Logics: Neutrosophic Logic, Neutrosophy, Neutrosophic set, Neutrosophic Probability and Statistics, 4th ed., Rehoboth, USA: American Research Press, vol. 1, 1999. [Google Scholar]
4. H. D. Cheng and Y. Guo, “A new neutrosophic approach to image thresholding,” New Mathematics and Natural Computation, vol. 4, no. 3, pp. 291–308, 2008. [Google Scholar]
5. Y. Guo and H. D. Cheng, “New neutrosophic approach to image segmentation,” Pattern Recognition, vol. 42, no. 5, pp. 587–595, 2009. [Google Scholar]
6. H. Wang, F. Smarandache, Y. Q. Zhang and R. Sunderraman, “Single valued neutrosophic sets, multispace and multistructure,” Infinity Study, 2010. [Google Scholar]
7. A. Kharal, “A neutrosophic multi-criteria decision making method,” New Mathematics and Natural Computation, vol. 10, no. 2, pp. 143–162, 2014. [Google Scholar]
8. P. Liu and L. Shi, “The generalized hybrid weighted average operator based on interval neutrosophic hesitant set and its application to multiple attribute decision making,” Neural Computing and Applications, vol. 26, no. 2, pp. 457–471, 2015. [Google Scholar]
9. J. J. Peng, J. Q. Wang, J. Wang, H. Y. Zhang and X. H. Chen, “Simplified neutrosophic sets and their applications in multi-criteria group decision-making problems,” International Journal of Systems Science, vol. 47, no. 10, pp. 2342–2358, 2016. [Google Scholar]
10. H. Wang, F. Smarandache, Y. Q. Zhang and R. Sunderraman, “Interval neutrosophic sets and logic: Theory and applications in computing,” Theory and Applications in Computing, Infinity Study, Arizona, USA: Hexis, 2005. [Google Scholar]
11. J. Ye, “Similarity measures between interval neutrosophic sets and their applications in multi-criteria decision-making,” Journal of Intelligent and Fuzzy Systems, vol. 26, no. 1, pp. 165–172, 2014. [Google Scholar]
12. M. Zhang, L. Zhang and H. D. Cheng, “A neutrosophic approach to image segmentation based on watershed method,” Signal Processing, vol. 90, pp. 1510–1517, 2010. [Google Scholar]
13. G. Freen, S. Kousar, S. khalil and M. Imran, “Multi-objective non-linear four-valued refined neutrosophic optimization,” Computational and Applied Mathematics, vol. 39, no. 1, pp. 35, 2020. [Google Scholar]
14. S. Khalil, F. Smarandache, S. Kousar and G. Freen, “Multiobjective nonlinear bipolar neutrosophic optimization and its comparison with existing techniques,” in Optimization Theory Based on Neutrosophic and Plithogenic Sets, Academic Press, pp. 289–314, 2020. [Google Scholar]
15. M. L. Vzquez, M. A. Q. Martnez, Y. P. Castell, J. R. H. Hernndez and E. G. Caballero, “A new model for the selection of information technology project in a neutrosophic environment,” Neutrosophic Sets and Systems, vol. 32, pp. 343, 2020. [Google Scholar]
16. M. L. Vzquez, M. A. Q. Martnez, Y. P. Castell, J. R. H. Hernndez and E. G. Caballero, “An interval valued neutrosophic decision-making structure for sustainable supplier selection,” Expert Systems with Applications, vol. 183, pp. 115354, 2021. [Google Scholar]
17. P. Bosc and O. Pivert, “On a fuzzy bipolar relational algebra,” Information Sciences, vol. 219, pp. 1–16, 2013. [Google Scholar]
18. G. Wei, C. Wei and H. Gao, “Multiple attribute decision making with interval-valued bipolar fuzzy information and their application to emerging technology commercialization evaluation,” IEEE Access, vol. 6, pp. 60930–60955, 2018. [Google Scholar]
19. K. M. Lee, “Bipolar-valued fuzzy sets and their operations,” in Int. Conf. on Intelligent Technologies, Bangkok, Thailand, pp. 307–312, 2000. [Google Scholar]
20. K. J. Lee, “Bipolar fuzzy subalgebras and bipolar fuzzy ideals of BCK/BCI-algebras,” Bulletin of Malaysian Mathematical Science Society, vol. 32, no. 3, pp. 361–373, 2009. [Google Scholar]
21. I. Deli, M. Ali and F. Smarandache, “Bipolar neutrosophic sets and their application based on multi-criteria decision making problems,” in Int. Conf. on Advanced Mechatronic Systems (ICAMechS), Beijing, China, pp. 249–254, 2015. [Google Scholar]
22. I. Deli, S. Yusuf, F. Smarandache and M. Ali, “Interval valued bipolar neutrosophic sets and their application in pattern recognition,” in IEEE World Congress on Computational Intelligence, Vancouver, Canada, 2016. [Google Scholar]
23. S. Broumi, A. Bakali, M. Talea, F. Smarandache and R. Verma, “Computing minimum spanning tree in interval valued bipolar neutrosophic environment,” International Journal of Modeling and Optimization, vol. 7, no. 5, pp. 300–304, 2017. [Google Scholar]
24. C. N. Wang, T. M. Le and H. K. Nguyen, “Application of optimization to select contractors to develop strategies and policies for the development of transport infrastructure,” Mathematics, vol. 7, no. 1, pp. 98–112, 2019. [Google Scholar]
25. W. Yang, L. Cai, S. A. Edalatpanah and F. Smarandache, “Triangular single valued neutrosophic data envelopment analysis: Application to hospital performance measurement,” Symmetry, vol. 12, no. 4, pp. 588–602, 2020. [Google Scholar]
26. M. Shehab, L. Abualigah, H. A. Hamad, H. Alabool, M. Alshinwan et al., “Mothflame optimization algorithm: Variants and applications,” Neural Computing and Applications, vol. 32, no. 14, pp. 9859–9884, 2020. [Google Scholar]
27. L. Abualigah, “Group search optimizer: A nature-inspired meta-heuristic optimization algorithm with its results, variants, and applications,” Neural Computing and Applications, vol. 33, no. 7, pp. 1–24, 2020. [Google Scholar]
28. G. Naseri and M. A. Koffas, “Application of combinatorial optimization strategies in synthetic biology,” Nature Communications, vol. 11, no. 1, pp. 1–14, 2020. [Google Scholar]
29. M. A. Qaness, M. A. Ewees, H. Fan and M. A. E. Aziz, “Optimization method for forecasting confirmed cases of COVID-19 in China,” Journal of Clinical Medicine, vol. 9, no. 3, pp. 674–689, 2020. [Google Scholar]
30. D. V. D. Berg, T. Savage, P. Petsagkourakis, N. Shah and E. A. D. R. Chanona, “Data-driven optimization for process systems engineering applications,” Chemical Engineering Science, vol. 248, pp. 117–135, 2022. [Google Scholar]
31. V. Guarrasi, N. C. Damico, R. Sicilia, E. Cordelli and P. Soda, “Pareto optimization of deep networks for COVID-19 diagnosis from chest X-rays,” Pattern Recognition, vol. 121, pp. 108242, 2022. [Google Scholar]
32. M. Alweshah, S. Alkhalaileh, M. A. A. Betar and A. A. Bakar, “Corona virus herd immunity optimizer with greedy crossover for feature selection in medical diagnosis,” Knowledge-Based Systems, vol. 235, pp. 107629, 2022. [Google Scholar]
33. V. I. Khabarov and O. G. Khabarova, “Efficiency of labor resources use and issues of transport supply and demand development in large cities and agglomerations,” Transportation Research Procedia, vol. 61, pp. 308–313, 2022. [Google Scholar]
34. F. Ahmad, “Interactive neutrosophic optimization technique for multi-objective programming problems: An application to pharmaceutical supply chain management,” Annals of Operations Research, vol. 311, pp. 551–585, 2022. [Google Scholar]
35. P. Day and T. K. Roy, “Multi-objective non-linear programming problem based on neutrosophic optimization technique and its application in riser design problem,” Neutrosophic Sets and Systems, vol. 9, pp. 88–95, 2015. [Google Scholar]
36. S. K. Bharati and S. R. Singh, “Solution of multi-objective linear programming problems in interval-valued intuitionistic fuzzy environment,” Soft Computing, vol. 23, no. 1, pp. 77–84, 2019. [Google Scholar]
37. H. J. Zimmermann, “Fuzzy programming and linear programming with several objective functions,” Fuzzy Sets and Systems, vol. 1, pp. 45–55, 1978. [Google Scholar]
38. P. P. Angelov, “Optimization in an intuitionistic fuzzy environment,” Fuzzy Sets and Systems, vol. 86, pp. 299–306, 1997. [Google Scholar]
39. D. S. Kumar, S. A. Edalatpanah and J. K. Dash, “A novel lexicographical-based method for trapezoidal neutrosophic linear programming problem, ” Neutrosophic Sets and Systems, vol. 46, no. 1, pp. 12–42, 2021. [Google Scholar]
40. Q. Wang, Y. Huang, S. Kong, X. Ma, Y. Liu et al., “A novel method for solving multiobjective linear programming problems with triangular neutrosophic numbers,” Journal of Mathematics, vol. 2021, 2021. https://doi.org/10.1155/2021/6631762. [Google Scholar]
41. C. Veeramani, S. A. Edalatpanah and S. Sharanya, “Solving the multiobjective fractional transportation problem through the neutrosophic goal programming approach,” Discrete Dynamics in Nature and Society, vol. 2021, 2021. https://doi.org/10.1155/2021/7308042. [Google Scholar]
42. H. Kamacı and S. Petchimuthu, “Some similarity measures for interval-valued bipolar q-rung orthopair fuzzy sets and their application to supplier evaluation and selection in supply chain management,” Environment, Development and Sustainability, pp. 1–40, 2022. https://doi.org/10.1007/s10668-022-021 https://30-y. [Google Scholar]
43. M. Navascus, C. Budroni and Y. Guryanova, “Disease control as an optimization problem,” PLOS One, vol. 16, no. 9, pp. 0257958–0257975, 2021. [Google Scholar]
44. M. Beaulieu and O. Bentahar, “Digitalization of the healthcare supply chain: A roadmap to generate benefits and effectively support healthcare delivery,” Technological Forecasting and Social Change, vol. 167, pp. 120717–120727, 2021. [Google Scholar]
45. D. Friday, D. A. Savage, S. A. Melnyk, N. Harrison, S. Ryan et al., “A collaborative approach to maintaining optimal inventory and mitigating stockout risks during a pandemic: Capabilities for enabling health-care supply chain resilience,” Journal of Humanitarian Logistics and Supply Chain Management, vol. 11, no. 2, pp. 248–271, 2021. [Google Scholar]
46. P. D. Singh, G. Dhiman and R. Sharma, “Internet of things for sustaining a smart and secure healthcare system,” Informatics and Systems, vol. 33, pp. 100622–100641, 2022. [Google Scholar]
47. J. C. Ho, M. K. Shalishali, T. L. B. Tseng and D. S. Ang, “Opportunities in green supply chain management,” The Coastal Business Journal,” vol. 8, no. 1, pp. 2–17, 2022. [Google Scholar]
48. 2020. http://data.worldbank.org/indicator/SP.DYN.CDRT.IN. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |