Computers, Materials & Continua DOI:10.32604/cmc.2022.030888
Article

Swarming Computational Efficiency to Solve a Novel Third-Order Delay Differential Emden-Fowler System

Wajaree Weera1, Zulqurnain Sabir2, Muhammad Asif Zahoor Raja3, Sakda Noinang4 and Thongchai Botmart1,*

1Department of Mathematics, Faculty of Science, Khon Kaen University, Khon Kaen, 40002, Thailand
2Department of Mathematics and Statistics, Hazara University, Mansehra, Pakistan
3Future Technology Research Center, National Yunlin University of Science and Technology, 123 University Road, Section  3, Douliou, Yunlin, 64002, Taiwan
4Department of Mathematics Statistics and Computer, Faculty of Science, Ubon Ratchathani University, Ubon Ratchathani, 34190, Thailand
*Corresponding Author: Thongchai Botmart. Email: thongbo@kku.ac.th
Received: 05 April 2022; Accepted: 25 May 2022

Abstract: The purpose of this research is to construct an integrated neuro swarming scheme using the procedures of the artificial neural networks (ANNs) with the use of global search particle swarm optimization (PSO) along with the competent local search interior-point programming (IPP) called as ANN-PSOIPP. The proposed computational scheme is implemented for the numerical simulations of the third order nonlinear delay differential Emden-Fowler model (TON-DD-EFM). The TON-DD-EFM is based on two types along with the particulars of shape factor, delayed terms, and singular points. A merit function is performed using the optimization of PSOIPP to find the solutions to the TON-DD-EFM. The effectiveness of the ANN-PSOIPP is certified through the comparison with the exact results for solving four examples of the TON-DD-EFM. The scheme’s efficiency is observed by performing the absolute error in suitable measures found around 10−04 to 10−07. Furthermore, the statistical-based assessments for 100 trials are provided to compute the accuracy, stability, and constancy of the ANN-PSOIPP for solving the TON-DD-EFM.

Keywords: Third-order nonlinear emden-fowler system; artificial neural network; statistical results; particle swarm optimization; numerical experimentations; local search programming

1  Introduction

The delayed form of the differential system is considered one of the noteworthy, historical, and significant equation, which has attracted the research community because of its massive applications. A few of them are biological models, dynamical-based population models, communication models, engineering/economical models, propagation, and transport systems [1–5]. To solve the delay differential models, many researchers suggested a numerical and analytical schemes to tackle the difficulty of the delay terms. Brunner et al. [6] proposed a numerical discontinuous Galerkin approach, and Hsiao et al. [7] applied the Haar wavelet scheme to handle the delay factor. Wang [8] proposed the Legendre wavelet approach to solving the delay differential scheme. Rach and Adomian [9] proposed the Adomian decomposition scheme to solve the delay form of the differential system. Shakeri et al. [10] solved the delay differential model with the homotopy perturbation approach. Erdogan et al. [11] applied the finite difference numerical scheme to solve the perturbed singular delay differential system. The generic form of the delay differential is given as [12,13]:

{d3vdε3=g(ε,v(ε−t),ddεv(ε−t),d2dε2v(ε−t)),v(0)=a,dv(0)dε=b,d2v(0)dε2=c,(1)

where g indicates the linear or nonlinear-based function and t represents the delayed factor. The singular investigations have achieved huge significance because of numerous applications in engineering, and physical and biological studies. It is not easy to solve the singularity-based systems because of their hard, difficult, challengeable, and grim nature. One significant, famous, singular, and historical form is the Emden-Fowler, which has many applications, like population growth, relativistic mechanics, pattern formation, fluid dynamics, and chemical reactors modeling. The Emden-Fowler system is mathematically given as [14–18]:

{d2vdε2+uεdudε+g(ε)h(v)=0,v(0)=a1,dv(0)dε=a2,(2)

where u≥1 indicates the shape vector and the Emden-Fowler model given in Eq. (2) can become the Lane-Emden for g(ε)=1. The Lane-Emden is one of the singular systems that derived a few centuries ago by the astrophysicists J. H. Lane and the R. Emden in their pioneer work. This prominent model designates the inner polytropic of structure stars, cluster galaxies, radiative cooling and model based on gas cloud. The Lane-Emden singular system has various applications in the isotropic based continuous media [19], physical scientific fields [20], density field of gaseous stars [21], dusty fluid systems [22], morphogenesis [23], stellar arrangement models [24], oscillating magnetic systems [25], catalytic diffusion reactions [26], isothermal gas sphere systems [27], mathematical sciences [28], electromagnetic theory [29] and quantum as well as classical mechanics [30]. The Lane-Emden model is given as:

{d2vdε2+uεdudε+h(v)=0,v(0)=a1,dv(0)dε=a2.(3)

The research community presented the solutions of the above model by applying different techniques. A few methods for presenting the solutions of the Lane-Emden system are the Adomian decomposition scheme suggested by Wazwaz and Shawagfeh [31,32]. Adel et al. [33] solved the pantograph Lane-Emden model using the Bernoulli collocation method. Abdelkawy et al. [34] solved the singular coupled functional Lane–Emden system using the famous spectral collocation scheme. Parand et al. [35] introduced a numerical approach for the singular equation of the Lane-Emden type. Using stochastic procedures, Sabir et al. [36] presented a nonlinear singular functional differential system.

In this study, the TON-DD-EFM is numerically discussed through the artificial neural networks (ANNs) by using the optimization procedure based on the global particle swarm optimization (PSO) aided with the local search-based interior-point programming (IPP), i.e., ANN-PSOIPP. The singular models are assumed to be tough by using the traditional and conventional schemes, like Runge-Kutta, Adams numerical method, Milne-Predictor-Corrector scheme, and many others. However, the researcher’s alternative and best choice are to solve the singular-based models using procedures based on the ANNs. There are several applications where ANNs have been exploited to solve many models in recent years; a few of them are the multi-singular higher-order Emden–Fowler system [37–43], nonlinear SIR dengue fever model [44], HIV infection system [45,46], third-order singular Emden–Fowler equation [47], SITR system [48], second kind of singular model [49], mosquito dispersal model [50] and many more [51–54]. By keeping the worth of these models, authors are interested in exploiting the singular TON-DD-EFM, which has never been solved before by using the stochastic ANN-PSOIPP. The general forms of the singular TON-DD-EFM are based on the two types given as [55]:

{d3dε3v(ε−t)+2χεd2dε2v(ε−t)+χ(χ−1)ε2ddεv(ε−t)+g(ε)h(v)=f(ε),v(0)=α,dv(0)dε=0,d2v(0)dε2=0,(4)

{d3dε3v(ε−t)+2χεd2dε2v(ε−t)+χ(χ−1)ε2ddεv(ε−t)+g(ε)h(v)=f(ε),v(0)=α,dv(0)dε=0,d2v(0)dε2=0,(5)

where χ is a real number always taken positive and f(ε) represents the forcing factor. The terms g(ε) and h(v) represent the ε and v functions. The singularity appears twice at ε = 0 in the first form of the model, represented in Eq. (4), while a single singularity occurs in the second type derived in Eq. (5). The shape factors in the 1st type are 2χ and χ(χ−1), whereas a single shape factor χ is observed in the 2nd type. Likewise, the delayed factors in the 1st type are noticed thrice than are observed in the first, second, and third factors. In the 2nd case, the delayed factors appeared twice in the first and second factors. The novel features of the proposed ANN-PSOIPP are concisely briefed as follows:

•   A novel design of ANN-PSOIPP is proposed to solve the singular TON-DD-EFM numerically along with its two types.

•   The detail about the delay factors, singular point, and shape factor is provided for solving the singular TON-DD-EFM.

•   The intersection of the exact/proposed solutions through ANN-PSOIPP proves the worth in the form of convergence to solve both cases of the singular TON-DD-EFM.

•   The correctness of the ANN-PSOIPP is observed through the good performance of the absolute error (AE) for solving the singular system.

•   The statistical performance is provided for the dependability of the stochastic ANN-PSOIPP by using the “Theil’s inequality coefficient (T.I.C)”, “root mean square error (R.MSE)”, and “Nash Sutcliffe efficiency (NSE)” for solving both the cases of the TON-DD-EFM.

•   Alongside the reasonable precise solutions of the cases of the singular TON-DD-EFM, stability, ease of understanding, robustness, specific applicability, and smooth operation are other valued advantages.

The other paper parts are provided as follows: Section 2 describes the procedures of the stochastic ANN-PSOIPP. Section 3 represents the performance operators. The results detail for solving the singular TON-DD-EFM are provided in Section 4. Finally, the conclusions are listed in the final section.

2  Designed Methodology

The designed ANN-PSOIPP approach is separated into two steps to demonstrate the performance of singular TON-DD-EFM. First, to introduce a fitness function (FF) for solving the model and the hybrid of the designed ANN-PSOIPP.

2.1 Modeling Based on ANNs

Several researchers implemented the modeling based on ANNs in various investigations to understand the nonlinear models in various fields. v(ε) indicates the results based on continuous mapping by implementing the FF, i.e., log-sigmoid s(ε)=(1+e−ε)−1 is written as:

v^(ε)=∑i=1kais(wiε+ci)=∑i=1kai(1+e−(wiε+ci))−1,dv^dε=∑i=1kaiddεs(wiε+ci)=∑i=1kaiwie−(wiε+ci)(1+e−(wiε+ci))−2,d2v^dε2=∑i=1kaid2dε2s(wiε+ci)=∑i=1kaiwi2(2e−2(wiε+ci)(1+e−(wiε+ci))−3−e−(wiε+ci)(1+e−(wiε+ci))−2),d3v^dε3=∑i=1kaid3dε3s(wiε+ci)=∑i=1kaiwi3(6e−3(wiε+ci)(1+e−(wiε+ci))−4−6e−2(wiε+ci)(1+e−(wiε+ci))−3+e−(wiε+ci)(1+e−(wiε+ci))−2),(6)

where a=[a1,a2,…,ak],w=[w1,w2,…,wk] and c=[c1,c2,…,ck] show the weight vectors. To solve the singular TON-DD-EFM given in Eqs. (4) and (5), the FF in the mean square error form is given as:

e=efit−1+efit−2,(7)

efit−1=efit−a+efit−b,(8)

efit−2=efit−c+efit−d,(9)

where efit−a and efit−b are the error based FFs in the form of differential model given in the Eqs. (4) and (5), while efit−c and efit−d represent the corresponding initial conditions (ICs), written as:

efit−a=1N∑k=1N(d3v^(εk−t)dεk3+2χεkd2v^(εk−t)dεk2+χ(χ−1)εk2dv^(εk−t)dεk+gkh(v^k)−fk)2,(10)

efit−b=1N∑k=1N(d3v^(εk−t)dεk3+χεkd2v^(εk−t)dεk2+gkh(v^k)−fk)2,(11)

efit−c=13((v^0−α)2+(dv^0dεk)2+(d2v^0dεk2)2),(12)

efit−d=13((v^0−α)2+(dv^0dεk−β)2+(d2v^0dεk2)2),(13)

where, Nh=1,v^k=v^(εk),gk=g(εk),fk=f(εk) and xk=kh.

2.2 Optimization: ANN-Psoipp

For the singular TON-DD-EFM given in Eqs. (4) and (5), the design of the ANN-PSOIPP scheme is presented.

Particle Swarm Optimization (PSO): It is an optimization process known as replacing a genetic algorithm [56]. PSO was introduced by Eberhart and Kennedy a few decades ago, which required short memory and was applied as an easy implementation process. PSO has been extensively applied as an optimization technique, like optical stuff based on multilayer thin films [57], electric daily peak-load forecasting [58], high-dimensional clustering statistics [59], prediction differential models [60], parameter approximation of chaotic plots [61], optimization of nonlinear benchmark model [62] and parameter estimate models in electromagnetic waves of the plane [63].

A particular candidate result for the optimization process is authenticated as a particle in space study. The network is revealed in the PSO scheme to make a swarm. For the ideal presentation of the approach, the primary swarms escalate larger. To adjust the parameters of the PSO, PLBn−1 and PGBn−1 indicates the swarm’s position as well as velocity. The mathematical notations are written as:

Xin=Xin−1+Vin−1,(14)

Vin=ωVin−1−n1r1(Xin−1−PLBn−1)−a2r2(Xin−1−PGBn−1).(15)

In the above equations, the particle and velocity components are Xi and Vi for the ith vector, ω is an inertia weight vector. The random vectors are r1 and r2, whereas the acceleration constants are n1 and n2. The velocity element vector lies in the interval [-vmax, vmax], (vmax shows the maximum velocity).

Interior-point programming (IPP): It adjusts the PSO parameters to converge more promptly by integrating the best global weights. These best global PSO weights are applied as an initial input. In recent years, IPP has been applied in numerous applications, e.g., riveting simulation in aircraft parts [64], complementarity monotone systems [65], viscoplastic fluidics system [66], dispatch system of the financial load [67], identification of the nonlinear stable system [68], non-smooth interaction dynamics [69], reactive optimal power flow problem with discrete control variables [70] and flow constraints in a pressure-dependent water distribution system [71]. This study is related presenting the hybrid form of the PSOIPP, which is pragmatic to compute the variables for the TON-DD-EFM. The pseudocode details using the ANN-PSOIPP are given in Tab. 1.

3  Statistical Performance

Three statistical measures T.I.C, R.MSE, and ENSE are presented in this section. The mathematical form of these operators by taking the exact and proposed solutions v and v^ are written as:

R.MSE=[1n∑m=1n(vm−v^m)2],(16)

T.I.C=ab,a=1n∑m=1n(vm−v^m)2,b=(1n∑m=1nvm2+1n∑m=1nv^m2)(17)

NSE = {1−cd,c=∑m=1n(vm−v^m)2,d=∑m=1n(vm−v¯m)2,v¯m=1n∑m=1nvm,(18)

ENSE = 1−NSE(19)

4  Results and Discussions

The detail for two examples of both the types of the singular TON-DD-EFM using the design ANN-PSOIPP scheme is provided in this section. The first two examples are obtained by taking the values of χ=2 and t=1 in Eq. (4), while the third and fourth examples are obtained by taking χ=1 and t=1 in Eq. (5).

Example 1: Consider the singular TON-DD-EFM having triple singular points is written as:

{d3dε3v(ε−1)+4εd2dε2v(ε−1)+2ε2ddεv(ε−1)+εv2=ε7+2ε4+ε+30−36ε+6ε2,v(0)=1,dv(0)dε=0,d2v(0)dε2=0.(20)

The true solution of the above Eq. (20) is 1+ε3.

Example 2: Consider the singular TON-DD-EFM having triple singular points involving trigonometric ratios are given as:

{d3dε3v(ε−1)+4εd2dε2v(ε−1)+2ε2ddεv(ε−1)+εv2=ε54−2ε2+6ε+ε2−2ε2sin⁡(ε−1)−4εcos⁡(ε−1)+ε3cos⁡ε+εcos2ε,v(0)=1,dv(0)dε=d2v(0)dε2=0.(21)

The true solution is cos⁡(ε+0.5ε2).

Example 3: Consider the singular TON-DD-EFM involving exponential based function is written as:

{d3dε3v(ε−1)+1εd2dε2v(ε−1)+εev=12−6ε+εe1+ε+ε3,v(0)=1,dv(0)dε=1,d2v(0)dε2=0.(22)

The true solution of Eq. (22) is 1+ε+ε3.

Example 4: Consider the singular TON-DD-EFM involving trigonometric based function is written as:

{d3dε3v(ε−1)+1εd2dε2v(ε−1)+εv2=εsin2ε+2εsin⁡ε+ε−cos⁡(ε−1)−1εsin⁡(ε−1),v(0)=dv(0)dε=1,d2v(0)dε2=0.(23)

1+sin⁡(ε) is the exact solution of Eq. (23).

The proposed procedure based on the ANN-PSOIPP is implemented for the singular TON-DD-EFM based Examples for 100 trials to get the system optimization of the model parameters. The best vectors are described to demonstrate the estimated forms of the TON-DD-EFM using ten neurons. The obtained numerical standards are given as follows:

v^1(ε)=−0.62811+e−(4.500ε+5.8496)+6.37471+e−(2.429ε+4.0923)−3.28901+e−(−3.4927ε−7.719)+…−5.99391+e−(1.187ε+0.0367),(24)

v^2(ε)=8.67411+e−(3.964ε−13.084)+8.32181+e−(−2.947ε−11.536)+1.44361+e−(−20.00ε+10.213)+…−9.98611+e−(5.377ε−7.163),(25)

v^3(ε)=1.52211+e−(−1.0355ε+5.657)+5.58441+e−(−0.805ε−2.2374)+0.44641+e−(1.8942ε+5.7719)+…−5.28121+e−(−2.0613ε−2.5638),(26)

v^4(ε)=−15.54171+e−(14.063ε−15.968)+6.9991+e−(−6.825ε−9.814)+7.35351+e−(0.942ε−1.5638)+…+1.07631+e−(−0.2511ε+14.2354).(27)

Optimization is performed for solving the singular TON-DD-EFM based examples 1-4 using the combination of the PSOIPP for 100 runs. Figs. 1a–1d signifies the optimized weight vectors of ANNs to solve each example of the singular TON-DD-EFM, and these weights are given in Eqs. (24)–(27). The result comparisons for all the examples of the singular TON-DD-EFM based on the obtained and exact solutions are provided using the proposed ANN-PSOIPP scheme in Figs. 1e–1h. The results are overlapped for the TON-DD-EFM, which specifies the exactness of ANN-PSOIPP. For the level of accuracy, the absolute error (AE) is calculated in Fig. 2. The second portion of Fig. 2 specifies the performance procedures of T.I.C, ENSE, and R.MSE, for each example of the singular TON-DD-EFM. It is indicated that the RMSE lies as 10−04 to 10−06. The TIC measures for each Example lies 10−08 to 10−10 , and the ENSE for each example lie 10−06 to 10−08, whereas, for example four the ENSE is found 10−10 to 10−12. These achieved results state the good tendency of routine using different measures for TON-DD-EFM.

Figure 1: Best weights and results comparison using the ANN-PSOIPP scheme for the TON-DD-EFM

Figure 2: AE and performance measures using the ANN-PSOIPP scheme for solving all examples of the singular TON-DD-EFM

Statistics presentations using 100 executions for the proposed ANN-PSOIPP scheme using the analysis of fitness, RMSE, TIC, and ENSE together with the histogram (Hist) plots are provided in Figs. 3–6 for solving the singular TON-DD-EFM. It is evident in the figures that the maximum values of these statistical operators lie in suitable ranges for solving all examples of the singular TON-DD-EFM.

Figure 3: Statistics measures of ANN-PSOIPP over Fit values together with the histogram for the TON-DD-EFM

Figure 4: Statistics measures based on ANN-PSOIPP through R.MSE values for the plots of the histogram for the TON-DD-EFM

Figure 5: Statistics measures for ANN-PSOIPP over TIC values using the plots of the histogram for the TON-DD-EFM

Figure 6: Statistics measures for the ANN-PSOIPP over ENSE values for the TON-DD-EFM

The convergence inquiries of the proposed ANN-PSOIPP scheme are shown further for global minimum and median performances of ‘G-FIT’, ‘G-TIC’, and ‘G-ENSE’ in Tab. 2. The Min G-FIT, G-TIC and G-ENSE lie 10−09-10−10, 10−09-10−11, 10−07-10−11, while the Med G-FIT, G-TIC, and G-ENSE were found as 10−06 to 10−08, 10−05 to 10−08, 10−02 to 10−06 for solving all examples of the singular TON-DD-EFM using the proposed ANN-PSOIPP scheme. The relative optimal performances enhance the accuracy of the ANN-PSOIPP scheme.

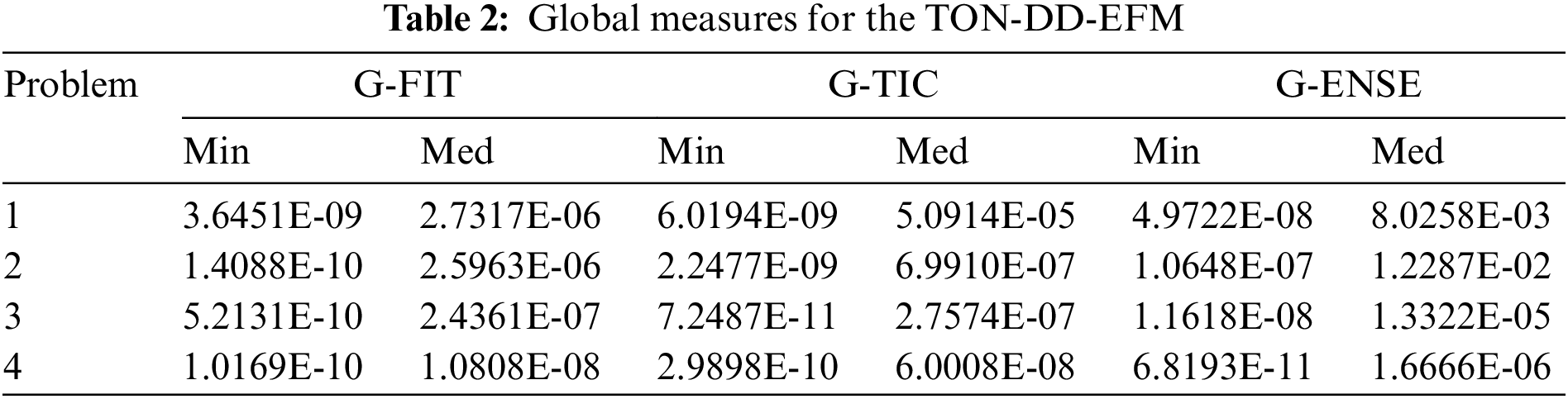
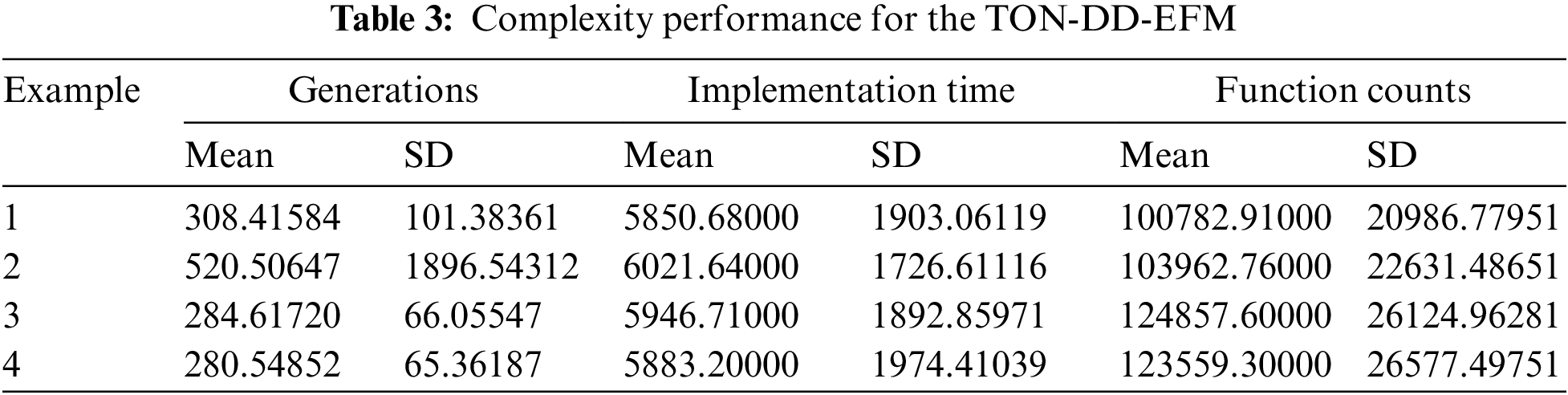
The complexity of the ANN-PSOIPP scheme is observed over the generations, execution time and count of functions. Complexity investigations for each example of the singular TON-DD-EFM are provided. Tab. 3 shows the average generations, implementation time, and function counts are 348.52201, 5925.55750, and 113290.64250, for each example of the singular TON-DD-EFM using the proposed ANN-PSOIPP scheme.

5  Conclusion

The present study shows that a precise, stable, accurate, and reliable ANN-PSOIPP scheme is accessible for the third-order delay differential Emden-Fowler model by applying the continuous mapping and approximation capability of ANNs. The optimization of the fitness/merit of these networks is obtained by applying the global and local search capabilities of PSO and the IPP approach. The ANN-PSOIPP scheme is viably executed to solve four examples of the third kind of singular delay differential singular system. The precise performances are examined using the numerical ANN-PSOIPP scheme for singular delay differential Emden-Fowler system based on AE with reliable precision of about 5-7 decimals of correctness from the true solutions. The statistical explanations are also obtainable in the form of Min, Mean and Median actions to authenticate the robustness of the numerical ANN-PSOIPP scheme for the singular model.

Funding Statement: This project is funded by National Research Council of Thailand (NRCT) and Khon Kaen University: N42A650291.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  T. Zhao, “Global periodic-solutions for a differential delay system modeling a microbial population in the chemostat,” Journal of Mathematical Analysis and Applications, vol. 193, no. 1, pp. 329–352, 1995. [Google Scholar]

 2.  R. P. Agarwal, O. Bazighifan, and M. A. Ragusa, M.A., “Nonlinear neutral delay differential equations of fourth-order: Oscillation of solutions,” Entropy, vol. 23, no. 2, pp. 129. [Google Scholar]

 3.  D. S. Li and M. Z. Liu, “Exact solution properties of a multi-pantograph delay differential equation,” Journal of Harbin Institute of Technology, vol. 32, no. 3, pp. 1–3, 2000. [Google Scholar]

 4.  W. Li, B. Chen, C. Meng, W. Fang, Y. Xiao et al., “Ultrafast all-optical graphene modulator,” Nano Letters, vol. 14, no. 2, pp. 955–959, 2014. [Google Scholar]

 5.  Z. Sabir, J. L. Guirao, and T. Saeed, “Solving a novel designed second order nonlinear Lane–Emden delay differential model using the heuristic techniques,” Applied Soft Computing, vol. 102, pp. 107105, 2021. [Google Scholar]

 6.  H. Brunner, Q. Huang and H. Xie, “Discontinuous galerkin methods for delay differential equations of pantograph type,” SIAM Journal on Numerical Analysis, vol. 48, no. 5, pp. 1944–1967, 2010. [Google Scholar]

 7.  C. H. Hsiao and S. P. Wu, “Numerical solution of time-varying functional differential equations via Haar wavelets,” Applied Mathematics and Computation, vol. 188, no. 1, pp. 1049–1058, 2007. [Google Scholar]

 8.  X. T. Wang, “Numerical solution of time-varying systems with a stretch by general Legendre wavelets,” Applied Mathematics and Computation, vol. 198, no. 2, pp. 613–620, 2008. [Google Scholar]

 9.  G. Adomian and R. Rach, “A nonlinear differential delay equation,” Journal of Mathematical Analysis and Applications, vol. 91, no. 2, pp. 301–304, 1983. [Google Scholar]

10. F. Shakeri and M. Dehghan, “Solution of delay differential equations via a homotopy perturbation method,” Mathematical and Computer Modelling, vol. 48, no. 3-4, pp. 486–498, 2008. [Google Scholar]

11. F. Erdogan, M. G. Sakar and O. Saldır, “A finite difference method on layer-adapted mesh for singularly perturbed delay differential equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 425–436, 2020. [Google Scholar]

12. A. Shvets and A. Makaseyev, “Deterministic chaos in pendulum systems with delay,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 1–8, 2019. [Google Scholar]

13. Z. Sabir, M. G. Sakar, M. Yeskindirova and O. Saldir, “Numerical investigations to design a novel model based on the fifth order system of Emden–Fowler equations,” Theoretical and Applied Mechanics Letters, vol. 10, no. 5, pp. 333–342, 2020. [Google Scholar]

14. R. H. Fowler, “Further studies of Emden’s and similar differential equations,” The Quarterly Journal of Mathematics, vol. 1, pp. 259–288, 1931. [Google Scholar]

15. Z. Sabir, F. Amin, D. Pohl and J. L. Guirao, “Intelligence computing approach for solving second order system of Emden–Fowler model,” Journal of Intelligent & Fuzzy Systems, vol. 38, no. 6, pp. 7391–7406, 2020. [Google Scholar]

16. Z. Sabir, H. A. Wahab, M. Umar, M. G. Sakar and M. A. Z. Raja, “Novel design of morlet wavelet neural network for solving second order Lane–Emden equation,” Mathematics and Computers in Simulation, vol. 172, pp. 1–14, 2020. [Google Scholar]

17. Z. Sabir, H. A. Wahab, S. Javeed, and H. M. Baskonus, “An efficient stochastic numerical computing framework for the nonlinear higher order singular models,” Fractal and Fractional, vol. 5, no. 4, pp. 176, 2021. [Google Scholar]

18. Z. Sabir, and H. A. Wahab, “Evolutionary heuristic with gudermannian neural networks for the nonlinear singular models of third kind,” Physica Scripta, vol. 96, no. 12, pp. 125261, 2021. [Google Scholar]

19. V. Radulescu and D. Repovs, “Combined effects in nonlinear problems arising in the study of anisotropic continuous media,” Nonlinear Analysis, Theory, Methods and Applications, vol. 75, no. 3, pp. 1524–1530, 2012. [Google Scholar]

20. V. B. Mandelzweig and F. Tabakin, “Quasi linearization approach to nonlinear problems in physics with application to nonlinear ODEs,” Computer Physics Communications, vol. 141, no. 2, pp. 268–281, 2001. [Google Scholar]

21. T. Luo, Z. Xin and H. Zeng, “Nonlinear asymptotic stability of the Lane-Emden solutions for the viscous gaseous star problem with degenerate density dependent viscosities,” Communications in Mathematical Physics, vol. 347, no. 3, pp. 657–702, 2016. [Google Scholar]

22. D. Flockerzi and K. Sundmacher, “On coupled Lane-Emden equations arising in dusty fluid models,” Journal of Physics: Conference Series, vol. 268, pp. 1–11, 2011. [Google Scholar]

23. M. Ghergu and V. Radulescu, “On a class of singular gierer–Meinhardt systems arising in morphogenesis,” Comptes Rendus Mathematique, vol. 344, no. 3, pp. 163–168, 2007. [Google Scholar]

24. A. Taghavi and S. Pearce, “A solution to the Lane–Emden equation in the theory of stellar structure utilizing the Tau method,” Mathematical Methods in the Applied Sciences, vol. 36, no. 10, pp. 1240–1247, 2013. [Google Scholar]

25. M. Dehghan and F. Shakeri, “Solution of an integro-differential equation arising in oscillating magnetic fields using he’s homotopy perturbation method,” Progress in Electromagnetics Research, vol. 78, pp. 361–376, 2008. [Google Scholar]

26. R. Rach, J. S. Duan and A. M. Wazwaz, “Solving coupled Lane–Emden boundary value problems in catalytic diffusion reactions by the adomian decomposition method,” Journal of Mathematical Chemistry, vol. 52, no. 1, pp. 255–267, 2014. [Google Scholar]

27. K. Boubaker and R. A. Van Gorder, “Application of the bPES to Lane–Emden equations governing polytropic and isothermal gas spheres,” New Astron, vol. 17, no. 6, pp. 565–569, 2012. [Google Scholar]

28. A. H. Bhrawy, A. S. Alofi and R. A. Van Gorder, “An efficient collocation method for a class of boundary value problems arising in mathematical physics and geometry,” Abstract and Applied Analysis, vol. 2014, pp. 1–9, 2014. [Google Scholar]

29. J. A. Khan, M. A. Z. Raja, M. M. Rashidi, M. I. Syam and A. M. Wazwaz, “Nature-inspired computing approach for solving non-linear singular Emden–Fowler problem arising in electromagnetic theory,” Connection Science, vol. 27, no. 4, pp. 377–396, 2015. [Google Scholar]

30. J. I. Ramos, “Linearization methods in classical and quantum mechanics,” Computer Physics Communications, vol. 153, no. 2, pp. 199–208, 2003. [Google Scholar]

31. A. M. Wazwaz, “A new algorithm for solving differential equations of Lane–Emden type,” Applied Mathematics and Computation, vol. 118, no. 2-3, pp. 287–310, 2001. [Google Scholar]

32. N. T. Shawagfeh, “Non-perturbative approximate solution for Lane–Emden equation,” Journal of Mathematical Physics, vol. 34, no. 9, pp. 4364–4369, 1993. [Google Scholar]

33. W. Adel and Z. Sabir, “Solving a new design of nonlinear second-order Lane–Emden pantograph delay differential model via Bernoulli collocation method,” The European Physical Journal Plus, vol. 135, no. 5, pp. 1–12, 2020. [Google Scholar]

34. M. A. Abdelkawy, Z. Sabir, J. L. Guirao and T. Saeed, “Numerical investigations of a new singular second-order nonlinear coupled functional Lane–Emden model,” Open Physics, vol. 18, no. 1, pp. 770–778, 2020. [Google Scholar]

35. K. Parand and M. Razzaghi, “Rational legendre approximation for solving some physical problems on semi-infinite intervals,” Physica Scripta, vol. 69, no. 5, pp. 353–357, 2004. [Google Scholar]

36. Z. Sabir, H. Günerhan and J. L. Guirao, “On a new model based on third-order nonlinear multisingular functional differential equations,” Mathematical Problems in Engineering, vol. 2020, pp. 1–9, 2020. [Google Scholar]

37. Z. Sabir, M. A. Z. Raja, J. L. Guirao and M. Shoaib, “Integrated intelligent computing with neuro-swarming solver for multi-singular fourth-order nonlinear Emden–Fowler equation,” Computational and Applied Mathematics, vol. 39, no. 4, pp. 1–18, 2020. [Google Scholar]

38. Z. Sabir, S. Saoud, M. A. Z. Raja, H. A. Wahab and A. Arbi, “Heuristic computing technique for numerical solutions of nonlinear fourth order Emden–Fowler equation,” Mathematics and Computers in Simulation, vol. 178, pp. 534–548, 2020. [Google Scholar]

39. T. Botmart and P. Niamsup, “Exponential synchronization of complex dynamical network with mixed time-varying and hybrid coupling delays via intermittent control,” Advances in Difference Equations, vol. 2014, no. 116, pp. 1–33, 2014. [Google Scholar]

40. T. Botmart, N. Yotha, P. Niamsup and W. Weera, “Hybrid adaptive pinning control for function projective synchronization of delayed neural networks with mixed uncertain couplings,” Complexity, vol. 2017, no. 4654020, pp. 1–19, 2017. [Google Scholar]

41. N. Boonsatit, G. Rajchakit, R. Sriraman, C. P. Lim, and P. Agarwal, “Finite-/fixed-time synchronization of delayed clifford-valued recurrent neural networks,” Advances in Difference Equations, vol. 2021, no. 1, pp. 1–25, 2021. [Google Scholar]

42. Z. Sabir, H. A. Wahab, T. G. Nguyen, G. C. Altamirano, F. Erdoğan et al., “Intelligent computing technique for solving singular multi-pantograph delay differential equation,” Soft Computing, pp. 1–13, 2022. [Google Scholar]

43. G. Rajchakit, R. Sriraman, N. Boonsatit, P. Hammachukiattikul, C. P. Lim et al., “Exponential stability in the lagrange sense for clifford-valued recurrent neural networks with time delays,” Advances in Difference Equations, vol. 2021, no. 1, pp. 1–21, 2021. [Google Scholar]

44. M. Umar, Z. Sabir, M. A. Z. Raja and Y. G. Sánchez, “A stochastic numerical computing heuristic of SIR nonlinear model based on dengue fever,” Results in Physics, vol. 19, pp. 1–9, 2020. [Google Scholar]

45. M. Umar, Z. Sabir, M. A. Z. Raja, H. M. Baskonus, S. W. Yao et al., “A novel study of morlet neural networks to solve the nonlinear HIV infection system of latently infected cells,” Results in Physics, vol. 25, pp. 104235, 2021. [Google Scholar]

46. Z. Sabir, M. Umar, M. A. Z. Raja, H. M. Baskonus, and W. Gao, “Designing of morlet wavelet as a neural network for a novel prevention category in the HIV system,” International Journal of Biomathematics, vol. 15, no. 4, pp. 2250012, 2022. [Google Scholar]

47. Z. Sabir, M. Umar, J. L. Guirao, M. Shoaib and M. A. Z. Raja, “Integrated intelligent computing paradigm for nonlinear multi-singular third-order Emden–Fowler equation,” Neural Computing and Applications, vol. 33, no. 8, pp. 3417–3436, 2021. [Google Scholar]

48. M. Umar, Z. Sabir, M. A. Z. Raja, M. Shoaib, M. Gupta et al., “A stochastic intelligent computing with neuro-evolution heuristics for nonlinear SITR system of novel COVID-19 dynamics,” Symmetry, vol. 12, no. 10, pp. 1–17, 2020. [Google Scholar]

49. Z. Sabir, D. Baleanu, M. Shoaib and M. A. Z. Raja, “Design of stochastic numerical solver for the solution of singular three-point second-order boundary value problems,” Neural Computing and Applications, vol. 33, no. 7, pp. 2427–2443, 2021. [Google Scholar]

50. M. Umar, M. A. Z. Raja, Z. Sabir, A. S. Alwabli and M. Shoaib, “A stochastic computational intelligent solver for numerical treatment of mosquito dispersal model in a heterogeneous environment,” The European Physical Journal Plus, vol. 135, no. 7, pp. 1–23, 2020. [Google Scholar]

51. T. Botmart and W. Weera, “Guaranteed cost control for exponential synchronization of cellular neural networks with mixed time-varying delays via hybrid feedback control,” Abstract and Applied Analysis, vol. 2013, no. 175796, pp. 1–13, 2013. [Google Scholar]

52. M. Umar, Z. Sabir, F. Amin, J. L. Guirao and M. A. Z. Raja, “Stochastic numerical technique for solving HIV infection model of CD4 + T cells,” The European Physical Journal Plus, vol. 135, no. 5, pp. 1–19, 2020. [Google Scholar]

53. N. Yotha, T. Botmart, K. Mukdasai and Weera, “Improved delay-dependent approach to passivity analysis for uncertain neural networks with discrete interval and distributed time-varying delays,” Vietnam Journal of Mathematics, vol. 45, no. 4, pp. 721–736, 2017. [Google Scholar]

54. M. Umar, Z. Sabir and M. A. Z. Raja, “Intelligent computing for numerical treatment of nonlinear prey–predator models,” Applied Soft Computing, vol. 80, pp. 506–524, 2019. [Google Scholar]

55. J. L. Guirao, Z. Sabir and T. Saeed, “Design and numerical solutions of a novel third-order nonlinear Emden–Fowler delay differential model,” Mathematical Problems in Engineering, vol. 2020, pp. 1–9, 2020. [Google Scholar]

56. Y. Shi and R. C. Eberhart, “Empirical study of particle swarm optimization,” in Proc. of the 1999 Congress on Evolutionary Computation-CEC99, Washington DC, USA, pp. 1945–1950, 1999. [Google Scholar]

57. A. Siabi-Garjan and R. Hassanzadeh, “A computational approach for engineering optical properties of multilayer thin films: Particle swarm optimization applied to bruggeman homogenization formalism,” The European Physical Journal Plus, vol. 133, no. 10, pp. 1–11, 2018. [Google Scholar]

58. S. Boubaker, “Identification of nonlinear hammerstein system using mixed integer-real coded particle swarm optimization: Application to the electric daily peak-load forecasting,” Nonlinear Dynamics, vol. 90, no. 2, pp. 797–814, 2017. [Google Scholar]

59. J. Tian, C. Sun, Y. Tan and J. Zeng, “Granularity-based surrogate-assisted particle swarm optimization for high-dimensional expensive optimization,” Knowledge-Based Systems, vol. 187, pp. 1–15, 2020. [Google Scholar]

60. Z. Sabir, T. Botmart, M. A. Z. Raja, R. Sadat, M. R. Ali et al., “Artificial neural network scheme to solve the nonlinear influenza disease model,” Biomedical Signal Processing and Control, vol. 75, no. 103594, pp. 1–13, 2022. [Google Scholar]

61. D. Yan, Y. Lu, M. Zhou, S. Chen and D. Levy, “Empirically characteristic analysis of chaotic PID controlling particle swarm optimization,” PLoS One, vol. 12, no. 5, pp. 1–24, 2017. [Google Scholar]

62. A. M. Ibrahim and M. A. Tawhid, “A hybridization of cuckoo search and particle swarm optimization for solving nonlinear systems,” Evolutionary Intelligence, vol. 12, no. 4, pp. 541–561, 2019. [Google Scholar]

63. S. Akbar, F. Zaman, M. Asif, A. U. Rehman and M. A. Z. Raja, “Novel application of FO-DPSO for 2-D parameter estimation of electromagnetic plane waves,” Neural Computing and Applications, vol. 31, no. 8, pp. 3681–3690, 2019. [Google Scholar]

64. M. Stefanova, S. Yakunin, M. Petukhova, S. Lupuleac and M. Kokkolaras, “An interior-point method-based solver for simulation of aircraft parts riveting,” Engineering Optimization, vol. 50, no. 5, pp. 781–796, 2018. [Google Scholar]

65. M. R. Sicre and B. F. Svaiter, “A O(1/k3/2) hybrid proximal extragradient primal–dual interior point method for nonlinear monotone mixed complementarity problems,” Computational and Applied Mathematics, vol. 37, no. 2, pp. 1847–1876, 2018. [Google Scholar]

66. H. Ilyas, I. Ahmad, M. A. Z. Raja, M. B. Tahir and M. Shoaib, “Intelligent computing for the dynamics of fluidic system of electrically conducting Ag/Cu nanoparticles with mixed convection for hydrogen possessions,” International Journal of Hydrogen Energy, vol. 46, no. 7, pp. 4947–4980, 2021. [Google Scholar]

67. M. Ettappan, V. Vimala, S. Ramesh and V. T. Kesavan, “Optimal reactive power dispatch for real power loss minimization and voltage stability enhancement using artificial bee colony algorithm,” Microprocessors and Microsystems, vol. 76, pp. 1–7, 2020. [Google Scholar]

68. J. Umenberger and I. R. Manchester, “Specialized interior-point algorithm for stable nonlinear system identification,” IEEE Transactions on Automatic Control, vol. 64, no. 6, pp. 2442–2456, 2018. [Google Scholar]

69. D. Mangoni, A. Tasora and R. Garziera, “A primal–dual predictor–corrector interior point method for non-smooth contact dynamics,” Computer Methods in Applied Mechanics and Engineering, vol. 330, pp. 351–367, 2018. [Google Scholar]

70. J. A. Delgado, E. C. Baptista, A. R. Balbo, E. M. Soler, D. N. Silva et al., “A primal–dual penalty-interior-point method for solving the reactive optimal power flow problem with discrete control variables,” International Journal of Electrical Power & Energy Systems, vol. 138, pp. 107917, 2022. [Google Scholar]

71. S. Elhay, O. Piller, J. W. Deuerlein, and A. R. Simpson, “An interior point method applied to flow constraints in a pressure-dependent water distribution system,” Journal of Water Resources Planning and Management, vol. 148, no. 1, pp. 04021090, 2022. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.