| Computers, Materials & Continua DOI:10.32604/cmc.2022.030927 |  |
| Article |
K-Banhatti Invariants Empowered Topological Investigation of Bridge Networks
1Department of Computer Science, Superior University, Lahore, 54000, Pakistan
2Department of Software Engineering, Superior University, Lahore, 54000, Pakistan
3Department of Software Engineering, Faculty of Information Technology, The University of Lahore, 54000, Pakistan
4Advanced Informatics Department, Razak Faculty of Technology and Informatics, Universiti Teknologi Malaysia, Kuala Lumpur, 54100, Malaysia
5Faculty of Informatics and Applied Mathematics, University Malaysia Terengganu, Malaysia
6Department of Computer Science & Information Technology, Faculty of Information Technology, The University of Lahore, 54000, Pakistan
*Corresponding Author: Muhammad Waseem Iqbal. Email: waseem.iqbal@superior.edu.pk
Received: 06 April 2022; Accepted: 26 May 2022
Abstract: Any number that can be uniquely determined by a graph is called graph invariants. During the most recent twenty years’ innumerable numerical graph invariants have been described and used for correlation analysis. In the fast and advanced environment of manufacturing of networks and other products which used different networks, no dependable assessment has been embraced to choose, how much these invariants are connected with a network graph or molecular graph. In this paper, it will talk about three distinct variations of bridge networks with great capability of expectation in the field of computer science, chemistry, physics, drug industry, informatics, and mathematics in setting with physical and synthetic constructions and networks, since K-Banhatti invariants are newly introduced and have various forecast characteristics for various variations of bridge graphs or networks. The review settled the topology of bridge graph/networks of three unique sorts with three types of K-Banhatti Indices. These concluded outcomes can be utilized for the modeling of interconnection networks of Personal computers (PC), networks like Local area network (LAN), Metropolitan area network (MAN) and Wide area network (WAN), the spine of internet and different networks/designs of PCs, power generation interconnection, bio-informatics and chemical structures.
Keywords: Bridge networks; invariants; k-banhatti indices; maple; network graph; molecular graph
The bridge networks are much important in computer science and other fields of sciences. These are used in the construction of memory interconnection, microchips, integrated circuits, power generation interconnection, robotics interconnection and chemical structures. A bridge graph is a graph acquired from number of graphs G1, G2, G3, Gm by partner the vertices vi and vi + 1 by an edge∀, I = 1, 2,., m − 1 [1]. V. R. Kulli in 2016, defined the possibility of various types of K-Banhatti invariants. Another vertex degree-based invariant graph named K-Banhatti index is utilized to catch the sharp lower and upper bounds of the associated networks and the attributes of the network arriving at the boundaries. K-Banhatti index is a topological invariant which is a number associated with a network graph [2] that catches the symmetry of the network structure and gives a logical language to anticipating the attributes of the network. K-Banhatti index is a degree-based topological index used for the solution of the topology of a certain network like a bridge network.
As one more emerging science is created with the assistance of computer science, math and chemistry called cheminformatics, whose huge fragments consolidate Quantitative structure-activity relationship (QSAR) and Quantitative structure-property relationships (QSPR). QSAR is a modeling tool used to tackle the topology of networks or structure of compounds, demonstrated the effective and best entertainer networks or structures. QSPR is likewise a modeling technique that corresponds to the properties of network structures with the assistance of numerical conditions or articulation. It gives the quantitative relationship between properties of networks or chemical structures [3].
Interconnected networks and graph theory give a point-by-point perception of these associated networks. Electric power interconnections prerequisite to unendingly screening the state of their structures by voltage size at loads and the machine stage point at generators. In electric power system, a vertex tends to be an electric center and an edge tends to be a transmission line joining two electrical focuses. In the design of a network interconnection point tends to processor and an edge tends to be a network way through which transmission is finished. This theory contributes an observable work in the fields of chemical sciences [4].
The topology of a graph concludes the way where vertices are associated by edges. From the geography of a network, certain properties can without much of a stretch be settled. In this heap of cases, this study can figure boundaries called Topological invariants (TIs) that numerically portrayed the connectedness plans structure between the centers or performers in a network. So, this study can build a mind-stunning network of general arrangements of regulations accomplice regulations centers those direct ordinary natural subjects for example; QSAR and QSPR are giving the establishment to these models [5].
In this article, a new arising study will figure out different indices of bridge networks. The outcomes will assume a crucial part in deciding the properties of these networks and their uses in the computer industry, robotics, chemistry, drug industry and so forth. It will likewise perform index analysis on certain networks which might be gainful for people groups who are working in the field of computer science, mathematics, robotics and chemical industry too [6].
The contribution of this research is to analyze how existing networks can be improved by optimizing their adaptability. During the said research certain networks were modeled through deduced results by topological invariants. These results will be developed over the solution of networks graphically by freshly prepared topological indices. Existing networks will be studied for topological perspectives, QSPR, QSAR models will be developed and analyzed. The relation between lower bounds and upper bounds of the network or graph will be discovered. Further, these relationships will be defined through optimization. Bridge networks and other certain computer networks are solved and evaluated with the help of topological invariants. Furthermore, contribution to research on developing advanced networks will facilitate the networks used in robotics and new architectures of computers in context with certain networks.
The study presents the adjusted first and second K-Banhatti indices of a graph. Likewise, the study presents the symphonious K-Banhatti index of a graph. The study figures out the adjusted first and second K-Banhatti indices and symphonious K-Banhatti index of a few standard graphs, TUC4C8[p, q] nanotubes and TUC4[p, q] nanotubes [7]. The Atom-bond connectivity (ABC) and Geometric number juggling (GA) correspond to different physical and chemical properties of chemicals having the above structures, similar to robustness and strain energy and the edge of boiling over and so forth Bunch theory and development of graphs can utilize the Cayley graphs (CG) of gatherings for deciding properties. In this review, they register conditions of the general randi’ c index for different potential gains of α, first zagreb index, ABC index, GA index, the fourth ABC index (ABC4 ), fifth GA index (GA5) for certain gatherings of graphs [8]. The topological indices or invariants are additionally numeric qualities related to computer networks, their interconnections and their properties, and so forth. It computes different topological indices of unpredictability based on the paired tree up to the k-level. The concluded results can be utilized for computer networks and chemical networks in topological portrayal [9].
The estimation of the irregularity indices of honeycomb networks, hexagonal networks, oxide networks and silicate networks is finished. The outcomes are extremely useful in understanding the conduct of various computer networks and chemical networks. After understanding these expressions various scientists can develop their own best networks in the chemical and computer industries likewise [10]. Further, the study explains that graph theory is a field through which they compute topological indices for tracking down the properties of various chemicals and networks without playing out any sorts of investigations on them. It likewise works out topological indices form-polynomial square shift networks which is a pieces of various chemical compounds with the assistance of division of edge [11].
Simonraj et al. portrayed the chemical network which is shown mathematically by topological indices in chemical graph theory. The study decided on one more kind of graph, which is named the third type of hex-construed network. It examined and as of late outlined a third type of hex-induced networks. As these interpreted results are valuable according to various chemical points of view similarly concerning drug sciences, these results furthermore give the reason to appreciate the significant essential geographies of the above networks [12].
Another review depicted that the m-polynomial is one of the arithmetical polynomials that are useful in theoretical chemistry. It plays significant work in handling the explanations of various degree-based topological indices. They got various degree-based topological indices for benzene rings introduced in thep-type-surface network and Tickysim spinnaker model (TSM) sheet. These results can accept a huge part to envision the geography of the aforementioned networks [13]. Further, computations of topological indices of confined pent-heptagonal nano-sheet are finished. QSARs address perceptive models got from the utilization of verifiable mechanical assemblies connecting with the natural activity (counting charming helpful effects and appalling side effects) of engineered materials (drugs/harms/biological poisons) with descriptors illustrative of molecular structure as well as properties [14]. There are a few certifiable hardships on HGR systems like affectability to upset, scale, lighting up, trouble and hindrance. There are utilized a particular and wide-range dataset with 31 kinds of tokens of various amounts of fingers with raising disengagement. It executed our computation for this dataset and got the mean accuracy up to 90%. Also, it differentiated the results and some datasets that for the most part share the photos of our dataset [15].
It elaborates those topological indices can be designed by changing over a chemical structure into a mathematical means. These topological indices accomplice certain chemical-substance properties like cutoff, security, strain energy and so on of synthetic mixes. Graph theory has found an amazing use around here of investigation. Interconnection networks of multiprocessor are routinely expected to communicate a large number of homogeneously imitated processor-memory consolidates, all of which is known as a handling center [16].
Physicochemical properties and topological indices are talked about and thoroughly analyzed in the QSAR/QSPR, for instance, Weiner index, Harary index and forms of Harary indices are used to predict the bioactivity of the manufactured blends. Graph theory has found huge use in computer science and chemistry, particularly in exhibiting substance structures [17]. The study kept an eye on the OTIS exchanged networks and bi traded networks and examined their topological indices. They determined complete randi ć, general total accessibility, first and second zagreb, first and second hyper zagreb, hyper zagreb atom bond and numerical indices for both the gathering of networks by considering the reason network as way Pn and k-standard graph Rk. They similarly gave express formulae for the ABC4 and GA5 indices of these networks with the reason Rk network [18].
Another review conveyed that since computer devices are utilized on the planet for the wellspring of data, they are expanding in numbers variously. So much, today, it is difficult to find any space, intelligent or other, which isn’t subject to their application. To be sure, even broad arrangements of regulations have been impacted by original handling and information systems. An impressive part of these QSAR strategies relies upon the usage of topological boundaries, which are numerical courses of action that order to accommodate primary information and sympathy relationships among structure and regular properties [19]. Accordingly, TIs are useful as commitments for QSPR models at every underlying level. Without a doubt, even broad arrangements of regulations may be advanced toward using figuring and information systems like networks. So, they can foster a flighty network of generally speaking arrangements of regulations partner regulations (hubs) that oversee fundamental natural focuses for instance. On the other hand, a precise legal structure is relied upon to provide legitimate and relevant guidance to addressing different enlisting methodologies as applied to coherent examination [20]. In this paper, researchers focused on different kinds of issues related to graph theory and their executions and ideas in the field of programming to show the ampleness of graph theory. These applications are familiar particularly with loosening up graph theory andshowing its goal and importance in network designing [21].
The speculative contemplations of the graph are particularly used by computer programming applications. Particularly in research spaces of programming such as data mining, picture division, gathering, picture getting, networking and so forth, for instance, a data configuration can be sorted out as a tree which thus used vertices and edges. Modeling of network geographies should be possible by utilizing graph considerations. This prompts the progress of new assessments and new speculations that can be utilized in enormous applications. It has been allocated to two locales [22]. The framework includes a depiction of unequivocal subjects from the theory of graph of the spaces of Computer science wherein they are utilized. Notwithstanding, for each depicted theory they show the fields wherein it is utilized. This paper gives a chart of the employments of graph theory in heterogeneous fields somewhat yet fundamentally programming is the field around which graph theory contemplations work. Graph theory has found sweeping applications in various fields [23].
Topological invariants engage us to assemble data about logarithmic structures and give us a numerical strategy to figure out the secret properties of various structures. Various strategies are available in history to check the nature of a topological index. There are two principal conflicts of topological indices, first one is the degree-based topological and the below-average is known as distance-based topological indices. There are many such invariants are available in history [24]. K-Banhatti index and its other variant have great capability of expectation in the field of computer science, math, chemistry, drugs, informatics and power generation in setting with physical and chemical structures and networks [25].
The methodology depends on quantitative requests. The reason for this study is to investigate and foster understanding with regards to basic and critical worries like blunder-free, faultless, best execution, and having advanced abilities in computer networks, interconnection networks of processors, chemical structures, robotics interconnections, and power interconnection networks.
The primary goal of this study is to examine the topological invariants of bridge computer networks. The review figures out the force of reality of topological indices in certain networks. The study makes sense of the k-banhatti indices, their reduced forms, and their advantages. This article makes sense of and mindful ongoing utilization of K-banhatti indices. Its great goal is to foster equations, so it can take a look at the topology, and execution of certain networks without performing tests and before before constructing them. The work concluded a few outcomes which are utilized in the modeling of certain computer networks [26].
The reading considers the accompanying hypothesis for the advancement of bridge networks utilized in computer networks, interconnection networks of processors, power interconnection networks, chemical structures and mechanical technology. The analysis gives the solidarity to create mistake-free, disappointing-free, best entertainer workstation networks, interconnection networks of processors, power interconnection networks and robotics interconnection networks.
In this deliberate study, it will take an existing bridge network, associate it with a graph, address the topology of the graph with the assistance of K-Banhatti indices and their other forms. The concluded results about the type of numeric expression will contrast with existing outcomes. This model is especially unsettling as it tackled the topology of a bridge network in numeric and graphical structure and gives exact outcomes. After analysis, a recreation apparatus maple is utilized for the confirmation and approval of results. The flow of systematic study of this article which takes existing bridge networks associates them with graph theory, solves the topology of the graph by K-Banhatti indices, compares the results and deduced results will be used for modeling of bridge networks utilized in certain networks [27]. This model is much concerning as it solved the topology of a bridge network numerically and give accurate results. The simulation tool maple is used for the verification and validation of results.
A bridge graph is a graph obtained from several s graphs G1, G2, G3,…Gm by associate the vertices vi and vi + 1 by an edge∀, i = 1, 2,…, m − 1 [28]. K Banhatti indices have two main forms first K Banhatti indices and second K Banhatti indices with different variants [29,30].
Eqs. (1)–(3) show the first K-Banhatti index, the first K Hyper Banhatti index, andthe modified first K-Banhatti index which will be used for the solution of bridge networks mentioned in Figs. 2, 5 and 8.
Eqs. (4)–(6) show the second K-Banhatti index, second K Hyper Banhatti index and modified second K-Banhatti index which will be used for the solution of bridge networks mention in Figs. 2, 5, and 8.
Tab. 1 describes the edge partitions of graph Gr (Ps, v) over Ps of the bridge graph given in Fig. 1.
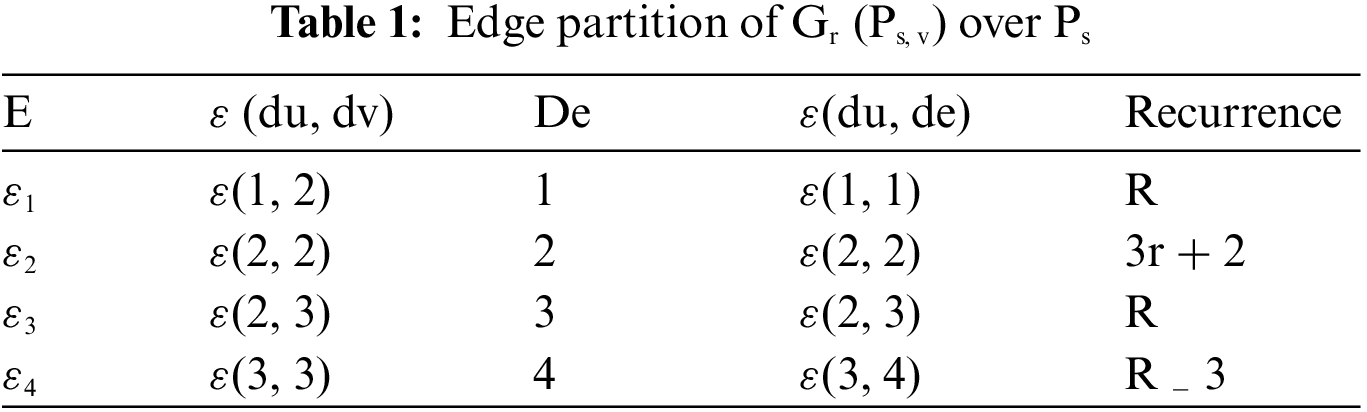
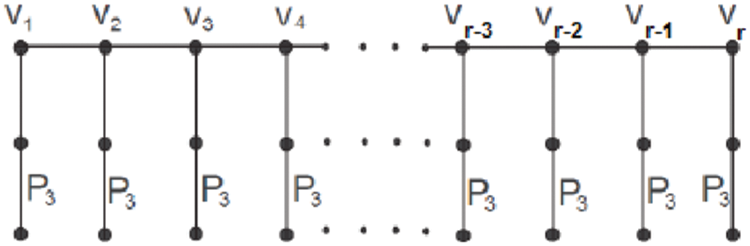
Figure 1: Gr (Ps, v) over Ps for Bridge Network
Fig. 1 shows the bridge networks in which bus networks and star networks bridge in a tree-like structure [31].
4.1.1 Bridge Graph Gr (Ps, v) Over Path
If the vertex set is V then by the observation of Fig. 1, it can order this vertex set into four subsets V1, V2, V3 and V4, Such that V = V1 + V2 + V3 + V4. If E represents the edge set. Fig. 1 shows that there are four distinct kinds of edges present in the graph bridge graph Gr (Ps, v) over the path of hybrid networks. Tab. 1, explains in detail the edges partition.
Let G be a graph of Gr (Ps, v) over Ps, then, FKBI, FKHBI, mFKBI SKBI, SKHBI, and mSKBI indices are.
Eqs. (7)–(12) represent the proven results of the graph of Gr (Ps, v) over Ps mentioned in Fig. 2.
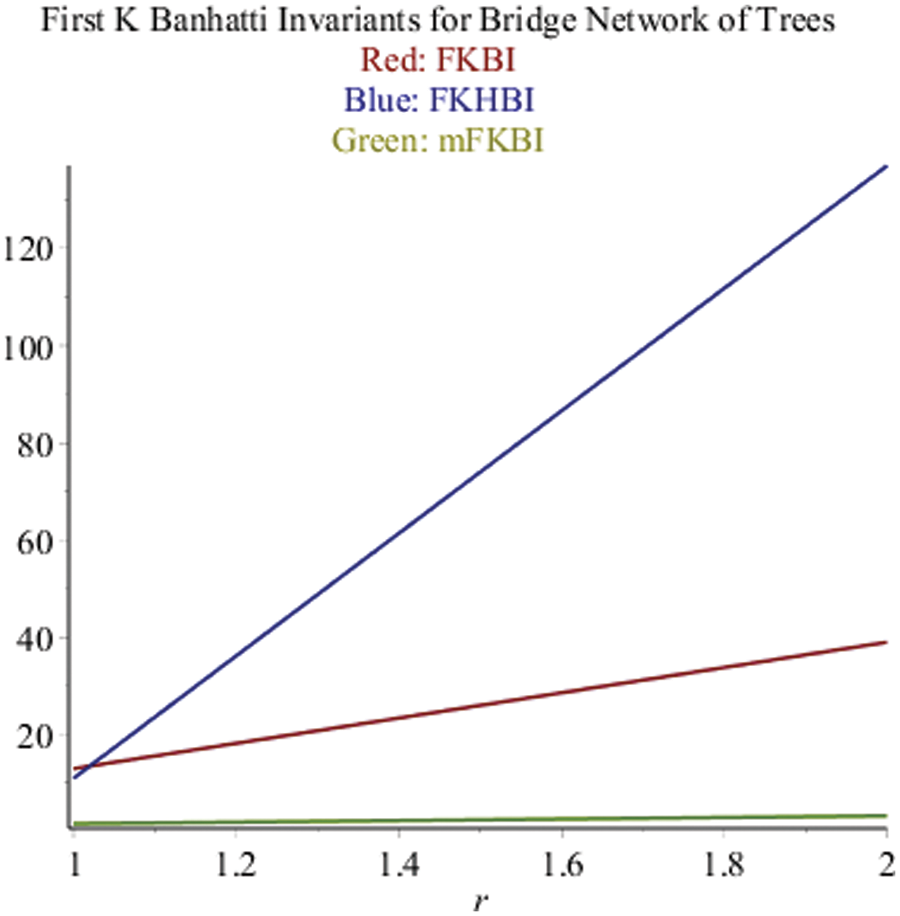
Figure 2: FKBI, FKHBI and mFKBI for Gr (Ps, v) over Ps
4.1.3 Investigation of Bridge Graphs by First K Banhatti Indices and Its Different Forms
Proof
Fig. 2 shows the results of Eqs. (1)–(3) of K-Banhatti indices and their forms in green and red lines respectively. It is the first K-Banhatti invariant for the bridge network of trees.
4.1.4 Investigation of Bridge Graphs by Second K Banhatti Indices and Its Different Forms
Proof
Fig. 3 shows the second k-banhatti invariants for the bridge network of trees.
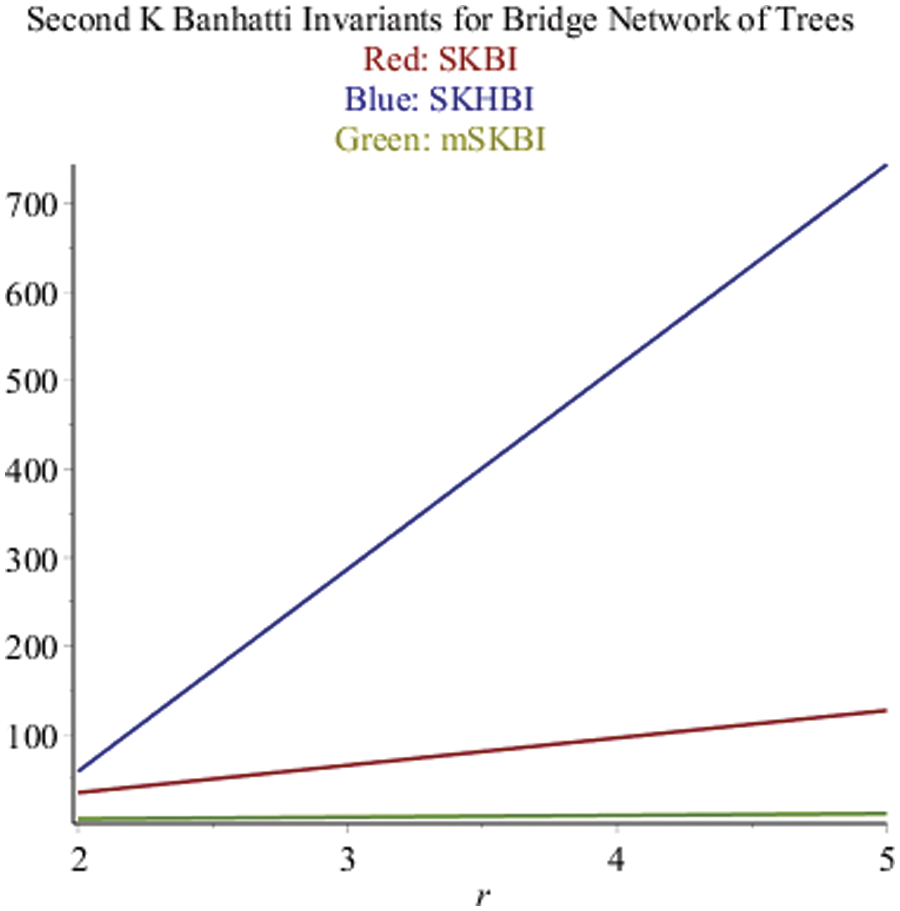
Figure 3: SKBI, SKHBI and mSKBI for Gr (Ps, v) over Ps
Tab. 2 describes the edge partitions of graph Gr (Ks, v) Over Ks of the bridge graph given in Fig. 4 with frequencies.
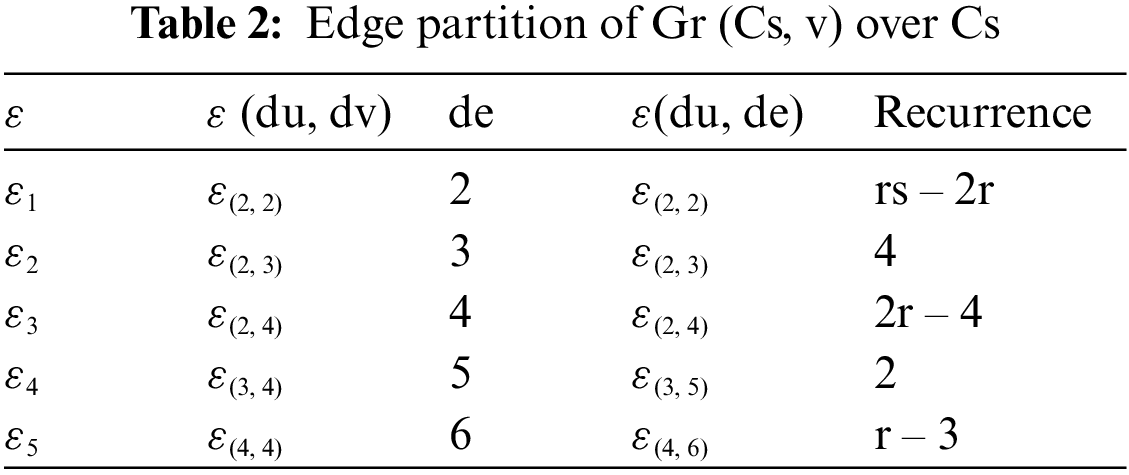
Figure 4: Gr (Cs, v) over Cs for Bridge Network
Fig. 4 shows the bridge networks in which bus networks and ring networks bridge together [32].
4.2.1 Bridge Graph Gr (Cs, v) Over Cycle
Assuming V is the arrangement of vertices seen in Fig. 4, this arrangement of vertices can be parted into four subsets V1, V2, V3 and V4 to V = V1 + V2 + V3 + V4. When ε (D2 (m)) addresses an edge set. Fig. 4 shows a half and half network cycle with five distinct kinds of edges in the network graph of the bridge graph Gr (Cs, v). Tab. 2 provides a detailed description of the edge set.
Let G be a graph of Gr (Cs, v) over Cs Then FKBI, FKHBI, mFKBI SKBI, SKHBI and mSKBI indices are;
Eqs. (13)–(18) represent the proven results of the graph of Gr (Cs, v) over the Cycle mentioned in Fig. 5.
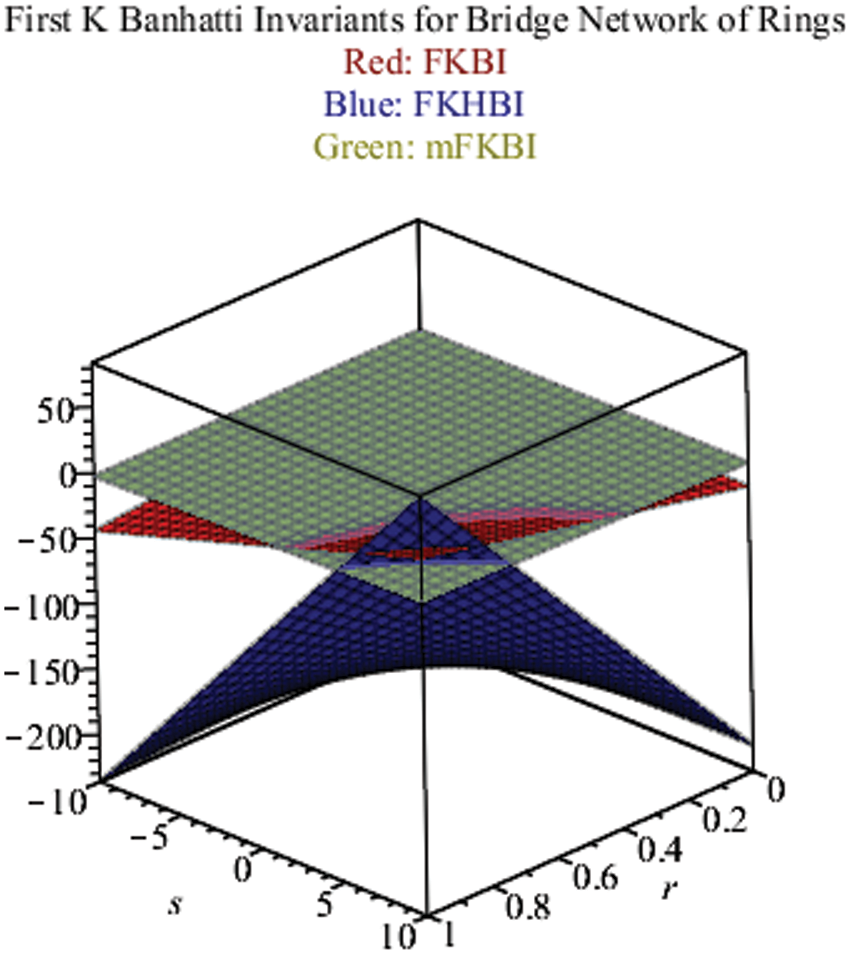
Figure 5: FKBI, FKHBI and mFKBI for Gr (Cs, v) over Cycle
4.2.3 Investigation of Bridge Graphs by K Banhatti Indices and Its Different Forms
Proof
Fig. 5 shows the results (Eqs. (1)–(3)) of the first K Banhatti indices and their other forms in green, red, and blue colors respectively in the 3D version.
Fig. 6 shows the results (Eqs. (4)–(6)) of the second K-Banhatti indices and their other forms in green, red and blue colors respectively in the 3D version.
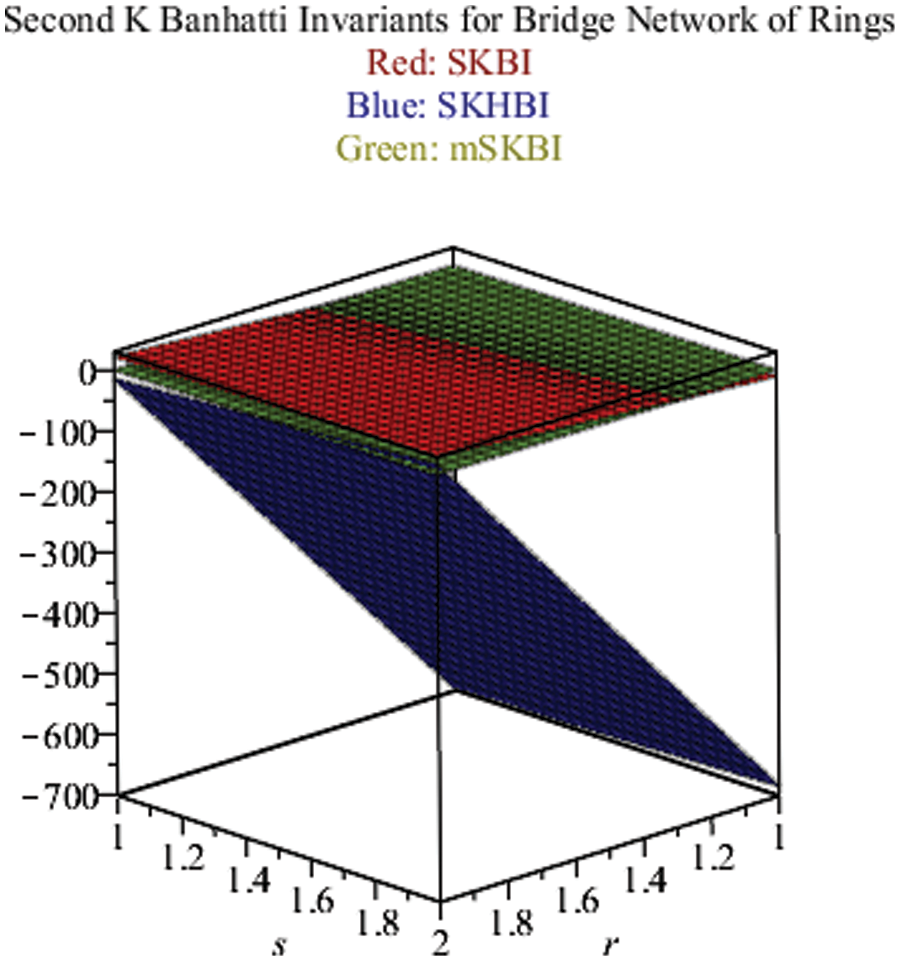
Figure 6: SKBI, SKHBI and mSKBI for Gr (Cs, v) over Cs
Tab. 3 describes the edge partitions of graph Gr (Ks, v) Over Ks of the bridge graph given in Fig. 7 with the number of occurrences.

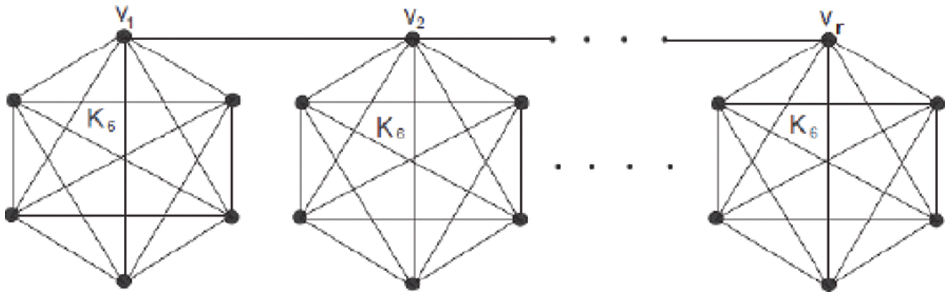
Figure 7: Gr (Ks, v) over Ks
Fig. 7 shows the bridge networks in which bus networks and fully connected networks are bridged together.
4.3.1 Bridge Graph Gr (Ks, v) Over Complete Graph
Assuming that the vertices set are V, understanding Fig. 6 allows us to sort this set of vertices into three subsets V1, V2 and V3 so that V = V1 + V2 + V3. If E shows the edge set, Fig. 6 shows the bridge graph Gr (Ks, v) of the complete graph of the hybrid network. The bridge graph of the network graph has five different edges. Tab. 3 provides a detailed description of the edge set.
Let G be a graph of Gr (Ks, v) over Ks. Then FKBI, FKHBI, mFKBI SKBI, SKHBI and mSKBI indices are;
Eqs. (19)–(24) represent the proven results of the graph of Gr (Ks, v) over the complete graph mentioned in Fig. 7.
4.3.3 Investigation of Bridge Graphs by First K Banhatti Indices and Its Different Forms
Proof
Fig. 8 shows the results (Eqs. (1)–(3)) of K Banhatti indices and their other forms in green, red and blue colors respectively in the 3D version.
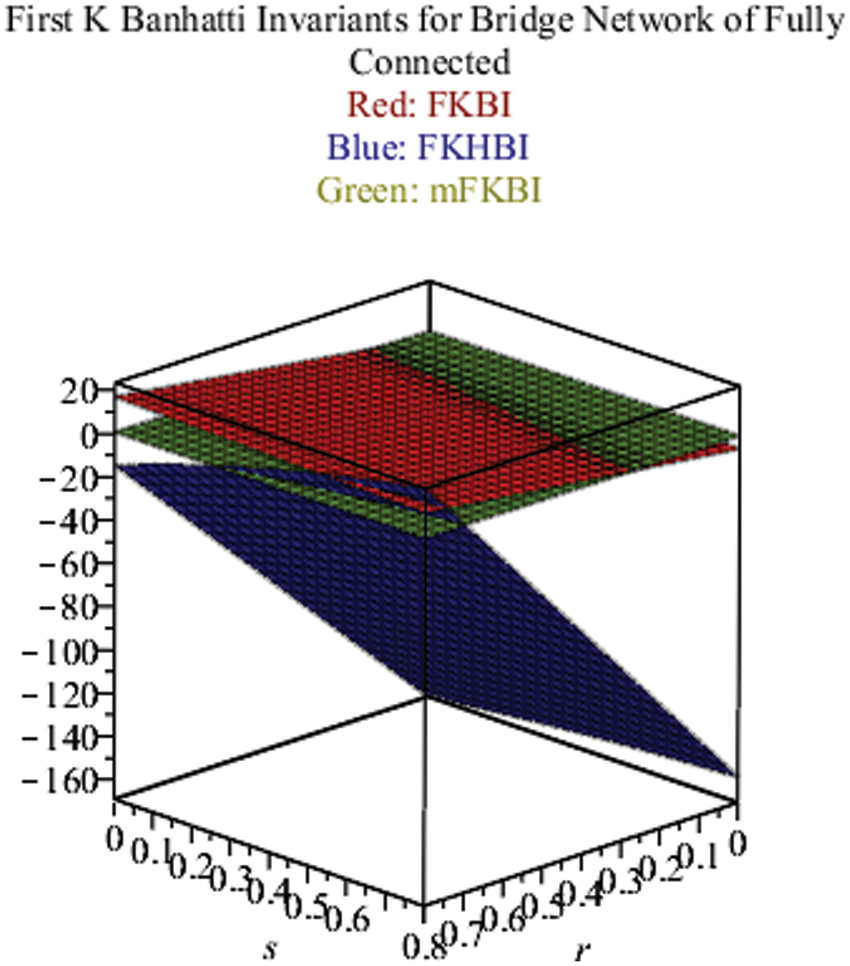
Figure 8: FKBI, FKHBI and mFKBI for Gr (Ks, v) over Ks
4.3.4 Investigation of Bridge Graphs by Second K Banhatti Indices and Their Different Forms
Proof
Fig. 9 shows the results (Eqs. (4)–(6)) of K-Banhatti indices and their other forms in green, red and blue colors respectively in the 3D version.
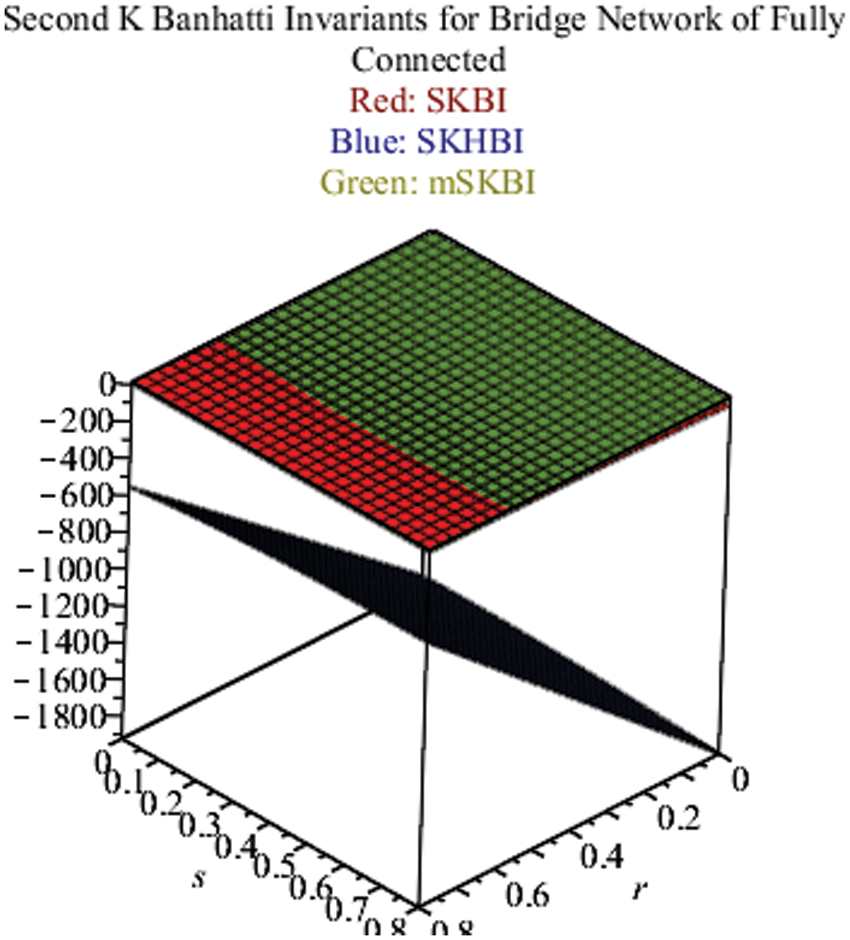
Figure 9: SKBI, SKHBI and mSKBI for Gr (Ks, v) over Ks
In the above results, the study analyzes that Topological invariants like k-banhatti invariants and their reduced forms enable us to collect information about bridge networks in the form of algebraic structures and gives us a mathematical technique to guess the hidden properties of different structures like certain networks There are two main clashes of topological indices, first one is the degree-based topological and the second class is known as distance-based topological indices but present study solved the networks with the help of degree-based topological indices and get best results as shown in graphs.
The research work concentrates on the topological properties and solutions of bridge networks for LAN, interconnection networks used in memory, microprocessors, MLP, power generation networks, chemical compounds, robotics, etc through topological invariants. The topological properties include lower bounds, upper bounds, and prediction qualities of deduced mathematical results. Though interconnection networks are modeled through these solved results. So, engineers and manufacturers foresee concerning products before manufactured or developing them.
TIs have lots of uses and implementations in many fields of computer science, chemistry, biology, informatics, arithmetic, material sciences, robotics, etc. But the utmost significant application is in the non-exact QSPR and QSAR. TIs are associated with the structure of networks, the backbone of the internet, local area networks and chemical structure. But the present article discusses the First and Second K Banhatti invariants with ‘their different forms which are freshly presented. These have numerous prediction qualities for different variants of bridge graphs or networks, i.e., Gr (Ps, v), Gr (Cs, v), and Gr (Ks, v). Figs. 2, 5, and 8 give the graphical representation of First K Banhatti invariants, Figs. 3, 6, and 9 give the graphical representation of Second K Banhatti invariants for the above-mentioned bridge graphs of networks. These deduced results will be used for the modeling of computer networks (like LAN, MAN, WAN and the backbone of the internet), interconnection networks, power generation networks, chemical structures, image processing, bioinformatics, memory interconnection networks and the assembly of robotics, etc.
Acknowledgement: We thank our families and colleagues who provided us with moral support.
Funding Statement: This research is fully funded by Universiti Teknologi Malaysia under the UTM Fundamental Research Grant (UTMFR) with Cost Center No Q.K130000.2556.21H14.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. X. Bei, S. Chen, J. Guan, Y. Qiao and X. Sun, “From independent sets and vertex colorings to isotropic spaces and isotropic decompositions another bridge between graphs and alternating matrix spaces,” SIAM Journal on Computing, vol. 50, no. 3, pp. 924–971, 2021. [Google Scholar]
2. A. F. Bouarab, J. P. Harvey and C. Robelin, “Viscosity models for ionic liquids and their mixtures,” Physical Chemistry Chemical Physics, vol. 23, no. 2, pp. 733–752, 2021. [Google Scholar]
3. J. F. Zhong, A. Rauf, M. Naeem, J. Rahman and A. Aslam, “Quantitative structure property relationships (qspr) of valency based topological indices with covid-19 drugs and application,” Arabian Journal of Chemistry, vol. 14, no. 7, pp. 103240, 2021. [Google Scholar]
4. V. Kulli, “New k banhatti topological indices,” International Journal of Fuzzy Mathematical Archive, vol. 12, no. 1, pp. 29–37, 2017. [Google Scholar]
5. M. Imran, M. A. Iqbal, Y. Liu, A. Q. Baig, W. Khalid et al., “Computing eccentricity based topological indices of 2 power interconnection networks,” Journal of Chemistry, vol. 2020, no. 1, pp. 1–7, 2020. [Google Scholar]
6. J. Liu, L. Cai, W. Akhtar, S. A. Maitla and Y. Wei, “Computation of irregularity indices of certain computer networks,” Mathematical Problems in Engineering, vol. 2020, no. 1, pp. 3–11, 2020. [Google Scholar]
7. M. Cancan, I. Ahmad and S. Ahmad, “Study of topology of block shift networks via topological indices,” Proyecciones (Antofagasta Online), vol. 39, no. 4, pp. 887–902, 2020. [Google Scholar]
8. M. S. Ahmad, W. Nazeer, S. M. Kang, M. Imran and W. Gao, “Calculating degree based topological indices of dominating david derived networks,” Open Physics, vol. 15, no. 1, pp. 1015–1021, 2017. [Google Scholar]
9. C. C. Wei, H. Ali, M. A. Binyamin, M. N. Naeem and J. B. Liu, “Computing degree based topological properties of third type of hex derived networks,” Mathematics, vol. 7, no. 4, pp. 368–377, 2019. [Google Scholar]
10. M. S. Ahmad, D. Afzal, W. Nazeer and S. M. Kang, “On topological indices of octagonal network,” Journal of Optoelectronics and Advanced Materials, vol. 18, no. 1, pp. 884–892, 2017. [Google Scholar]
11. M. Naeem, M. K. Siddiqui, J. L. Guirao and W. Gao, “New and modified eccentric indices of octagonal grid omn,” Applied Mathematics and Nonlinear Sciences, vol. 3, no. 1, pp. 209–228, 2018. [Google Scholar]
12. Z. Hussain, M. Munir, S. Rafique and S. M. Kang, “Topological characterizations and index analysis of new degree based descriptors of honeycomb networks,” Symmetry, vol. 10, no. 10, pp. 478–491, 2018. [Google Scholar]
13. W. Zhang, S. A. Kirmani, M. K. Siddiqui, A. Rauf, M. Aleem et al., “On degree based topological indices of polycyclic certain interconnection networks,” Polycyclic Aromatic Compounds, vol. 1, no. 1, pp. 1–8, 2021. [Google Scholar]
14. S. Mondal, D. E. Nilanjan and P. A. L. Anita, “Topological properties of networks using m polynomial approach,” Konuralp Journal of Mathematics, vol. 8, no. 1, pp. 97–105, 2020. [Google Scholar]
15. F. Deng, X. Zhang, M. Alaeiyan, A. Mehboob and M. R. Farahani, “Topological indices of the pent heptagonal nanosheets VC5C7 and HC5C7,” Advances in Materials Science and Engineering, vol. 2019, no. 1, pp. 3–6, 2019. [Google Scholar]
16. N. Mirehi, M. Tahmasbi and A. T. Targhi, “Hand gesture recognition using topological features,” Multimedia Tools and Applications, vol. 78, no. 10, pp. 13361–13386, 2019. [Google Scholar]
17. J. B. Liu, J. Zhao, S. Wang and J. Cao, “On the topological properties of the certain neural networks,” Journal of Artificial Intelligence and Soft Computing Research, vol. 8, no. 4, pp. 257–268, 2018. [Google Scholar]
18. A. Hussain, M. Numan, N. Naz, S. I. Butt, A. Aslam et al., “On topological indices for new classes of benes network,” Journal of Mathematics, vol. 2021, no. 1, pp. e6690053, 2021. [Google Scholar]
19. M. Šestak, M. Heričko, T. W. Družovec and M. Turkanović, “Applying k vertex cardinality constraints on a neo4j graph database,” Future Generation Computer Systems, vol. 115, no. 1, pp. 459–474, 2021. [Google Scholar]
20. A. H. Göller, L. Kuhnke, A. T. Laak, K. Meier and A. Hillisch, “Machine learning applied to the modeling of pharmacological and absorption, distribution, metabolism, excretion and toxicity (admet) endpoints,” in Proc. of Artificial Intelligence in Drug Design, New York, United States, pp. 61–101, 2022. [Google Scholar]
21. V. V. Mitic, G. Lazovic, B. Randjelovic, V. Paunovic, I. Radovic et al., “Graph theory applied to microelectronics intergranular relations,” Ferroelectrics, vol. 570, no. 1, pp. 145–152, 2021. [Google Scholar]
22. B. Huang, L. Ge, G. Chen, M. Radenkovic, X. Wang et al., “Nonlocal graph theory based transductive learning for hyperspectral image classification,” Pattern Recognition, vol. 116, no. 1, pp. 107967, 2021. [Google Scholar]
23. D. Hwang, H. J. Kim, S. P. Lee, S. Lim, B. K. Koo et al., “Topological data analysis of coronary plaques demonstrates the natural history of coronary atherosclerosis,” Cardiovascular Imaging, vol. 14, no. 7, pp. 1410–1421, 2021. [Google Scholar]
24. Y. H. Pan, A. Khalid, P. Ali, A. U. Rehman, M. K. Siddiqui et al., “Topological study of polycyclic silicon carbide structure,” Polycyclic Aromatic Compounds, vol. 1, no. 1, pp. 1–12, 2022. [Google Scholar]
25. D. T. Hoang, H. R. Maimani, A. Mousivand and M. R. Pournaki, “Cohen macaulayness of two classes of circulant graphs,” Journal of Algebraic Combinatorics, vol. 53, no. 3, pp. 805–827, 2021. [Google Scholar]
26. C. Durell and S. Forcey, “Level 1 phylogenetic networks and their balanced minimum evolution polytopes,” Journal of Mathematical Biology, vol. 80, no. 5, pp. 1235–1263, 2020. [Google Scholar]
27. A. J. M. Khalaf, M. Farhan, M. Siddiqui and M. Farahani, “On degree based topological indices of bridge graphs,” Journal of Discrete Mathematical Sciences and Cryptography, vol. 23, no. 1, pp. 1139–1156, 2020. [Google Scholar]
28. D. Afzal, S. Ali, F. Afzal, M. Cancan, S. Ediz et al., “A study of newly defined degree based topological indices via m polynomial of jahangir graph,” Journal of Discrete Mathematical Sciences and Cryptography, vol. 24, no. 2, pp. 427–438, 2021. [Google Scholar]
29. K. Hamid, M. W. Iqbal, A. R. Virk, M. U. Ashraf, A. M. Alghamdi et al., “K-Banhatti sombor invariants of certain computer networks,” Computers, Materials & Continua (CMC), vol. 73, no. 1, pp. 15–31, 2022. [Google Scholar]
30. M. Azari, “Multiplicative sum Zagreb index of splice bridge and bridge cycle graphs,” Boletim da Sociedade Paranaense de Matemática, vol. 39, no. 3, pp. 3–8, 2021. [Google Scholar]
31. X. R. Zhang, W. Z. Zhang, W. Sun, H. L. Wu, A. G. Song et al., “A Real-time cutting model based on finite element and order reduction,” Computer Systems Science and Engineering, vol. 43, no. 1, pp. 1–15, 2022. [Google Scholar]
32. X. R. Zhang, J. Zhou, W. Sun and S. K. Jha, “A lightweight CNN based on transfer learning for COVID-19 diagnosis,” Computers, Materials & Continua (CMC), vol. 72, no. 1, pp. 1123–1137, 2022. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |