| Computers, Materials & Continua DOI:10.32604/cmc.2022.032087 |  |
| Article |
Computational Stochastic Investigations for the Socio-Ecological Dynamics with Reef Ecosystems
1Department of Mathematics, Faculty of Science, Khon Kaen University, Khon Kaen 40002, Thailand
2Department of Mathematical Sciences, United Arab Emirates University, P.O.Box 15551, Al Ain, UAE
3Department of Mathematics and Statistics, Hazara University, Mansehra, Pakistan
4Department of Biological Sciences, Rabigh College of Science and Arts, King Abdulaziz University, Jeddah, Saudi Arabia
5Graduate Program in Administration, Federal University of Santa Maria, Santa Maria 93458, Brazil
*Corresponding Author: Wajaree Weera. Email: wajawe@kku.ac.th
Received: 06 May 2022; Accepted: 07 June 2022
Abstract: The motive of this work is to present a computational design using the stochastic scaled conjugate gradient (SCG) neural networks (NNs) called as SCGNNs for the socio-ecological dynamics (SED) with reef ecosystems and conservation estimation. The mathematical descriptions of the SED model are provided that is dependent upon five categories, macroalgae M(v), breathing coral C(v), algal turf T(v), the density of parrotfish P(v) and the opinion of human opinion X(v). The stochastic SCGNNs process is applied to formulate the SED model based on the sample statistics, testing, accreditation and training. Three different variations of the SED have been provided to authenticate the stochastic SCGNNs performance through the statics for training, accreditation, and testing are 77%, 12% and 11%, respectively. The obtained numerical performances have been compared with the Runge-Kutta approach to solve the SED model. The reduction of mean square error (MSE) is used to investigate the numerical measures through the SCGNNs for solving the SED model. The precision of the SCGNNs is validated through the comparison of the results and the absolute error performances. The reliability of the SCGNNs is performed by using the correlation values, state transitions (STs), error histograms (EHs), MSE measures and regression analysis.
Keywords: Socio-ecological state; conservation estimation; neural networks; reef ecosystems; scaled conjugate gradient; numerical study
The study of coral reef ecology systems (CRESs) or complex aquatic networks along with the composed construction based on the Scleractinia corals have located on their reigns skeletons [1]. CRES is the assortment of individuals, which provides the services to the nearby populace. CRES comprises on the number of polyps that are established into a large domain to perform as an electromagnet for both tourism and fishing. A major feature of coral growth is zooxanthellae algae (ZA), which is also recognized as a unicellular creature and proficient in using the photosynthetic process. During the CRESs procedure, ZA is produced with the interdependent connotation of coral polyps in the process of isolation. For the nutrients, CRES is used as an organic indication, which establishes ZA in the form of a coral substance to generate the chemical combinations in the photosynthesis process [2]. This combined response series approves the growth and development of each category of the model.
The Caribbean form the CRESs demonstrates the elasticity in the contradiction of the past conflicts and recovered quickly after the Hurricane Allen (1980–1983) [3–6]. The mutual connotation between the urchins and CRESs is authenticated with the urchin entities using the algal turf nutrition. Parrotfish performs the main grazers procedure based on the ecosystem, which is used to emphasize the conditions of operative protection [7]. The Algal progresses are considered dangerous due to the authenticity of the CRESs. The macroalgae spread is documented to evade the development of reef along with the potential growth.
The mathematical form of the systems along with the diverse perceptions have been functional in numerous submissions of the religion, non-physical form of the models (psychology, sociology, political science, economics), linguistics, engineering studies (computer science, mechanical, electrical), philosophy, and in the dynamics of the natural science (earth sciences, biology, chemistry, physics). A mathematical model is applied to scrutinize the influences of numerous apparatuses. The mathematical systems have been provided in several measures, like game theory, statistics, and well as dynamic systems. In general, mathematical systems can indicate the logical strategies, while the scientific measures exhibit the brilliance of the models that indicate the theoretical performances to support the consequences of the repeatable actions. The mathematical form of the systems has been illustrated in the ecosystem management [8,9], vaccination [10,11], land-use variations [12] and forestry [13–16] and prediction differential model [17].
The human conducts and the dynamic impacts based on the CRESs require more investigations to model the theoretical form of the systems. Several anthropogenic influences have been used to reproduce the present work based on the reef protection along with the covered areas of marine [18]. The human presentations have been dynamically modeled, adaptively evolving the phenomenon, a deeper and richer shape of the anthropogenetic pressures in a system over a long time. The mathematical models based on the biological systems have also been used in [19–25].
The mathematical form of the socio-ecological dynamics (SED) using the reef ecosystems and the conservation estimation model is provided in five categories, Macroalgae M(v), breathing coral C(v), algal turf T(v), the density of parrotfish P(v) and the opinion of human opinion X(v) [26]:
The starting four dynamics in the Eq. (1) represent the same behavior as presented by Blackwood et al. [27], which is used to exclude the constant parrotfish concentration values. These values alter with the coupling

The motive of the present work is to provide a computational design using the stochastic scaled conjugate gradient (SCG) neural networks (NNs) called as SCGNNs for the SED with reef ecosystems and conservation estimation. The stochastic frameworks have been used to provide the results of several evolutionary/swarming schemes [28–34]. The advanced topographies have never been exploited before to solve the SED with reef ecosystems and conservation estimation using the SCGNNs. Few major novel points of this study are given as:
• A novel design of the SCGNNs is presented to solve the SED with reef ecosystems and conservation estimation using the SCGNNs.
• The comparison of the achieved performances via SCGNNs and the database Runge-Kutta solutions has been presented to solve the SED model.
• The overlapping of the outcomes designates the accuracy and correctness of the proposed stochastic SCGNNs procedure for solving the mathematical SED nonlinear model.
• The precise and accurate absolute error (AE) presentations designate the excellence of the stochastic designed SCGNNs approach to solving the SED mathematical model.
• The presentations via correlation values, STs, EHs, MSE measures and regression analysis provide the accurateness of the stochastic designed SCGNNs approach for the nonlinear SED systems.
The remaining sections of the paper are organized as: Section 2 is based on the stochastic methodology. Section 3 provides the numerical procedures of the SED model. Section 4 derives the concluding remarks of the present study.
2 Designed Method Through SCGNNs
The proposed methodology based on the SCGNNs is described in two phases for solving the SED with reef ecosystems and conservation estimation. The process of optimization based on the multi-layer procedures is provided in Fig. 1. The SCGNNs procedure is applied by using the stochastic SCGNNs performance through the statics for training, accreditation, and testing are 77%, 12% and 11%, respectively.
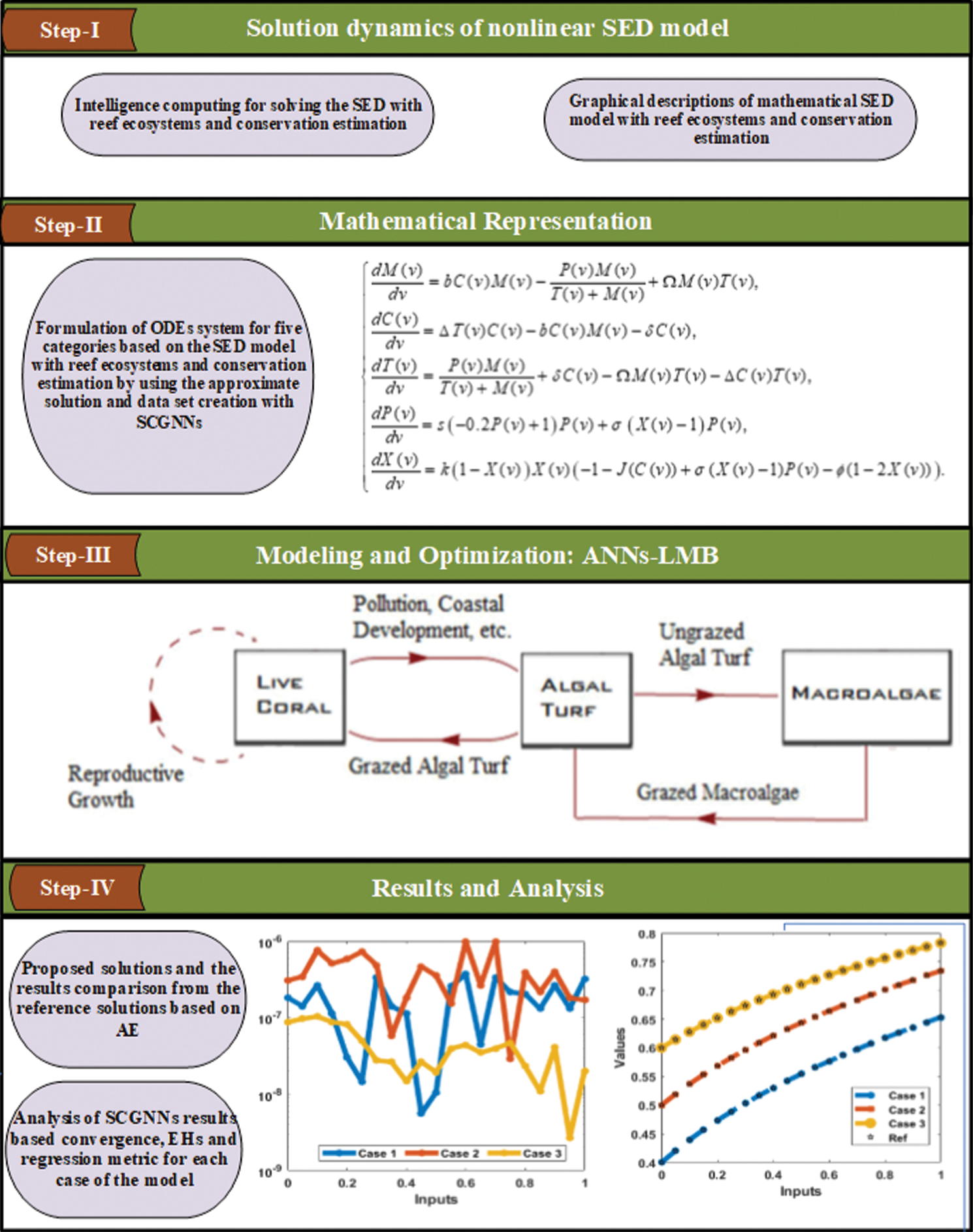
Figure 1: Workflow diagram of SCGNNs for solving the SED mathematical system
Fig. 1 shows the dataset is designed for different variants of SED mathematical system based on the Runge-Kutta scheme (invoking ‘NDSolve’ solver in the Mathematica software). The Runge-Kutta method is applied as a default parameter setting in ‘NDSolve’ to check the execution and terminating tolerances. The statics designed for SED mathematical system is applied in the process of comparison throughout the study.
The designed SCGNNs is implemented using the ‘nftool’ solver in ‘Matlab’ for the appropriate portions of hidden neurons, testing statistics, learning methods and verification statics. While the process of implementation based on the SCGNNs for solving the SED mathematical system based on the parameter setting is provide in Tab. 2. The networks training is directed with SCGNNs process, where the backpropagation is oppressed to improve the Jacobian ‘jZ’ based on the presentation, i.e., MSE, to adjust the weight along with the variables of bias Z. The modification or adaptation for each decision variable by taking the SCG process is presented below as:
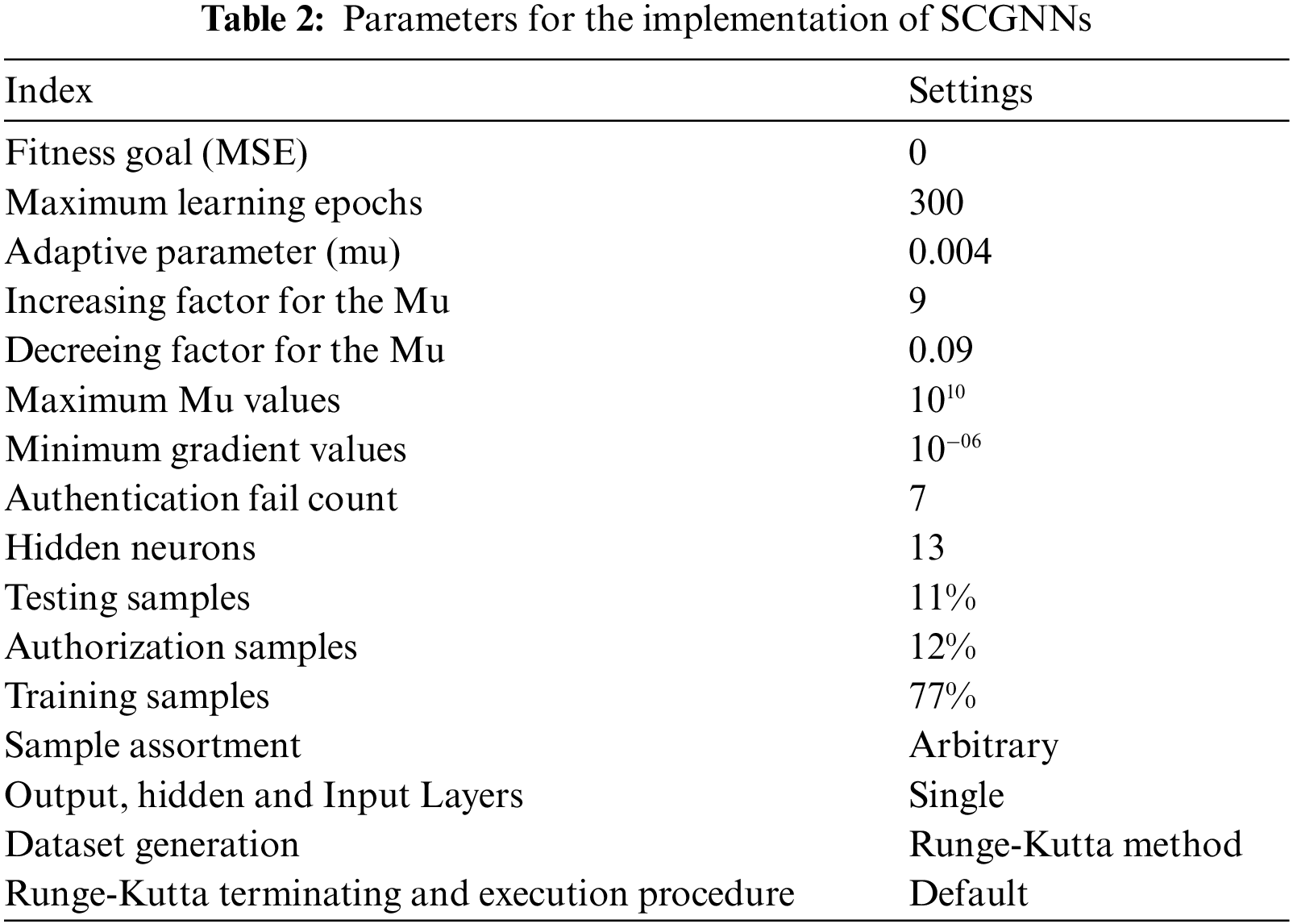
Fig. 2 shows the formulation of the proposed LMBNNs procedure using the generic perception based on the single neurons.
Figure 2: Generic structure based on a single neuron
This section presents the numerical representations using the proposed SCGNNs for three different variations based on the mathematical form of the SED with reef ecosystems and conservation estimation are mathematically given as:
Case-1: Suppose a SED model by taking
Case-2: Suppose a SED model by taking
Case-3: Suppose a SED model by taking
The obtained results from the SCGNNs have been calculated with interval [0, 1] to solve the SED model with reef ecosystems and conservation estimation by taking 13 numbers of neurons with the statical assessments of training, accreditation, and testing have been used as 77%, 12% and 11%, respectively. The input, output, and hidden layer’s structure of the SED model is shown in Fig. 3. The different measures for the selection of these data can also be chosen. If the training performances have been chosen as >77%, then one can get the better performances due to the values of bias input. Furthermore, if the statics for the training samples is selected <77%, then the correctness of the SCGNNs is degraded significantly for SED model with reef ecosystems and conservation estimation. Therefore, the sample statics for the unbiased and bias inputs should be selected with care and concentration to avoid both premature convergence and divergence.

Figure 3: Stochastic SCGNNs procedure for the SED system
The illustrations based on the SED mathematical system are presented in Figs. 4–12. The MSE measures and STs representations are illustrated in Figs. 4 and 5 to present the solutions of the SED system. The MSE measures for testing, best curve, training, and corroboration are shown in Fig. 4. The Epochs for the mathematical SED system have calculates using the SCGNNs scheme as 68, 58 and 38, which found as 7.6689 × 10−11, 5.8828 × 10−11 and 1.6161 × 10−13. The gradient presentations are derived in Fig. 5 for the SED model based on the SCGNNs. These representations are measured as 9.578 × 10−08, 9.570 × 10−08 and 9.729 × 10−08 for case 1 to 3. These illustrations designate the accuracy of the SCGNNs for the SED mathematical system. The fitting curves performances are shown in Figs. 6–8 for each variant of the SED mathematical system, which has been performed by using the comparison of references and achieved solutions. The error based maximum values have been plotted through the training, testing, and corroboration measures by using the SCGNNs procedure for the SED mathematical system. The EHs representations have been provided in Figs. 9a–9c, whereas the regression performances have been illustrated in Figs. 10–12 for the SED nonlinear system. The correlation measures are derived to authenticate the regression that is measured as 1 for each case of the SED. The training, corroboration, and testing measures show the correctness of the stochastic SCGNNs scheme for the SED. Furthermore, the MSE convergence has been provided in Tab. 3 for training, endorsement, epochs, complexity measures and backpropagation.
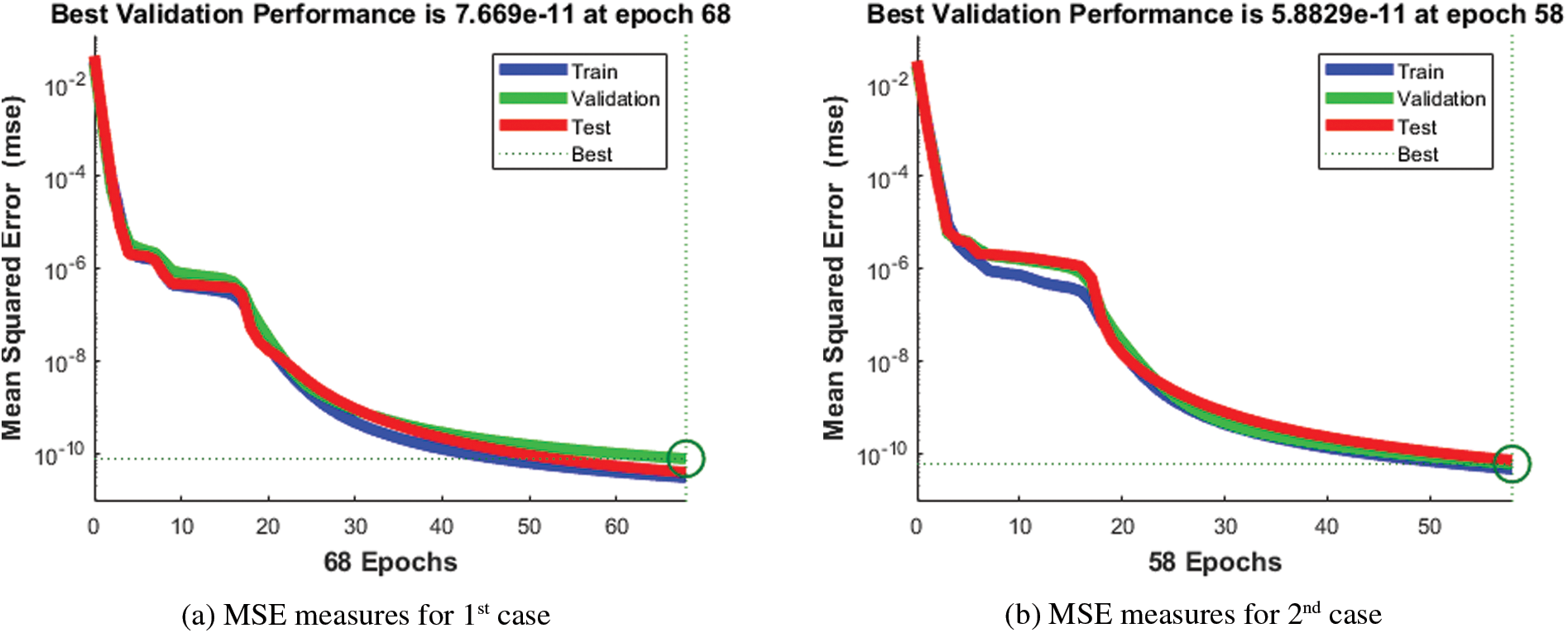

Figure 4: MSE measures using the SCGNNs performances to solve the SED model
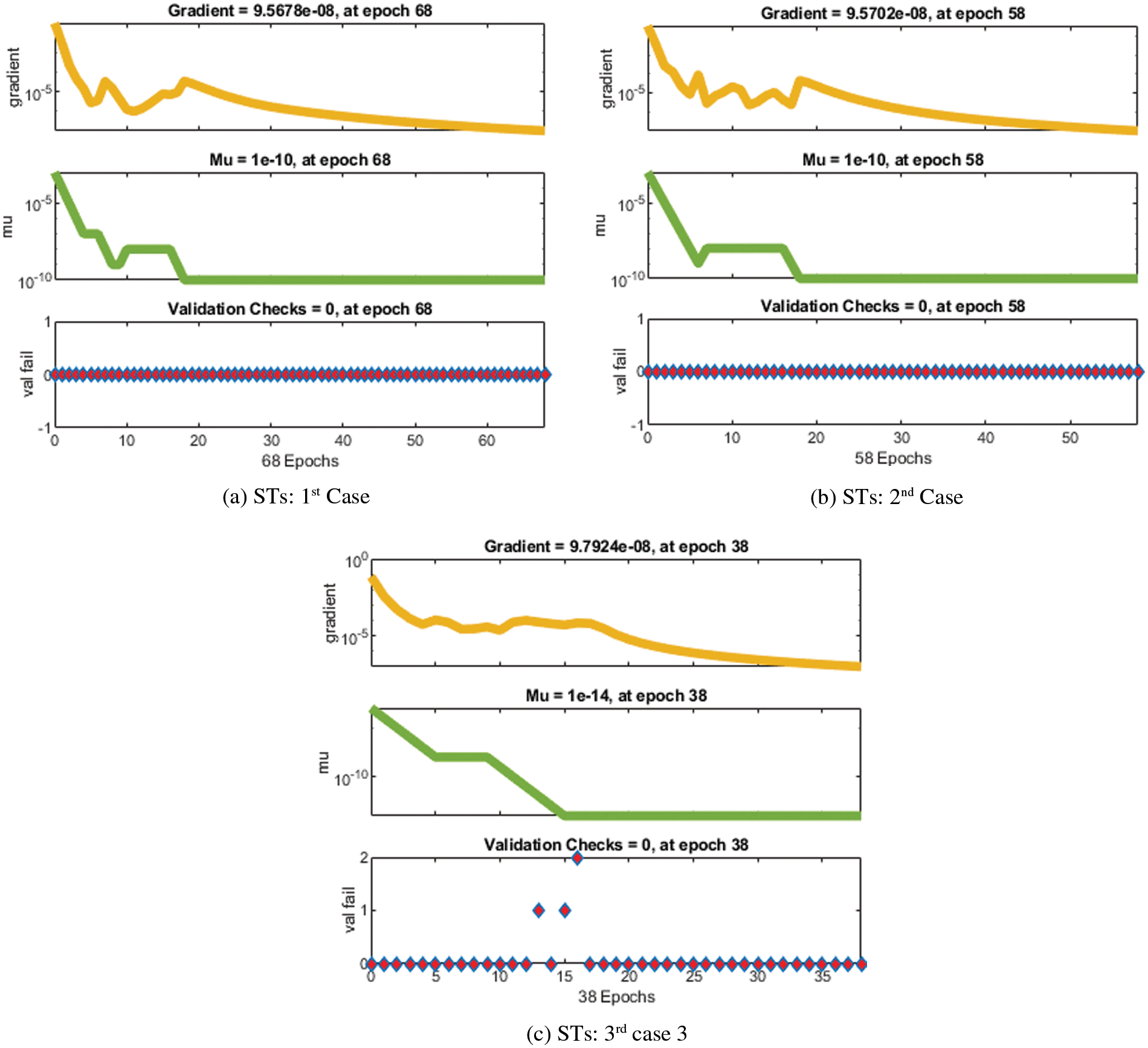
Figure 5: Values of the STs using the SCGNNs performances to solve the SED model
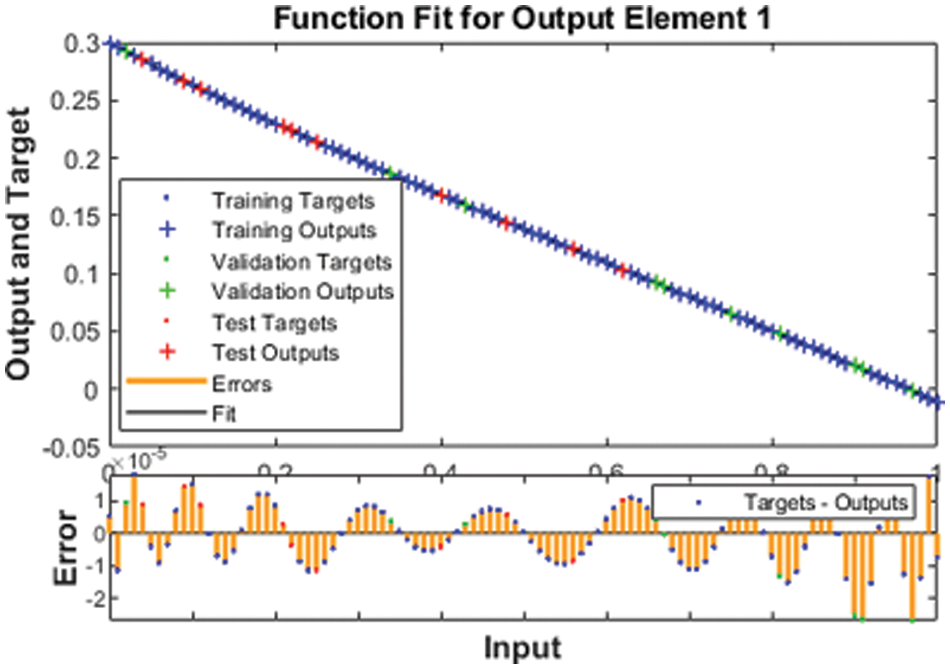
Figure 6: Fitness designs for the SED model based 1st case
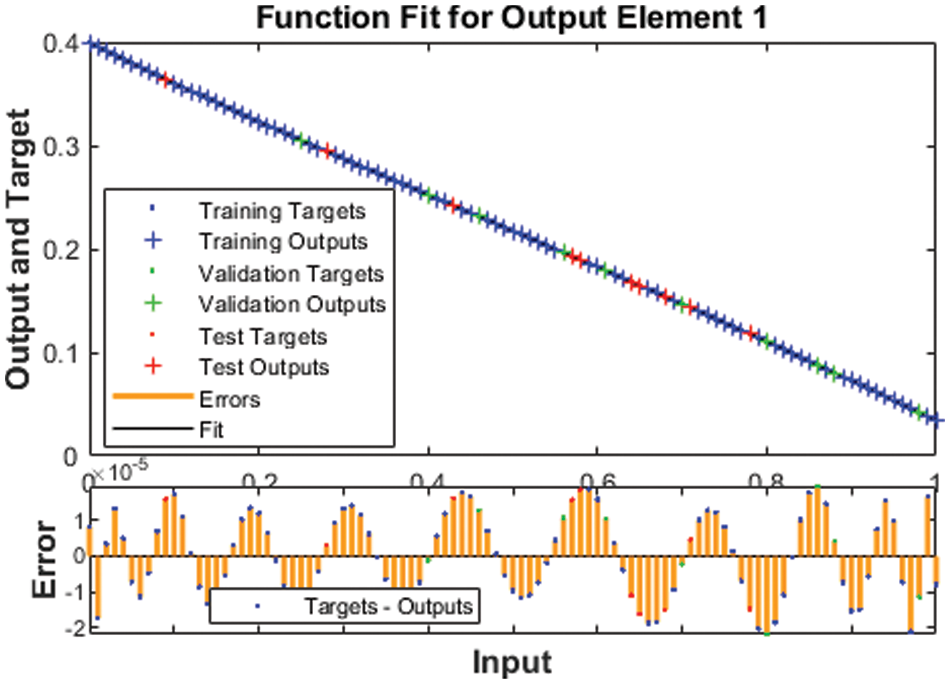
Figure 7: Fitness designs for the SED model based 2st case

Figure 8: Fitness designs for the SED model based 3rd case
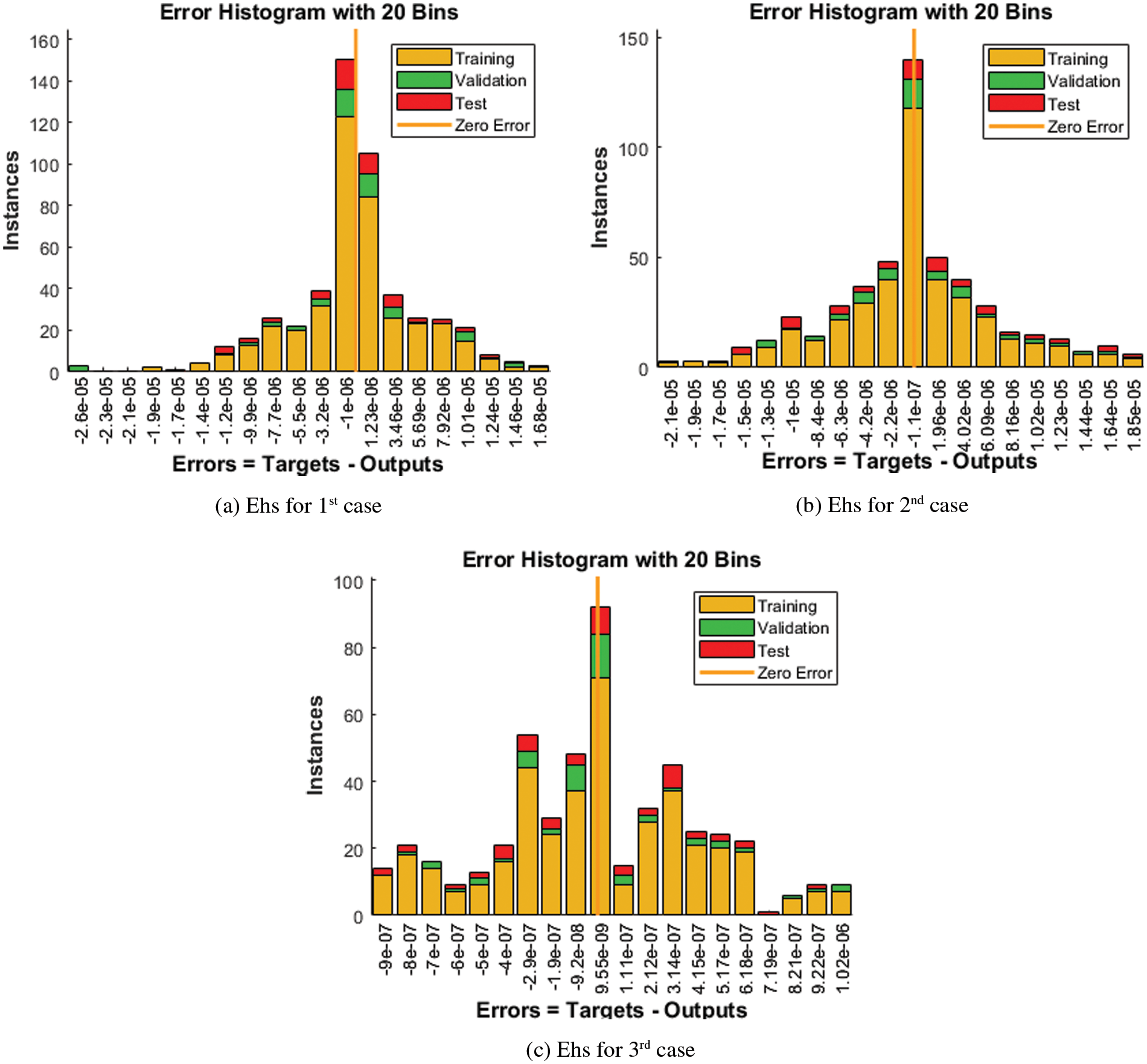
Figure 9: EHs using the SCGNNs performances to solve the SED model
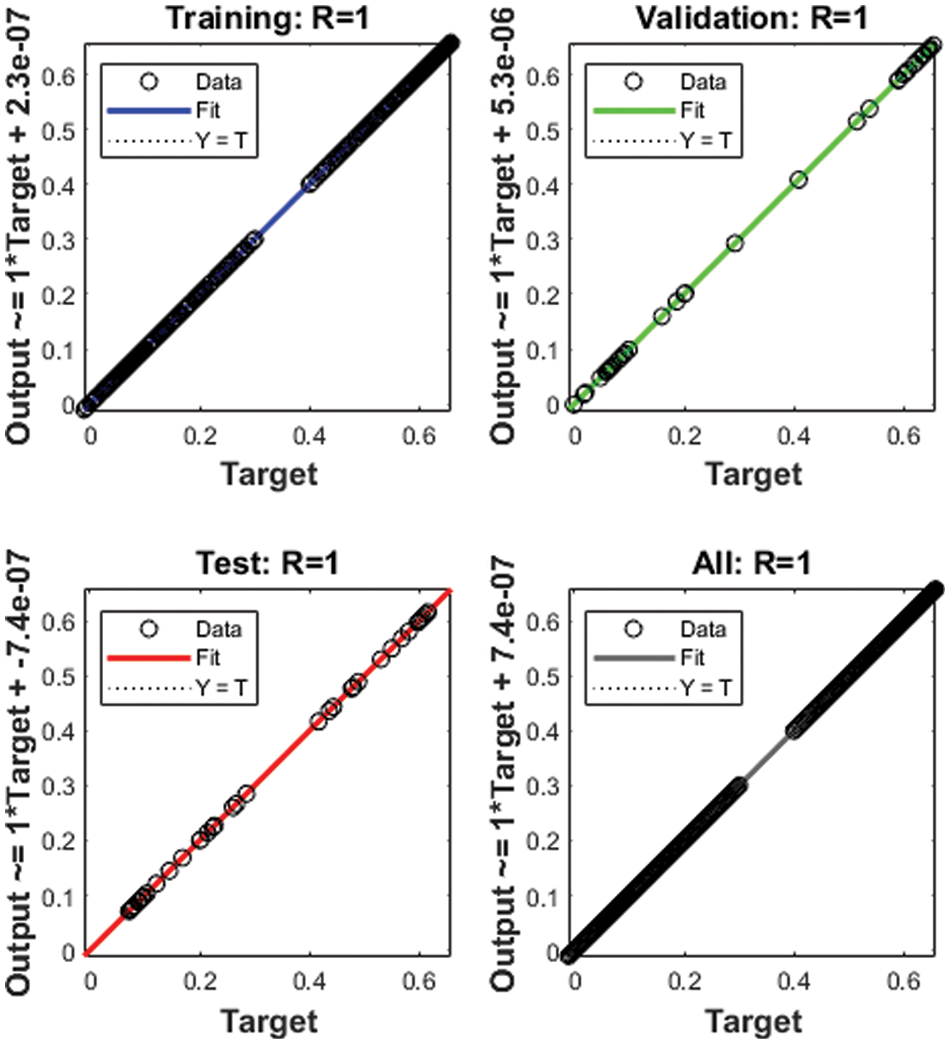
Figure 10: Regression measures of case 1 for the SED system

Figure 11: Regression measures of case 2 for the SED system

Figure 12: Regression measures of case 3 for the SED system
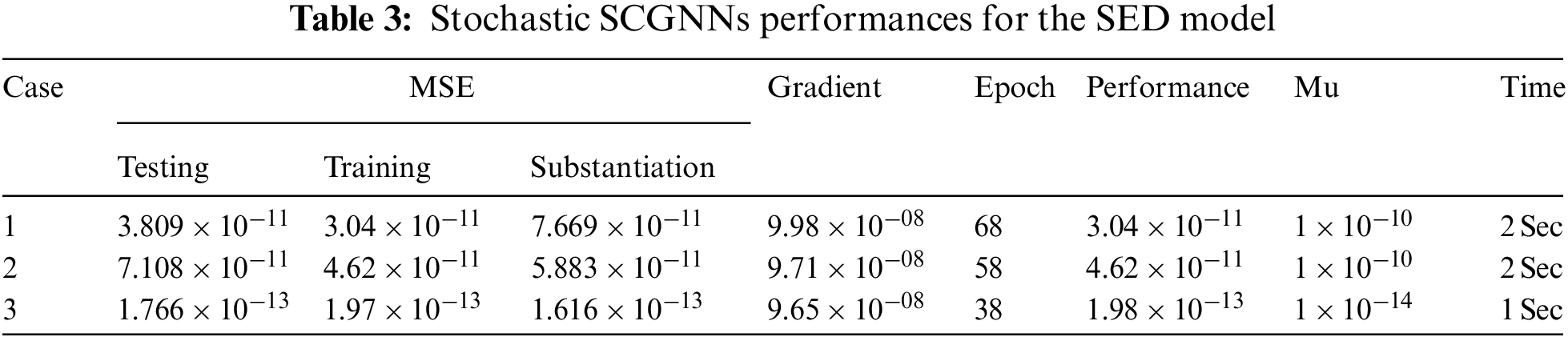
The results (reference and obtained) comparisons are presented in Fig. 13 and the AE for each case of the SED system is illustrated in Fig. 14. The results for the classes of the SED based Macroalgae M(v), breathing coral C(v), algal turf T(v), density of parrotfish P(v) and the opinion of human opinion X(v) are presented in Figs. 13a–13e. The overlapping of the solutions is performed for all cases and each dynamic of the SED model, which represent the perfection and correctness of the stochastic SCGNNs. The AE illustration have been provided in Figs. 14a–14e based on the Macroalgae M(v), breathing coral C(v), algal turf T(v), density of parrotfish P(v) and the opinion of human opinion X(v) of the SED mathematical system. It is observed in the Fig. 14a, that plots of AE for the class M(v) lie as 10−05 to 10−06, 10−04 to 10−06 and 10−06 to 10−07 for 1st to 3rd case. The AE for the class C(v) are derived in Fig. 14b that are calculated around 10−05 to 10−07, 10−05 to 10−08 and 10−07 to 10−09. The AE for the class T(v) are presented in Fig. 14c, which are found as 10−05 to 10−07, 10−05 to 10−06 and 10−06 to 10−07. The AE for the class P(v) are given in Fig. 14d that found around 10−07 to 10−08, 10−06 to 10−07 and 10−07 to 10−09. Moreover, the AE measures for the category X(v) are derived in Fig. 14e, which are calculated as 10−05 to 10−08, 10−05 to 10−06 and 10−06 to 10−08 for 1st to 3rd case of the SED mathematical model. These overlapping of the calculated and reference results as well as the AE values perform the accuracy of the proposed SCGNNs for solving the SED nonlinear mathematical system.
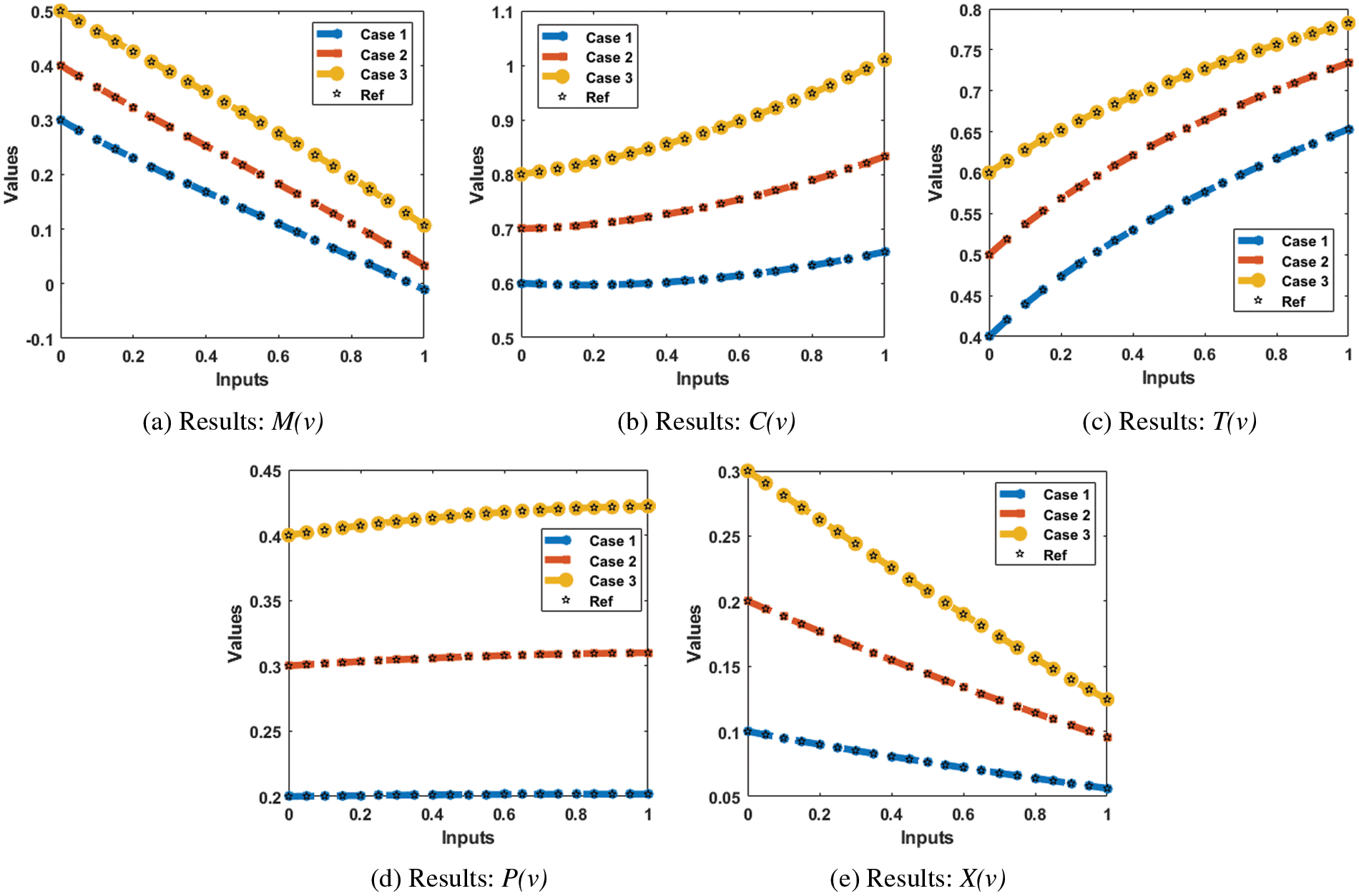
Figure 13: Result comparisons illustrations using the SCGNNs performances to solve the SED mathematical model
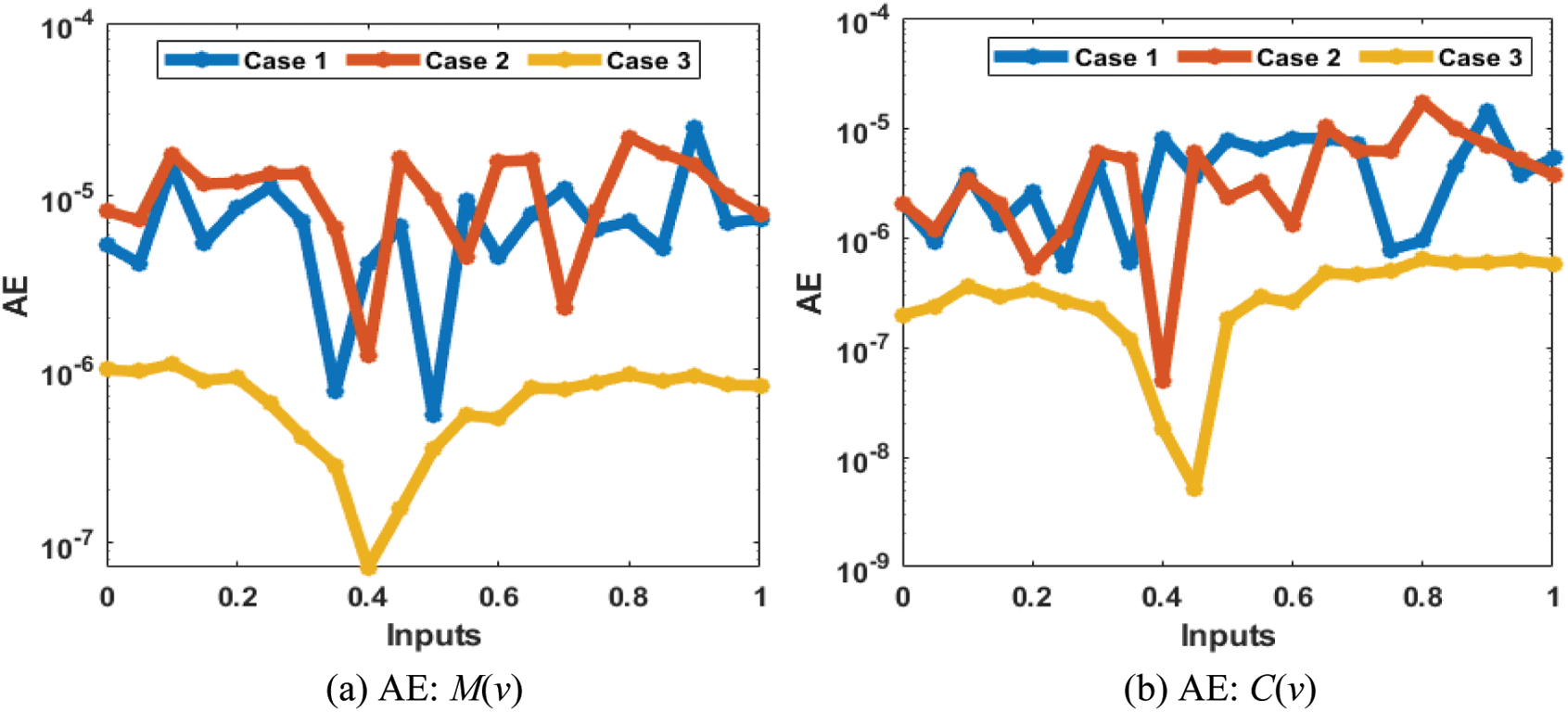
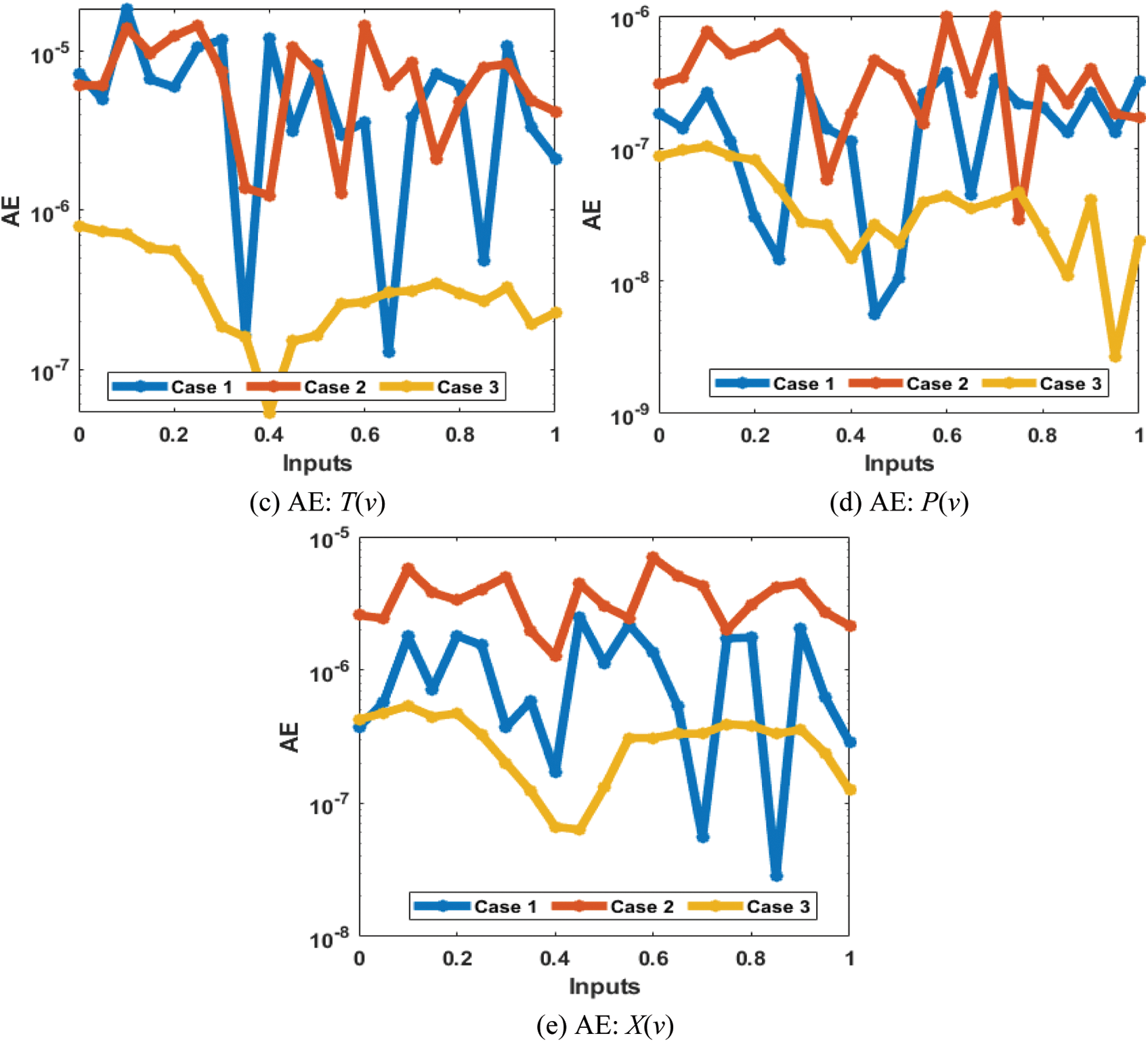
Figure 14: AE using the SCGNNs performances to solve the nonlinear SED mathematical model
The motive of current investigations is to provide a computational structure using the stochastic procedure based on the scaled conjugate gradient neural networks for the socio-ecological dynamics with reef ecosystems and conservation estimation. The mathematical formulations of the SED using the reef ecosystems and conservation estimation have been presented with five categories, Macroalgae M(v), breathing coral C(v), algal turf T(v), density of parrotfish P(v) and the opinion of human opinion X(v). The stochastic procedure based on the SCGNNs has been implemented to formulate the socio-ecological dynamics using the sample statistics, testing, accreditation, and training. Three different classes of the socio-ecological dynamics have been used to validate the stochastic SCGNNs measures through the training, accreditation, and testing statics that has been chosen as 77%, 12% and 11%, respectively along with thirteen numbers of neurons. The comparison of the obtained results has been presented with the reference solutions (Runge-Kutta) for the socio-ecological dynamics system. The AE has been performed in good measures for solving each class of the socio-ecological dynamics with reef ecosystems and conservation estimation, which indicates the correctness of the stochastic approach. The reduction of mean square error has been provided to investigate the numerical measures through the SCGNNs for solving the SED system. The trustworthiness results based on the SCGNNs have been validated through the values of the correlation, state transitions, error histograms, MSE measures and regression analysis.
The designed SCGNNs scheme can be applied in the future to solve the various fluid systems, lonngren-wave networks [35–37], fractional models [38–42], delayed neural networks [43–46] and nonlinear models [47–50].
Funding Statement: This project is funded by National Research Council of Thailand (NRCT) and Khon Kaen University: N42A650291.
Conflicts of Interest: The authors declare that there have not conflicts of interest.
References
1. D. R. Bellwood, T. P. Hughes, C. Folke and M. Nyström, “Confronting the coral reef crisis,” Nature, vol. 429, pp. 827–833, 2004. [Google Scholar]
2. J. E. Sanfilippo, L. Garczarek, F. Partensky and D. M. Kehoe, “Chromatic acclimation in cyanobacteria: A diverse and widespread process for optimizing photosynthesis,” Annual Review of Microbiology, vol. 73, pp. 407–433, 2019. [Google Scholar]
3. T. A. Gardner, I. M. Côté, J. A. Gill, A. Grant and A. R. Watkinson, “Hurricanes and Caribbean coral reefs: Impacts, recovery patterns, and role in long-term decline,” Ecology, vol. 86, no. 1, pp. 174–184, 2005. [Google Scholar]
4. P. J. Mumby, A. Hastings and H. J. Edwards, “Thresholds and the resilience of Caribbean coral reefs,” Nature, vol. 450, no. 7166, pp. 98–101, 2007. [Google Scholar]
5. H. A. Lessios, “Mass mortality of diadema antillarum in the Caribbean: What have we learned” Annual Review of Ecology and Systematics, vol. 19, no. 1, pp. 371–393, 1988. [Google Scholar]
6. M. R. M. S. Nagdee, L. Nurse, L. Inniss, A. Chadwick and T. Johnson, “Historical shoreline mapping: Application of the digital shoreline analysis system to the evolution of worthing beach, Barbados, following Hurricanes Allen (1980) and Ivan (2004),” Journal of Coastal Research, vol. 36, no. 2, pp. 313–318, 2020. [Google Scholar]
7. R. T. Yarlett, C. T. Perry, R. W. Wilson and A. R. Harborne, “Inter-habitat variability in parrotfish bioerosion rates and grazing pressure on an Indian Ocean reef platform,” Diversity, vol. 12, no. 10, pp. 381, 2020. [Google Scholar]
8. L. A. Barlow, J. Cecile, C. T. Bauch and M. Anand, “Modelling interactions between forest pest invasions and human decisions regarding firewood transport restrictions,” PloS One, vol. 9, no. 4, pp. 1–12, 2014. [Google Scholar]
9. S. J. Lade, A. Tavoni, S. A. Levin and M. Schlüter, “Regime shifts in a social-ecological system,” Theoretical Ecology, vol. 6, pp. 359–372, 2013. [Google Scholar]
10. T. Oraby, V. Thampi and C. T. Bauch, “The influence of social norms on the dynamics of vaccinating behaviour for paediatric infectious diseases,” Proceedings of the Royal Society of London B: Biological Sciences, vol. 281, pp. 1–8, 2014. [Google Scholar]
11. C. T. Bauch, “Imitation dynamics predict vaccinating behavior,” Proceedings of the Royal Society of London B: Biological Sciences, vol. 272, pp. 1669–1675, 2005. [Google Scholar]
12. K. A. Henderson, C. T. Bauch and M. Anand, “Alternative stable states and the sustainability of forests, grasslands, and agriculture,” Proceedings of the National Academy of Sciences, vol. 113, no. 51, pp. 14552–14559, 2016. [Google Scholar]
13. C. Innes, M. Anand and C. T. Bauch, “The impact of human-environment interactions on the stability of forest-grassland mosaic ecosystems,” Scientific Reports, vol. 3, no. 1, pp. 1–10, 2013. [Google Scholar]
14. A. Satake and T. K. Rudel, “Modeling the forest transition: Forest scarcity and ecosystem service hypotheses,” Ecological Applications, vol. 17, no. 7, pp. 2024–2036, 2007. [Google Scholar]
15. K. A. Henderson, M. Anand and C. T. Bauch, “Carrot or stick? Modelling how landowner behavioural responses can cause incentive-based forest governance to backfire,” PloS One, vol. 8, no. 10, pp. 1–13, 2013. [Google Scholar]
16. S. Levin, T. Xepapadeas, A. S. Crépin, J. Norberg, A. De Zeeuw et al., “Social-ecological systems as complex adaptive systems: Modeling and policy implications,” Environment and Development Economics, vol. 18, no. 2, pp. 111–132, 2013. [Google Scholar]
17. A. P. Galvani, C. T. Bauch, M. Anand, B. H. Singer and S. A. Levin, “Human–environment interactions in population and ecosystem health,” Proceedings of the National Academy of Sciences, vol. 113, no. 51, pp. 14502–14506, 2016. [Google Scholar]
18. Z. Sabir, J. L. Guirao, T. Saeed and F. Erdoğan, “Design of a novel second-order prediction differential model solved by using adams and explicit Runge–Kutta numerical methods,” Mathematical Problems in Engineering, vol. 2020, pp. 1–7, 2020. [Google Scholar]
19. K. S. Nisar, K. Logeswari, V. Vijayaraj, H. M. Baskonus and C. Ravichandran, “Fractional order modeling the Gemini virus in capsicum annuum with optimal control,” Fractal and Fractional, vol. 6, no. 2, pp. 1–19, 2022. [Google Scholar]
20. W. Gao, P. Veeresha, C. Cattani, C. Baishya and H. M. Baskonus, “Modified predictor–corrector method for the numerical solution of a fractional-order SIR model with 2019-nCoV,” Fractal and Fractional, vol. 6, no. 2, pp. 1–13, 2022. [Google Scholar]
21. Z. Sabir, “Stochastic numerical investigations for nonlinear three-species food chain system,” International Journal of Biomathematics, vol. 15, no. 4, pp. 2250005, 2022. [Google Scholar]
22. H. Sun and R. Grishman, “Lexicalized dependency paths based supervised learning for relation extraction,” Computer Systems Science and Engineering, vol. 43, no. 3, pp. 861–870, 2022. [Google Scholar]
23. M. Umar, Z. Sabir, M. A. Z. Raja, H. M. Baskonus, S. W. Yao et al., “A novel study of Morlet neural networks to solve the nonlinear HIV infection system of latently infected cells,” Results in Physics, vol. 25, pp. 1–13, 2021. [Google Scholar]
24. Y. G. Sánchez, Z. Sabir, H. Günerhan and H. M. Baskonus, “Analytical and approximate solutions of a novel nervous stomach mathematical model,” Discrete Dynamics in Nature and Society, vol. 2020, pp. 1–9, 2020. [Google Scholar]
25. P. Veeresha, E. Ilhan, D. G. Prakasha, H. M. Baskonus and W. Gao, “A new numerical investigation of fractional order susceptible-infected-recovered epidemic model of childhood disease,” Alexandria Engineering Journal, vol. 61, no. 2, pp. 1747–1756, 2022. [Google Scholar]
26. V. A. Thampi, M. Anand and C. T. Bauch, “Socio-ecological dynamics of Caribbean coral reef ecosystems and conservation opinion propagation,” Scientific Reports, vol. 8, no. 1, pp. 1–11, 2018. [Google Scholar]
27. J. C. Blackwood, A. Hastings and P. J. Mumby, “The effect of fishing on hysteresis in Caribbean coral reefs,” Theoretical Ecology, vol. 5, pp. 105–114, 2012. [Google Scholar]
28. Z. Sabir, M. A. Z. Raja, A. S. Alnahdi, M. B. Jeelani and M. A. Abdelkawy, “Numerical investigations of the nonlinear smoke model using the Gudermannian neural networks,” Mathematical Biosciences and Engineering, vol. 19, no. 1, pp. 351–370, 2022. [Google Scholar]
29. Z. Sabir, H. A. Wahab, S. Javeed and H. M. Baskonus, “An efficient stochastic numerical computing framework for the nonlinear higher order singular models,” Fractal and Fractional, vol. 5, no. 4, pp. 1–14, 2021. [Google Scholar]
30. M. Umar, Z. Sabir, M. A. Z. Raja, M. Shoaib, M. Gupta et al., “A stochastic intelligent computing with neuro-evolution heuristics for nonlinear SITR system of novel COVID-19 dynamics,” Symmetry, vol. 12, no. 10, pp. 1–17, 2020. [Google Scholar]
31. M. Umar, Z. Sabir, M. A. Z. Raja, F. Amin, T. Saeed et al., “Integrated neuro-swarm heuristic with interior-point for nonlinear SITR model for dynamics of novel COVID-19,” Alexandria Engineering Journal, vol. 60, no. 3, pp. 2811–2824, 2021. [Google Scholar]
32. J. L. Guirao, Z. Sabir and T. Saeed, “Design and numerical solutions of a novel third-order nonlinear Emden–Fowler delay differential model,” Mathematical Problems in Engineering, vol. 2020, pp. 1–9, 2020. [Google Scholar]
33. Z. Sabir, H. A. Wahab and J. L. Guirao, “A novel design of gudermannian function as a neural network for the singular nonlinear delayed, prediction and pantograph differential models,” Mathematical Biosciences and Engineering, vol. 19, no. 1, pp. 663–687, 2021. [Google Scholar]
34. Z. Sabir and H. A. Wahab, “Evolutionary heuristic with gudermannian neural networks for the nonlinear singular models of third kind,” Physica Scripta, vol. 96, no. 12, pp. 125261, 2021. [Google Scholar]
35. E. İlhan and İ. O. Kıymaz, “A generalization of truncated M-fractional derivative and applications to fractional differential equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 171–188, 2020. [Google Scholar]
36. H. M. Baskonus, H. Bulut and T. A. Sulaiman, “New complex hyperbolic structures to the lonngren-wave equation by using sine-gordon expansion method,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 129–138, 2019. [Google Scholar]
37. K. Vajravelu, S. Sreenadh and R. Saravana, “Influence of velocity slip and temperature jump conditions on the peristaltic flow of a Jeffrey fluid in contact with a Newtonian fluid,” Applied Mathematics and Nonlinear Sciences, vol. 2, no. 2, pp. 429–442, 2017. [Google Scholar]
38. M. S. M. Selvi and L. Rajendran, “Application of modified wavelet and homotopy perturbation methods to nonlinear oscillation problems,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 2, pp. 351–364, 2019. [Google Scholar]
39. N. H. Aljahdaly, R. P. Agarwal, R. Shah and T. Botmart, “Analysis of the time fractional-order coupled burgers equations with non-singular kernel operators,” Mathematics, vol. 9, no. 18, pp. 1–24, 2021. [Google Scholar]
40. Z. Sabir, M. A. Z. Raja and D. Baleanu, “Fractional mayer neuro-swarm heuristic solver for multi-fractional order doubly singular model based on lane–emden equation,” Fractals, vol. 29, no. 5, pp. 1–15, 2021. [Google Scholar]
41. K. A. Touchent, Z. Hammouch and T. Mekkaoui, “A modified invariant subspace method for solving partial differential equations with non-singular kernel fractional derivatives,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 2, pp. 35–48, 2020. [Google Scholar]
42. M. Alesemi, N. Iqbal and T. Botmart, “Novel analysis of the fractional-order system of nonlinear partial differential equations with the exponential-decay kernel,” Mathematics, vol. 10, no. 4, pp. 1–17, 2022. [Google Scholar]
43. T. Botmart, N. Yotha, P. Niamsup and W. Weera, “Hybrid adaptive pinning control for function projective synchronization of delayed neural networks with mixed uncertain couplings,” Complexity, vol. 2017, no. 4654020, pp. 1–19, 2017. [Google Scholar]
44. W. Adel and Z. Sabir, “Solving a new design of nonlinear second-order Lane–Emden pantograph delay differential model via Bernoulli collocation method,” The European Physical Journal Plus, vol. 135, no. 5, pp. 1–12, 2020. [Google Scholar]
45. A. Shvets and A. Makaseyev, “Deterministic chaos in pendulum systems with delay,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 1–8, 2019. [Google Scholar]
46. F. Erdogan, M. G. Sakar and O. Saldır, “A finite difference method on layer-adapted mesh for singularly perturbed delay differential equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 425–436, 2020. [Google Scholar]
47. T. Botmart, Z. Sabir, M. A. Z. Raja, M. R. Ali, R. Sadat et al., “A hybrid swarming computing approach to solve the biological nonlinear leptospirosis system,” Biomedical Signal Processing and Control, vol. 77, pp. 1–15, 2022. [Google Scholar]
48. M. T. Gençoğlu and P. Agarwal, “Use of quantum differential equations in sonic processes,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 21–28, 2021. [Google Scholar]
49. A. Aghili, “Complete solution for the time fractional diffusion problem with mixed boundary conditions by operational method,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 9–20, 2021. [Google Scholar]
50. Z. Sabir, M. Umar, M. A. Z. Raja, H. M. Baskonus and W. Gao, “Designing of Morlet wavelet as a neural network for a novel prevention category in the HIV system,” International Journal of Biomathematics, vol. 15, no. 4, pp. 2250012, 2022. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |