| Computers, Materials & Continua DOI:10.32604/cmc.2022.032229 |  |
| Article |
Optimized Weighted Ensemble Using Dipper Throated Optimization Algorithm in Metamaterial Antenna
1Department of Computer Sciences, College of Computer and Information Sciences, Princess Nourah bint Abdulrahman University, P.O. Box 84428, Riyadh, 11671, Saudi Arabia
2Department of Communications and Electronics, Delta Higher Institute of Engineering and Technology, Mansoura, 35111, Egypt
3Faculty of Artificial Intelligence, Delta University for Science and Technology, Mansoura, 35712, Egypt
4General Information Technology Department, Ministry of Defense, The Executive Affairs, Excellence Services Directorate,Riyadh, 11564, Saudi Arabia
5Computer Engineering and Control Systems Department, Faculty of Engineering, Mansoura University, Mansoura, 35516, Egypt
6Department of Computer Science, Faculty of Computer and Information Sciences, Ain Shams University, Cairo, 11566, Egypt
7Department of Computer Science, College of Computing and Information Technology, Shaqra University, 11961, Saudi Arabia
*Corresponding Author: Faten Khalid Karim. Email: fkdiaaldin@pnu.edu.sa
Received: 11 May 2022; Accepted: 12 June 2022
Abstract: Metamaterial Antennas are a type of antenna that uses metamaterial to enhance performance. The bandwidth restriction associated with small antennas can be solved using metamaterial antennas. Machine learning is gaining popularity as a way to improve solutions in a range of fields. Machine learning approaches are currently a big part of current research, and they’re likely to be huge in the future. The model utilized determines the accuracy of the prediction in large part. The goal of this paper is to develop an optimized ensemble model for forecasting the metamaterial antenna’s bandwidth and gain. The basic models employed in the developed ensemble are Support Vector Regression (SVR), K-Nearest Regression (KNR), Multi-Layer Perceptron (MLP), Decision Trees (DT), and Random Forest (RF). The percentages of contribution of these models in the ensemble model are weighted and optimized using the dipper throated optimization (DTO) algorithm. To choose the best features from the dataset, the binary (bDTO) algorithm is exploited. The proposed ensemble model is compared to the base models and results are recorded and analyzed statistically. In addition, two other ensembles are incorporated in the conducted experiments for comparison. These ensembles are average ensemble and K-nearest neighbors (KNN)-based ensemble. The comparison is performed in terms of eleven evaluation criteria. The evaluation results confirmed the superiority of the proposed model when compared with the basic models and the other ensemble models.
Keywords: Metamaterial antenna; dipper throated optimization; feature selection; parameters prediction
In all sectors of science and engineering, machine learning (ML) has been widely used to automate everyday tasks and provide breakthrough insights. Practitioners of machine learning have changed the foundations of various industries and fields of study. One of the newest fields is the design and optimization of metamaterial antennas. Given the current state of the world’s huge data, machine learning (ML) has received a lot of attention. In the design and prediction of antenna behavior, machine learning has a lot of promise since it allows for a lot of speed while maintaining high accuracy [1–10].
Closed-form solutions are uncommon in metamaterial antennas due to their complex shapes. The function of electromagnetic fields in the construction of antennas is described using Maxwell’s equations in computational electromagnetics (CEM). To get a physical understanding of the antenna’s design, a series of approximate solutions is usually used. Integral equations, for example, may be used to solve linear antennas using sophisticated numerical methods. Maxwell’s equations were later solved using differential and integral equation solvers as computer technology evolved [11–13]. The two most frequent CEM approaches in the design of metamaterial antennas are numerical techniques and high-frequency methods. Three approaches are often used in modeling and testing antenna parameters: the method of moments (MoM), the finite element method (FEM), and the finite difference time domain (FDTD). In addition, the radiation field of high-frequency reflector antennas may be calculated using the physical optics approximation method. The majority of antenna simulation work involves using computers to tackle problems with specified boundaries and partial differential equations [14–16].
Due to the inherent nonlinearities of antenna designs, machine learning (ML) has been extensively investigated as a supplement to CEM in enhancing and creating a wide range of antenna designs. Because statistics and data science are frequently referenced, ML is a subset of artificial intelligence (AI) that focuses on extracting useful information from data. Researchers have been able to create systems using machine learning’s data-driven methodology, bringing us closer to fully autonomous systems that can match, compete with, and occasionally surpass human abilities and intuition. Machine learning approaches, on the other hand, rely on data quality, quantity, and accessibility, which might be difficult to come by in some cases [17–19].
For metamaterial antennas, such as those used in computer vision, there is no standardized dataset available. From the aspect of antenna design, this dataset must be collected if it isn’t already accessible. This may be done by simulating the intended antenna over a wide range of values using CEM simulation software. Training, testing, and cross-validation may all be done with the same dataset. These components are used to train and test the capacity of the machine learning model to generalize to new inputs. At this point, it is up to the designer’s vision and talent to find out how to validate the model and improve its generality. In this case, normal processes include plotting learning curves and evaluating bias and variance values. In most cases, the designer’s intuition plays a big influence in improving a model’s performance [20–24].
The application of machine learning to antenna parameter optimization considerably accelerates the design process. Traditional methods of getting ideal parameters for a particular antenna design, as shown in Fig. 1, take far too long when utilizing present modeling tools. However, if machine learning is employed to carry out the parameter optimization process, a near approximation of these parameters may be obtained quickly. As a result of this benefit, some academics have devoted their research to implementing machine learning models into antenna design. This section covers the research and outcomes in this field.
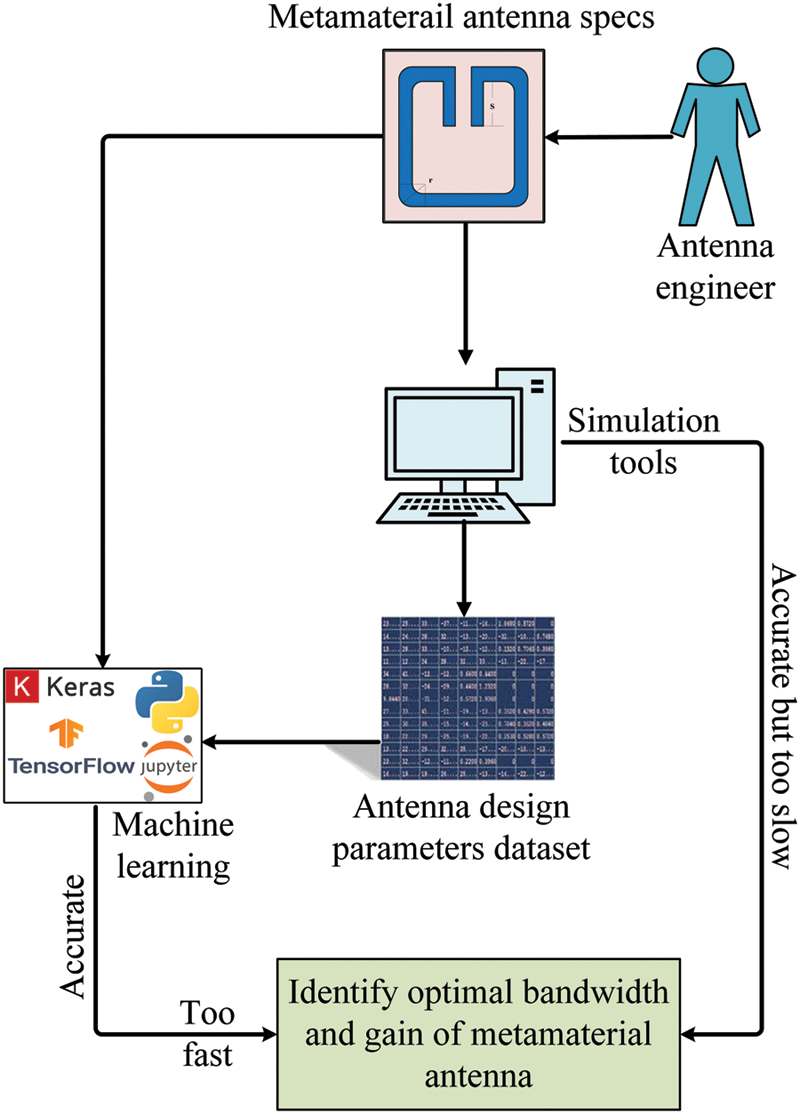
Figure 1: The process of optimizing metamaterial antenna bandwidth and gain
To apply machine learning into the antenna design challenge, follow the methods below in general. A series of simulations is used to estimate an antenna’s electromagnetic characteristics. These characteristics are subsequently kept in a database and fed into a machine learning algorithm. Finally, according on the designer’s specifications, the algorithm selects the Antenna that gives the best results.
2.1 Machine Learning Techniques
Machine learning (ML) is a technology that uses algorithms to learn from data without having to pre-program them. There are three forms of reinforcement learning: supervised, unsupervised, and reinforcement. Extensive interconnections of neurons; which are fundamental processing cells, are employed to achieve excellent performance in Artificial Neural Networks (ANN). When complex functions with numerous features are identified, neural networks may be used to do machine learning. An input layer, an output layer, and hidden layers between the input and output layers are all layers in a neural network [25]. A different type of directed learning algorithm is the support vector machines (SVM) approach. It is mostly utilized in classification and makes use of kernel approaches to deal with a difficult issue involving non-linearly separable patterns. One of the most basic machine learning approaches is the KNN. This algorithm uses the outputs of its closest neighbors in the training set to estimate the result of each new input after remembering the training set.
Machine learning algorithms have been employed in smart grid networks to predict dangerous occurrences, wireless networks to forecast wireless users’ mobility patterns and content demands, and voice recognition. Training a learning algorithm on data from previous simulations to enhance antenna parameters is one way to use machine learning in antenna design.
Because they are intelligent and have past knowledge of random search, metaheuristic algorithms tackle unanticipated problems. These algorithms are either versatile, straightforward, or capable of avoiding local perfection. The aspects of population-based heuristic algorithms include exploration and exploitation. Exploration and exploitation are chosen by the metaheuristic algorithm. The approach extensively inspects the search space while exploring. Local search in the region is currently being used. In recent decades, several natural-inspired global optimization algorithms have been created. A number of scenarios can benefit from population-based metaheuristics, sometimes known as general-purpose algorithms. Metaheuristics can be metaphor-based or non-metaphor-based. Metaphors, on the other hand, use algorithms to reflect natural events or human behavior in today’s society [26].
2.2 Selection of Significant Features
The process of feature selection and extraction are referred to as feature engineering. This process is essential to all machine learning operations. Although extraction and selection of features are similar in certain aspects, they are frequently used interchangeably. The feature selection approach aims to find the most consistent, relevant, and nonredundant qualities. The search area for feature selection is limited to two binary values: 0 and 1. Consequently, the binary version of the optimization algorithm should be employed to fit the feature selection task. The main idea of the binary version is to employ the sigmoid function to get the binary values from the continuous results of the optimizer.
When it comes to artificial intelligence problems, ensemble strategies are becoming more popular. The average ensemble is one of the most fundamental ensemble algorithms for integrating and computing the mean of base regressor outputs. This approach computes the mean value by combining the results of several regressors. This type of ensembles is used in conjunction with KNN-based ensemble to prove the effectiveness of the proposed weighted ensemble model. The proposed weighted ensemble for bandwidth and gain prediction is based on three phases namely, preprocessing, selection of relevant features, and optimization of the weighted outputs of five regression models, as illustrated in Fig. 2. Instead of choosing one ideal version among the possibilities, the ensemble model mixes all of the designs by giving each one a weight. The ensemble methodology has been proven to be one of the most effective ways to improve the predictive capacity of traditional models. The outcome variable of the best ensemble member is chosen in the first step to generate the final forecast in an ensemble model. The mixed formula is used in the second step to blend the ensemble members’ output variables [27].
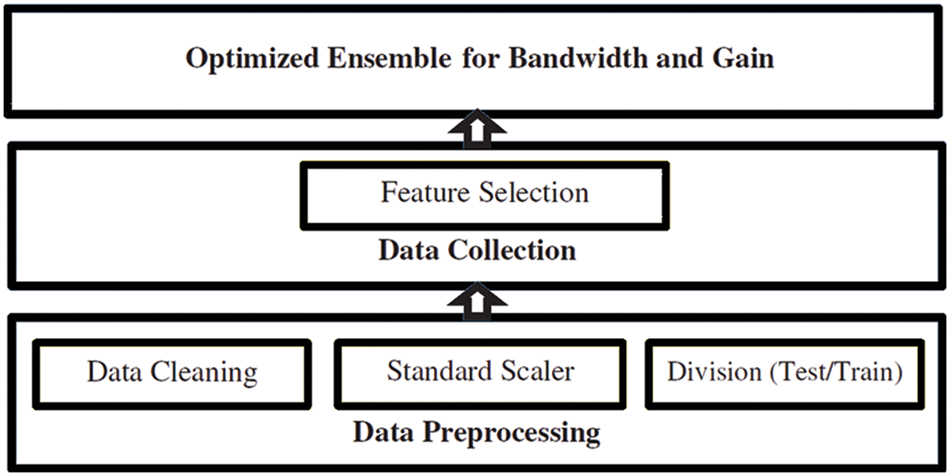
Figure 2: The proposed approach based on three stages namely, data preprocessing, data collection, and optimized ensemble
Eleven Metamaterial Antenna properties are included in the dataset used in this investigation. The collection of antenna designs is available on the Kaggle dataset which is employed in this research [28]. This collection contains 572 recordings. The distance between rings, The height and width of the split ring resonator, antenna bandwidth, antenna gain, rings’ gap, rings’ width, the number of array cells in split ring resonator, the distance between the antenna patch, and the distance between array cells in split ring resonator are all included in each record about the metamaterial antenna. The correlation between these features is represented by the matrix shown in Fig. 3. Using machine learning techniques, these properties are used to predict the gain and bandwidth of metamaterial antenna. The distributions of gain and bandwidth features is depicted in Fig. 4.
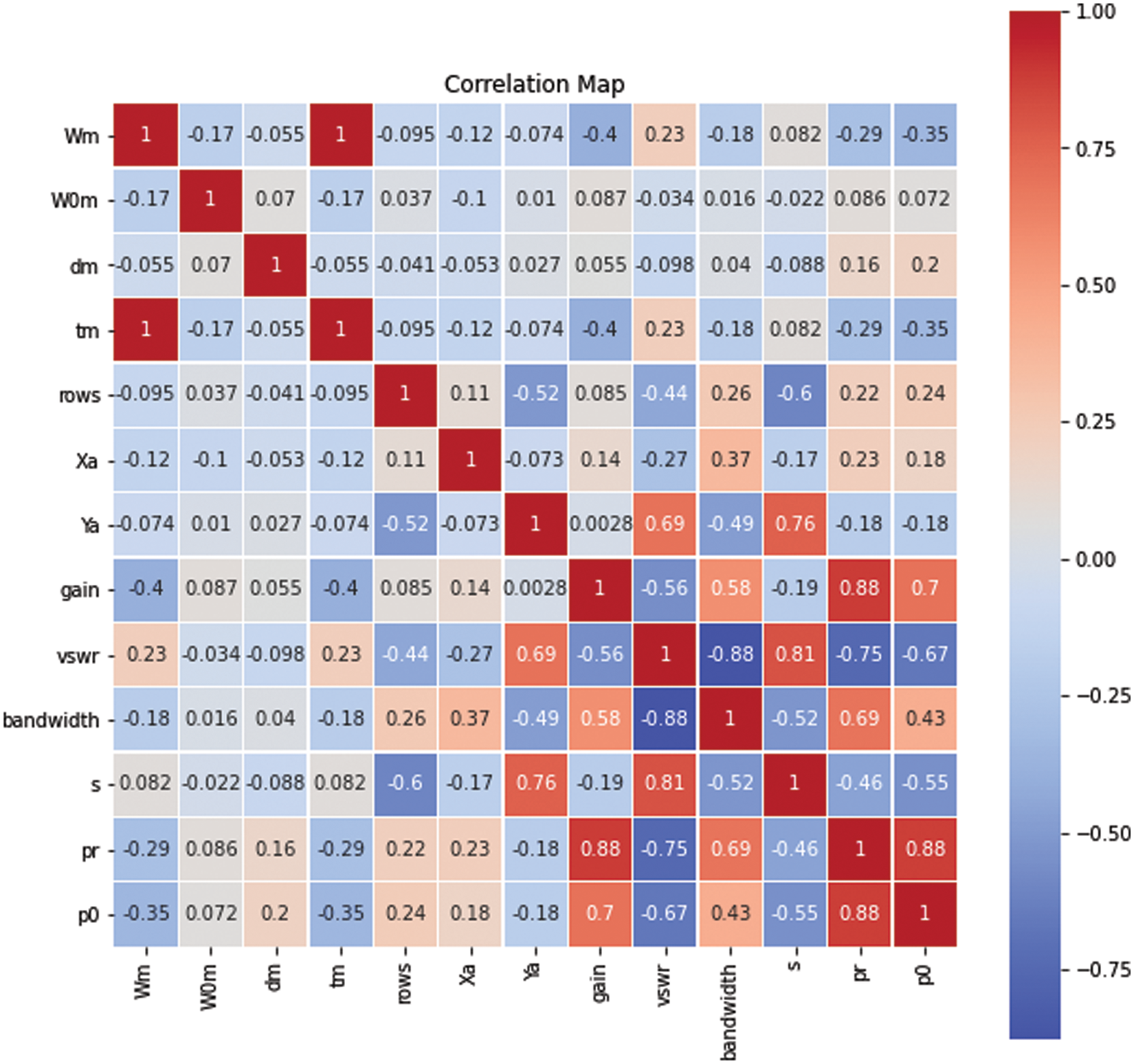
Figure 3: Metamaterial features correlation matrix
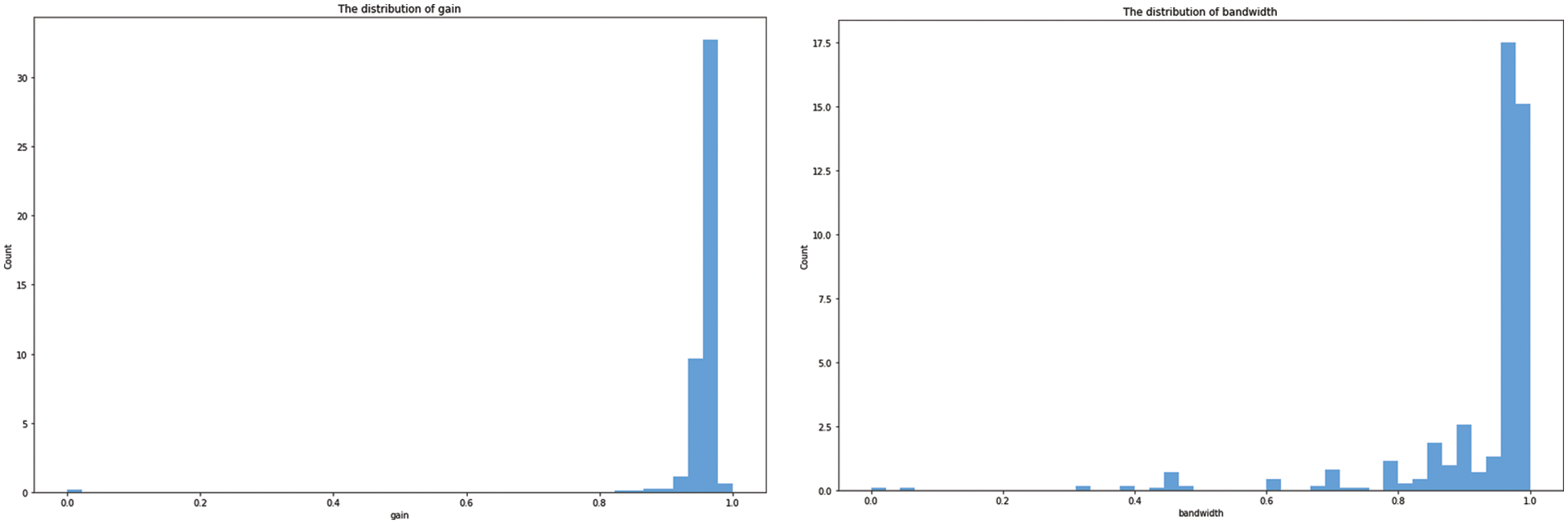
Figure 4: The gain and bandwidth features distributions
The preprocessing of the dataset is performed in terms of three steps. Firstly, data cleaning, in which the null values are replaces with the average between the surrounding values for each feature. Secondly, scaling the features values using the min-max scaler. Thirdly, the split of the dataset into training and testing based on the 80% and 20% recommendation rule.
3.3 Dipper Throated Optimization Algorithm
This algorithm is proven to be an effective metaheuristic optimization algorithm based on the hunting dipper throated bird’s quick bending motions [29]. The steps of this algorithm are represented by the flowchart depicted in Fig. 5. The steps of presented in the flowchart are based on the following equations, where X, Y, and h are the bird location, velocity, and fitness function, respectively.
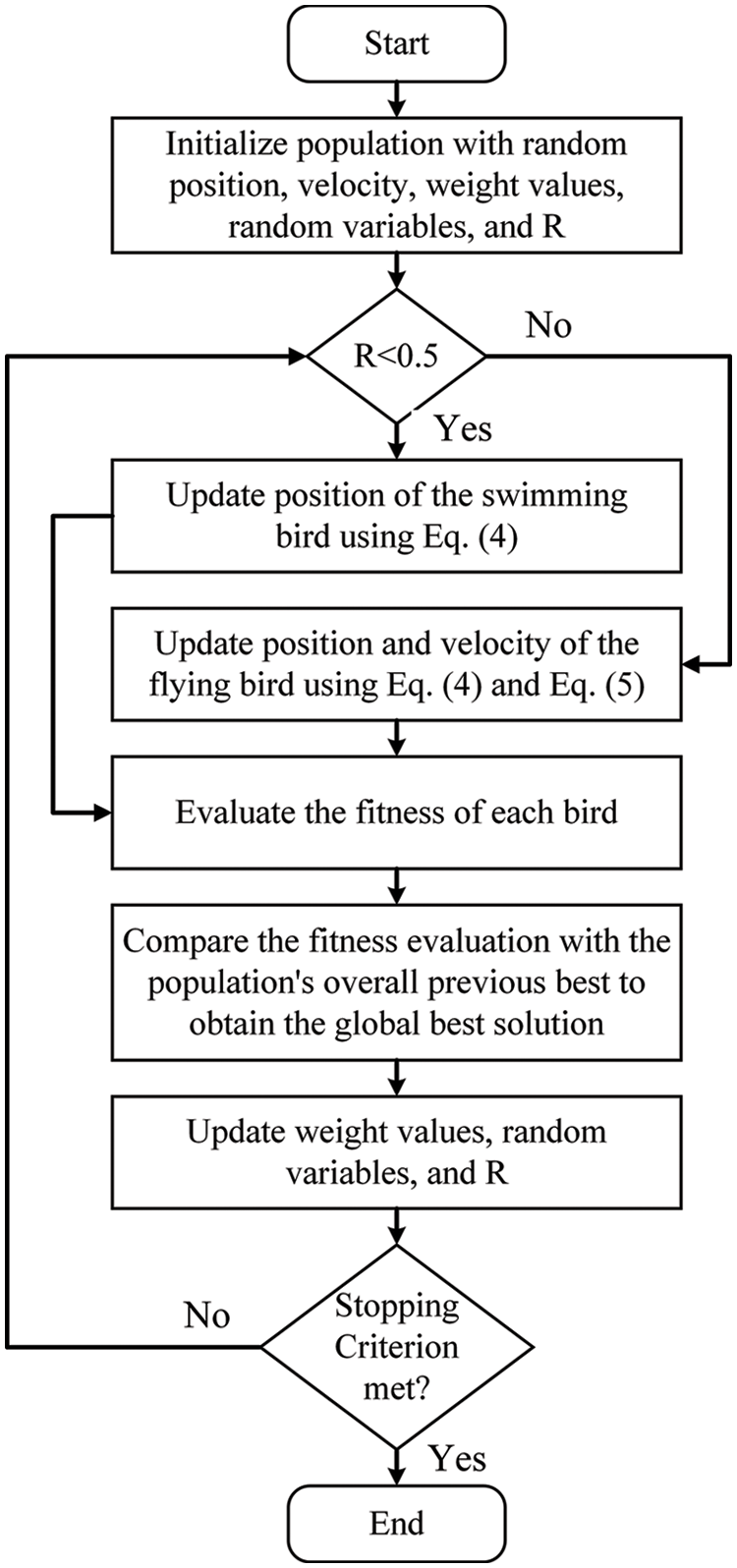
Figure 5: Flowchart of the dipper throated optimization algorithm
where the location and speed of the
Because the search space is confined to two binary values, 0 and 1, picking features presents a unique problem. As a result, we employed the sigmoid function to transform the output of the conventional optimizer into binary values. The following equation is used to convert the continuous answer to binary in order to fit the feature selection task.
where the updated binary position at iteration i is denoted by
These are the explanations behind the outcomes in this section. The findings are described using support vector regression (SVR), k-nearest regressor (KNR), random forest (RF), decision tree (DT), and multi-layer perceptron (MLP) regressors, as well as the suggested weighted average ensemble model. After that, the outcomes of feature selection are used to offer the suggested model’s performance.
The evaluation metrics employed in this research are presented in Tab. 1. These metrics include: average fitness size, average error, standard deviation, worst, best, and average fitness. These metrics are used to evaluate the performance of feature selection methods. On the other hand, Tab. 1 includes other metrics for performance assessment of the optimized models and ensembles. These metrics are the root mean square error (RMSE), the mean absolute percentage error (MAPE), the relative root mean square error (RRMSE), and Pearson’s correlation coefficient (r). In addition, the modified agreement index (d) was employed to determine agreement (WI), where M is the number of observations in the subset;

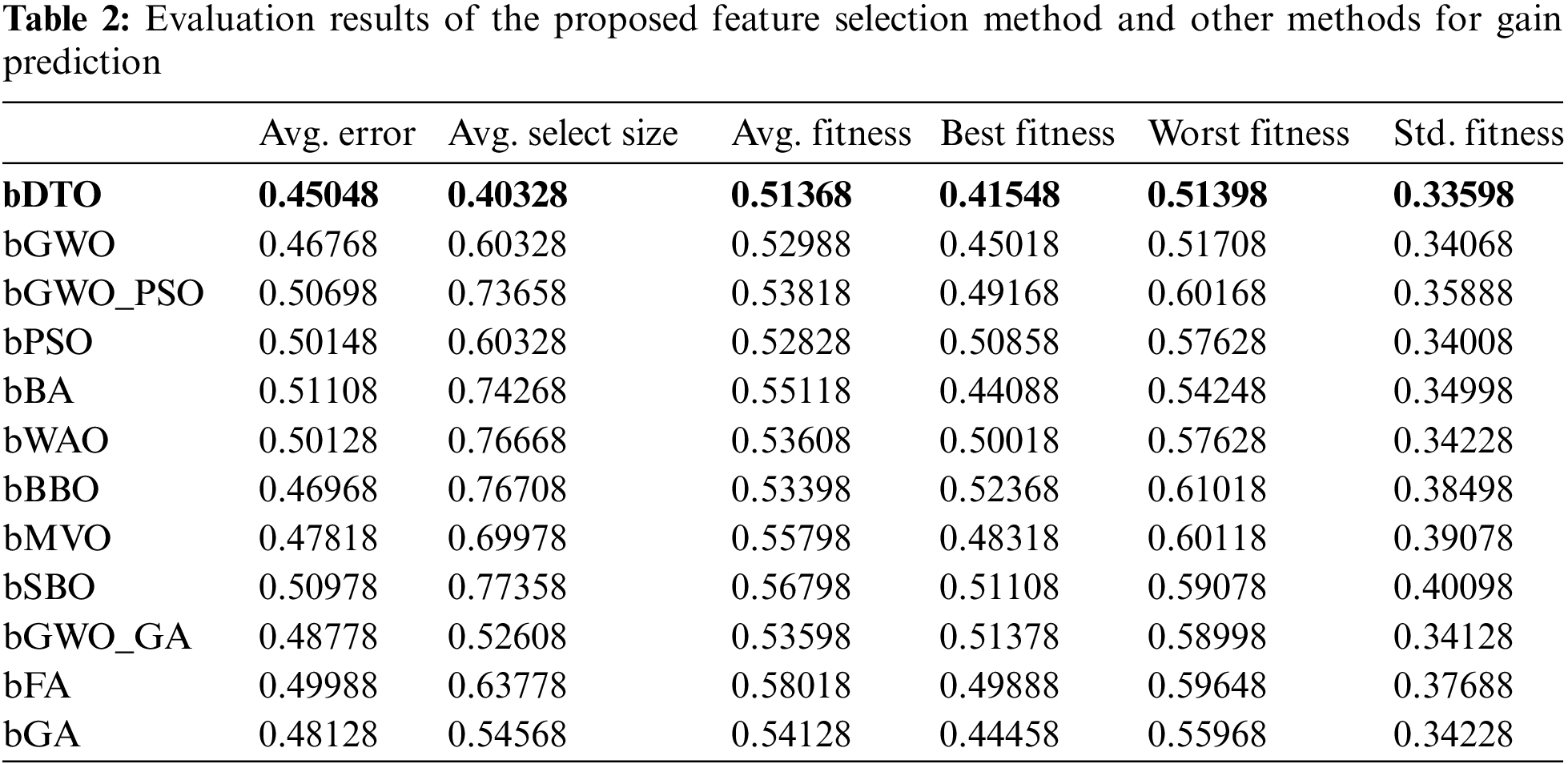
The first set of experiments was conducted to measure the performance of the feature selection methods. Tab. 2 presents the assessment of the results achieved by the proposed bDTO and other feature selection methods. As shown in the table, the proposed bDTO could achieve the minimum error and the best fitness.
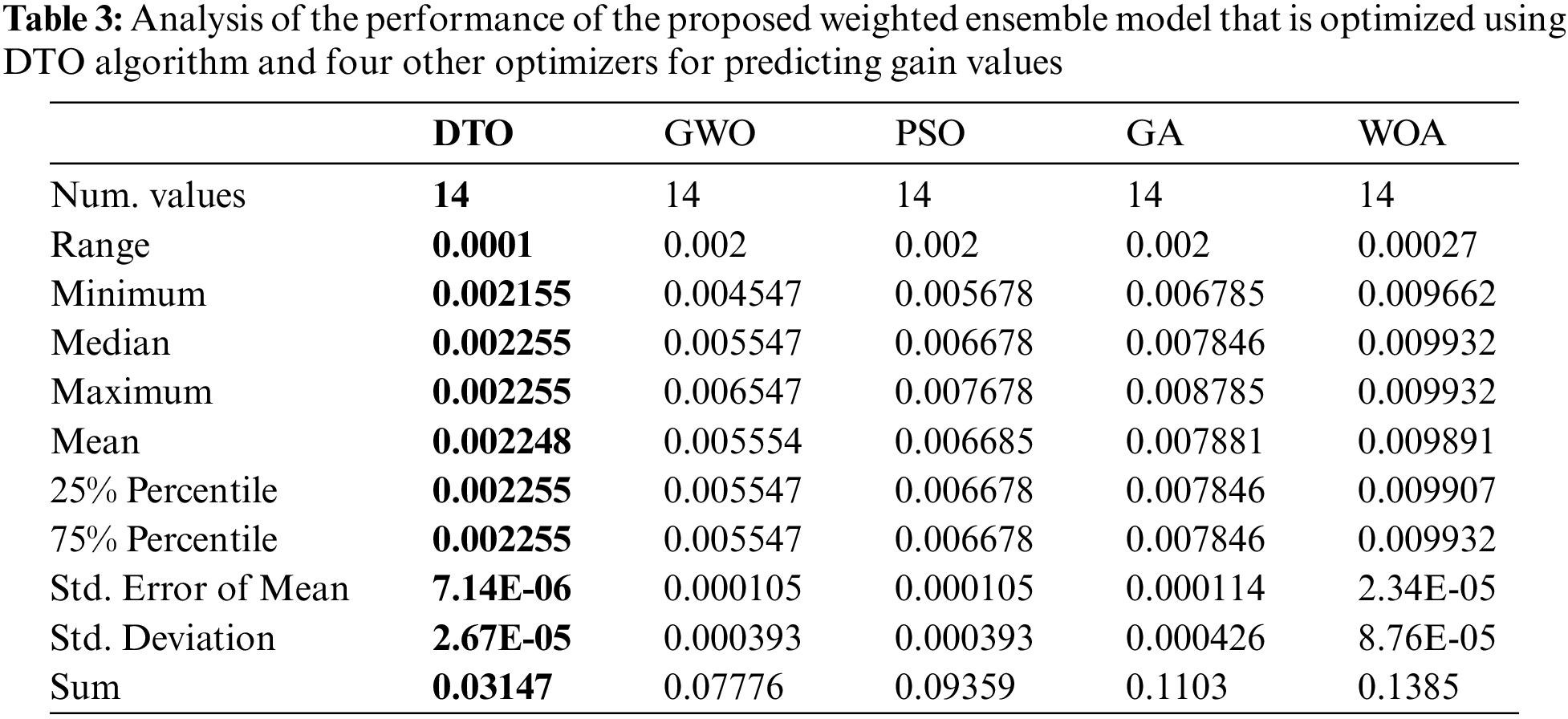
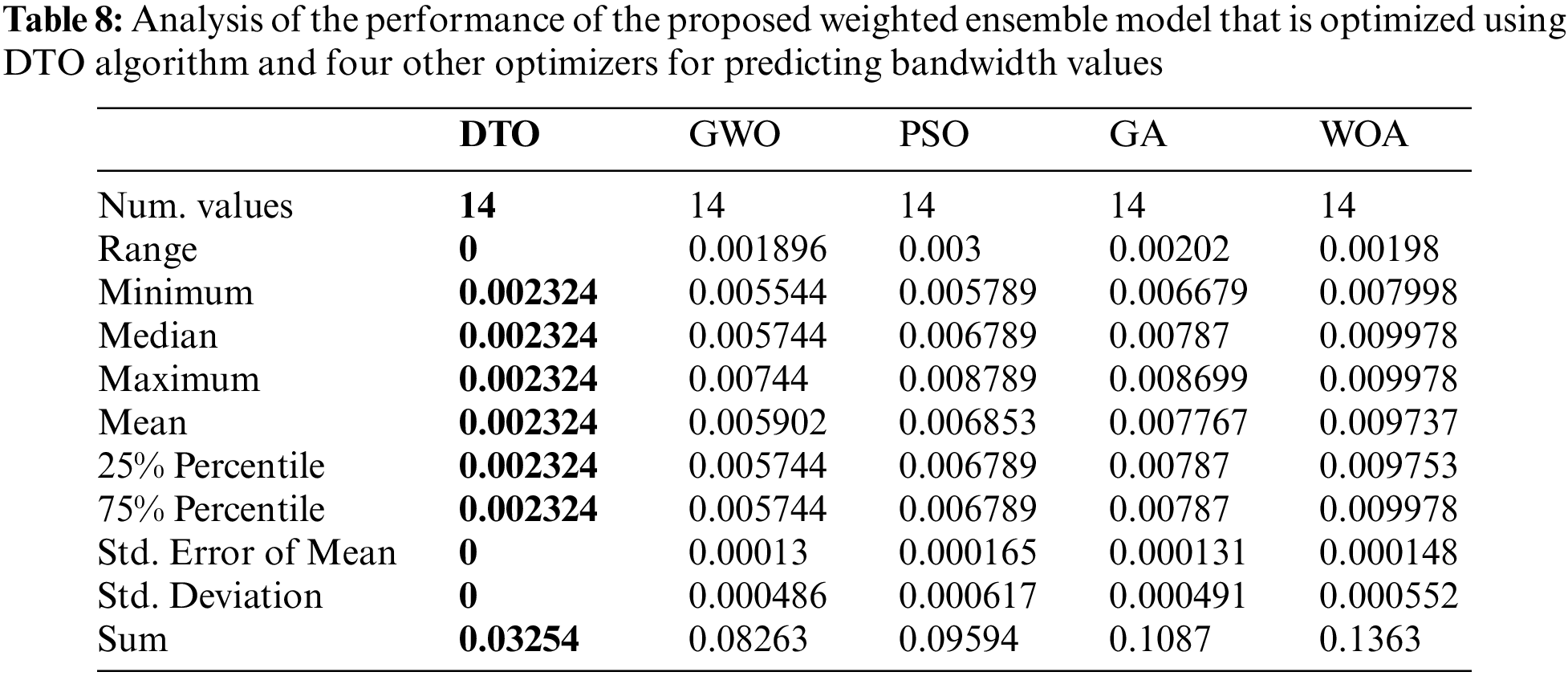
Once the significant features are selected, the optimized weighted ensemble model is employed to predict the gain values of metamaterial antenna. The prediction results are analyzed and presented in Tab. 3. The weighted ensemble is optimized using DTO and four other optimizers. The best performance is achieved by the DTO optimization algorithm.
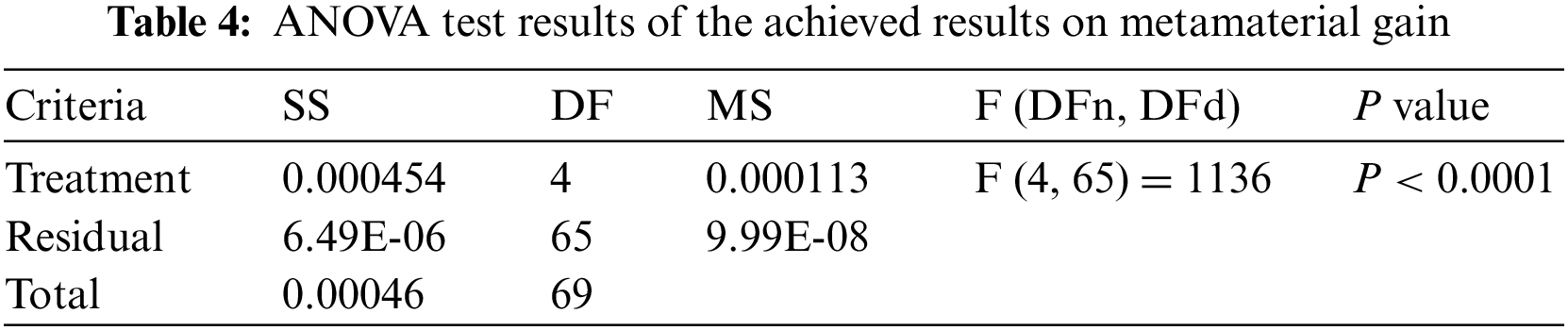
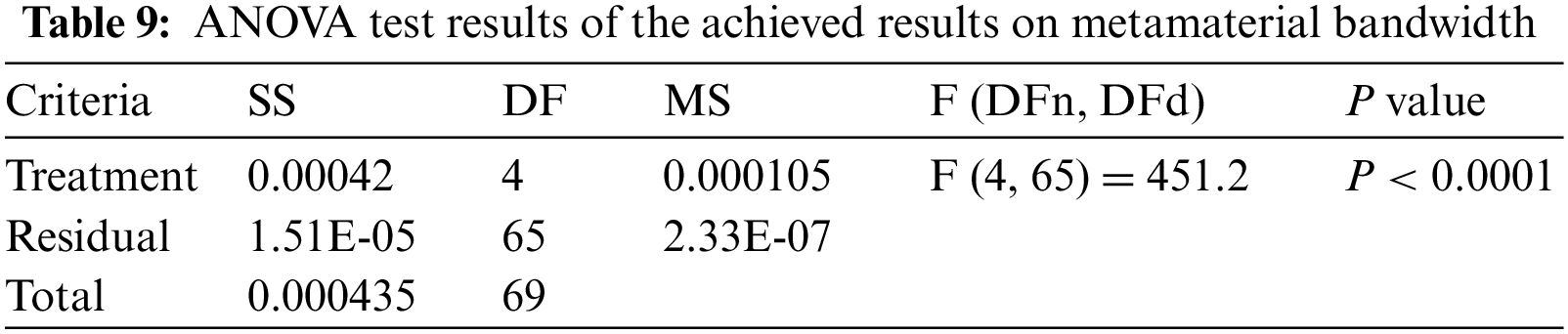
The null and alternative hypotheses are analyzed using a one-way analysis of variance (ANOVA) test. For the null hypothesis H0 (i.e., DTO = GWO = PSO = GA = WOA), the algorithm’s mean values are set equal. Under the alternative hypothesis, H1, the means of the algorithms are not similar. The results of the ANOVA test are presented in Tab. 4.
The statistical difference between each two algorithms is used to compute the p-values between the optimization of the weighted ensemble using DTO and four other optimization techniques. This study used Wilcoxon’s rank-sum test. The two basic hypotheses in this test are the null and alternative hypotheses. For the null hypothesis given by H0, DTO = GWO, DTO = PSO, DTO = GA, DTO = WOA Under the alternative hypothesis, H1, the algorithms’ means aren’t similar. The Wilcoxon rank-sum test’s findings are shown in Tab. 5.
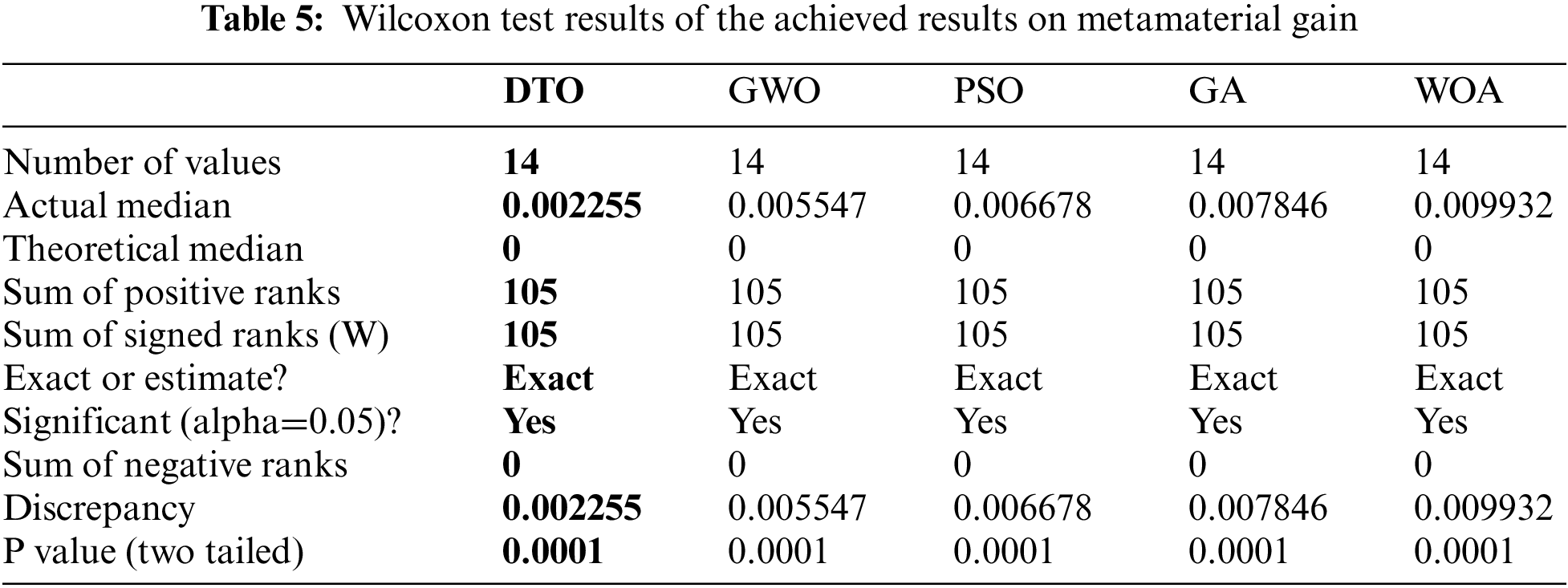
On the other hand, the prediction results of the metamaterial gain are recorded using five separate machine learning regressors and two ensemble models in addition to the proposed weighted ensemble model. These results are analysis using eight evaluation criteria and the results are presented in Tab. 6. Moreover, Fig. 6 shows the prediction vs. the actual gain values using the proposed approach.
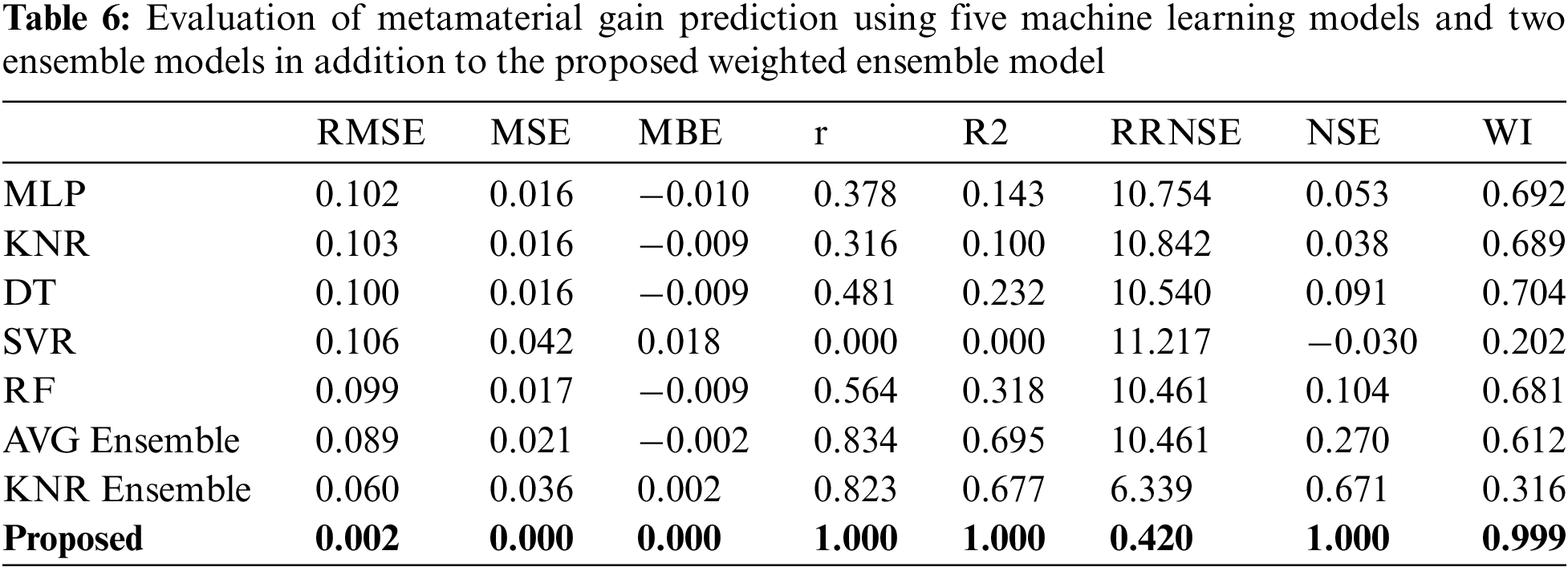
Figure 6: The actual (red) and predicted (green) gain values using the proposed weighted ensemble
The histogram of the gain values using the proposed weighted ensemble model that is optimized by DTO algorithm and four other optimizers and the RMSE of the predicted gain values using the proposed weighted ensemble model that is optimized by DTO algorithm and four other optimizers are presented in Figs. 7 and 8, respectively, to show the effectiveness of the proposed approach.
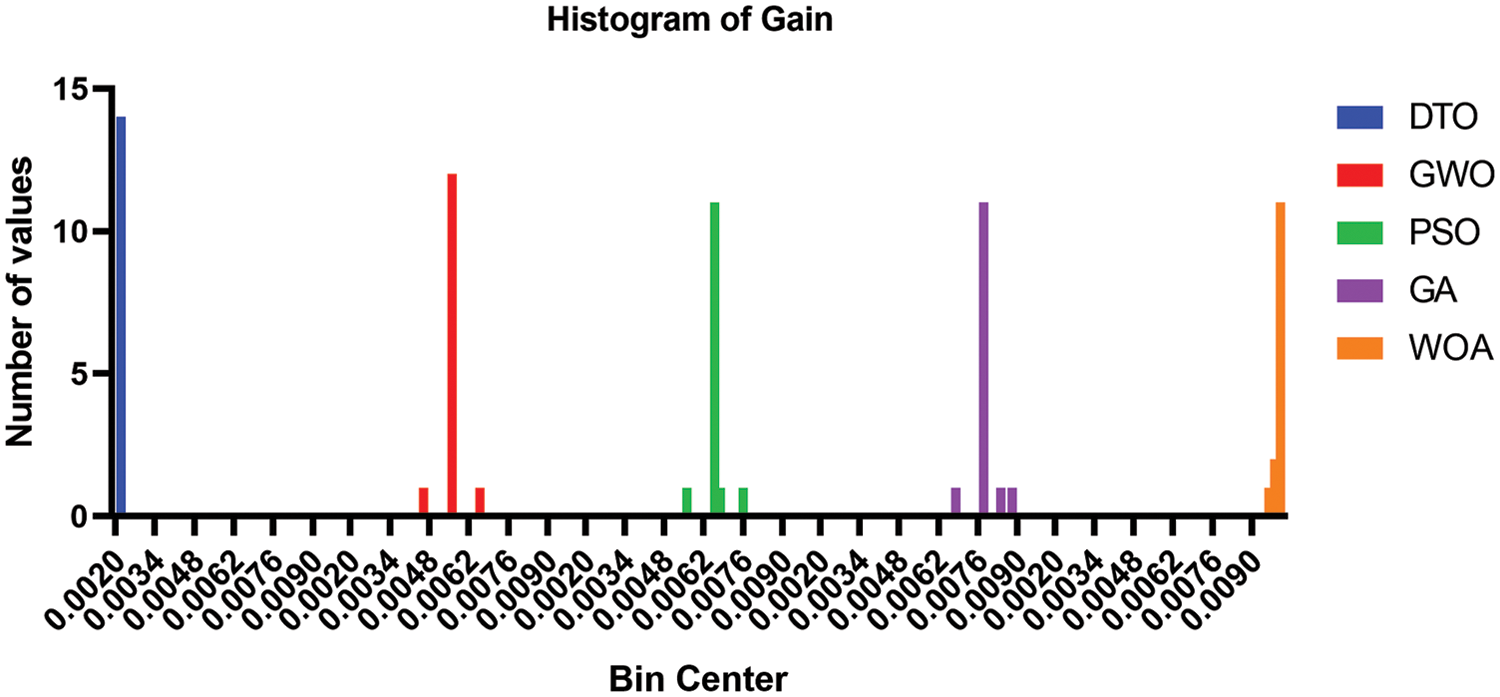
Figure 7: Histogram of the gain values using the proposed weighted ensemble model that is optimized by DTO algorithm and four other optimizers
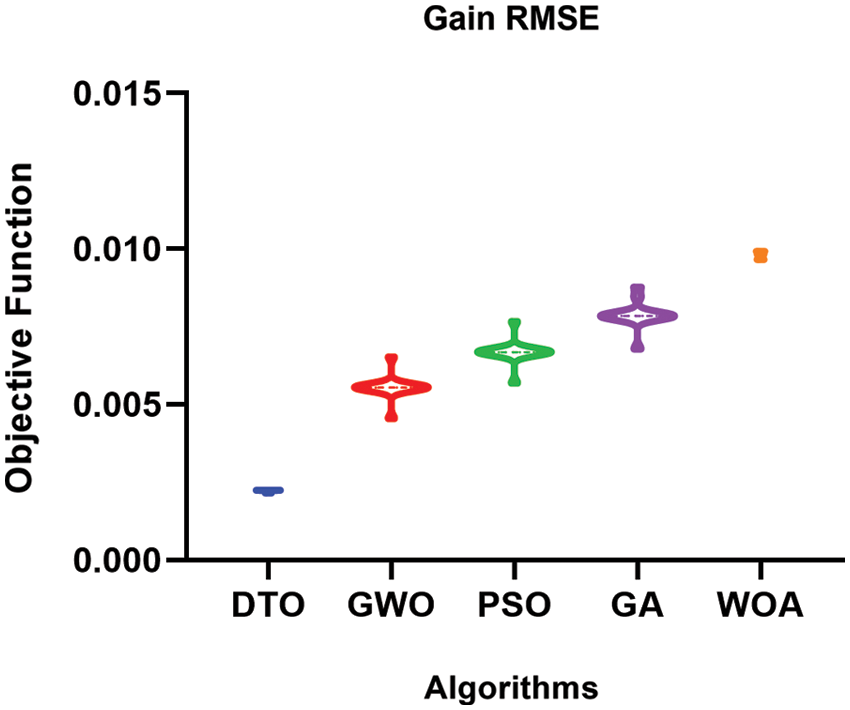
Figure 8: RMSE of the predicted gain values using the proposed weighted ensemble model that is optimized by DTO algorithm and four other optimizers
4.3 Metamaterial Bandwidth Results
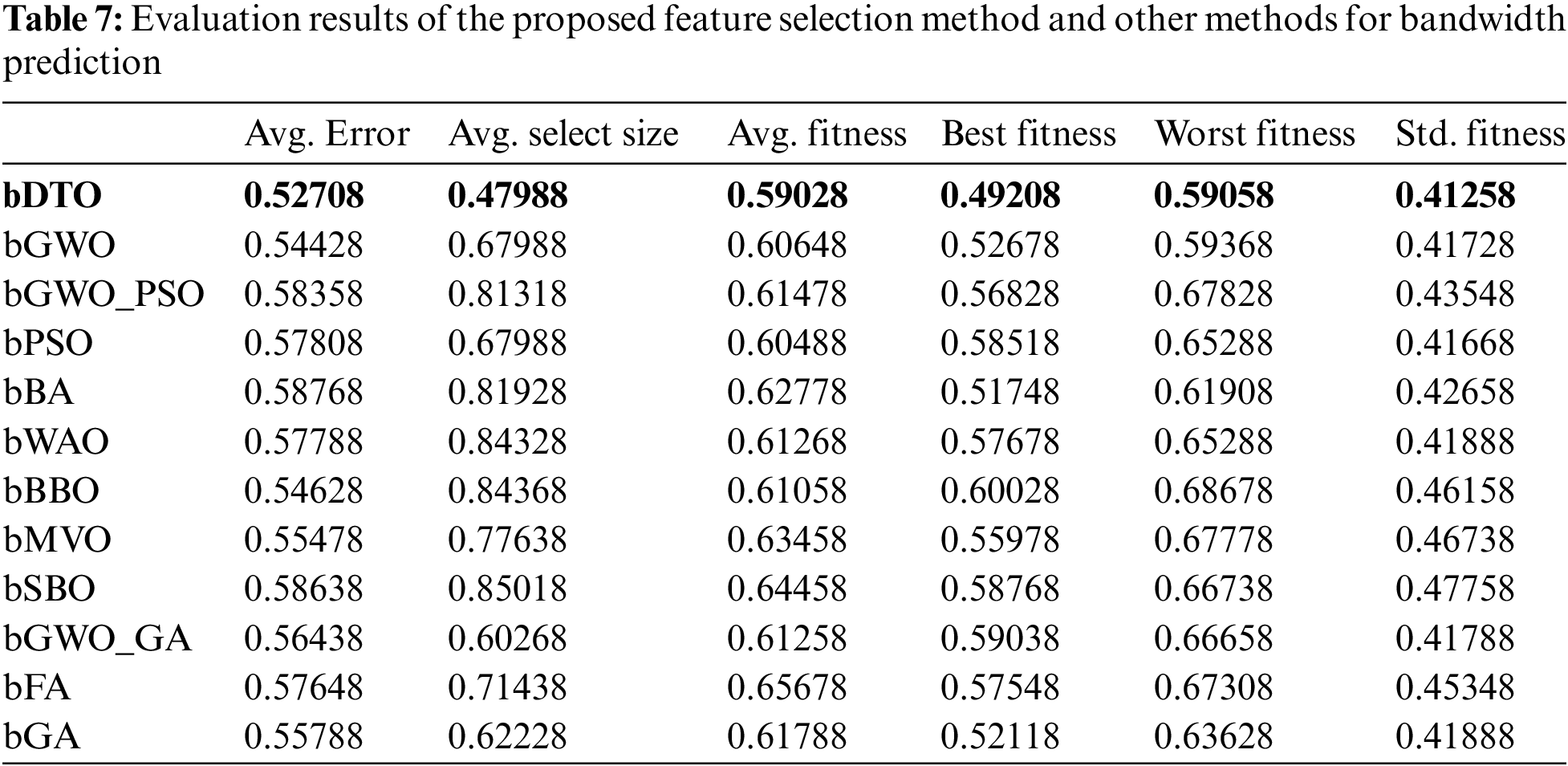
To prove the generalization of the proposed approach, the bandwidth of the metamaterial antenna is predicted using the proposed weighted ensemble model. The first step is to select the significant features from the given dataset. The feature selection is performed using bDTO, and the evaluation of the performance of features selection for this task is presented in Tab. 7, and the analysis of the performance of the proposed ensemble model in predicting metamaterial antenna bandwidth is presented in Tab. 8.
The ANOVA test and Wilcoxon test results are presented in Tabs. 9 and 10 to show the superiority and stability of the proposed approach in predicting the bandwidth of metamaterial antenna.
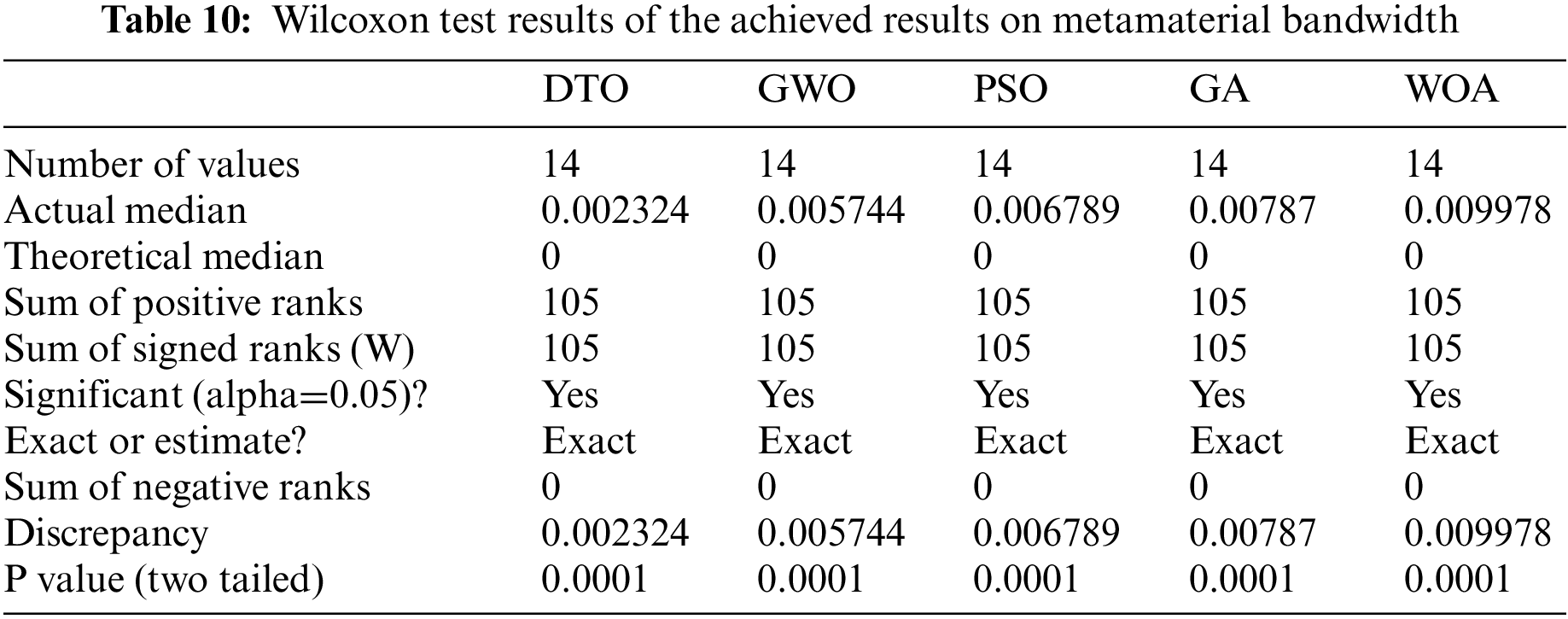
On the other hand, the prediction results of the metamaterial bandwidth are recorded using five separate machine learning regressors and two ensemble models in addition to the proposed weighted ensemble model. These results are analysis using eight evaluation criteria and the results are presented in Tab. 11. Moreover, Fig. 9 shows the prediction vs. the actual gain values using the proposed approach.
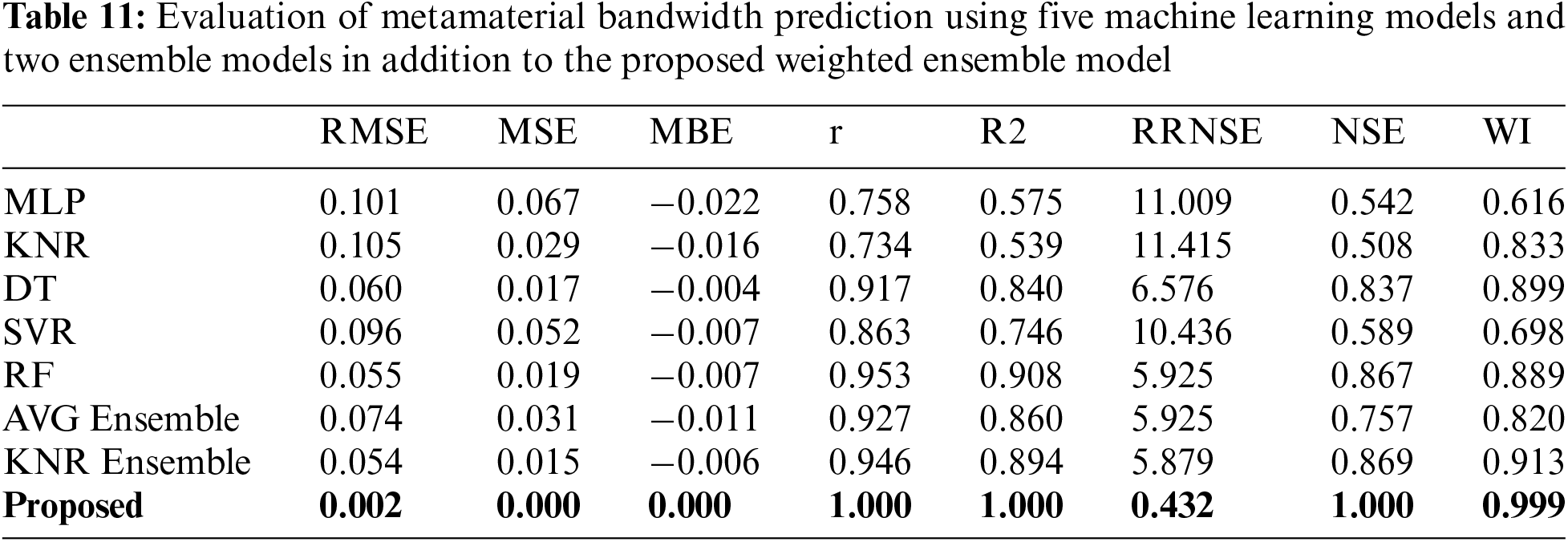
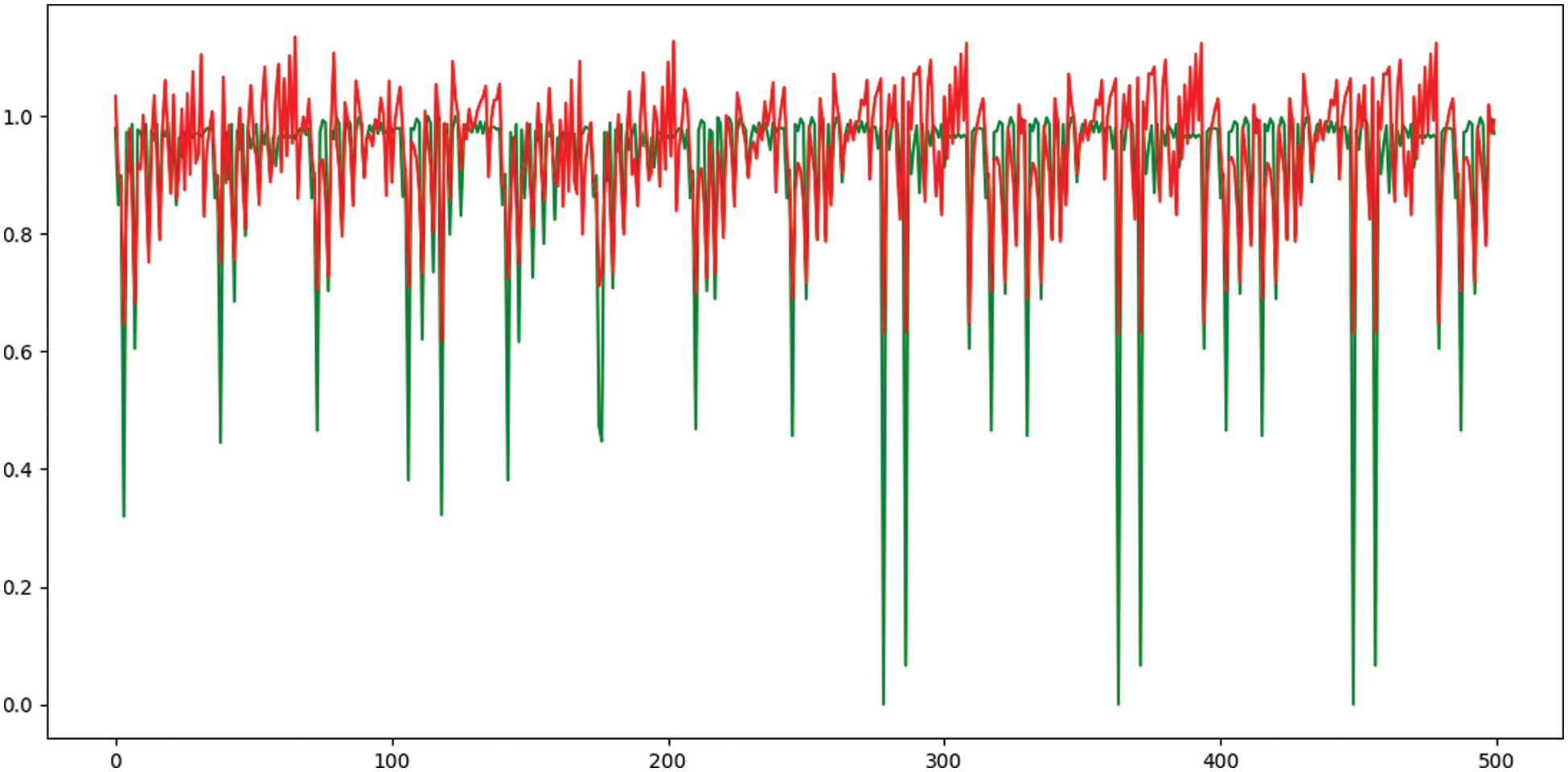
Figure 9: The actual (red) and predicted (green) bandwidth values using the proposed weighted ensemble
The histogram of the gain values using the proposed weighted ensemble model that is optimized by DTO algorithm and four other optimizers and the RMSE of the predicted bandwidth values using the proposed weighted ensemble model that is optimized by DTO algorithm and four other optimizers are presented in Figs. 10 and 11, respectively, to show the effectiveness of the proposed approach.
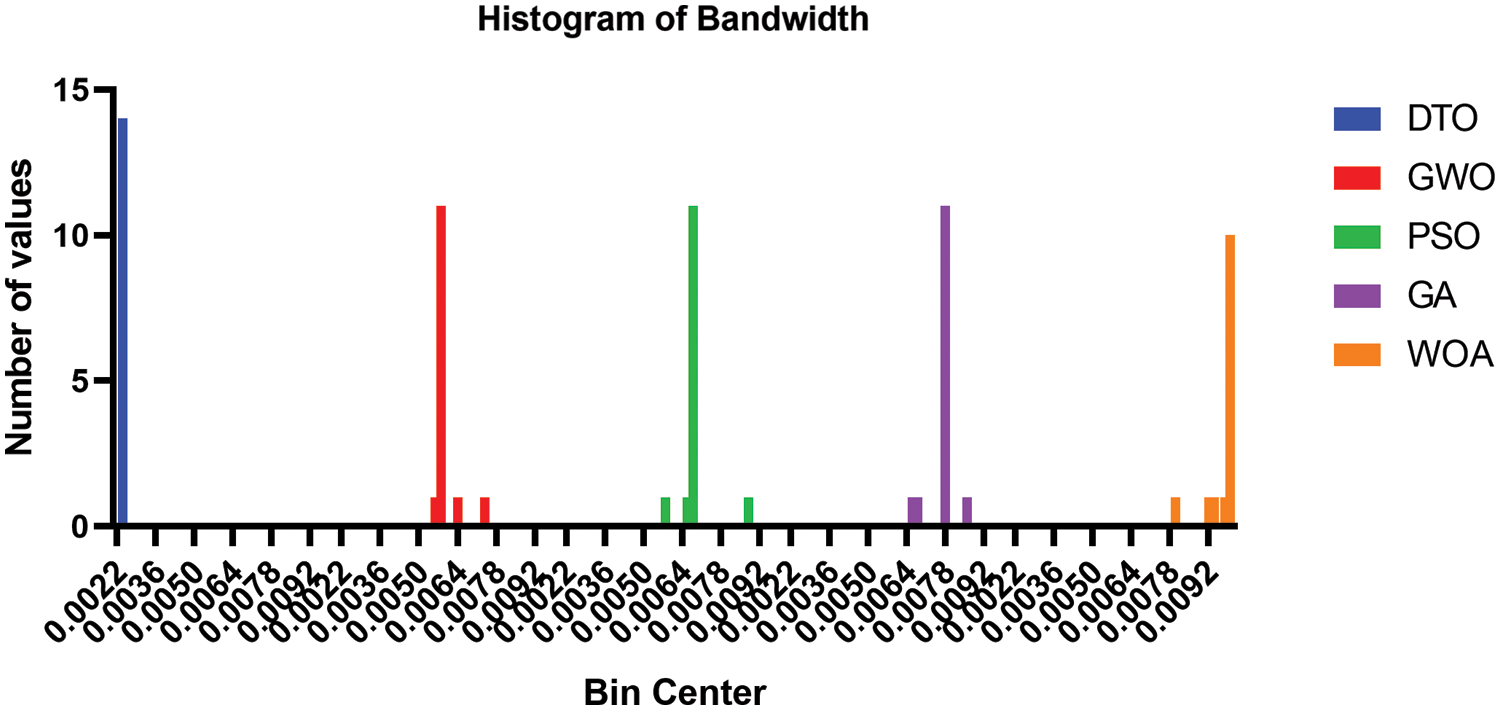
Figure 10: Histogram of the bandwidth values using the proposed weighted ensemble model that is optimized by DTO algorithm and four other optimizers
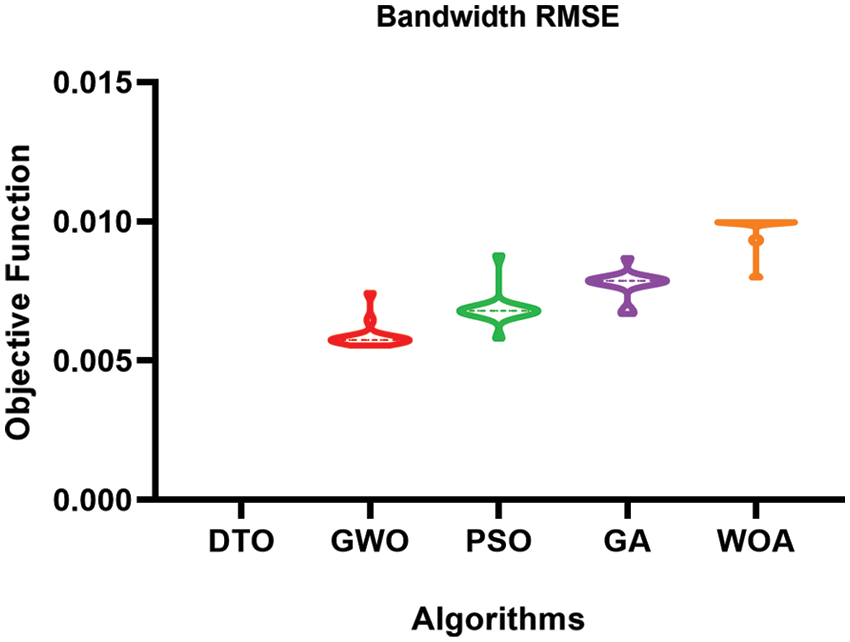
Figure 11: RMSE of the predicted bandwidth values using the proposed weighted ensemble model that is optimized by DTO algorithm and four other optimizers
Machine learning approaches are currently a big part of current study, and they’re likely to be huge in the future. The model utilized determines the accuracy of the forecast in large part. To choose the best characteristics from the metamaterial antenna dataset, this research use the DTO method. Metamaterial antennas are able to overcome the gain and bandwidth limitations of small antennas. Machine learning is attracting a lot of attention for its potential to improve solutions in a range of fields. For estimating the bandwidth and gain of the metamaterial antenna, the optimum ensemble model produced satisfactory results. SVR, RF, KNR, DT, and MLP are the fundamental models that have been examined. The best characteristics from the datasets were chosen using the DTO method. Five regression models were tested against the suggested technique. According to the data, the proposed method is better to others in terms of properly predicting antenna bandwidth and gain.
Acknowledgement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R300), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R300), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. J. Suganthi, T. Kavitha and V. Ravindra, “Survey on metamaterial antennas,” IOP Conference Series: Materials Science and Engineering, vol. 1070, no. 1, pp. 12086, 2021. [Google Scholar]
2. M. Alibakhshikenari, B. S. Virdee, L. Azpilicueta, M. Naser-Moghadasi, M. O. Akinsolu et al., “A comprehensive survey of metamaterial transmission-line based antennas: Design, challenges, and applications,” IEEE Access, vol. 8, pp. 144778–144808, 2020. [Google Scholar]
3. H. M. E. Misilmani and T. Naous, “Machine learning in antenna design: An overview on machine learning concept and algorithms,” in 2019 Int. Conf. on High Performance Computing & Simulation (HPCS), Dublin, Ireland, pp. 600–607, 2019. [Google Scholar]
4. K. Sun, R. Fan, X. Zhang, Z. Zhang, Z. Shi et al., “An overview of metamaterials and their achievements in wireless power transfer,” Journal of Materials Chemistry, vol. 6, no. 12, pp. 2925–2943, 2018. [Google Scholar]
5. A. Abdelhamid and S. Alotaibi, “Optimized two-level ensemble model for predicting the parameters of metamaterial antenna,” Computers, Materials & Continua, vol. 73, no. 1, pp. 917–933, 2022. [Google Scholar]
6. A. Abdelhamid, E. M. El-Kenawy, B. Alotaibi, G. Amer, M. Abdelkader et al., “Robust speech emotion recognition using CNN+LSTM based on stochastic fractal search optimization algorithm,” IEEE Access, vol. 10, pp. 49265–49284, 2022. [Google Scholar]
7. G. Geetharamani and T. Aathmanesan, “Design of metamaterial antenna for 2.4 GHz WiFi applications,” Wireless Personal Communications, vol. 113, no. 4, pp. 2289–2300, 2020. [Google Scholar]
8. W. Naktong, A. Ruengwaree, N. Fhafhiem and P. Krachodnok, “Resonator rectenna design based on metamaterials for low-RF energy harvesting,” Computers, Materials & Continua, vol. 68, no. 2, pp. 1731–1750, 2021. [Google Scholar]
9. E. S. M. El-kenawy, H. F. Abutarboush, A. W. Mohamed and A. Ibrahim, “Advance artificial intelligence technique for designing double T-shaped monopole antenna,” Computers, Materials & Continua, vol. 69, no. 3, pp. 2983–2995, 2021. [Google Scholar]
10. M. M. Fouad, A. I. El-Desouky, R. Al-Hajj and E. -S. M. El-Kenawy, “Dynamic group-based cooperative optimization algorithm,” IEEE Access, vol. 8, pp. 148378–148403, 2020. [Google Scholar]
11. E. S. M. El-Kenawy, A. Ibrahim, S. Mirjalili, M. M. Eid and S. E. Hussein, “Novel feature selection and voting classifier algorithms for COVID-19 classification in CT images,” IEEE Access, vol. 8, pp. 179317–179335, 2020. [Google Scholar]
12. E. S. M. El-Kenawy, M. M. Eid, M. Saber and A. Ibrahim, “Mbgwo-SFS: Modified binary grey wolf optimizer based on stochastic fractal search for feature selection,” IEEE Access, vol. 8, pp. 107635–107649, 2020. [Google Scholar]
13. A. Ibrahim, S. Mohammed, H. A. Ali and S. E. Hussein, “Breast cancer segmentation from thermal images based on chaotic salp swarm algorithm,” IEEE Access, vol. 8, pp. 122121–122134, 2020. [Google Scholar]
14. A. Ibrahim, M. Noshy, H. A. Ali and M. Badawy, “PAPSO: A power-aware VM placement technique based on particle swarm optimization, Luthra,” in IEEE Access, A. Luthra, 6th ed., vol. 8, ECG Made Easy Jaypee Brothers Medical Publishers, pp. 81747–81764, 2020. [Google Scholar]
15. A. Ibrahim, H. A. Ali, M. M. Eid and E. -S. M. El-kenawy, “Chaotic harris hawks optimization for unconstrained function optimization,” in 2020 16th Int. Computer Engineering Conf. (ICENCO), Cairo, Egypt, pp. 153–158, 2020. [Google Scholar]
16. M. M. Eid, E. -S. M. El-kenawy and A. Ibrahim, “A binary sine cosine-modified whale optimization algorithm for feature selection,” in 2021 National Computing Colleges Conf. (NCCC), Taif, Saudi Arabia, pp. 1–6, 2021. [Google Scholar]
17. E. -S. M. El-Kenawy, S. Mirjalili, A. Ibrahim, M. Alrahmawy, M. El-Said et al., “Advanced meta-heuristics, convolutional neural networks, and feature selectors for efficient COVID-19 X-ray chest image classification,” IEEE Access, vol. 9, pp. 36019–36037, 2021. [Google Scholar]
18. A. Abdelhamid and S. R. Alotaibi, “Robust prediction of the bandwidth of metamaterial antenna using deep learning,” Computers, Materials & Continua, vol. 72, no. 2, pp. 2305–2321, 2022. [Google Scholar]
19. H. Lin, W. -Y. Shin and J. Joung, “Support vector machine-based transmit antenna allocation for multiuser communication systems,” Entropy, vol. 21, no. 5, pp. 471, 2019. [Google Scholar]
20. N. Kurniawati, D. N. N. Putri and Y. K. Ningsih, “Random forest regression for predicting metamaterial antenna parameters,” in 2020 2nd Int. Conf. on Industrial Electrical and Electronics (ICIEE), Lombok, Indonesia, pp. 174–178, 2020. [Google Scholar]
21. E. S. M. El-Kenawy, S. Mirjalili, S. S. M. Ghoneim, M. M. Eid, M. El-Said et al., “Advanced ensemble model for solar radiation forecasting using sine cosine algorithm and Newton’s laws,” IEEE Access, vol. 9, pp. 115750–115765, 2021. [Google Scholar]
22. A. Ibrahim, S. Mirjalili, M. El-Said, S. S. M. Ghoneim, M. Alharthi et al., “Wind speed ensemble forecasting based on deep learning using adaptive dynamic optimization algorithm,” IEEE Access, vol. 9, pp. 1–18, 2021. [Google Scholar]
23. E. M. El-Kenawy, S. Mirjalili, F. Alassery, Y. Zhang, M. Eid et al., “Novel meta-heuristic algorithm for feature selection, unconstrained functions and engineering problems,” IEEE Access, vol. 10, pp. 40536–40555, 2022. [Google Scholar]
24. S. S. M. Ghoneim, T. A. Farrag, A. A. Rashed, E. -S. M. El-Kenawy and A. Ibrahim, “Adaptive dynamic meta-heuristics for feature selection and classification in diagnostic accuracy of transformer faults,” IEEE Access, vol. 9, pp. 78324–78340, 2021. [Google Scholar]
25. A. A. Salamai, E. -S. M. El-kenawy and A. Ibrahim, “Dynamic voting classifier for risk identification in supply chain 4. 0,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3749–3766, 2021. [Google Scholar]
26. A. Ibrahim, A. Tharwat, T. Gaber and A. E. Hassanien, “Optimized superpixel and AdaBoost classifier for human thermal face recognition,” Signal Image and Video Processing, vol. 12, no. 4, pp. 711–719, 2018. [Google Scholar]
27. T. Gaber, A. Tharwat, A. Ibrahim, V. Snáel and A. E. Hassanien, “Human thermal face recognition based on random linear oracle (RLO) ensembles,” in 2015 Int. Conf. on Intelligent Networking and Collaborative Systems, Taipei, pp. 91–98, 2015. [Google Scholar]
28. R. Machado, “Antennas. Florianópolis, State of Santa Catarina, Brazil: FotonTech,” accessed: 2022-05-01, 2019. [Online]. Available: https://www.kaggle.com/renanmav/metamaterial-antennas. [Google Scholar]
29. A. Takieldeen, E. M. El-kenawy, E. Hadwan and M. Zaki, “Dipper throated optimization algorithm for unconstrained function and feature selection,” Computers, Materials & Continua, vol. 72, no. 1, pp. 1465–1481, 2022. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |