Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2021.016871

ARTICLE

P-Indeterminate Vector Similarity Measures of Orthopair Neutrosophic Number Sets and Their Decision-Making Method with Indeterminate Degrees

Mailing Zhao1 and Jun Ye1,2,*

1Department of Electrical Engineering and Automation, Shaoxing University, Shaoxing, 312000, China
2School of Civil and Environmental Engineering, Ningbo University, Ningbo, 315211, China
*Corresponding Author: Jun Ye. Email: yejun1@nbu.edu.cn
Received: 04 April 2021; Accepted: 07 May 2021

1  Introduction

Since intuitionistic fuzzy sets (IFSs) [1] were proposed by Atanassov in incomplete and uncertain situations, they have been wildly applied in various fields [2–8]. Particularly, similarity measures play important roles in decision making (DM), pattern recognition, and clustering analysis. For instance, various similarity measures of IFSs, such as the Dice measures and the cosine measures of IFSs [9–12], were proposed and used for DM problems in IFS setting. Then, many researchers [13–17] also introduced different similarity measures of IFSs and applied them to pattern recognitions. Also, the Jaccard and Dice measures of IFSs [18,19] were presented and applied to clustering analyses.

It is known that IFS is depicted by both the truth membership degree and the falsity membership degree. Then, it can be also denoted as an orthopair fuzzy set regarding the truth and falsity membership degrees. There may be a situation where the sum of the truth membership degree and falsity membership degree are more than one. To solve this issue, Yager [20,21] presented the Pythagorean fuzzy set (PFS) as the extension of IFS. Then Wei et al. [22] introduced the cosine similarity measure of PFSs and applied them in pattern recognition and medical diagnosis. Nguyen et al. [23] introduced exponential similarity measures of PFSs and utilized them in pattern recognition and DM problems. As the further extension of IFS and PFS, Yager et al. [24,25] proposed the concept of q-rung orthopair fuzzy set (q-ROFS), which gives decision makers more flexibility to represent the information expression range of the truth and falsity membership degrees by choosing a suitable value of the parameter q. Then, Liu et al. [26] introduced some cosine similarity measures and distance measures between q-ROFSs and used them for DM problems in orthopair fuzzy setting.

Due to the complexity and indeterminacy of current DM environments, IFS, PFS, and q-ROFS also indicate some limitations in describing the decision information. For instance, if decision makers believe that their truth and falsity membership degrees contain their partial determinacy and partial indeterminacy owing to their hesitancy, inconsistence, and indeterminacy. In the partial certain and partial uncertain situations, IFS, PFS, and q-ROFS cannot express them. Then, a neutrosophic number (NN) [27–29] composed of its certain term a and its uncertain term bI can effectively express the partial certain and partial uncertain information, which is denoted as u = a + bI for indeterminacy I ∈ [I−, I+] and a, b ∈ R (all real numbers). The NN u = a + bI changes with the changes of I ∈ [I−, I+], which implies a changeable interval number depending on the interval ranges of I ∈ [I−, I+]. Therefore, NN is more suitable for indeterminate information expression and applications in indeterminate environments [30,31], which shows its advantage. Based on the hybrid concept of both IFS and NN, Ye et al. [32] originally proposed orthopair indeterminate sets/neutrosophic number sets (OISs/ONNSs) and their aggregation operators, then applied them to multiple attribute DM problems under indeterminate environments. Although the indeterminate DM method introduced in [32] demonstrated its advantages in the indeterminate information expression, aggregations and decision process, the existing research [32] lacks a similarity measure between ONNSs, which is an essential mathematical tool and plays a crucial role in DM, pattern recognition, and clustering analysis. Therefore, it is necessary to propose some similarity measures between ONNSs to supplement the gap. To do so, we propose the p-indeterminate cosine measure, p-indeterminate Dice measure, p-indeterminate Jaccard measure of ONNSs in vector space (the three parameterized indeterminate vector similarity measures/p-indeterminate vector similarity measures of ONNSs). Then, we develop a DM method based on the proposed p-indeterminate vector similarity measures of ONNSs to solve indeterminate DM problems with the small indeterminate degree (p = 0) or the moderate indeterminate degree (p = 0.5) or the big indeterminate degree (p = 1) specified by decision makers. However, the developed DM method not only gives decision makers much more flexibility to express the information of the troth and falsity indeterminacy degrees by choosing the value/range of the indeterminacy I ∈ [I−, I+], but also deals with indeterminate DM problems by choosing the indeterminate degrees of p by the decision makers, which show its evident advantages.

The rest of the paper is indicated below. Section 2 introduces preliminaries of IFS, NN and ONNS. Section 3 proposes the p-indeterminate cosine measure, p-indeterminate Dice measure, p-indeterminate Jaccard measure of ONNSs in vector space. In Section 4, a DM method based on the p-indeterminate vector similarity measures of ONNSs is developed to solve indeterminate DM problems with the small indeterminate degree (p = 0) or the moderate indeterminate degree (p = 0.5) or the big indeterminate degree (p = 1) of the decision makers. In Section 5, an actual DM example on choosing a suitable logistics supplier is provided to demonstrate the flexibility and efficiency of the developed DM approach in indeterminate DM problems. Conclusions and further study are contained in Section 6.

2  Preliminaries of IFS, NN and ONNSs

Since there are the indeterminacies of the truth membership degree and the falsity membership degree in the real-life situations, Ye et al. [32] proposed an ONNS concept based on hybrid concepts of IFS and NN as the generalization of the IFS concept in incomplete and indeterminate situations.

Under incomplete and uncertain situations, an IFS D in a universe set X = {x1, x2, …, xn} is defined as the following form [1]:

where TD(xi) ∈ [0, 1] and FD(xi) ∈ [0, 1] for xk ∈ X (k = 1, 2, …, n) are the truth membership degree and the falsity membership degree of the element xk to D, respectively, such that the condition 0 ≤ TD(xk) + FD(xk) ≤ 1. Then, IFS can be also considered as an orthopair fuzzy number, denoted by 〈 TD(xk), FD(xk)〉.

In indeterminate situations, NN [27–29] is defined as u = a + bI for indeterminacy I ∈ [I−, I+] and a, b ∈ R, where a is its certain term and bI is its uncertain term. NN indicates either a single value u = a + bI for I = I− = I+ or an interval number u = [a + bI−, a + bI+] for I = [I−, I+]. Especially, there is u = a if bI = 0 (no indeterminate term) or u = bI if a = 0 (no determinate term). Obviously, one does not doubt the superiority of NN over the unique interval expression due to its expressional flexibility in determinate and/or indeterminate cases.

Regarding the hybrid concept of IFS and NN, Ye et al. [32] defined ONNS to express the orthopair indeterminate information composed of both truth indeterminate degrees and falsity indeterminate degrees.

Definition 2.1 [32]. Let X = {x1, x2, …, xn} be a fixed universe set. An ONNS O is defined as the following form:

where T~O(xk,I)=ak+bkI⊆[0,1] and F~O(xk,I)=ck+dkI⊆[0,1] for xk ∈ X (k = 1, 2, …, n) and I ∈ [I−, I+] are the truth indeterminate degree and the falsity indeterminate degree of the element xk to O, respectively, such that the condition 0≤supT~O(xk,I)+supF~O(xk,I)≤1. Then its intuitionistic indeterminate index is U~(xk,I)=1−T~O(xk,I)−F~O(xk,I)=[1−(ak+bkI++ck+dkI+),1−(ak+bkI−+ck+dkI−)]⊆[0,1].

For convenient representation, the component ⟨xk,T~O(xk,I),F~O(xk,I)⟩ in the ONNS O for xk ∈ X (k = 1, 2, …, n) and I ∈ [I−, I+] is denoted simply by ⟨T~k(I),F~k(I)⟩=⟨ak+bkI,ck+dkI⟩, which is called the orthopair NN (ONN).

Obviously, the ONNS O is reduced to the IFS or interval-valued IFS as a special case of the ONNS O corresponding to some specified single value or interval value of I ∈ [I−, I+]. In fact, ONNS can be considered as an IFS (orthopair fuzzy set) family or an interval-valued IFS (orthopair interval-valued fuzzy set) family depending on a group of single values or interval values of I ∈ [I−, I+].

Set o1=⟨T~1(I),F~1(I)⟩=⟨a1+b1I,c1+d1I⟩ and o2=⟨T~2(I),F~2(I)⟩=⟨a2+b2I,c2+d2I⟩ for I ∈ [I−, I+] as two ONNs. Then, there exist the following relations [32]:

(1) o1 ⊆ o2 ⇔ T~1(I)⊆T~2(I), F~1(I)⊇F~2(I);

(2) o1 = o2 ⇔ o1 ⊆ o2 and o2 ⊆ o1;

(3) (o1)C=⟨F~1(I),T~1(I)⟩ (Complement of o1);

(4) o1⊕o2=⟨[infT~1(I)+infT~2(I)−infT~1(I)infT~2(I),supT~1(I)+supT~2(I)−supT~1(I)supT~2(I)],[infF~1(I)infF~2(I),supF~1(I)supF~2(I)]⟩;

(5) o1⊗o2=⟨[infT~1(I)infT~2(I),supT~1(I)supT~2(I)],[infF~1(I)+infF~2(I)−infF~1(I)infF~2(I),supF~1(I)+supF~2(I)−supF~1(I)supF~2(I)]⟩;

(6) αo1=⟨[1−(1−infT~1(I))α,1−(1−supT~1(I))α],[(infF~1(I))α,(supF~1(I))α]⟩ for α > 0;

(7) o1α=⟨[(infT~1(I))α,(supT~1(I))α],[1−(1−infF~1(I))α,1−(1−supF~1(I))α]⟩ for α > 0.

Set ok=⟨T~k(I),F~k(I)⟩=⟨ak+bkI,ck+dkI⟩ for I ∈ [I−, I+] (k = 1, 2, …, n) as a group of ONNs. Then, Ye et al. [32] proposed the ONN weighted arithmetic averaging (ONNWAA) and ONN weighted geometric averaging (ONNWGA) operators:

ONNWAA(o1,o2,…,on)=∑k=1nαkok=⟨1−∏k=1n(1−ak−bkI)αk,∏k=1n(ck+dkI)αk⟩ (1)

ONNWGA(o1,o2,…,on)=∏k=1nokαk=⟨∏k=1n(ak+bkI)αk,1−∏k=1n(1−ck−dkI)αk⟩ (2)

where αk ∈ [0, 1] (k = 1, 2, …, n) is the weight of ok for ∑k=1nαk=1.

For any ONN ok=⟨T~k(I),F~k(I)⟩=⟨ak+bkI,ck+dkI⟩ for I ∈ [I−, I+], Ye et al. [32] defined its score and accuracy functions with I ∈ [I−, I+], respectively, as follows:

S(ok)={infT~k(I)−infF~k(I)+supT~k(I)−supF~k(I)}/2={2ak+bk(I−+I+)−[2ck+dk(I−+I+)]}/2,S(ok)∈[−1,1] (3)

H(ok)={infT~k(I)+infF~k(I)+supT~k(I)+supF~k(I)}/2={[2ak+bk(I−+I+)]+[2ck+dk(I−+I+)]}/2,H(ok)∈[0,1] (4)

Regarding the two functions S(ok) and H(ok), the ranking method of two ONNs ok=⟨T~k(I),F~k(I)⟩=⟨ak+bkI,ck+dkI⟩ (k = 1, 2) for I ∈ [I−, I+] is defined as the following laws [32]:

(1) o1 > o2 if S(o1) > S(o2);

(2) o1 > o2 if S(o1) = S(o2) and H(o1) > H(o2);

(3) o1 = o2 if S(o1) = S(o2) and H(o1) = H(o2).

3  New p-Indeterminate Vector Similarity Measures of ONNSs

This section presents new p-indeterminate vector similarity measures of ONNSs in vector space, including the p-indeterminate cosine measure, p-indeterminate Dice measure, and p-indeterminate Jaccard measure of ONNSs.

Definition 3.1. Set o1k=⟨T~1k(I),F~1k(I)⟩=⟨a1k+b1kI,c1k+d1kI⟩O1={o11,o12,…,o1n} and O2={o21,o22,…,o2n} as two ONNSs, where and o2k=⟨T~2k(I),F~2k(I)⟩=⟨a2k+b2kI,c2k+d2kI⟩ are ONNs for I ∈ [I−, I+]. Let p ∈ [0, 1] be an indeterminate parameter. Then, the p-indeterminate vector similarity measures between ONNSs O1 and O2 with indeterminate degrees of p ∈ [0, 1] are presented as the following p-indeterminate cosine measure, p-indeterminate Dice measure and p-indeterminate Jaccard measure:

Cp(O1,O2)=1n∑k=1n([a1k+b1kI−+b1kp(I+−I−)][a2k+b2kI−+b2kp(I+−I−)]+[c1k+d1kI−+d1kp(I+−I−)][c2k+d2kI−+d2kp(I+−I−)])([a1k+b1kI−+b1kp(I+−I−)]2+[(c1k+d1kI−+d1kp(I+−I−)]2×[a2k+b2kI−+b2kp(I+−I−)]2+[a2k+b2kI−+d2kp(I+−I−)]2) (5)

Dp(O1,O2)=1n∑k=1n2([a1k+b1kI−+b1kp(I+−I−)][a2k+b2kI−+b2kp(I+−I−)]+[c1k+d1kI−+d1kp(I+−I−)][c2k+d2kI−+d2kp(I+−I−)])([a1k+b1kI−+b1kp(I+−I−)]2+[(c1k+d1kI−+d1kp(I+−I−)]2+[a2k+b2kI−+b2kp(I+−I−)]2+[a2k+b2kI−+d2kp(I+−I−)]2) (6)

Jp(O1,O2)=1n∑k=1n([a1k+b1kI−+b1kp(I+−I−)][a2k+b2kI−+b2kp(I+−I−)]+[c1k+d1kI−+d1kp(I+−I−)][c2k+d2kI−+d2kp(I+−I−)])(([a1k+b1kI−+b1kp(I+−I−)]2+[(c1k+d1kI−+d1kp(I+−I−)]2+[a2k+b2kI−+b2kp(I+−I−)]2+[a2k+b2kI−+d2kp(I+−I−)]2)−([a1k+b1kI−+b1kp(I+−I−)][a2k+b2kI−+b2kp(I+−I−)]+[c1k+d1kI−+d1kp(I+−I−)][c2k+d2kI−+d2kp(I+−I−)])) (7)

Especially when p is specified as any value, the p-indeterminate cosine measure, p-indeterminate Dice measure and p-indeterminate Jaccard measure are reduced to the cosine measure [15], Dice measure [19] and Jaccard measure [18] of IFSs, respectively. Hence, based on the properties of the vector similarity measures [15,18,19], the p-indeterminate cosine measure, p-indeterminate Dice measure and p-indeterminate Jaccard measure also obviously contain the following properties:

(1) Cp(O1, O2) = Cp(O2, O1), Dp(O1, O2) = Dp(O2, O1) and Jp(O1, O2) = Jp(O2, O1);

(2) Cp(O1, O2) = Dp(O1, O2) = Jp(O1, O2) = 1 if O1 = O2;

(3) Cp(O1, O2), Dp(O1, O2), Jp(O1, O2) ∈ [0, 1].

When the importance of each ONN ojk (j = 1, 2; k = 1, 2, …, n) in O1 and O2 is taken into account and specified by its weight αk with 0 ≤ αk ≤ 1 and ∑k=1nαk=1, the weighted p-indeterminate cosine measure, weighted p-indeterminate Dice measure, and weighted p-indeterminate Jaccard measure of ONNSs O1 and O2 can be given, respectively, as follows:

Cwp(O1,O2)=∑k=1nαk([a1k+b1kI−+b1kp(I+−I−)][a2k+b2kI−+b2kp(I+−I−)]+[c1k+d1kI−+d1kp(I+−I−)][c2k+d2kI−+d2kp(I+−I−)])([a1k+b1kI−+b1kp(I+−I−)]2+[(c1k+d1kI−+d1kp(I+−I−)]2×[a2k+b2kI−+b2kp(I+−I−)]2+[a2k+b2kI−+d2kp(I+−I−)]2) (8)

Dwp(O1,O2)=∑k=1nαk2([a1k+b1kI−+b1kp(I+−I−)][a2k+b2kI−+b2kp(I+−I−)]+[c1k+d1kI−+d1kp(I+−I−)][c2k+d2kI−+d2kp(I+−I−)])([a1k+b1kI−+b1kp(I+−I−)]2+[(c1k+d1kI−+d1kp(I+−I−)]2+[a2k+b2kI−+b2kp(I+−I−)]2+[a2k+b2kI−+d2kp(I+−I−)]2) (9)

Jwp(O1,O2)=∑k=1nαk([a1k+b1kI−+b1kp(I+−I−)][a2k+b2kI−+b2kp(I+−I−)]+[c1k+d1kI−+d1kp(I+−I−)][c2k+d2kI−+d2kp(I+−I−)])(([a1k+b1kI−+b1kp(I+−I−)]2+[(c1k+d1kI−+d1kp(I+−I−)]2+[a2k+b2kI−+b2kp(I+−I−)]2+[a2k+b2kI−+d2kp(I+−I−)]2)−([a1k+b1kI−+b1kp(I+−I−)][a2k+b2kI−+b2kp(I+−I−)]+[c1k+d1kI−+d1kp(I+−I−)][c2k+d2kI−+d2kp(I+−I−)])) (10)

Obviously, the weighted p-indeterminate cosine, weighted p-indeterminate Dice and weighted p-indeterminate Jaccard measures also contain the following properties:

(1) Cwp(O1, O2) = Cwp(O2, O1), Dwp(O1, O2) = Dwp(O2, O1) and Jwp(O1, O2) = Jwp(O2, O1);

(2) Cwp(O1, O2) = Dwp(O1, O2) = Jwp(O1, O2) = 1 if O1 = O2;

(3) Cwp(O1, O2), Dwp(O1, O2), Jwp(O1, O2) ∈ [0, 1].

However, the weighted p-indeterminate cosine measure of ONNSs, the weighted p-indeterminate Dice measure of ONNSs and the weighted p-indeterminate Jaccard measure of ONNSs imply the cosine measure family of IFSs, the Dice measure family of IFSs, and the Jaccard measure family of IFSs, respectively, regarding a group of p values, then the existing cosine, Dice and Jaccard measures of IFSs [15,18,19] are the special cases of the three p-indeterminate vector similarity measures (4)–(6) corresponding to the each value of p ∈ [0, 1]. It is obvious that the parameterized indeterminate vector similarity measures of ONNs with indeterminate degrees of p ∈ [0, 1] show their measure flexibility in different indeterminate ranges of I and indeterminate degrees of p.

4  DM Method Using the Proposed p-Indeterminate Vector Similarity Measures of ONNSs

This section develops a multiple attribute DM method with indeterminate degrees (decision risks) of decision makers based on the proposed p-indeterminate vector similarity measures under ONNS environment.

Regarding a multiple attribute DM problem, there is a set of alternatives L = {L1, L2, …, Lm}, which is assessed by a set of attributes X = {x1, x2, …, xn}. Then, the weight of each xk is specified by αk with 0 ≤ αk ≤ 1 and ∑k=1nαk=1. Decision makers are required to satisfactorily assess each alternative Lj (j = 1, 2, …, m) with respect to each attribute xk (k = 1, 2, …, n) by the ONN ojk=⟨T~jk(I),F~jk(I)⟩=⟨ajk+bjkI,cjk+djkI⟩, where T~jk(I)=ajk+bjkI⊆[0,1] and F~jk(I)=cjk+djkI⊆[0,1] for 0≤supT~jk(I)+supF~jk(I)≤1 and I ∈ [I−, I+] are the truth and falsity indeterminate degrees. Thus, all ONNs can be constructed as the decision matrix of ONNs O = (ojk)m × n.

To solve multiple attribute DM problems with ONN information, we present a multiple attribute DM method using the weighted p-indeterminate vector similarity measures (the weighted p-indeterminate cosine, weighted p-indeterminate Dice, weighted p-indeterminate Jaccard measures) with indeterminate degrees of p ∈ [0, 1] specified by decision makers and give the following decision steps:

Step 1: An ideal solution/alternative O∗={o1∗,o2∗,…,on∗} is yielded from the decision matrix O by the ideal ONNs ok∗=⟨Tk∗,Fk∗⟩=⟨maxj(ajk+bjkI+),minj(cjk+djkI−)⟩ (k = 1, 2, …, n; j = 1, 2, …, m) for I ∈ [I−, I+].

Step 2: By applying one of Eqs. (8)–(10) corresponding to the small indeterminate degree (p = 0) or the moderate indeterminate degree (p = 0.5) or the big indeterminate degree (p = 1) of the decision makers, the weighted p-indeterminate cosine measure or the weighted p-indeterminate Dice measure or the weighted p-indeterminate Jaccard measure between Oj (j = 1, 2, …, m) and O* is presented by the following formula:

Cwp(Oj,O∗)=∑k=1nαk[ajk+bjkI−+bjkp(I+−I−)]Tk∗+[cjk+djkI−+djkp(I+−I−)]Fk∗[ajk+bjkI−+bjkp(I+−I−)]2+[(cjk+djkI−+djkp(I+−I−)]2(Tk∗)2+(Fk∗)2 (11)

Or

Dwp(Oj,O∗)=∑k=1nαk2([ajk+bjkI−+bjkp(I+−I−)]Tk∗+[cjk+djkI−+djkp(I+−I−)]Fk∗)[ajk+bjkI−+bjkp(I+−I−)]2+[(cjk+djkI−+djkp(I+−I−)]2+(Tk∗)2+(Fk∗)2 (12)

Or

Jwp(Oj,O∗)=∑k=1nαk[ajk+bjkI−+bjkp(I+−I−)]Tk∗+[cjk+djkI−+djkp(I+−I−)]Fk∗(([a1k+b1kI−+b1kp(I+−I−)]2+[(c1k+d1kI−+d1kp(I+−I−)]2+(Tk∗)2+(Fk∗)2)−([ajk+bjkI−+bjkp(I+−I−)]Tk∗+[cjk+djkI−+djkp(I+−I−)]Fk∗)) (13)

Step 3: The alternatives are ranked and the best one is chosen corresponding to the values of the weighted p-indeterminate vector similarity measure according to the indeterminate degree p = 0 or p = 0.5 or p = 1 specified by the decision makers.

Step 4: End.

5  Actual DM Example

5.1 Multiple Attribute DM Problem on Choosing a Suitable Logistics Supplier

A suitable third part logistics supplier is selected to play a key role because it can improve efficiency, market share and service quality and reduce costs in business development. In this section, we consider a multiple attribute DM problem on choosing a suitable logistics supplier as the third part for a manufacturing company to show the practicability and effectiveness of the proposed DM method in ONNS setting.

Suppose that four possible logistics suppliers are chosen as a set of their alternatives L = {L1, L2, L3, L4} for a manufacturing company, which must be evaluated by the three requirements/attributes: the efficiency (x1), the service quality (x2), and the cost (x3). Then, the weight vector of the three attributes is given as α = (0.35, 0.32, 0.33). Thus, the satisfactory assessment of each alternative Lj (j = 1, 2, 3, 4) are given over the attributes xk (k = 1, 2, 3) by decision makers, and then the assessment information of the truth indeterminacy degree and the falsity indeterminacy degree is expressed as the ONN ojk=⟨T~jk(I),F~jk(I)⟩=⟨ajk+bjkI,cjk+djkI⟩, where T~jk(I)=ajk+bjkI⊆[0,1], F~jk(I)=cjk+djkI⊆[0,1], and 0≤supT~jk(I)+supF~jk(I)≤1 (j = 1, 2, 3, 4 and k = 1, 2, 3) for the indeterminacy I ∈ [0, 1]. Thus, all ONNs can be established as their decision matrix:

Therefore, the developed DM approach is applied in the indeterminate DM problem with I ∈ [0, 1] and indicated by the following decision process:

First of all, an ideal solution/alternative O∗={o1∗,o2∗,o3∗}={⟨0.8,0.1⟩,⟨0.8,0.1⟩,⟨0.8,0.0⟩} is obtained from the decision matrix O for I ∈ [I−, I+] = [0, 1].

Then by applying one of Eqs. (11)–(13) regarding the small indeterminate degree (p = 0) or the moderate indeterminate degree (p = 0.5) or the big indeterminate degree (p = 1) presented by the decision makers, the values of the weighted p-indeterminate cosine measure or the weighted p-indeterminate Dice measure or the weighted p-indeterminate Jaccard measure between Oj (j = 1, 2, …, m) and O* and decision results are shown in Tab. 1.

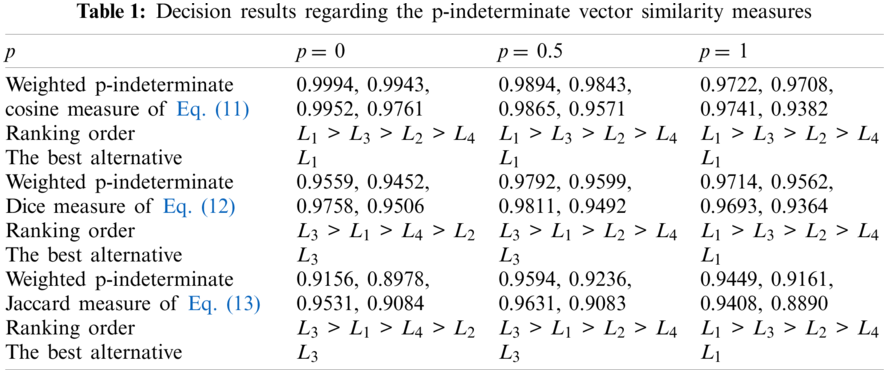
As for decision results in Tab. 1, the ranking orders and the best alternatives obtained by the weighted p-indeterminate Dice measure and the weighted p-indeterminate Jaccard measure are identical and then both indicates their sensitivity and ranking changeability corresponding to the different indeterminate degrees (p = 0, 0.5, 1); while the ranking order and the best alternative obtained by the weighted p-indeterminate cosine measure are different from the ones obtained by both the weighted p-indeterminate Dice measure and the weighted p-indeterminate Jaccard measure and indicate some robustness corresponding to the different indeterminate degrees (p = 0, 0.5, 1). But, the weighted p-indeterminate cosine measure lacks some sensitivity to the different indeterminate degrees. From the perspective of decision flexibility, the weighted p-indeterminate Dice measure and the weighted p-indeterminate Jaccard measure are superior to the weighted p-indeterminate cosine measure. Then, their final decision results indicate that the best alternative is L1 or L4 depending on an indeterminate degree and a similarity measure specified by the decision makers.

5.2 Comparison with Related DM Methods

In the setting of IFSs, existing vector similarity measures of IFSs in the literature [15,18,19] only are the special cases of the proposed p-indeterminate vector similarity measures of ONNSs when p takes some specified indeterminate degree (i.e., p = 0 or 0.5 or 1). Then, the DM method based on the proposed p-indeterminate vector similarity measures shows its better flexibility and practicability depending on decision makers’ indeterminate degrees in indeterminate DM problems, while the existing related DM methods [15,18,19] cannot deal with the indeterminate DM problems with ONNS information. Therefore, the developed DM method is more generalized suitability and superior to the existing DM methods, and also shows the advantages in its flexibility, efficiency and practicability under indeterminate DM environments.

To compare the proposed DM method with the existing DM method [32] in the setting of ONNSs, we apply the existing DM method [32] to the above DM example in the setting of ONNSs. By using Eqs. (1) and (2), the aggregated values of the ONNWAA and ONNWGA operators are calculated when the indeterminate ranges are I = [I−, I+] = [0, 0], [0, 0.5], [0, 1]. Then, the score values of S(oj) (j = 1, 2, 3, 4) are calculated by Eq. (3) and the decision results are shown in Tabs. 2 and 3, respectively.

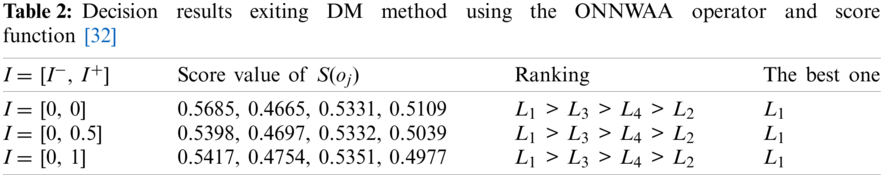
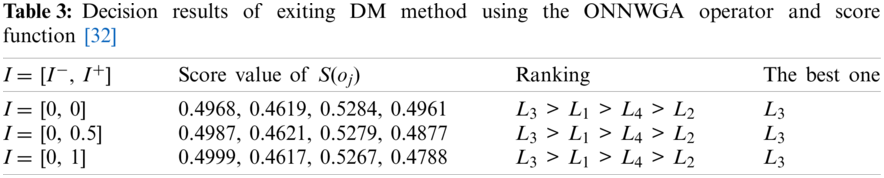
From the ranking results of Tabs. 2 and 3, the exiting DM method [32] reflects ranking difference based on the ONNWAA operator and the ONNWGA operator. Then, two kinds of ranking orders are always unchanged corresponding to different indeterminate ranges I = [I−, I+] = [0, 0], [0, 0.5], [0, 1], which demonstrates no sensitivity to the different indeterminate ranges. Obviously, the indeterminate ranges cannot affect the ranking order of alternatives in the DM example under the environment of ONNSs.

Compared with the proposed DM method, there is the same ranking order between the exiting DM method using the ONNWGA operator and score function [32] and the proposed DM method using Eqs. (12) and (13) for the indeterminate degree of p = 0, but the other ranking orders show their difference. Then, the best alternative L1 or L4 is the same between the proposed DM method and the existing one [32] in the DM example. However, the proposed DM method shows its advantages in some decision flexibility and efficiency corresponding to decision makers’ various indeterminate degrees (decision risks). But the existing DM method cannot result in the ranking change of alternatives corresponding to decision makers’ different indeterminate ranges in the DM example, and then it lacks the decision flexibility, which show its insufficiency. Therefore, it is obvious that the proposed DM method is superior to the existing one in indeterminate DM problems with ONNS information.

6  Conclusion

Due to the lack of similarity measures of ONNSs in the existing literature [32], this study proposed the p-indeterminate vector similarity measures of ONNSs, including the p-indeterminate cosine measure, the p-indeterminate Dice measure, and the p-indeterminate Jaccard measure of ONNSs to provide effective mathematical tools for flexible DM in indeterminate problems. Then, a multiple attribute DM approach with the different indeterminate degrees (p = 0, 0.5, 1) of the decision makers was developed by using the p-indeterminate vector similarity measures under the indeterminate DM environment. Lastly, an actual DM example on choosing a suitable logistics supplier was presented to demonstrate the flexibility, efficiency and practicability of the developed DM approach in indeterminate DM situations. By comparison with the existing DM methods, the superiority of this study is that the established DM approach indicates its flexibility, efficiency, and practicability depending on decision makers’ indeterminate degrees in ONNS setting.

In this study, however, we only use the proposed p-indeterminate vector similarity measures of ONNSs for DM problems, but lack more applications. Therefore, it is necessary for us to extend the p-indeterminate vector similarity measures to medical diagnosis, pattern recognition, and clustering analysis as further research directions in ONNS setting.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.