DOI:10.32604/csse.2021.014810

| Computer Systems Science & Engineering DOI:10.32604/csse.2021.014810 |  |
| Article |
On Edge Irregular Reflexive Labeling of Categorical Product of Two Paths
1Centre for Advanced Studies in Pure and Applied Mathematics, Bahauddin Zakariya University, Multan, Pakistan
2College of Computer Science and Information Technology, Jazan University, Jazan, Saudi Arabia
*Corresponding Author: Muhammad Ibrahim. Email: mibtufail@gmail.com
Received: 19 October 2020; Accepted: 13 November 2020
Abstract: Among the huge diversity of ideas that show up while studying graph theory, one that has obtained a lot of popularity is the concept of labelings of graphs. Graph labelings give valuable mathematical models for a wide scope of applications in high technologies (cryptography, astronomy, data security, various coding theory problems, communication networks, etc.). A labeling or a valuation of a graph is any mapping that sends a certain set of graph elements to a certain set of numbers subject to certain conditions. Graph labeling is a mapping of elements of the graph, i.e., vertex and/or edges to a set of numbers (usually positive integers), called labels. If the domain is the vertex-set or the edge-set, the labelings are called vertex labelings or edge labelings respectively. Similarly, if the domain is V (G)[E(G), then the labeling is called total labeling. A reflexive edge irregular k-labeling of graph introduced by Tanna et al.: A total labeling of graph such that for any two different edges ab and a'b' of the graph their weights has 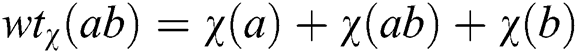 and
and 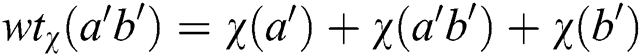 are distinct. The smallest value of k for which such labeling exist is called the reflexive edge strength of the graph and is denoted by res(G). In this paper we have found the exact value of the reflexive edge irregularity strength of the categorical product of two paths
are distinct. The smallest value of k for which such labeling exist is called the reflexive edge strength of the graph and is denoted by res(G). In this paper we have found the exact value of the reflexive edge irregularity strength of the categorical product of two paths  for any choice of
for any choice of 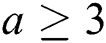 and
and 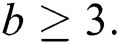
Keywords: Edge irregular reflexive labeling; reflexive edge strength; categorical product of two paths
The area of graph theory has experienced fast developments during the last 60 years. Among the huge diversity of concepts that appear while studying this subject one that has gained a lot of popularity is the concept of labeling of graphs with more than 1700 papers in the literature and a very complete dynamic survey by Gallian [1]. This new branch of mathematics has caught the attention of many authors and many new labeling results appear every year. This popularity is not only due to the mathematical challenges of graph labeling, but also for the wide range of its application, for instance X-ray crystallography, coding theory, radar, astronomy, circuit design, network design and communication design. In fact, Bloom et al. studied applications of graph labeling to other branches of science and it is possible to find part of this work in Bloom et al. [2] and Bloom et al. [3].
All charts discussed in this paper are simple, finite and not directed. In Chartrand et al. [4] suggest a very nice problem. Set positive integer tags from the set 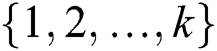 to the edges of a linked graph directly with at least three in this path, so that the graph becomes sporadic. Any weight (sum of the label) on each special edge. The question is what is the base estimate for the largest
to the edges of a linked graph directly with at least three in this path, so that the graph becomes sporadic. Any weight (sum of the label) on each special edge. The question is what is the base estimate for the largest 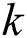 on all this unexpected task? This parameter is for the graph
on all this unexpected task? This parameter is for the graph 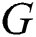 is known as the irregularity strength of the
is known as the irregularity strength of the 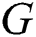 and is denoted by
and is denoted by 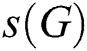 . A very nice comprehensive overview on the irregularity strength is given by Lahel [5]. For more further recent results, see the papers by Amar et al. [6], Dimitz et al. [7], Gyarfas [8], and Nierhoff [9].
. A very nice comprehensive overview on the irregularity strength is given by Lahel [5]. For more further recent results, see the papers by Amar et al. [6], Dimitz et al. [7], Gyarfas [8], and Nierhoff [9].
There is an attraction arise from these papers as, an edge irregular k-labeling defined by 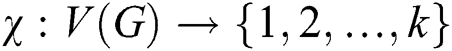 such that for every two different edges
such that for every two different edges 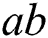 and
and 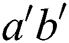 there weights
there weights  , where the weight of an edge
, where the weight of an edge  is
is  . If there exist such labeling for smallest value of
. If there exist such labeling for smallest value of  then it is known as the edge irregularity strength of the graph
then it is known as the edge irregularity strength of the graph 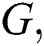 denoted by
denoted by 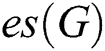 . The parameter and lower bound of edge irregularity strength was introduced by Ahmad et al. [10] and found the exact value of the edge irregularity strength for several families of graphs.
. The parameter and lower bound of edge irregularity strength was introduced by Ahmad et al. [10] and found the exact value of the edge irregularity strength for several families of graphs.
The total labeling of graph introduced by Bača et al. [11] by taking the domain of mapping as the union of node and links of chart to positive integers up to 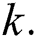 This labeling of graph is called the total
This labeling of graph is called the total 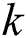 labeling of the chart
labeling of the chart 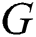 if for every two different links
if for every two different links 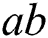 and
and 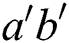 of
of 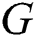 one has
one has 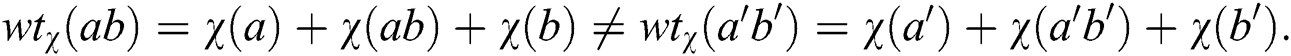 The total edge irregularity strength denoted by
The total edge irregularity strength denoted by 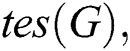 is defined as the minimum
is defined as the minimum 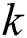 for which
for which 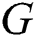 has an edge irregular total k-labeling.
has an edge irregular total k-labeling.
Keeping in view the problem imposed in Chartrand et al. [4] is there possible to find such labeling of the graph for a distinct degree. It seems to be impossible to construct a chart in which every node has a unique degree for a simple chart; however, it is possible for multigraphs (graphs in which we allow loops or multiple edges between the adjacent vertices). The question then became: What is the smallest number of parallel edges between two vertices required to ensure that the graph display vertex irregularity? This problem is equivalent to the labeling problem as described at the beginning of this section.
Using both Chartrand et al. [4] and Ahmad et al. [10] as motivation, in Ryan et al. [12], the authors decreed that the vertex labels should represent loops at the vertex. The consequence was two-fold; first, each vertex label was required to be an even integer, since each loop added two to the vertex degree; and second, unlike in total irregular labeling, the label 0 was permitted as representing a loopless vertex. Edges continued to be labelled by integers from one to 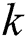 .
.
Thus, for a graph 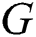 , in Ryan et al. [12,13] are defined labelings
, in Ryan et al. [12,13] are defined labelings 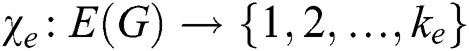 and
and  , and then, labeling
, and then, labeling 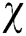 is a total k-labeling of
is a total k-labeling of 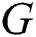 defined such that
defined such that 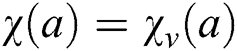 if
if 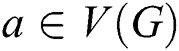 and
and 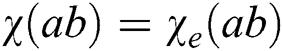 if
if 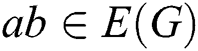 , where
, where 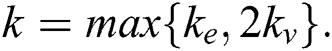 The total k-labeling
The total k-labeling  is called an edge irregular reflexive k-labeling of the graph
is called an edge irregular reflexive k-labeling of the graph 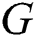 if for every two different edges
if for every two different edges 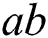 and
and 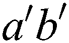 of
of 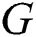 , one has
, one has  . The smallest value of
. The smallest value of  for which such labeling exists is called the reflexive edge irregularity strength of the graph
for which such labeling exists is called the reflexive edge irregularity strength of the graph 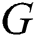 and is denoted by
and is denoted by 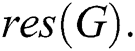 In Ivanco et al. [14] purposed the following. Any graph
In Ivanco et al. [14] purposed the following. Any graph 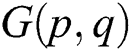 with maximum degree
with maximum degree 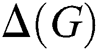 other than
other than 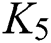 satisfies
satisfies
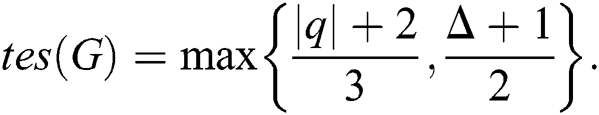
In term of 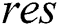 , Ryan et al. [12] purpose the following: Any graph
, Ryan et al. [12] purpose the following: Any graph  with maximum degree
with maximum degree 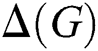 satisfies
satisfies

where 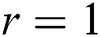 for
for 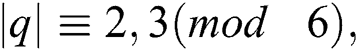 and zero otherwise.
and zero otherwise.
2 Constructing an Edge Irregular Reflexive Labeling
Let us recall the following lemma proven in Ryan et al. [12]. For every graph 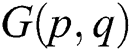 ,
,
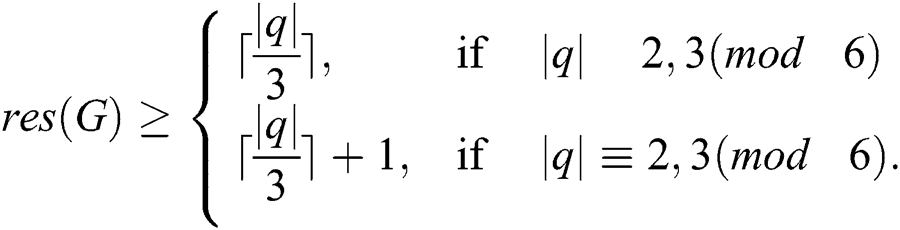
From the above lemma it is noted that the minimum weight under  of a link is one and the minimum of the maximal weight of a link is equal to the number of edges/links of the graph. Further the labeling of a link can be obtained as the sum of three numbers in which at least two must be even.
of a link is one and the minimum of the maximal weight of a link is equal to the number of edges/links of the graph. Further the labeling of a link can be obtained as the sum of three numbers in which at least two must be even.
In this paper, we investigate the  for the categorical product of two paths
for the categorical product of two paths 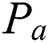 and
and 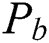 for
for 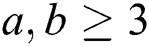 .
.
3 Categorical Products of Two Paths
As far as the category of graphs and full graph homomorphisms is concern, the categorical product was introduced by Culik et al. [15] and called it as the cardinal product. After then it was defined by Weichsel [16] and name it as the Kronecker product and studies the connectedness of products of finitely many factors. Stephen et al. [17] were the first to who called the cardinal product as a categorical product. Moreover, the categorical product was extensively studied many researchers in the history of graph labeling. Ahmad et al. [18] found the total edge irregularity strength for a categorical product of two paths. Ahmad et al. [19] find the edge irregular total labeling for categorical product of two cycles. Victor et al. [20] studied the categorical product of two s-valued graphs. For the definition of categorical product of two graphs we refer [18].
Theorem 1: Let 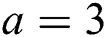 and
and 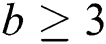 be positive integers and
be positive integers and  be the categorical product of two paths then
be the categorical product of two paths then
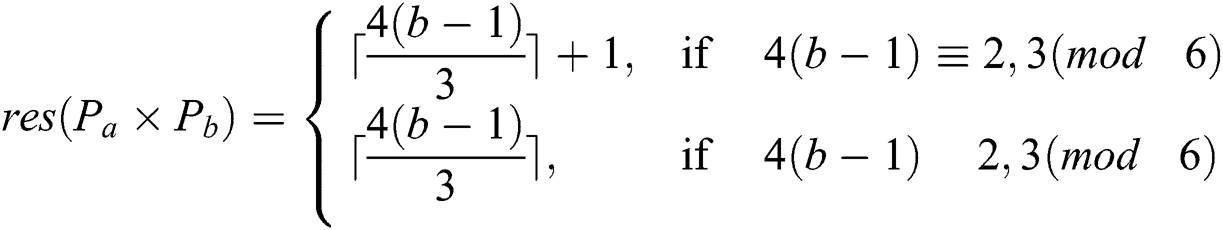
Proof. Since  has
has 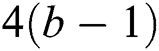 edges. Therefore, from Lemma 2 we get
edges. Therefore, from Lemma 2 we get
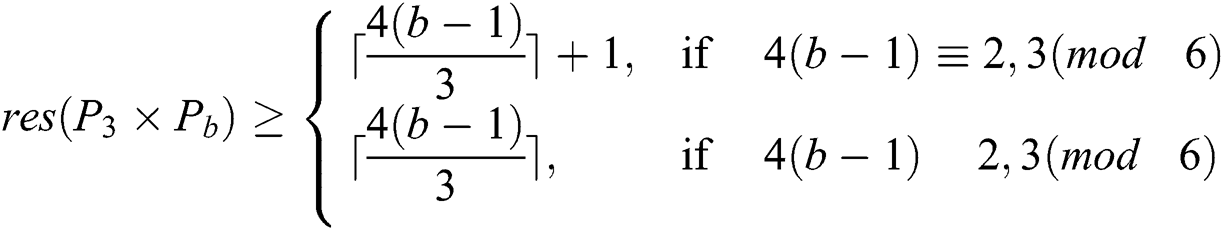
Next, we will show that
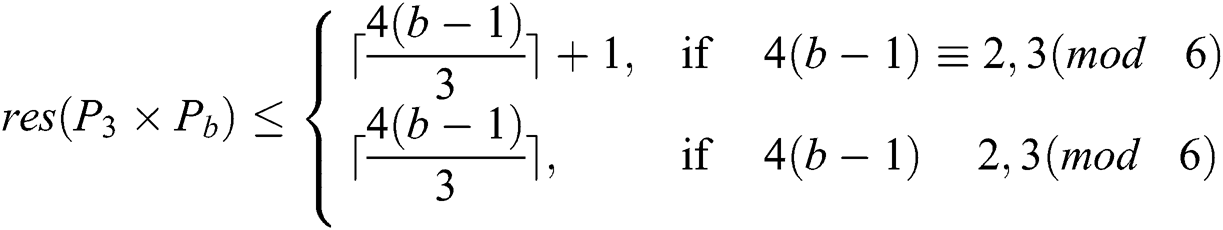
For this we define a  -labeling on
-labeling on  as follows:
as follows:
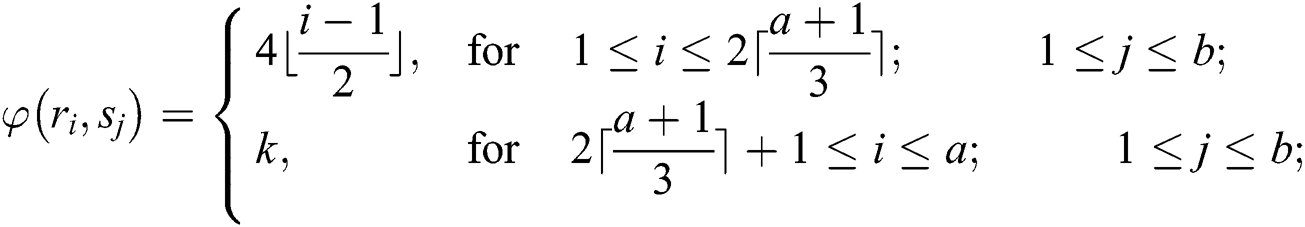
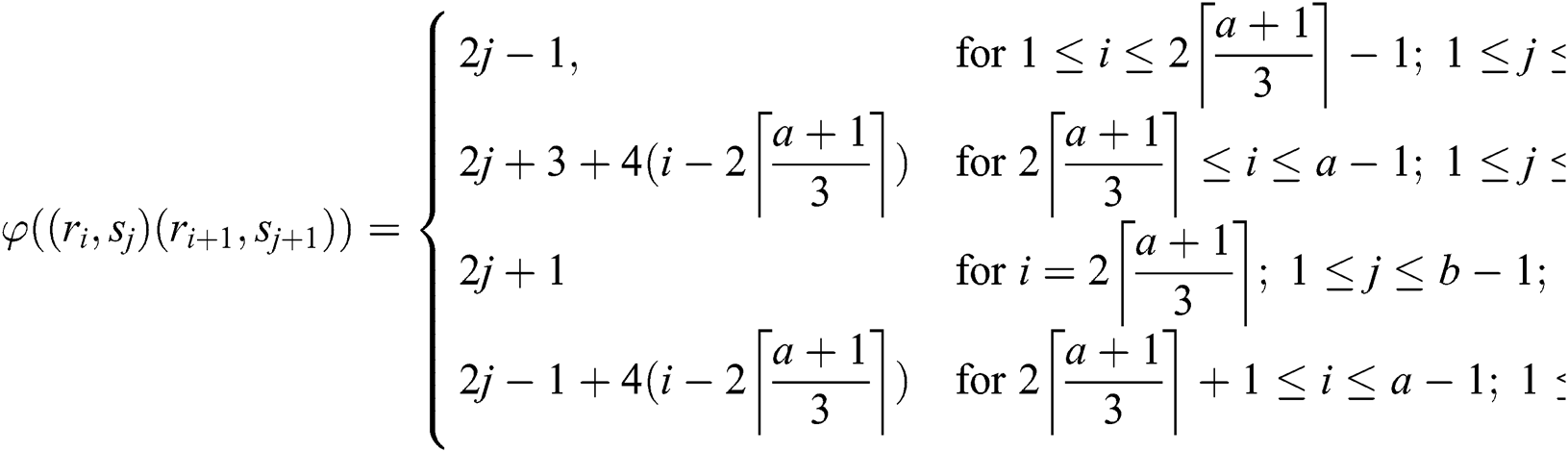
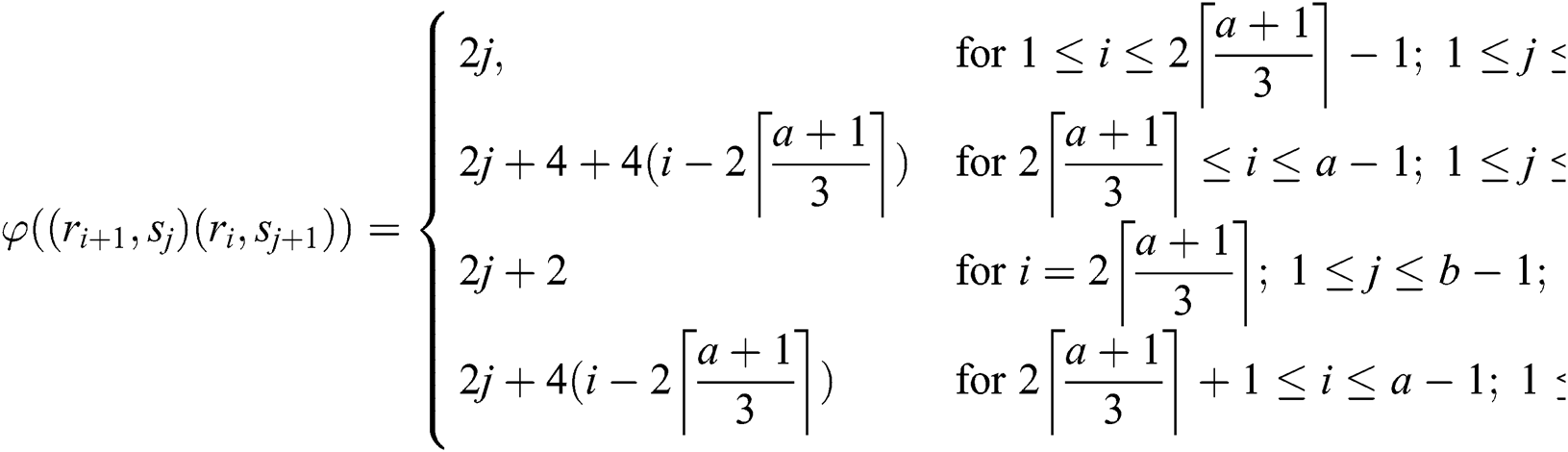
The weights of the edges are given as under:
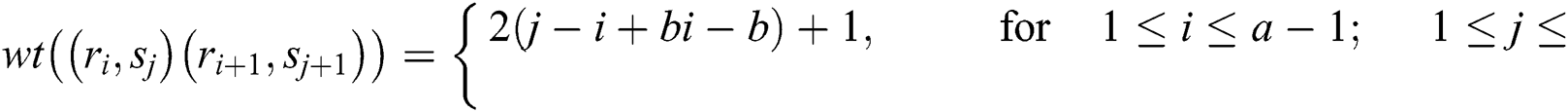
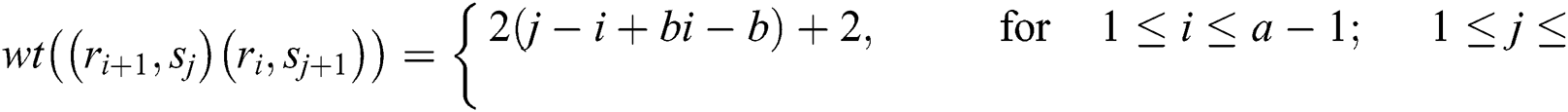
Observe that the weights of all the links receive distinct values. So,  is an edge irregular reflexive labeling of
is an edge irregular reflexive labeling of  for
for 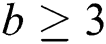 . As required:
. As required:
Theorem 2: Let 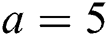 and
and 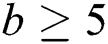 be positive integers and
be positive integers and  be the categorical product of two paths
be the categorical product of two paths 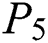 and
and 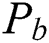 then
then
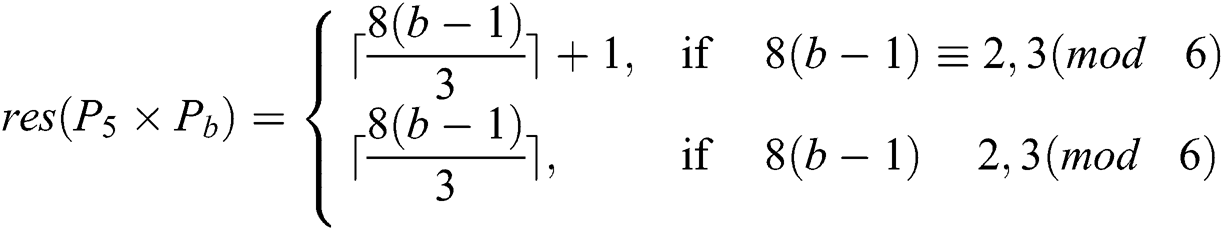
Proof. Since  has
has  edges. Therefore, from Lemma 2 we get
edges. Therefore, from Lemma 2 we get
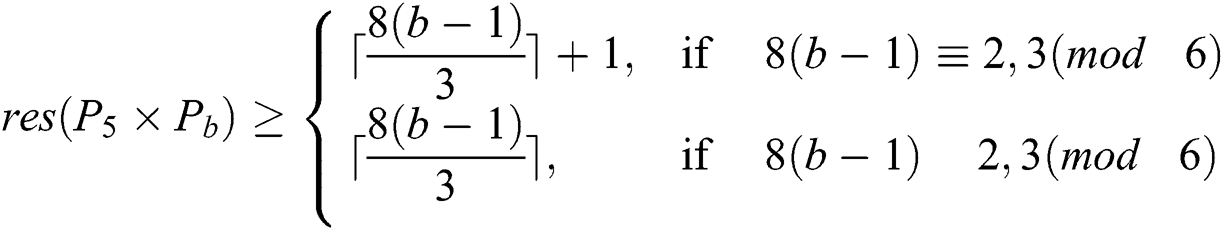
Next, we will show that
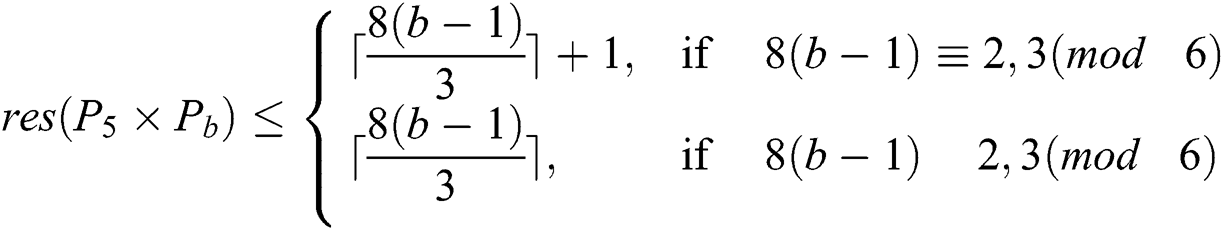
For this we define a 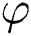 -labeling on
-labeling on  as follows:
as follows:
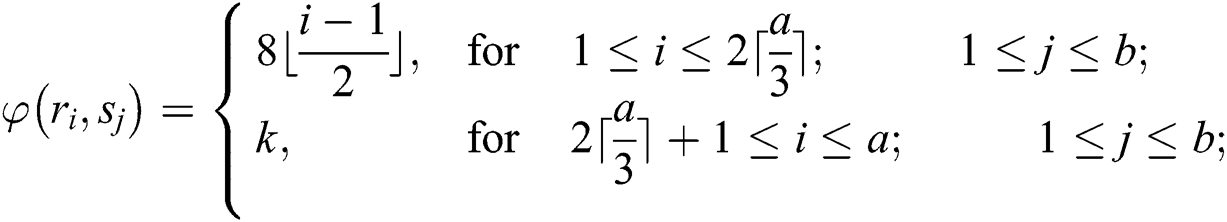
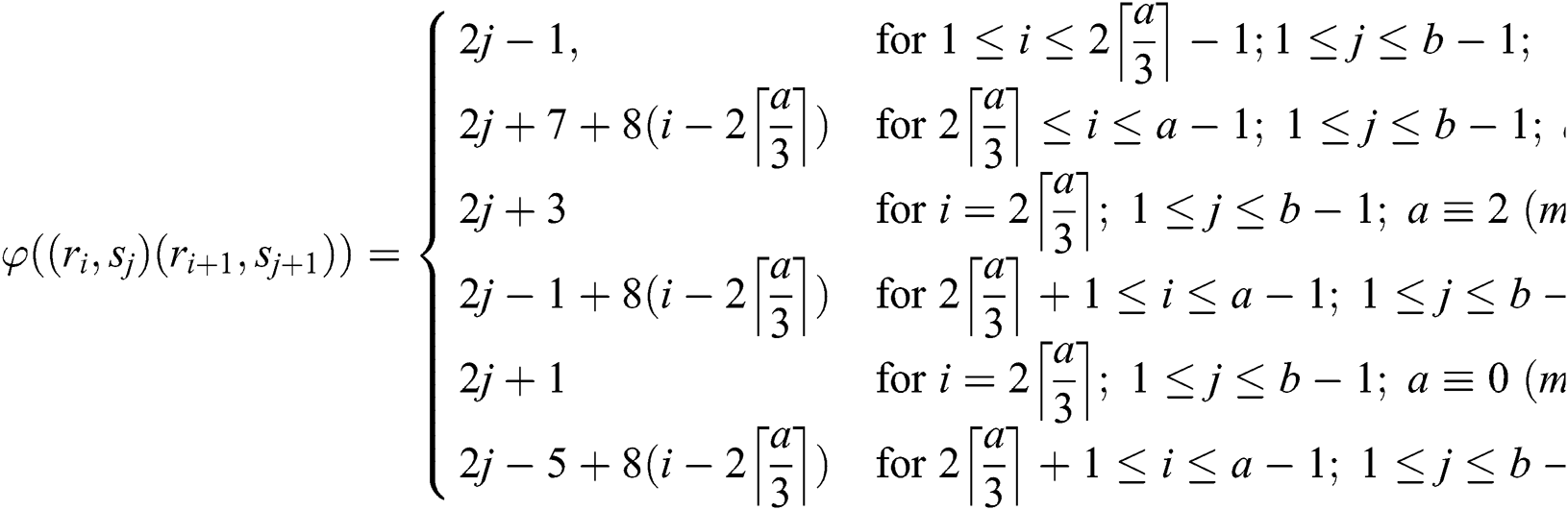
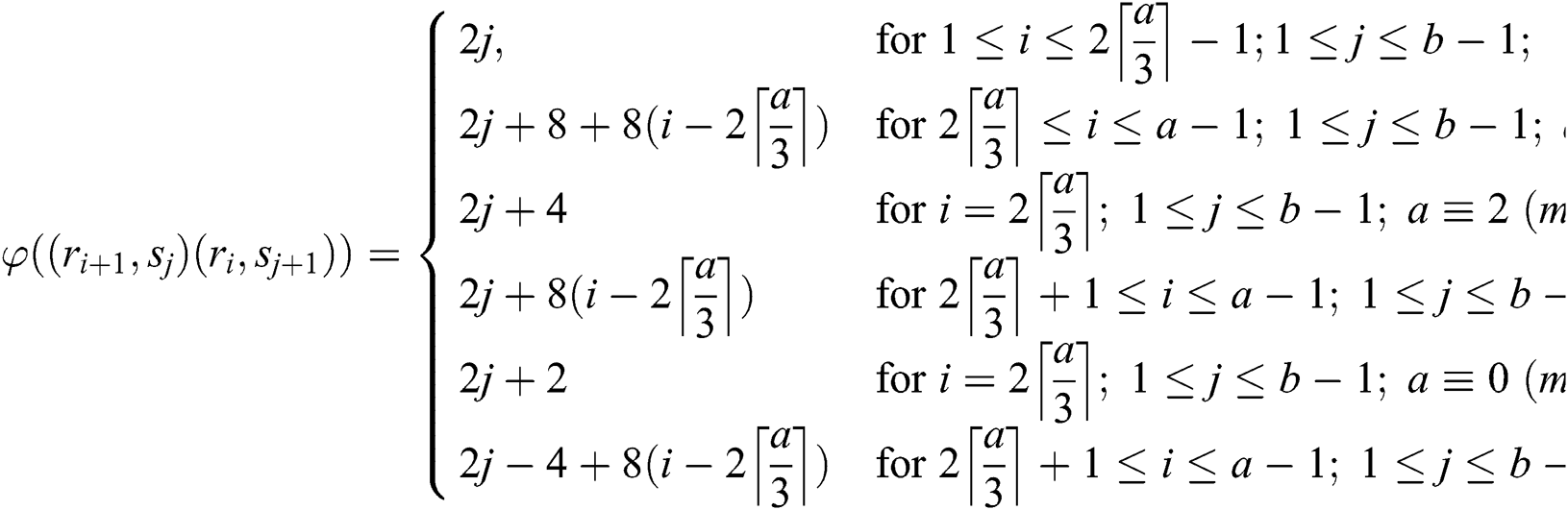
The weights of reflexive edges are given as under:
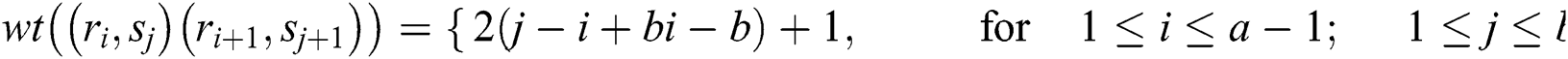

Observe that the weights of all the links receive distinct values. So, 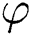 is an edge irregular reflexive labeling of
is an edge irregular reflexive labeling of  for
for 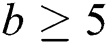 . As required:
. As required:
Theorem 3: Let for all 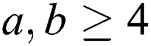 and
and 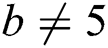 be positive integers and
be positive integers and  be the categorical product of two paths
be the categorical product of two paths 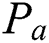 and
and 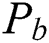 then
then

Proof. Since  has
has 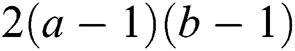 edges. Therefore, from Lemma 2 we get
edges. Therefore, from Lemma 2 we get
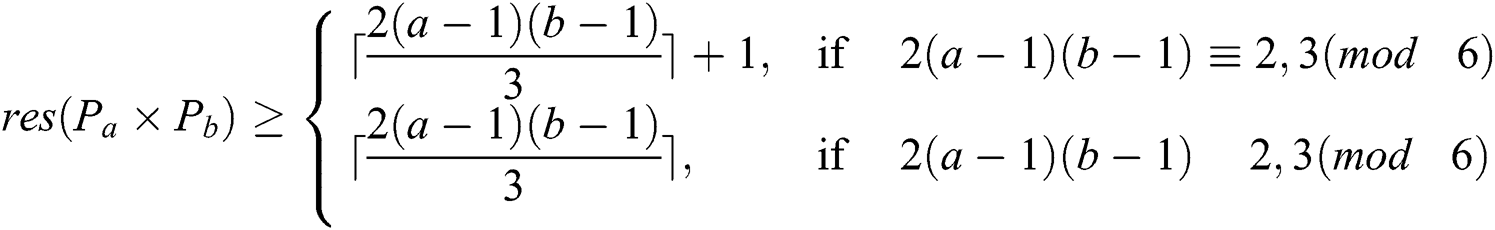
Next, we will show that
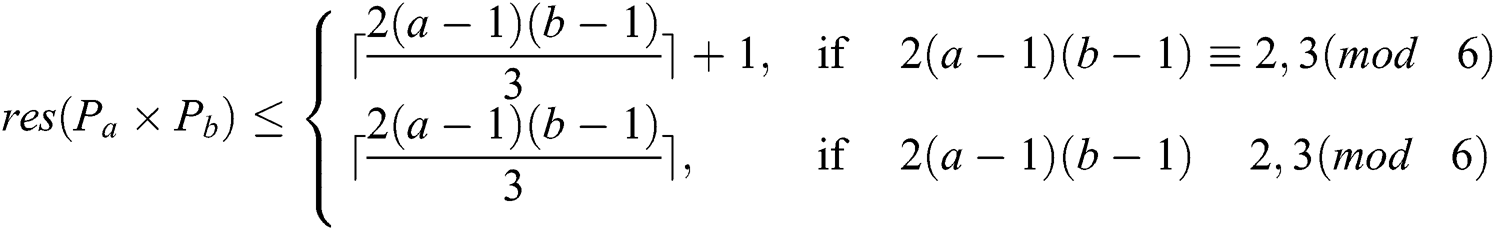
For this we define a  -labeling on
-labeling on  as follow:
as follow:
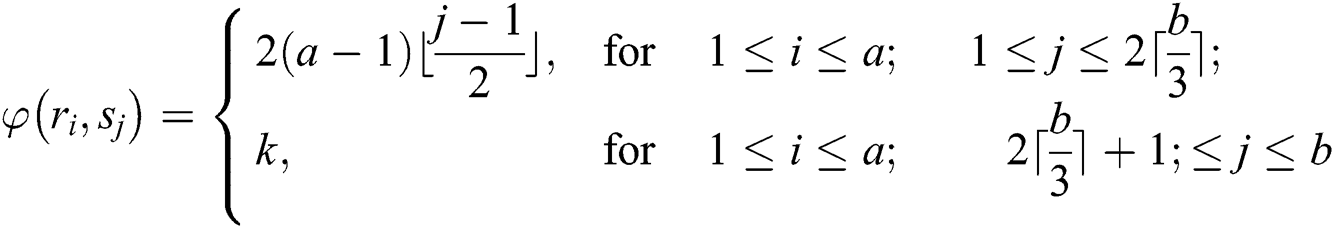
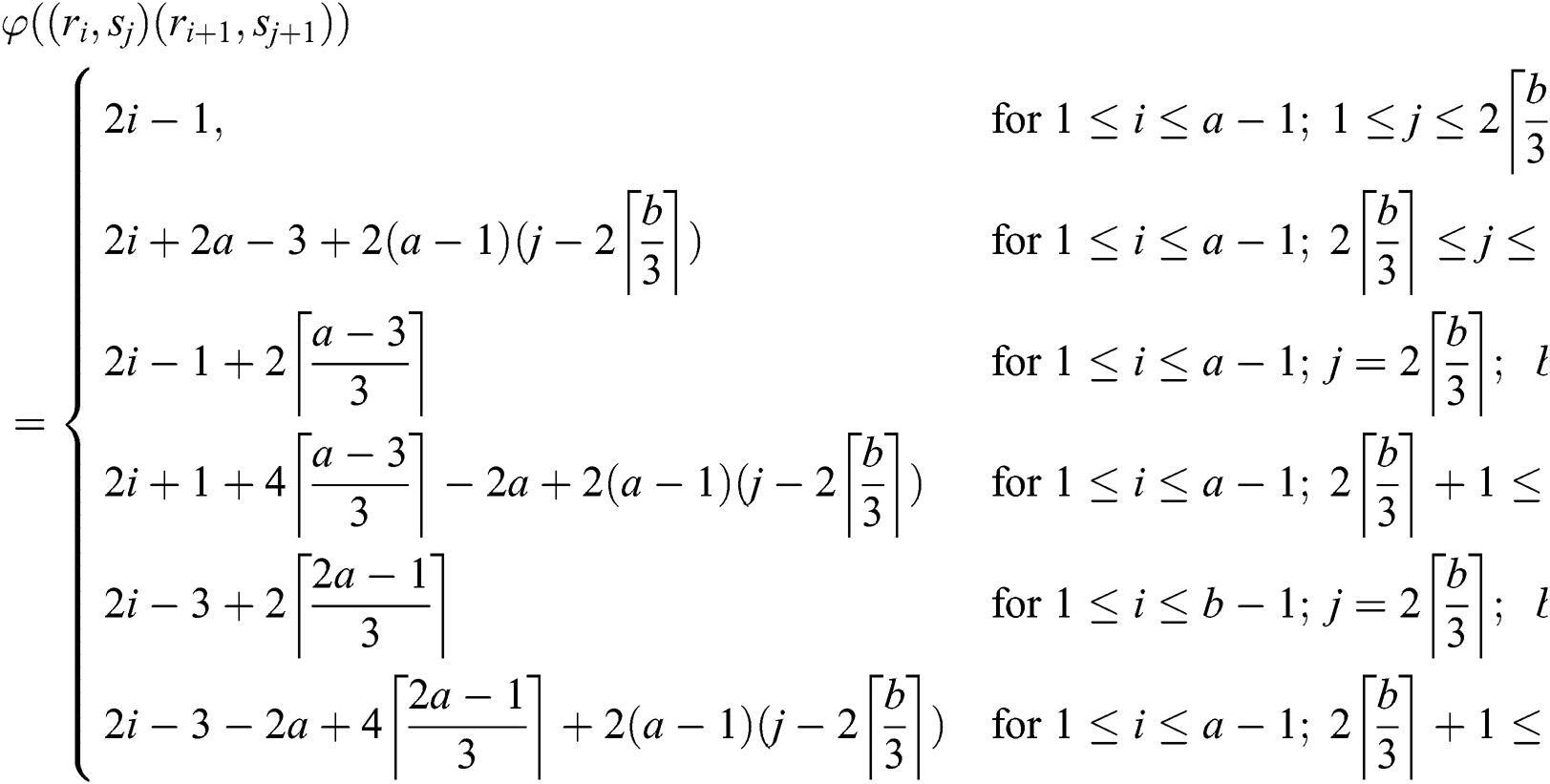
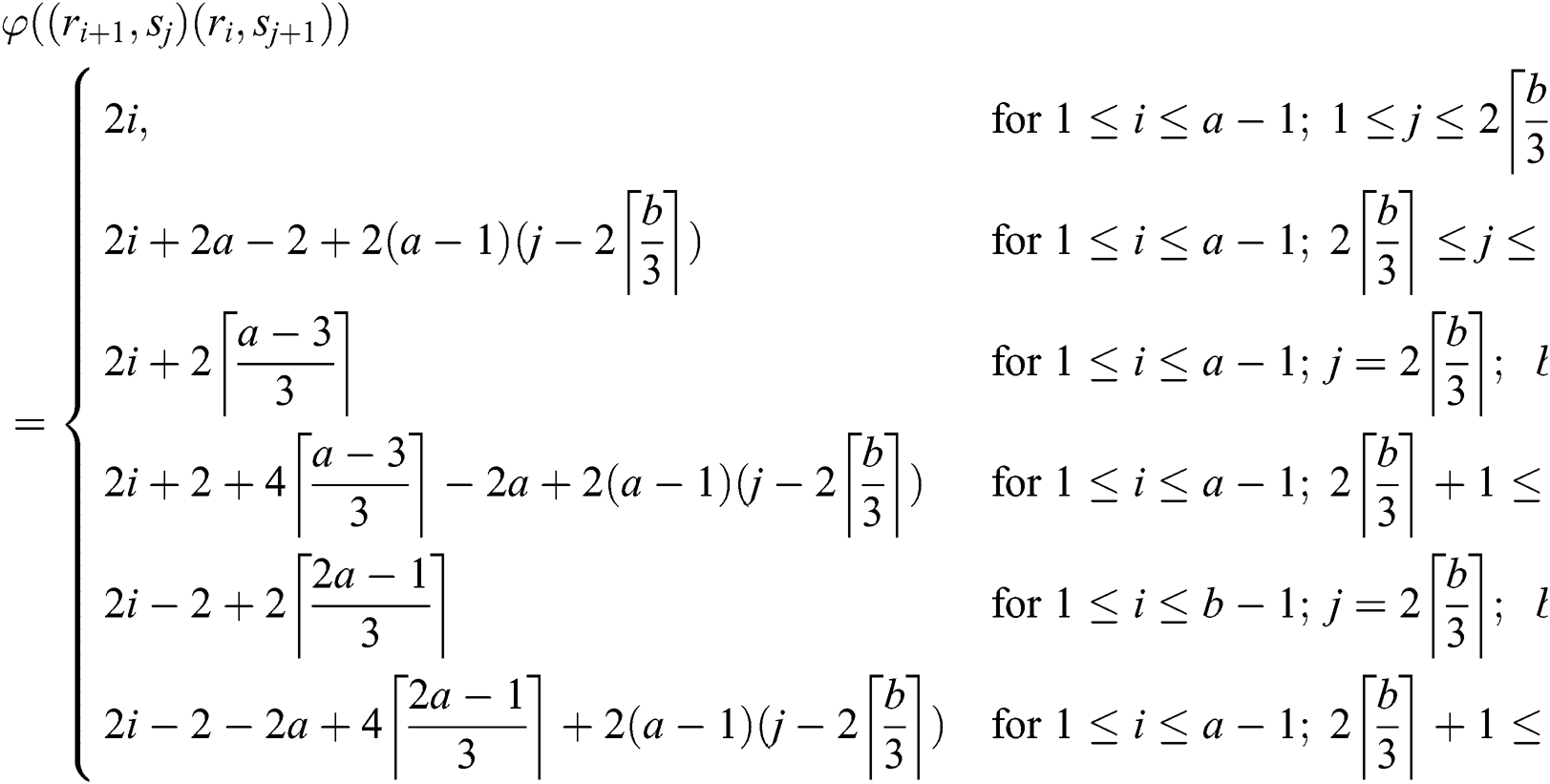
The weights of reflexive edges are given as under:
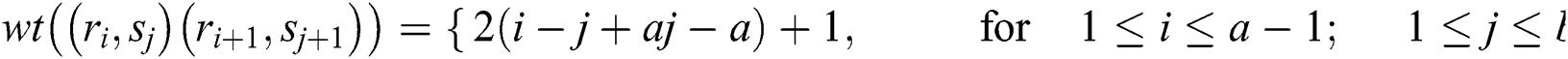
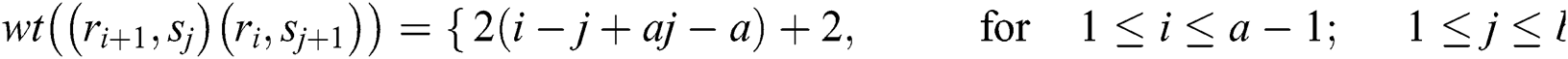
Observe that the weights of all the links receive distinct values. So, 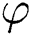 is an edge irregular reflexive labeling of
is an edge irregular reflexive labeling of  for
for  and
and 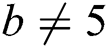 . As required.
. As required.
In this paper we have found the exact value of the reflexive edge irregularity strength of the categorical product of two paths  for any choice of
for any choice of 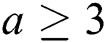 and
and 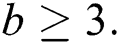 In future we are interested to found the reflexive edge irregularity strength of some grid related graphs.
In future we are interested to found the reflexive edge irregularity strength of some grid related graphs.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. A. Gallian. (2019). “A dynamic survey of graph labeling,” Electronic Journal of Combinatorics, vol. 19, DS6, . [Online]. Available: http://www.combinatorics.org/surveys/ds6.pdf. [Google Scholar]
2. G. S. Bloom and S. W. Golomb. (1977). “Applications of numbered undirected graphs,” in Proc. IEEE, vol. 65, no. 4, pp. 562–570. [Google Scholar]
3. G. S. Bloom and S. W. Golomb. (1978). “Numbered complete graphs, unusual rules, and assorted applications,” in Theory and Applications of Graphs, Lecture Notes in Mathematics, Springer-Verlag, vol. 642, pp. 53–65. [Google Scholar]
4. G. Chartrand, M. S. Jacobson, J. Lehel, O. R. Oellermann, S. Ruiz et al. (1988). , “Irregular networks,” Congressus Numerantium, vol. 64, pp. 187–192. [Google Scholar]
5. J. Lahel. (1991). “Facts and quests on degree irregular assignment,” in Graph Theory, Combinatorics and Applications, New York, NY, USA: Wiley, pp. 765–782. [Google Scholar]
6. D. Amar and O. Togni. (1998). “On irregular strenght of trees,” Discrete Mathematics, vol. 190, no. 1–3, pp. 15–38. [Google Scholar]
7. J. H. Dimitz, D. K. Garnick and A. Gyárfás, “On the irregularity strength of the m × n grid,” Journal Graph Theory, vol. 16, no. 4, pp. 355–374. [Google Scholar]
8. A. Gyárfás, “The irregularity strength of Kmm 4 for odd m,” Discrete Mathematics, vol. 71, pp. 273–274, 1998. [Google Scholar]
9. T. Nierhoff. (2000). “A tight bound on the irregularity strength of graphs,” SIAM Journal on Discrete Mathematics, vol. 13, no. 3, pp. 313–323. [Google Scholar]
10. A. Ahmad, O. Al Mushayt and M. Baa. (2014). “On edge irregularity strength of graphs,” Applied Mathematics and Computation, vol. 243, pp. 607–610. [Google Scholar]
11. M. Bača, S. Jendrolˇ, M. Miller and J. Ryan. (2007). “On irregular total labellings,” Discrete Mathematics, vol. 307, no. 11–12, pp. 1378–1388. [Google Scholar]
12. J. Ryan, B. Munasinghe and D. Tanna. (2017). “Reflexive irregular labeling,”. [Google Scholar]
13. M. Bača, M. Irfan, J. Ryan, A. Semaničová-Feňovčíková, D. Tanna et al. (2019). , “Note On reflexive irregular edge labelings of graphs,” AKCE International Journal of Graphs and Combinatorics, vol. 16, no. 2, pp. 145–157. [Google Scholar]
14. J. Ivančo and S. Jendrolˇ. (2006). “Total edge irregularity strength of trees,” Discussiones Mathematicae Graph Theory, vol. 26, no. 3, pp. 449–456. [Google Scholar]
15. K. Culik. (1958). “Zur Thorie der Graphen,” Casopis Pest. Mat., vol. 83, pp. 133–155. [Google Scholar]
16. P. M. Weichsel. (1962). “The Kronecker product of graphs,” in Proc. of the American Mathematical Society, vol. 18, no. 1, pp. 47–52. [Google Scholar]
17. S. T. Hedetniemi. (1965). “Homomorphisms of graphs,” University of Michigan Technical Report 03105-42-T, December, it is stated there that “the complete report is available in the major Navy technical libraries and can be obtained from the Defense Documentation Center”. [Google Scholar]
18. A. Ahmad and M. Bača. (2014). “On total edge irregularity strength of a categorical product of two paths,” Ars Combinatoria, vol. 114, pp. 203–212. [Google Scholar]
19. A. Ahmad, M. Bača and M. K. Siddiqui. (2014). “On edge irregular total labeling of categorical product of two cycles,” Theory of Computing Systems, vol. 54, no. 1, pp. 1–12. [Google Scholar]
20. P. Victor and M. Chandramouleeswaran. (2018). “Categorical product of two s-valued graphs,” Ars Mathematica Contemporanea, vol. 15, no. 1, pp. 113–126. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |