DOI:10.32604/csse.2021.015700
| Computer Systems Science & Engineering DOI:10.32604/csse.2021.015700 | |
| Article |
A Hybrid Artificial Intelligence Model for Skin Cancer Diagnosis
1Research Scholar, Anna University, Chennai, Tamil Nadu, 600025, India
2Velammal Engineering college, Chennai, Tamil Nadu, 600066, India
*Corresponding Author: V. Vidya Lakshmi. Email: vidyalakshmi.phd@gmail.com
Received: 03 December 2020; Accepted: 06 January 2021
Abstract: Melanoma or skin cancer is the most dangerous and deadliest disease. As the incidence and mortality rate of skin cancer increases worldwide, an automated skin cancer detection/classification system is required for early detection and prevention of skin cancer. In this study, a Hybrid Artificial Intelligence Model (HAIM) is designed for skin cancer classification. It uses diverse multi-directional representation systems for feature extraction and an efficient Exponentially Weighted and Heaped Multi-Layer Perceptron (EWHMLP) for the classification. Though the wavelet transform is a powerful tool for signal and image processing, it is unable to detect the intermediate dimensional structures of a medical image. Thus the proposed HAIM uses Curvelet (CurT), Contourlet (ConT) and Shearlet (SheT) transforms as feature extraction techniques. Though MLP is very flexible and well suitable for the classification problem, the learning of weights is a challenging task. Also, the optimization process does not converge, and the model may not be stable. To overcome these drawbacks, EWHMLP is developed. Results show that the combined qualities of each transform in a hybrid approach provides an accuracy of 98.33% in a multi-class approach on PH2 database.
Keywords: Skin cancer; multi-directional systems; curvelet; contourlet; shearlet; multi-layer perceptron
A Computer Aided Diagnosis (CAD) system can be seen as a system that analyzes medical images or signals and identifies any deviations from the normal patterns. Though building a successful CAD system is very difficult, there are many different approaches taken for building CAD systems for skin cancer diagnosis. Statistical features based systems [1–5] are one of the earliest types of the CAD system. In general, the CAD system relies on the assumption that there exists a statistical disparity between normal and abnormal images. Statistical models developed may take into account individual features [1–5] or studying the interrelationship between pixels [6,7]. Many statistical measures are available to detect abnormalities such as ABCD rule [1], colour [2,4,5], shape [3], and texture features [3,4], local binary pattern [6] and Haralick features [7]. However, the overlapping measures could lead to low classification results. Reviews on different use of statistics to develop a CAD system is discussed in Maglogiannis et al. [8].
Recently, frequency domain analysis in the medical domain leads to the development of CAD system using spectral features such as wavelet-based analysis [9], multi-wavelet analysis [10], curvelet [11] and contourlet [12]. The various textural features such as singularities, curves and contours in smooth and non-smooth regions of medical images are represented by the analysis as mentioned above based on the filters used in the decomposition stage and their arrangements. With the different advantages offered by the different analyses, it is very difficult to identify a single approach that is the most successful. More recently, many researchers have moved towards building hybrid supervised CAD. By fusing different techniques to tackle different components of CADs, they hope to overcome some of the disadvantages that a specific technique possesses while retaining any advantage. To achieve this goal, a HAIM is developed that combines three multi-directional representation systems.
The available CAD systems can be categorized into supervised or unsupervised systems based on the classifier used in the detection stage. Currently, neural network based supervised CAD systems [13–19] are most successful. However, they are not very efficient at learning and adopting continuous changes. A review of different implementations of neural networks for skin cancer diagnosis is provided in Brinker et al. [20]. Also, support vector machine [6,10,21], Bayes [11], Random forest [21], AdaBoost [12] and k-nearest neighbour [21] supervised classifiers also used in skin cancer diagnosis. A Self Organizing Map (SOM) [22] is a method of unsupervised learning that differs from other neural network techniques in that the desired output need not be specified. Instead, it can cluster a variety of training inputs and compare the testing data to it. CAD systems to segment the abnormalities for skin cancer detection are SOM [22] and Fuzzy c-means algorithm [23].
This study aims to build an effective dermoscopic image classification system to diagnose skin cancer. To achieve this goal, a HAIM is developed for dermoscopic image classification that combines three multi-directional representation systems with a modified MLP for successful classification. The rest of the paper is organized as follows: In Section 2, the development of HAIM is described with the mathematical backgrounds of directional systems such as CurT, ConT and SheT and EWHMLP. In Section 3, the investigation of the performance of HAIM is described, and the key findings are highlighted, and the final Section 4 provides a summary of this study.
An automated skin cancer detection/classification system is required for early detection and prevention of skin cancer. In this study, skin cancer classification from dermoscopic images is considered as a multi-class classification problem with the help of HAIM. It uses diverse multi-directional representation systems for feature extraction and EWHMLP for the classification. Fig. 1 shows the overall approach for skin cancer classification by the proposed HAIM.
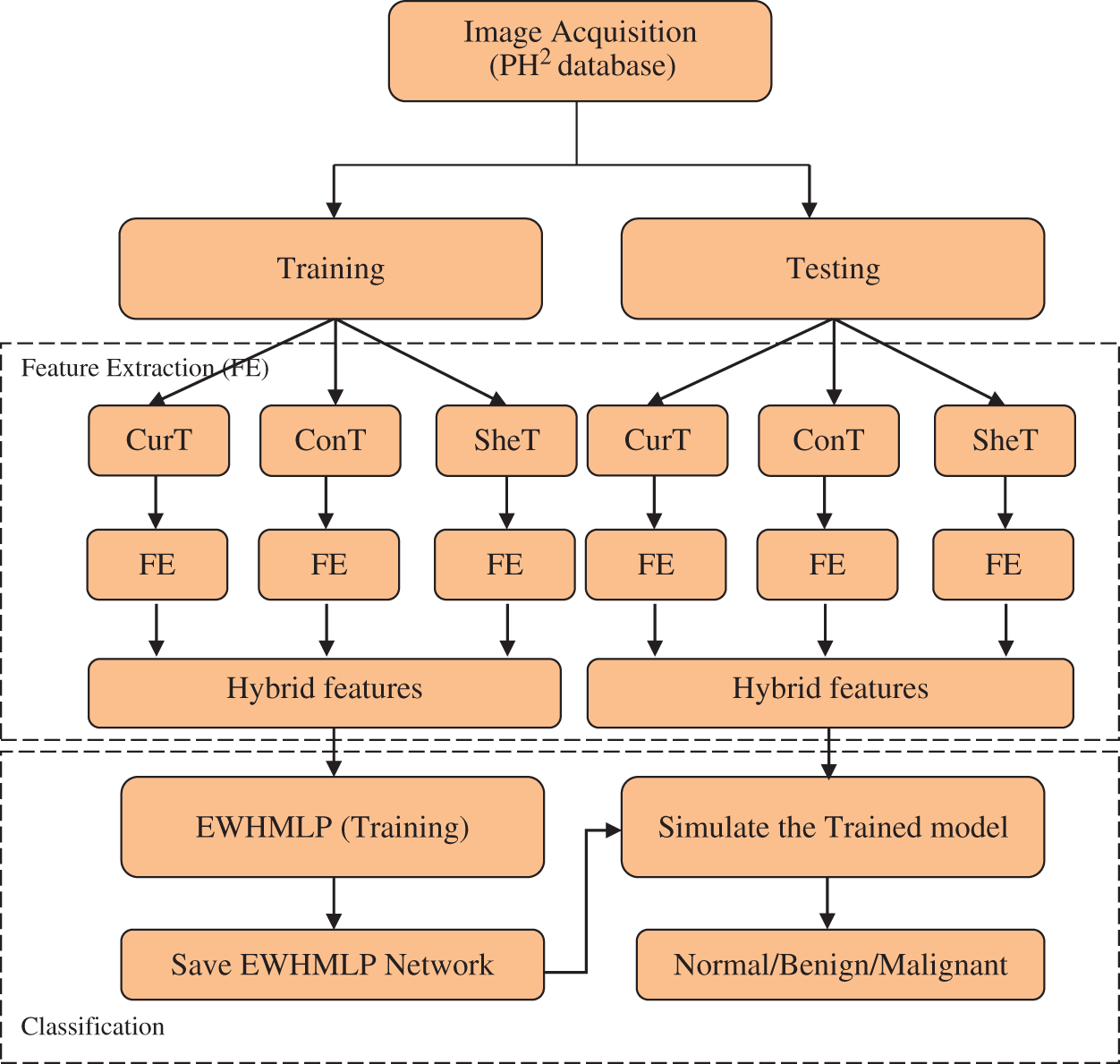
Figure 1: HAIM for skin cancer classification
Though the wavelet transform is a powerful tool for signal and image processing, it is unable to detect the intermediate dimensional structures of a medical image. Thus the proposed HAIM uses CurT [24], ConT [25] and SheT [26] transforms as feature extraction techniques. Among these diverse multi-directional representation systems, CurT provides optimal sparse representation on curved singularities, whereas ConT transform provides the same on contours as well. Also, the SheT transform can detect non-smooth corner points where the CurT and ConT fail. Hence, the textural features extracted from these systems provide information about the different kinds of tissues in the medical images that are separated by non-smooth and smooth curves. It is well known that better system performance can be achieved when combining the qualities of each technique in a hybrid approach.
In general, the Multi-Scale Analysis (MSA) of any signal is controlled by translation and scaling functions and is given by,
where the translation operator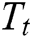 
is defined by 
. Different MSA can be developed by defining a new scaling operator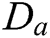 
at scale a. In CurT, parabolic dilation is introduced which is in the form of Donoho et al. [24]
where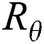 
is a 2 × 2 rotation matrix which shows the rotation by 
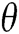radians. Using the parabolic dilation in Eq. (2), the CurT family by a basic element 
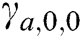is generated [24].
where scale a > 0, orientation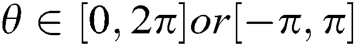 
and b is the location. Based on the above details, CurT can be defined as Donoho et al. [24]
Though the construction of CurT in the continuous domain is simple, the discretized construction is very difficult, i.e., the critical sampling in a rectangle grid. To overcome this, ConT is developed in the discrete domain directly, which uses the Directional Filter Bank (DFB) and Laplacian Pyramid (LP). The decomposition by LP algorithm generates a low pass image and bandpass images. To get directional information, the bandpass images are further decomposed by DFB. The translation of impulse responses of synthesis filters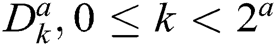 
in DFB provides a family of filters in Eq. (5) that provides both localization and directional properties [25].
where S is the sampling lattices in the space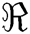 
. Though CurT and ConT locate the boundaries precisely, they are unable to detect the non-smooth corner points on the curve. The SheT has the ability to detect them and the scaling operator 
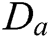is multiplied by the shearing matrix (s). It is defined by
where
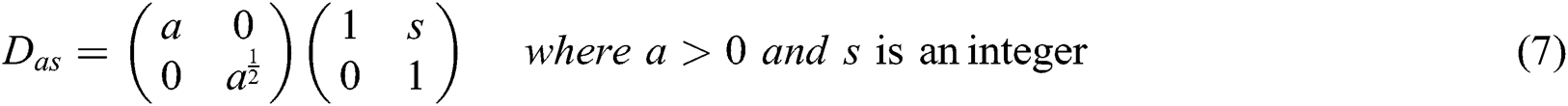
The frequency planes induced by CurT, ConT and SheT are shown in Fig. 2. More information about CurT can be found in Donoho et al. [24] and for ConT in Do et al. [25] and SheT in Lim [26]. To avoid the high dimensional feature space in the form of sub-bands for a particular level of representation of these systems, energies of each sub-band are extracted as features, and all are hybridized serially. The mean of the magnitude of directional sub-bands in each transform is computed as its energy and also used as features. The extracted energy feature EF, from the sub-band B of size M × N from the transformations such as CurT, ConT and SheT is defined by
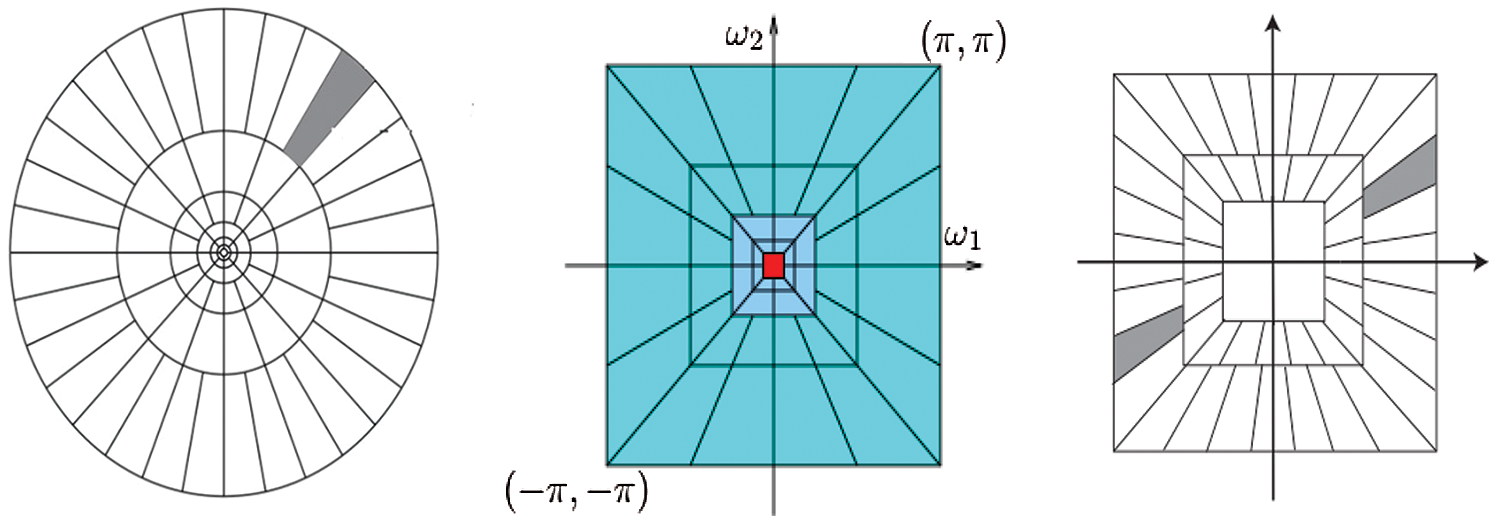
Figure 2: Frequency plane by CurT (Left Image) [24], ConT (Middle Image) [25] and SheT (Right Image) [26]
As the dermoscopic images contain unwanted information such as noise and hairs, a preprocessing step is required to remove them before feature extraction. This increases the performance of the system as the features are extracted only from the abnormalities in the skin. A simple and effective median filtering approach is used to remove noises in the dermoscopic images. Fig. 3 shows the sample acquired dermoscopic images and their corresponding median filtered images.
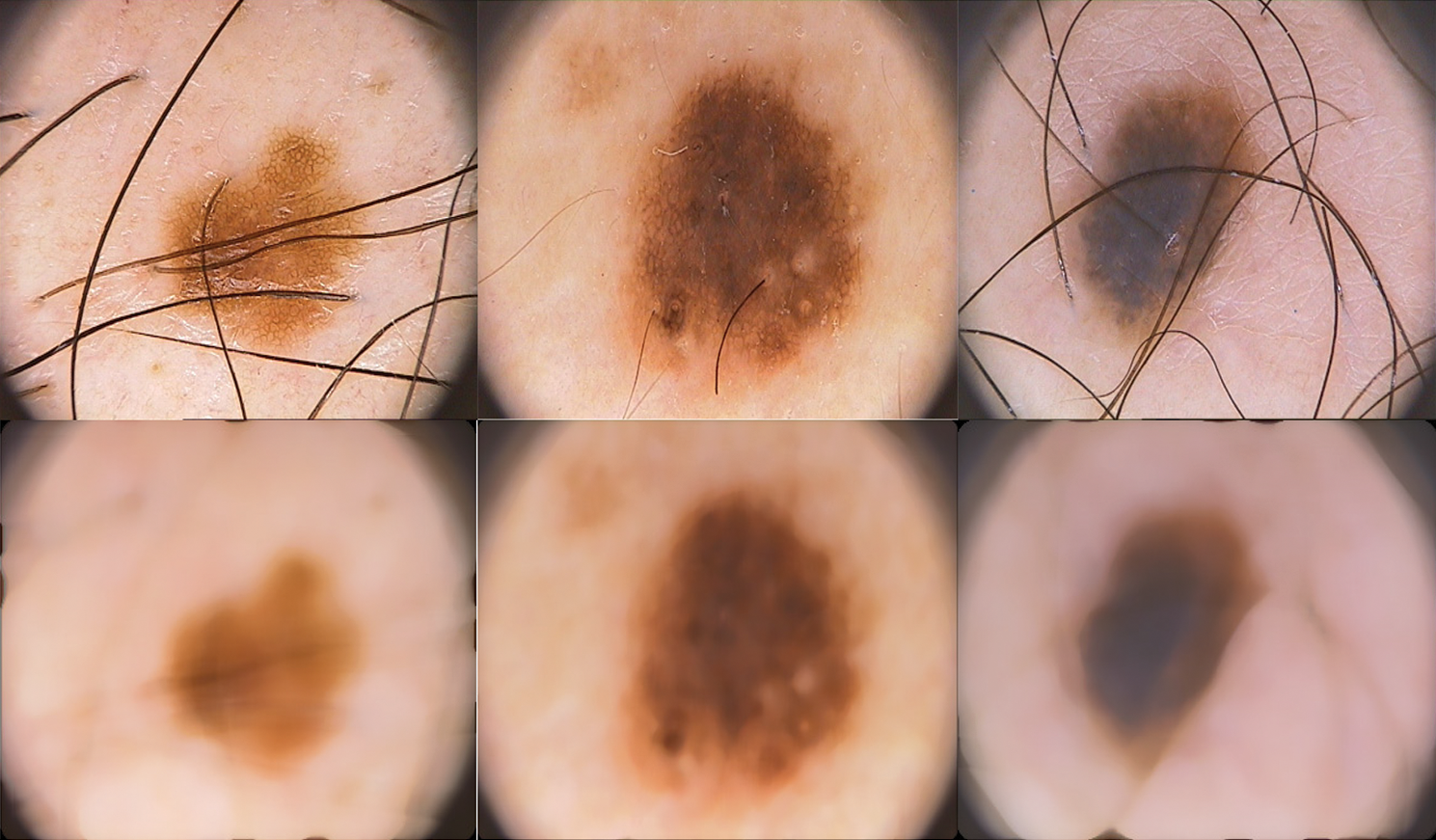
Figure 3: Acquired dermoscopic images (top row) and preprocessed dermoscopic images (bottom row)
Neural network based CADs are probably the most successful supervised based medical diagnosis system [13–19] in terms of their accuracy. In general, a neural network based CAD works as follows: The memory of the system is the neural network. The neural network consists of a set of artificial neurons, with input and output units. In between the input and output units is a set of neurons. The neurons are connected by a set of edges, and through training with normal data, the network organizes itself by determining the ‘strength’ of these connections. Decision making is determined by the network. Given an input for testing, the network determines the output decision (i.e., either normal or abnormal). One of the implementations of a neural network based supervised CAD employs an MLP approach. As MLP is very flexible and well suitable for the classification problem, the proposed HAIM for skin cancer classification model uses MLP as a base model.
The learning of weights is a challenging task in the MLP model and has many good solutions. Due to this stochastic nature, the optimization process does not converge, and the model may not be stable. To overcome these drawbacks, EWHMLP is developed. Tab. 1 shows the MLP parameters used in EWHMLP.
Table 1: MLP parameters used in this study
The assignment of weights of designed EWHMLP is as follows: The first step is to run the base MLP model and find the best one which gives a more optimistic and realistic performance on the given dataset. To obtain the weights for the proposed EWHMLP, the weights from the last ten epochs are kept during the training process. For each layer, the weighted average is calculated based on the weights of each model for the same layer. Finally, the exponential average weight is assigned to the new MLP model with different decay rates to achieve stable and more accurate architecture for skin cancer classification. Fig. 4 shows the architecture of EWHMLP. The ReLu function returns the input value directly or zeroes if the input is less than 0 which is defined as
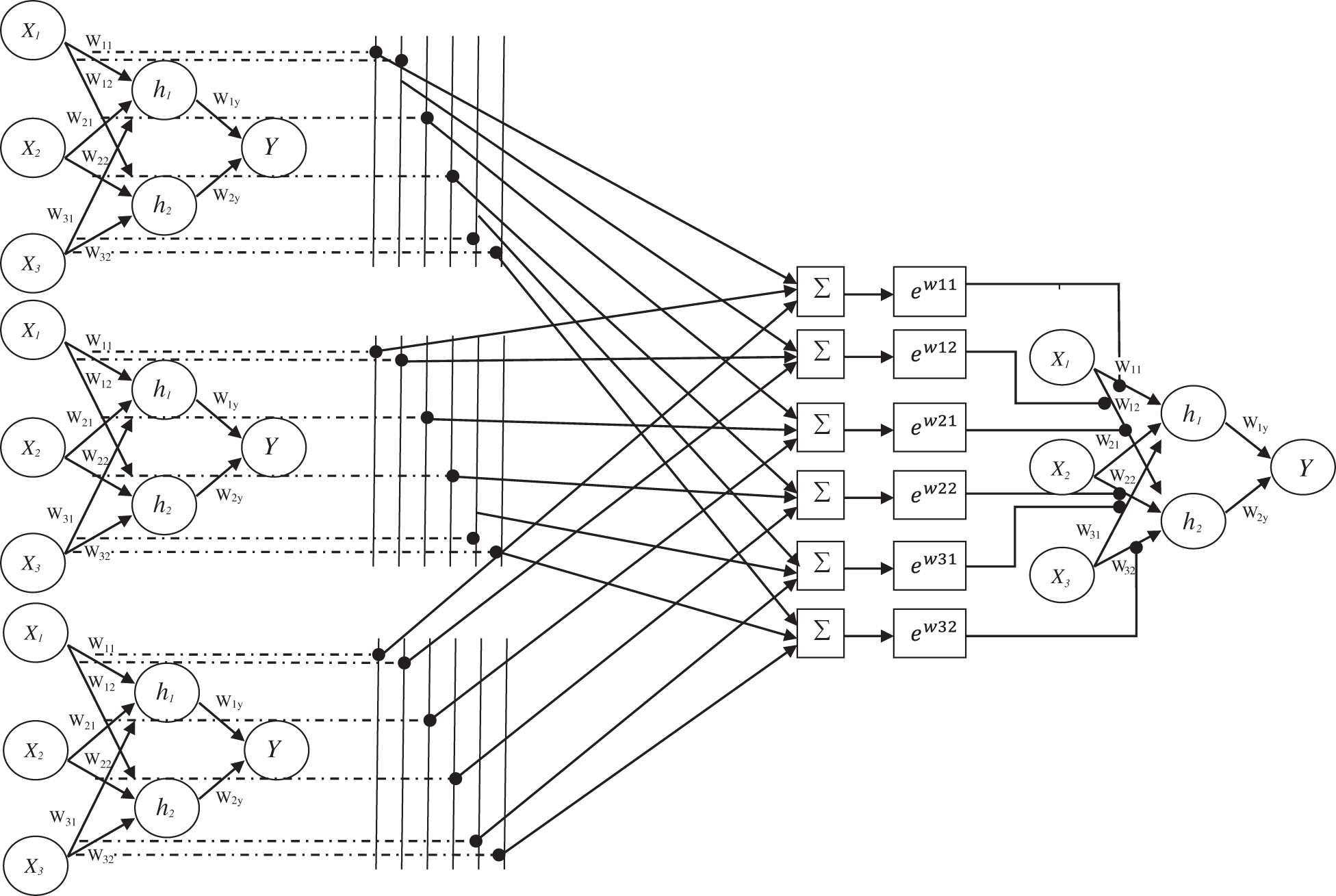
Figure 4: Architecture of EWHMLP
Among the different activation functions such as sigmoid, tanh and softmax function used in the output layer, softmax function is chosen as it supports multiclass classification whereas other functions are mainly used in binary classification. Also, the network gets stuck while using sigmoid function at training. The softmax function in the output layer j for the input layer i is defined as
Finally, the class which has a high probability is assigned as a predicated class.
In this section, the new HAIM for skin cancer diagnosis is explored empirically. Firstly, how the data is set up for the experiments and then investigates the ability of HAIM for classification.
3.1 Experimental Data and Setup
The proposed HAIM for skin cancer diagnosis is analyzed using the PH2 database [27,28]. The database has 80 normal, 80 benign and 40 malignant images and each dermoscopic image is of resolution 768 × 560 pixels. Fig. 5 shows sample images in the database. In order to test the ability of HAIM from experimental data, the training data need to be provided periodically so that HAIM learns continuously. Also, there has to be different training data between periods. To achieve this, 10-fold cross-validation is employed, and HAIM is run over a number of periods (ten times). At each period, HAIM is provided with a batch of training data. A new EWHMLP trained network is generated to diagnose skin cancer. Fig. 6 shows the learning procedure for HAIM.
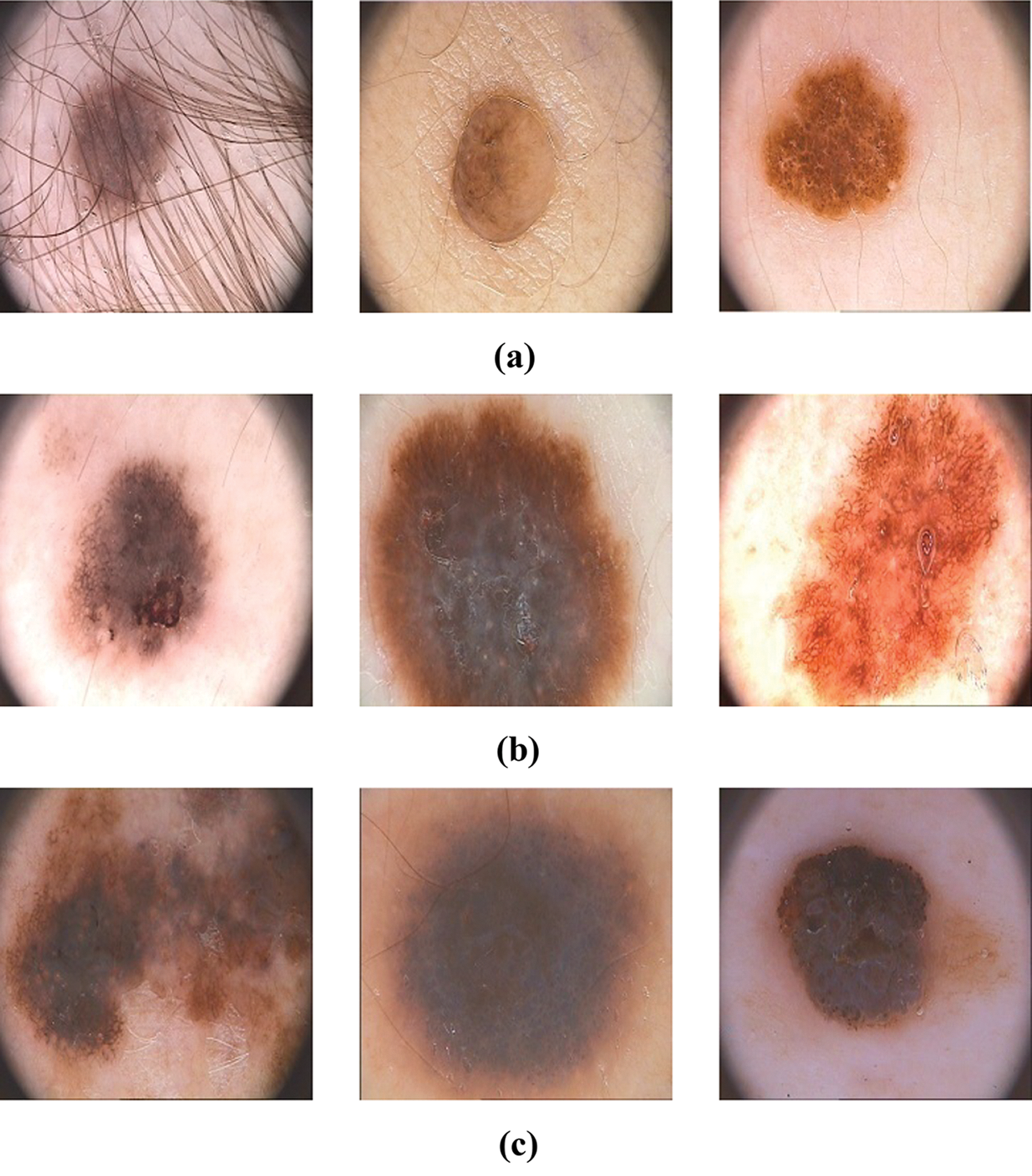
Figure 5: Sample images in the PH2 database (a) Normal (b) Benign (c) Malignant
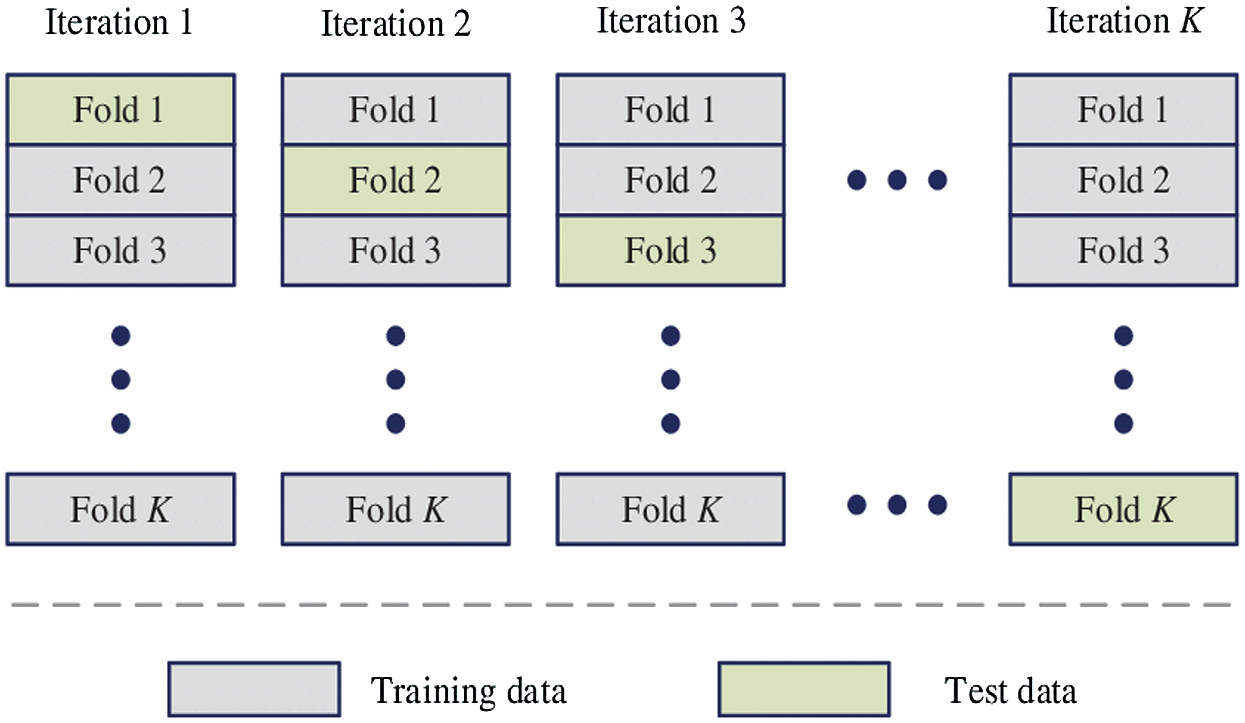
Figure 6: Learning procedure of HAIM
In order to provide HAIM with sufficient number of training data, the database is partitioned into ten folds. Each fold can then be fed into HAIM sequentially, starting from 1st fold to 10th fold. The ten folds of data provide a good scenario for testing the classifier with different training images. The ten folds are determined as follows:
Firstly, all normal images (80) is split into ten folds where the first fold contains the first eight (8) normal images and the second fold contains the second eight (8) normal images and so forth the final fold contains the remaining normal images. This process is repeated for benign and malignant group of images as well. It is intended that each fold is given to HAIM for testing and remaining fold for training starting from the first fold through to 10th fold. This implies that all images in the database are exploited into the training and testing phase of the system.
The performance of HAIM is evaluated based on its classification accuracy, sensitivity and specificity at each fold. The computations of these parameters are illustrated in Tab. 2
Table 2: Illustration of the confusion matrix of the 3-class problem
It is observed from Tab. 2 that the confusion matrix parameters are obtained for each class, and thus, the performance metrics can be computed for each class involved in this study. The overall performance of the system can be obtained by averaging the performances. Tab. 3 shows the performance metrics involved in this study.
There are mainly two parameters that affect the performance of HAIM. They are the level or scale of decomposition and the number of directional features. A set of experiments is carried out with varying these two parameters for each multi-directional representation system before hybridizing them. At first, the dermoscopic images are represented by CurT into five different scales from 1 to 5 and 8 different angles. Then, the energies are computed from the curvelet coefficients at each orientation and later concatenated to construct the input feature vector. After the feature construction, the modified MLP, EWHMLP is employed to classify the dermoscopic images into normal, benign or malignant. Tab. 4 shows the performance of CurT- EWHMLP for dermoscopic image classification.
Table 4: Performance of CurT- EWHMLP for dermoscopic image classification
As the level of CurT representation of dermoscopic images increases, the performance of CurT- EWHMLP increases. This is because increasing CurT representation increases the number of features for training, and hence there are more chances to increase the performance. A maximum of 87.33% accuracy is attained at 3rd level CurT representation. When the representation of dermoscopic images by CurT increases above 3rd level, it provides redundant information. This causes a fall in the correct classification, which in turn reduces the system performance. After analyzing the performance of EWHMLP by CurT, the same set of experiments are repeated for ConT representation of skin images. Tab. 5 shows the performance of ConT- EWHMLP for dermoscopic image classification.
Table 5: Performance of ConT- EWHMLP for dermoscopic image classification
It can be seen from Tabs. 4 and 5 that a significant improvement is observed over CurT. It is reasonable to expect that the ConT features would lead to higher accuracy of 92% since it provides texture information on contour as well. Also, it is noted that 7.5% and 3.6% increase in sensitivity and specificity is attained by ConT based features over CurT at 3rd level representation. Tab. 6 shows the performance of SheT- EWHMLP for dermoscopic image classification. In this study, 32 directional features are extracted in each level of representation.
Table 6: Performance of SheT- EWHMLP for dermoscopic image classification
It can be seen that there is a large variation in the performance of SheT- EWHMLP system over CurT- EWHMLP and ConT- EWHMLP. This is because of the ability of SheT to detect smooth and non-smooth corner points and curvature in the dermoscopic images. It is observed that the SheT features provide 96% accuracy, 93.75% sensitivity and 97.01% specificity. In order to further analyze the system, the system uses features from the above three representation systems. Tab. 7 shows the performance of HAIM- EWHMLP for dermoscopic image classification.
Table 7: Performance of HAIM- EWHMLP for dermoscopic image classification
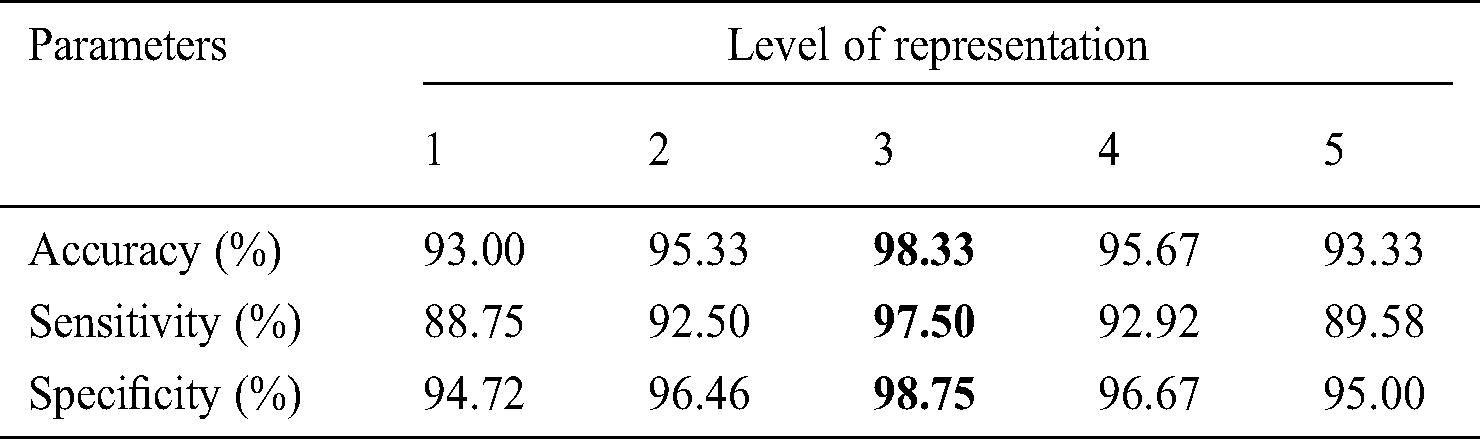
It can be inferred from Tab. 7 that the HAIM provides the highest accuracy of 98.33% for the same dataset for training EWHMLP classifier. The combined texture features from the three representation systems increase the accuracy to a maximum when compared to their counterpart. It can be noticed from Tabs. 3–7 that the performance of features of 1st and 2nd representation levels are low compared to other levels. This is because the features that can be generated are not capable of classifying the skin images. Tab. 8 shows the number of features extracted from each transform and used for performance analysis in each model.
Table 8: Performance of HAIM- EWHMLP for dermoscopic image classification
Fig. 7 shows a summary of the best performance obtained from each transform and HAIM. A comparative study is also made to analyze the performance of the HAIM further. Fig. 8 shows the comparative analysis with the NN ensemble approach [18], SVM with colour and texture features [4] and Bayes with ConT features [12]. It can be seen from Fig. 8 that the HAIM outperforms other classification methods for skin cancer diagnosis.
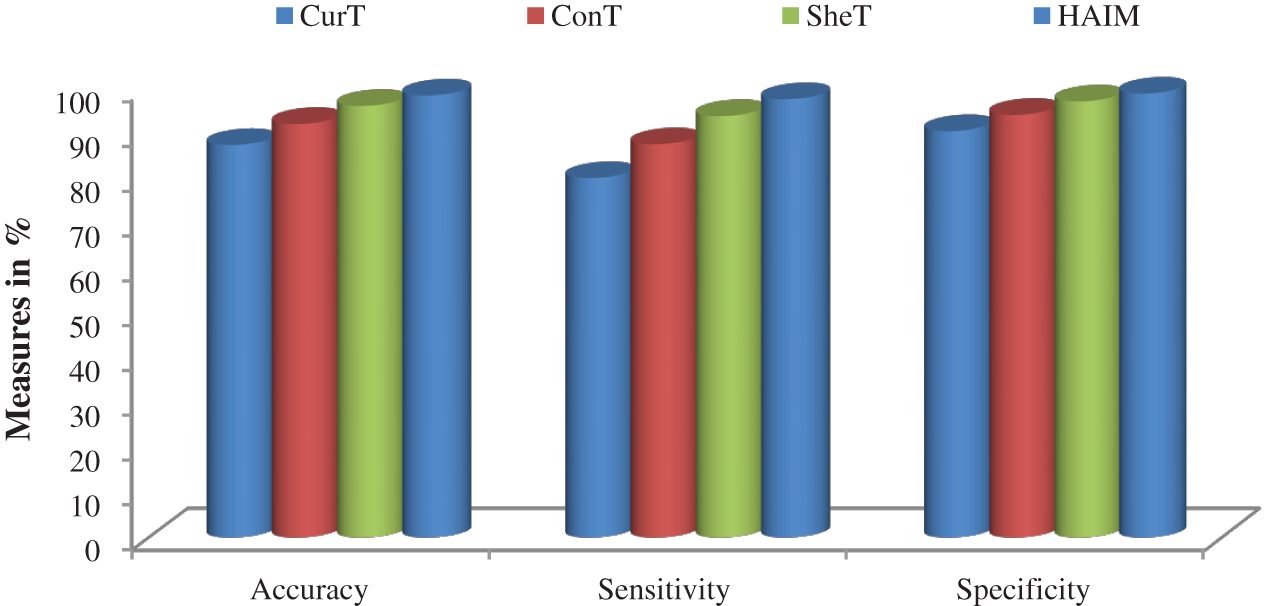
Figure 7: Best performance attained by the features of CurT, ConT, SheT and HAIM with EWHMLP
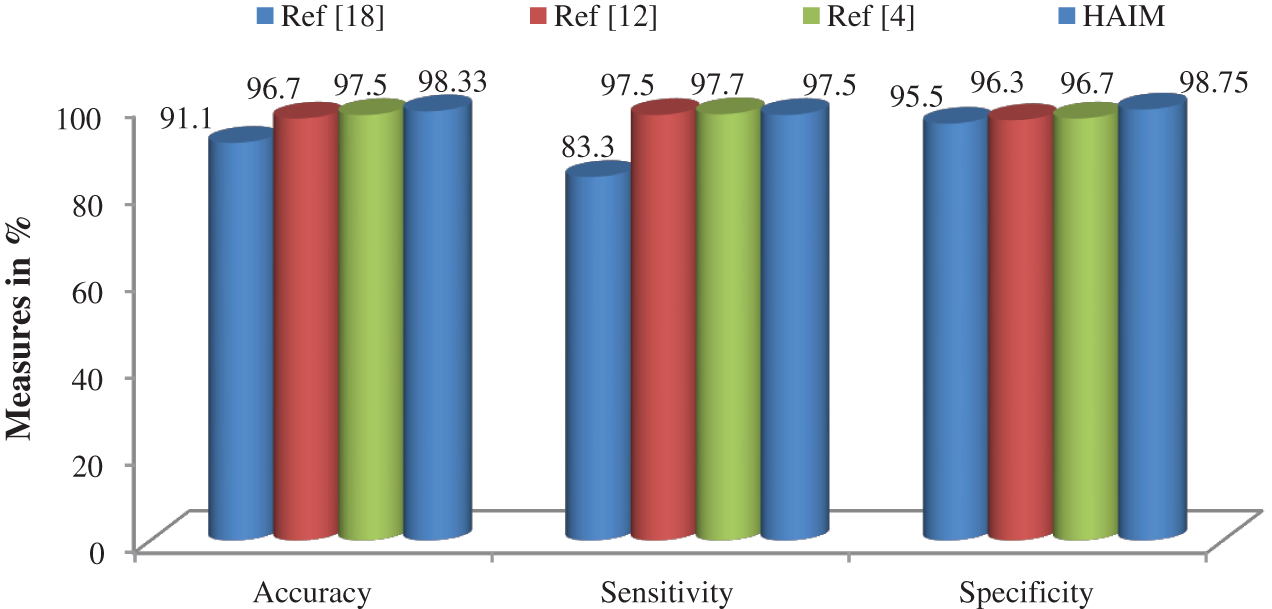
Figure 8: Comparative analysis
The use of coupling of features from three multi-directional representation systems with a modified MLP can lead to the development of an effective HAIM for the problem of skin cancer diagnosis. Also, the classification results obtained using HAIM are shown to be more comprehensible. Three transforms; CurT, ConT and SheT are used in the feature extraction stage, and EWHMLP is developed for classification. The drawbacks of existing MLP algorithm such as learning of weights and the optimization problem are reduced by the EWHMLP. A series of experiments are conducted to test the effectiveness of HAIM for dermoscopic image classification. It is demonstrated using PH2 dataset that HAIM improves on the accuracy of existing systems to diagnose skin cancer and successfully reduce the false positive rate.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. W. Stolz, A. Riemann and A. Cognetta. (1994). “ABCD rule of dermatoscopy: A new practical method for early recognition of malignant melanoma,” European Journal of Dermatology, vol. 4, pp. 521–527. [Google Scholar]
2. T. Schindewolf, W. Stolz and R. Albert. (1993). “Classification of melanocytic lesions with color and texture analysis using digital image processing,” American Society of Cytology, vol. 15, pp. 1–11. [Google Scholar]
3. M. E. Celebi, H. A. Kingravi, B. Uddin, H. Iyatomi, Y. A. Aslandogan et al. (2007). , “A methodological approach to the classification of dermoscopy images,” Computerized Medical Imaging and Graphics, vol. 31, no. 6, pp. 362–373. [Google Scholar]
4. M. Nasir, M. Attique Khan, M. Sharif, I. U. Lali, T. Saba et al. (2018). , “An improved strategy for skin lesion detection and classification using uniform segmentation and feature selection based approach,” Microscopy Research and Technique, vol. 6, no. 6, pp. 528–543. [Google Scholar]
5. M. E. Celebi and A. Zornberg. (2014). “Automated quantification of clinically significant colors in dermoscopy images and its application to skin lesion classification,” IEEE Systems Journal, vol. 8, no. 3, pp. 980–984. [Google Scholar]
6. F. Adjed, I. Faye, F. Ababsa, S. J. Gardezi and S. C. Dass. (2016). “Classification of skin cancer images using local binary pattern and SVM classifier,” AIP Conference Proceedings, vol. 1787, no. 1, pp. 080006. [Google Scholar]
7. F. Ghali. (2019). “Skin cancer diagnosis by using fuzzy logic and GLCM,” Journal of Physics: Conference Series, vol. 1279, no. 1, pp. 012020. [Google Scholar]
8. I. Maglogiannis and C. Doukas. (2009). “Overview of advanced computer vision systems for skin lesions characterization,” IEEE Transactions on Information Technology in Biomedicine, vol. 13, no. 5, pp. 721–733. [Google Scholar]
9. R. Garnavi, M. Aldeen and J. Bailey. (2012). “Computer-aided diagnosis of melanoma using border- and wavelet-based texture analysis,” IEEE Transactions on Information Technology in Biomedicine, vol. 16, no. 6, pp. 1239–1252. [Google Scholar]
10. S. Kumarapandian. (2018). “Melanoma classification using multiwavelet transform and support vector machine,” International Journal of MC Square Scientific Research, vol. 10, no. 3, pp. 01–07. [Google Scholar]
11. M. Machado, J. Pereira and R. Fonseca-Pinto. (2016). “Reticular pattern detection in dermoscopy: An approach using curvelet transform,” Research on Biomedical Engineering, vol. 32, no. 2, pp. 129–136. [Google Scholar]
12. R. Sonia. (2016). “Melanoma image classification system by NSCT features and Bayes classification,” International Journal of Advances in Signal and Image Sciences, vol. 2, no. 2, pp. 27–33. [Google Scholar]
13. M. A. Albahar. (2019). “Skin lesion classification using convolutional neural network with novel regularizer,” IEEE Access, vol. 7, pp. 38306–38313. [Google Scholar]
14. N. Moura, R. Veras, K. Aires, V. Machado, R. Silva et al. (2019). , “ABCD rule and pre-trained CNNs for melanoma diagnosis,” Multimedia Tools and Applications, vol. 78, no. 6, pp. 6869–6888. [Google Scholar]
15. A. Mahbod, G. Schaefer, C. Wang, R. Ecker and I. Ellinge. (2019). “Skin lesion classification using hybrid deep neural networks,” in IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSPBrighton, United Kingdom, pp. 1229–1233. [Google Scholar]
16. M. Q. Khan, A. Hussain, S. U. Rehman, U. Khan, M. Maqsood et al. (2019). , “Classification of melanoma and nevus in digital images for diagnosis of skin cancer,” IEEE Access, vol. 7, pp. 90132–90144. [Google Scholar]
17. S. Serte and H. Demirel. (2019). “Gabor wavelet-based deep learning for skin lesion classification,” Computers in Biology and Medicine, vol. 113, pp. 103423. [Google Scholar]
18. F. Xie, H. Fan, Y. Li, Z. Jiang, R. Meng et al. (2017). , “Melanoma classification on dermoscopy images using a neural network ensemble model,” IEEE Transactions on Medical Imaging, vol. 36, no. 3, pp. 849–858. [Google Scholar]
19. S. Justin and M. Pattnaik. (2020). “Skin lesion segmentation by pixel by pixel approach using deep learning,” International Journal of Advances in Signal and Image Sciences, vol. 6, no. 1, pp. 12–20. [Google Scholar]
20. T. J. Brinker, A. Hekler, J. S. Utikal, N. Grabe, D. Schadendorf et al. (2018). , “Skin cancer classification using convolutional neural networks: Systematic review,” Journal of Medical Internet Research, vol. 20, no. 10, pp. e11936. [Google Scholar]
21. A. Murugan, S. A. H. Nair and K. S. Kumar. (2019). “Detection of skin cancer using SVM, random forest and kNN classifiers,” Journal of Medical Systems, vol. 43, no. 8, pp. 269–275. [Google Scholar]
22. A. D. Mengistu and D. M. Alemayehu. (2015). “Computer vision for skin cancer diagnosis and recognition using RBF and SOM,” International Journal of Image Processing, vol. 9, no. 6, pp. 311–319. [Google Scholar]
23. A. R. Ali, M. S. Couceiro and A. E. Hassenian. (2014). “Melanoma detection using fuzzy C-means clustering coupled with mathematical morphology,” in 14th International Conference on Hybrid Intelligent Systems, Kuwait, pp. 73–78. [Google Scholar]
24. D. Donoho and E. Candes. (2005). “Continuous curvelet transform: II. Discretization and frames,” Applied and Computational Harmonic Analysis, vol. 19, no. 2, pp. 198–222. [Google Scholar]
25. M. N. Do and M. Vetterli. (2005). “The contourlet transform: An efficient directional multiresolution image representation,” IEEE Transactions on Image Processing, vol. 14, no. 12, pp. 2091–2106. [Google Scholar]
26. W. Q. Lim. (2010). “The discrete shearlet transform: A new directional transform and compactly supported shearlet frames,” IEEE Transactions on Image Processing, vol. 19, no. 5, pp. 1166–1180. [Google Scholar]
27. T. Mendonça, P. M. Ferreira, J. S. Marques, A. R. Marcal and J. Rozeira. (2013). “PH2-A dermoscopic image database for research and benchmarking,” in 35th Annual International Conference on Engineering in Medicine and Biology Society, Osaka, Japan, pp. 5437–5440. [Google Scholar]
28. PH2 Database Link. Available: https://www.fc.up.pt/addi/ph2%20database.html. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |