Computer Systems Science & Engineering DOI:10.32604/csse.2021.014130
Article

Optimal Solution of Fuzzy Transportation Problem Using Octagonal Fuzzy Numbers

D. Gurukumaresan1,*, C. Duraisamy1 and R. Srinivasan2

1Department of Mathematics, Kongu Engineering College, Erode, 638060, India
2Department of Ancient Science, Faculty of Science, Tamil University, Thanjavur, 613010, India
*Corresponding Author: D. Gurukumaresan. Email: gurukumaresan2020@gmail.com
Received: 01 September 2020; Accepted: 13 January 2021

Abstract: In this paper a fuzzy transportation problem under a fuzzy environment is solved using octagonal fuzzy numbers. The transportation problem is significant and has been widely studied in the field of applied mathematics to solve a system of linear equations in many applications in science. Systems of concurrent linear equations play a vital major role in operational research. The main perspective of this research paper is to find out the minimum amount of transportation cost of some supplies through a capacitated network formerly the availability and the demand notes are octagonal fuzzy numbers. Octagonal fuzzy numbers are used and showed a membership function. To illustrate this method, a fuzzy transportation problem is solved by using octagonal fuzzy numbers using the ranking technique. It is shown that it is the best optimal solution and it is demonstrated with a numerical example.

Keywords: Linear equation; transportation problem; fuzzy transportation problem; ranking technique; trapezoidal fuzzy numbers

1  Introduction

Transportation problems (TPs) encompass possibly the most pro use of interest research. Transportation models consist of full applications within the stock and-provide chain to lowering the well worth calculations which are had been produced for finding out a TP once the price coefficients and consequently the natural market quantities are known explicitly. The commonness of global irregularity and estimation is unavoidable due to sudden situations. There exists rectangular-measure cases in which the really worth coefficients just because the offer-and-request quantities of a TP ought to likewise be dubious due to some factors. To manage unfastened data in selecting alternatives [1], the idea of fluffiness changed into offered. In Ref. [2], a fuzzy set speculation changed into created. In Ref. [3], fuzzy straight fragmentary writing pc programs was brought wherein usage of fuzzy transportation troubles turned into furthermore applicable to transportation fashions and vast global problems addressed. A fuzzy TP is probably one at which the transportation expenses and deliver and-request area devices are fuzzy amounts. Amaliah and Fatichah [4] added an underlying vital possible arrangement (IBFS), that is one of the significant strides in obtaining a really perfect answer for TP. As a characteristic of this examination paintings, a proposed new technique called TOCM-MT turned into created to decide the IBFS of TPs. The TOCM-MT is coded using the C++ programming language and may accomplish an all out expense, which incorporates values similar or nearer to the right association. In Ref. [4], a method was developed for solving the feasibility of a new fuzzy method and finding the IBFS for a fuzzy TP. In Ref. [5], an algorithm was developed for solving the intuitionistic fuzzy TP. In Ref. [6], an innovative approach was presented to optimize TPs using generalized trapezoidal numbers in a fuzzy environment. After this pioneering work, many authors [7–10] proposed many different methods for obtaining the solution of fuzzy TPs. In Ref. [11], the idea of the optimum answer for TPs with a fuzzy constant expressed as fuzzy numbers was advanced. A solution for a fully fuzzy TP was presented in Ref. [12], while a solution for a fuzzy TP using the zero-points maximum allocation method was given in Muruganandam and Srinivasan [13]. A fuzzy linear fractional programming method was given in [14–16], in which utilization of fuzzy TPs is additionally applicable to being modeled and to solve important global TPs. A fuzzy TP may be a TP in which the transportation prices and provide-and-demand area units are fuzzy quantities. In Ref. [17], a solution for a fully fuzzy TP was presented. In Ref. [18], a solution of a fuzzy TP problem using the zero-point maximum allocation method was given. Zadeh [19] advanced the idea of a higher cognitive process in fuzzy surroundings and Zimmermann [20] developed a fuzzy set theory.

2  Preliminaries

In this section, we are using various basic definitions.

2.1 Definition – Fuzzy Set

The fuzzy set is defined by 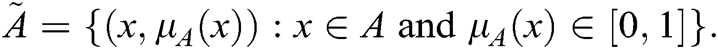Where is called the membership function [16].

2.2 Definition – Octagonal Fuzzy Number

A fuzzy number is a octagonal fuzzy number denoted by ,

= (a1, a2, a3, a4, a5, a6, a7, a8) are where (a1, a2, a3, a4, a5, a6, a7, a8) real numbers and its membership function [19] are given by

where

2.3 Definition – Ranking Technique

A positioning procedure that fulfills praise, linearity and addictive homes offers consequences that depend upon human instinct. If ã is a fuzzy number [16,17], after that the place is distinct by .

3  Formulation of Fuzzy Linear Programming

The fuzzy linear programming (LP) model [18–20], can be expressed as follows:

“Minimize

Subject to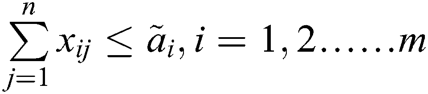

”

Here, for all “” and “” are assumed to be positive, “” are commonly known as resources, and are commonly known as demands. The fuzzy costs, “”, are all non-negative. If “”, then the given problem is balanced TP. If this above mentioned condition is not satisfied, introduced a dummy origin or destination is to balance the problem. The proposed new method does not require the TP to be balanced later; it can be applied to both balanced and unbalanced TPs. The constraint set (1) is represented as “≤” and the constraint set (2) as “≥”, instead of ‘=’, for both cases in a balanced problem. This is one of the advantages of the proposed method, which is called the “stepping stone” method. The unbalanced problem is not required to be converted into a balanced problem, and no dummy origin or destination is introduced, so time and space are saved.

Let the TP consist of m origins and n destinations, where

= is the number of goods transported from the ith origin to the jth destination

is cost involved in transporting per unit product from the ith origin to the jth destination,

is the number of units available at the ith origin and

is the number of units required at the jth destination

4  Mathematical Formulation of Fuzzy TP

Mathematically, a TP can be stated as follows.

“Minimize

subject to

where is the cost of transportation of a unit from the ith resource to the jth destination, and the quantity is to be some positive integer or zero, which is to be transported from the ith origin to the jth destination. A visible necessary and sufficient condition that the linear programming problem given in (1) has a solution

Mathematically, a fuzzy TP can be explicitly expressed as follows.

Minimize

subject to

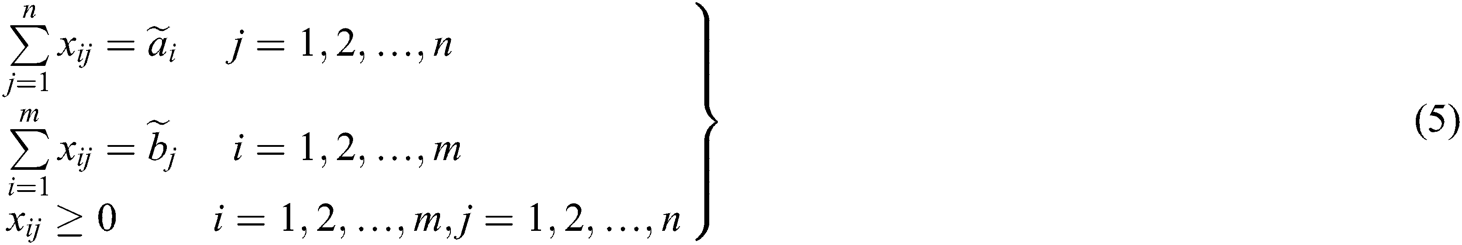
in which the transportation costs , supply and demand quantities are fuzzy quantities. An obvious necessary and sufficient condition for the fuzzy linear programming problem given in (4) and (5) to each a solution is that

This problem can also be represented as shown in Tab. 1.

Table 1: Problem Statement

5  Method for Solving TP

The following steps are used to solve the TP

Step – 1: From the given TP, switch the values in fuzzy to crisp using the ranking function.

Step – 2: Find the minimum cell values from each of the cell value of every row/column of the TP and place them on the right-top/right-bottom of the corresponding cost.

Step – 3: Add the right-top and right-bottom values and place the summation value in the corresponding cell value.

Step – 4: Identify the smallest element in each row and column of the transportation table and subtract from their corresponding row and column.

Step – 5: Calculate the sum the values in the rows and columns. Choose the maximum value and assign the minimum value of supply/demand in the smallest element of the rows and columns. Remove the columns or rows corresponding to where the supply or demand is satisfied.

Step – 6: Repeat steps 4 and 5 until the supply-and-demand is totally met.

Step – 7: Replace the original transportation value with the satisfied cell value.

Step – 8: Workout the minimum cost.

(i.e.), Total Cost = “”

5.1 Numerical Example

Tab. 2 shows the fuzzy transportation table

Table 2: Fuzzy Transportation Table

5.2 Solution

The octagonal fuzzy numbers are converted into crisp numbers presented in Tab. 3 with using the proposed ranking method.

Table 3: Iteration – 1

With the help of the proposed algorithm, the optimal solution is obtained and shown in Tab. 4

Table 4: Optimal solution

The total cost of the IBFS is calculated as a below total cost of 120, which is a basic feasible solution. The solution was obtained using the NCM, LCM, VAM and MODI/stepping stone methods separately. Hence, the basic feasible solution obtained using the proposed method is a free solution.

6  Conclusions

In this research paper, a method for solving octagonal fuzzy numbers is projected to solve the fuzzy optimal solutions of fuzzy TPs. Since the projected algorithm is a new and easy way to switch the uncertainty in the crisp environment numerical examples are presented that show that the proposed this technique is very easy to understand and to apply to classical TPs to obtain an optimum solution. In the future, the proposed method can be applied to real-world problems in the fields that include job assignments and job scheduling.

Acknowledgement: We thank LetPub (www.letpub.com) for its linguistic assistance during the preparation of this manuscript.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  H. Arsham and A. B. Kahn. (1989). “A simplex type algorithm for general transportation problems: An alternative to stepping-stone,” Journal of Operational Research Society, vol. 40, no. 6, pp. 581–590. [Google Scholar]

 2.  A. R. Babu and B. R. B. Reddy. (2019). “Feasibility of fuzzy new method in finding initial basic feasible solution for a fuzzy transportation problem,” Journal of Computer and Mathematical Sciences, vol. 10, no. 1, pp. 43–54. [Google Scholar]

 3.  R. E. Bellman and L. A. Zadeh. (1970). “Decision making in a fuzzy environment,” Management Science, vol. 17, no. 4, pp. 141–164. [Google Scholar]

 4.  B. Amaliah, C. Fatichah and E. Suryani. (2019). “Total opportunity cost matrix – minimal total: A new approach to determine initial basic feasible solution of a transportation problem,” Egyptian Informatics Journal, vol. 20, no. 2, pp. 131–141. [Google Scholar]

 5.  D. Kuchta and S. Chanas. (1996). “A concept of the optimal solution of the transportation problem with Fuzzy cost co efficient,” Fuzzy Sets and Systems, vol. 82, no. 9, pp. 299–305. [Google Scholar]

 6.  S. Chanas, W. Kolodziejczyk and A. Machaj. (1984). “A fuzzy approach to the transportation problem,” Fuzzy Sets and Systems, vol. 13, no. 3, pp. 211–221. [Google Scholar]

 7.  C. S. Dinesh, B. P. Kumar and P. K. Srivastava. (2020). “Trisectional fuzzy trapezoidal approach to optimize interval data based transportation problem,” Journal of King Saud University - Science, vol. 32, no. 1, pp. 195–199. [Google Scholar]

 8.  S. Ganeshkumar, M. Venkatachalapathy and R. Pandiarajan. (2017). “A special type of solving transportation problems using generalized quadratic fuzzy number,” International Journal of Scientific & Technology Research, vol. 9, no. 2, pp. 6344–6348. [Google Scholar]

 9.  A. Kaur and A. Kumar. (2011). “A new method for solving fuzzy transportation problems using ranking function,” Applied Mathematical Modelling, vol. 35, no. 12, pp. 5652–5661. [Google Scholar]

10. R. Kumar, S. A. Edalatpanah and S. Jha. (2019). “A Pythagorean fuzzy approach to the transportation problem,” Complex & Intelligent System, vol. 5, no. 2, pp. 255–263. [Google Scholar]

11. S. T. Liu. and C. Kao. (2004). “Solving Fuzzy transportation problems based on extension principle,” European Journal of Operational Research, vol. 153, no. 3, pp. 661–674. [Google Scholar]

12. M. Zangiabadi and H. R. Maleki. (2013). “Fuzzy goal programming technique to solve multiobjective transportation problems with some non-linear membership functions,” Iranian Journal of Fuzzy Systems, vol. 10, no. 1, pp. 61–74. [Google Scholar]

13. S. Muruganandam and R. Srinivasan. (2016). “A method of solution to intuitionistic fuzzy transportation problem,” Asian Journal of Research in Social Sciences and Humanities, vol. 6, no. 5, pp. 753–761. [Google Scholar]

14. N. Mathur and P. K. Srivastava. (2020). “An inventive approach to optimize fuzzy transportation problem,” International Journal of Mathematical, Engineering and Management Sciences, vol. 5, no. 5, pp. 985–994. [Google Scholar]

15. P. Pandian and G. Natarajan. (2010). “A new algorithm for finding a fuzzy optimal solution for fuzzy transportation problems,” Applied Mathematical Sciences, vol. 4, no. 2, pp. 79–90. [Google Scholar]

16. R. Srinivasan. (2020). “On solving fuzzy linear fractional programming in material aspects,” Materials Today: Proceedings, vol. 21, pp. 155–157. [Google Scholar]

17. D. S. Dinagar and B. Christoper Raj. (2019). “A method for solving fully fuzzy transportation problem with generalized quadrilateral fuzzy numbers,” Malaya Journal of Matematik, vol. S, no. 1, pp. 24–27. [Google Scholar]

18. L. Sujatha, P. Vinothini and R. Jothilakshmi. (2018). “Solving fuzzy transportation problem using zero point maximum allocation method,” International Journal of Current Research, vol. 7, no. 1, pp. 173–178. [Google Scholar]

19. L. A. Zadeh. (1965). “Fuzzy sets,” Information and Control, vol. 8, no. 3, pp. 338–353. [Google Scholar]

20. H. J. Zimmermann. (2001). Fuzzy Set Theory and its Applications. Fourth Edition. Norwell, MA: USA Kluwer Academic. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.