Computer Systems Science & Engineering DOI:10.32604/csse.2021.015624
Article

Improved Attribute Chain Sampling Plan for Darna Distribution

Harsh Tripathi1, Amer Ibrahim Al-Omari2, Mahendra Saha1 and Ayed R. A. Alanzi3,*

1Department of Statistics, Central University of Rajasthan, Rajasthan, India
2Department of Mathematics, Faculty of Science, Al al-Bayt University, Mafraq, Jordan
3Department of Mathematics, College of Science and Human Studies at HotatSudair, Majmaah University, Majmaah 11952, Saudi Arabia
*Corresponding Author: Ayed R. A. Alanzi. Email: a.alanzi@mu.edu.sa
Received: 30 October 2020; Accepted: 09 February 2021

Abstract: Recently, the Darna distribution has been introduced as a new lifetime distribution. The two-parameter Darna distribution represents is a mixture of two well-known gamma and exponential distributions. A manufacturer or an engineer of products conducts life testing to examine whether the quality level of products meets the customer’s requirements, such as reliability or the minimum lifetime. In this article, an attribute modified chain sampling inspection plan based on the time truncated life test is proposed for items whose lifetime follows the Darna distribution. The plan parameters, including the sample size, the acceptance number, and the past lot result of the proposed sampling plan, are determined with the help of the two-point approach considering the acceptable quality level (AQL) and the limiting quality level (LQL). The plan parameters and the corresponding operating characteristic functions of a new plan are provided in tabular form for various Darna distribution parameters. Also, a few illustrated examples are presented for various distribution parameters. The usefulness of the proposed attribute modified chain sampling plan is investigated using two real failure time datasets. The results indicate that the proposed sampling plan can reduce the sample size when the termination ratio increases for fixed values of the producer’s risk and acceptance number. Hence, the proposed attribute modified chain sampling inspection plan is recommended to practitioners in the field.

Keywords: Attribute chain sampling inspection plan; consumer’s risk; Darna distribution; operating characteristic curve; producer’s risk; truncated life test

1  Introduction

All manufacturing industries in this competitive world solely rely on the quality of products manufactured by the company. The quality of products is the main metric that matters the same for both consumers and producers. The greatest challenge for the manufacturing industry is to stay in the competitive market with high revenue and market value of the products. High market value and revenue can be achieved only by producing good-quality products. Therefore, quality control is an indispensable part of the ongoing manufacturing process or full finished product. Hence, there is nothing more important than product quality in the manufacturing industry. Therefore, several tools and techniques have been proposed for statistical quality control (SQC) to handle the product quality at various levels of production. Two major types of SQC techniques are statistical process control and statistical product control. The statistical process control is achieved using the techniques of the histogram, Pareto chart, design of experiment, control chart, and process capability indices, while the statistical product control is achieved using the technique of acceptance sampling inspection plan. The hundred percent inspection method of items of a lot is another way to inspect the lot to control the quality of products. However, the hundred percent inspection is not feasible in practice because it has high costs in terms of time, money, and labor. Besides, when the quality of a product is tested by destructive testing (e.g., the life of a candle or testing of electrical fuses), the hundred percent inspection will result in the destruction of products.

The acceptance sampling inspection plan (AcSIP) represents an alternative solution to the hundred percent inspection. The AcSIP can be classified as AcSIP by attributes and AcSIP by variables. The AcSIP development for different probability models has been increasing in recent years. A variety of AcSIPs have been present in the literature of SQC, including the single acceptance sampling inspection plan (SaSIP), double acceptance sampling inspection plan (DaSIP), group acceptance sampling inspection plan (GaSIP), sequential acceptance sampling inspection plan (SeSIP), and multiple acceptance sampling inspection plan (MaSIP). Many studies have been focused on the development of an extension of the existing AcSIPs [1–4]. The time truncation technique is very useful when the nature of products is destructive. The methodology of the time truncated AcSIP is that life test terminates at a predefined time point t0 or when a cumulative number of failures larger than a given acceptance number c are observed. If the observed cumulative number of failures is smaller than a given acceptance number c, then the lot is accepted; otherwise, the lot is rejected. In recent times, exhaustive work has been done to develop the time truncated AcSIP. In [5–8], the methods for Weibull distribution, Sushila distribution, transmuted generalized inverse Weibull distribution, and Garima distribution have been developed, respectively. In Aslam and Jun [9], the generalized log-logistic distribution was studied, and in Rao [10], the Marshall-Olkin extended exponential distribution was analyzed. The generalized exponential distribution [11], Maxwell distribution [12], half normal distribution [13], ASP with gamma distribution, Weibull distribution, and Pareto distribution of the second type [14–16] have also been widely studied. In addition, the generalized half-normal distribution with a single ASP and inverse log-logistic distribution with the group and double ASP was examined in [17,18]. In Al-Omari et al. [19], an ASP based on truncated life tests for Akash distribution was proposed. Further, in Al-Omari et al. [20], the authors proposed an ASP when the lifetime follows the Rama distribution. The ASP based on the new Weibull-Pareto distribution was presented in Al-Omari et al. [21], and the ASP for Ishita distribution was reported in Al-Nasser et al. [22].

In Dodge [23], a special AcSIP known as the chain sampling inspection plan (ChSP) was designed. The usage of the past lot quality information is the crucial part of the ChSP, which reduces the consumer and producer’s risks significantly. In the ChSP, the decision on lot acceptance or rejection is based not only on the quality of the current sample but also on the quality of the past-submitted lots. The ChSP is also known as ChSP-1. An extended version of the ChSP denoted as MChSP-1 was proposed in Govindaraju and Balamurali [24]. In 2018, Luca developed a re-extended version of the MChSP-1 that is referred to as the modified chain sampling plan (MChSP). The MChSP is suitable for both to attribute and variable inspection plans. In addition, Luca showed that the MChSP could be preferable over the other existing plans; more details about the MChSP can be found in Luca [25]. The modified group chain sampling plans for lifetimes following the Rayleigh distribution were presented in Jamaludin et al. [26]. The chain sampling plan for variables inspection was studied in [27,28].

To the best of the authors’ knowledge, in the SQC-related literature, there has been no study on the development of MChSP time truncated life test for the Darna probability distribution in the case of attribute quality characteristic. In order to address this shortcoming, this paper presents an attribute MChSP for the time truncated life test under the assumption of the Darna distribution (DD). Also, using the attribute MChSP of the DD, estimation of the suggested parameters plan is studied with the help of the two-point approaches, the acceptable quality level (AQL) and the limiting quality level (LQL).

The rest of the paper is organized as follows. In Section 2, the design of the proposed attribute sampling plan is presented. A brief description of the DD and the proposed plan are described in detail in Section 3. In Section 4, a study of the tables and hypothetical examples are provided to understand the methodology of the proposed plan. In Section 5, the proposed plan is verified using two real datasets. Finally, concluding remarks and future scope of the proposed ChSP are given in Section 6.

2  Darna Distribution

The DD that was proposed in Shraa and Al-Omari [29] is explained in the following. The DD represents a special mixture of the exponential and gamma distributions (i.e., Exp(θλ) and Gamma(3,θλ) distributions) with a mixing factor 2λ22λ2+θ2 . The DD is a widely used lifetime distribution due to its flexible properties. In Shraa and Al-Omari [29], several statistical properties of the Darna distribution were derived. The probability density function (PDF) and cumulative distribution function (CDF) of the two parameters DD are respectively given by:

f(x;λ,θ)=θ2λ2+θ2(2λ+θ4x22λ3)e−θxλ;x>0,λ>0,θ>0,,θ≠λ, (1)

F(x;λ,θ)=1−(4λ4+2λ2θ2+θ4x2+2λθ3x2λ2(2λ2+θ2))e−θxλ;x>0,λ>0,θ>0, (2)

where λ and θ denote the shape and scale parameters of the DD, respectively, and the mean is expressed as:

μ=E(X)=λ(4λ2+6θ2)2θ(2λ2+6θ2). (3)

The reliability and hazard functions of the DD distribution are respectively given by:

R(x;θ,α)=4α4+2α2θ2+θ4x2+2αθ3x2α2(2α2+θ2)e−θxα;x>0,α>0,θ>0, (4)

H(x;θ,α)=4α4θ+θ5x24α5+2α3θ2+αθ4x2+2α2θ3x. (5)

It has been observed that the DD possesses different characteristics, for instance, the increasing and decreasing hazard rate functions depend on the distribution parameters. The behavior of the hazard rate function of the DD is quite similar to some real-life situations. Hence, it is better to use the DD for the truncated life test of the MChSP.

3  Truncated Plan for DD

This section discusses the proposed plan when the time of the items follows the DD. The main part of designing the proposed plan is to estimate the plan parameters. The plan parameters characterize the AcSIP, and they include the sample size n , acceptance number C , and the number of previous lots i . The design steps of the proposed plan are as follows:

1.    Select a sample of size n from the current lot and test it for time τ0 .

2.    Observe the number of defective units D till τ0 and reject the lot if D>C .

3.    If D≤C, the lot is accepted provided that there is at most one lot among the preceding i lots in which the number of defective units exceeds the criterion C ; otherwise, the lot is rejected.

The acceptance probability in the proposed AcSIP is based on the plan parameters, i.e., the operating characteristic (OC) function of the MChSP ([21]), which is given by:

Pa(p;n,C,i)=[r{ri+iri−1(1−r)}], (6)

where r=P(D≤C) is defined by the probability that the observed number of defective units found in a lot is less than the criterion C . In Luca [25], the special case of MChSP −(n,C,i) has been discussed, and it has been stated that special case is as follows: the OC-curve of an MChSP −(n,0,i) plan will approximate that of an MChSP −1−(n,i) plan. The mathematical expression of the OC function can be obtained by Eq. (2) as follows:

Pa(p;n,C,i)=(∑j=0C⁡(nj)pj(1−p)n−j)×[(∑j=0C⁡(nj)pj(1−p)n−j)i+i(∑j=0C⁡(nj)pj(1−p)n−j)i−1{1−(∑j=0C⁡(nj)pj(1−p)n−j)}]. (7)

The probability of item failure before the predefined termination time τ0 can be expressed in the form of CDF of a Darna distribution as p=F(τ0) .

A main part of the MChSP is to determine the sampling plan parameters. The problem of determining the plan parameters (n,C,i) can be handled by the two-point approach considering the AQL and LQL. A certain condition associated with the two-point approach is that the OC curve passes approximately through the two points [AQL,(1−α)],[LQL,β] and satisfies the following non-linear conditions simultaneously:

Pa(p0;n,C,i)≥(1−α), (8)

Pa(p1;n,C,i)≤β. (9)

Two risks are associated with the AcSIP, the producer’s risk that is denoted as α ,which represents the probability of rejection of a good lot, and consumer’s risk that is denoted as β , which represents the probability of acceptance of a bad lot. Basically, the two-point approach result depends on the two risks. The acceptance probabilities of a lot regarding the values of AQL (p0) and LQL (p1) denoted as Pa(p0;n,C,i) and Pa(p1;n,C,i) , respectively, are beneficial to determine the plan parameter by the two-point approach as follows:

Pa(p0;n,C,i)=(∑j=0C⁡(nj)p0j(1−p0)n−j)×[(∑j=0C⁡(nj)p0j(1−p0)n−j)i+i(∑j=0C⁡(nj)p0j(1−p0)n−j)i−1{1−(∑j=0C⁡(nj)p0j(1−p0)n−j)}], (10)

Pa(p1;n,C,i)=(∑j=0C⁡(nj)p1j(1−p1)n−j)×[(∑j=0C⁡(nj)p1j(1−p1)n−j)i+i(∑j=0C⁡(nj)p1j(1−p1)n−j)i−1{1−(∑j=0C⁡(nj)p1j(1−p1)n−j)}]. (11)

Hence, the suggested plan parameters can be determined with the help of the two-point approach for various values of AQL, LQL, α and β. In this way, the acceptance probability of a good lot is larger than the producer’s confidence level (1−α), and that the acceptance probability of a bad lot is smaller than the consumer’s risk (β).

4  Proposed Plan Tables and Hypothetical Example

This section describes the proposed plan tables for various combinations of distribution parameters λ and θ . The plan parameters of the proposed time truncated MChSP for the DD parameters of λ=1,θ=2 , and producer’s risk α = 0.05 and for the predefined values of termination ratio τ0/μ=0.5,0.75,1.00 and the quality level μ/μ0=2,3,4,5,6,7,8 are given in Tab. 1. The acceptance probability (Pa(p;n,C,i)) of a lot for some pre-specified values of λ,θ,a , and μ/μ0 is also presented in Tab. 1. As shown in Tab. 1, in most of the cases, when the value of termination ratio increases, the required sample size decreases, and this result holds for all the values of quality level μ/μ0 and β . In practice, the required sample size for the decision is directly related to the lot quality and the number of non-conforming units present in the lot, so if the quality level increases and the tolerable number of non-conforming units in a lot decreases, then the required sample size to make a decision on a lot at a particular β value decreases with the predefined value of the termination ratio a .

Table 1: Plan parameters of the MChSP for the DD when λ=1,θ=2 , and α=0.05

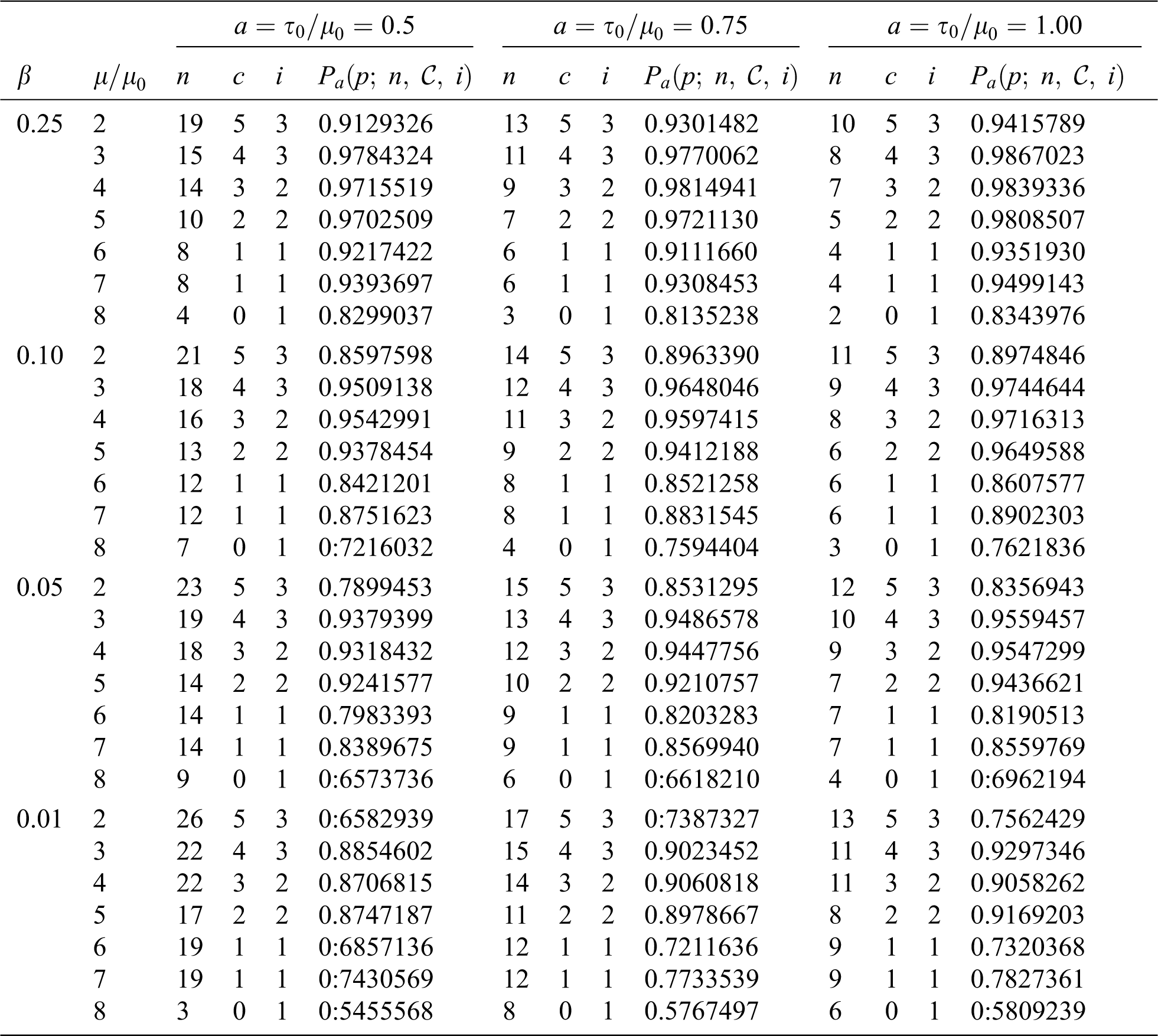
Similarly, as shown in Tab. 2 the required sample size (n), acceptance number (C) , and past information (i) are in favor of the predefined values of termination ratio (a) , quality level (μ/μ0) , and producer’s risk (α=0.05) when λ=2 and θ=2. The trend of the required sample size in Tab. 2 is similar to that in Tab. 1, where it can be noted that the quality level increases and the acceptance number decreases when the required sample size decreases. Also, the acceptance probability of a lot for specific parameters of the proposed plan and predefined values of λ,θ,a, and μ/μ0 is given in Tab. 2.

Table 2: Plan parameters of the MChSP for the DD at λ=2,θ=2 , and α=0.05

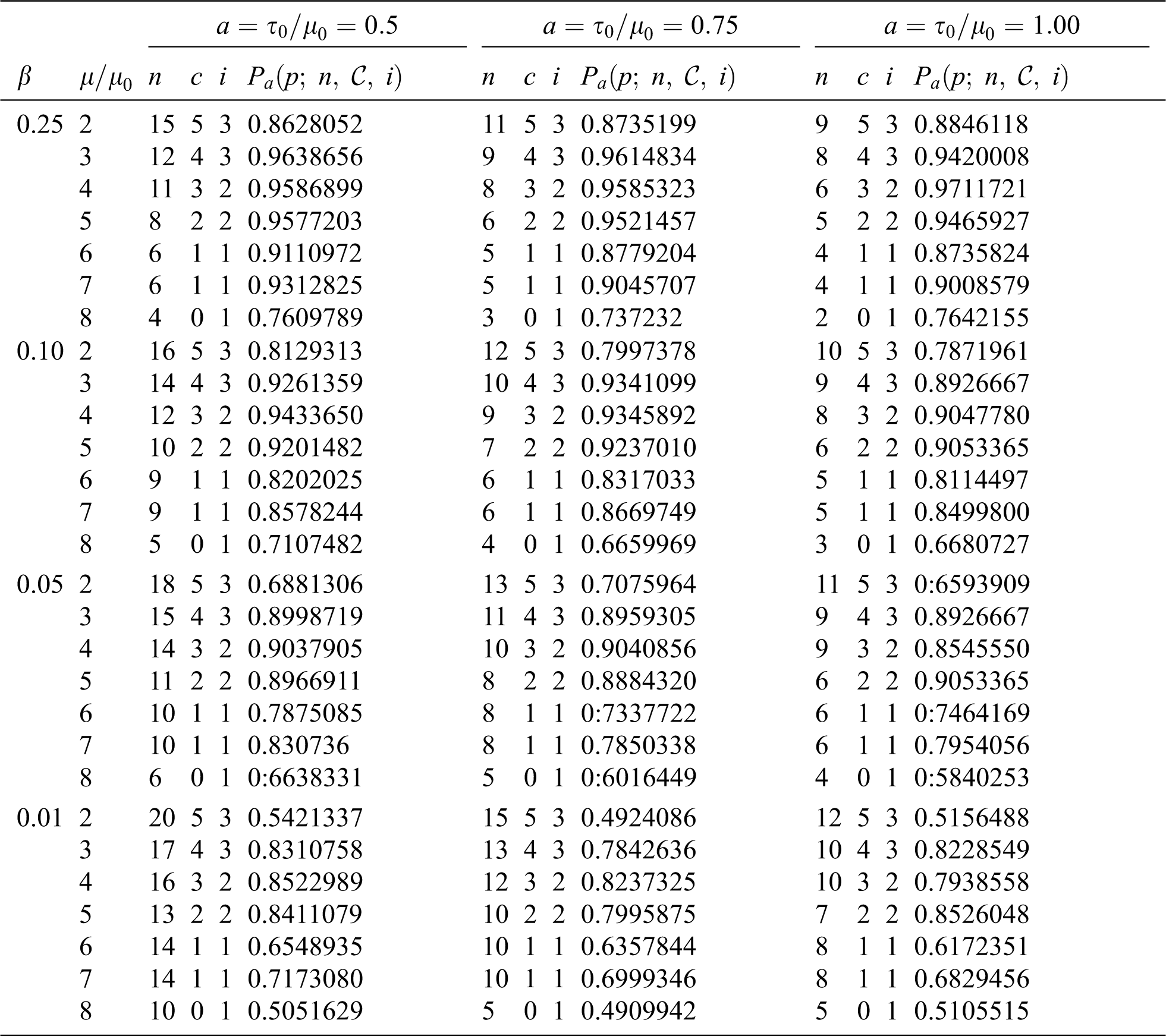
For λ=3 and θ=4 , the plan parameters (n,C,i) for predefined values of termination ratio (a) , quality level (μ/μ0) , and producer’s risk (α=0.05) are given in Tab. 3. Based on values given in Tab. 3, when the termination ratio increase, the required sample size decreases for all values of quality level μ/μ0 and β. This result is similar to those in Tabs. 1 and 2.

Table 3: Plan parameters of the MChSP for the DD at λ=3,θ=4 , and α=0.05

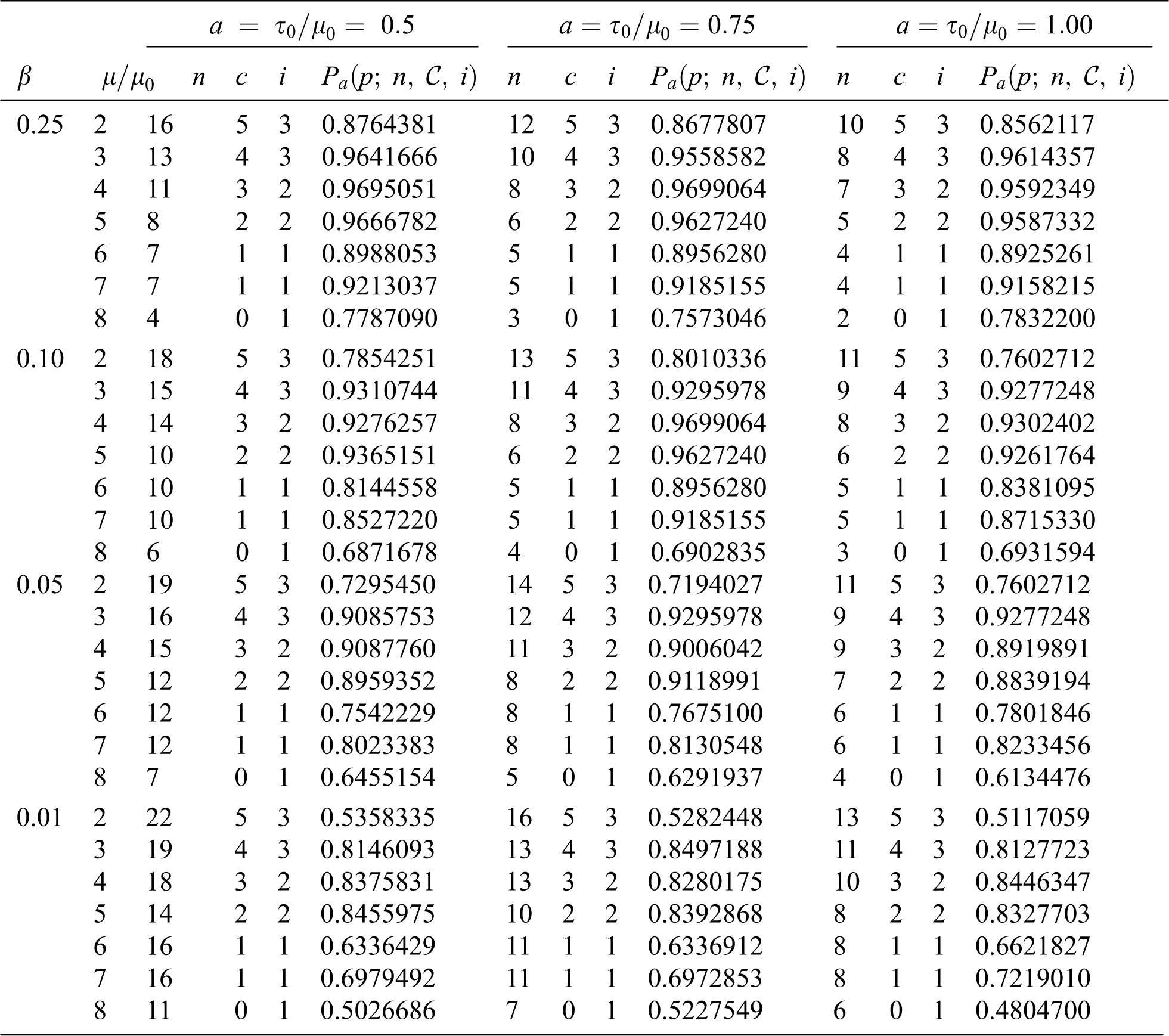
Hypothetical example: Suppose that the lifetime of an item follows the DD with parameters λ and θ as given in Tab. 1 when the producer’s risk is α=0.05 and the consumer’s risk is β . Also, suppose that the termination ratio and quality level are 0.5 and 4 , respectively. Then, the plan parameters (n,C,i) of the proposed plan are (14,3,2) , and the probability of lot acceptance is 0.9715519 . Assume the sample size is 14 , and that all 14 units are tested. Truncate the lifetime test of 14 selected units of the sample at time t . Record the number of failures from the lifetime test and reject the lot if the number of failures is D>C . Accept the lot if D≤C(=3) and if there is at-most one lot among the preceding two lots in which the number of defective units D exceeds the criterion of C=3 .

5  Proposed Plan Evaluation using Real Data

In this section, two real-life situations are discussed and the descriptions of these examples are presented. The descriptive statistics of the data includes the minimum, first quartile (Q1) , median, mean, third quartile (Q3) , maximum, CS (coefficient of skewness), and CK (coefficient of kurtosis), as given in Tab. 4. Before the verification of the proposed plan using these data, it was checked whether the considered datasets supported the DD by conducting the goodness-of-fit test. The goodness-of-fit test based on the Kolmogorov-Smirnov (K-S) statistics compares the empirical and theoretical models by computing the maximum absolute difference between the empirical and theoretical CDFs, and it is defined as Dn=Supx|Fn(x)−F(x;Θ)| , where, Θ=(θ,λ) , Supx represents the supremum of the set of distances, Fn(x) denotes the empirical distribution function, and F(x;Θ) is the cumulative distribution function. The two discrimination criteria, Akaike information criteria (AIC) and Bayesian information criteria (BIC), were considered based on the likelihood function evaluated at the maximum likelihood estimates (MLEs). The criteria were defined as AIC=−2l(Θ^)+2k and BIC=−2l(Θ^)+2ln(n) , where l(Θ^) denoted the log-likelihood function evaluated at the MLEs, k was the number of model parameters, and n denoted the sample size. The model with the lowest values of AIC and BIC was chosen as the best model to fit the data. The MLE values of l(Θ^),AIC,BIC,K−S statistic, and p are given in Tab. 5. The plots of histogram densities, empirical versus theoretical CDFs, and P-P plots for datasets I and II are displayed in Figs. 1 and 2, respectively.

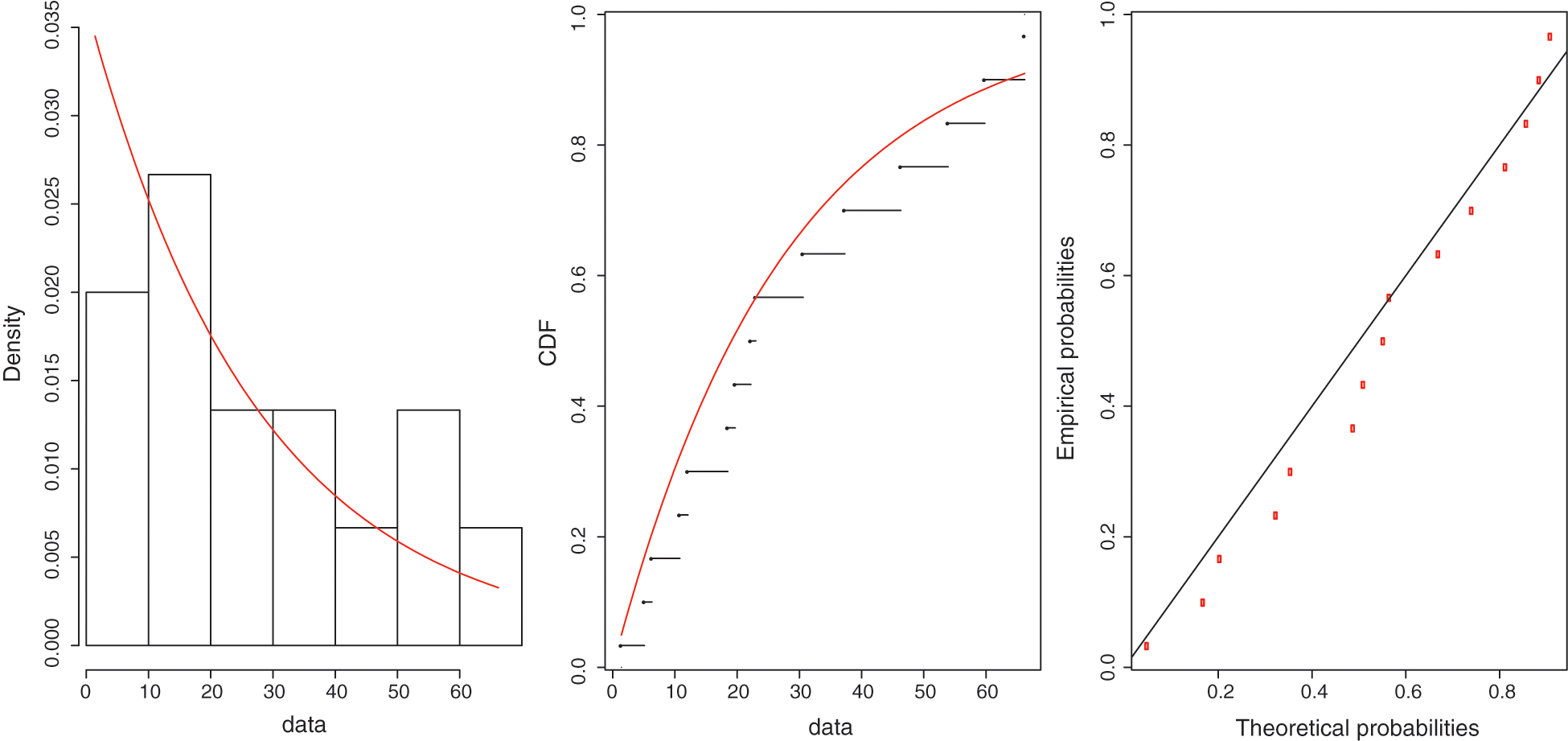
Figure 1: Histogram-density, CDFs, and P-P plots for dataset I

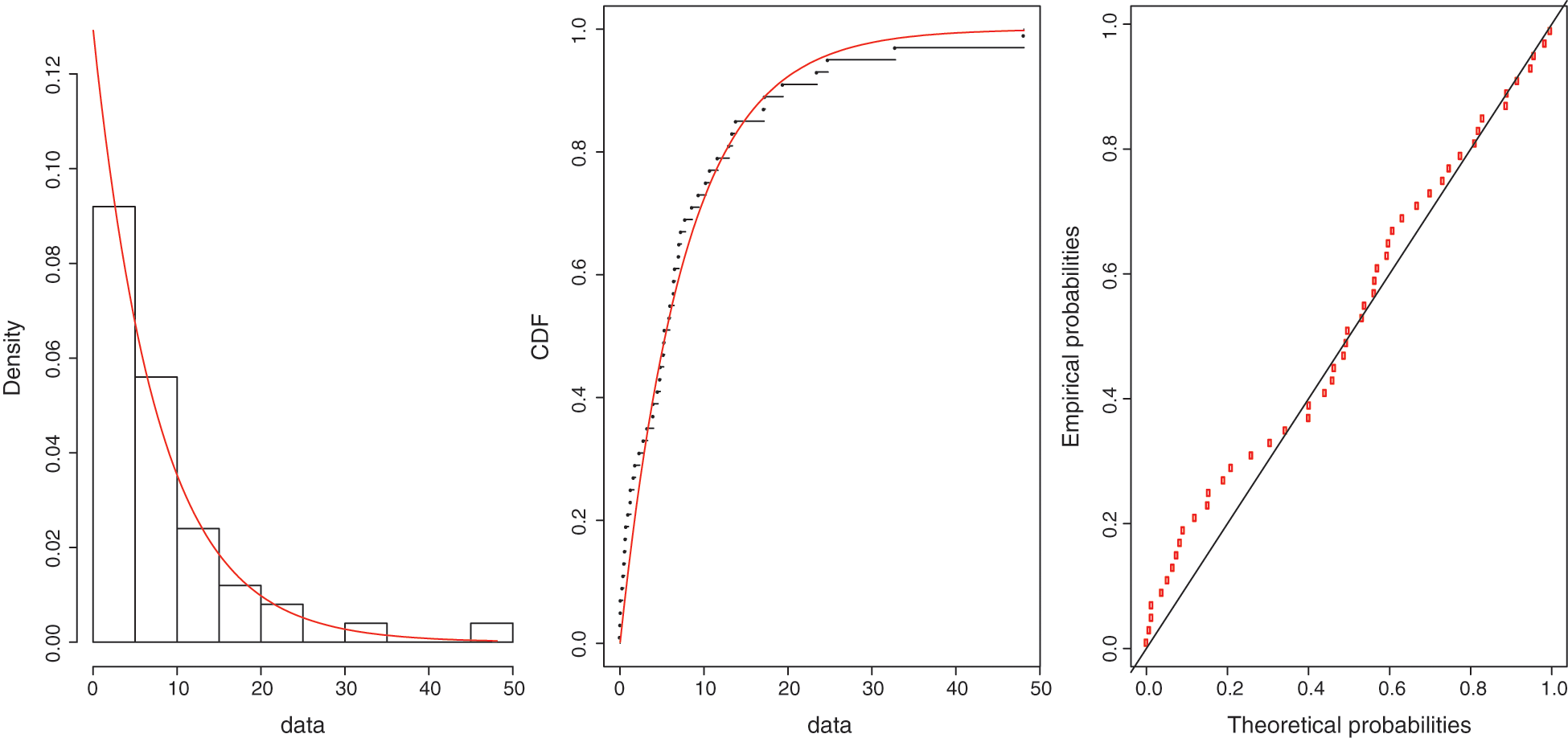
Figure 2: Histogram-density, CDFs, and P-P plots for dataset II

Table 4: Descriptive summary of real datasets

Table 5: Model fitting results of real datasets

Dataset I: The dataset I was taken from Lawless [30], and it included the failure times in minutes for 15 electronic components obtained by the accelerated life test, which were as follows: 1.4, 5.1, 6.3, 10.8, 12.1, 18.5, 19.7, 22.2, 23, 30.6, 37.3, 46.3, 53.9, 59.8, and 66.2. This dataset follows the DD, and the maximum likelihood estimates of the distribution parameters were λ^=2.10832758 and θ^=0.07659991 . The mean lifetime (μ0) of the dataset based on the estimated parameters was 27.5602 . It was supposed that an experimenter set the termination ratio (t/μ0) at 0.5 ; then, the termination time was 13.7801 when the consumer’s risk was 0.25 . The optimal parameters of the suggested sampling plan for the considered specifications were n=13,C=6, and i=11 . When the experimenter set up the MChSP plan according to the above-mentioned specifications, the MChSP was as follows:

•   Select a sample of size 13 from a submitted lot and start with the normal inspection; then, test the units up to the truncation time of 13.7801 minutes.

•   Record the number of non-conforming units (D) from the selected sample of the submitted lot and reject the lot if D>C .

•   If D>C(6) , accept the lot if there is at-most one lot among the preceding 11 lots in which the number of defective units D exceeds the criterion C(6) .

At the true mean lifetime of 82.6806 minutes, i.e., the quality ratio of μ/μ0=3, the probability of lot acceptance was 0.9984183 .

Dataset II: The second dataset consisted of the failure times (in weeks) of 50 components. This dataset was considered by Jose and Paul [31], and the failure times in this dataset were as follows: 0.013, 0.065, 0.111, 0.111, 0.613, 0.309, 0.426, 0.535, 0.684, 0.747, 0.997, 1.284, 1.304, 1.647, 1.829, 2.336, 2.838, 3.269, 3.997, 3.981, 4.52, 4.789, 4.849, 5.202, 5.291, 5.349, 5.911, 6.018, 6.427, 6.456, 6.572, 7.023, 7.087, 7.291, 7.787, 8.596, 9.388, 10.261, 10.731, 11.658, 13.006, 13.388, 13.842, 17.152, 17.283, 19.418, 23.471, 4.777, 32.795, and 48.105.

The lifetime of this dataset followed the Darna distribution, and the maximum likelihood estimates were λ^=2.0432835 and θ^=0.2666318 . Accordingly, based on the estimated parameters, the mean lifetime (μ0) of the dataset was 7.792705 . It was supposed that the termination ratio (t/μ0) was set at 0.5; then, the termination time was 3.896352 for the consumer’s risk of 0.01 . For these specifications, the optimal design parameters were n=50,C=20 , and i=12 . Based on these assumptions, the MChSP was as follows:

•   Select a sample of size 50 from a submitted lot with the normal inspection and test the units up to the truncation time of 3.896352 minutes.

•   Record the number of non-conforming units (D) from the selected sample of the submitted lot and reject the lot if D>C .

•   If D>C(20), accept the lot if there is at-most 1 lot among the preceding 12 lots in which the number of defective units D exceeds the criterion C(=20) .

At the true mean lifetime of 15.58541 minutes, i.e., the quality ratio of μ/μ0=2, the probability of lot acceptance was 0.9984634 .

6  Conclusions

In this paper, an MChSP for the time truncated test when the lifetime of products follows the DD is proposed. The proposed plan parameters at the producer’s risk of α=0.05 and consumer’s risk of β=0.25,0.10,0.05,0.01 are provided. A hypothetical example is also presented for a better understanding of the proposed MChSP. Also, examples of two rel data sets are considered to show the usefulness of the suggested plan. In addition, the proposed method for the DD can be used as a reference for the development of MChSP for other non-normal distributions. Also, the suggested MChSP in this paper can be modified by using other sampling methods, such as the ranked set sampling methods [32–35].

Acknowledgement: The authors are grateful to the Editor and anonymous reviewers for their valuable comments and suggestions.

Funding Statement: A.R.A. Alanzi would like to thank the Deanship of Scientific Research at Majmaah University for financial support and encouragement.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. I. Al-Omari and A. D. Al-Nasser, “A two parameter quasi Lindley distribution in acceptance sampling plans from truncated life test,” Journal of Statistic and Operation Research, vol. 1, pp. 39–47, 2019. [Google Scholar]

 2.  A. I. Al-Omari and S. A. Al-Hadhrami, “Acceptance sampling plans based on truncated life tests for extended exponential distribution,” Kuwait Journal of Science, vol. 45, no. 2, pp. 89–99, 2018. [Google Scholar]

 3.  M. Aslam, C. H. Jun and M. Ahmad, “New acceptance sampling plans based on life tests for Birnbaum–Saunders distributions,” Journal of Statistical Computation and Simulation, vol. 81, no. 4, pp. 461–470, 2011. [Google Scholar]

 4.  G. S. Rao, “A group acceptance sampling plans for lifetimes following a generalized exponential distribution,” Economic Quality Control, vol. 24, no. 1, pp. 75–85, 2009. [Google Scholar]

 5.  C. H. Jun, S. Balamurali and S. H. Lee, “Variables sampling plans for Weibull distributed lifetimes under sudden death testing,” IEEE Transactions on Reliability, vol. 55, no. 1, pp. 53–58, 2006. [Google Scholar]

 6.  A. I. Al-Omari, “Acceptance sampling plans based on truncated life tests for Sushila distribution,” Journal of Mathematical and Fundamental Sciences, vol. 50, no. 1, pp. 72–83, 2018. [Google Scholar]

 7.  A. I. Al-Omari, “The transmuted generalized inverse Weibull distribution in acceptance sampling plans based on life tests,” Transactions of the Institute of Measurement and Control, vol. 40, no. 16, pp. 4432–4443, 2018. [Google Scholar]

 8.  A. I. Al-Omari, “Improved acceptance sampling plans based on truncated life tests for Garima distribution,” International Journal of System Assurance Engineering and Management, vol. 9, no. 6, pp. 1287–1293, 2018. [Google Scholar]

 9.  M. Aslam and C. H. Jun, “A double acceptance sampling plan for generalized log-logistic distributions with known shape parameters,” Journal of Applied Statistics, vol. 37, no. 3, pp. 405–414, 2010. [Google Scholar]

10. G. S. Rao, “Double acceptance sampling plan based on truncated life tests for Marshall-Olkin extended exponential distribution,” Austrian Journal of Statistics, vol. 40, no. 3, pp. 169–176, 2011. [Google Scholar]

11. A. S. Ramaswamy and P. Anburajan, “Double acceptance sampling based on truncated life tests in generalized exponential distribution,” Applied Mathematical Sciences, vol. 6, no. 64, pp. 3199–3207, 2012. [Google Scholar]

12. W. Gui, “Double acceptance sampling plan for truncated life tests based on Maxwell distribution,” American Journal of Mathematical and Management Sciences, vol. 33, no. 2, pp. 98–109, 2014. [Google Scholar]

13. A. I. Al-Omari, A. D. Al-Nasser and F. S. Gogah, “Double acceptance sampling plan for time-truncated life tests based on half normal distribution,” Economic Quality Control, vol. 31, no. 2, pp. 93–99, 2016. [Google Scholar]

14. M. Aslam, C. H. Jun and M. Ahmad, “A group sampling plan based on truncated life test for gamma distributed items,” Pakistan Journal of Statistics, vol. 25, no. 3, pp. 333–340, 2009. [Google Scholar]

15. M. Aslam and C. H. Jun, “A group acceptance sampling plan for truncated life test having Weibull distribution,” Journal of Applied Statistics, vol. 36, no. 9, pp. 1021–1027, 2009. [Google Scholar]

16. M. Aslam, A. R. Mughal, M. Ahmed and Y. Zafar, “Group acceptance sampling plans for Pareto distribution of the second kind,” Journal of Testing and Evaluation, vol. 38, no. 2, pp. 143–150, 2010. [Google Scholar]

17. H. Tripathi, M. Saha and V. Alha, “An application of time truncated single acceptance sampling plan based on generalized half-normal distribution,” Annals of Data Science, vol. 8, no. 1, pp. 189–195, 2021. [Google Scholar]

18. H. Tripathi, S. Dey and M. Saha, “Double and group acceptance sampling plan for truncated life test based on inverse log-logistic distribution,” Journal of Applied Statistics, vol. 31, pp. 1–16, 2020. [Google Scholar]

19. A. I. Al-Omari, N. Koyuncu and A. R. A. Al-anzi, “New acceptance sampling plans based on truncated life tests for Akash distribution with an application to electric carts data IEEE,” Access, vol. 8, pp. 201393–201403, 2020. [Google Scholar]

20. A. I. Al-Omari, A. D. Al-Nasser and E. Ciavolino, “Acceptance sampling plans based on truncated life tests for Rama distribution,” International Journal of Quality & Reliability Management, vol. 36, no. 7, pp. 1181–1191, 2019. [Google Scholar]

21. A. I. Al-Omari, A. Santiago, J. M. Sautto and C. N. Bouza, “New Weibull-Pareto distribution in acceptance sampling plans based on truncated life tests,” American Journal of Mathematics and Statistics, vol. 8, no. 5, pp. 144–150, 2016. [Google Scholar]

22. A. D. Al-Nasser, A. I. Al-Omari, A. Bani-Mustafa and K. Jaber, “Developing single-acceptance sampling plans based on a truncated lifetime test for an Ishita distribution,” Statistics in Transition New Series, vol. 19, no. 3, pp. 393–406, 2018. [Google Scholar]

23. H. F. Dodge, “Chain sampling inspection plan,” Industry Quality Control, vol. 11, no. 4, pp. 10–13, 1995. [Google Scholar]

24. K. Govindaraju and S. Balamurali, “Chain sampling plan for variables inspection,” Journal of Applied Statistics, vol. 25, no. 1, pp. 103–109, 1998. [Google Scholar]

25. S. Luca, “Modified chain sampling plans for lot inspection by variables and attributes,” Journal of Applied Statistics, vol. 45, no. 8, pp. 1447–1464, 2018. [Google Scholar]

26. A. F. Jamaludin, Z. Zain and N. Aziz, “A modified group chain sampling plans for lifetimes following a Rayleigh distribution,” Global Journal of Pure and Applied Mathematics, vol. 12, no. 5, pp. 3941–3947, 2016. [Google Scholar]

27. K. Govindaraju and S. Balamurali, “Chain sampling plan for variables inspection,” Journal of Applied Statistics, vol. 25, no. 1, pp. 103–109, 1998. [Google Scholar]

28. A. R. S. Ramaswamy and A. R. M. Priya, “Sampling risks for chain sampling plans with non-constant defective probability,” Stochastics and Quality Control, vol. 22, no. 1, pp. 117–126, 2007. https://www.degruyter.com/view/journals/eqc/22/1/article-p117.xml?language=en-affiliation0. [Google Scholar]

29. D. H. Shraa and A. I. Al-Omari, “Darna distribution: Properties and application,” Electronic Journal of Applied Statistical Analysis, vol. 12, no. 2, pp. 520–541, 2019. [Google Scholar]

30. J. F. Lawless, Statistical models and methods for lifetime data. New York, USA: John Wiley and Sons, 2003. [Google Scholar]

31. K. K. Jose and A. Paul, “Marshall-Olkin exponential power distribution and its generalization: Theory and application,” IAPQR Transaction, vol. 43, no. 1, pp. 1–29, 2018. [Google Scholar]

32. A. Haq, J. Brown, E. Moltchanova and A. I. Al-Omari, “Partial ranked set sampling design,” Environmetrics, vol. 24, no. 3, pp. 201–207, 2013. [Google Scholar]

33. A. Haq, J. Brown, E. Moltchanova and A. I. Al-Omari, “Mixed ranked set sampling design,” Journal of Applied Statistics, vol. 41, no. 10, pp. 2141–2156, 2014. [Google Scholar]

34. A. Haq, J. Brown, E. Moltchanova and A. I. Al-Omari, “Ordered double ranked set samples and applications to inference,” American Journal of Mathematical and Management Sciences, vol. 33, pp. 239–260, 2014. [Google Scholar]

35. E. Zamanzade and A. I. Al-Omari, “New ranked set sampling for estimating the population mean and variance,Hacettepe,” Journal of Mathematics, and Statistics, vol. 45, no. 6, pp. 1891–1905, 2016. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.